KIRGIZİSTAN-TÜRKİYE MANAS ÜNİVERSİTESİ
FEN BİLİMLER ENSTİTÜSÜ
MATEMATİK ANABİLİM DALI
STİELTJES İNTEGRALİNDE SAYISAL YAKLAŞIM
METODLARI
(YÜKSEK LİSANS TEZİ)
Murat SEZER
BİŞKEK 2010
KIRGIZİSTAN-TÜRKİYE MANAS ÜNİVERSİTESİ
FEN BİLİMLER ENSTİTÜSÜ
MATEMATİK ANABİLİM DALI
STİELTJES İNTEGRALİNDE SAYISAL YAKLAŞIM
METODLARI
(YÜKSEK LİSANS TEZİ)
Murat SEZER
Danışman
Prof.Dr.Avıt ASANOV
BİŞKEK 2010
İntihal Yapılmadığını Belirten İfade
Ben bu tezdeki bütün bilgileri akademik ve etik kurallara göre aldığımı ve sunduğumu
belirtiyorum.Bu çalışmaya özgün olmadan kullandığım bütün materyal ve bilgilere akademik ve
etik kurallar gereğince atıfta bulunduğumu ve hiçbir şekilde intihal yapmadığımı açıkça
bildiriyorum.
İSİM,SOYAD:
İMZA:
TARİH:
Плагиат жасалбагандыгы тууралуу билдируу
Мен бул эмгекте алынган бардык маалыматтарды академияалык жана этикалык
эрежелерге ылайык колдондум.Тагыраак айтганда бул эмгекте колдонулган бирок мага
тишелүү болбогон малыматтардын бардыгын тиркеьеде так көрсөттүм жана эч кайы
жерден плагиат жасалбагандыгына ынандырып кетким келет.
АТЫ,ЖӨНҮ:
КОЛУ:
ДАТАСЫ:
KIRGIZİSTAN TÜRKİYE
MANAS ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ MÜDÜRLÜĞÜNE
Matematik Anabilim dalı, Matematik Bilim dalı’nda 0851Y03003 numaralı Murat
Sezer in hazırladığı “Stieltjes integralinin değerini Simpson kuralını kullanarak yaklaşık
olarak bulma” konulu Yüksek Lisans ile ilgili tez savunma sınavı, .../.../ 2010 günü ...-...
saatleri arasında yapılmış, sorulan sorulara alınan cevaplar sonunda adayın tezinin ...
olduğuna ... ile karar verilmiştir.
ЧЕЧИМ
Кыргыз-Түрк Манас университетинин Коомдук Илимдер Институтунун
экзамендик инструкциясынын ...- жобосуна ылайык, ... № жыйында
уюшулган
комиссия,
педагогика
бөлүмүнүн
магистранты ... темасында жазган дипломдук проектин анализдеп, .../.../ 2010 ж.
Саат ... дө жактоого кабыл алды.
Магистрант ... минута убакыт ичинде дипломдук проектин жактап,
комиссия
деген чечим чыгарды.
КЫСКАЧА МАЗМУНУ
Даярдаган
: Мурат СЕЗЕР
Университет
: Кыргызстан-Туркия Манас Университети
Институт
: Табигий Илимдер Институту
Багыты
: Математика
Иштин сыпаты
: Магистрстура
Беттердин саны
: XI+17
Бүтүрүү датасы
: Май 2010
Диссертация жетекчиси
: Проф.Др.Авыт Асанов
Стильтестин интегралын Симпсон методу менен
жакындаштырып эсептөө
Математикалык эсептерде же математика колдонулган көп жерлерде берилген
функциялардын туундуларын алуу же интегралдык эсептөөлөр бар. Бирок бул
функциялардын туундуларын алуу же болбосо интегралдарын эсептөө абдан
татаал болгон учурлар болот, кээдэ болсо мүмкүн болбогон учурлар болот.
Мындай учурларда башка бир функцияга карата туунду алынганда туундулары
бар экендиги көрүлдү. Мындай туунду алуу Стильтьес интегралынын тескери
операциясы экендиги көрсөтүлгөн, Стильтьес интегралынын айрым учуру Риман
интегралы болушу, бул интегралдын керектүүлүгүн көрсөтөт. Бирок бул
Стильтьес интегралын чыгарылышы ар дайым бар экендиги билинсе дагы, буну
эсептөө ар дайым мүмкүн болбойт. Ошондуктан интегралды жакындаштырып
эсептөө методдору колдонулат. Риман интегралын жакындаштырып эсептөөдө
колдонулган Симпсон методу Стильтьес интегралына да колдонулушу мүмкүн
экендиги көрсөтүлдү. Албетте жакындаштырып эсептөөнүн так чыгарылыштан
айырмасы болот, ушул катасын кантип табуу жана кандай шарттар коюш
керектиги көрсөтүлдү.Алгач, биринчи бөлүмдө башка бир өсүүчү үзгүлтүксүз
функцияга карата туунду алуунун аныктамасы жана бул туунду алуунун кээ бир
теоремалары каралды. Кийинки бөлүмдө, бул туунду алуунун тескери функциясы
болгон Стильтестин интегралын аныктамасы берилди. Акыркы үчүнчү бөлүмдө
болсо, жакындаштырып эсептөө методдорунан Симпсон методунун аныктамасы
менен бирге бул методдун бир гана Риман интегралына эмес, Стильтестин
интегралына да колдонууга болоору көрсөтүлдү.
Ачкыч сөздөр: Стильтьес интегралы, Риман интегралы, жакындаштырып
эсептөө, туунду, интеграл, Симпсон методу
V АБСТРАКТ
Автор
: Мурат СЕЗЕР
Университет
: Кыргызстан-Турция Манас Университети
Институт
: Естественных Наук
Кафедра
: Математика
Качество диссертации
: Магистрaтура
Количество страниц
: XI + 17
Дата выпуска
: Май 2010
Руководитель диссертации : Проф.Др.Авыт Асанов
Приблеженное вычисление интеграла Стильтеса методом
Симпсона
Во многих Математических и Научных вычислений или же в Прикладной
Матиматике нужно взять производную или интеграл какой либо функции. Но как
известно не все функции могут быть дифференцированны или же
интегрированны методом Рейманна. Если у какой нибуть фунции существует
производная относительно другой функции, то производная может существовать.
В дополнение, если первообразная относительно функции которая равна
интегралу Стилтьеса, то можно вычислить интеграл некоторых не
диференцируемых функций. Но к сожелению, даже при гарантии существования,
крайне тяжело вычислить интеграл методом Стилтьеса. Это всё ведёт к методом
приближение. В интегралле Реймана сущестует множество методов приближения.
И одно из них это метод Симпсона. В этой статье, пытается опредилить
возможно ли использование метода Симпсона в вычисление интегала методом
Стильеса. Так как здесь используется метот приближения то тут нужно ожидать
погрешности вычисления. Так же в этой статье высчитываются все формулы и
нужные условия для снижения погрешности.
Первая глава посвещенна производной относительна безприрывной и
возрастающей функции. Здесь данны несколько законов производных и теорема
расширения Тейлора. Далее во второй главе, интеграл Стильтеса определяется как
первообразная относительна функции. После фундоментальных определений в
третьей главе определяется и закон приближения метод Симпсона, и
вычитывается погрешность для этого метода. Далее даётся приложения метода
вычисления с использованием интеграла Стильтеса.
Ключевые слова: интеграл Стилтьеса, интеграл Римана, Приблеженное
вычисление, метод Симпсона, производная, интеграл
VI ABSTRACT
Prepared by
: Murat SEZER
University
: Kyrgyzstan-Turkey Manas University
Institute
: Natural Sciences
Department
: Mathematics
Thesis Level
: Master Thesis
Number of Pages
: XI + 17
Graduate Date
: May 2010
Thesis Advisor
: Prof.Dr. Avit Asanov
Approximate Integration of Stieltjes Integral
by using the Simpson`s Rule
In many parts of Mathematical computations, Scientific computations or in Applied
Mathematics it is needed to differentiate a function or integrate a function. However, it
is known that many functions are not differentiable and cannot be integrable by using
Riemann integrations methods. If some of this kind of functions are differentiated with
respect to another function, derivative may exists. In addition, as an antiderivative with
respect to function that is Stieltjes integral, some of unintegrable functions can be
integrated with respect to function above. Unfortunately, it is again difficult to integrate
many functions by using this Stieltjes integral, even though the existence is guaranteed.
This leads to use approximation methods. In Riemann integral, there are many
approximation methods. One of these methods is the Simpson`s Rule. In this paper, it is
tried to find whether it is possible to use this Simpson`s method in Stieltjes integral or
not. Since this is an approximation method, it can be thought immediately about the
error bound in this calculation. In this paper, the Formula and needed conditions fort he
error bound are also obtained.
As a preliminary section, the first section is devoted to derivative with respect to a
continuous and increasing function. Here some of the differentiation rules are given.
Then, Stieltjes integral is defined as an antiderivative of this differentiation. After these
fundamental studies, one of the approximation methods The Simpson`s Rule is defined
and error bound is obtained. And then, this method is applied to Stieltjes integral.
Keywords: Differentiation, Integral, Stieltjes integral, Riemann integral, approximation
methods, error bounds, The Simpson`s Rule.
VII ÖNSÖZ
Bu eserde Riemann integralinin hesaplanmasında kullanılabilecek sayısal metodlardan
birisi olan Simpson`s Yaklaşım Kuralı ve hata payı üzerinde duruldu.Sonra bu sayısal
b
yaklaşım kuralı ve hata payı
∫ f ( x )dϕ ( x) olarak tanımlanan Stieltjes integraline
a
uygulandı. f(x) , (a,b) aralığında sürekli bir fonksiyon ve ϕ ( x)
artan sürekli bir
b
fonksiyon olmak üzere
I s = ∫ f ( x ) d ϕ ( x ) Stieltjes integralini düşünelim.Biliyoruz ki
a
I s nin varlığı garanti olsada,hesaplanması çok zor hatta bazen imkansız olabilir.Bu
durumlarda,
I s yi simpson`syaklaşım kuralını kullanarak hesaplayabiliriz.
Bu tez çalışmamda,sabırla bana yardımcı olan,yol gösteren,değerli hocam Prof.Dr.Avıt
ASANOV Bey’e teşekkürü bir borç bilirim.
Bişkek 2010
Murat SEZER
İÇİNDEKİLER:
TEZ ONAY SAYFASI…………………………………………………….. II
ÖZ………………………………………………………………………….. IV
КЫСКАЧА МАЗМУНУ.............................................................................. V
АБСТРАКТ................................................................................................... VI
ABSTRACT………………………………………………………………... VII
ÖNSÖZ……………………………………………………………………... VIII
İÇİNDEKİLER……………………………………………………………... IX
KISALTMALAR…………………………………………………………… X
SEMBOLLER………………………………………………………………. XI
GİRİŞ……………………………………………………………………….. 1
BİRİNCİ BÖLÜM
(ARTAN VE SÜREKLİ BİR FONKSİYONA GÖRE TÜREV)
1.ARTAN VE SÜREKLİ BİR FONKSİYONA GÖRE BİR FONKSİYONUN
TÜREVİ................................................................................................... 2
1.1 Artan Ve Sürekli Bir Fonksiyona Göre Türevin Tanımı..................
2
1.2 Artan Ve Sürekli Bir Fonksiyona Göre Türev Alma Kuralları .......
4
1.3 Artan Ve Sürekli Bir Fonksiyona Göre Taylor Açılımı.................... 5
İKİNCİ BÖLÜM
(STİELTJES İNTEGRALİ)
2. ARTAN VE SÜREKLİ BİR FONKSİYONA GÖRE TERS TÜREV VE
STİELTJES İNTEGRALİ.....................................................................
6
ÜÇÜNCÜ BÖLÜM
(SIMPSON YAKLAŞIM KURALI VE RİEMANN İNTEGRALİ)
3. SIMPSON YAKLAŞIM KURALININ RİEMANN İNTEGRALİNE
UYGULANMASI..............................................................................
8
3.1 Simpson Yaklaşım Kuralı İle İntegral Hesaplama.................... 8
3.2 Simpson Yaklaşım Kuralındaki Hata Payı............................... 9
DÖRDÜNCÜ BÖLÜM
(SIMPSON YAKLAŞIM KURALI VE STİELTJES İNTEGRALİ)
4. SIMPSON YAKLAŞIM KURALININ STİELTJES İNTEGRALİNE
UYGULANMASI........................................................................
10
4.1. Simpson Yaklaşım Kuralını Kullanarak Stieltjes İntegralini
Hesaplama.....................................................................................
10
SONUÇ……………………………………………………………………
14
ÖZET………………………………………………………………………
15
КЫСКАЧА БАЯН ……………………………………………………….
16
KAYNAKLAR……………………………………………………………
17
SEMBOLLER LİSTESİ
[ a, b ]
a , b kapalı aralığı
( a, b )
a , b açık aralığı
∈
elemanıdır
fϕ′
ϕ ( x ) fonksiyonuna göre türev
→
yaklaşır
∆x
x in çevresindeki en küçük aralık
∫ f ( x) dϕ ( x)
ϕ ( x ) fonksiyonuna göre integral
max
[ ]
[ a, b] aralığındaki
sup
verilen şarta göre en küçük üst sınır
x∈ a ,b
x in maksimum değeri
x − y ≤δ
GİRİŞ
Matematiğin önemli konularından birisi olan İntegral,uygulamalı
matematik,fizik,mühendislik,vs gibi alanların bir çok bölümünde kullanılmaktadır.
Riemann integralinin genel hali olan Stieltjes integralide olasılık ve eşitsizliklerin ispatı
gibi uygulamalı matematiğin bir çok bölümünde kullanılmaktadır.
İntegrale başlamadan önce bu integralin tersi olan diferansiyele göz atmak faydalı
olacaktır.Bu diferansiyelde türev x e göre değil,bir fonksiyona göre alınacaktır.Bu
teknik x e göre türevi olmayan fonksiyonların türevlenebilmesinde bize yardımcı
olacaktır.Burada kendisine göre türev alacağımız fonksiyonun [a,b] aralığında artan
sürekli bir fonksiyon olma gibi sınırlılığı vardır.Bu fonksiyonun tersi Stieltjes integrali
veya bir fonksiyona göre integral alma olarak adlandırılır.
X e göre türev almak güç olduğunda,bu integral alma tekniği çok kullanışlı olacaktır.Bu
integrali var olsa bile Stieltjes integralini hesaplamanın her zaman mümkün olduğu
anlamına gelmez.Bu durumlarda,yaklaşım metodlarıyla integral istenilen kesinlikte
hesaplanabilir.
Riemann integralinde Yamuk sayısal yaklaşım kuralı,Orta nokta kuralı,Simpson
kuralı,vs gibi bir çok yaklaşım metodu bulunmaktadır.Her bir yaklaşım metodunun
kendine özgü şartları ve sınırlılıkları mevcuttur.Mesela hata payının hesaplanabilmesi
için Simpson kuralında fonksiyonun dördüncü türevi,Orta nokta kuralında ikinci türevi
var olması gerekir.Bu çalışmada Simpson Yaklaşım Kuralının Stieltjes integralinde
kullanılması gösterilmeye çalışılacak.Eğer bu kuralın,Stieltjes integralinde kullanımının
mümkün olduğunu ispat edebilirsek,o zaman bir çok integrali,istediğimiz kesinlikte,bu
yaklaşım kuralı ile hesaplayabiliriz.
BİRİNCİ BÖLÜM
(ARTAN VE SÜREKLİ BİR FONKSİYONA GÖRE TÜREV)
1.ARTAN VE SÜREKLİ BİR FONKSİYONA GÖRE BİR FONKSİYONUN
TÜREVİ
1.1. Artan Ve Sürekli Bir Fonksiyona Göre Türevin Tanımı:
Tanım 1: f ( x ) , ( a, b ) aralığında tanımlı bir fonksiyon ve ϕ ( x ) , ( a, b ) aralığında
düzenli artan sürekli bir fonksiyon olsun. ∆ x ≠ 0 olmak üzere ( a, b ) aralığından x
noktası alınsın.Bu durumda f ( x ) fonksiyonunun ϕ ( x ) e göre türevi
fϕ ′ ( x ) =
∆f ( x )
f ( x + ∆x ) − f ( x )
df
olarak tanımlanır.
= lim
( x ) = ∆lim
x → 0 ∆ϕ ( x )
∆x → 0 ϕ ( x + ∆x ) − ϕ ( x )
dϕ
Teorem 1:
x0 ∈ ( a, b ) için f ( x ) fonksiyonu ϕ ( x ) e göre türevlenebilir ise f ( x ) , x0 da
süreklidir.
İspat:
Eğer f ( x) fonksiyonu x0 da ϕ ( x) e göre türevlenebilir bir fonksiyon ise,1.tanımdan
lim
∆x → 0
∆f ( x0 ) df
=
( x0 ) = fϕ′ ( x0 ) yazılır.Bu durumda, ∆x → 0 iken α (∆x)
∆ϕ ( x0 ) dϕ
olabildiğince küçük olmak üzere
∆f ( x0 )
= fϕ ′ ( x0 ) + α (∆x) dir veya
∆ϕ ( x0 )
∆f ( x0 ) = fϕ ′ ( x0 ) ∆ϕ ( x0 ) + α (∆x)∆ϕ ( x0 ) dır. ∆x → 0 iken
∆f ( x0 ) = f ( x0 + x) − f ( x0 ) → 0 olur ki bu da f ( x) in x0 da sürekli olduğunu gösterir.
2 Örnek: f ( x ) = x fonksiyonunun x = 0 noktasında türevlenemez olduğu
gösterilebilir.Ama aynı f ( x ) = x fonksiyonu ( −∞, ∞ ) aralığında düzenli artan sürekli
1
⎧
3 , x<0
x
−
⎪
bir ϕ ( x ) = ⎨
1
⎪ x3 , x≥0
⎩
fonksiyonuna göre türevlenebilir.
Çözüm:
x < 0 olmak üzere
f ( x + ∆x ) − f ( x )
x + ∆x − x
= lim
∆x → 0 ϕ ( x + ∆x ) − ϕ ( x )
∆x →0 ϕ ( x + ∆x ) − ϕ ( x )
fϕ ′ ( x ) = lim
3
3
1
1
1
2
1
1
2
⎛
⎞ ⎛ 13 ⎞
⎛
⎞ ⎛
⎞
3
3 − x 3 ⋅ x + ∆x 3 + x + ∆ x 3 ⋅ x 3 + x 3
x
x
x
x
x
+
∆
−
+
∆
⎜
⎟ ⎜
⎟
⎜
⎟ ⎜
⎟
⎠ ⎝
⎠ = lim ⎝
⎠ ⎝
⎠
= lim ⎝
1
1
1
1
∆x → 0
∆x → 0
⎛
⎞
⎛
⎞
− ⎜ x + ∆x 3 − x 3 ⎟
− ⎜ x + ∆x 3 − x 3 ⎟
⎝
⎠
⎝
⎠
2
2
1
1
2
⎞
⎛
= − lim ⎜ x + ∆x 3 + x + ∆x 3 ⋅ x 3 + x 3 ⎟ = −3 ⋅ x 3
∆x → 0
⎠
⎝
ve x > 0 olmak üzere
fϕ ′ ( x ) = lim
∆x → 0
f ( x + ∆x ) − f ( x )
x + ∆x − x
= lim
∆
x
→
0
ϕ ( x + ∆x ) − ϕ ( x )
ϕ ( x + ∆x ) − ϕ ( x )
3
3
1
1
1
2
1
1
2
⎛
⎞ ⎛ 1⎞
⎛
⎞ ⎛
⎞
⎜ x + ∆x 3 ⎟ − ⎜ x 3 ⎟
⎜ x + ∆x 3 − x 3 ⎟ ⋅ ⎜ x + ∆x 3 + x + ∆x 3 ⋅ x 3 + x 3 ⎟
⎠ ⎝
⎠ = lim ⎝
⎠ ⎝
⎠
= lim ⎝
1
1
1
1
∆x → 0
∆
x
→
0
⎛
⎞
⎛
⎞
⎜ x + ∆x 3 − x 3 ⎟
⎜ x + ∆x 3 − x 3 ⎟
⎝
⎠
⎝
⎠
2
2
1
1
2
⎛
⎞
= lim ⎜ x + ∆x 3 + x + ∆x 3 ⋅ x 3 + x 3 ⎟ = 3 ⋅ x 3
∆x → 0
⎝
⎠
Ve x = 0 , ∆x > 0 olmak üzere
∆x
f ( ∆x ) − f ( 0 )
= lim
=0
1
∆x → 0 ϕ ( ∆ x ) − ϕ ( 0 )
∆x → 0
∆x 3
fϕ ′ ( 0 ) = lim
3 Şimdi ∆x < 0 alalım.
∆x
f ( ∆x ) − f ( 0 )
= lim
=0
1
∆x → 0 ϕ ( ∆x ) − ϕ ( 0 )
∆x → 0
3
− ∆x
fϕ ′ ( 0 ) = lim
buradan fϕ′ ( 0 ) = 0 olur.
Bu durumda f ( x ) = x fonksiyonu ϕ ( x ) e göre ( −∞, ∞ ) aralığında türevlenebilir.
2
⎧
3 , x<0
3
x
−
⋅
⎪
fϕ ′ ( x ) = ⎨
2
⎪ 3⋅ x 3 , x > 0
⎩
1.2. Artan Ve Sürekli Bir Fonksiyona Göre Türev Alma Kuralları:
1) C herhangi bir sabit olmak üzere ( C )ϕ ′ = 0
2)
( u + v )ϕ′ = uϕ′ + vϕ′
3)
( u ⋅ v )ϕ′ = uϕ′ ⋅ v + u ⋅ vϕ′
⎛ u ⎞ ′ u ′ ⋅ v − u ⋅ vϕ ′
4) ⎜ ⎟ = ϕ
v2
⎝ v ⎠ϕ
5) Chain Rule: u ( x) , x = x0 noktasında ϕ ( x) e göre türevlenebilir fonksiyonu için
u ( x0 ) = u0 , uϕ ′ ( x0 ) = α ve f ( u ) fonksiyonu u ( x) e göre u = u0 noktasında
türevlenebilir bir fonksiyon olmak üzere f ′ ( u0 ) = β olsun.
Bu durumda v ( x ) = f ( u ( x ) ) fonksiyonu x = x0 noktasında ϕ ( x) e göre
türevlenebilir öyle ki
vϕ′ ( x ) = f ′ ( u0 ) ⋅ uϕ′ ( x0 ) = β ⋅ α
4 1.3. Artan Ve Sürekli Bir Fonksiyona Göre Taylor Açılımı:
f ( x ) fonksiyonu x = x0 noktasında ϕ ( x ) e göre n-1 defa türevlenebilen ve fϕ( n ) ( x0 )
e sahip bir fonksiyon olsun. ∆ϕ = ϕ ( x ) − ϕ ( x0 ) olmak üzere
q ( x ) = f n ( x0 , x ) = f ( x0 ) +
fϕ ′ ( x0 )
1!
∆ϕ +
fϕ ′′ ( x0 )
2!
( ∆ϕ )
2
+ ... +
fϕ (
n)
( x0 )
n!
( ∆ϕ )
n
dir.
5 İKİNCİ BÖLÜM
(STİELTJES İNTEGRALİ)
2. ARTAN VE SÜREKLİ BİR FONKSİYONA GÖRE TERS TÜREV VE
STİELTJES İNTEGRALİ
x
Teorem 2: f ( x ) fonksiyonu [ a, b] aralığında sürekli ve F ( x ) = ∫ f ( t ) ⋅ dϕ ( t ) ,
a
x ∈ [ a, b] olsun.Bu durumda Fϕ ′ ( a ) = lim+
∆x → 0
Fϕ ′ ( b ) = lim−
∆x → 0
F ( a + ∆x ) − F ( a )
ve
ϕ ( a + ∆x ) − ϕ ( a )
⎛x
⎞′
F ( b + ∆x ) − F ( b )
olmak üzere Fϕ ′ ( x ) = ⎜ ∫ f ( t ) ⋅ dϕ ( t ) ⎟ = f ( x )
ϕ ( b + ∆x ) − ϕ ( b )
⎝a
⎠ϕ
x ∈ [ a, b ] olur.
⎛ x +∆x
⎞
⎜ ∫ ( f ( x) − f (t ) ) dϕ ⎟
⎠ olmak üzere diferansiyel tanımından
İspat: lim ψ ( x, ∆x) = ⎝ x
∆x → 0
ϕ ( x + ∆x ) − ϕ ( x )
x +∆x
x +∆x
⎛
⎞
lim ⎜ f ( x) ∫ dϕ − ∫ ( f ( x) − f (t ) ) dϕ ⎟
∆x → 0
x
x
⎝
⎠ = f ( x) − lim ψ ( x, ∆x) yazılır.
Fϕ′ ( x) =
∆x → 0
ϕ ( x + ∆x ) − ϕ ( x )
ω f (δ ) = sup f ( x) − f (t ) olmak üzere
t − x ≤δ
ϕ ( x) fonksiyonu [ a, b ] aralığında artan olduğundan
⎛ x +∆x
⎞
dϕ ⎟
⎝ x
⎠ = ω (∆x ) dır.
ψ ( x , ∆x ) ≤
f
ϕ ( x + ∆x ) − ϕ ( x )
ω f ( ∆x ) ⎜
∫
6 Buradan açıkça görülür ki Fϕ′ ( x) = f ( x) olmak üzere lim ω f (δ ) = 0 , den
δ →0
lim ψ ( x, ∆x) ≤ lim ω f ( ∆x ) = 0 dır.
∆x → 0
∆x → 0
Teorem 3: (Newton-Leibnitz) fϕ′ ( x ) = f ( x) fonksiyonu [ a, b] aralığında sürekli
b
olmak üzere
∫ fϕ′ ( x ) ⋅ dϕ ( x ) = f ( b ) − f ( a ) dir.
a
İspat: a = x0 < x1 < x2 < ... < xn = b ve i = 1, 2,..., n için ξi sayısı [ xi −1 , xi ] dan
herhangi bir sayı olmak üzere Stieltjes integralinin tanımından integral
n
S n = ∑ fϕ′ (ξi ) [ϕ ( xi ) − ϕ ( xi −1 ) ] toplamı şeklindedir.
i =1
ci ∈ [ xi −1 , xi ] , i = 1, 2,..., n olmak üzere , Lagranj teoreminden,
f ( xi ) − f ( xi −1 ) = fϕ′ (ci ) [ϕ ( xi ) − ϕ ( xi −1 )] olur.Eğer Sn toplamında ci yi ξi ile
n
değiştirirsek Sn = ∑ [ f ( xi ) − f ( xi −1 ) ] = f ( xn ) − f ( x0 ) = f (b) − f (a) olur.
i =1
Sonuç: fϕ′ ( x ) fonksiyonu [ a, b] aralığında sürekli bir fonksiyon olmak üzere
∀x ∈ [ a, b ] için
x
∫ fϕ′ ( s ) ⋅ dϕ ( s ) = f ( x ) − f ( a ) dir.
a
Teorem 4: (Parçalı türev)
fϕ′ ( x ) ve gϕ ′ ( x ) fonksiyonları [ a, b] aralığında sürekli fonksiyonlar olmak üzere
b
∫
a
b
f ( x ) ⋅ gϕ ′ ( x ) ⋅ dϕ ( x ) = ⎡⎣ f ( x ) ⋅ g ( x ) ⎤⎦ − ∫ g ( x ) ⋅ fϕ ′ ( x ) ⋅ dϕ ( x ) dir.
b
a
a
İspat: Stieltjes ile integral alınır
[ f ( x) ⋅ g ( x)]ϕ′ =
fϕ ′ ( x) ⋅ g ( x) + f ( x) ⋅ gϕ ′ ( x)
7 ÜÇÜNCÜ BÖLÜM
(SIMPSON YAKLAŞIM KURALI VE RİEMANN İNTEGRALİ)
3. SIMPSON YAKLAŞIM KURALININ RİEMANN İNTEGRALİNE
UYGULANMASI
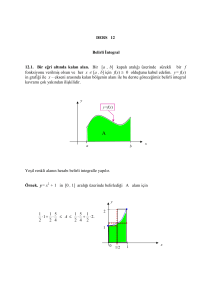
3.1 Simpson Yaklaşım Kuralı İle İntegral Hesaplama:
(0,y1)
h
A=
(h,y2)
∫ ( ax
2
+ bx + c ) dx
−h
(‐h,y0) ‐h y0 = ah 2 − bh + c
y1 = c
⎛ ax3 bx 2
⎞h
=⎜
+
+ cx ⎟
2
⎝ 3
⎠ −h
h =
2ah3
+ 2ch
3
=
h
2ah 2 + 6c )
(
3
y0 + 4 y1 + y2 = 2ah 2 + 6c
⇒ A=
h
( y0 + 4 y1 + y2 )
3
y2 = ah 2 + bh + c
Şimdi kapalı [ a, b ] aralığını eşit N = 2n parçaya bölelim
b−a
⎧
i,
⎪ xi = a +
Burada ⎨
N
⎪⎩ fi = f ( xi ) ,
ve h =
i = 0,1, 2,..., N
b−a b−a
=
N
2n
Demek x j ≤ x ≤ x j + 2h
8 x j+2 h
∫
f ( x)dx ≈
xj
h
( f j + 4 f j +1 + f j +2 )
3
Genel olarak
b
x2
x4
xN
a
x0
x2
xN −2
∫ f ( x ) dx = ∫ f ( x)dx + ∫ f ( x)dx + ... + ∫
≈
f ( x)dx
h
( f0 + 4 f1 + 2 f 2 + 4 f3 + ... + 4 f N −1 + f N )
3
Burada f j = f ( x j ) = f ( a + jh ) j = 0,1, 2,..., N
3.2.Simpson Yaklaşım Kuralındaki Hata Payı:
f ( x) = f j +1 + ( x − x j +1 ) f '( x j +1
x j+2 h
∫
xj
xj
j +1
2!
2
f ''( x j +1 ) + ...
⎡
⎤
1 h2
1 h 4 (4)
f ( x)dx = 2h ⎢ f j +1 +
f ''( x j +1 ) +
f ( x j +1 ) + ...⎥
3 2!
5 4!
⎣
⎦
x j+2 h
∫
(x − x )
)+
f ( x)dx ≈
*
h
( f j + 4 f j +1 + f j +2 )
3
⎞
⎛
⎞⎤
h ⎡⎛
h2
h2
= ⎢⎜ f j +1 − hf '( x j +1 ) +
f ''( x j +1 ) − ... ⎟ + 4 f j +1 + ⎜ f j +1 + hf '( x j +1 ) +
f ''( x j +1 ) + ... ⎟ ⎥
3 ⎣⎝
2!
2!
⎠
⎝
⎠⎦
⎛
⎞
1 h2
1 h 4 (4)
f ''( x j +1 ) +
f ( x j +1 ) + ... ⎟
= 2h ⎜ f j +1 +
3 2!
3 4!
⎝
⎠
Şimdi şu farka bakalım
* - **
**
= ES
4
⎛ 1 1 ⎞ h ( 4)
Es = 2 h ⎜ − ⎟
f ( x j +1 ) + ...
⎝ 5 3 ⎠ 4!
ES = −
h5 ( 4 )
f ( x j +1 ) + ...
90
9 DÖRDÜNCÜ BÖLÜM
(SIMPSON YAKLAŞIM KURALI VE STİELTJES İNTEGRALİ)
4. 1.SIMPSON YAKLAŞIM KURALININ STİELTJES İNTEGRALİNE
UYGULANMASI
Verilen aralığı n parçaya bölelim a= x0 < x1 < x 2 < . . . < xN =b
Her bir aralık ⎡⎣ x j , x j +1 ⎤⎦ , x j +1 = x j + h , j = 0,1,..., N = 2n.
Taylor Açılımını kullanırsak,
2
⎡⎣ϕ(x) −ϕ(x*j+1)⎤⎦
ı
ıı *
*
*
*
f ( x) = f ( xj+1 ) + fφ ( xj+1 ) ⎣⎡ϕ(x) −ϕ(xj+1)⎦⎤ + fϕ (xj+1)
+
2!
3
4
⎡⎣ϕ(x) −ϕ(x*j+1)⎤⎦
⎡⎣ϕ(x) −ϕ(x*j+1)⎤⎦
ııı *
(ıv)
*
*
+ fϕ (xj+1)
+ fϕ ⎡⎣xj+1 +θ(x − xj+1)⎤⎦
3!
4!
ϕ ( x j +2 ) + ϕ ( x j )
⎛ ϕ ( x j +2 ) + ϕ ( x j ) ⎞
*
burada x*j +1 = ϕ −1 ⎜
⎟ ⇒ ϕ ( x j +1 ) =
2
2
⎝
⎠
∫
x j +2h
xj
+
f (x)dϕ(x) = ∫
x j + 2h
xj
fϕııı ( x*j +1 )
3!
⎡ *
fϕıı (x*j+1)
2
ı *
*
⎡⎣ϕ(x) −ϕ(x*j+1)⎤⎦ +
⎢ f (x j+1) + fϕ (x j+1) ⎡⎣ϕ(x) −ϕ(x j+1)⎤⎦ +
2
⎢⎣
3
⎡⎣ϕ ( x) − ϕ ( x ) ⎤⎦ + fϕ
*
j +1
( ıv )
⎡⎣ x
*
j +1
4
⎡⎣ϕ ( x) − ϕ ( x*j +1 ) ⎤⎦ ⎤
⎥ dϕ ( x ) =
+ θ ( x − x ) ⎤⎦
⎥
4!
⎦
*
j +1
10 2 x j +2h
Ij = ∫
x j +2h
xj
⎡⎣ϕ ( x) − ϕ ( x*j +1 )⎤⎦
*
ı
*
+
f ( x)dϕ ( x) = f ( x j +1 ) ⎣⎡ϕ ( x j +2 ) − ϕ ( x j )⎦⎤ + fϕ ( x j +1 )
2!
xj
144444244444
3
=0
( x*j +1 )
ıı
⎡⎣ϕ ( x) − ϕ ( x*j +1 )⎤⎦
3!
+ fϕ
3 x j +2h
xj
4 x j +2h
⎡⎣ϕ ( x) − ϕ ( x*j +1 )⎤⎦
ııı
*
+ fϕ ( x j +1 )
+
4!
xj
144444244444
3
=0
4
+∫
x j +2h
xj
⎡ϕ ( x) − ϕ ( x*j +1 )⎤⎦
dϕ ( x).
fϕ(ıv) ⎡⎣ x*j +1 + θ ( x − x*j +1 )⎤⎦ ⎣
4!
Sonra
Ij = ∫
x j +2h
xj
f ( x)dϕ ( x) = f ( x*j +1 ) ⎡⎣ϕ ( x j + 2 ) − ϕ ( x j ) ⎤⎦ + fϕıı
( x*j +1 )
3!
3
⋅ 2 ⋅ ⎡⎣ϕ ( x j + 2 ) − ϕ ( x*j +1 ) ⎤⎦ +
4
+∫
x j +2h
xj
⎡⎣ϕ ( x) − ϕ ( x*j +1 ) ⎤⎦
( ıv )
*
*
fϕ ⎡⎣ x j +1 + θ ( x − x j +1 ) ⎤⎦
dϕ ( x )
4!
Taylor Açılımından
f (xj ) = f (x
*
j +1
fϕ ( x
ııı
+
) + fϕ ( x
ı
*
j +1
3!
)
*
j +1
) ⎡⎣ϕ ( x j ) − ϕ ( x *j +1 ) ⎤⎦ +
3
⎡⎣ϕ ( x j ) − ϕ ( x *j +1 ) ⎤⎦ +
fϕ
( ıv )
f ( x j + 2 ) = f ( x*j +1 ) + fϕı ( x*j +1 ) ⎡⎣ϕ ( x j + 2 ) − ϕ ( x*j +1 ) ⎤⎦ +
+
fϕ ııı ( x*j +1 )
3!
3
⎡⎣ϕ ( x j + 2 ) − ϕ ( x*j +1 ) ⎤⎦ +
f ϕ ıı ( x *j +1 )
(x
*
j +1
2!
+ θ ( x j − x *j +1 ) )
4!
fϕ ıı ( x*j +1 )
⎡⎣ϕ ( x j ) − ϕ ( x *j +1 ) ⎤⎦
2
⎡⎣ϕ ( x j + 2 ) − ϕ ( x*j +1 ) ⎤⎦ +
2!
fϕ (ıv ) ( x*j +1 + θ ( x j + 2 − x*j +1 ) )
4!
2
⎡⎣ϕ ( x j ) − ϕ ( x *j +1 ) ⎤⎦ +
⎡⎣ϕ ( x j + 2 ) − ϕ ( x*j +1 ) ⎤⎦
4
11 4
Sonra
⎡ ϕ ( x j + 2 ) − ϕ ( x j ) ⎤⎦
⎡⎣ f ( x j ) + 4 f ( x *j + 1 ) + f ( x j + 2 ) ⎤⎦ =
Aj = ⎣
6
x j+2
=
∫
xj
1
⎡ f ( x j ) + 4 f ( x*j +1 ) + f ( x j + 2 ) ⎤⎦ dϕ ( x) =
6⎣
⎧
⎫
fϕ ıı ( x*j +1 )
2
ı
*
*
*
⎡
⎤
⎡⎣ϕ ( x j ) − ϕ ( x*j +1 ) ⎤⎦ +
⎪ f ( x j +1 ) + fϕ ( x j +1 ) ⎣ϕ ( x j ) − ϕ ( x j +1 ) ⎦ +
⎪
2!
⎪
⎪
( ıv )
*
*
⎪ f ııı ( x* )
⎪
f
x
(
x
x
)
+
−
θ
3
4
( j +1
j
j +1 )
ϕ
j +1
⎪+ ϕ
⎡⎣ϕ ( x j ) − ϕ ( x*j +1 ) ⎤⎦ +
⎡⎣ϕ ( x j ) − ϕ ( x*j +1 ) ⎤⎦ + ⎪
3!
4!
⎪
x j +2 ⎪
1 ⎪
⎪
*
= ∫ ⎨+4 f ( x j +1 ) +
⎬ dϕ ( x )
6 xj ⎪
⎪
ıı
*
⎪+ f ( x* ) + f ı ( x* ) ⎡ϕ ( x ) − ϕ ( x* ) ⎤ + fϕ ( x j +1 ) ⎡ϕ ( x ) − ϕ ( x* ) ⎤ 2 +
⎪
j+2
j +1 ⎦
j +1
j +1 ⎣
j+2
j +1 ⎦
ϕ
⎪
⎪
2! ⎣
⎪
⎪
ııı
*
fϕ (ıv ) ( x*j +1 + θ ( x j + 2 − x*j +1 ) )
3
4⎪
⎪ fϕ ( x j +1 )
*
*
⎡⎣ϕ ( x j + 2 ) − ϕ ( x j +1 ) ⎤⎦ +
⎡⎣ϕ ( x j + 2 ) − ϕ ( x j +1 ) ⎤⎦ ⎪
⎪+
3!
4!
⎩
⎭
Buradan
Aj = f ( x*j +1 ) +
+
fϕ
( ıv )
Şimdi
(x
*
j +1
fϕ ıı ( x*j +1 )
3
⎡⎣ϕ ( x j + 2 ) − ϕ ( x*j +1 ) ⎤⎦ +
3
+ θ ( x j + 2 − x*j +1 ) )
4!
5
⋅ 2 ⋅ ⎡⎣ϕ ( x j + 2 ) − ϕ ( x*j +1 ) ⎤⎦ . farkına bakalım ,
4
⎧
⎫
⎡⎣ϕ ( x) − ϕ ( x*j +1 ) ⎤⎦
ıv
(
)
*
*
⎡⎣ x j +1 + θ ( x − x j +1 ) ⎤⎦ .
dϕ ( x ) − ⎪
x j + 2 ⎪ fϕ
⎪
⎪
4!
Es ( j ) = I j − A j = ∫ ⎨
dϕ ( x).
5⎬
( ıv )
*
*
+
−
f
x
θ
(
x
x
)
−
ϕ
(
x
)
ϕ
(
x
)
(
)
⎡
xj ⎪
ϕ
j +1
j+2
j +1
j +2
j ⎤ ⎪
⋅2⋅⎢
⎥ ⎪
⎪−
4!
2
⎣
⎦ ⎭
⎩
12 Şimdi
M = sup fϕ (ıv ) ( x ) x∈[ a ,b ]
Sonra x j +2
∫
Es ( j ) ≤
fϕ
( ıv )
(x
xj
4
*
j +1
⎡⎣ϕ ( x) − ϕ ( x*j +1 ) ⎤⎦
dϕ ( x ) +
+ θ (x − x ))
4!
*
j +1
+ fϕ (ıv ) ( x*j +1 + θ ( x j + 2 − x*j +1 ) )
⎡⎣ϕ ( x) − ϕ ( x*j +1 ) ⎤⎦
≤M⋅
5!
5
1
⎡ϕ ( x j + 2 ) − ϕ ( x j ) ⎤⎦
4 ⎣
4!.2
5 x = x j +2
+
M
⋅ ⎡ϕ ( x j + 2 ) − ϕ ( x j ) ⎤⎦ =
4!.24 ⎣
5
x= x j
5⎛1
M
⎞
⋅ ⎡ϕ ( x j + 2 ) − ϕ ( x j ) ⎤⎦ ⎜ + 1⎟ ,
4 ⎣
4!.2
⎝5 ⎠
=
j = 0,1, 2,......., N − 2
Şimdi ise
W (δ ) = sup ϕ ( x) − ϕ ( y )
x − y ≤δ
n −1
n −1
ϕ ( x2 j + 2 ) − ϕ ( x2 j )
j =0
j =0
6
I ( x) = ∑ I 2 j = ∑
⎡⎣ f ( x2 j ) + 4 f ( x2* j +1 ) + f ( x2 j + 2 ) ⎤⎦
b
I = ∫ f ( x)dϕ ( x)
a
n −1
E (n) = I − I n = ∑ ES (2 j ),
buradan
j =0
n −1
E (n) ≤ ∑ E2 j
j =0
4
M 6 n −1
6M
≤
⋅ ∑ ⎣⎡sup (ϕ ( x j + 2 ) − ϕ ( x j ) ⎦⎤ ⎡⎣ϕ ( x j + 2 ) − ϕ ( x j ) ⎤⎦ =
[W (2h)] (b − a)
16.4! 5 j =0
16 ⋅ 5!
13 SONUÇ
Artan ve sürekli bir fonksiyona göre bir fonksiyonun türevinin tanımı ele
alındı.Türev-süreklilik teoremi ispatlandı.
Türevi bulunamayan bir fonksiyonun,başka artan ve sürekli bir
fonksiyon( ϕ ( x ) ) altında türevlenebilir olduğu aktarıldı ve örnek verildi.Bu artan ve
sürekli fonksiyonun ( ϕ ( x ) ) türevinde kullanılan kural ve teoremler ele alındı.Taylor
açılımına uygulanabilirliği görüldü.
Artan ve sürekli fonksiyonun ( ϕ ( x ) ) ters türevi ve Stieltjes integrali
incelendi.Bu integralde ve bağlantılı teoremlerde ϕ ( x ) in uygulanabilir olduğu
gözlemlendi.
Simpson kuralının Riemann integralinde görüldü.Ardından Simpson kuralının
Stieltjes integralinede uygulanabilir olduğu anlaşıldı.
İleride yapılacak çalışmalarla başka kurallarında Stieltjes integraline
uygulanabilir olduğu/olmadığının incelenebileceği kanaatine varıldı.
14 ÖZET
Birinci bölümde temel olarak artan ve sürekli bir fonksiyona göre bir fonksiyonun
türevinin tanımı ve ilgili teoremler ele alındı. Türevlenemeyen bir fonksiyonun,başka
artan ve sürekli bir fonksiyon( ϕ ( x ) ) altında türevlenebilir olduğu aktarıldı ve örnek
verildi.Bu artan ve sürekli fonksiyonun ( ϕ ( x ) ) türevinde kullanılan kural ve teoremler
ele alındı.Taylor açılımına uygulanabilirliği görüldü.
Daha sonra, artan ve sürekli fonksiyonun ( ϕ ( x ) ) ters türevi ve Stieltjes integrali
incelendi.Bu integralde ve bağlantılı teoremlerde ϕ ( x ) in uygulanabilir olduğu
gözlemlendi.
Son olarak da, Simpson kuralı Riemann integralinde görüldü.Ardından Simpson
kuralının Stieltjes integralinede uygulanabilir olduğu anlaşıldı.
15 КЫСКАЧА БАЯН
Биринчи бөлүмдө, кадимки туунду алуудан кенээнирек болгон башка бир
үзгүлтүксүз өсүүчү функцияга карата туунду алуу менен башталды. Кадимки
туундусу жок болгон жерде башка бир үзгүлтүксүз өсүүчү функцияга карата
туундусу бар экендиги көрсөтүлдү. Кадимки туунду алуунун касиеттери жана
теоремалары башка бир функцияга карата туунду алууда дагы иштеши
көрсөтүлдү.
Экинчи бөлүмдө болсо, бул башка бир функцияга карата туунду алуунун тескери
операциясы болгон Стильтес интегралы каралды.
Акыркы бөлүмдө, Риман интегралындагы жакындаштырып эсептөө методдорунан
Симнсон методу жана анын ката формуласы табылды. Бул методдун Стильтес
интегралында да колдонууга болоору далилденди.
16 KAYNAKLAR:
[1] Asanov, A. (2001). Proizvodnaya Funktsii po Vozrastayushey Funktsii .
University Manas, 1(2): 18-45
[2] Bender, E. Deriving the Trapezoidal Rule Error. University of California,
Department of Mathematics, San-Diego
http://math.ucsd.edu/~ebender/20B/77_Trap.pdf
[3] Conte S. and C. de Boor. (1972). Elementary Numerical Analysis. McGraw-Hill.
New York
[4] First Step in Numerical Analysis. Mahidol Physics Education Centre.
http://mpec.sc.mahidol.ac.th/numer/STEP31.HTM
[5] Jensen J. and Rowland J., (1975). Methods of Computation. Scott. Foresman.
Glenview
[6] Rozema, E. (Feb., 1980). Estimating the Error in the Trapezoidal Rule. The
American Mathematical Monthly, 87(2):124-128
[7] Silverman, R.A. (1985). Calculus with Analytic Geometry. Prentice-Hall, Inc.,
New Jersey, 413-423
17 KIRGIZİSTAN-TÜRKİYE MANAS ÜNİVERSİTESİ
FEN BİLİMLER ENSTİTÜSÜ
MATEMATİK ANABİLİM DALI
STİELTJES İNTEGRALİNDE SAYISAL YAKLAŞIM
METODLARI
(YÜKSEK LİSANS TEZİ)
Murat SEZER
BİŞKEK 2010