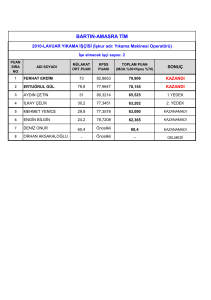
Haliç Üniversitesi, Uygulamalı Matematik Bölümü
Math 103 Lineer Cebir Ödev Çözümü
3. Ödevin Çözümü
1. Sorunun Çözümü: Ben şu iki vektörü seçiyorum:
2
r 1
1
r 2
−1
3
a) Bu vektörlerin Euclidean iç çarpımı şöyledir:
⟨r1 , r 2 2 −1
1
−1
3
b) Bu vektörlerin W tarafından yaratılan iç çarpıma göre çarpımları da şöyledir:
⟨r1 , r 2 2 −1
5 0
5 0
1
0
0
3
1
1
7
Değerlendirme: Çözümünüz soruda tarif edildiği gibi değerlendirilecektir.
2. Sorunun Çözümü: Ben şöyle bir matrisler seçtim:
1
M1
0
M2
−2 1
1
0
−1 1
Bu durumda
⟨M 1 , M 1 2 1 1 0 0 2 −2−2 1 1 11
‖M 1 ‖
⟨M 1 , M 1
11
⟨M 2 , M 2 2 1 1 0 0 2 −1−1 1 1 5
‖M 2 ‖
⟨M 2 , M 2
5
⟨M 1 , M 2 2 1 1 0 0 2 −2−1 1 1 7
Buradan
cos
⟨M 1 , M 2
‖M 1 ‖‖M 2 ‖
7
11 5
arccos0. 94 20 ∘
buluruz. Dikkat ederseniz seçtiğim M 1 ve M 2 matrisleri birbirlerine benzediği için
aralarındaki açı da küçük çıktı.
Değerlendirme: ⟨M 1 , M 2 çarpımını alma ve ‖M 1 ‖ ve ‖M 2 ‖ değerlerini bulma
işlemi 1’er puan, açıyı hesaplamak 2 puandır. İşlem hatasından 1 puan kırılacaktır.
3. Sorunun Çözümü: Ben şu r 2 vektörünü şu şekilde seçtim:
−1
r 2
1
Gram-Schmidt yöntemini iki adımda uygulayacağım.
1. Adım:
e 1 r1
‖r1 ‖
‖r1 ‖
22 62
40 2 10
Bu durumda
e1
1
2 10
2. Adım:
e2
⟨r2 , e 1
r 2 − ⟨r2 ,
e 1 e 1
2
1
10
6
3
10
r 2 − ⟨r2 ,
e 1 e 1
‖r2 − ⟨r2 , e 1 e 1 ‖
1
10
−1 1
−1
1
−
2
10
3
10
1
10
2
10
− 65
3
10
2
5
Bu vektörün boyunu
‖r2 − ⟨r2 , e 1 e 1 ‖
olarak buluruz. Buradan da
−6
5
2
2
5
2
4
10
e2
r 2 − ⟨r2 ,
e 1 e 1
‖r2 − ⟨r2 , e 1 e 1 ‖
1
− 65
4
10
2
5
−
3
10
1
10
bulunur.
Bulduğumuz vektörlerin birbirlerine ortogonal olup olmadığını kontrol edelim:
⟨e 1, e 2
1
10
3
10
−
3
10
1
10
0
Buradan bu vektörlerin birbirlerine ortogonal olduğunu görmüş oluyoruz.
Değerlendirme: Birinci adım 1 puan ve ikinci adım 3 puandır. İşlem hatasından
1 puan kırılacaktır. Bu soruda yaptığınız işlemi şekil üzerinde göstermeniz de
gerekmektedir ve bu da 1 puandır. Ben ne yazık ki burada şekil çizemiyorum ancak bu
şekli derste pek çok defa çizmiştik.