D - Belirli integralin uygulamaları.qxp - Soruhane.com

Belirli Ýntegralin Uygulamalarý
Örnek 1
A) EÐRÝ ALTINDAKÝ ALAN
1.
f:[a , b] → R’ye tanýmlý ve sürekli olmak
þartýyla y = f(x) eðrisi x = a ve x = b
doðrularý ve ox–ekseni arasýnda kalan
düzlemsel bölgenin alaný
A=
i)
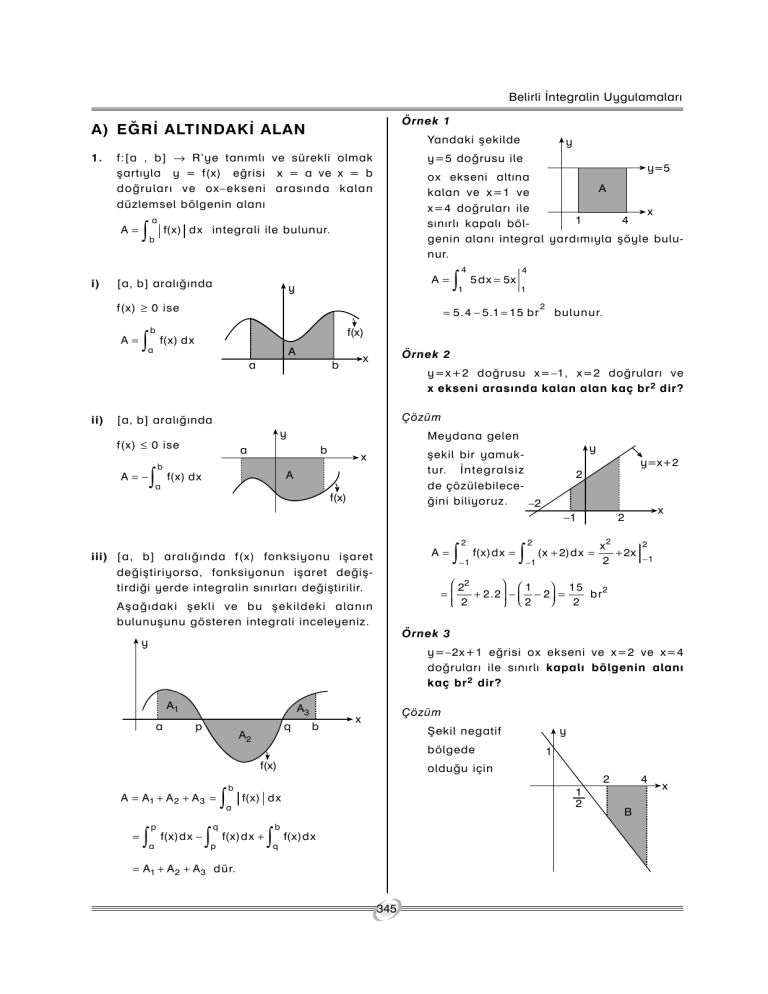
Yandaki þekilde
∫
a
y=5 doðrusu ile
y=5
ox ekseni altýna
A
kalan ve x=1 ve
x=4 doðrularý ile
x
1
4
sýnýrlý kapalý bölgenin alaný integral yardýmýyla þöyle bulunur.
f(x) dx integrali ile bulunur.
b
[a, b] aralýðýnda
A=
y
f(x) ≥ 0 ise
A=
∫
b
A
∫
a
2
bulunur.
y=x+2 doðrusu x=–1, x=2 doðrularý ve
x ekseni arasýnda kalan alan kaç br 2 dir?
Çözüm
y
f(x) ≤ 0 ise
b
1
Örnek 2
x
b
[a, b] aralýðýnda
A=−
1
4
5 dx = 5x
f(x)
a
ii)
∫
4
= 5. 4 − 5.1 = 15 br
f(x) dx
a
y
Meydana gelen
a
b
A
f(x) dx
y
þekil bir yamuktur. Ýntegralsiz
de çözülebileceðini biliyoruz.
−2
x
f(x)
y=x+2
2
−1
A=
iii) [a, b] aralýðýnda f(x) fonksiyonu iþaret
deðiþtiriyorsa, fonksiyonun iþaret deðiþtirdiði yerde integralin sýnýrlarý deðiþtirilir.
∫
2
−1
(x + 2)dx =
x2
+ 2x
2
2
−1
Örnek 3
y
y=–2x+1 eðrisi ox ekseni ve x=2 ve x=4
doðrularý ile sýnýrlý kapalý bölgenin alaný
kaç br 2 dir?
A1
a
A3
p
q
A2
b
Çözüm
x
Þekil negatif
bölgede
f(x)
A = A1 + A 2 + A 3 =
∫
−1
f(x)dx =
⎛ 22
⎞ ⎛1
⎞ 15
=⎜
+ 2.2⎟ − ⎜ − 2⎟ =
br 2
⎠
2
⎝ 2
⎠ ⎝2
Aþaðýdaki þekli ve bu þekildeki alanýn
bulunuþunu gösteren integrali inceleyeniz.
=
∫
2
x
2
p
a
f(x)dx −
∫
q
p
∫
b
a
f(x)dx +
∫
q
1
olduðu için
1
2
f(x) dx
b
y
f(x)dx
= A1 + A 2 + A 3 dür.
345
2
4
B
x
Belirli Ýntegralin Uygulamalarý
B=−
∫
4
2
⎛
⎞
x2
( − 2x + 1)dx = − ⎜ − 2
+x⎟
⎜
⎟
2
⎝
⎠
= (x 2 − x)
4
2
a)
4
2
Yukarýda verilen f(x) fonksiyonuna göre
∫
= (4 2 − 4) − (2 2 − 2)
6
−3
f(x)dx
integralinin deðeri nedir? denildiðinde
alanlarýn cebirsel toplamý yapýlýr, yani;
= 12 − 2 = 10 br 2 bulunur.
∫
Þekli çizmeden, alanýný bulacaðýmýz bölgenin yerini tesbit etmeden integral alsaydýk
sonuç –10 çýkacaktý alan mutlaktýr, negatifle
ifade edilemeyeceðinden |–10| kabul edip
alaný 10 br 2 olduðu söylenebilirdi.
b)
f(x)=x 2 –2x–8 eðrisi ile ox ekseni arasýnda
kalan kapalý bölgenin alanýný bulunuz.
−3
f(x)dx = − 5 + 20 = 15
[–3, 6] aralýðýnda f(x) ve x ekseni arasýndaki taralý alan nedir? denildiðinde ise
mutlak deðerce toplam yapýlýr, yani;
∫
Örnek 4
6
6
f(x) dx = − 5 + 20 = 25 br 2 dir.
−3
Çözüm
x 2 –2x–8=0 ⇒ (x+2) . (x–4)=0
Örnek 5
x=–2 ve x=4 bulunur.
A=
4
∫ (x
2
−2
=
x2
eðrisi ile ox ekseni arasýnda
2
kalan kapalý bölgenin alaný kaç br 2 dir?
f(x) = 2 −
)
− 2x − 8 dx
x3
x2
−2
− 8x
3
2
Çözüm
4
f(x)=2–x 2 / 2 eðrisinin
−2
grafiðini çizelim. Ýstenilen alan grafikteki
taralý alandýr. Buna
−2
göre,
⎡ 43
⎤ ⎡ ( − 2)2
⎤
=⎢
− 42 − 8.4 ⎥ − ⎢
− ( − 2)2 − 8( − 2) ⎥
⎢⎣ 3
⎥⎦ ⎢⎣ 3
⎥⎦
⎛ 64
⎞ ⎛4
⎞
=⎜
− 16 − 32 ⎟ − ⎜ − 4 + 16 ⎟
⎝ 3
⎠ ⎝3
⎠
=
64
4
− 48 − − 12
3
3
A=
= 20 − 60 = − 40
∫
2
−2
⎛
x2 ⎞
1 x3
⎜2 −
⎟ dx = 2x − .
⎜
2 ⎟⎠
2 3
⎝
y
2
2
x
2
−2
⎛
23 ⎞ ⎡
( − 2)3 ⎤
= ⎜ 2.2 −
⎟ − ⎢2.( − 2) −
⎥
⎜
6 ⎟⎠ ⎣⎢
6 ⎦⎥
⎝
A = − 40 = 40 br 2 dir.
= 4−
=
Uyarý : (Aklýnýzda bulunsun)
4
4
+4−
3
3
16
br 2 dir.
3
f(x)
20 br2
−3
5 br2
−1
6
Örnek 6
x
y=x 3 eðrisi ile x=–2 ve x=1 doðrularý
arasýnda kalan kapalý bölgenin alaný kaç
br 2 dir?
346
Belirli Ýntegralin Uygulamalarý
Örnek 8
Çözüm
∫
A=
1
y
x 3 dx
−2
y
y=x3
f(x)
−2
x
1
−3
2
−1
x
4
Yukarýda f(x) fonksiyonunun grafiði verilmiþtir. Buna göre;
=
∫
=−
0
− x 3 dx +
−2
4
x
4
0
+
−2
4
x
4
∫
1
∫
x 3 dx
0
−1
∫
f(x)dx = 6 ve
4
−3
f(x)dx = −5
olduðuna göre þekildeki tüm taralý alanlarýn toplamý kaç br 2 dir?
1
0
Çözüm
⎡
( − 2)4 ⎤ ⎡ 14 0 ⎤
= − ⎢0 −
⎥+⎢ − ⎥
4 ⎦⎥ ⎣⎢ 4 4 ⎥⎦
⎣⎢
= 4+
2
Alanlarý bulurken mutlak deðerce toplam
yapýldýðýný biliyoruz. Buna göre;
1 17
br 2 bulunur.
=
4
4
∫
4
−3
f(x)dx =
∫
−1
−3
f(x)dx +
∫
2
−1
f(x)dx +
∫
4
2
f(x)dx
–5 = –A + 6 – B
A + B = 11 olup tüm alanlar toplamý,
Örnek 7
Yandaki þekilde
taralý alan 14
dir.
∫
2
−2
br 2
∫
y
f(x)
2
f(x)dx = 0
−2
−3
f(x) dx = 11 + 6 = 17 br 2
Örnek 9
y=4x–x 2 eðrisi ile x=–2 ve x=2 doðrularý ve
ox ekseni arasýnda kalan bölgenin alaný
kaç br 2 dir?
x
olduðuna göre,
∫
4
y
2
f(x)dx in deðeri kaçtýr?
0
−2
∫
2
−2
f(x)dx =
∫
0
−2
f(x)dx −
∫
2
0
f(x)dx
Çözüm
0 = A – A dýr.
Soruda bahsedilen alan þekilde görülmektedir. Buna göre;
Yani üst bölgedeki pozitif alan ile alt
bölgedeki negatif alanlar birbirine eþittir.
Taralý alan =
O halde;
∫
2
0
x
2
Çözüm
∫
2
−2
=−
f(x)dx = − 7 dir.
347
∫
4x − x 2 dx
0
−2
(4x − x 2 )dx +
∫
2
0
(4x − x 2 )dx
Belirli Ýntegralin Uygulamalarý
ii)
2
3
⎛ x
x ⎞
= − ⎜ 4.
−
⎟
2
3 ⎠
⎝
2
0
−2
⎛ 4x
x ⎞
+⎜
−
⎟
2
3 ⎠
⎝
⎡
8⎞ ⎤ ⎛
⎛
= − ⎢ (0) − ⎜ 8 + ⎟ ⎥ + ⎜ 8 −
⎝
3⎠ ⎦ ⎝
⎣
= 8+
3
2
0
[m,n] aralýðýnda
y
g(y) ≤ 0
n
A=−
8⎞
⎟ − (0)
3⎠
∫
n
m
A
g (y) dy
x
m
8
8
+ 8 − = 16 br 2
3
3
iii) [m,n] aralýðýnda
Örnek 10
Yandaki þekilde
3
eðrisi x = 2
y=
x
ve x = 8 doðrularý
3
y=
x
x = g(y) fonksiyonu
iþaret deðiþtiriyorsa
n
A = A1 – A2
k
A1
x
A2
ile ox ekseni arasýn-
2
da kalan kapalý
y
8
m
bölgenin alaný kaç br2 dir?
A=
∫
n
k
g (y)dy −
∫
k
m
g (y)dy
= A1 − A 2 dir.
Çözüm
A=
y
∫
8
2
3
dx = 3
x
∫
= 3 ln x
8
2
8
2
1
dx
x
Örnek 11
= 3 ⎣⎡ ln 8 − ln 2 ⎦⎤
= 3.2ln 2 = 6.ln 2 br
2
y = lnx eðrisi, y = 1 ve y = 3 doðrularý
ve oy ekseni arasýnda kalan kapalý bölgenin alaný kaç br 2 dir?
dir.
Çözüm
2.
x = g(y) eðrisi y = m ve y = n doðrularý
ve oy ekseni arasýnda kalan bölgenin alaný
A=
∫
n
m
g(y) dy =
∫
n
m
Soruda istenilen kapalý bölge yandaki
þekilde görülmektedir.
x .dy dir.
y = ln x ⇒ x =
i)
[m,n] aralýðýnda
g(y) ≥ 0 ise
A=
∫
n
m
n
g (y) dy
ey
3
y
1
x
1
dir.
y=lnx
Buna göre,
y
x=g(y)
A=
A
∫
3
1
x dy =
∫
3
1
ey dy = ey
3
1
= e3 − e br 2 bulunur.
m
Örnek 12
x
x = y 2 – 4 eðrisi ile oy ekseni arasýnda
kalan kapalý bölgenin alaný kaç br 2 dir?
348
Belirli Ýntegralin Uygulamalarý
ÝKÝ EÐRÝ ARASINDA KALAN ALAN
Çözüm
x=0 için y = ∓ 2
y
y=0 için x=–4
olup aranan bölge yandaki gibidir. Buna göre
taralý alan
1.
x=y2 − 4
2
−4
y = f(x) , y = g(x) eðrileri ile x = a ve x = b
doðrularý tarafýndan sýnýrlanan bölgenin
alaný
x
y
y
K
−2
g(x)
A=
∫
2
x.dy =
−2
3
⎛y
⎞
=⎜
− 4y⎟
3
⎝
⎠
∫
2
−2
L
(y2 − 4)dy
a
3
2
−2
a
b
b
L
g(x)
3
⎛2
⎞ ⎛ ( − 2)
⎞
=⎜
− 4.2⎟ − ⎜
− 4.( − 2)⎟
3
3
⎝
⎠ ⎝
⎠
K
y
f(x)
b
a
= 8 − 16 = − 8 olup
x
L
A = − 8 = 8 br 2 dir.
g(x)
Yukarýdaki üç þekilde de görüldüðü gibi
taralý alan
Örnek 13
y = e x eðrisi ile y = 2 doðrusu ve oy ekseni
arasýnda kalan kapalý bölgenin alaný kaç
br 2 dir?
A lan =
Soruda istenilen
2
ki þekilde görülmektedir.
1
∫
1
x dy =
u = lny
ise
dv = dy
ise
∫
2
1
∫
2
1
y=ex
du = dy / y
v =y
2.
dy
lny dy = y.lny − y.
y
= ( y lny − y)
∫
b
a
⎣⎡ f(x) − g(x)⎦⎤ dx dir.
Ýki eðri arasýndaki alan þekildeki gibi ise
∫
1
⎣⎡ f(x) − g(x)⎦⎤ dx dir.
Eðer aþaðýdaki þekilde görüldüðü gibi bu
þeridin alt ve üst ucu fonksiyon deðiþtiriyorsa integral parçalanýr.
lny dy dir.
2
a
Yukarýdaki þekillerde taralý alanlarý bulurken oy eksenine parelel KL þeridi çizilir. Bu
þeridi kendisine parelel olarak kaydýrarak
bölgeyi taradýðýmýzda üst ucu hep y = f(x)
eðrisi üzerinde alt ucu da hep g(x) eðrisi
üzerinde deðiþmesi gerekir.
y=2
x
y = e x ⇒ lny = x dir.
2
A lan =
y
taralý alan yanda-
∫
b
Eðer f(x) – g(x)>0 ise mutlak deðerin içi
pozitif olduðundan formül
Çözüm
A=
x
x
8
⎛8
⎞ ⎛ −8
⎞ 8
= ⎜ − 8⎟ − ⎜
+ 8⎟ = − 8 + − 8
⎝3
⎠ ⎝ 3
⎠ 3
3
A=
f(x)
K
f(x)
y
K
L
= (2.ln2 − 2) − (1 ln1 − 1)
= 2.ln2 − 2 + 1 = ln 4 − 1
a
= ln 4 − lne
L
b
f(x)
c
K
= ln 4 / e br 2 bulunur.
g(x)
349
x
Belirli Ýntegralin Uygulamalarý
A=
∫
=
3.
∫
c
a
b
a
x2 − 4 = − 3
f(x) − g(x) dx
⎡⎣ g(x) − f(x) ⎤⎦dx +
∫
c
b
x 2 = 1 ise x = ∓ 1 dir. A lan ne gatif bölg e de,
⎡⎣ f(x) − g(x) ⎤⎦dx
x=f(y) ve x=g(y)
eðrileri ile y=m ve
A=−
1
∫ ⎡⎣⎢(x
y
=−
n
y=n doðrularý ile
sýnýrlý taralý böl-
m
genin alaný
A=
∫
n
m
∫
)
− 4 − ( − 3 ) ⎤ dx
⎦⎥
1
( x 2 − 1)dx =
−1
⎛
x3 ⎞
= ⎜x −
⎟
⎜
3 ⎟⎠
⎝
x
x=f(y)
x=g(y)
2
−1
= 1−
1
−1
1
∫
(1 − x 2 )dx
−1
1⎞ ⎛
1⎞
⎛
= ⎜ 1 − ⎟ − ⎜ − 1+ ⎟
3
3
⎝
⎠ ⎝
⎠
1
1
2 4
+ 1− = 2 − =
bulunur.
3
3
3 3
f (y) − g(y) dy dir.
Örnek 16
Örnek 14
y=
y=x 2 eðrisi ile y=4 doðrusu arasýnda kalan
kapalý bölgenin alaný kaç br 2 dir?
kalan kapalý bölgenin alaný kaç br 2 dir?
Çözüm
Çözüm
Ortak çözüm
y
yaparak kesim
Ortak çözüm yaparak kesim noktalarýný bulalým.
y=x2
y=4
noktalarýný
4
= −x + 5
x
bulalým.
x2
=4
2
−2
x
∫
2
−2
x2
(4 − x 2 )dx = 4x −
x3
3
4
y= x
y=−x+5
− 5x + 4 = 0
x = 1 ve x = 4
2
−2
⎛
23 ⎞ ⎛
( − 2)3 ⎞
= ⎜ 4.2 −
⎟ − ⎜ 4.( − 2) −
⎟
3 ⎠ ⎝
3 ⎠
⎝
= 8−
y
4 = − x 2 + 5x
x = ∓ 2 dir.
A=
4
eðrisi ile y=–x+5 doðrusu arasýnda
x
A=
∫
1
x
4⎛
1
4⎞
⎜ 5 − x − x ⎟ dx
⎝
⎠
⎛
⎞
x2
= ⎜ 5x −
− 4.ln x ⎟
⎜
⎟
2
⎝
⎠
8
8
16 32
+ 8 − = 16 −
=
3
3
3
3
4
4
1
⎛
⎞ ⎛
⎞
42
12
= ⎜ 5. 4 −
− 4.ln 4 ⎟ − ⎜ 5.1 − − 4 ln1⎟
⎜
⎟ ⎜
⎟
2
2
⎝
⎠ ⎝
⎠
Örnek 15
y=x 2 –4 eðrisi ile y=–3 doðrusu arasýnda
kalan kapalý bölgenin alaný kaç br 2 dir?
= 20 − 8 − 8 ln 2 − 5 +
Çözüm
= 7+
Ortak çözüm yaparak integralin sýnýrlarýný
tesbit edelim.
=
350
1
+0
2
1
− 8 ln 2
2
15
− 8 ln 2 br 2 bulunur.
2
Belirli Ýntegralin Uygulamalarý
Örnek 17
A=
y=x 2
eðrisi ile y=x+2 doðrusu arasýnda
kalan kapalý bölgenin alaný kaç br 2 dir?
∫
3
−2
Bu iki fonksiyonu ortak çözerek kesim noktalarýný bulalým ve grafik çizip aradýðýmýz
bölgeyi görelim.
, y=x+2
∫
b
a
−2
−1
[ f(x) − g(x) ]dx
f(x)=x 2 –x , g(x)=3x–x 2 eðrileri arasýnda
kalan kapalý bölgenin alanýný bulunuz.
Çözüm
de n
2
Ýki eðriyi ortak çözüp integral sýnýrlarýný
bulalým.
2
−1
f(x) = g(x) ⇒ x 2 − x = 3x − x 2 ise
8⎞ ⎛ 1
1⎞
⎛
= ⎜2 + 4 − ⎟ − ⎜ − 2+ ⎟
⎝
3⎠ ⎝ 2
3⎠
= 6+2−
2x 2 − 4x = 0
x = 0, x = 2 dir.
1 8 1
1
− − = 5−
2 3 3
2
∫
2
=
∫
2
=
∫
2
A=
9
=
br 2
2
Örnek 18
y 2 =x eðrisi ile y=x−6 doðrusu arasýnda
kalan kapalý bölgenin alaný kaç br 2 dir?
=
Bu iki fonksiyonun grafiklerini çizip aradýðýmýz bölgeyi görelim.
y 2 =y+6
0
0
⎡⎣g(x) − f (x) ⎤⎦dx
(3x − x 2 − x 2 + x)dx
4x 2
x3
−2
2
3
(4x − 2x 2 )dx =
2
0
8
br 2 dir.
3
Örnek 20
y
y=x − 6
3
f(x) fonksiyo-
y
nunun grafiði
(y+2)(y–3)=0
y=–2 , y=3
0
8⎞
16
⎛
= ⎜ 2.4 − 2. ⎟ − 0 = 8 −
3⎠
3
⎝
Çözüm
y 2 –y–6=0
11 125
br 2 dir.
=
6
6
Örnek 19
x
2
x2
x3
+ 2x −
A=
(x + 2 − x 2 )dx =
2
3
−1
∫
−2
9
8
9 8
+ 9 + 10 − = 19 + −
2
3
2 3
= 19 +
y=x2
2
(x+1)(x–2)=0
A=
3
y=x+2
x 2 –x–2=0
x=–1 , x=2
=
y
x 2 =x+2
y2
y3
+ 6y −
2
3
27 ⎞ ⎛ 4
8⎞
⎛9
= ⎜ + 18 −
−
− 12 + ⎟
⎝2
3 ⎟⎠ ⎜⎝ 2
3⎠
Çözüm
y=x 2
(y + 6 − y2 )dy =
x
yanda verilmiþtir. Buna göre;
−2
y2=x
∫
Yukarýdaki þekilden de biliyoruz ki y ekseni
arasýnda kalan alaný bulmalýyýz.
c
a
is e
351
f(x)dx = 10 v e
∫
c
b
a
∫
f(x)
b
c
a
f(x) dx = 18
f( x)dx 'in de ðer i nedir ?
c
Belirli Ýntegralin Uygulamalarý
Örnek 22
Çözüm
∫
c
a
|y|=4–x 2 eðrisi ile sýnýrlý kapalý bölgenin
alaný kaç br 2 dir?
f(x) dx = 18
þekilde görülen taralý alanlarýn toplamýdýr.
∫
c
a
f(x)dx = 10 ise üstteki pozitif alan ile alt-
Çözüm
taki negatif alanýn cebirs el toplamýdýr.
∫
∫
∫
b
a
c
a
c
a
∫
f(x)dx = A
c
b
y>0 ise y=4–x 2
y
y=x 2 –4
4
y<0 ise
f(x)dx = B → (B < 0)
Parabol simetrik
olduðundan taralý
f(x) dx = A − B = 18
2
−2
x
alan,
−4
f(x)dx = A + B = 10
A − B = 18 ⎫⎪
⎬
A + B = 10 ⎪⎭
yani
∫
c
b
A=4
A = 14
∫
⎛
x3 ⎞
(4 − x 2 )dx = 4 ⎜ 4x −
⎟
3⎠
⎝
2
0
2
0
⎡⎛
⎤
8⎞
16 64
br 2
= 4. ⎢⎜ 4.2 − ⎟ − (0)⎥ = 4.
=
⎝
⎠
3
3
3
⎣
⎦
B = −4
f(x)dx = − 4 bulunur.
bulunur.
Örnek 23
x<0
⎧⎪ x + 2 ,
f(x) = ⎨
⎪⎩ x 2 − 4x + 4 , x ≥ 0
Örnek 21
Yanda grafiði verilen
y=x2+2x
f(x) fonksiyonu, x=2
fonksiyonunun grafiði ile ox ekseni arasýnda kalan kapalý bögenin alaný kaç br 2 dir?
doðrusu ve x ekseni
arasýnda kalan taralý
2
−2
alan kaç br 2 dir?
x
Çözüm
Soruda istenilen
y
alan yandaki þekil-
∫
∫
2
−2
2
−2
2
de görülmektedir.
Çözüm
Buna göre taralý
f(x) dx = A 1 + A 2
2
x + 2x dx = −
⎛ x3
⎞
A = −⎜
+ x2 ⎟
⎝ 3
⎠
∫
0
−2
alan A = A 1 + A 2 ,
2
(x + 2x)dx +
⎛ x3
⎞
+⎜
+ x2 ⎟
−2
⎝ 3
⎠
0
∫
2
0
−2
2
A 1 dik üçgenin alaný olup,
2
(x + 2x)dx
A=
1
.2. 2 +
2
2
0
⎡
⎤
⎛ 8
⎞ ⎤ ⎡⎛ 8
⎞
= − ⎢0 − ⎜ − + 4 ⎟ ⎥ + ⎢⎜ + 4 ⎟ − 0 ⎥
3
3
⎝
⎠
⎝
⎠
⎣
⎦ ⎣
⎦
∫
2
0
2
1
(x − 2)3
3
= 2+
1 ⎡
. (0) − ( − 2)3 ⎤
⎦
3 ⎣
1
8
.8 = 2 +
3
3
4 20
+
3 3
= 2+
=
24
= 8 br 2
3
=
352
(x − 2)2 dx
= 2+
=
14
br 2
3
A1 A2
0
x
Belirli Ýntegralin Uygulamalarý
Örnek 24
Çözüm
Yandaki þekilde
Soruda istenilen
rilmiþtir.
y
verilenlere göre
y=x2
2
taralý alan kaç
br 2 dir?
y2 3
+
2 2
2y2 =
1
y= x
bölge
þekilde
x=2y2
y
1
2x=y2 + 3
4y2 = y2 + 3
3y2 = 3
2
Çözüm
Soruda verilen
A 3 gibi üç par-
y=x2
çaya bölelim.
A1 A2
1
∫
A2 =
0
∫
2
1
x 2 dx =
x3 1
3
1
dx = ln x
x
0
2
1
=
A=2
y= 1
x
1
olsun.
A1 =
Paraboller simetrik olduðundan,
A3
A=A 1 +A 2 +A 3
2
∫
1
1
0
Örnek 26
Þekilde taralý alan
y
integralle nasýl
2
ifade edilebilir?
x
2
−2
2
1
−2
y=−x
Çözüm
⎛2
⎞ ⎛2
⎞
= ⎜ 23 / 2 − ln2⎟ − ⎜ − 0⎟
⎝3
⎠ ⎝3
⎠
Merkezi orjinde yarýçapý 2 birim olan bir
çember denkleminin ikinci bölgedeki
parçasýný fonksiyon olarak yazabiliriz.
2
2
2 2 − ln2 −
3
3
A = A1 + A 2 + A 3 oldu ðundan
=
⎞
6
⎛ 1+ 9 − 4 ⎞
= 2. ⎜
= 2. = 2 bulunur.
⎟
⎝
⎠
6
6
= ln2 − ln1 = ln2
1⎞
− lny
⎜⎝ y − y ⎟⎠ dy = 1
+1
2
=
2
⎡⎛ 1 3 2 ⎞
⎤
= 2 ⎢⎜ + − ⎟ − (0)⎥
⎣⎝ 6 2 3 ⎠
⎦
1
1
−0 =
3
3
1
+1
2
y
=
3
0
x
1
1
⇒ x=
y=
x
y
A3 =
1 ⎛ y2
∫ ⎜⎝ 2 + 2 − 2y ⎟⎠ dy
⎛ 1 y3 3
y3 ⎞
= 2. ⎜ .
+ .y − 2. ⎟
3⎠
⎝2 3 2
y = x2 ⇒ x = y
2⎛
−1
y = ±1
2
x
3
y2 = 1
y
bölgeyi A 1 , A 2 ,
1
x
göste-
A=
1
4
2
+ ln2 +
2 − ln2 −
3
3
3
=
4 2 1 4 2 −1
− =
bulunu r.
3
3
3
∫
∫
0
− 2
0
⎡ 4 − x 2 − ( − x)⎤ dx
⎢⎣
⎥⎦
denklem
⎛ 4 − x 2 + x ⎞ dx dir.
⎠
x 2 + y2 = 4,
− 2⎝
y = 4 − x2
y = −x
x2 + x2 = 4
2x 2 = 4
Örnek 25
x2 = 2
x = 2y2 ve 2x = y2 + 3 eðrileri ile sýnýrlý kapalý
bölgenin alaný kaç br 2 dir?
x=± 2
353
Belirli Ýntegralin Uygulamalarý
y
y
3.
x
x
−r
Ýki eðri arasýnda kalan alanýn ox ekseni
etrafýnda 360° döndürülmesinden elde
edilen cismin hacmi
r
y
y = r2 − x 2
r
g(x)
y = − r2 − x 2
f(x)
y
r
y
x
a
x
−r
−r
x = r 2 − y2
Vx = π
x = − r 2 − y2
4.
2. HACÝM HESABI
1.
∫
b
a
x
b
⎡ f(x)2 − g(x)2 ⎤ dx dir.
⎣
⎦
y=f(x) eðrisi ile y=t , x=a , x=b doðrularý
tarafýndan sýnýrlanan bölgenin y=t doðrusu
etrafýnda döndürülmesiyle meydana gelen
dönel cismin hacmi
y=f(x)
y
y=f(x)
a
x
b
y=t
a
y=f(x) denlemiyle temsil edilen eðrinin
[a, b] aralýðýna ait parçanýn ox ekseni etrafýndan döndürülmesiyle elde edilen cismin
hacmi
Vx = π
∫
b
a
f(x)2 dx = π
2.
∫
b
a
Vt = π
y=x 2 eðrisi ile x=2 doðrusu ve x ekseni
arasýnda kalan alanýn ox ekseni etrafýnda
döndürülmesinden oluþan cismin hacmi
kaç br 3 dür?
d
f(a)=c
f(b)=d
Çözüm
c
a
b
y
x
Ayný þekilde y=f(x) denklemiyle temsil
edilen [c, d] aralýðýna ait parçanýn oy
ekseni etrafýnda döndürülmesiyle meydana
gelen cismin hacmi
Vy = π
∫
c
f(y)2 dy = π
∫
c
( f(x) − t )2 dx dir.
Örnek 1
y=f(x)
d
a
y2 dx
y
d
∫
b
x
b
y=x2
∫
2
=π
∫
2
=π
x5
5
Vx = π
x
x=2
x 2 dy
Vx = π
354
0
0
y2 dx
x 4 dx
2
0
32
br 3 dür.
5
Belirli Ýntegralin Uygulamalarý
Örnek 4
Örnek 2
y=e x
eðrisi ve x=1 doðrusu ve eksenler
arasýnda kalan bölgenin ox ekseni etrafýnda döndürülmesinden oluþan cismin
hacmi kaç br 3 dür?
f(x)=
x2
eðrisine x=1 apsisli noktadan çi2
zilen teðeti ile eksenler arasýndaki düzlemsel bölgenin oy ekseni etrafýnda döndürül-
Çözüm
mesinden oluþan þeklin hacmi kaç br3 dür?
Vx = π
=π
=π
=
∫
∫
∫
1
0
1
0
1
0
Çözüm
y
y2 dx
Meydana gelen düzlemsel bölgenin alanýný
þekil çizerek görelim.
y=ex
(e x )2 dx
Önce f(x) in x=1 noktasýndaki teðetini bulalým.
e2x dx
π 2x
e
2
1
0
=
x
1
− 2x .2
4
=−
x4
x3
f '(x) =
π 2 π 0 π 2
e − e = (e − 1) br 3
2
2
2
y
6
Eðim=m=f ‘(1)=–4
x=1
için
y=−4x+6
f(1)=2
A(1 , 2)
Teðetin denklemi
x
y–y 1 =m(x–x 1 )
3
−
2
y–2=–4(x–1)
Örnek 3
3
2
y=–4x+6
y=cosx eðrisinin x=0 , x=π doðrularý ve x
ekseni arasýnda kalan alanýn yine ox ekseni etrafýnda döndürülmesinden meydana
gelen cismin hacmi kaç br 3 dür?
I. Yol:
Þekilden de görüldüðü gibi taralý alanýn oy
ekseni etrafýnda döndürüldüðünde meydana gelen þekil bir konidir ve koninin hacmini bulalým.
Çözüm
2
π
2
y=cosx
π
V=
x
0
=
0 ve π/2 arasýndaki alan, π/2 ile π arasýndaki alana eþittir. x ekseni etrafýnda dönmesinden oluþan hacimlerde eþit olacaðýndan;
Vx = 2 π
Vx = 2 π
∫
π/2
∫
π/2
0
0
y2 dx = 2 π
∫
π/ 2
0
1
⎛
⎞
= π ⎜ sin2x. + x ⎟
⎝
⎠
2
π/2
0
∫
π/ 2
0
3
=
π .9.6
4.3
9π
br 3 bulunur.
2
II. Yol:
Vy = π
c os 2 x dx
c os 2x + 1
dx = π
2
π r2 .h
=
3
⎛ 3⎞
π . ⎜ ⎟ .6
⎝ 2⎠
( c os 2x + 1)dx
⎡⎛
⎤
π 1 π⎞
= π ⎢⎜ sin2 . + ⎟ − (0) ⎥
⎝
⎠
2
2
2
⎣
⎦
π π2
=π =
br 3 bulunur.
2
2
355
∫
6
0
x 2 dy = π
6
∫
6 ⎛ y − 6⎞ 2
0
⎜⎝ − 4 ⎟⎠ dy
=
π
16
=
⎞
π ⎛ y3 12y2
−
+ 36y⎟
⎜
16 ⎝ 3
2
⎠
=
⎞
π ⎛ 63
− 6.62 + 36.6⎟ − (0)
⎜
16 ⎝ 3
⎠
∫
0
(y2 − 12y + 36)dy
6
0
Belirli Ýntegralin Uygulamalarý
=
π
(72 − 63 + 63 )
16
x y
+ = 1 ⇒ x r + hy = hr
h r
=
π .72 9 π
br 3 bulunur.
=
16
2
Burdan y = r −
xr
bulunur.
h
bu doðru altýnda ve eksenler arasýndaki kapalý bölgeyi ox ekseni etrafýnda döndürdüðümüzde meydana gelen þekil bir konidir.
Örnek 5
y=5–x 2 parabolü ile y=2 , x=0 ve x=1
doðrularý tarafýndan sýnýrlanan bölgenin
y=2 doðrusu etrafýnda döndürüldüðünde
meydana gelen cismin hacmini bulunuz.
Buna göre;
Vx = π
xr ⎞
⎜ r − h ⎟ dx
0⎝
⎠
∫
Çözüm
=π
Soruda istenilen
y
5
kapalý bölge þe-
=π
kilde gösterilmiþtir. Buna göre,
2
h⎛
∫
h⎛
0
∫
⎜ r2 −
⎜
⎝
2x r 2 x 2r 2
+
h
h2
2x 2 r 2 x 3r 2
−
⎜ r2 x −
⎜
2h
3h2
⎝
h⎛
0
y=2
x
V=π
∫
0
(5 − x 2 − 2)2 dx = π
=π
∫
1
0
1
2
0
Vx =
(9 − 6x 2 + x 4 )dx
⎛
x3 x5 ⎞
= π ⎜ 9x − 6
+
⎟
3
5 ⎠
⎝
1
π .r2 h
br 3 bulunmu º olur.
3
Çözüm
∫
3
∫
3
Vy = π
Örnek 6
koninin
=π
hacmini
1
1
Çözüm
y
h ve taban yarýçapýna r diyelim ve |AB|
doðrusunun denklemini bulalým.
A(0, r)
y
x 2 dy
y=3
(y − 1)dy
⎛ y2
⎞
= π⎜
− y⎟
2
⎝
⎠
Koninin yüksekliðine
0
3
y=x 2 +1 eðrisi y=3 doðrusunun sýnýrladýðý
düzlemsel bölgenin oy ekseni etrafýnda
döndürülmesinden oluþan cismin hacmini bulunuz.
1 ⎞ 36 π
⎛
br 3
= π.⎜ 7 + ⎟ =
⎝
5⎠
5
yardýmýyla
2
Örnek 7
0
⎡⎛
⎤
1⎞
= π ⎢ ⎜ 9 − 2 + ⎟ − (0)⎥
⎝
⎠
5
⎣
⎦
Ýntegral
bulunuz.
h
⎛
r2 h ⎞
= π ⎜ r2 h − r2 h +
⎟
⎜
3 ⎟⎠
⎝
∫ (3 − x ) dx
2
⎞
⎟
⎟
⎠
⎡⎛
⎤
r
r h ⎞
.
= π ⎢⎜ r 2 h − .h2 +
⎟ − (0)⎥
2
⎜
⎟
h
⎢⎣⎝
⎥⎦
h 3 ⎠
2
1
⎞
⎟ dx
⎟
⎠
3
1
1
⎡⎛ 3 2
⎞ ⎛ 1 ⎞⎤
= π ⎢⎜
− 3⎟ − ⎜ − 1⎟ ⎥
⎢⎣⎝ 2
⎠ ⎝ 2 ⎠ ⎥⎦
x
B(h, 0)
⎡ 3 1⎤
= π . ⎢ + ⎥ = 2π br 3 bulunur.
⎣2 2⎦
A(0 , r) , B=(h , 0)
noktalarý verildiðine göre,
356
x
ALIÞTIRMALAR 4
Belirli Ýntegralin Uygulamalarý
1. Yandaki þekilde A1
ve A 2 bulunduklarý
bölgenin alanlarýný
gösterdiðine göre,
A2 – A1= ?
7. y = 2 – x2 ile y = x2 eðrileri tarafýndan sýnýr-
y=x2
A2
lanan kapalý bölgenin alaný kaç br2 dir?
C e v ap :
A1
2
8
3
x
8. f(x) = lnx eðrisinin x = e noktasýndan çizilen te-
C e vap : 8 / 3
ðeti ile x ekseni ve f(x) = lnx eðrisi arasýnda
kalan kapalý bölgenin alaný kaç br2 dir?
2. f (x) = 4 – 1 . x2 eðrisi ile x + y = 4 doðrusu ara-
C e v ap :
4
e−2
2
sýnda kalan kapalý bölgenin alaný kaç br2 dir?
9. Yandaki þekilde taralý alan 1 br 2 olduðuna göre,
a’nýn deðeri kaçtýr?
8
C e v ap :
3
3. y = lnx ile y = –lnx eðrileri x = c (c>1) doðrusu
x
a
arasýnda kalan kapalý bölgenin alaný 2c+2 br2
olduðuna göre, c’ nin deðeri kaçtýr?
C e vap : 3 3
C e vap : e 2
10. y = lnx eðrisi ve x = e doðrusu ile ox ekseni
arasýnda kalan kapalý bölgenin ox ekseni etrafýnda döndürülmesinden elde edilen cismin hacmi
kaç br3 dür?
4. y = x2 – 2x eðrisi x = 0 ve x = 3 doðrusu ve ox
ekseni arasýnda kalan kapalý bölge kaç br2 dir?
C e v ap :
y=(x−a)2
C e vap : π(e − 2)
8
3
11. y = x eðrisi y = 2 doðrusu ve oy ekseni arasýnda kalan kapalý bölgenin oy ekseni etrafýnda
döndürülmesinden oluþan cismin hacmi kaç br3
dür?
5. y = x3 –1 eðrisi y = 3 doðrusu ve oy ekseni
arasýnda kalan alan kaç br2 dir?
C e v ap :
32 π
5
C e v ap : 3 3 4
12. y = x3 eðrisi y = 2 , y = 0 doðrularý ve oy ekseni
arasýnda kalan kapalý bölgenin alaný oy ekseni
etrafýnda döndürülmesinden elde edilen cismin
hacmi kaç br3 dür?
6. y = lnx eðrisi ox ekseni ve x = e doðrusu
arasýnda kalan kapalý bölgenin alaný kaç br2
dir?
C evap :
C e vap : 1
357
6π 3
. 4
5
TEST 4
1.
Belirli Ýntegralin Uygulamalarý
Yandaki taralý
alan kaç br2 dir?
5.
y=x3
Yandaki taralý
alan kaç br2 dir?
y
y=x3
−2
1 2
A)
2.
15
4
B)
14
3
C)
13
2
D)
11
4
E)
Yandaki taralý
alan kaç br2 dir?
10
4
6.
y=sinx
3.
1
2
B) 1
C)
2
2
D)
3
3
C) 7
D) 8
E) 9
Yandaki taralý
alan kaç br2 dir?
y=x
y=x2−4x+4
x
E)
A) 2
3
2
7.
y
Yandaki taralý
alan kaç br2 dir?
B) 6
x
π π
6 2
A)
A) 5
x
2
x
y=ex
B) 5
C) 12
D) 9 / 2
E) 64 / 3
Yandaki taralý
alan kaç br2 dir?
y=x2−2x
1
x
1
A) 1
B) e
D) e − 1
4.
C) 2e + 1
E)
Yandaki taralý
alan kaç br2 dir?
y=6x−x2
x
A)
e −1
2
8.
y=2
75
4
B)
64
3
C)
33
2
D)
Yandaki taralý
alan kaç br2 dir?
17
3
E)
13
3
y
y3=x2
x
y=2−x2
x
y=lnx
A) e 2
B) 2e + 1
D) e2 + 1
C) 3e 2 + 1
A)
E) e 2 − 1
358
10
3
B)
18
15
C)
32
15
D)
27
14
E)
26
11
Belirli Ýntegralin Uygulamalarý
TEST 4
9.
Yandaki taralý alan
kaç br2 dir?
14. x = –2 – y + y2 eðrisi ile y ekseni arasýnda
kalan bölgenin alaný kaç br2 dir?
y
3
2
A) 1
B) 2
C) 5 / 3
D) 4 / 3
A) 3
x
1
6
B)
C)
y=x
2
9
D)
7
3
8
3
D)
E)
9
2
15. f(x) = x2 – 2x ve g(x) =– x2 + 2x eðrileri
arasýndaki alan kaç br2 dir?
y
y=ax2
x
1
2
C)
E) 8 / 3
10. Þekildeki taralý alan
6 br2 ise a ’ nýn deðeri
kaçtýr?
A)
B) 4
3
10
E)
11. Yandaki taralý
alan kaç br2 dir?
A)
5
4
7
2
B)
C)
8
3
D)
9
4
E)
11
3
4
7
16. y = cosx eðrisi ile x = π / 2 doðrusu ve eksenler
arasýndaki kapalý bölgenin ox ekseni etrafýnda
döndürülmesinden oluþan cismin hacmi kaç br3
dür?
y
y=x2
(2, 4)
A)
x
π2
2
B)
π2
4
C)
π
8
D)
π
2
E)
π
4
−4
A) 2
B) 8
C) 9 / 2
D) 16 / 3
E) 8 / 3
12. Þekildeki taralý alan kaç
br2 dir?
17. f(x) = –x2 , g(x) = x2 – 2 eðrileri arasýnda kalan
alanýn ox ekseni etrafýnda döndürülmesinden
elde edilen cismin hacmi kaç br3 dür?
A)
π
2
B)
π
6
C)
π
12
D)
8π
3
E)
16 π
3
y=x
y=−x
y=x2
x
18.
A)
1
3
B)
1
6
C)
4
3
D)
5
3
E)
5
6
A) 2
3
C)
2
4
D)
3
∫
dx
,
x
f(1)=2 olmak üzere f(x) eðrisi x ekseni ve x =e
doðrusu arasýnda kalan bölgenin yine ox ekseni
etrafýnda döndürülmesinden oluþan cismin
hacmi kaç br3 dür?
13. y = 2x – x2 parabolü ve x ekseni arasýnda
kalan alan kaç br2 dir?
2
B)
3
f(x) =
A) 2
5
E)
2
B) 2e − 1
D) e − 4
C) e − 2
E) − 3e − 2
Cevaplar: 1-A 2-E 3-D 4-E 5-D 6-D 7-B 8-C 9-A 10-B 11-E 12-A 13-D 14-E 15-C 16-B 17-E 18-B
359