AMPERMETRE VE VOLTMETRENİN DEVREYE

D.NO: 1
DENEY ADI : AMPERMETRE VE VOLTMETRENİN DEVREYE BAĞLANMASI
ÖĞR. ADI ve NO :
TARİH : .. /.. / 2005
G.NO :
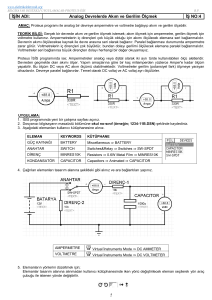
D. AMACI : Ampermetre ve Voltmetrenin devreye bağlanması , direnç ve güç ölçümü , hatalar
TEMEL BİLGİ :
Ampermetreler, bir devreden geçen akım şiddetini ölçeler. Ampermetreler, akım şiddeti ölçülecek devreye seri
bağlanırlar. Ampermetre devreye paralel bağlanacak olursa, iç direnci çok küçük olduğundan üzerinden büyük akım
geçer ve alet yanar. Devre, ampermetre üzerinden kısa devre olur.
Gerilim, iki nokta arasındaki potansiyel farkıdır. Bu iki nokta arasındaki potansiyel farkını ölçmek için voltmetre, bu iki
noktaya bağlanmalıdır. Voltmetreler, yanlışlıkla devreye seri bağlanacak olursa, iç dirençleri büyük olduğundan
devre direncini önemli ölçüde arttırırlar. Direnç büyük olunca, geçen akım küçük olur. Bu küçük akım, alıcının normal
gücü ile çalışmasına yetmez. Dolayısıyla devre normal çalışamaz. Bu nedenle voltmetreler hiçbir zaman devreye
seri olarak bağlanamazlar.
A – AMPERMETRE ÖNDE BAĞLAMA : Ampermetre önce bağlamada, ampermetre ölçtüğü akım, voltmetre ve
dirençten geçen akımların toplamıdır. Bu ölçmede voltmetreden geçen akım dirençten geçen akıma nazaran çok
küçük olmalı ki, ölçmede en az hata olsun. Direnç akımının voltmetre akımına nazaran büyük olması, direnç
değerinin küçük olması demektir. Bu nedenle değeri küçük olan dirençlerin ölçülmesinde, ampermetreyi önde
bağlayarak ölçme yapılmalıdır.Küçük direnç demek büyük akım çeken direnç demektir. Büyük akım çeken direnç ise
gücü büyük olan alıcı demektir. O halde bu usulle küçük direnç ve büyük güçler ölçülebilir sonucu ortaya çıkar.
R
Mp
i
ix
A
Px
iv
V
U
X
X
X
X
Devrenin gücü : P=U.I
Alıcının gücü : Px=U.Ix
Akım kanununa göre : I=Iv + Ix buradan Ix = I - Iv çekilip Px de yerine konursa alıcın gücü ( gerçek güç) ortaya
çıkar.
Px= U.Ix = U.( I - Iv ) = U.I – U. Iv olur. Iv =U / Rv olduğundan yerine koyarsak ;
2
Px= U.I – U. Iv = U.I – U. (U / Rv) = U.I – U / Rv
2
Ölçmedeki hatayı U / Rv
meydana getirmektedir . Bunu küçültmek tek yolu Rv direncinin çok büyük olmasıyla
gerçekleşebilir. Bu da bize Rx << Rv olması sonucunu ortaya çıkarır. Bu ise bize iki temel sonucu vermektedir.
1.
Rx << Rv olması KÜÇÜK DEĞERDE DİRENÇ ölçümünü,
2
2
( Iv << Ix ve Px= Ix .Rx = U /Rx ) ve
Rx << olması ise , Büyük akım yük akımı Ix
dolayısıyla BÜYÜK DEĞERDE DİRENÇLERİN ölçümünün
gerçekleşebileceği sonucunu çıkarır.
2.
1
hyön = −
HATA DEĞERİ ise ;
Rx`
ile belirlenir.
Rv
B – AMPERMETREYİ SONRA BAĞLAMA : Voltmetre önce bağlamada, ampermetre de okunan akım değeri,
dirençten geçen akım gerçek akımdır. Ancak, voltmetrede okunan gerilim değeri, direnç ve ampermetredeki gerilim
düşümlerinin toplamı olmaktadır. Ampermetre direnci çok küçük olduğundan, üzerindeki gerilim düşümü de küçük
olur. Ölçme esnasında bu gerilim düşümü, direnç üzerindeki gerilim düşümüne oranla ne kadar küçük olursa, deney
sonundaki hata payı da o kadar azdır. Hesaplamada bulunan direnç değeri de o kadar gerçeğe yakındır. Bu
bağlantıda, voltmetrenin önde bağlanması ile büyük değerli dirençlerin ölçülmesinde daha kesine sonuçlar alınır. Bu
ise akımın küçük olması gerektirir. Akının küçük olması demek de, gücün küçük olasını sağlar. O halde bu
bağlama ile ; büyük direnç ve küçük gücün ölçümü gerçekleşir.
R
Mp
A
V
Px
U
X
X
X
X
Devrenin gücü : P=U.I
Alıcının gücü : Px=Ux.I
Gerilim kanununa göre ; U = Ua + Ux olup buradan Ux = U - Ua çekip Px de yerine koyarsak ;
Px=Ux.I =( U - Ua ).I = U.I – Ua.I bulunur. Burada ; Ua.= I.Ra olduğuna göre eşitlikte yerine konursa ,
Px= U.I – Ua.I
2
= U.I – I . Ra
bulunur. Gerçek Px
sarfiyati en küçük değere indirebilmek
Ra
direnci
2
değerini etkileyen ampermetrenin sarfiyatıdır. (I . Ra ) bu
sabit olduğundan
sadece I
akını
küçük olmasıyla
gerçekleşebilir. Vede ölçüm hatasının küçük olabilmesi için Ra << Rx olmak zorundadır. Bu ise bize iki temel
sonucu vermektedir.
1. Ra << Rx olması BÜYÜK DEĞERDE DİRENÇ ölümlerini,
2
2
2. Ra << Rx olması I<< olmasını sağlar buda GÜCÜN KÜÇÜK olmasını Px= I .Rx = U /Rx yanı küçük
güçte güç ölçümlerini, bu yöntemle gerçekleştirebiliriz.
Yaptığımız hatayı ise ;
2
hyön =
Ra`
bulabiliriz.
Rx
KULLANILAN ALETLER:
123456-
Ampermetre
Voltmetre
Kablolar
Gerilim Kaynağı
Sigortalı Şalter Tablosu
4 x 100W ( paralel bağlı ) ampul + 2000 W ısıtıcı
DENEY YAPILIŞI ve İŞLEM BASAMAKLARI :
AMPERMETRE ÖNCE BAĞLAMA :
1. Gerekli ölçü aletleri ve diğer elemanları özellikleri ile tespit ediniz.
2. Şekilde görülen bağlantı yapınız.
3. Bağlantılar kontrol ediniz
4. Ra direncine bir değeri tespit edilip ve her değere bağlı olarak diğer ölçü aletlerini değerlerini okunarak not
ediniz
5. Çeşitli güçte lambalar yakılarak her defasında ölçü aletlerinin değerlerini yazınız.
VOLTMETRE ÖNCE BAĞLAMA :
1. Gerekli ölçü aletleri ve diğer elemanları özellikleri ile tespit ediniz.
2. Şekilde görülen bağlantı yapınız.
3. Bağlantılar kontrol ediniz.
4. Ra direncine bir değeri tespit edilip ve her değere bağlı olarak diğer ölçü aletlerini değerlerini okunarak not
ediniz
5. Çeşitli güçte lambalar yakılarak her defasında ölçü aletlerinin değerlerini yazınız.
DEVRE MONTAJ ŞEMASI :
R
Mp
R
Mp
i
ix
A
V
a). Ampermetre önce bağlama.
A
Px
iv
U
X
X
X
X
V
Px
U
X
X
X
X
b). Ampermetre sonra bağlama.
3
ÖLÇÜLEN DEĞERLER :
1. Bağlama için : (Lambalar Paralel)
Önce Bağlama:
Sonra Bağlama:
U=
U=
I=
I=
Rv= 50 K
Rv= 50 K
Ra=1 Ohm
Ra=1 Ohm
I=
I=
Rv= 50 K
Rv= 50 K
Ra=1 Ohm
Ra=1 Ohm
I=
I=
Rv= 50 K
Rv= 50 K
Ra=1 Ohm
Ra=1 Ohm
2. Bağlama İçin : (Lambalar Seri)
Önce Bağlama:
Sonra Bağlama:
U=
U=
3. Bağlama İçin : (Isıtıcı)
Önce Bağlama:
Sonra Bağlama:
U=
U=
HESAPLAMALAR :
SONUÇ :
No: Bağ.Şekli:
1.
2.
3.
4
Önce
Sonra
Önce
Sonra
Önce
Sonra
U
(v)
I
(A)
Px
(W)
Rx
(ohm)
Ra
Rv
(ohm) (ohm)
1 Ohm 50 K
1 Ohm 50 K
1 Ohm 50 K
1 Ohm 50 K
1 Ohm 50 K
1 Ohm 50 K
Hyö
(%)
Açıklama
Lambalar
Paralel
Lambalar
Seri
Isıtıcı
D.NO: 2
DENEY ADI : WESTON KÖPRÜSÜ İLE DİRENÇ ÖLÇÜMÜ
TARİH: .. / .. / 2005
ÖĞR. ADI ve NO :
G.NO :
D. AMACI : Westorn tipi ohmetre çalışma prensibinin öğrenilmesi, köprü denge konumunun ispatı.
TEMEL BİLGİ : Ohmetreler, direnci doğrudan ölçen aletlerdir. Çeşitli tipleri olmakla birlikte günümüzde en çok
kullanılan Weston tipi ohmetrelerdir. Bu tip ohmetrelerde biri bilinmeyen ( Rx ) üçü bilinen ( R1, R2, R3 )olmak üzere
dört direnç vardır. İlk önce aşağıdaki montaj şemasında 1 no’lu anahtar kapatılır. 1 no’lu anahtar kapalı iken 2 no’lu
anahtar kapatılırsa genellikle denge olmayacağından galvanometreden bir akım geçer. Dirençleri ayarlamak suretiyle
galvanometreden akım geçirmek mümkündür. Bu durumda galvanometre sapmaz. Galvanometrenin sapmaması
galvanometre üzerinde bir potansiyel fark olmaması demektir. O halde R2 direnci üzerindeki potansiyel fark R1
üzerindeki potansiyel farkına eşit demektir. Buna göre;
i1 . R1 = i2 . R2
i1 . Rx = i3 . R3
her iki denklemi taraf tarafa bölersek ;
i1 .R1 i2 .R2
R
R
R
=
⇒ 1 = 2 ⇒ R x = 1 .R3
i.R x i2 .R3
R x R3
R2
olur.
İŞLEM BASAMAKLARI :
1.
2.
3.
4.
5.
6.
7.
Westorn ohmetre incelendi.
Ölçmek istenilen direnç alet üzerinde Rx yazılı uçlara bağlandı.
Önce 1 no’lu anahtar kapatıldı.
1 no’lu anahtar 2 no’lu anahtarda kapatıldı (2 no’lu anahtar butondur).
R3 direncini ayar alanının sonuna kadar yavaş döndürüldü ve dengeleme ayarlanmaya çalışıldı.
Denge sağlanmadığı zaman R1/R2 arası değiştirildi. R3 direnci ile tekrar denge arandı.
R1/R2 oranının bütün kademeleri denendiği halde denge sağlanmadığı zaman ölçmek istenilen direnç ölçü
aletinin ölçme sınırı direncinde olduğu unutulmamalıdır.
8. Denge sağlandığı zaman alet üzerinde R1/R2 oranı ile R3 direncinin değeri ile çarpıldı ve ölçmek istenilen
direncin değeri hesaplanmaya çalışıldı.
DEVRE MONTAJ ŞEMASI :
R1
Rx
I1
G
2
I2
R3
R2
I
1
a
b
SONUÇ : Çeşitli tipleri olmakla birlikte, günümüzde en çok kullanılmakta olan direnç ölçme köprü türüdür. Genelde
orta ölçekte dirençler ( 10 –100k ) doğru bir şekilde ölçülebilmektedir.
5
D.NO: 3
DENEY ADI : ÖZ İNDÜKLEME KATSAYISI VE KAPASİTE ÖLÇÜMLERİ
ÖĞR. ADI ve NO :
TARİH : .. /.. / 2005
G.NO :
D. AMACI :Temel devre elemanlarından endüktansın (bobin) ve kapasitansın (Kondansatör) ölçümünün öğrenilmesi
TEMEL BİLGİ : Doğru akım ve Alternatif akım devrelerinde üç çeşit devre elemanı vardır. Bunlar direnç, bobin ve
kondansatördür.
Bobinler, kapasiteden gelen akımın kompanza edilmesi, radyo frekansı, güç devresi (kaynağı), ses kartı vb.
devrelerde parazitlerin girmesini engellemede, ayar devreleri gibi çok çeşitli uygulamalarda..
Kondansatörler ise, doğrultma devreleri, filtre devreleri, AC ve DC birleştirici devreleri, AC ve DC ayırıcı
devrelerinde , ayar devrelerinde frekans süzme, bilgisayar RAM’larında gibi sayısız uygulama alanlarında
kullanmaktayız.
Direnç bulunan AC devreler, DC devreler gibi çözülürler. Bobin ve kondansatör bulunan alternatif akım devrelerinin
çözümünde ise “reaktans” veya “reaktif direnç” adı verilen bir cins direncin bilinmesi gerekir. Reaktans , bobin ve
kondansatörlerin alternatif akıma karşı gösterdikleri dirençtir.
Bu direncin ölçülmesi ile bu elemanlardan bobinin öz indükleme katsayısını ve kapasitenin (değerini) sığasını
hesaplama ile bulabiliriz.
Bobin:
Bobinler bir makara üzerine sarılan teller ile meydana getirildiğinden, bu tellerin bir direnci vardır. Bu dirence
bobinin omik direnci adı verilir. Çok küçük değerlerde ise ihmal edilebilir ve bu tür omik direnci sıfır olan devrelere
SAF ENDÜKTİF DEVRE adı verilir. Bu kabulle bobin uçlarında yalnız akımın değişmesinden dolayı meydana
gelen emk görülür. Ve bobin akımı bu emk dan 90 derece geridedir.
Ohm kanununa göre, bir bobinin gerilimi ile akımının etkin değerlerinin oranı ( U / I ) sabittir.Ve bu oran alternatif
akıma karşı bobinin gösterdiği zorluğu temsil eder. Yalnız bu zorluğa direnç yerine “ENDÜKTİF REAKTANS” adı
verilir.
XL : endüktif reaktans
(ohm)
R : bobin telinin direnci (ohm) (ihmal edilebilir)
ZL : bobinin toplam direnci (ohm)
L : bobinin endüktansı (henry)
ZL2 = R2 + XL2
R ≈ 0 ise ,
XL=ω.L
ZL = XL = UL / IL
Kondansatör :
Bobinde olduğu gibi kondansatörde de içinden geçen akımla geçen akım ile uçları arasında 90 derecelik faz farkı
bulunmaktadır. Fakat faz farkının yönü bobinin tersinedir. Yani akım, gerilimden 90 derece, ileri fazdadır.
Kondansatörün uçların çok küçük omik direnç görülmekle birlikte, bu dikkate alınmaz. Kondansatörün alternatif
akıma geçişe karşı gösterdiği zorluğa ise “KAPASİTİF REAKTANS” adı verilir.
6
Xc : kapasitif reaktans
(ohm)
R : kondansatörün omik direnci (ohm) (ihmal)
ZC : kondansatörün toplam direnci (ohm)
C : kondansatörün kapasitesi (farad))
ZC2 = R2 + XC2
R ≈ 0 ise ,
XC=1 / ω.C
ZC = XC = UC / IC
KULLANILAN ALETLER:
1- Ampermetre
2- Voltmetre
3- Kablolar
4- Gerilim Kaynağı
5- Sigortalı Şalter Tablosu
6- Bobin (balast)
7- Kondansatör
DENEY YAPILIŞI ve İŞLEM BASAMAKLARI :
ÖZ İndükleme katsayısının ölçülmesi :
1- Deney bağlantı şeması :
2- Bobinin ilk önce ohmetre yardımıyla omik direncinin ölçülmesi,
3- Bobinin alternatif akımdaki ZL direncinin , devrede ölçülen akım ve gerilim bilgileri ile hesaplanması,
ZL = U / I
hesaplanıp, yandaki formülde yerine konulursa
ZL2 = R2 + XL2
,
XL=ω.L
4- ZL2 = R2 + XL2 ve XL=ω.L formülleri yardımıyla öz indükleme katsayısını veren formül yardımıyla bobin öz
indükleme değerinin hesaplanması ,
L= √( ZL2 - R2 ) /2.∏.f
Henry bulunur.
7
5-Bobinin omik direnci ile endüktansı arasındaki açının hesaplanması,
ZL = R + JXL den : Ф =-tan -1 (XL/ R) derece bulunur.
KAPASİTE ölçülmesi :
1- Deney bağlantı şeması :
2- Kondansatörün omik direnci ihmal edilecek kadar küçük olduğundan dikkate alınmaz,
3- Akım ve gerilim bilgisi ölçülerek bu bilgiler yardımıyla kapasitif reaktans elde edilmesi,
ZC = XC = U / I
4- Hesaplanan kapasitif reaktans formülünden yararlanılarak kondansatörün kapasitesinin hesaplanması,
XC=1 / ω.C förmülünde ω=2.∏.f
C= I/2.∏.f.U
farad bulunur.
konarak C
çekilirse
5- Kapasitenin açısı ise ;
ZC = R + JXC den : Ф =-tan -1 (XC/ R) derece bulunur.
ÖLÇÜLEN DEĞERLER :
8
HESAPLAMALAR :
SONUÇ :
9
D.NO: 4
DENEY ADI : OSILOSKOPUN DEVREYE BAĞLANMASI
ÖĞR. ADI ve NO :
TARİH : .. /.. / 2005
G.NO :
D. AMACI : Osiloskopun yapısı, çalışması ve devreye bağlayarak ölçüm yapılmasının öğrenilmesi..
TEMEL BİLGİ : Elektriksel işaretlerin ölçülüp değerlendirilmesinde kullanılan aletler içinde en geniş ölçüm
olanaklarına sahip olan osiloskop, işaretin dalga şeklinin, frekansının ve genliğinin aynı anda belirlenebilmesini
sağlar. Başka bir ifade ile; periyodik veya periyodik olmayan elektriksel işaretlerin ölçülmesi ve gözlenmesini
sağlayan, çok yönlü bir elektronik cihazdır. Osiloskop ile ölçülen bazı elektriksel bazı elektriksel büyüklükler
şunlardır.
1 - AC ve DC gerilimler,
2 - AC ve DC akımın dolaylı ölçümü,
3 - Periyot, frekans, ve faz ölçümü,
4 - Yükselme zamanı ve düşme zamanı ölçme,
5 - Transdüser kullanarak, basınç ,gerilme ve sıcaklık ölçümü gibi.
Bu uygulamalar dışında, kullanıcının kabiliyeti ve ilgi alanına bağlı olarak osiloskop, daha değişik alanlarda da
kullanılabilir.
Şekil : Osiloskop
ÇALIŞMASI :
Osiloskopun en önemli parçaları ,
1- Katod ışınlı tüp veya CRT ( CATHODE Ray Tube )
2- Düşey amplifikatör
3- Yatay amplifikatör
4- Tarama osilatörü
5- Tetikleme devresi
6- Çeşitli besleme devreleri şeklinde özetlenebilir.
Çalışması, hareket halindeki elektronların yörüngelerinin bir elektrik alan içerisinden geçerken sapmaları temel
prensibine dayanır. Katod ışın tüpündeki saptırma plakaları adı verilen düzlemsel levhalara uygun potansiyellerde
gerilimler uygulanarak oluşturulan elektrik alanlar, plakalar arasından geçen elektronları (elektron demetini)
saptırarak fosfor ekrana çarptığı noktanın yerini değiştirir. Bu noktanın konumu saptırma plakalarına uygulanan
gerilimin ani değeri ve dalga şekline bağlı olarak değişecek ve ekranda ışıklı bir çizgi oluşacaktır.
10
Şekil : Bir katod ışınlı tüpün iç yapısı
Osiloskop devreye daima paralel bağlanır. Çok yüksek olan iç direnci nedeniyle seri bağlanması halinde ölçüm
yapılmak istenen devreden akım akmasını engelleyecektir. Akım dalga şekillerini incelemek için akımın aktığı
devreye küçük değerli bir direnç (ölçüm direnci, şönt direnç) seri bağlanarak uçlarında düşen gerilimin dalga şekli
incelenir. Bir omik dirençte içinden akan akım ve uçlarında düşen gerilimin dalga şekilleri ve fazlarının aynı oldukları
göz önüne alınarak ve ohm kanunu gereği V=I.R bağıntısı da göz önünde tutularak akım incelenir. Dikkat edilmesi
gereken nokta, kullanılan direncin değerinin devre akımını çok fazla sınırlamayacak kadar küçük seçilmesi
(genellikle akıma bağlı olarak 10 ile 200 miliohm arası) ve gücünün bu akıma dayanabilecek kadar büyük olmasıdır.
Osiloskop çalıştırıldıktan sonra bir kaç dakika ısınması beklenir. Bu esnada timebase komütatorünün ortalarda bir
konumda (örneğin 5mS/div) olması iyi olur. Eğer bu sürenin sonunda ekranda ışıklı çizgi belirmediyse;
Şekil : Osiloskop ekranı ( yatay =time, düşey=genlik )
Parlaklık (Intensity) potansiyometresi yeterince açık değildir. Saat yönüne tam turunun 3/4 ü kadar çevrilmelidir.
Çizgi belirdikten sonra parlaklık yine bu düğme yardımı ile istenilen şekilde ayarlanabilir. Hala çizgi belirmediyse;
Xpos ve Ypos düğmeleri ile oynanarak çizgi ekran üzerine düşürülmeye çalışılır. Sonuç olumsuzsa;
11
Şekil : Intens (parlaklık ) ve focus ( odaklama )
Şekil : Xpos, Ypos düğmeleri
AT/NORM TRIGGER anahtarı AT konumuna getirilir ve yukarıdaki işlemler tekrarlanır.
Işıklı çizginin parlaklığı ayarlandıktan sonra gerekiyorsa netliği de FOCUS düğmesi yardımıyla sağlanır.
Şekil : Prob
Şekil :Prob kalibre etme ve Kompanzasyon ayar vidası
Işıklı çizgi ekranda belirdikten sonra Y INPUT girişine (osiloskop çok kanallı ise Y1 girişine) bir prob takılır.
Günümüzde bütün problarda BNC tipi konnektörler (fişler) kullanılmaktadır. Bu fişler yerlerine oturtulduktan sonra
dış taraflarındaki hareketli kısım saat yönünde bir miktar çevrilerek kilitlenir. Problar X1, X10 ve X100 olmak üzere
birkaç çeşittir. Bir prob üzerindeki bir anahtar yardımı ile hem X1 hem de X10 özelliği gösterebilir. X1 tipi problarda
ölçülen işaret olduğu gibi osiloskoba uygulanır. X10 ve X100 tipleri ise sırasıyla işareti 10 ve 100 kez zayıflatıp
osiloskoba gönderir. X10 veya X100 tipi bir prob kullanılmadan önce aşağıdaki şekilde kompanze edilmelidir.
Prob, osiloskop üzerindeki kare dalga üretecine bağlanır ve üzerindeki ayar vidası, ekranda köşeleri düzgün bir kare
dalga görülene kadar çevrilir. Bu işlemden sonra hatasız bir ölçüm yapmak mümkündür. X1 tipi probların bu işleme
ihtiyacı yoktur.
12
Şekil : Kalibre edilmiş probun ekrana yansıyan görüntüsü
1 - OSİLOSKOPTA GERİLİM ÖLÇÜLMESİ
Ekrandaki işaretin genliği Y (düşey) ekseninde ölçülür. Ölçülecek olan gerilim doğrudan veya bir prob üzerinden
osiloskopun düşey girişine uygulanır. Kazanç, tarama hızı ve tetikleme düğmeleriyle ayarlamalar yapılarak , ekranı
dolduracak kararlı bir işaret elde edilir. Yatay ve düşey pozisyon kontrolü ile kolay okunabilecek şekilde işaret
ekrana yerleştirilir.
Genlik, ilk önce ekran üzerindeki kareler cinsinden belirlenir. Daha sonra VOLTS/DIV giriş zayıflatıcısı
komütatörünün üzerindeki işaretin gösterdiği değer ile kare sayısı çarpılarak gerilimin gerçek değeri belirlenir. Bu
esnada eğer varsa kesintisiz genlik ayar düğmesi "cal" konumunda veya saat istikametinin tersi yönünde en sona
kadar çevrilmiş olmalıdır. Eğer zayıflatıcılı ( X10 veya X100) bir prob kullanılıyorsa zayıflatma katsayısı da hesaba
katılmalıdır. Osiloskobun hassasiyeti VOLTS/DIV komutatörünü saat yönünde çevirerek arttırılır.
Şekil : Komütatörler( genlik ve zaman ) ve cal düğmesi
Tepeden tepeye genlik (Utt), gerilim kademesi ile kullanılan probun çarpımına eşittir.
Tepe değeri ; Ut =
U tt
' dir.
2
Efektif değeri; Ueff = Ut x 0,707 ‘dir.
Ortalama değeri; Uort = Ut x 0,636 ‘dır.
Eğer doğru gerilim ölçülecekse, gerilim seçici anahtar DC konuma getirilmelidir. Osiloskopta oluşacak sapma ile DC
gerilim ölçülür. Tarama işareti yukarı sapmış ise gerilim pozitif, aşağıya sapmış ise gerilim negatiftir.
13
2- OSİLOSKOPTA PERİYOT ( FREKANS ) ÖLÇME
Modern osiloskoplarda frekans yerine periyot ölçülmektedir. Periyot ölçümleri X (yatay) ekseninde yapılır. Dalga
şeklinin bir periyodunun X ekseni yönündeki uzunluğu kareler sayılarak belirlenir. Daha sonra TIMEBASE
komutatörünün gösterdiği değer ( sn / div, msn / div ya da µsn / div ) ile kare sayısı çarpılarak işaretin periyodu
belirlenir. Eğer varsa kesintisiz TIMEBASE ayar düğmesi "cal" konumunda veya saat istikametinin tersi yönünde en
sona kadar çevrilmiş olmalıdır. Kullanılan prob (X1, X10 veya X100) zaman ölçümlerini etkilemez.
Şekil :Timebase düğmesi
Peryodu (T) osiloskoptaki tarama aralığı ile tarama hızı kademesinin birbirine çarpımına eşittir. Frekansta (F)
peryodun bire bölümünden elde edilir.
F=
Ölçülen
veya
bilinmeyen
frekans
10/1 ‘lık prob
Düşey
giriş
1
Hz.
T
Yatay
giriş
Bilinen
frekans
Şekil : Bilinen ferkansla – bilinmeyen frekansın karşılaştırılması yöntemi
Frekans ölçümlerinde bir diğer hassas ölçüm ise, karşılaştırma metodu ile yapılan ölçmedir. Bu metodla bilinmeyen
frekans ile bilinmeyen frekans karşılaştırılır. Bu ölçümde osiloskobun yatay taraması kaldırılır. x-y modunda düşey
girişe bilinmeyen frekans işaret, yatay girişe de frekansı bilinen uygulanır. Ekranda kapalı eğriler elde edilir.
14
Şekil : x-y mod anahtarı , iki işaretin karşılaştırılmasında kullanılır.
Eğer
Eğer
fd = fy ise ekranda daire veya elips elde edilir.
fd > fy ise ekranda değişik şekiller elde edilir.
fd t y
=
bağıntısı yardımı ile istenilen frekans değeri hesaplanır.
fy t d
Şekil : fd=fy durumu daire
Şekil : fd=fy durumu elips
Şekil : fd>fy durumu
3- OSİLOSKOPTA FAZ ( AÇI ) ÖLÇÜMÜ
Faz ölçümü iki değişik şekilde yapılır. Bunlardan birincisi, faz farkı ölçülecek olan olan işaretlerden biri, osiloskobun
bir kanalına, diğeride diğer kanala uygulanır. Bu iki işaret arasındaki gecikme (td) ve peryod ölçülerek farkı
hesaplanır. Derece olarak faz farkı;
⎛ td ⎞
⎟ ’dir.
⎝T ⎠
θ = 360 x⎜
İkinci yöntem ise; faz farkı ölçülecek olan işaretlerden biri osiloskobun yatay girişine, diğeri ise düşey girişine
uygulanır. Ekrandaki eğrinin max değerleri (Ym) ile düşey eksenin simetrik olarak kesildiği noktalar arasındaki
mesafeler ölçülür. Aşağıdaki formülden de faz farkı bulunur.
−1
⎛ Y ⎞
⎟
⎝ Ym ⎠
θ = Sin ⎜
15
Y
Ym
Ym
Y
Ym
Y
Y
Ym
0
0 (Y/Ym)= 0
60
0
30
(Y/Ym)= 0,5
0
0
0
90
(Y/Ym)= 1
120
(Y/Ym)= 0,866
0
180
(Y/Ym)= 0
0
150
Şekil : İki işaretin karşılaştırılarak faz farkının tespitindeki ekran görüntüleri.
4- OSİLOSKOPLA AKIM ÖLÇÜMÜ
Osiloskopun giriş direnci çok büyük olduğu için; böyle bir cihaz ampermetre gibi kullanılamaz. Bu sebepten dolayı
dolaylı ölçme yapılamaz. Değeri belli olan bir direnç akımı ölçülecek olan devreye seri bağlanır. Bu direncin uçları da
gerilim osiloskop ile ölçülecek olan akım;
I=
V
R
’dir.
5- OSİLOSKOPLA GÜÇ ÖLÇÜMÜ
Uçlarındaki gerilimi belli olan bir R direnci üzerinde harcanan güç;
2
⎛ Utt ⎞ 1
P=⎜
⎟ x
⎝ 2,282 ⎠ R
bağıntısıyla hesaplanabilir. Utt: sinüzoidal işaretin tepeden tepeye değeri.
Mesela ; 50 Ω luk bir yük direncine bir işaret kaynağı bağlanmış ve sasiloskop yardımıyla tepeden tepeye 0.2 V luk
bir gerilim ölçülmüş ise yük direncinde P= [ 0.2 / 2.2.82 ]2.[1/50] = 0.1 mw değerinde bir güç kaybı vardır.
KULLANILAN ALETLER :
1.
2.
3.
4.
5.
16
Osiloskop
Osilatör ( AC)
Varyak
DC çıkışlı ayarlı adaptor.
Prob
D. YAPILIŞI ve İŞLEM BASAMAKLARI :
AC ve DC GERİLİM ÖLÇÜMÜ ;
1. Ölçülecek olan gerilim doğrudan veya bir prob üzerinden osiloskopun düşey girişine uygulanır.
2. Kazanç, tarama hızı ve tetikleme anahtarıyla ayarlandırma yapılır.
3. Ekranı dolduracak kararlı bir ışık elde edilir.
4. Yatay ve düşey pozisyon kontrolu ile kolay okunacak şekilde işaret ekrana getirilir.
5. Düşey kareler işaretin tepeden tepeye genliğine göre sayılarak, gerilim kademesi ve prob değerleri dikkate
alınarak gerilim değeri bulunur.
FREKANS ÖLÇÜMÜ ;
A- DİREK ÖLÇÜM
1- Ölçülecek olan gerilim doğrudan veya bir prob üzerinden osiloskopun düşey girişine uygulanır.
2- Kazanç, tarama hızı ve tetikleme anahtarıyla ayarlandırma yapılır.
3- Ekranı dolduracak kararlı bir ışık elde edilir.
4- Yatay ve düşey pozisyon kontrolu ile kolay okunacak şekilde işaret ekrana getirilir.
5- Yatay kareler işaretin bir tekrarı boyunca sayılarak tımebase kademesindeki değer ile çarpılarak işaretin
frekansı vede periyodu hesaplanır.
12345-
B- KARŞİLAŞTIRMA YÖNTEMİ İLE,
Bilinmeyen frekans, bilinen frekansla karşılaştırılır.
Bu ölçümde osiloskobun yatay taramasını kaldırınız.
Düşey girişe bilinmeyen frekanslı işaret, yatay girişe de frekansı belli olan işareti uygulayınız.
Ekranda kapalı eğriler elde ediniz.
Fd ve fy değerleri sayılarak, bilinmeyen frekansa ulaşılır.
DEVRE MONTAJ ŞEMASI :
Ölçülen
veya
bilinmeyen
frekans
10/1 ‘lık prob
Düşey
giriş
Yatay
giriş
Bilinen
frekans
Şekil : Karşılaştırma metoduyla frekans ölçme deney düzeneği.
17
ÖLÇÜLEN DEĞERLER :
HESAPLAMALAR :
SONUÇ :
18
D.NO: 5
DENEY ADI : GÜÇ KOMPANZASYONU
ÖĞR. ADI ve NO :
TARİH : .. /.. /2005
G.NO :
D. AMACI : Lokol Güç kompanzasyonunun nasıl yapıldığının öğrenilmesi.
TEMEL BİLGİ : Kompanzasyonda kullanılan en önemli tanımlardan biri güç faktörüdür veya cosφ’dır. Aktif akımın
toplam akıma oranıdır. Diğer bir tanım ise güç üçgeninden akmaktadır.
P
olacaktır.
S
P = S .CosΦ
P = S → max güç
cosφ =
Generatör , transformatör, motor, bobin gibi elektrik cihazlarının çalışması için gerekli manyetik alan meydana
gelmek zorundadır. Manyetik alanı meydana getiren mıknatıslanma akımı endüktif (geri-fazda) karakterde
olduğundan şebekeden çekilir ve akımın sıfırdan geçtiği anda alan ortadan kalkacağından tekrar şebekeye ilave
edilir. Bu nedenle reaktif güç üretici ile tüketici arasında sürekli olarak şebeke frekansının iki katı bir frekansla
sağlanır.
Şekil : Endüktif devre vektör diyagramı (akım gerilimden geridedir).
Şekil : Endüktif devre ile omik devre ile karşılaştırması
19
Şekil : Kapasitif devre vektör diyagramı (akım gerilimden ileridedir).
Şekil : Kapsitif devre ile omik devre ile karşılaştırması
Düşük güç faktörünün etkileri,
1. Generatör ve trafoların daha büyük seçilmelerine,
2. İletkenlerin kalın kesitli olmasına,
3. Şebekeden daha çok reaktif gücün çekilmesine,
4. İletkenlerden kayıpların ve gerilim düşümünün artmasına,
5. Üretim, dağıtım ve iletimde kapasite ve verimin düşmesine,
6. Üretim maliyetinin artmasına sebep olur.
Bazı kuruluşların ortalama güç değerleri;
Otomativ sanayi
: 0.72
Un sanayi
: 0.64
Demir döküm fabrikaları : 0.70
Meskenler
: 0.74 – 0.88
Resmi daireler
: 0.60 – 0.8
Türkiye Elektrik Kurumu ( TEK ) GÜÇ FAKTÖRÜ : 0.857 DEĞERİNE KADAR ÜCRETLENDİRME YAPMAKTADIR.
Bu değerin altında reaktif güç bedelini almaktadır.
20
İki tür güç faktörü kompanze edilir;
1) Ip sabit tutularak ( P=sbt ) ;
I1
I2 haline getirilir, buda Ic akımı ile sağlanır.
Q1 = Px tan Φ 1
Q2 = Px tan Φ 2
QC = Q1 − Q2
QC = 3 xU n xI C
QC = P(tan Φ 1 − tan Φ 2 ) = kxP
2
I
QC = C Δ
wxC Δ
2
QC = 3xU Δ xwxCΔ
2) S veya I sabit tutularak ;
QC = Q1 − Q2
Q1 = Sx sin Φ 1
Q2 = Sx sin Φ 2
QC = S (sin Φ 1 − sin Φ 2 )
QC = P1 x tan Φ 1 − P1 x tan Φ 2
ΔP = P1 − P2 = S (cos Φ 2 − cos Φ 1 )
D.YAPILIŞI ve İŞLEM BASAMAKLARI :
1.
2.
3.
4.
5.
6.
Kullanılacak olan malzemeler hazırlayınız.
A1 ampermetresi devreye uygulanacak akımı ölçebilecek şekilde devreye seri olarak bağlayınız.
A2 ampermetresi flüoresan lamba üzerine düşecek olan akımı ölçebilecek şekilde devreye bağlayınız.
C kondansatörü bir anahtar yardımıyla devreye bağlayınız.
Devreye enerji veriniz.
A1 ampermetresindeki değer okuyarak, not ediniz.
21
7.
8.
9.
10.
11.
A2 ampermetresindeki değer okuyarak, not ediniz.
Devreye anahtar yardımıyla kondansatörü devreye sokunuz.
Kondansatörün devreye girmesiyle flüoresan lamba üzerine düşen akımın düştüğü gözlemleyiniz.
Bu durumda A2 ampermetresinde okunan değer not ediniz.
Devrede kondansatör varken şebekeden çekilen akımla (A1) azalma olduğu, A2 ampermetresinin
gösterdiği değerde değişiklik olmadığı tespit ediniz.
KULLANILAN ALETLER :
1.
2.
3.
4.
5.
6.
7.
2 Adet ampermetre.
Voltmetre
2 adet 40x40W flüoresan lamba
Balast
Bağlantı için kablolar
Kondansatör
Adi anahtar.
DENEY MONTAJ ŞEMASI :
Şekil : Deney bağlantı şeması
ÖLÇÜLEN DEĞERLER :
22
HESAPLAMALAR :
SONUÇ :
23
D.NO: 6
DENEY ADI : GÜÇ KATSAYISININ ÖLÇÜLMESİ.
ÖĞR. ADI ve NO :
TARİH : .. /.. /2001
G.NO :
D. AMACI : Güç katsayısının ölçülmesinin öğrenilmesi.
TEMEL BİLGİ : AA devrelerinde güç ölçerken, devre indüktif veya kapasitif yüklü ise böyle bir devrenin akımı ile
gerilimi arasında bir faz farkı meydana gelmektedir. Bu farkın açı ile gösterilmesi bu açının cos’inise güç katsayısı
denilmektedir.
Güç katsayısı aşağıdaki metotlardan biri ile ölçülebilir.
a. Ampermetre – Voltmetre ve Wattmetre metodu ile,
b. Üç ampermetre metodu ile,
c. Üç voltmetre metodu ile,
d. Doğrudan cosϕ metre ile ölçme.
a. Ampermetre – Voltmetre - Wattmetrenin devreye bağlanarak güç ölçülmesi (1 fazlı) :
Gücü ölçmek için elektriğin iki ana büyüklüğünü ölçmek gerekir. Buda akım ve gerilim şiddetidir.
AA devrelerinde endüktif ve kapasitif devrelerde güç;
P = U .I . cos ϕ (W)
P = U .I (W)
DC devrelerde ise; P = U .I (W)
Omik devrelerde ise;
cos ϕ =
P
U .I
radyan değeri hesaplanır .
ϕ = arc. cos ϕ derce olarak bulunur.
b. Üç ampermetre metodu ile cosϕ ölçülmesi :
Üç ampermetre metodunda ise, R direncinin değeri alıcı akımın çektiği akımı vermelidir. I1≅I2 olmalıdır. I1 akımı ile U
gerilimi aynı fazda, I2 akımı ile U gerilimi arasında ise ϕ açısı kadar bir faz farkı vardır. I1 akımı ile I2 akımının
vektörel bileşeni I akımını vermektedir.
24
I 2 = I 1 + I 2 + 2.I 1 .I 2 . cos ϕ
2
2
2
(A)
2
I 2 − I1 − I 2
olur.
cos ϕ =
2 .I 1 .I 2
c. Üç voltmetre metodu ile cosϕ ölçülmesi :
Üç voltmetre metodunda ise, U1 gerilimi ile I akım aynı fazda, U2 gerilimi ise I akımına göre akımına göre ϕ açısı
kadar ilerdedir.
U 2 = U 1 + U 2 + 2.U 1 .U 2 . cos ϕ (V)
2
cos ϕ =
2
2
2
U 2 − U1 − U 2
olur.
2.U 1 .U 2
d- Doğrudan cosϕ metre ile ölçme:
Bir fazlı cosϕ metrenin devreye bağlanışı
25
D. YAPILIŞI VE İŞLEM BASAMAKLARI :
a. Ampermetre – Voltmetre - Wattmetrenin devreye bağlanarak güç ölçülmesi (1 fazlı) :
1. Devreye seri bir şekilde akımı ölmek için bir A ampermetresi bağlandı.
2. Devreye paralel bir şekilde gerilimi ölçmek için bir V voltmetresi bağlandı.
3. Akım bobini devreye seri, gerilim bobini devreye seri bağlanarak devrenin gücünü ölçmek için bir W
wattmetresi bağlandı.
4. Devreye enerji verildi.
5. Ölçülen değerler not edildi.
b. Üç voltmetre metodu ile cosϕ ölçülmesi :
1. Devreye ilk olarak bir R direnci ile L bobini bağlandı.
2. R direnci üzerine düşecek olan gerilimi ölçmek için paralel bir şekilde bir V1 voltmetresi bağlandı.
3. L bobini üzerine düşecek olan gerilimi ölçmek için paralel bir şekilde bir V2 voltmetresi bağlandı.
4. Devre üzerine düşecek olan gerilimi ölçmek için V voltmetresi devreye bağlandı.
5. Devre akımını ölçmek için de devreye A ampermetresi bağlandı.
6. Devreye enerji verildi.
7. Ölçülen değerler not edildi.
c. Üç ampermetre metodu ile cosϕ ölçülmesi :
1. Devreye ilk olarak bir R direnci ile L bobini bağlandı.
2. R direnci üzerine düşecek olan akımı ölçmek için seri bir şekilde bir I1 voltmetresi bağlandı.
3. L bobini üzerine düşecek olan akımı ölçmek için seri bir şekilde bir I2 voltmetresi bağlandı.
4. Devre üzerine düşecek olan akımı ölçmek için I voltmetresi devreye bağlandı.
5. Devreye enerji verildi.
6. Ölçülen değerler not edildi.
KULLANILAN ALETLER :
a. Ampermetre – Voltmetre - Wattmetrenin devreye bağlanarak güç ölçülmesi (1 fazlı) :
1. Yük olarak flüoresan lamba.
2. Ampermetre
3. Voltmetre
4. Wattmetre
5. Bağlantılar için kablolar.
6.
b. Üç voltmetre metodu ile cosϕ ölçülmesi :
1. Direnç olarak lamba
2. Bobin olarak flüoresan balastı.
3. 3 adet voltmetre.
4. Bağlantılar için kablo.
c. Üç ampermetre metodu ile cosϕ ölçülmesi :
1. Direnç olarak lamba
2. Bobin olarak flüoresan balastı.
3. 3 adet ampermetre.
4. Bağlantılar için kablo.
d. Direk cosϕ’metre ile cosϕ ölçülmesi :
1. Yük olarak flüoresan lamba.
2. cosϕ’metre.
3. Bağlantılar için kablo.
26
DENEY MONTAJ ŞEMASI :
a- Ampermetre – Voltmetre - Wattmetrenin devreye bağlanarak güç ölçülmesi (1 fazlı) :
b- Üç voltmetre metodu ile cosϕ ölçülmesi :
d. Üç ampermetre metodu ile cosϕ ölçülmesi :
ÖLÇÜLEN DEĞERLER :
27
HESAPLAMALAR :
SONUÇ :
28
D.NO: 7
DENEYADI : İŞ ÖLÇÜMÜ, SAYAÇ, FREKANSMETRE, WATMETRE, TARİH :.. /.. /2005
TAKOMETRE DEVRE BAĞLANTILARI
ÖĞR. ADI ve NO :
G.NO :
D. AMACI : Çeşitli ölçü aletlerininçalışması,yapısı ve kullanımının öğrenilmesi...
TEMEL BİLGİ :
Elektrik İşini Ölçme ( Sayaçlar ) : Tüketilen elektrik enerjisini ölçen aygıtlara sayaç adı verilir. Aslında elektrik işi
W=P.t dir. Yani ( güç.zaman ) dır. Burada güç birimi vat, zaman birimi de saat olarak yazılırsa, elektrik işi vat-saat
olarak ortaya çıkar.
Sayaç etiketinde , çalışma gerilimi, akımı, frekansı, 1 Kwh için devir sayısı gibi bilgiler bulunur. Bu bilgilerin ışığı
altında sayacı doğru olarak devreye bağlamak ve bazı sayaç kontrollerini ile ilgili hesaplamalar yapmak
mümkündür. Bu işlemleri basit olarak yapabilmek için bir formül bulunur. Aslında bu formül üçlü bir orantının
çözümünden bulunmuştur. Bunu bir örnekle açıklarsak ;
1kwh enerji tüketimi için 1200 devir yapan bir fazlı sayaca, akkor telli lambalar bağlanmıştır. Sayaç bir dakikada 10
devir yaptığına göre, lambaların gücü nedir diye sonucu arasaydık basit bir oranla bulabilirdik.
1000 W
P W
3600 sn
60 sn
1200 devir
10 devir
P.t.K = 1000.3600. n
P= 1000.3600.10 / 60.1200 = 500 Vat bulunur.
Burada; ( P ) : Aktif Güç
( t ) : Disk devrinin ölçüldüğü süre sn.
( n ) : Disk devir sayısı
( K ) : Saycın etiketindeki sabit değer ( devir sayısı )
Periyot Ölçme ( Frekansmetre ) : Frekans ölçen cihazlara frekansmetre diyoruz. Genellikle elektriki ve mekaniki
rezonans ilkelerine göre çalışırlar. Bu aygıtlar da, voltmetreler gibi, şebekeye paralel bağlanırlar. Şebek
frekansının sabit tutulmasına özen gösterilir.Eğer şebek frekansı değişirse , asenkron motorlarının devir sayıları
değişecektir. Aynı şekilde ampuller düşük frekanslarda gözleri yoracak şekilde aydınlatmayı etkileyecektir.Elektrikli
zaman saatlerinin çalışması aksayacak. Transformatörler ve motorlar ısınacak. Verimleri düşer. Bu ve bunun gibi
sakıncalara neden olmaması için şebekeyi besleyen alternatörlerin frekansları her zaman ölçmek gerekmektedir.
Çalışma şekillerine göre ,
a- Dilli Frekansmetre : Mekaniki rezonans ilkesine göre çalışır. Bir elektro mıknatısın karşısına,
değişik frekanslarda titreşim yapan, sıra sıra çelik şerit diller yerleştirilir. Bu dillerin herbiri 0.5 hertz’lık titreşim
ferkansı farkları için yapılmışlardır.Magnetik alanın en büyük genlikte titreştiği dilin hizasındaki frekans değeri, o
gerilimin frekansıdır. Çok duyarlı değillerdir.
b- İbreli Frekansmetreler : Elektriki rezonans ilkesine göre çalışır. Çok çeşitleri vardır. Hareketli ve
sabit bobinlerden oluşan iki elektro magnetik düzenek mevcuttur. Basit bir şekilde ibreli frekansmetrenin yapısı
aşağıda şekilde verilmiştir.
29
Devir Sayısını Ölçmek ( Takometre) : Elektrik makinalarının veya diğer dönen makinaların devir sayısını ölçen
aygıtlara Tokometre veya Turmetre adı verilir.Bu aletler atelye, laboratuvar ve fabrikalarda çok çeşitli olarak
kullanılmaktadır. Bunlar Kademeli( Universal ) , Saatlı, Generatörlü, Dilli, Strosboskobik ... tiplerde yapılmışlardır. Biz
atelyemizde optik olarak vede direk temaslı olarak çalışan universal tip takometrenin kullanımını göreceğiz..
Güç Ölçme ( Wattmetre ) : Güç ;Birim zamanda ( saniye ) yapılan elektrik işidir. Doğru akım vede alternatif akımın
omik devrelerinde P=U.I. dir.
Güç ölçmek için, elektriğin iki ana büyüklüğü olan gerilim ve akım şiddetinin ölçülmesi gerekir. A.A. endüktif ve
kapasitif ve karışık durumlarında P=U.I.cosΦ dir CosΦ güç katsayısıdır. Güç katsayısını ölçümü bir evvelki
deneyde gösterilmiştir. Gücü çeşitli metotlarla ölçebiliriz. Ama direk olarak doğrudan ölçen aletlere Watmetre adı
vermekteyiz.Yapıları elktrodinamik, indüksiyon, elektro statik sistemlere göre dizayn edilmişlerdir. Devreye
bağlanışı hem akım hemde gerilim bilgisini işlediği için akım bobinini ampermetre gibi devreye seri, gerilim bobinini
voltmetre gibi paralel bağlamak zorundayız.( Sayaçlarda olduğu gibi.)
KULLANILAN ALETLER:
1-)Sayaç (1 ∼)
2-)Wattmetre (220V 10A)
3-)Ampermetre (2 Ad)
4-)Voltmetre
5-)Frekansmetre
6-)Takometre
7-)CosinüsΦ’metre
8-)Yük
D. YAPILIŞI ve İŞLEM BASAMAKLARI :
1-)Deney için gerekli aletleri temin ediniz.
2-)Şekilde görülen devre şemasının bağlantısını yapınız.
3-)Bağlantı yapıldıktan sonra devreye gerilim uygulayınız.
4-)Devrede ölçülen değerleri not alınız.
30
DEVRE MONTAJ ŞEMASI :
ÖLÇÜLEN DEĞERLER:
31
HESAPLAMALAR:
SONUÇ:
32
D.NO: 8
DENEYADI : SAYAÇ BAĞLANTISI VE HATA TESPİTLERİ
ÖĞR. ADI ve NO :
TARİH :.. /.. /2005
G.NO :
D. AMACI : Sayaç bağlantısının yapılmasının ve hataların bulunmasının öğrenilmesi
TEMEL BİLGİ :
Üretilen veya tüketilen elektrik enerjisini watt saat yada katları olan kilowat saat gibi birim ile ölçen ölçü
aletidir.Genelde ikiye ayrılır ;
1- A.A. Sayaçları
a- Tek Fazlı Sayaçlar
- Çift Tarifeli Sayaçlar
- Reaktif Sayaçlar
Normal Sayaçlar
b- Üç Fazlı Sayaçlar
- 3 Fazlı 3 Telli
- 3 Fazlı 4 Telli
- 3 Fazlı 3 Telli Aron Bağlı
- 3 Fazlı 3 Telli Reaktif
- 3 Fazlı 3 Telli Ters Reaktif
2- D.A. Sayaçları
33
Elektrik enerjisini ölçmek için kullanılan bütün sayaçlar döner disk temeline ve indüksiyon tip olarak adlandırılır.Bu
aletlerde de gene iki bobin bulunur, fakat bobinlerin her ikiside sabit olup,her ikisinin de magnetik alanından
etkilenen küçük ve hafif bir alüminyum disk döner.Diski döndüren moment şöyle doğar.(Birinci bobinin magnetik
alanının disktte yarattığı indüksiyon akımlarına ikinci bobinin magnetik alanı ve ikinci bobinin magnetik alanının
diskte yarattığı indüksiyon akımlarına da birinci bobinin magnetik alanı kuvvet etki ettirir.Yalnız bileşke bir momentin
doğabilmesi için bu magnetik alanların hem diski farklı bölgelerinden delmesi ve hem de faz farklı olması
gerekmektedir.Hemen görülür ki indüksiyon olayının doğup aletin çalışabilmesi için alternatif akımların söz konusu
olması gerekir ve döndürme momentinin değerine frekans da etkir.Bu yüzden;bu aletler,sadece ölçeklendiği belli bir
frekansta doğru ölçme yapabilirler.
Doğacak döndürme momentinin ortalama değeri bobinlerden geçen akımların efektif değerleriyle aralarındaki faz
farkının sinüsü çarpımına bağlı olur.Bu yüzden,indüksiyonlu aletlerle ortalama güç ölçecek wattmetre yapmadığı ya
da aktif enerji sayacı yapmayı istersek gerilim elektromagneti o şekilde yapılır ki gerilim elektromagnetinin diski
delen akısı gerilim bobinine uygulanan gerilimden tam 90 derece geri fazda olur.Bu yüzden,gerilim elektromagneti
olabildiği kadar indüktif yapıldıktan başka kosinüsfi ayarı denen ayarla şekilde görülen φu akısı U geriliminden 90
derece geri faz getirilir.
Diski frenleyen mıknatısın kutuplarını dönme eksenine yaklaştırıp uzaklaştırmakla sayacın tam yük ayarı
yapılır.Gerilim elektromagnetinin altına doğru küçük bir alüminyum levhacığı az ya da çok iterek statik sürtünmeleri
dengeliyecek ek bir döndürme momenti yaratılmış olur ki bu da sayacın küçük yük ayarını oluşturur.
Sayaçların bu ayarları aşağıda gösterilen koşullar altında ve aşağıda anlatıldığı gibi yapılır:
Önce,sayaç nominal yüküyle tam yüklü olarak çalıştırılır.Bu amaçla,gerilim elektromagnetine uygulanan gerilim
sayaç üzerinde yazılı olan Us nominal gerilimine eşit yapılır.Akım elektromagnetinden de bu gerilim ile aynı fazda
olan sayacın,nominal akımı In kadar bir akım geçirilir.Sayaçtan geçirilen güç bir wattmetre ile doğru olarak
ölçülür.Yukarıda belirlenen tam yük ayarı koşulları altında bu güç Pn = Un *In kadar olmalıdır.Sayacın
üzerinde,sayaç doğru yazdığı zaman ; 1 Kwh enerjinin kaç disk dönüşüne karşılık olacağı K değeri de verilir.Bu
belirli değerler yardımıyla, eğer sayaç doğru yazsaydı diskin n dönüşünü yapması için geçmesi gerekecek olan t
süresi;
34
tn = 3600.1000.n/K.PN
formülünden hesaplanır.Bir kronometre ile diskin n dönüşünü tamamlaması geçen t süresi ölçülür.Bu süre t’den
küçük ise mıknatıs kutupları dönme ekseninden uzaklaştırılacak frenleme momenti büyütülür ve disk yavaşlatılarak
n dönüşü tn kadar sürede yapması sağlanır.
Bundan sonra,sayacın küçük yük ayarını yapmak için, akım elektromagnetinden, U = Un gerilimi ile aynı fazda,fakat I
= In/20 olur.Sayaç enerjiyi gene doğru yazıyorsa,bu kere n/20 dönüşünü gene yukarıda hesaplanan tn süresinde
yapması gerekir.Daha uzun ya da daha kısa sürede yapıyorsa hesaplanan tn süresinde yapması gerekir.Daha uzun
ya da daha kısa sürede yapıyorsa yukarıda anlatılan küçük yük ayarı ile ayarlanılır ve tam tn kadar sürede yapması
sağlanır.
Son olarak,sayacın kosinüsfi ayarını yapmak için ,gerilim elektromagnetine U = Un gerilimi uygulanır;fakat akım
elektromagnetinden geçirilen I = In akımı yukarki gerilimden 90 derece faz farklı yapılır.Bunun olması için
wattmetrenin sıfır göstermesi sağlanır.Küçük yük ayarıda tekrar kontrol edilir.
Sayaç Ayarları :
Hata = %∈=( tn- tı ) / tn (+ yada -)
1-)Tam yükte
2-)1/20 Yükte
3-)cos ϕ ayarı
tn> tı ..... sayaç hızlı döner.
tn> tı......sayaç yavaş döner.
tn = tı.....hata yoktur.
tn = 3600.1000.n / K.P
Ör: Nominal karakteristiği 110V/5A K =200 d/kwh olan bir aktif enerji sayacı U/Un= 1, I =In =%50 cosϕ = 1 yük
durumunda çalışırken ;
a-)80 devri kaç sn’de yapar?
b-)Kronometrede 80 devir için 500sn tutulsa sayaç az mı çok mu yazar,hata varsa % kaçtır?
Çözüm:
a-) K = 3600.1000.n/P.t
P = U.I = 110.2,5 = 275 W
tn = 3600.1000.n /K.P =3600.1000.80/2000.275 = 523.6 sn
b-) %∈ = tn –tı /tn = 523,6-500/523.6 = %4.76 (+)
35
KULLANILAN ALETLER:
1-)Sayaç (1 ∼)
2-)Wattmetre (220V 10A)
3-)Ampermetre (2 Ad)
4-)Voltmetre
5-)Frekansmetre
6-)Yük
D. YAPILIŞI ve İŞLEM BASAMAKLARI :
1-)Deney için gerekli aletleri temin ediniz.
2-)Şekilde görülen devre şemasının bağlantısını yapınız.
3-)Bağlantı yapıldıktan sonra devreye gerilim uygulayınız.
4-)Devrede ölçülen değerleri not alınız.
DEVRE MONTAJ ŞEMASI :
36
ÖLÇÜLEN DEĞERLER:
P1 =........ W
P2 =........ .W
P3 =........ W
K = 675 d/kwh,
t1 =..... sn
t2 =..... sn
t3 =..... sn
U =......V,
I1 =...A ,
n1 =... tur
n2 =... tur
n3 =... tur
I2 =...A ,
I3 = ....A
HESAPLAMALAR:
SONUÇ:
37