KONU TESTİ
ÖABT Analitik Geometri
1.
4.
a+3 = b−3
−a − 3 =b − 3
Noktanın Analitik İncelemesi
0 + a − b − a − b =−2b
a+b =
0
Cevap D
2.
Cevap C
A ( a + 4, 1 − a ) noktası y ekseni üzerinde ise,
a+4 =
0
A ( 0, 5 )
a = −4
B ( b + 2, b − 10 ) noktası x ekseni üzerinde ise
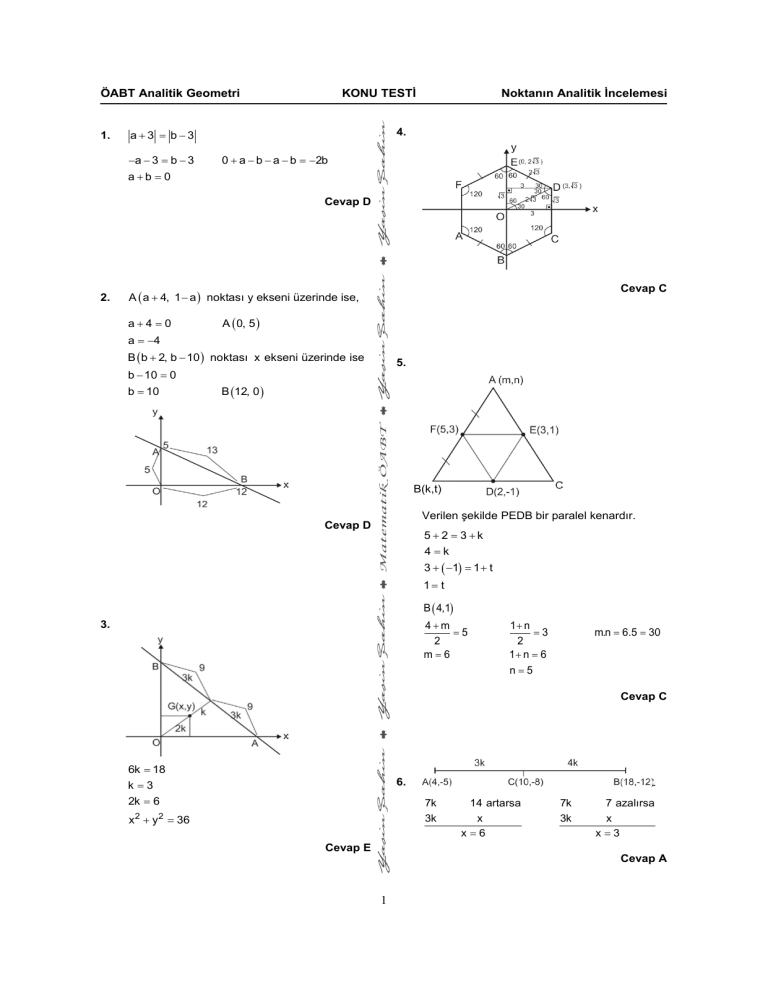
5.
b − 10 =
0
b = 10
B (12, 0 )
B(k,t)
Verilen şekilde PEDB bir paralel kenardır.
Cevap D
5+2 = 3+k
4=k
3 + ( −1) = 1 + t
1= t
B ( 4,1)
4+m
1+ n
= 5
= 3
2
2
=
m 6
=
1+ n 6
n=5
3.
m.n
= 6.5
= 30
Cevap C
6k = 18
k=3
2k = 6
2
2
x +y =
36
6.
.
7k
14 artarsa
7k
7 azalırsa
3k
x
3k
x
=
x 6=
x 3
Cevap E
Cevap A
1
ÖABT Analitik Geometri
KONU TESTİ
7.
Noktanın Analitik İncelemesi
9.
( x − 2 )2 + ( 0 − ( −3 ) )
2
=
( x − 3 )2 + ( 0 − ( −4 ) )
2
x 2 − 4x + 4 + 9 = x 2 − 6x + 9 + 16
2x = 12
x=6
3+4 7
0+2
= =
,
1
2
2
2
7
D ,1
2
4 + ( −1) 3
2+6
= =
,
4
2
2
2
3
E , 4
2
Cevap E
3 + ( −1)
0+6
= 1,= 3
2
2
F (1,3 )
7
2
1
1
2
3
2
1
=
3
1 21
3 9 28
+ 4 + − 1+ +
2 4
2 2 2
4
=
1
39
16 −
2
2
=
1 7 7
=
.
2 2 4
Cevap A
10.
8.
( x − 1)2 + ( y − 2 )2 = ( x − 0 )2 + ( y − ( −3 ) )
2
x 2 − 2x + 1 + y 2 − 4y + 4 = x 2 + y 2 + 6y + 9
0 =2x + 10y + 4
0 =x + 5y + 2
Cevap E
Cevap A
2
ÖABT Analitik Geometri
KONU TESTİ
Noktanın Analitik İncelemesi
12.
11.
A ile L arası uzaklık 5 birimdir.
A ile K arası uzaklık 5 birimdir.
15 + 15 + 2a =
40
2a = 10
a=5
15 12
= =
x 4
5
x
Cevap A
4 + ( −15 ) =−11
Cevap B
3
ÖABT Analitik Geometri
1.
(
KONU TARAMA SINAVI – 1
)
A −a2 + 3a − 4, a2 + 2a + 4 = A ( −, + ) → II. bölge
−
+
Noktanın Analitik İncelemesi
5.
Cevap B
2.
AB = OB
( 0 − ( −6 ) )2 + ( y − 2)2= ( 0 )2 + ( y − 0 )2
36 + y 2 − 4y + 4 =
y2
40 = 4y ⇒ y = 10
∆
A ( AOB )=
AD=
( 3 − 2 )2 +
(0 − ( −1) =)
2
2
12 + 1=
⇒
2
1
60 =
30
2
Cevap C
Cevap B
3.
−6 2
1
1
( −60 + 0 + 0 ) − 0
0 10=
2
2
0 0
A ( +3, − 3 ) → IV. bölgede
P(x,y)
( x − 3 )2 + ( y + 3 )2 = ( x − 0 )2 + ( y − 0 )2
x 2 − 6x + 9 + y 2 + 6y + 9 = x 2 + y 2
−6x + 6y + 18 = 0 ⇒ 6y = 6x − 18 ⇒ y = x − 3
Cevap B
4.
6.
A ( 6, −4 ) noktasının x ekseni üzerindeki dik
izdüşümü P(6, 0)
B (3, -8) noktasının y ekseni üzerindeki dik
izdüşümü Q(0, -8)
PQ=
(6 − 0)
2
+ ( 0 − ( −8 ) )=
2
2.3 = 6
36 + 64
= 10
Cevap C
Cevap E
4
KONU TESTİ
ÖABT Analitik Geometri
1.
m2 > m1, m3 ise negatiftir.
4.
Doğrunun Analitiği
2x − 3y + 1 =
0
(paralel
doğruların
eğimleri
eşittir.)
m3 < m1 < m2
m=
Cevap E
2
3
y +1=
2
( x − 3 ) ⇒ 3y + 3 = 2x − 6 ⇒ 2x − 3y − 9 = 0
3
Cevap C
2.
5.
tan135 = −1
iki noktası ve eğimi bilinen doğru
m = −1
denklemi
-2
y − 3 =−1( x + 2 )
y − 3 =− x − 2 ⇒ y =− x + 1 ⇒ y + x − 1 =0
y − 3 =−2 ( x − 2 )
Cevap B
y − 3 =−2x + 4
y + 2x − 7 =
0
x − 2y =
6
7
+ 2 / y + 2x =
5x = 20
x=4
4 − 2y =
6
−2 =
2y
−1 =y
3.
x.y =4 ( −1) =−4
Cevap B
t + 3 + t − 2 2t − 1 + t + 5 2t + 1 3t + 4
,
= 2 ,
2
2
2
x
y
6.
2t + 1
3t + 4
=
x =
y
2
2
=
=
2x − 1 2t
2y − 4 3t
2x − 1
2y − 4
= t= t
2
3
2x − 1 2y − 4
=
2
3
6x − 3 = 4y − 8
6x − 4y + 5 =
0
x 2 − 2xy − 3y 2 + 3x − 5y + 2 =
0
0
( x − 3y ) . ( x + y ) + 2 ( x − 3y ) + x + y + 2 =
0
( x − 3y )( x + y + 2 ) + x + y + 2 =
0
( x + y + 2 ) . ( x − 3y + 1) =
1
m1 =
−1, m2 =
3
1
2
m1 + m2 =−1 + =−
3
3
Cevap A
Cevap B
5
KONU TESTİ
ÖABT Analitik Geometri
7.
m = -1 için,
10.
−3y + 2 + 1 =
0
−3y =−3 ⇒ y =1
m = 2 için,
3x − 4 + 1 =
0
3x − 3 = 0 ⇒ x = 1
Doğrunun Analitiği
3x − 2y + 5 =
0
0
3x − 2y + 5 + k ( 2x + y + 2 ) =
2x + y + 2 =
0
A (1, 0 ) için
3.1 − 2.0 + 5 + k. ( 2.1 + 0 + 2 ) =
0
3 − 0 + 5 + k ( 4) =
0
8 + 4k =0 ⇒ 4k =−8 ⇒ k =−2
3x − 2y + 5 − 2 ( 2x + y + 2 ) =
0
0
⇒ 3x − 2y + 5 − 4x − 2y − 4 =
⇒ − x − 4y + 1 =0
0
⇒ x + 4y − 1 =
Cevap C
AO =
(1 − 0 )2 + (1 − 0 )2 =
2
Cevap B
8.
p = 0 için
11.
y + 2 =0 ⇒ y =−2
p = 1 için
4x + y + 3 =
0
x eksenine paralel ise x i yok
3x + 2y + 1 =
0
edelim.
x+y+5 =
0
x = −3
0
− 3 / 4x + y + 3 =
0
+ 4 / 3x + 2y + 1 =
5y = 5 ⇒ y = 1
A ( −3, −2 )
y= x + c
−2 =−3 + c
c =1
y= x + 1
Cevap D
Cevap B
9.
2x − 3y + 5 + k ( x + 2y − 3 ) =
0
( 0,0 )
12.
için
2.0 − 3.0 + 5 + k ( 0 + 2.0 − 3 ) =
0
5 + k ( −3 ) =
0
k=
5
3
5
0
( x + 2y − 3 ) =
3
6x − 9y + 15 + 5x + 10y − 15 =
0
11x + y =
0
2x − 3y + 5 +
Cevap A
Cevap C
6
ÖABT Analitik Geometri
KONU TESTİ
Doğrunun Analitiği
16.
13.
2.a =
1
1
− .a =
−1
3
=
a
1
a=
a=
3
−
2
5
1
3 + − =+
2
2
22 − ( −1) + 5
10 10 10 5
= = =
= 2 5
2
5
5
5
22 + ( −1)
2
A ( ABCD=
4.5
= 20
) a=
Cevap C
Cevap D
14.
17.
3x − 2y + 1
32 + ( −2 )
2
=
2x − 3y + 4
22 + ( −3 )
2
⇒ 3x − 2y + 1 = 2x − 3y + 4
3x − 2y + 1 =
2x − 3y + 4 ve 3x − 2y + 1 =
−2x + 3y − 4
x+ y−3 0
5x − 5y + 5 0
=
=
x − y +1=
0
y − 2= 3 ( x + 1)
0 − 2 = 3x + 3
−5 =
3x
5
x= −
3
Cevap A
Cevap B
15.
18.
3x − 4y − 5
32 + ( −4 )
2
=
4x + 3y − 7
42 + ( 3 )
2
4x + 3y − 7
=
5
5
3x − 4y − 5 = 4x + 3y − 7
0 =x + 7y − 2
3x − 4y − 5 =−4x − 3y + 7
7x − y − 12 =
0
⇒
Verilen şekil bir dikdörtgen olduğu için
x y
+ =
1
4 6
3x − 4y − 5
Cevap B
Cevap A
7
KONU TESTİ
ÖABT Analitik Geometri
19.
Doğrunun Analitiği
22.
−2 + 1 0 + 3 1 3
2 , 2 = − 2 , 2
3−0
3
m=
= = 1
1
1 − ( −2 ) 3
m1.m2 = −1
m2 = −1
3
1
=
−1 x +
2
2
2y − 3 =−2x − 1
2y + 2x − 2 =
0
y−
5x − y − 12 =
0
5.a − ( −a ) − 12 =0
y + x −1=
0
6a = 12
a=2
Cevap E
=
= 8
Ç ( OABC
) 4.2
23.
Cevap D
20.
T.A
=
y + 2y + y + 2y =
60
6y = 60
5.2
= 5
2
Cevap C
y = 10
24.
Cevap C
21.
2.0 + 3.0 − 13
=
22 + 32
13
13 13
=
=
13
13
13
Alan
=
Cevap C
3.6
= 9
2
Cevap D
8
KONU TESTİ
ÖABT Analitik Geometri
25. 3x − 2y + 1 =
0
m1 =
Doğrunun Analitiği
27.
3
2
3
3
m+
2 = 1,
2 = −1
3
3
1 + m.
1 − m.
2
2
2m − 3
2m + 3
= 1
= −1
2 + 3m
2 − 3m
2m − 3 =2 + 3m
2m + 3 =−2 + 3m
=
−5 m =
5 m
m−
−1
m2 ( −5 ) =
yada
1
5
1
y − 1 = ( x − 2)
5
5y − 5 =x − 2
0 = x − 5y + 3
=
m
(B ve C noktalarından birini kullanarak denklemi yazalım.)
y+2 =
−1
m2 ( 5 ) =
1
5
=
h
1
y − 1 =− ( x − 2 )
5
5y − 5 =− x + 2
5y + x − 7 = 0
m2 =
1 − ( −2 ) 3
=
1 − ( −3 ) 4
m2 = −
3
( x + 3 ) ⇒ 4y + 8 = 3x + 9
4
4y − 3x − 1 =
0
−3. ( 2 ) + 4 ( −2 ) − 1
= 3
5
Cevap C
Cevap A
26.
28.
2x − y
y
=
5
1
2x − y =y 5
(
)
yada
2x =
y 1+ 5
y
(
2x − y =− y 5
(
3x
A ( x )= x 6 −
⇒ 2 ( 6 − 3 )= 6
2
)
2x =
y 1− 5
3x 2
2
=6 − 3x =0
x=2
2x
2x
= y
5 +1
1− 5
(
)
5 +1
)
(1+ 5 )
(
= 6x −
)
5 −1
1+ 5 x
=
.x y= y
−2
2
Cevap C
Cevap D
9
KONU TESTİ
ÖABT Analitik Geometri
29.
Doğrunun Analitiği
31.
4= 8 − a2
a=2
8−4
= −2
0−2
m −1
m −1
⇒ =
3
1 + m.1
1+ m
3 + 3m =−
m 1
tan 60
=
(
3 +=
1 m 3− 3
)
Cevap B
3 +1
=m
1− 3
ve
m −1
=− 3 ⇒ m − 1 =− 3 (1 + m )
1 + m.1
(
)
m 1+ 3 =
− 3 +1
m=
− 3 +1
1+ 3
3 +1 − 3 +1
.
= +1
1− 3 1+ 3
Cevap D
32.
30.
x y
1
=
+
6 3
x y
1
+ =
3 6
y + 1 −1 − 0
=
0−4 4−6
y + 1 −1
y +1 1
= ⇒
=
−4
−2
−4
2
2y + 2 =−4
2y = −6
y = −3
x + 2y 6
=
2x + y =
6
3x + 2y =
12
x+y =
4
y=2
x=2
a+b =
4
+
Cevap E
Cevap C
10
ÖABT Analitik Geometri
1.
3x + 4y + 5 =
0
m= −
4.
3x − 2y + 1
3 + ( −2 )
2
3
4
3
− .m1 =−1
4
4
=
m1
3
2
=
3x − 2y − 7
32 + ( −2 )
2
⇒ 3x − 2y + 1 = 3x − 2y − 7
4
y − 2 = ( x + 2)
3
m.m1 =−1
Doğrunun Analitiği
KONU TARAMA SINAVI – 2
⇒ 3x − 2y + 1 = 3x − 2y − 7
yada
3x − 2y + 1 =−3x + 2y + 7
6x − 4y − 6 =
0
3x − 2y − 3 =
0
3y − 6 =4x + 8
3y
=
− 4x − 14 0
4x − 3y + 14 =
0
Cevap C
Cevap E
5.
2.
y + 4 =+1( x − 3 )
x + y =3
y+4 = x−3
y=
x−7
3
a−4
=
b−3
4
12
(b − 3 ) . ( a − 4 ) =
y − x =−7
2y = −4
−2
y=
x=5
5 + ( −2 ) =3
Cevap B
Cevap C
3.
6.
Paralel iki doğru arasındaki uzaklık formülü
uygulanırsa;
=l
c1 − c 2
2
a +b
2
⇒
=l
−1 − 9
=
32 + 12
10
=
10
10
2a = 6
=
Alan
=
a 3
=
10. 10 10
=
A 3.3
= 9
Cevap C
Cevap B
11
ÖABT Analitik Geometri
1.
KONU TESTİ
A ( 5,12 ) x
eksB
( 5, −12 )
5.
A ( 5,12 ) y
eks C ( −5,12 )
Analitik Düzlemde Simetri
− ( −1) ) Aı ( 3,3 )
A (=
3, −1) y1Aı ( 3,2.1=
3.a + 2.3 − 3 =
0
A ( 5,12 ) arjin
D ( −5, −12 )
3a + 6 − 3 =
0
Alan = 24.10 = 240
a = −1
3a = −3
Cevap A
Cevap C
6.
A ( t − 2, t + 1)
x= t − 2
2.
y= x + 1
0
⇒ x−y+3 =
x − y =−3
=
h
x =−1 ters simetri ( 2. ( −1) − x ) − y + 3 =0
0
−x − y + 1 =
2 ( −8 ) − 5 + 1 20
= = 4 5
2
5
22 + ( −1)
x + y −1=
0
Cevap E
Cevap C
7.
3.
p = −2 için;
A ( 3, −2 ) y
=
− x B ( 2, −3 )
0x − 5y − 4 − 1 =
0
y = −1
p = 3 için
5x + 5 =0 ⇒ x =−1
y + 3= 1( x − 2 )
y =x − 5 ⇒ x =0 için y =−5
Cevap A
Cevap A
8.
4.
0
2x + 3y − 6 =
A ( 2,1)
3x − 2y + 4 =
0 x
=−2 ters simetri
3 ( −4 − x ) − 2y + 4 =0
2x + 3y + k − 7 =
0
2x + 3y + c − 8 =
0
2.2 + 3.1 + k =
0
k = −7
2x + 3y − 8 = 0 ⇒ 2x + 3y = 8
−12 − 3x − 2y + 4 =
0
3x + 2y + 8 =
0
Cevap B
Cevap A
12
ÖABT Analitik Geometri
9.
KONU TESTİ
A ( 3t,2t + 1)
12.
Analitik Düzlemde Simetri
2x − y + 1 =
0
x
x = 3t ⇒ t =
3
y = 2t + 1 ⇒ y = 2
x
+ 1 ⇒ 3y = 2x + 3
3
2x − y − 3 =
0
2x − y + k =
0
2x − y − 7 =
0
3. ( −1) − 2 ( 3 ) + k =
0
Cevap D
−3 − 6 + k =0
k=9
3y − 2x + 21 =
0
2x − 3y − 21 =
0
Cevap D
a .a + b1.b2
13. d1 − 2 1 22
0
d =
a +b 2 2
2
2
10.
3 −1
3x − y − 8 − 2 2 2 . ( x + y − 4 ) =
0
1 +1
3x − y − 8 − 2 ( x + y − 4 ) =
0
0
⇒ 3x − y − 8 − 2x − 2y + 8 =
x − 3y =
0
y − 2 =−1( x − 3 )
Cevap B
y − 2 =− x + 3
y + x =−5
y+x =
5
x − y =−1
2x = 4
=
x 2,=
y 3
1+ 4 =
5
Cevap D
2.3 + 3 ( −1)
( 3x − y − 7 ) =0
14. 2x + 3y − 1 − 2
( 3 )2 + ( −1)2
11.
3
2x + 3y − 1 − 2 ( 3x − y − 7 ) =0
10
20x + 30y − 10 − 18x + 6y + 42 =
0
2x + 36y + 32 = 0 ⇒ y = 0 için
2x = −32
5x − 12y + 2 =
0
=
5.3 − 12 ( −4 ) + 2 65
= = 5
2
13
52 + ( −12 )
2 = 10
x = −16
Cevap E
Cevap B
13
ÖABT Analitik Geometri
KONU TESTİ
Analitik Düzlemde Simetri
17. y =
x3 − x 2 + x − 1
y=
−x − x =
( −y ) − ( −y ) + ( −y ) − 1
3
15.
2
− x =− y3 − y 2 − y − 1
x = y3 + y 2 + y + 1
Cevap A
c = −7
3 ( −1) − 4.0 + k =
0
k=3
=
13 − 3
=
3 + ( −4 )
2
2
10
= 2
5
=
= 4
2 2.2
Cevap C
18.
16.
y = x 2 − 2x + 3 y
= x x = y 2 − 2y + 3
y =x3 − 3x + 1
yeks göre y =( − x ) − 3 ( − x ) + 1
3
y=
− x3 + 3x + 1
Cevap A
Cevap A
14
ÖABT Analitik Geometri
1.
KONU TARAMA TESTİ – 3
A ( 3, −2 )
y = x B ( −2,3 )
4.
3x − y + 2 =
0
m1 = 3
Analitik Düzlemde Simetri
4.3 + 1. ( −1)
( 3x − y − 4 ) =
4x + y − 3 − 2
0
32 + ( −1)2
11
4x + y − 3 − 2 ( 3x − y − 4 ) =
0
10
40x + 10y − 30 − 66x + 22y + 88 =
0
y − 3= 3 ( x + 2 )
y − 3 = 3x + 6
0 = 3x − y + 9
−26x − 32y + 58 =
0
⇒ 13x − 16y − 29 =
0
Cevap C
Cevap A
2.
5.
=
x1
2x − 3y + 5
= 0
=
y 2 2x − 3 ( 4 − y ) + 5
= 0
2x − 12 + 3y + 5 =
0
2x + 3y − 7 =
0
−1 + 4 + 3
2 + 3 +1
= 2,=
= 2
y1
3
3
=
G
x 3 Gı ( 2.3 − 2,2 )
( 2,2 )
Cevap E
Gı ( 4,2 )
Cevap C
3.
A ( 3,=
4 )
x 0 B ( 3, −4 )
A ( 3, 4=
y 0 C ( −3, 4 )
)
6.
y = x2 − x + 1
A ( 2, −1)
−2−y =
( 4 − x )2 − ( 4 − x ) + 1
−2 − y = 16 − 8x + x 2 − 4 + x + 1
−2 − y = x 2 − 7x + 13 ⇒ − y = x 2 − 7x + 15
x = 0 için y = −15
Cevap B
Alan
= 6.8
= 48
Cevap D
15
KONU TESTİ
ÖABT Analitik Geometri
1.
2x < y
4.
Analitik Düzlemde Eşitsizlikler
3≤ x + y ≤5
x≥0
y≥0
(5 2 ) − (3 2 )
2
2
= 50 − 18 = 32
Cevap E
Cevap A
5.
3x + 4y ≤ 24
x.y ≤ 0
2.
24 + 24 = 48
y−x ≥0
y+x ≥0
Cevap B
( y − x).( y + x) ≥ 0
y2 − x2 ≥ 0
Cevap E
6.
3.
( 4m − 8 ) . (16 − m − 7 ) > 0
( 4m − 8 ) . ( 9 − m ) > 0
x + y ≤2
0 2
4
−2 0
0 −2
2
0
F ( x1.y1 ) .F ( x 2.y 2 ) > 0
1 − 1
4
1
−1
−1 − 1
1
1
=
m 2=
m 9
0 1
4
−1 0
0 −1
1
0
4 + 4 + 4 +1=
13 tane kafes noktası vardır.
2<m<9
3, 4,5,6,7,8
Cevap C
Cevap C
16
KONU TESTİ
ÖABT Analitik Geometri
7.
F ( x1, y1 ) .F ( x 2.y 2 ) > 0
Analitik Düzlemde Eşitsizlikler
9.
( a − 3 ) . ( −1 − a ) > 0
a = 3,
a = −1
-1 < a < 3
mAB = mBP
0, 1, 2
9−5 5−0
=
3 − 1 1− x
4
5
=
⇒ 2 − 2x
= 5
2 1− x
−2x =
3
3
x= −
2
Cevap B
Cevap B
10.
8.
F ( x1.y1 ) .F ( x 2.y 2 ) < 0
( −9 + m ) . ( 7 + m ) < 0
m = 9,
m = −7
7 − 0 0 − ( −5 )
=
7−x
x −1
7
5
=
7 − x x −1
7x − 7 = 35 − 5x
12x = 42
7
x=
2
-7 < m < 9
-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8
7 + 8 = 15
Cevap C
Cevap E
17
ÖABT Analitik Geometri
KONU TESTİ
11.
12.
Analitik Düzlemde Eşitsizlikler
4−y
y +1
=
−12 + 2 −2 − 3
4 − y y +1
=
−10
−5
4 − y = 2y + 2
2 = 3y
y=
2
3
−5 − 1 1 − 7
=
6−x x+2
−6x − 12 =
−36 + 6x
24 = 12x
2=x
Cevap D
Cevap D
18
ÖABT Analitik Geometri
Analitik Düzlemde Eşitsizlikler
KONU TARAMA SINAVI – 4
1.
3.
2
mPA = mAB
y−6
=
0−2
y−6
=
−2
6−3
2−8
3
⇒ y − 6= 1
−6
y=7
mAP = mPBı
0 − ( −6 )
3−0
3
6
=
⇒
=
−2 − x
−2 − x x − 1
x −1
x − 1 =−4 − 2x
3x = −3
x = −1
Cevap E
Cevap D
2.
4.
x + y ≤2
x≥0
mPB = mAP
0 − 4 −2 − 0
=
x − 3 −1 − x
2
1
=
⇒ −2 − 2x = x − 3
x − 3 −1 − x
1 = 3x
1
=x
3
Alan
=
Cevap A
4.2
= 4
2
Cevap C
19
ÖABT Analitik Geometri
KONU TARAMA SINAVI – 4
6.
5.
Analitik Düzlemde Eşitsizlikler
F ( x1.y1 ) .F ( x 2.y 2 ) < 0
( a + 1) . ( 4 + a ) < 0
a=
−1, a =
−4
−4 < a < −1
−3, − 2
y < 3x
y≤0
Cevap B
Cevap B
20
KONU TESTİ
ÖABT Analitik Geometri
1.
r2
( x − a )2 + ( y − b )2 =
4.
Çemberin Analitik İncelenmesi
x 2 + y 2 − 4x + 6y − 12 =
0
25
( x − 2 )2 + ( y + 3 )2 =
M ( 2, −3 ) , r =
5
3 ( 2 ) − 4 ( −3 ) + 17
48
( x − 4 )2 + y 2 =
m ( 4,0 ) .r = 4 3
=
(
a2 + 42 =
4 3
)
= 7
2
32 + ( −4 )
2
Cevap E
a = 4 2 ⇒ 2a = 8 2
Cevap E
2.
x2 + y2 + x =
0
+
0
− / x2 + y2 − y =
x+y =
0
y = − x I. denklemde yazarsak
5.
x2 + x2 + x =
0
x − 3 =− 4y − y 2
2x + x = 0 ⇒ x ( 2x + 1) = 0
2
x =0⇒ y =0
0
( x − 3 )2 + y2 − 4y =
A ( 0,0 )
22
( x − 3 )2 + ( y − 2 )2 =
m ( 3,2 ) , r = 2
1
1
1 1
x=
− ⇒ y = B− ,
2
2
2 2
2
x =−
3
4y − y 2
2
1
2
1 1
AB = − + = =
2
2
2 2
Cevap D
3.
x 2 + y 2 + x + 2y + m =
0
−
2πr
2
2π.2
=
= 2π
2
eğrinin uzunluğu =
x 2 + y 2 − 2x − y − m + 1 =
0
3x + 3y + 2m − 1 =
0
denklemde A ( 2, −3 ) noktasını yazarsak;
6 − 9 + 2m − 1 = 0 ⇒ m = 2
Cevap B
Cevap E
21
KONU TESTİ
ÖABT Analitik Geometri
Çemberin Analitik İncelenmesi
9.
6.
R=5
r=
5
2
Om = 4 2
OT → 60 'ın karşısı → 2 6
Cevap C
Cevap E
7.
m ( 0,0 ) , r = 2 olan bir çemberin denklemi
( x − 0 )2 + ( y − 0 )2 =
( 2)
10.
y=
− x ve y =
x
2
x2 + y2 =
2
2
Cevap B
8.
( 2)
2
= m.m ⇒ m2 = 2
a2 + a2 =
4m2
a2 = 2m2
a2 = 2.2
a = 2
m ( 2,0 ) veya m ( −2,0 )
r 2 = 16 + 1 ⇒ r 2 = 17
( x − a)
2
+ ( y − b) =
r
2
2
+ y2
( x − 2)=
2
17
( x − 2 )2 + ( y + 1)2 =
+ y2 2
2 veya ( x + 2 )=
2
Cevap A
Cevap D
22
KONU TESTİ
ÖABT Analitik Geometri
Çemberin Analitik İncelenmesi
13.
11.
2r de 10 artmış
m= 1
m = −1
( −2,3 )
( −2,3 )
y−3 =
1( x + 2 )
y − 3 =−1( x + 2 )
m=4
y=
x+5
1
1
x=
, y=
2
2
3x – 2y + 4 = 0
r de 5 artar
=
y 3x − 1
=
x 3,=
y 8
Cevap B
( 3,8 )
Cevap B
12.
14.
md1 = 1
md2 = −1
y =x + 3
y=
−2x + 3
x = 0, y = 3
y =− x + 1
y=
−2x + 3
x = 2, y = −1
r = 0 − ( −1) = 1
r = 2 − ( −1) = 3
r =3 − 2 =
1
r =−1 − 2 =3
y−2 =
1( x + 1)
y − 2 =−1( x + 1)
Cevap A ve E
5
( x − 2 )2 + ( y + 1)2 =
Cevap A
23
KONU TESTİ
ÖABT Analitik Geometri
Çemberin Analitik İncelenmesi
17.
15.
2−4
2
= −
2 +1
3
2 −1 1
mAC =
=
çarpımları − 1 olduğu için AB ⊥ BC
2+3 5
4 −1 3
=
mAB =
−1 + 3 2
mBC =
3x − y − 1 =
0
3.1 − y − 1 =
0
2=y
m (1,2 ) ,r = 4
1 3
−3 + 2 1 + 2 1 3
m
,
= − 2,2 ⇒ − 2 + 2 = 1
2
2
16
( x − 1)2 + ( y − 2 )2 =
Cevap C
Cevap E
18.
16.
5x + 12y + 6 =
0
5x + 12 ( −3 ) + 6 = 0 ⇒ 5x = 30
x=6
x = 0 için y = −12
=
y 0=
için x 4
3.r + r − 12 =0
r =3
m ( 6, −3 )
r=
c1 − c 2
2
a +b
2
=
−7 − 6
13
= 1= r
m ( 3, −3 )
1
( x − 6 )2 + ( y + 3 )2 =
9
( x − 3 )2 + ( y + 3 )2 =
Cevap A
Cevap B
24
ÖABT Analitik Geometri
KONU TESTİ
Çemberin Analitik İncelenmesi
21. 3x − y − 6 =
0
19.
−6
x=
0⇒y=
y =0⇒ x =2
−15
x=
0⇒y=
15
4
4r + r − 15 =0
r =3
y =0⇒ x =
( 2 )2 + ( −6 )2 =( 2r )2
m ( 3, −3 )
4 + 36 =
4r 2
40 = 4r 2
Cevap B
10 = r 2
10
( x − 1)2 + ( y + 3 )2 =
Cevap D
2x − y =
5
20.
+
22.
x+y =
1
x=2
b+2 = 0
a + 3 = 2a + 1
b=
2=
a
−2
y = −1
5x 2 + 5y 2 + 2x + 2y + c =
0
2
2
c
x2 + y2 + x + y + =
0
5
5
5
Not :
∆ < 0 → sanal çember belirtir.
∆ = 0 → nokta belirtir.
∆ > 0 → reel çember belirtir.
m ( 2, −1)
=
r
0
( a + 3 ) x2 + (b + 2) xy + ( 2a + 1) y2 + ax − by + c =
3.2 − 4 ( −1) + 5
= 3
2
32 + ( −4 )
x 2 + y 2 + ∆x + Ey + F = 0
D2 + E2 − 4F =
∆
2
2
c
2
2
2 2
5 +5 −45 ≥ 0 ⇒ 5 ≥ c ⇒ c =
5
9
( x − 2 )2 + ( y + 1)2 =
Cevap E
Cevap C
25
ÖABT Analitik Geometri
KONU TESTİ
25.
23.
Çemberin Analitik İncelenmesi
xy − 3x + 5y − 15 =
0
x ( y − 3) + 5 ( y − 3) =
0
0
( x + 5 )( y − 3 ) =
x=
3
−5 y =
( y eksenine teğet )
m ( −5,3 ) ve r =
5
25
( x + 5 )2 + ( y − 3 )2 =
Cevap A
m ( 3,7 )
6.12= 4.D ⇒ D = 18
DC = 18 + 4 = 22
BA =6 + 12 =18
26.
72 + 92 =
r2
130 = r 2
130
( x − 3 )2 + ( y − 7 )2 =
Cevap E
m ( 3, −4 ) ,r =
5
25
( x − 3 )2 + ( y + 4 )2 =
24.
Cevap C
27.
42 = 2 OC ⇒ OC = 8
( −3 )2 + 42 =
x=
− 7 5 cos θ → ( x − =
7)
25 cos2 θ
2
y +=
24 5 sin θ → ( y + 24=
) 25 sin2 θ
2
r2 ⇒ r = 5
25
( x − 7 )2 + ( y + 24 )2 =
Cevap D
Cevap C
26
ÖABT Analitik Geometri
KONU TESTİ
28. =
x 2 + y 2 9, m=
( 0,0 ) ,r1 3
Çemberin Analitik İncelenmesi
31.
x 2 + y 2 + 8x − 6y + 24 =0 → m2 ( −4,3 ) r2 =1
16
( x − 3 )2 + ( x + 1)2 =
x 2 − 6x + 9 + x 2 + 2x + 1 =
16
m1m2=
16 + 9= 5
2x 2 − 4x =
6
x 2 − 2x − 3 =
0
Cevap A
29.
x =3⇒ y =3
A ( 3,3 )
x =−1 ⇒ y =−1
B ( −1, −1)
AB =
( −1 − 3 )2 + ( −1 − 3 )2 =
4 2
Cevap B
Cevap D
30.
32. =
y mx − 2
m=
0 için ⇒ y =
−2
m = 1 için ⇒ y = x − 2
y=
−2 için ⇒ m =
0
y 3 = −x
1
y= −
x
3
1
−
=
m=
tan α
3
tan α =150
(
( −3 − 0 )2 + ( 2 − ( −2 ) )
m ( 0, −2 ) , r =
5
mA =
)
m −2,2 3 ,r =
2
−2.2 3 =
−4 3
2
= 5= r
x2 + ( y + 2) =
25
2
Cevap C
Cevap E
27
KONU TESTİ
ÖABT Analitik Geometri
33. m ( −3,1) , r =
4
mA =
2
35.
( −3 − 2 )2 + (1 − 0 )2 =
x + 16 = 26 ⇒ x =
Çemberin Analitik İncelenmesi
=
r 2.m1 ( −1,0 )
26
x 2 + y 2 + 2x − 6y − 3 =
0
10
x 2 + 2x + 1 + y 2 − 6y + 9 =
13
Cevap D
13
( x + 1)2 + ( y − 3 )2 =
m ( −1,3 ) .r =
13
=
y 0 için x 2 +=
2x − 3 0
−3, x =
x=
1
4
( x + 1)2 + y2 =
Cevap A
36.
x 2 + y 2 − 8x + 6y =
0
52
( x − 4 )2 + ( y + 3 )2 =
34.
x 2 + y 2 + 4x − 10y + 25 =
0
22
( x + 2 )2 + ( x − 5 )2 =
m1m2 = a2 + 32 = 5 ⇒ a2 + 9 = 25
a = 4
a > 0 ise a =
4
mm =
2
36 + 64 = 10
3 + x = 102 ⇒ x=
Cevap C
2
91
Cevap E
28
ÖABT Analitik Geometri
KONU TARAMA SINAVI – 5
1.
4.
Çemberin Analitik İncelenmesi
52
( x − 2 )2 + y 2 =
m ( 2,0 ) , r = 5
3<r <7
4,5,6
Cevap D
Cevap B
2.
x 2 + ( ax + b ) =
r2
2
5.
x 2 + a2 x 2 + 2axb + b2 − r 2 =
0
−2ab
= 0 ⇒ −2ab = 0
a2 + 1
a.b = 0
x 2 + y 2 + 6x − 4y + 8 =
0
−
x 2 + y 2 − 2y + 6 =
0
6x − 2y + 2 =
0
3x − y + 1 =
0
Cevap D
Cevap A
3.
6.
y+7 y−4
.
= −1
x+3 x−2
2
42
( x − 2 )2 + ( y + 3 )2 =
2
y + 3y − 28 =− x − x + 6
x 2 + y 2 + x + 3y − 34 =
0
Cevap C
Cevap A
29
ÖABT Analitik Geometri
KONU TARAMA SINAVI – 5
10.
7.
Çemberin Analitik İncelenmesi
x 2 +=
y 2 − 12x 0, m=
( 6,0 ) , r 6
2
k)
( x + 2 )2 + ( y − =
mm =
64, m ( −2,k=
) ,r 8
82 + k 2 = 10
=
k 2 100 − 64
k 2 = 36 ⇒ k = 6
2
( x − 3 )2 + (mx + 1)2 =
x 2 − 6x + 9 + m2 x 2 + 2mx + 1 =
2
x 2 + m2 x 2 + x ( −6 + 2m ) + 8 =0
( −6 + 2m )2 − 4 (1 + m2 ) 8 =0
7m2 + 6m − 1 = 0 ⇒ ( 7m − 1)( m + 1) = 0
Cevap D
m = −1
y =− x + 1
11. m (1, −2 ) , r =
4
y + x −1=
0
Cevap A
8.
82 + 82 =
( 2r )
2
r 2 = 32
32
( x − 1)2 + ( y + 2 )2 =
Cevap B
Cevap B
12.
9.
20
( x + 1)2 + ( y + 3 )2 =
20
( x + 1)( x1 − a ) + ( y + 3 )( y1 + b ) =
( x + 1) ( 3 − ( −1) ) + ( y + 3 ) ( −1 − ( −3 ) ) =20
4x + 4 + 2y + 6 =
20
4x + 2y =
10
2x + y =
5
m = −2
=
3 ( −2 ) + 4 ( −3 ) − 12
5
=6
Cevap A
Cevap A
30
ÖABT Analitik Geometri
KONU TESTİ
4.
1.
Elips
2
x=
+ y 2 25, =
a 5
2
x=
+ y 2 9,
=
b 3
b
a
3 2
=1 − =
5 5
basıklık = 1 −
Cevap B
x2
52
+
y2
32
=
1
5.
9x 2 + 25y 2 =
225
Cevap B
2.
e=
c
a
15
= 5
3
15
y=
−
=
−5
3
=
y
x2
y2
+
=
1
0,64 1
2
a=
b2 + c 2
=
12
( 0,8 )2 + c 2
Cevap E
c 2 = 0,36
c = 0,6
0,6
=
e = 0,6
1
6.
Cevap C
3.
x2
2
2
+
y2
(
2 5
)
2
2x 2 + 3y 2 =
30
x.x1 y.y1
x2 y2
3x 2y
+
=⇒
1
+
=⇒
1
+
=
1
15 10
15
10
15 10
x y
+ =1 ⇒ x + y = 5
5 5
=
1
F ( 0, 4 )
8 birim
F ' ( 0, −4 )
Cevap D
TA
=
5.5 25
=
2
2
Cevap C
31
KONU TESTİ
ÖABT Analitik Geometri
7.
x.x0 y.y0
x2 y2
+
=⇒
+
=
1
1
16 4
16
4
3
3
10.
Elips
4x 2 + 5y 2 =
100
x2 y2
1
+
=
25 20
2x y ( −1)
1 ⇒ 6x − 4y =
16
+
=
16
4
3
3x − 2y =
8
3
m=
2
2
mN = −
3
y − y=
1 mN ( x − x1 )
a 5=
b 2 5
=
2
( x − 2)
3
3y + 3 =−2x + 4
y − ( −1) =−
2
a=
b2 + c 2
2x + 3y − 1 =
0
y 0=
için x
=
= 20 + c 2
25
1
2
c2 = 5 ⇒ c = 5
4
Cevap D
( 5)
2
+ 5.y 2= 100 ⇒ y= 4
( 4 + 4) (
)
5+ 5
= 8 5
2
=
T.A
Cevap E
8.
4x 2 + y 2 =
16
x2 y2
+
=
1
4 16
11. 2x 2 + y 2 =
4
elips alanı =
π.a.b
x2 y2
1
+
=
2
4
=
b =
2, a 2
= π.4.2
= 8π
2
a=
b2 + c 2
Cevap C
=
22
( 2)
2
+ c2
2 = c2
c= 2
( )
F ( 0, − 2 )
F 0, 2
ı
9.
4x 2 + 9y 2 =
1
2
2
x
y
1
1
+
=1 ⇒ a2 = → a =
1
1
4
2
4
9
1
1
⇒ b2 = → b =
9
3
m ( 0,0 ) r = 2 olan çember denklemi
1
x = cos θ
2
y=
2
x 2 + y=
1
sin θ
3
( 2)
2
2
⇒ x 2 + y=
2
Cevap B
Cevap D
32
ÖABT Analitik Geometri
KONU TESTİ
Elips
15. mx 2 + 9y 2 =
225
12.
x2
y2
asal ekseni x = 0 doğrusu ise
+
=
1
225 225
↓
m
9
15
15
= b
= 5= a
elips y ekseni üzerinde
3
m
2
b
2 b
= 1− ⇒ 1− =
5
a
5 a
15
3 b 3
= ⇒ = m
5 a 5
5
5.15
15 =
m
x=6
x2
102
+
y2
82
=⇒
1
x2 y2
+
=
1
100 64
m =5 ⇒ m =25
Cevap A
Cevap E
13.
4x 2 + y 2 =
25
x2 y2
+
=
1
25 25
5
a2 = 25
a = 5
25
b2 =
4
5
b=
2
5 5
+ =
5
2 2
16.
x
= cos θ 2
y2
x
8
+
=
1
y
64 36
= sin θ
6
Cevap C
14. Doğrunun basıklığı _________ sadece asal
eksen var.
Fı.F − 0
Fı.F
= 1 ⇒ doğrunun basıklığı
çemberin basıklığı :
2r − 2r
=0
2r
Elip sin basıklığı : 0 < b3 < 1
2
8=
62 + x 2
x 2 = 28
x = 2 7
b1 > b3 > b2
ı
=
+ 4 7
F=
F 2 7 +2 7
Cevap D
Cevap C
33
KONU TESTİ
ÖABT Analitik Geometri
17.
20.
x2 y2
+
=
1
8 12
12= 8 + c 2
m ( 0,0 ) r = 5
2
Elips
c2 = 4
c = 2
2
⇒x +y =
25
Cevap E
Cevap E
21.
18.
x 2 + y 2= 100 ⇒ a= 10
x 2 + y 2 = 64 ⇒ b = 8
c
6 3
=
e= =
a 10 5
2
a=
b2 + c 2
100 = 64 + c 2 ⇒ c 2 = 36
c = 6
Cevap C
r2
( x − a )2 + ( y − b )2 =
F ( c,0 ) , r = 2a
( x − c )2 + y 2 =
( 2a )2
Fı ( −c,0 ) , r =
2a
19.
( x + c )2 + y 2 =
( 2a )2
( x − c )2 + y 2 =
( 2a )2
( x + c )2 + y 2 =
( 2a )2
( x − 0)
2
+ ( y − 2)
x 2 + y 2 − 4y +=
4
2
1
=
2 2
(
y − 16
8x = 0 → x = 0
x = 0 için
02 + y 2
64
( −2 )2 + y2 =
1 2
y − 32y + 256
8
)
y = 2 15
(
)(
kesişim noktaları 0, −2 15 0,2 15
8x 2 + 8y 2 − 32y + 32 =y 2 − 32y + 256
)
4 15
8x 2 + 7y 2 =
224
Cevap E
Cevap C
34
KONU TESTİ
ÖABT Analitik Geometri
22.
( x − ( −2) )2 + ( y − 0 )2 =62
Fı ( −2,0 ) ,
24.
2a =
6
Elips
x2 y2
+
= 1
k
4
( a2 ) 12
2
y = 2x ⇒ m = 2
(b )
a=3
b2 + ( −2 ) =32
2
b2 = 5
b= 5
m1.m2 = −
b2
a2
12
x
b2 1
1
x=
− ⇒ 2 = ⇒ k =
2
8
4
4
4
a m
a
k = 12
−b2
Cevap E
x2 y2
+
=
1
9
5
Cevap A
25.
23.
m=
x + ( y − 3) =
100
2
2
y−0 y−0
9
= −
.
x − ( −2 ) x − 2
4
2a = 10
=
a 5=
b 4
y2
F ( 0,3 )
x2
42
2
+
y 2 − y1
x 2 − x1
4−x
y2
52
2
=
9
4
2
4y=
36 − 9x 2
=
1
y2 x2
+
=
1
9
4
2
x
y
+
=
1
16 25
Cevap C
Cevap B
35
KONU TESTİ
ÖABT Analitik Geometri
26.
∆ =0
Elips
29.
b2 + m2a2 =
n2
x2 y2
+
=
1
25 16
a2
b2
16 + 25m2 =
52
25m2 = 9
9
m2 =
25
3
m=
5
7k = 14
k=2
x
cos θ = 2
y2
6 x
+
=
1
y 36 64
sin θ =
8
Cevap B
Cevap A
27.
x2
a2
+
y2
b2
=
1
2
24
5
x
y
8
=
1
1
+
=→
+
100
102 b2
b2
24.24 1
9
.
=
→ b2 = 64
25 b2 25
2
2
2
30.
x2 y2
+
=
1
100 64
Cevap A
28.
=
r
a2 + b2
=
r
16 + 9
r =5
x2 + y2 =
25
Cevap D
2
a=
b2 + c 2
100 = 64 + c 2 → c = 6
36 18
62 = x.10 ⇒ x =
=
10
5
II. yol
x.x1 + y.y1 =
36
10x + 0y = 36 ⇒ x =
18
5
Cevap B
36
ÖABT Analitik Geometri
1.
( x + 3 )2 + y 2
KONU TARAMA SINAVI – 6
1 x + 12
=
.
2
12
Elips
4.
HATALI
1
( x + 3 ) + y = ( x + 12 )2
4
1 2
2
x 2 + 6x + 9 + y=
x + 24x + 144
4
2
2
(
)
4x 2 + 24x + 36 + 4y 2 =x 2 + 24x + 144
3x 2 + 4y 2 = 144 − 36
3x 2 + 4y 2 =
108
Cevap A
5.
2.
e=
x2 y2
1
+
=
4 12
x.x0 y.y0
2.x y
+
=⇒
−
=
1
1
4
12
4 12
(3)
6x − y = 12 ⇒ 6x − y − 12 = 0
c 3k
6
=
=
a 5k 10
= 6
3k
2
a=
b2 + c 2
=
k 2
= b2 + 36
100
Cevap B
64 = b2
yedek çemberin denklemi
x2 + y2 =
64
Cevap D
6.
3x + y − 7 =
0
m=
m1.m =
−3
−1
3.
x
=
cos θ
3
y
= sin θ
5
x2
=
cos2 θ
9
m1 =
1
3
y mx + n
=
1
y
x+n
=
3
y2
= sin2 θ
25
b2 + a2m2 =
n2 ( teğetlik şartı)
+
2
2
x
y
+
=
1
9 25
a=5
b=3
basıklık =1 −
2
1
5 + 36 =
n2
3
5+4 =
n2
9 = n2 ⇒ n = 73
1
1
y=
x + 3 yada y =
x−3
3
3
3y =
x+9
3y =
x−9
0 =x − 3y − 9
0 =x − 3y − 9
b
3
=1 −
a
5
2
=
5
Cevap C
Cevap B
37
ÖABT Analitik Geometri
KONU TARAMA SINAVI – 6
Elips
9.
7.
x
4
y
sin θ =
6
cos θ =
= 48 + c 2
64
c 2 = 16
c = 4
x2 y2
+
=
1
16 36
Fı ( −4,0 ) ,F ( 4,0 ) ⇒
Cevap B
16 y 2
+
=
1
64 48
y 2 48
48
=
⇒ y=
⇒ y= 6
48 64
8
ı
= ML
= 12
F=
.F 8 ve NK
=
= 96
Alan (KLMN
) 12.8
Cevap D
10.
4x 2 + 5y 2 =
80
x2 y2
1
+
=
20 16
8.
x2 y2
1
+
=
4 12
20m2 + 16 =
36
monj çemberinin denklemi
2
m = 1
2
x + y = 12 + 4
CEvap D
x2 + y2 =
16
Cevap A
38
ÖABT Analitik Geometri
1.
2a
= 12
2
c=
b2 + a2
=
a 6
2
8=
62 + b2
28 = b2
x2
a2
−
y2
b2
2
KONU TESTİ
4.
=
a =
2 3
b 2
=
1
b
x
a
2
2
y=
+
x,
y=
−
x
2 3
2 3
x
x
y=
,
y= −
3
3
1
tan 30 =
3
1
tan150 = −
3
y=
2
Cevap A
y=
x2 y2
−
=
1
12 4
=
a2 12
=
b2 4
x
y
−
=
1
36 28
2.
Hiperbol
b = 3k → b = 9
b
b 3
x⇒ = ⇒
a = 4k → a = 12
a
a 4
2
c=
b2 + a2
225
= 9k 2 + 16k 2
225 = 25k 2
9 = k 2 → k = 3
x2
122
−
y2
92
=⇒
1
x2 y2
−
=
1
144 81
Cevap D
Cevap C
3.
x2 y2
−
=
1 ⇒ c2 =
b2 + a2
18 18
2
a=
18
2
c=
18 + 18
2
b=
18
= a2
2
c=
36
c = 6
5.
x2
=
x 2 9 tan2 θ ⇒ = tan2 θ
9
=
y2 4
y2
1
⇒
=
2
4
cos θ
cos2 θ
1
x2 y2
y2 x2
−
=
−1 ⇒
−
=
1
9
4
4
9
9y 2 − 4x 2 =
36
Cevap A
Cevap C
39
KONU TESTİ
ÖABT Analitik Geometri
6.
Hiperbol
x2 − y2 =
36
=
x 3y − 6
x2 y2
−
=
1
48 12
36
( 3y − 6 )2 − y2 =
=
a2 48
=
b2 12
8y 2 − 36y =
0
2
c=
a2 + b2
c = 2 15
y ( 2y − 9 ) =
0
(2 5 )
y=0
2
− 4y 2 = 48 ⇒ y = 3
AıB=
y=
9
9
⇒ x = 3. − 6
2
2
27 − 12 15
=
x =
2
2
2
2
9 10
15
9
2 + 6 + 2 − 0 =
2
Cevap C
8.
II. yol
x2 y2
−
=
1
9
3
Bu kirişin uzunluğuna hiperbolün parametresi
denir ve
x 2 − 3y 2 =
9
2b2
ile hesaplanır.
a
2.12
24
6 3
= = = 2 3
3
48 4 3
Cevap E
Cevap A
7.
=
x 0=
için y 2
y = 0 için x = −6
9.
F ( 7,0 ) ve Fı ( −7,0 )
x ekseni üzerinde olup asal eksende x te
2b = yedek eksen
2b = 6 ⇒ b = 3
c=7
2
c=
b2 + a2
= 32 + a2
49
Hiperbolün denklemi
x2
a2
−
y2
a2
40 = a2
=
1
x2 + y2 =
40
Cevap A
40
KONU TESTİ
ÖABT Analitik Geometri
13.
10.
Hiperbol
A (1,a ) noktası 4y 2 − 3x 2 =
33 üzerinde ise
4a2 − 3 (1) =
33
2
4a2 = 36
a2 = 9 → a = 3
üzerindeki nokta → A (1,3 ) yada A (1, −3 ) olabilir.
( x − 10 )2 + ( y − 0 )2 =
x−4
5
2 12 + 02
4y ( 3 ) − 3x.1 =
33
⇒ 120 = 3x 2 − 2y 2
4y ( −3 ) − 3x.1 =
33
24y = 0 → y = 0
Cevap A
Cevap C
11.
y = mx + n
4x 2 − ( mx + 4 ) = 8
4 = m.0 + n
4x 2 − m2 x 2 − 8mx + 16 = 8
=
4 n
2
(
(
14. =
y mx → köşegen denklemi
)
)
b2
=
x eşleniğin denklemi
1 2m
a2m
4
1
=
y
x ⇒ 4x −=
y 0
= m
1
2
2.
2
2
y
=
− 8mx − 16 − 8 0
x 2 4 − m=
∆ =0
(
)
64m2 − 4 4 − m2 ( −24 ) =
0
2
(
64m + 96 4 − m
2
0
)=
Cevap A
32m2 = 96.4
m2 = 12 → m = 2 3
−12
( 2 3 ) . ( −2 3 ) =
Cevap B
15.
36
( x − 6 )2 + y 2 =
F ( 6,0 )
12.
4x 2 − y 2 =
15
2a
= 6
2
c=
b2 + a2
=
a 3
36
= b2 + 9
27 = b2
Teğet denklemi 4x.2 − y ( −1) =
15
x2 y2
−
=
1
9 27
8x + y =
15
Cevap B
Cevap A
41
KONU TESTİ
ÖABT Analitik Geometri
x2 y2
16.
=
−
1
64 36
asimptot
=
denklemi y
=
a2 64
=
b2 36
=
y
b
x
a
3
x
4
=
a =
8 b 6
6.4
= 12
2
Alan
=
Cevap E
x2 y2
=
−
1
a2 a2
17. 2a 8
=
x2 y2
=
−
1 yada
16 16
=
a 4
y2 x2
−
=
1
16 16
y2 − x2 =
16
Cevap E
2
18. c=
b2 + a2
2
c=
a2 + a2
2
2
)
2
x
y
=
−
1
9
9
=
c 2 2a2
3 2)
(=
(
F 3 2,0 asal eksen x te
2a2
2
− y2 9
x=
a=3
Cevap D
42
Hiperbol
ÖABT Analitik Geometri
1.
2a
= 6
2
c=
b2 + a2
=
a 3
= b2 + 9
16
KONU TARAMA SINAVI – 7
4.
Hiperbol
2y 2 − 3x 2 =
−19
2y.yo − 3x.xo =
−19 ( teğet denklemi )
2y ( −2 ) − 3x.3 =
−19
7 = b2
4y + 9x − 19 =
0
F ( 0, 4 ) ve Fı ( 0, −4 ) odak y ekseni üzerinde
9
4
m1.m2 = −1
m1 = −
y2 x2
−
=
1
9
7
9
− .m2 =
−1
4
4
m2 =
9
Normal denklemi ise;
4
y + 2=
( x − 3)
9
9y + 18 = 4x − 12
4x − 9y − 30 =
0
Cevap A
Cevap B
2.
=
x a tan θ
hiperbolün parametrik denklemi
=
y b sec θ
y2 x2
− = 1
16 9
5.
x = 3 tan θ
=
y 4 sec θ
Cevap E
y2 x2
−
=
1
64 36
2
c=
b2 + a2
2
c=
36 + 64
3.
e=
c 2k
=
a k
c 2 = 100
c = 10
2k= 8
F ( 0,10 ) ve Fı ( 0, −10 )
c 8=
k 4
=
a=4
odak
noktalarından
birini hiperbol denkleminde yazarsak;
(10 )2 − x2
2
c=
b2 + a2
64
64
= b2 + 16
36
= 1⇒
100
x2
−1=
64
36
2
36 x
36 9
=
⇒ x=
=
64 36
8
2
9
x= −
2
A ( ABCD
=
= 180
) 20.9
48 = b2
yedek çember denklemi
x2 + y2 =
48
Cevap D
Cevap C
43
ÖABT Analitik Geometri
KONU TARAMA SINAVI – 7
6.
x2 y2
−
=
1
12 4
2
c=
a2 + b2
2
c=
12 + 4
c = 4
F ( 4,0 ) ve Fı ( −4,0 )
noktalarından birini hi-
perbol denkleminde yazarsak;
16 y 2
1
−
=
12 4
16
y2
−1=
12
4
4
y2
16
=
⇒ y2 =
12
4
12
4
y=
2 3
2 3
2 3
4.
4.
8 3 8 3
3
3 =
Alan =
+
+
2
2
6
6
=
16 3 8 3
=
6
3
Cevap E
44
Hiperbol
KONU TESTİ
ÖABT Analitik Geometri
1.
3.
Parabol
y2 =
−32x
y2 =
2px
p = 2mn teğet olma şartı
2p =
−32
y=
mx + n
p=
−16
−16 =
2.1.n
−8 =
n
Cevap B
4.
y 2 = 2px paralel denklemi
p
F ,0
2
p
= −2
2
p=
y2 =
2 ( −4 ) .x
−4
y 2 = −8x
a2= 12x ⇒ x=
Cevap C
a2
12
a
a2
= y,= x
2
24
a = 2y,
2.
y 2 = 6x
y.y1 = p ( x + x1 ) → Teğet denklemi
y 2 = 4x
Cevap C
= 2 ( x + 1)
y.2
=
2p 4
y= x + 1
=
=
x 0 için ⇒
y 1
−1
y=
0 için ⇒ x =
5.
4
= 2p
Alan
=
a2 = 24x ⇒ 4y 2 = 24x
1.1 1
=
2
2
p
⇒p
= 2
2
y 2 = 4x
y 2 = −4x
m = 4
Cevap B
Cevap B
45
ÖABT Analitik Geometri
KONU TESTİ
6.
8.
Parabol
x 2 = 8y
y= −
x 2 = 2py
y= −
p= 4
p
doğrultman denklemi
2
4
2
y = −2
Cevap D
p
p
D , y ⇒ y2 =
4
2
2
y 2 = 2p
y 2 = 4x
2p = 4
p=2
9.=
p 3=
y 2 2px
y 2= 4 ⇒ y 2
3.2 = 6
y 2 = 2.3x ⇒ y 2 = 6x
−6x
y2 =
2. ( −3 ) x ⇒ y 2 =
Cevap D
7.
Cevap C
p
F 0,=
F ( 0, −2 )
2
p
=−2 ⇒ p =−4
2
10.
2
x=
ay
= 2py
a = 2p
a=
2 ( −4 ) =
−8
x 2 = −8y parabolü
m
= x ⇒ m =2x
2
x =−
( −2x )2 − 2
y 2 = 2px
8
2
=y
p
=
3 ⇒ p =−6
2
y 2= 2 ( −6 ) x
x 2 + 4y + 4 =
0
y 2 = −12x
Cevap A
Cevap A
46
KONU TESTİ
ÖABT Analitik Geometri
11.
x =−
p
=−2 ⇒ p =4
2
Parabol
14.
y 2 = 2px ⇒ y 2 = 8x
Bu doğrunun geometrik yer denklemi y ekseni
üzerindedir.
y 2 = 8.4
y 2 = 32
Cevap A
y=4 2
Cevap D
12. 2p = 8
x.4 = y ( 9 + 2 ) → teğet denklemi
p= 4
x= y + 2
x−2 =
y
mT = 1 mN = −1
y − y1 =mN ( x − x1 ) ⇒ y − 2 =−1( x − 4 )
x = 0 için y − 2 = 4 ⇒ y = 6
Cevap E
13. 2p = 2
p=1
15.
p
m
1
1
−2 = ⇒ m =−
m
2
1
y + 2 =− ( x − 3 )
2
x + 2y + 1 =
0
y=
A ( x, y )
x=a
→ ( 2 − x, y )
x =1
y2 =
−6 ( 2 − x )
y2 6 ( x − 2)
=
Cevap B
Cevap A
47
KONU TESTİ
ÖABT Analitik Geometri
18. =
10 2p
16.
=
p 5
Parabol
=
p 2mn → Teğet şartı
=
5 2m ( 2m − 4 )
0 = 4m2 − 8m − 5
m1 + m2 =
2
A ( x1.? ) → x12 = 4y ⇒
x12
=y
4
x2
A x1, 1
4
B ( x 2.? ) → x 22 = 4y ⇒
x 22
=y
4
Cevap C
B x2
4
x2
, 2
=
x 2 4 ( mx + m )
x 2 − 4mx − 4n =
0
x1 + x 2 =
4m
x1 + x 2
=4 ⇒ x1 + x 2 =8
2
4m =8 ⇒ m =2
=
y 2x + n
C ( 4,2 )
=
6 2.4 + n
n = −2
m+n =
0
Cevap E
17.
2p = 4
F (1,0 )
p=2
y 2 = 4.1
y = 2
Cevap C
48
ÖABT Analitik Geometri
1.
y−4
=
x2 + ( y + 4 )
y − 4=
x2 + ( y + 4 )
12
KONU TARAMA SINAVI - 8
Parabol
4.
2
2
y 2 − 8y + 16 = x 2 + y 2 + 8y + 16
−16y =
x2
6x = ( −6 − x )
Cevap D
2
6x
( x + n )2 =
2
x + ( 2n − 6 ) x + n2 =
0
0
( 2n − 6 )2 − 4.1.n2 =
2.
−
4n2 − 24n + 36 − 4.n2 =
0
36 6 3
n=
= =
24 4 2
p
→ doğrultman denklemi
2
Cevap D
p
p
=3 ⇒ =−3 ⇒ x =−3
2
2
p=6
5.
Cevap B
p = 2mn
2 = 2m.m
=
1 m → Aradaki açı 90o
3.
Cevap D
6.
36 = 2p.4
9
p=
2
9
2
y = 2. x
2
y 2 = 12x
2p = 12
p=6
p 6
y= = =6⇒y=6
m 1
y 2 = 9x
Cevap C
Cevap A
49
KONU TESTİ
ÖABT Analitik Geometri
4.
1.
Düzlemde Vektörler
p = ( x, y ) olsun
PA = A − P = ( −1 − x, 2 − y )
2
2
PA = ( −1 − x ) + ( 2 − y ) = 3
9
( x + 1)2 + ( y − 2 )2 =
Cevap A
GB + GC =
−GA
GB + GC + GA =
0
Cevap E
5.
2
mp = =
−2
−1
−2.m =
−1
m=
1
2
eğimi ve geçtiği nokta belli doğru denklemi
y − y1= m ( x − x1 )
2.
AB =
( −2 − a )2 + ( −3 )2
1
( x − 2)
2
2y + 6 = x − 2 ⇒ 0 = x − 2y − 8
y + 3=
⇒ ( a + 2 ) + 9 = 25
2
16
( a + 2 )2 =
Cevap A
a+2 = 4⇒ a = 2
− 12
a + 2 =−4 ⇒ a =−6
Cevap C
6.
3.
paralel vektörlerin eğimleri eşittir.
mA = mB
tan x 4 sin x
=
⇒ tan x.cot x =
4 sin x.cos x
cos x
cot x
1 = 2 sin 2x
1
= sin 2x
2
→ 2x =
30
x = 15
OC.OB
( 3, 4 ) . ( 6,2 ) = 3.6 + 4.2 = 26
Cevap A
Cevap C
50
KONU TESTİ
ÖABT Analitik Geometri
7.
Bir vektöre paralel olan doğruya doğrultman
10.
Düzlemde Vektörler
A
=
( 3, −4 )
B = (10,0 )
A.B ( 3, −4 ) . (10,0 ) 30 + 0
=
= = 6
2
5
A
32 + ( −4 )
denir.
Cevap D
Paralel doğruların eğimi eşit.
(4k, 3k) vektörü A olsun.
=
A= 15
( 4k )2 + ( 3k )2
11.
ya (12,9 )
yada ( −12, −9 )
A.B ( 3, −2 ) . (1,2 )
1
1 2
.B =
. (1,2 ) =
− . (1,2 ) =
− 5 ,− 5
2
2
5
12 + 22
B
Cevap B
Cevap A
8.
2x − y + 1 =
0
m= 2
2m1 = −1
1
m1 =
−
yani ( 2k, − k ) vektörü
2
12.
Başlangıç
( 2k )2 + ( −k )2
=
2 5
2
=
2 5
4k + k
20 = 5k
A için konum vektörü;
(0,−( −2),
Bitiş
B
( 3,1)
( 0,3 )
2
3 −1) =( 2,2 )
B için konum vektörü;
( 3 −0, 1−3 ) = ( 3,−2)
Bitiş
A.B = ( 2,2 ) . ( 3, −2 ) = 2.3 + 2. ( −2 ) = 6 − 4 = 2
Başlangıç
2
4 = k2
( 4, −2 )
k =2
A
( −2,1)
( 0,3 )
yada ( −4,2 )
Cevap D
Cevap B
9.
A
=
( 3, −4 )
m= −
13.
4
3
− .m =−1 ⇒ m =
3
4
=
100 16k + 9k
1
3
( 3k,k ) bu vektör birim vektör ise normu 1 dir.
( 4k,3k )
1
( 3k )2 + k =
2
k=
100 = 25k 2
1
10
1
3
1
3
,
,−
yada −
10
10
10 10
4 = k2
( 8,6 )
−3.m1 =
−1
m1 =
( 4k )2 + ( 3k )2
2
=
k 2
(1, −3 )
−3
m=
4
3
=
10
A=
yada ( −8, −6 )
Cevap A
Cevap B
51
KONU TESTİ
ÖABT Analitik Geometri
14. 3y
= 13 − 2x
Düzlemde Vektörler
17.
13 2
− x
3 3
2
m= −
3
2
− .m1 =
−1
3
3
m1 =
( 2k,3k ) birim vektörün normu 1 dir.
2
A
=
y
( 2k )2 + ( 3k )2
+
2
+ 2A.B + B
− 2A.B + B
4A.B = 20
A.B = 5
2
−/ A
2
=
36
2
16
=
Cevap A
=
1
1
13
1
=
13
2
3
2
3
,
, −
veya −
13 13
13
13
k2 =
k
18.
A − B =( −3, 4 )
A.B = 5
2
A −B =
Cevap A
A
2
( −3 )2 + 42
+ B
2
− 2A.B
2
= x − 2.5 ⇒ x = 35
Cevap E
15.
A=
( −2, 5 )
2
A = ( −2 ) + 5
2 5
A
= − ,
3 3
A
( )
2
=3 olup
19.
A +B
+
2
=
A −B
A
2
=
(
2
A
42 + =
62 2 A
Cevap A
+ B
2
2
2
+ 2A.B
+ B
+ B
2
2
− 2A.B
)⇒ A
2
2
+ B= 26
Cevap B
A = ( −1,5 )
16.
( 3, −4 )
AB =
B = ( 2,1)
AB =
5
20.
AB ile zıt yönlü olan birim vektör.
AB
3 4
− =
− 5,5
AB
( A + B )2 =( A − B )2 − 4AB
A +B
2
= A −B
2
− 4A.B
A ⊥ B ⇒ A.B =
0
62 = x 2 ⇒ x = 6
Cevap D
Cevap E
52
ÖABT Analitik Geometri
KONU TESTİ
21.
Düzlemde Vektörler
A +B
23.
(
34
)
2
2
A − 2B
=
A
2
+ B
2
+ 2A.B
=
−9
42 + 62 + 2A.B ⇒ A.B =
2
= A
2
+4 B
2
− 4A.B
x 2 = 42 + 4.62 − 4 ( −9 )
x2 =
16 + 4.36 + 36
x 2= 196 ⇒ x= 14
x 6
=
2 y
x.y = 12
Cevap E
24.
AB.DC = − x.y cos 60
=
−12.
1
=
−6
2
Cevap B
OD = ( 9,3 )
BE = ( −8, 4 )
−60
OD.BE =
9 ( −8 ) + 3.4 =
Cevap A
22.
BE.BF = 4 3.8.cos 30
3
= 4=
3.8.
48
2
Cevap C
53
ÖABT Analitik Geometri
KONU TARAMA SINAVI – 9
5.
1.
Düzlemde Vektörler
u = ( 3,2 )
v ( 2, −1)
=
u.v ( 3,2 ) . ( 2, −1)
4
8 4
.v=
. ( 2, −1)=
( 2, −1)= , −
2
5
5
5 5
v
Cevap C
AB + BC =
AC
BD
+ AD =
+ BA
BC + AD = AC + BD
Cevap A
2.
m=
6.
2
= 2
1
y − 4= 2 ( x − 3 )
y − 4 = 2x − 6
y − 2x + 2 =
0
Cevap C
BA. BC + AC
BA.BC + BA.AC
4.x.cos θ + 0
4
4.x. = 16
x
(
3.
12x + 5y + 3 =
0
12
5
( 5k, − 12k ) yada ( −5k,12k )
m= −
25k 2 + 144k 2 =
132
( 5, −12 )
)
Cevap D
yada ( −5,12 )
Cevap A
4.
A ( −4,3 ) .B ( −2,3 ) =
17
Cevap C
54
KONU TESTİ
ÖABT Analitik Geometri
1.
B−A=
Uzayda Vektörler
A.B
5.
=
.B
2
B
( 2, −3, +4 )
C − B =( −1,1, −2 )
C − A = (1, −2, −2 )
AC = 1 + 4 + 4 = 9
CA = 3
+
( 2, 4, −6 ) . (1, −1,0 ) . 1, −1,0
(
)
2
−1. (1, −1,0 ) =
( −1,1,0 )
Cevap B
Cevap B
6.
u=
(1, −2,2 )
v
=
2.
9 u
2
+ 16 v
2
+ 144 w
2
( 0,3, −4 )
u.v (1, −2,2 )( 0,3, −4 )
=
=
=
13
5
v
−
14
5
14
uzunluğu
5
Cevap C
Cevap A
3.
−4,2, −6 )
( 2, −1,3 ) . (=
14. 56 cos θ
7.
−8 −=
2 − 18 2.14.cos θ
−=
1 cos θ
θ =180
B − A=
(1,2, −5 )
B − (1, −1,3 )= (1,2, −5 )
B= (1,2, −5 ) + (1, −1,3 )= ( 2,1, −2 )
−2 ) 2 1 2
( 2,1,=
B
=
3 , 3 ,− 3
3
B
Cevap E
Cevap A
4.
y ekseni üzerinde herhangi bir vektör alalım.
u = ( 0,1,0 )
( 0,1,0 ) . (
8.
A
=
=
B
)
=
3,2,3 4.1.cos θ
( 2, −3, 4 )
(10, 4, −2 )
=
20 − 12 − 8
1
= cos θ
2
θ =60
29. 120.cos θ
=
0 cos θ
θ =30
Cevap C
Cevap C
55
KONU TESTİ
ÖABT Analitik Geometri
9.
Uzayda Vektörler
A.A − A.B + A.C
Cevap C
32 − 3.4 cos 60o =
3
13.
Cevap A
x 2 − 4x + 4 + y 2 − 6y + 9 + z2 + 8z + 16 =
9
9
( x − 2 )2 + ( y − 3 )2 + ( z + 4 )2 =
r =3
Cevap C
10.
14.
x 2 − 6x + 9 + y 2 − 4y + 4 + z2 =
25
25
( x − 3 )2 + ( y − 2 )2 + z 2 =
( x − 2) + ( y + 1)
2
2
+ z = ( x − 4 ) + ( y − 3 ) + ( z + 2)
2
2
2
yüzey alanı =4πr 2 =4π25 =100π
2
Cevap D
4x + 8y − 4z =
24
z + 2y − z =
6
Cevap A
15.
11. r =
( −2 )2 + 02 + 32
x 2 + 2x + 1 + y 2 − 4y + 4 + z2 − 6z + 9 =9
9
( x + 1)2 + ( y − 2 )2 + ( z − 3 )2 =
m ( −1,2,3 ) ,r =
3
⇒ r 2 = 13
x 2 + y 2 + z2 =
13
Cevap E
Cevap D
12. m1 ( −1,0,2 ) ,r1 =
4
m2 ( 2, 4, −10 ) .r2 =
5
16.
AB=
(1, −1,1)
AC = ( 0,2,2 )
1
1
AB + AC =
( −4i, −2j,2k ) =
2
2
m1.m2 = 13
24
=
2
6
Cevap A
56
KONU TESTİ
ÖABT Analitik Geometri
1
17.
0
3
A,BxC = 2 −1 0 = 1( −2 ) + 0 + 3.8 = 22
0
4
2
Cevap C
18.
i j k
AxB = 1 0 3 =( −6i, −4j,2k )
0 2 4
=
36 + 16 + 4= 2 14
Cevap D
57
Uzayda Vektörler
ÖABT Analitik Geometri
1.
KONU TARAMA SINAVI – 10
X2 − 2X + 1 + Y 2 + 4Y + 4 + Z2 − 6Z + 9 =9
5.
9
( x − 1)2 + ( y + 2 )2 + ( z − 3 )2 =
m (1, −2,3 ) .r =
3
Uzayda Vektörler
1 2 3
A.BxC = 0 −1 2 = 1( −3 ) − 2 ( −6 ) + 3.3 = 18
3 0 3
Cevap C
yüzey alanı = 4πr 2 = 4π9 = 36π
Cevap E
2.
x 2 − 2x + 1 + y 2 − 6y + 9 + z2 =4
6.
Cevap E
MA = 5
Cevap D
A=
22 + 12 + ( −2 )= 3
2
Doğrultman ko sinüsleri
=
2 1
2
, ,−
3 3
3
Cevap A
4.
=
OA
A.B
=
2
B
)
( 7, −4,3 ) . ( 0,0,3
=
3
k
0 =
( −2i,0.j, −4k ) =4 + 16 =2 5
2 0 −1
4
( x − 1)2 + ( y − 3 )2 + z2 =
m (1,3,0 ) ,r = 2
3.
i j
AxB =0 2
( 0,0,3 )
02 + 02 + 32 =
3
Cevap B
58
KONU TESTİ
ÖABT Analitik Geometri
1.
x − x1 y − y1 z − z1
= =
formunda olmalı
a
b
c
6.
Uzayda Doğru Denklemleri
A ( 3,2, −1) , B ( a, 4,2 )
3a + 2.4 − 1.2 =
0
1
3
y−
z+
x+2
3
2
= =
4
5
3
3
2
4 5
3, 3 , 2 ⇒ (18,8,15 )
3a + 8 − 2 =
0
3a = −6
a = −2
Cevap A
Cevap C
2.
A ( 2, −1,0 ) ve B ( 5,2, −3 )
AB = ( 3,3, −3 ) yada BA = ( −3, −3,3 )
BA = ( −1, −1,1)
7.
x +1 y − 2 z
d2 : = =
3
m
n
2
1
3
=
− ⇒m=
−
3
m
2
2 4
= ⇒n= 6
3 n
3
m.n =− − 6 =−9
2
Cevap B
3.
x − 3 y +1 z − 4
d1 : = =
2
−1
4
x − 3 y − 2 z −1
= =
−1
2
4
Cevap B
Cevap A
4.
x−2 z−3
,=
y +1 0
=
1
2
8. =
d1
Cevap D
d2 =
x − 2 y −1 z −1
= =
→ (1,1,n )
1
1
n
x−3 y−5
, z − 4 = 0 → (1,1,0 )
=
1
1
(1,1,n )(1,1,0 ) =
5.
=
2
x−2 y−3
z +1
= =
3 − 2 1 − 3 2 − ( −1)
2 + n2 . 2.
12 + 12 + 12 . 12 + 12 + 02 .cos 60
1
2
(
)
4 = 2 + n2 . 2 ⇒ 16 = 2 + n2 .2
x − 2 y − 3 z +1
= =
1
−2
3
2
8 =2+n ⇒ n = 6
Cevap D
Cevap C
59
KONU TESTİ
ÖABT Analitik Geometri
12.
9.
Uzayda Doğru Denklemleri
y = 1 için
x − 2 1+ 1
1+ 1
=
= z − 3,
,
3
2
2
=
x 5=
z 4
z = −1 için
x − 3 =− y + 1 =−1 + 2
=
=
−y + 1 1
x − 3 1,
=
x 4=
y 0
( 3, −3,0 ) . ( 2, −2,1=)
B ( 4,0, −1)
32 + ( −3 ) + 02 . 22 + ( −3 ) + 12 .cos α
2
2
AB=
6=
+ 6 + 0 3 2.3cos α
=
12 9 2 cos α
4
= cos α
3 2
Cevap B
z−
1
2
1
2
x − 2 y +1 z − 3
=
=
⇒ 3x − 6 = y + 1 = 2z − 6
1
1
1
3
2
Cevap A
11.
v1 = ( 2,1,3 )
v 2=
( 5 − 4 )2 + (1 − 0 )2 + ( 4 + 1)2 =
3 3
Cevap E
h= 2
x y+2
10.= =
1
1
3
A ( 5,1, 4 )
(1, −1,2 )
i
j k
v1xv 2 = 2 1 3 = 5i − j − 3k
1 −1 2
( 5, −1, −3 )
x−3 y−0 z+3
= =
5
−1
−3
Cevap D
60
ÖABT Analitik Geometri
1.
KONU TARAMA SINAVI – 11
A ( 2,1,0 )
5.
Uzayda Doğru Denklemleri
A ( 2,3,1)
B ( −3, −1,2 )
Cevap A
2 ( −3 ) + 3 =
( −1) + 1.2
14. 14 cos θ
=
−7 14 cos θ
1
−= cos θ ⇒=
θ 120
2
Cevap D
2.
x−0 y−0 z−0
x
y z
=
=
⇒
= =
−2
3
1
−2 3 1
Cevap B
6.
3.
( 2,2, −1) . (1,1,1=)
x−0
y−0 z−0
= =
yada
−2 − 0 1 − 0 3 − 0
x + 2 y −1 z − 3
= =
0 + 2 0 −1 0 − 3
−x − 2
z−3
= y −1=
2
3
=
3 3 3 cos α
3
= cos α
3
h= 6
Cevap D
Cevap D
4.
9. 3 cos α
x −1 y + 2
=
= z−3
2
3
x −1
= k ⇒ x − 1 = 2k
2
=
x 2k + 1
y+2
= k ⇒ y + 2 = 3k
3
=
y 3k − 2
z−3 =k ⇒ z =k +3
Cevap A
61
ÖABT Analitik Geometri
1.
KONU TESTİ
2 ( x − 3 ) + ( −1)( y − 2 ) + 3 ( z − 1) =
0
6.
Uzayda Düzlem Denklemleri
3 ( x + 1) + 2 ( y − 0 ) + 1( z − 2 ) =
0
3x + 3 + 2y + z − 2 =
0
3x + 2y + z + 1 =
0
2x − y + 3z − 7 =
0
Cevap A
Cevap B
7.
2.
1( x − 0 ) − 1( y − 0 ) + 2 ( z − 0 ) =
0
x − y + 2z =
0
Cevap A
( x − 1)2 + ( y − 2)2 + ( z − 3 )2 = ( x − 0 )2 + ( y − 1)2 + ( z + 2)2
−2x − 2y − 10z + 9 =
0
2z + 2y + 10z − 9 =
0
3.
Cevap B
2x + y + 3z + 2 =
0
( 2,1,3 )
2k + 1( k + 3 ) + 3 ( k + 1) =
0
2k + k + 3 + 3k + 3 =
0
6k + 6 =
0
k = −1
8.
x − 1 3 −2
y +1 2 0 =
0
z−2 1 1
2x − 5y + 4z − 15 =
0
Cevap D
Cevap E
4.
=
N
( 2, −3,1)
V = ( 3,2,k )
2.3 − 3.2 + 1.k =
0
k=0
9.
x −1 y − 2 z − 3
−2
0
−3 =
0
2
−4
−2
6x + 5y − 4z − 4 =
0
Cevap C
Cevap D
5.
10.
2x + y − z + 1 =
0
=
V ( 2,1, −1)
( a, 4,2 )
( a,a,2 )
a.a + 4a + 4 =
0
2 ( x + 2 ) + 1( y + 1) − 1( z − 3 ) =
0
0
( a + 2 )2 =
2x + 4 + y + 1 − z + 3 =0
2x + y − z + 8 =
0
a = −2
Cevap A
Cevap A
62
ÖABT Analitik Geometri
11.
KONU TESTİ
m
n +1 k −1 2
= = =
m +1 n −1 k + 2 4
15.
Uzayda Düzlem Denklemleri
A ( 4,2, −1) ,
B ( 0, −1, −1)
BA = ( 4,3,0 )
m
1
n +1 1
k −1 1
,
,
= =
=
4.2 −=
1.3 + 2.0 5.3 cos ( 90 − α )
m +1 2
n −1 2
k+2 2
=
5 15 cos ( 90 − α )
m=
1
n=
k=
4
−3
m + n + k = 1− 3 + 4 = 2
1
= sin α
3
Cevap B
Cevap A
4 a
4
3
16.
= =
,
2 3
2 −b
12. 3x − 2y − z + 5 =
0
a= 6
2 / x + y + 2z =
0
5x + 5z + 5 =
0
x + z +1=
0
x=k
=
y 2k + 3
z =−k − 1
x y − 3 z +1
= =
−1
1
2
y −1
=− z
x +1=
2
+
b= −
6
4
a
6
=
= −4
b −6
4
Cevap B
17.
x + 2y − z =
3
2 / 2x − y + z =
0
5x + z =
3
x=k
z= 3 − 5k
y= 3 − 3k
+
Cevap E
(k,3 − 3k,3 − 5k )
13. =
h
3k + 2 ( 3 − 3k ) + 4 ( 3 − 5k ) + 5 =
0
2 (1) + 2 − 2 ( −1) + 9 15
= = 5
2
3
22 + 12 + ( −2 )
3k + 6 − 6k + 12 − 20k + 5 =
0
k =1
(1,0, −2 )
Cevap D
Cevap C
18.
2x − 4y + 6z + 1 =
0
2x − 4y + 6z + 14 =
0
2z − 4y + 6z + 1 =
0
14. d1 ( −1,1,2 )
d2 (1,2,1)
−1.1
=
+ 1.2 + 2.1
x − 2y + 3z + 7 =
0
14 + 1 15
15
=
→ 2x − 4y + 6z +
2
2
2
4x − 8y + 12z + 15 =
0
6. 6 cos ( 90 − α )
1
= sin α
2
30 = α
Cevap A
Cevap B
63
ÖABT Analitik Geometri
1.
KONU TARAMA SINAVI – 12
0 ( x − 2 ) + 2 ( y + 1) + 1( z − 3 ) =
0
5.
Uzayda Düzlem Denklemleri
( 3, −2,1)
( 4,5, −2 )
3.4 + 5 ( −2=
) + 1( −2 )
2y + 2 + z − 3 =
0
2y + z − 1 =
0
14. 45 cos α
=
− 10 − 2
12
14. 45 cos α
=
α 90
0 cos α ⇒ =
Cevap D
Cevap A
2.
3 −2 1
= =
6 m n
3m =
−12,
3n =
6
m=
−4
n=
2
m.n = −8
6.
2x + y − z − 1 + k ( 3x − y − 2z − 4 ) =0
2 ( 2 ) + ( −1) − 3 − 1 + k ( 3.2 − ( −1) − 2 ( 3 ) − 4 ) =
0
Cevap C
4 − 1 − 4 + k ( 6 + 1 − 6 − 4 ) =0
k= −
1
3
1
( 3x − y − 2z − 4 ) =0
3
3x + 4y − z + 1 =
0
2x + y − z − 1 −
3.
Cevap D
( x − 1)2 + ( y + 1)2 + ( z − 2 )2
⇒
=
( x − 2 )2 + ( y + 0 )2 + ( z − 4 )2
⇒ 2x + 2y + 4z =
14
⇒ x + y + 2z − 7 =
0
Cevap E
4.
x−0
2
−1
y−0
1
1 =0 ⇒ 4x − 5y + 3z =0
z − 0 −1 3
Cevap A
64
KONU TESTİ
ÖABT Analitik Geometri
1.
B ( 3, 4,5 ) , C ( −3, −4,5 )
BC
=
2
( 6 )2 + 82 + 0=
Uzayda Simetri
Koordinat Dönüşümleri
Koniklerin Genel Denklemi
3.
10
Cevap E
a +1 b −1 c + 3
C
,
,
2
2
2
a + 1 b − 1
c +3
−
0
+ 2 2 − 5 =
2
2
a + 1 − b + 1 + 2c + b − 10 =0
a − b + 2c − 2 =
0
AB / /N
a −1 b +1 c − 3
= = = k
−1
1
2
a =k + 1, b =−k − 1, c =2k + 3
k + 1 − ( −k − 1) + 2 ( 2k + 3 ) − 2 =0
6k + 6 =0 ⇒ k =−1
=
a 0,=
b 0,=
c 1
( 0,0,1)
Cevap A
4.
2.
x =−1 + 4 =3
( 3, 4 )
y = 3 +1= 4
( 3 − 0 )2 + ( 4 − 0 )2
=
5
Cevap C
5.
=
y 3x + 2
A ( 0,2 )
B (1,5 )
a b +1 c + 2
= = = k
2
2
2
a =2k, b =2k − 1, c =2k − 2
AB.V = 1( a − 0 ) + 1( b − 1) + 1( c − 2 ) = 0
A ( 0,2 ) → ( 2,1)
B (1,5 ) → ( 3, 4 )
4 −1 3
= = 3
3−2 1
y −=
1 3 ( x − 2)
m=
a + b − 1 + c − 2 =0
2k + 2k − 1 − 1 + 2k − 2 − 2 =0
6k = 6 ⇒ k = 1
y 3x − 5
=
( 2,1,0 )
Cevap E
Cevap D
65
KONU TESTİ
ÖABT Analitik Geometri
6.
xı= x − 2
11.
yı= y + 1
( x − 2)
2
2
(x ) + (y )
ı
ı
2
x 2 − 2xy + y 2 − 6x + 6y + 9 =
0
B2 − 4AC
4 − 4.1.1 =
0
4
+ ( y + 1) =
2
Uzayda Simetri
Koordinat Dönüşümleri
Koniklerin Genel Denklemi
0
( x − y )2 − 6 ( x − y ) + 9 =
4
=
0
( x − y − 3 )2 =
çakışık iki doğru
Cevap B
Cevap E
7.
xı = 3 cos 45 − 1sin 45 =
2
yı =3 sin 45 + 1.cos 45 =2 2
(
2,2 2
12.
)
Cevap A
8.
B
A −C
tan 2θ=
2
2
= = 1
1 − ( −1) 2
tan 2θ=
π
π
⇒ θ=
4
8
Cevap A
xı =1cos 90 − ( −2 ) sin 90 =+2
=
yı 1sin 90 + ( −2 ) cos
=
90 1
( 2,1)
Cevap B
9.
tan 2θ =
2x + y − 2 =
0 doğrusunun orijin etrafında saa-
tin tersi yönünde 90 döndürülmesi ile oluşan
doğru denklemi x − 2y + 2 =
0
Cevap C
10. 5x 2 + 5y 2 + 6x + 8y + 5 =
0
B2 − 4AC
02 − 4.5.5 < 0
Cevap B
66
ÖABT Analitik Geometri
1.
KONU TARAMA TESTİ - 13
B ( 2,1, −3 ) , C ( −2,1,3 )
BC=
2
( 2 + 2)2 + (1 − 1)2 + ( −3 − 3 )=
4.
Uzayda Simetri
Koordinat Dönüşümleri
Koniklerin Genel Denklemi
−3 cos 270 − 4 sin 270 =
xı =
4
yı =
−3 sin 270 + 4 cos 270 =
3
52
= 2 13
( 4,3 )
Cevap E
Cevap A
2.
5.
tan 2θ =
2=
θ
−2
−2
=
= −1
4−2
2
3π
3π
⇒=
θ
4
8
Cevap B
a + 2 b + 3 −c − 1
= = = k
2
2
2
a = 2k − 2,
b = 2k − 3,
c = −2k − 1
AB.V = ( a − 2 ) 1 + ( b − 3 ) .1 + ( −1) . ( c − 1) = 0
6.
B2 − 4AC > 0
a − 2 + b − 3 − c +1=
0
2k − 2 − 2 + 2k − 3 − 3 + 2k + 1 + 1 =
0
4
6k − 8 = 0 ⇒ k =
3
2
1
11
− , c=
−
a=
, b=
3
3
3
Verilen denklem hiperbol belirtir.
Cevap B
Cevap E
3.
x 2 + 3xy − 4y 2 − 9 =
0
y = 2x
( 0,0 ) → (1,3 )
(1,2 ) → ( 2,5 )
5−3 2
= = 2
2 −1 1
y − 3= 2 ( x − 1)
m=
y − 3 = 2x − 2
y 2x + 1
=
Cevap B
67
KONU TESTİ
ÖABT Analitik Geometri
1.
x = f ( t ) + k.a ⇒ x = 0 + k.3
4.
Yüzeyler
{( t, t, t ) t ∈ }
v=
y= g ( t ) + k.b ⇒ y= 2 cos t + k.0
( −1,3,2 )
x =t + k. ( −1)
z= h ( t ) + k.c ⇒ z= 3 sin t + k.0
2x + z
y=
t + k.3 y =+ 3k
3
z = t + k.2
3y = 2x + z + 9k
y 2 z2
+
=
1
4
9
Cevap C
3y = 2x + z + 9 ( y − z )
0 = 6y + 2x − 8z
z=
3y + x
4
Cevap D
2.
x =f ( t ) + k.a ⇒ x =t + k.2
y =g ( t ) + k.b ⇒ y =t + k.0
z =h ( t ) + k.c ⇒ z =t + k.1
5.
z= y + k
z−y =
k
x=
(1 − k ) .2 + k.0
y=
(1 − k ) cos t + k.0
x =+
y 2 (z − y)
z=
(1 − k ) sin t + k.0
x =y + 2z − 2y
x+y
x = 2z − y ⇒
= z
2
y 2 + z2 =(1 − k ) ⇒ y 2 + z2 =
2
x2
4
⇒ 4y 2 + 4z2 =
x2
Cevap A
3.
Cevap A
x = cos t
y = 2 sin t
z
0
{( cos t, 2 sin t, 0 ) t ∈ }
6.
{( cos t,
sin t, 3 )}
x=
(1 − k ) .cos t + k.0 x2 + y2 =(1 − k )2
y=
(1 − k ) .sin t + k.0
z2
2
2
z=
(1 − k ) .3 + k.0 x + y =
9
x cos t + k.1
=
=
y 2 sin t + k.0
z= 0 + k.1
x−z =
cos t
2
2 y
1
=
( x − z) +
y
4
= sin t
2
9x 2 + 9y 2 =
z2
Cevap E
Cevap B
68
KONU TESTİ
ÖABT Analitik Geometri
=
x 3ϑt
2
7.
=
y t=
3yz
x
z= ϑ
Yüzeyler
11. 2x 2 + y 2 =
1
2x 2 = 1 − y 2
x2
=
Cevap C
1 − y2
1 − y2
x
⇒=
2
2
1 − y 2 + z2
x =f y 2 + z2 , x =
2
(
1 − y 2 + z2
⇒ x2 =
2
2
)
2x 2 + y 2 + z2 =
1
Cevap B
8.
x=0
y=
t
1 + y 2, z =
f x 2 + y 2
z =
z= 1 + t2
z =1 + x 2 + y 2
Cevap A
12.
x 2 + 3y + 2 =
0
x 2 =−3y − 2 ⇒ x = −2 − 3y
x= −2 − 3 y 2 + z2
x 2 =−2 − 3 y 2 + z2
x=t
2
2
2
=
y t=
y f x 2 + z2
y x , =
9.
z = 0
2
=
y x +z
x 2 + 2 =−3 y 2 + z2
(x
2
2
+2
)
2
(
= 9 y 2 + z2
)
Cevap E
Cevap C
y=0
=
z =
x x f y 2 + z2
10.
z2 = x
=
x y 2 + z2
Cevap D
69
ÖABT Analitik Geometri
1.
KONU TARAMA SINAVI – 14
x= 0 + k.1
6.
y = t + k.0
z=
t 2 + k.0
1 − z2
1 − z2
3y 2 =1 − z2 ⇒ y 2 =
⇒ y =
3
3
z=
y2
⇒y=
Cevap B
Yüzeyler
(
1 − x 2 + z2
)
3
1 − x 2 − z2
y2 =
3
3y 2 + x 2 + z2 =
1
=
x cos t + k.0
y2
2.
y= 2 sin t + k.0 x 2 + = 1
4
z= 0 + k.2
Cevap D
Cevap A
3.
x=
(1 − k ) 2 cos t + k.0 2 2
x
z
z =(1 − k ) 2 sin t + k.0
+
=y 2
4
4
y =(1 − k ) 1 + k.0
x 2 + z2 =
4y 2
Cevap B
x=
(1 − k ) 0 + k.1
4.
2
y =(1 − k ) sin t + k.0 y 2 + z2 =(1 − k )
z=
(1 − k ) cos t + k.0
y 2 + z2 = ( x − 1)
2
Cevap E
5.=
x t 2=
x f y 2 + z2
y= 0
z=t
x = z2 ⇒ x = y 2 + z2
Cevap A
70
ÖABT Analitik Geometri
GENEL TARAMA SINAVI
1.
4.
( −1)2 + ( Y + 1)2 =
22 + Y 2
1
( x − 3)
2
2y + x − 1 =
0
2x − y + 3 =
0
x = −1
y + 1 =−
1 + y 2 + 2y + 1 = 4 + y 2
2y = 2
y =1
+
Cevap D
Cevap B
2.
5.
px + py − p + 2x − y − 5 =
0
x ( p + 2 ) + y ( p − 1) − p − 5 =
0
p =−2 için − 3y − 3 =0
y = −1
=
=
−6 0
p 1 için 3x
x=2
y = − x ikinci açıortay doğrusu
m1 = −1
m1.m2 = −1
m2 = 1
y + 1= 1( x − 2 )
Cevap C
y = x − 2 −1
y = x−3 ⇒ x−y−3 = 0
Cevap A
3.
6.
3 / 3x − 2y + 5 =
0
2 / 2x + 3y − 1 =
0
13x = −13
x =−1 x + 1 =0
∆
5.2
=
A ( AOB
) = 5
2
Cevap B
Cevap B
71
ÖABT Analitik Geometri
GENEL TARAMA SINAVI
7.
11.
m1 =
0 − ( −2 )
1− 3
m1.m2 =−1
m2 = 1
=
2
= −1
−2
y + 1 =1( x − 2 )
y +1= x − 2
3 ( −2 ) + 4 ( 3 ) + 9 15
= = 3
5
32 + 42
2l = 6
y−x+3 =
0
x−y−3 =
0
=l
Cevap E
Cevap D
8.
2.1 + 1( −3 )
( x − 3y + 4 ) =0
12. 2x + y − 1 − 2
12 + ( −3 )2
1
2x + y − 1 − 2 − ( x − 3y + 4 ) =
10
20x + 10y − 10 + 2x − 6y + 8 =
0
22x + 4y − 2 =
0
11x + 2y − 1 =
0
Cevap C
9.
Cevap A
2
2b − 2a
13
=
3
( a − b )2 +
a−b =
3
Cevap C
10.
13.
3x + 2y − 5 =
0
A (1,2 )
3x + 2y + c1 =
0
3x + 2y + c 2 =
0
3 (1) + 2.2 + c1 =
0
c1 = −7
3x + 2y − 9 =
0
Cevap B
Cevap C
72
ÖABT Analitik Geometri
14.
GENEL TARAMA SINAVI
( 2 + 2 + m )( −1 − 6 + m ) < 0
17.
( 4 + m )( −7 + m ) < 0
Cevap C
m1m2 ≤ 5
( a − 2 )2 + ( −2 − 1)2
15.
(a − 2)
2
≤5
≤ 25 − 9
( a − 2 )2 ≤ 16
a − 2 ≤ 4 ⇒ −4 ≤ a − 2 ≤ 4
−2 ≤ a ≤ 6
Cevap C
18.
mBA = mAP
6−4 4−0
=
2 − 1 1− x
2
4
=
⇒ 2 − 2x
= 4
1 1− x
−2x =
2
x = −1
72
( x − 3 )2 + ( y − 0 )2 =
Cevap B
49
( x − 3 )2 + y 2 =
Cevap C
16.
19.
(
x 2 + 42 =26
−4 6
1
8
2 1 =0⇒ y =
2
3
0 y
)
2
x 2 + 16 =
26
x 2 = 10
x = 10
Cevap A
Cevap E
73
ÖABT Analitik Geometri
GENEL TARAMA SINAVI
x 2 + y 2 − 6x − 4y + 5 =
0
20.
−
23.
x 2 + y 2 − 2x + 2y − 3 =
0
0
−4x − 6y + 8 =
0
−2x − 3y + 4 =
2x + 3y − 4 =
0
Cevap B
b2 + a2.m2 =
n2
64 + 9m2 =
100
m = 2
=
y 2x + 10
y=
−2x + 10
21.
Cevap A
24.
x2 y2
1
+
=
5
4
y+2 y+4
= −1
.
x −1 x − 3
y 2 + 6y + 8 + x 2 − 4x + 3 =
0
2
( x − 2 )2 + ( y + 3 )2 =
Cevap B
x2 + y2 =
32
x2 + y2 =
9
22.
Cevap E
25.
x
cos β = 2
y2
6 x
+
=1 ⇒ x 2 + 9y 2 =36
y 36 4
sin β =
2
2x 2 = 62 + 42 −
82
2
2x 2 = 20
x 2 = 10 ⇒ x =
Cevap A
10
Cevap B
74
ÖABT Analitik Geometri
26.
GENEL TARAMA SINAVI
( x + 4 )2 + ( y − 0 )2 = ( x − 4 )2
29.
2
x=
mx + n
x 2 − mx − n =
0
x1 + x 2 =
m
x 2 + 8x + 16 + y 2 = x 2 − 8x + 16
y 2 = −16x
Cevap C
27. 2c 4=
=
10
y
x1 + x 2
=1 ⇒ x1 + x 2 =2
2
m=2
=
y 2x + n
=
5 2.1 + n
n=3
= 2.3
= 6
m.n
b → 3k
x
a → k
c = 2 10
Cevap D
2
c=
b2 + a2
40 9k 2 + k 2
=
40 = 10k 2
4 = k 2 ⇒ k = 2
x2 y2
1
−
=
4 36
9x 2 − y 2 =
36
Cevap C
30.
28.
x2 y2
1
−
=
4 12
y2
=⇒
1 y2 =
36
12
y=6
6.6
A ( TAF
=
) = 18
2
4−
Cevap C
Cevap A
75
ÖABT Analitik Geometri
GENEL TARAMA SINAVI
31.
35.
AC.BD
y−x =
0
( 4,3 ) . ( −4,3 ) =−16 + 9 =−7
2−4
=
2
=
h
2
Cevap A
Cevap D
A.B + A.C
32.
=
36.
A . B .cos 60 + A . C .cos180
1
= 6.4. + 6.2. ( −1)
2
=0
Cevap B
33. C / =
A 4B + 3C
A.C
= 4BC + 3CC
A . C cos α =3 C
CE.CF
( −3, −6 ) . ( −6, −3 ) =
18 + 18 = 36
Cevap E
2
6 C . C cos α =3 C
2
37.
1
6 cos α = 3 ⇒ cos α
2
α =60
A ( 3, −4,7 )
B (1,1,1)
A.B
=
.B
2
B
Cevap C
( 3, −4,7 ) . (1,1,1) =
. (1,1,1)
3
34. B / A= B + C
=
A.B
B
2
2=
(1,1,1)
( 2,2,2)
Cevap D
+ B.C
2
=
B + B .2 B cos α
2
2
−=
B
2 B .cos α
38.
1
cos α = − ⇒ α = 120
2
u + v + w=
u2 + v 2 + w 2=
32 + 42 + 52= 5 2
Cevap B
Cevap D
76
ÖABT Analitik Geometri
GENEL TARAMA SINAVI
39. z = 0
42.
20
( x + 3 )2 + ( y − 1)2 + 4 =
a
b
c
,
,
A
A A
3
4
5
1
,
,
=
5 2 5 2 5 2
2
16
( x + 3 )2 + ( y − 1)2 =
r=4
Cevap A
Cevap E
43.
40.
2
3 −3 1
=
− ,
=
a
2 2 b
4
2
a=
−
b=
−
3
3
4 2
a + b =− − =−2
3 3
Cevap D
2. 3.cos α
2. 3.
2
3
=2
Cevap D
44.
(1, −1,0 ) . (1,0,0 ) = 2.1.cos α
1
=
2 cos α
1
cos=
α
⇒=
α 45
2
41.
Cevap B
x −1
y+3
z−0
45.
= =
2 − 1 −1 − ( −3 ) 0 + 2
=
CA.CB CA . CB .cos α
=
−1)
( −3,0, −4 ) . ( −7,0,
x −1 y + 3 z
= =
1
2
2
0 −1 y + 3
=
1
2
y =−5, z =−2
5.5 2.cos α
25 25 2 cos α
=
1
cos=
α
⇒=
α 45
2
( 0, −5, −2 )
Cevap E
Cevap B
77
ÖABT Analitik Geometri
46.
GENEL TARAMA SINAVI
x − y + 2z + 5 =
0
49. 3x − y + z − 5 =
0
(1, −1,2 )
2 ( x + 2 ) − 1( y − 1) + 2 ( z − 3 ) =
0
2x + y − 2z =
0
5x − z =
5
( 5,0, −1)
+
x + 2 − y + 1 + 2z − 6 =0
=
x k olsun, =
z 5k − 5
x − y + 2z − 3 =
0
− x + 2y − az + 1 =0
( −1,2, −a )
Cevap C
2x + y − 2z = 0 doğrusunda x = k ve z = 5k − 5
2k + y − 2 ( 5k − 5 ) =
0
2k + y − 10k + 10 =
0
=
y 8k − 10
47.
x y + 10 z + 5
=
= = k
1
8
5
1 + 2.8 − a.5 = 0 ⇒ a = 3
i
j
k
2 3 4 = i ( 5 ) − j ( −6 ) + k ( −7 )= 0
1 −2 −1
Cevap D
( 5,6, −7 )
5 ( x − 1) + 6 ( y − 0 ) − 7 ( z − 2 ) =
0
5x − 5 + 6y − 7z + 14 =
0
5x + 6y − 7z + 9 =
0
Cevap D
50.
48.
a +1 b + 2 c + 3
= = = k
1
1
−1
a= k − 1
b =−k − 2
c= k − 3
AB.V = ( a − 1) 1 + ( b − 2 )( −1) + ( c − 3 ) .1 = 0
x
y
z
=
= = k
1 −1 2
x=k
y = −k
z = 2k
x − y + 2z + 6 =
0
a − 1 − b + 2 + c − 3 =0
a−b+c =
2
k − 1+ k + 2 + k − 3 =
2
4
3k = 4 ⇒ k =
3
1
10
5
a=
,b =
− , c=
−
3
3
3
k − ( −k ) + 2 ( 2k ) + 6 =0
6k + 6 =
0
k = −1
( −1,1, −2 )
Cevap B
Cevap C
78
ÖABT Analitik Geometri
GENEL TARAMA SINAVI
54.
51.
x = 2 +1= 3
B ( 3, −4 )
y =−3 − 1 =−4
C ( 3,2 )
BC=
2
( 3 − 3 )2 + ( −4 − 2 )=
6
Cevap C
a+2
b + 1 c
− 2
3
0
+ +3 =
2
2 2
3a + 6 − 2b − 2 + c + 6 =
0
3a − 2b + c + 10 =
0
a − 2 b −1 c − 0
= = = k
−2
3
1
=
a 3k + 2
−2k + 1
b=
c =k
55. 3x − 2y + 6 =
0 doğrusunun
etrafında
saatin dönme yönünde 90 derece döndürüldüğünde oluşan doğru 2x + 3y − 6 =
0
Cevap B
3 ( 3k + 2 ) − 2 ( −2k + 1) + k + 10 =
0
56.
14k = 14
k = −1
4x 2 − xy − 3y 2 − 9 =
0
B2 − 4AC > 0
1 − 4 ( 4 ) . ( −3 ) > 0
( −1,3, −1)
hiperbol
Cevap A
52.
orijin
Cevap B
2y − x + 1 =
0 doğrusu üzerinde olan iki nokta
seçelim.
(1,0 ) → ( 2, −1)
1
3
0, − 2 → 1, − 2
57.
3
+1
2= 1
=
m
1− 2
2
1
y +=
1
( x − 2)
2
2y + 2 = x − 2
⇒ x − 2y − 4 =
0
−
x 2 + xy − 2y 2 − 3x + 3y =0 ⇒ B2 − 4AC > 0
0
( x + 2y )( x − y ) − 3 ( x − y ) =
0
( x + 2y )( x − y − 3 ) =
kesişen iki doğru
Cevap B
Cevap D
58.
(
)
53. 3 y 2 − 6y + 9 − x − 2 =
0
3 ( y − 3) =
x+2
2
( )
2
3 yı = xı
tan 2θ =
B
A −C
4
= =
1
4
3+
3
3
tan 2=
θ 60 ⇒ =
θ 30
tan =
2θ
yı =
y−3
xı= x + 2
4
3
Cevap B
Cevap A
79
ÖABT Analitik Geometri
59.
GENEL TARAMA SINAVI
x=t
y=k
2
=
z kt ⇒=
z x.y ⇒ z=
xy
Cevap C
60.
x2 − y + 1 =
0
x 2 = y − 1 ⇒ x = f y 2 + z2
x2 =
y 2 + z2 − 1
( x + 1)
2
2
= y 2 + z2
Cevap E
80
