x-+t+x

1.
f: {-1, 0,1, 2} ~ Bye tanrmh f fonksiyonu
blr olduguna gore, s(B) en az ka(: olabillr?
bire
f(x) = Ixl-1
fonkslyonu orten olduguna
gldakilerden hanglsldlr?
A) R -{1}
B) [-1, 00)
D)R
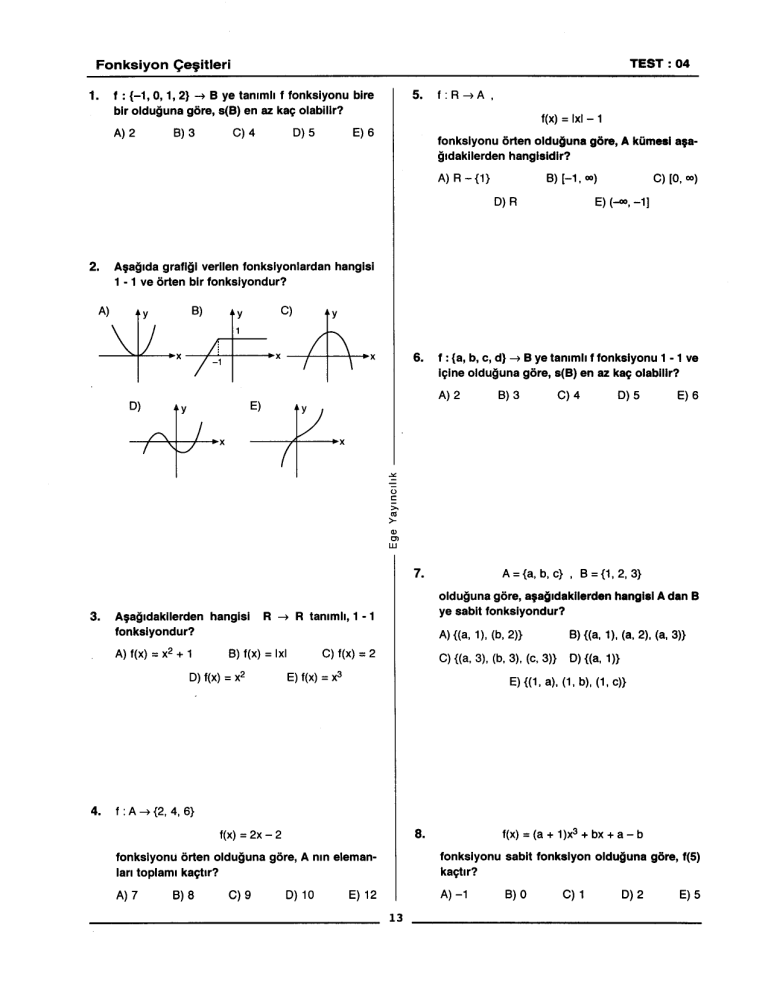
2.
A,aglda graflgl verllen fonkslyonlardan
1 - 1 ve orten blr fonksiyondur?
gore, A kumesl a,a-
C) [0, 00)
E) (-00, -1]
hanglsi
C)~
~,B)
x-+t+x
-1
6.
f : {a, b, c, d} ~ Bye tanrmh f fonkslyonu 1 -1 ve
1(:lne olduguna gore, s(B) en az ka(: olablllr?
A = {a, b, c} , B = {1, 2, 3}
3.
A,agldakllerden
fonkslyondur?
hanglsi
A) f(x) = x2 + 1
R ~
B) f(x) = Ixl
D) f(x) =
x2
R tanrmh, 1 - 1
C) f(x)
=2
olduguna gore, a,agldakllerden
ye sabit fonkslyondur?
A) {(a, 1), (b, 2)}
B) {(a, 1), (a, 2), (a, 3)}
C) {(a, 3), (b, 3), (c, 3)}
D) {(a. 1)}
E) f(x) = x3
E) {(1, a), (1, b), (1, c)}
f(x) = 2x - 2
fonkslyonu
Ian toplaml
orten olduguna
ka(:tlr?
gore, A nm eleman-
hanglsl A dan B
f(x)
fonkslyonu
ka(:tlr?
= (a + 1)x3 + bx + a -
sa bit fonkslyon
b
olduguna
gore, f(5)
f(x) = (a - 2)x2 - (3b + 6)x - 3
f(x) = 2ax - b
fonkslyonu blrlm fonkslyon
f(a.b) ka~tlr?
fonkslyonu sablt blr fonkslyon Ise, a - b ka~tlr?
olduguna
gore,
f(x) = 3x - 4
2x + k
fonkslyonu
ka~lr?
A) ~
14. f(x) birim fonksiyon olmak uzere,
sablt fonkslyon olduguna gore, k
f(x - 2) + f(x - 1) = 11
B) - ~
C) -
2.
D) -2
E) -~
533
2
f(x) = (a + 1)x - 1
x+1
f(g(x» + f(x) = 2x - 1
olduguna gore, g(11) ka~tlr?
fonkslyonu sablt fonkslyon olduguna gore, f(2)
ka~lr?
D) ~
B) -~
2
12.
2
16. f(x) dogrusal fonksiyon,
f(x) = (a - b - 3)x + a + b
fonkslyonu
ka~tlr?
A)-2
f(2) =3 , f(1) =-1
blrlm fonkslyon olduguna gore, b
olduguna gore, f(5) ka~tlr?
B) -1
D) 1
C)O
E) 2
A)10
B) 12
C)15
D) 16
E) 18
14
11.C
2.E
3.E
4.C
5.8
6.D
7.C
8.A
9.8
10.8
11.A
12.A
13.8
14.C
15.8
16.C
I
Fonksiyonlarda i,lemler
= {(1,
f
3), (3, 2), (4, 1)}
9 ={(1, -1), (3, 4), (4, -2)}
olduguna gore, (f + g)(3) kaertlr?
R, f(x)
9 : {1, 2} ~
R, g(x) = 2x - 3
olduguna gore, f + 2g fonksiyonu nedlr?
A) {(2, 5)}
B) {(2, 8)}
0) {(1, 7)}
f
= {(2,
5), (3. 4), (4, 1)}
9
= {(2,
3), (3, -1), (5, 2)}
2.
f(x)
B)3
C)2
= 2x -
C) {(2, 7)}
E){(3, 6)}
1 , g(x)
= 4x + m
fonkslyonlarl veriliyor. (2f + g)(2) = 10 olduguna
gore, m kaertlr?
olduguna gore, (2f - 3g)(2» kaertlr?
A)4
= x2 + 1
f : {2, 3} ~
0)1
f = {(1, 2), (2, 3), (4, -1)}
3.
9
= {(2,
(f.g)(x) = x3 + 4x - 1 , g(x) = 2x + 1
1), (3, 2), (4, O)}
olduguna gore, f.g fonkslyonu a~agldakllerden
hanglsldlr?
olduguna gore, f(2) kaertlr?
A) {(2, 3), (4, -1)}
B)
{(2, 3), (3, 6), (4, O)}
C)
{(2, 3), (4, O)}
0) {(2, 6), (4, -1)}
E) {(3, 2), (2, 6),(4, O)}
(f + g)(x)
= 2x + 4
(f - 2g)(x) = 1 - 4x
4.
f(x)
= 3x
+ 1 , g(x)
= x2 -
4
olduguna gore,
{f} (2)
5..
C)Q.
O)L
3
5
3
olduguna gore, (1.g)(1)kaertlr?
A)-15
B)-12
C)-10
0)-8
A)~
3
B)
kaertlr?
f(x) ve g(x) fonksiyonlannln grafikleri verilmi~tir.
13.
f(x)
olduguna gore, f(x + 1) In f(x) clnslnden degerl
nedlr?
Buna gore,
A) f(x) + 1
(f - 2g)(-1) + f(g(-3»
y = f(x)
= x-3
B) f(x) + 2
D) 2f(x) + 1
C) f(x) - 1
E) 2f(x)
toplaml ka~tlr?
f(x)
= x+1
2
olduguna gore, f(x - 2) nln f(x) clnslnden deOeri
nedlr?
(f + g)(x + 1) = 2x + 3 . f(3) = -4
A) 2f(x) - 1
olduguna gore, g(3) ka~tlr?
B) f(x) + 1
D) 2f(x) + 1
C) f(x) - 1
E) f(x) - 2
.>l:
0
c:
>0as
>-
Q)
Cl
w
= 3x
g(x) = 2x2 -
11.
2-
f(x)
4x + 2
B) 7x - 7
x-2
A)
B) f(x) + 1
f(x) - 1
f(x)
f(x + 2)
E) 7x - a
g(x)
f(x)
= x2 + 2x + 1
B) x2 +
X
C) x2
D) x
A) 9f2(x)
20D
3.C
40B
50C
60C
70C
80B
= 32x-1
B) 9f(x)
D) 3f(x)
E) x + 1
16
'1.E
f(x)
olduguna gore, f(2x) In f(x) clnslnden degerl
nedlr?
olduguna gore, (f - g)(x -1» fonkslyonu a,agldakllerden hanglsldlr?
A) x2 - x
E) 2f(x) - 1
f(x)
f(x) - 2
f(x) = x2 + 3x + 2
12.
C) f(x) - 1
f(x) + 1
C) 7x + a
D)
D) ax + 7
= _x_
olduguna gore, f(x + 2) nln f(x) clnslnden degerl
nedlr?
5x + 4
olduguna gOre, (21- 3g)(x) fonkslyonu atagldakllerden hanglsldlr?
A) ax - 7
f(x)
15.
9.B
100D
1101:
E) f2(x)
Fonksiyonlarln Tersi
3.
=
=
A {a, b, c} kumeslnden B {1, 2, 3} kumeslne
tammlanan fonkslyonlardan
hanglslnln ters
fonkslyonu vardlr?
5.
f(x + 2) = 2x - 3
r-1(5)
olduguna gore, f(4) kac;tlr?
Ifadeslnln sonucu
A) {(a, 1), (a, 2), (a, 3)}
B)
{(a, 1), (b, 1), (c, 2)}
C)
{(a, 3), (b, 1), (c, 3)}
0)
{(a, 3), (b, 2), (c, 1)}
E) {(b, 1), (c, 1), (a, 3)}
f(x)
olduguna gore,
= 5x -
2
r1 ( x2)
r-1(25) kac;tlr?
olduguna gore,
A)5
= 3x
r-1(4) + f(3) kac;tlr?
B)6
C)7
0)8
f(x) =~
3x - 2
f(x)=2x-4,
r1(x)=g(X-1)
olduguna gore, g(1) kac;tlr?
B)
5.
C)L
3
5
A)1
B)2
C)3
x-3
f(x) =--
8.
2x + a
fonkslyonu
kac;tlr?
1c;ln f(x)
= r- (x) olduguna
1
gore, a
f(x) dogrusal fonksiyondur.
1(1)=3,
olduguna gore,
r1(5)=2
r-1(9) kac;tlr?
0)4
f(x) + 1 = f(x) - 1
x- 1
f(x) = x - 1
a
fonksiyonlarl
kac;tlr?
r-1(x) = g(x)
olduguna
gore, a
C)~
B) ~
2
4
f(x) = _3_
2x -1
f-1(3) =5
f(ax;1)=2X_1"
11.
ic;in
f (~)
2x - 1
•
g(x) = x + m
= 2x + 1
x + 2
f(x) = ax + 4
2x - b
B) §.
C)...2...
5
11
D)~
11
fonksiyonu
kac;tlr?
E)JL
birebir
ve orten
olduguna
gore, a
11
f(x) = x2 + 6x - 4
fonksiyonunun
(1 - 1) ve orten oldugu arahk
ic;in, tersi a~agldakilerden
hangisi olabilir?
r1(2x)
olduguna
= g(2x - 1) • g(3) = 1
A) Y =
gore, f(1) kac;tlr?
v'i<+13 -
3
C)y=~-3
D)Y=~+3
E) y=~
18
9.0
B) y = VX + 13 + 3
+13