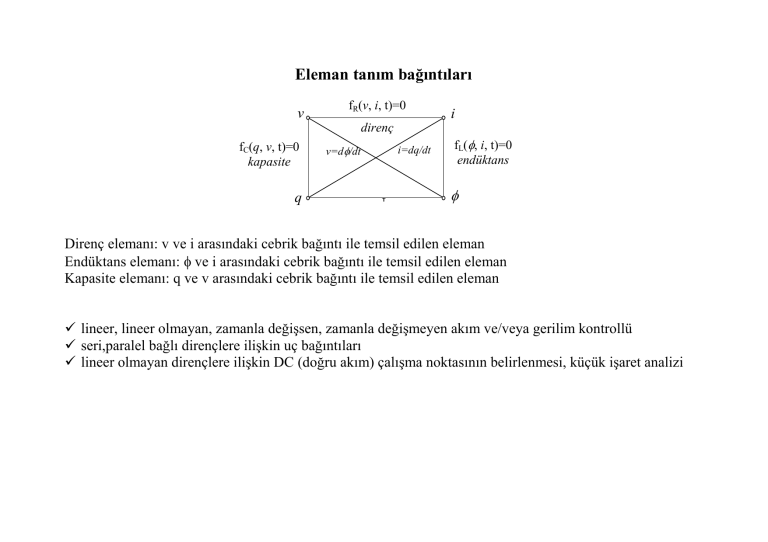
Eleman tanım bağıntıları
v
fR(v, i, t)=0
i
direnç
fC(q, v, t)=0
kapasite
q
v=dφ/dt
i=dq/dt
φ
fL(φ, i, t)=0
endüktans
φ
Direnç elemanı: v ve i arasındaki cebrik bağıntı ile temsil edilen eleman
Endüktans elemanı: φ ve i arasındaki cebrik bağıntı ile temsil edilen eleman
Kapasite elemanı: q ve v arasındaki cebrik bağıntı ile temsil edilen eleman
lineer, lineer olmayan, zamanla değişsen, zamanla değişmeyen akım ve/veya gerilim kontrollü
seri,paralel bağlı dirençlere ilişkin uç bağıntıları
lineer olmayan dirençlere ilişkin DC (doğru akım) çalışma noktasının belirlenmesi, küçük işaret analizi
Lineer direnç
i
v(t)=R i(t)
i(t)=G v(t)
+
v
R:direnç (Ω)
G:iletkenlik (siemens, S)
–
i
v
v
i
i-v düzlemi
akım kontrollü
v - i düzlemi
gerilim kontrollü
Özel lineer dirençler
açık-devre elemanı
f(v,i)=i=0
v
R=∞
i
i
kısa-devre elemanı
v
f(v,i)=v=0
v
R=0
R=0
i
i
G=∞
v
Not: açık-devre ve kısa-devre elemanlarının karakteristikleri arasındaki nasıl bir ilişki var?
Tanım: (Dual dirençler)
A direncinin v-i karakteristiği B direncinin i-v karakteristiği ile aynıdır
⇔
A direnci B direncinin dualidir.
Lineer direnç elemanına ait ani güç: p(t) = v(t) i(t)
p(t)=Ri2(t)=Gv2(t)
R>0, p(t)>0
R<0, p(t)<0
pasif
aktif
Lineer olmayan direnç
i
+
f(v,i,t) = 0
v
ℜR={ (v,i) : f(v,i)=0}
f(v,i) = 0
–
Bazı özel lineer olmayan dirençler
İdeal diyot
i
ℜID={ (v,i) : v.i=0, i=0 ve v<0 ve v=0, i>0}
+
v
–
i = 0 ( v < 0 ) iken açık-devre elemanı
v = 0 ( i > 0 ) iken kısa-devre elemanı gibi davranır.
i
v
v
i
i-v düzlemi
v-i düzlemi
i
pn-jonksiyon diyodu
i
+
v
v
IS
–
ℜD={ (v,i) : i=IS . [ expv/Vt - 1 ] }
IS: ters doyma akımı,
VT=kT/q ≈ 26 mV
k: Boltzman sabiti,
q: elektron yükü,
K: ortam sıcaklığı (Kelvin)
Tünel diyodu
i
i= î (v)
+
v
I1
I2
–
ℜD={ (v,i) : i=î (v) },
i1<i<i2
v1 v2
v1<v<v2 eğim negatif
her i akımına karşı 3 farklı v düşüyor ⇒
v
⇒ osilatör, kuvvetlendirici
hafıza, anahtarlama
Bağımsız kaynaklar
Bağımsız gerilim kaynağı
i
vs(t)
i
ℜvs={ (v,i) : v=vs(t), -∞<i<∞ }
E
+
–
i
i
v
-Vm
-Vm/2
Vm/2 Vm
v
E=3 V
vs(t)=Vm sinωt
Bağımsız akım kaynağı
–
is(t)
v
+
ℜis={ (v,i) : i=is(t), -∞<v<∞ }
