DENEY 7 – AKIM KAYNAKLARI VE AKTİF YÜKLER
DENEY 1 – DİYOT KARAKTERİSTİKLERİ
7.1 DENEYİN AMACI
Bu deneyde kuvvetlendirici devrelerde kullanılan entegre devre beslemesi ve aktif yük olarak
kullanılabilen akım kaynakları incelenecektir.
7.2 TEORİK BİLGİ
Sabit akım kaynakları entegre transistörleri beslemek için sıkça kullanılır. Ayrıca bu devreler
kuvvetlendiricilerde aktif yük olarak da kullanılabilir. Sabit akım devreleri BJT ve FET devrelerinde
toplayıcı ve akaç dirençlerinin yerini almıştır. Dirençler yerine aktif yüklerin kullanılması daha yüksek
küçük-işaret kazancı elde edilmesini sağlamıştır.
7.2.1 Temel İki Transistörlü BJT Akım Kaynağı
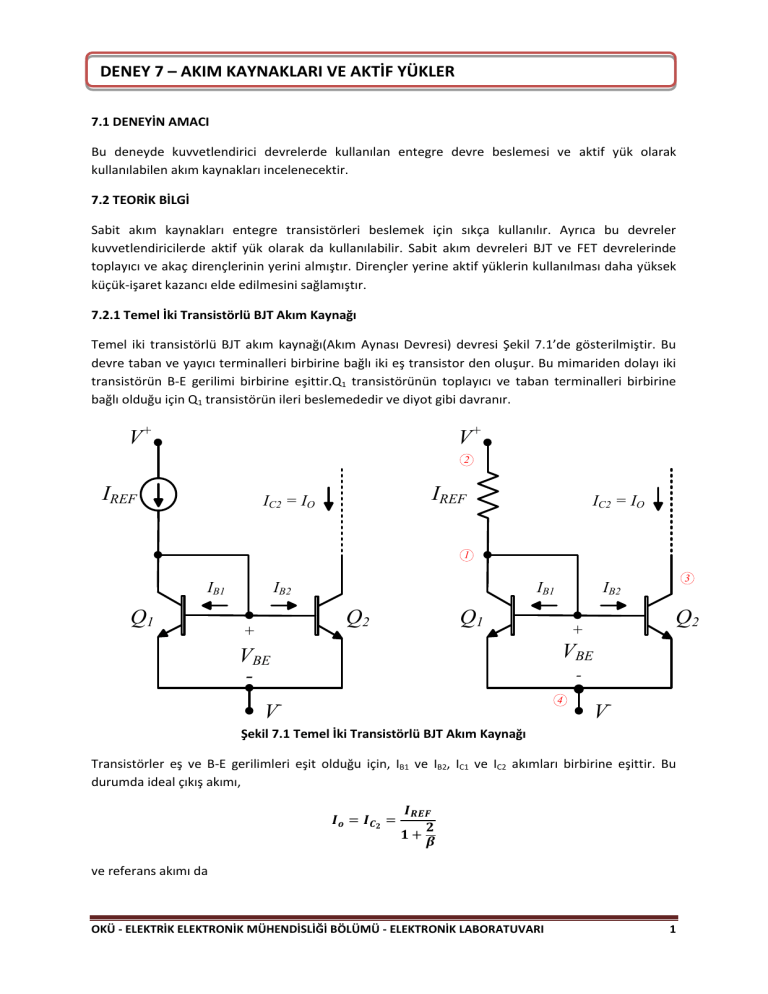
Temel iki transistörlü BJT akım kaynağı(Akım Aynası Devresi) devresi Şekil 7.1’de gösterilmiştir. Bu
devre taban ve yayıcı terminalleri birbirine bağlı iki eş transistor den oluşur. Bu mimariden dolayı iki
transistörün B-E gerilimi birbirine eşittir.Q1 transistörünün toplayıcı ve taban terminalleri birbirine
bağlı olduğu için Q1 transistörün ileri beslemededir ve diyot gibi davranır.
V+
V+
2
IREF
IREF
IC2 = IO
IC2 = IO
1
IB1
Q1
IB2
IB1
Q2
+
Q1
VBE
V-
3
IB2
Q2
+
VBE
4
V-
Şekil 7.1 Temel İki Transistörlü BJT Akım Kaynağı
Transistörler eş ve B-E gerilimleri eşit olduğu için, IB1 ve IB2, IC1 ve IC2 akımları birbirine eşittir. Bu
durumda ideal çıkış akımı,
ve referans akımı da
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
1
olarak hesaplanır
7.2.2 Temel İki Transistörlü MOSFET Akım Kaynağı
Temel iki-transistörlü NMOS akım kaynağı iki tane eş NMOS transistörlerden oluşur. Bu transistörlerin
geçit ve kaynak terminalleri birbirine bağlıdır. Bu yapıdan dolayı iki transistor ün G-S gerilimleri
birbirine eşittir. Temel iki transistörlü NMOS akım kaynağının devre şeması Şekil 7.2’de gösterilmiştir.
M1 transistörünün akaç ve kaynak terminalleri birbirine bağlı olduğu için bu transistör her zaman
doyum bölgesinde beslemededir.
V+
IREF
ID2 = IO
M1
+
VGS
-
M2
V-
Şekil 7.2 Temel İki-Transistölü NMOS Akım Kaynağı
λ’nın sıfır olduğunu varsayarsak, G-S gerilimi
olarak hesaplanır. Çıkış akımı ise
M1 ve M2 transistörleri eş olduğu için VTN1 ve VTN2, kn1 ve kn2 birbirine eşit olur. Çıkış akımı ise
olur.
Referans akımını belirlemek için devreye bir transistör daha eklenebilir. Temel üç-transistörlü akım
kaynağının devre şeması Şekil 7.3’te gösterilmiştir.
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
2
V+
2
M3
1
ID2 = IO
+
-
VGS3
3
M1
+
VGS1=VGS2
4
M2
V-
Şekil 7.3 Temel Üç-Transistörlü NMOS Akım Kaynağı
λ’nın sıfır olduğunu varsayarsak, M2 transistörünün G-S gerilimi
olarak bulunur. Çıkış akımı ise
olarak hesaplanır.
7.2.3 BJT Aktif Yük Devresi
BJT aktif yük devresi şekil 7.42te gösterilmiştir. Giriş gerilim kaynağı QO transistorünü besleyen DC
bileşen ve AC giriş sinyalinden oluşur.
DC Analiz: DC analizde kapasiteler açık devre gibi davranır. Eğer bütün AC kaynakları sıfıra eşitlersek
Şekil 7.4(b)’deki devreyi elde ederiz. Q1 ve Q2 transistörleri eş ise, çalışma noktasındaki C-E gerilimi
Yukarıdaki eşitlik Qo ve Q2’nin beslemeleri ileri aktif bölgede olduğu sürece geçerlidir.
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
3
V+
V+
Q2
Q2
Q1
C
Q1
R1
Vo
Vo
R1
VI
QO
VIdc
RL
QO
(a)
(b)
Şekil 7.4 (a) BJT Aktif Yük Devresi, (b) DC Eşdeğer Devresi
AC Analiz: AC analiz yaparken kapasitelerinin kapasite değerlerinin yeterince büyük olduğunu kabul
edeceğiz, böylece devrede kapasiteleri kısa devre olarak göstereceğiz. Bütün DC kaynakları sıfıra
götürüp, devrede yerlerine kısa devre konur. Transistörlerin yerine de kısa işaret model yerleştirilir.
Devrenin, küçük işaret devre eşdeğer devresi Şekil 7.5’te gösterilmiştir.
Vo
+
hie
VIac
hfeib
1/ho0
1/ho1
RL
Şekil 7.5 BJT Aktif Yük Devresi Küçük İşaret Devresi
BJT aktif yük devresinin küçük işaret gerilim kazancı
olarak hesaplanır.
7.2.4 MOSFET Aktif Yük Devresi
MOSFET aktif yük devresi Şekil 7.6’da gösterilmiştir.??? Giriş gerilim kaynağı, VI, MO transistörünü
besleyen DC bileşen ve AC giriş sinyalinden oluşur.
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
4
DC Analiz: DC analizde kapasiteler açık devre gibi davranır. Bütün AC kaynaklar sıfıra götürülür. DC
eşdeğer devresi Şekil 7.6’da gösterilmiştir.
M1 ve M2 transistörleri eş transistörler ise, λ1= λ2= λP, VTP1=VTP2=VP ve kP1=kP2=kP olur. Çalışma
noktasındaki D-S gerilimi
olarak hesaplanır.
V+
M2
M2
M1
C
Vo
VI
MO
M1
4
IREF
VI
1
IREF
Vo
2
R1
RL
V+
3
R1
MO
5
(a)
(b)
Şekil 7.6 (a) MOSFET Aktif Yük Devresi, (b) DC Eşdeğer Devresi
AC Analiz: Kapasitelerin kapasite değerlerinin yeterince büyük olduğunu kabul edilir, böylece AC
analizde kısa devre gibi davranır. Bütün Dc kaynaklar sıfıra götürülüp devrede kısa devre olarak
gösterilir. Transistörlerin eşdeğer devresi de devrenin içine yerleştirilirse, devrenin küçük işaret
eşdeğer devresi elde edilir. Küçük işaret eşdeğer devresi Şekil 7.7’de gösterilmişitir.
Vo
+
VIac
gmVGS
rd1
rd2
RL
Şekil 7.7 MOSFET Aktif Yük Devresinin Küçük İşaret Eşdeğer Devresi
MOSFET aktif yük devresinin küçük işaret gerilim kazancı
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
5
7.3 ÖN ÇALIŞMA
7.3.1 Şekil 7.1’de, IREF ve IO’yu hesaplayınız ve PSpice analizini yapınız.( ayarlanabilir direnç 0<RL<10kΩ
, V+=5V, V-=0V).
NETLIST
1.0 mA
0.8 mA
0.6 mA
0.4 mA
0.2 mA
0 mA
0
1K
2K
3K
4K
5K
6K
7K
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
8K
9K
6
10 K
7.3.2 Şekil 7.3’de, IREF ve IO’yu hesaplayınız ve PSpice analizini yapınız.( Ayarlanabilir direnç
0<RL<30kΩ , V+=10V, V-=0V).
NETLIST
500 uA
400 uA
300 uA
200 uA
100 uA
0 mA
0
2K
4K
6K
8K
10 K
12 K
14 K
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
16 K
18 K
7
20 K
7.3.3 Şekil 7.6(b)’deki devrenin PSpice analizini yapınız, küçük işaret kazancı Av’yi elde ediniz. Vodc ve
IREF’i bulunuz.( Vin = 2.8+0.05sin(2π100t) V and V+=10 V).
AV =
VOdc =
IREF =
7.4 İŞLEM BASAMAKLARI
7.4.1 Deneyde Kullanılacak Malzemeler
Direnç
IC
: 1 kΩ, 2.2 kΩ, 4.7 kΩ, 6.9 kΩ
: CD4007, CA3146
Standart Laboratuvar Ekipmanları:
Osiloskop, DC Güç Kaynağı, Sinyal Jeneratörü, Dijital Multimetre, Protoboard.
7.4.2 Şekil 7.1(b)’deki devreyi kurunuz. Aşağıdaki tabloyu doldurunuz.(V+ = 5 V, V-=0 V)
RL
IO
VCE2
0
1 KΩ
2.2 KΩ
4.7 KΩ
7.4.3 Şekil 7.3’deki devreyi kurunuz. Aşağıdaki tabloyu doldurunuz.(V+ = 5 V, V-=0 V)
RL
IO
VDS2
0
2.2 KΩ
4.7 KΩ
6.9 KΩ
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
8
7.4.4 Şekil 7.6(b)’deki devreyi kurunuz. Küçük işaret kazancı Av, IREF ve Vodc’yi elde ediniz. Vodc ve.( Vin =
2.8 + 0.05sin(2π100t) V and V+=10 V)
4.7 k
Vin
AV =
+
VS
2.2 k
VOdc =
IREF =
7.5 SONUÇ
7.5.1 Ön çalışma sonuçları ile deney sonuçlarını karşılaştırınız. Farklar varsa nedenlerini
açıklayınız.
7.5.2 Bu deneyde ne öğrendiniz açıklayınız.
OKÜ - ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ - ELEKTRONİK LABORATUVARI
9