ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
06. HAZİRAN. 1996
Şekil 1
3. Şekil 1 deki iki ucu ankastre kirişin sol ve sağ mesnetlerinde ortaya çıkan reaksiyonları ve kiriş
boyunca eğim ve sehim denklemlerini Mohr Alan-Moment metodunu veya Macaulay metodunu
kullanarak bulunuz.
ÇÖZÜM :
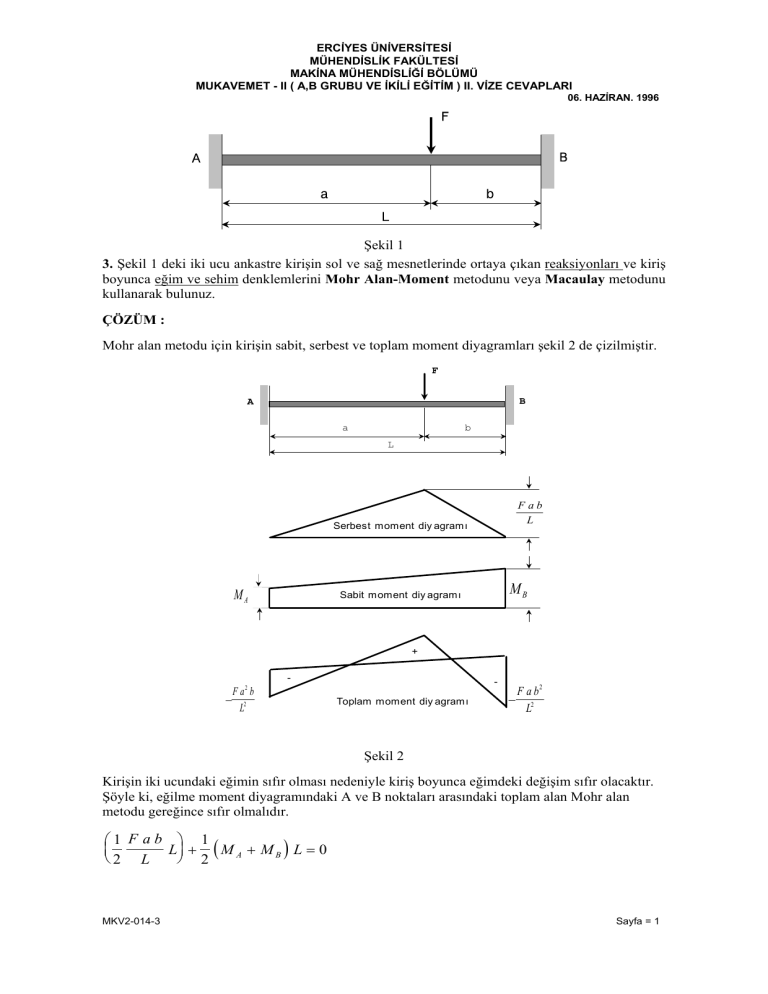
Mohr alan metodu için kirişin sabit, serbest ve toplam moment diyagramları şekil 2 de çizilmiştir.
F
B
A
b
a
L
F ab
L
Serbest moment diy agramı
MA
MB
Sabit moment diy agramı
+
-
F a2 b
− 2
L
Toplam moment diy agramı
−
F a b2
L2
Şekil 2
Kirişin iki ucundaki eğimin sıfır olması nedeniyle kiriş boyunca eğimdeki değişim sıfır olacaktır.
Şöyle ki, eğilme moment diyagramındaki A ve B noktaları arasındaki toplam alan Mohr alan
metodu gereğince sıfır olmalıdır.
1 F ab
2 L
MKV2-014-3
1
L + ( M A + M B ) L = 0
2
Sayfa = 1
ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
06. HAZİRAN. 1996
F ab
M A + MB = −
L
(1)
Ayrıca B noktasına izafeten A nın çökme miktarıda sıfır olur. Bu nedenle A civarında A ve B
noktaları arasındaki eğilme moment diyagramının momenti sıfır olmalıdır.
b
1 F a b 2 a 1 F a b
L 1
2 L
a
b a + + ( M A L) + ( M B − M B ) L
+
=0
2 2
3
2 L
3 2 L
3
b 1
1 F a b 2 a 1 F a b
L 1
2 L
a
b a + + M A L + M B L
=0
+
3 2
3
2 L
3 2 L
3 2
F a 3 b F a b2
b
L2
+
MA + 2 MB ) +
a + = 0
(
6
3L
3L
3
M A + 2 MB = −
Fab
(2 a 2 + 3 a b + b2 )
L3
(2)
(1) nolu denklem (2) nolu denklemden çıkarılırsa
MB = −
F ab
Fab
2 a 2 + 3 a b + b2 ) +
(
3
L
L
MB = −
Fab
2 a 2 + 3 a b + b 2 − L2 )
(
3
L
bulunur. Şekil 2 den L = a + b
MB = −
(
MB = −
F a2 b
L2
(3)
eşitliği (3) nolu ifadede yerine konulursa
)
F ab
F ab
2
2 a 2 + 3 a b + b 2 − ( a + b) = −
( 2 a 2 + 3 a b + b 2 − a 2 − 2ab − b 2 )
3
L
L3
F ab
Fab
F a2 b
2
MB = −
a
+
a
b
=
−
a
a
+
b
=
−
L
(
)
(
)
L3
L3
L3
(4)
bulunur. Son ifadede (1) nolu ifade yerine konulursa
MA −
F a2 b
Fab
=−
2
L
L
Fab
F a2 b
Fab
F a2 b
F ab
(
)
MA = −
L+
= − 2 a +b +
= − 2 ( a + b − a)
2
2
2
L
L
L
L
L
MA = −
F a b2
L2
(5)
bulunur. Şekil 3 de gösterildiği gibi A noktasına göre moment alınırsa
M A + F a − RB L − M B = 0
MKV2-014-3
Sayfa = 2
ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
06. HAZİRAN. 1996
Şekil 3
RB =
Fa
1
1 F a b2 F a 2 b
−
M
+
F
a
−
M
=
+
+ F a = 3 ( − b 2 + ab + l 2 )
(
2
2
A
B)
L
L
L
L
L
RB =
Fa
Fa
Fa
2
− b 2 + ab + ( a + b) = 3 ( − b 2 + ab + a 2 + 2ab + b 2 ) = 3 ( 3ab + a 2 )
3
L
L
L
(
)
F a2
(a + 3b)
RB =
L3
bulunur.
∑F
y
(6)
= 0 dan F = R A + RB
yazılabilir. O halde
F a2
F
F
(a + 3b) = 3 ( l 3 − a 3 − 3a 2 b) = 3
RA = F −
3
L
L
L
(( a + b )
3
− a 3 − 3a 2 b
RA =
F
F
3
2
2
3
3
2
( 3ab 2 + b 3 )
3 ( a + 3a b + 3ab + b − a − 3a b ) =
L
L3
RA =
F b2
( 3a + b)
L3
)
(7)
bulunur. A noktasının referans alındığı Macaulay metoduna göre eğilme moment denklemi
M ( x ) = EI zz
d2y
= R A x + M A − F ( x − a)
dx 2
( 0 ≤ x < L)
(8)
( 0 ≤ x < L)
(9)
( 0 ≤ x < L)
(10)
eğim denklemi
( x − a)
dy
x2
EI zz
= RA
+ MAx − F
+ c1
dx
2
2
2
sehim denklemi
( x − a)
x3
x2
EI zz y = R A
+ MA
−F
+ c1 x + c2
6
2
6
3
şeklinde yazılabilir. Şekil 3 den sınır şartları
x = 0 da
MKV2-014-3
dy
= 0 ve y = 0
dx
(11a,b)
Sayfa = 3
ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
06. HAZİRAN. 1996
dy
x = L de
= 0 ve y = 0
dx
(12a,b)
olacaktır. (9) nolu denkleme (11a) sınır şartı uygulanırsa
( 0 − a)
dy
02
0 = EI zz
= RA
+ MA0− F
+ c1
dx
2
2
2
c1 = 0
(13)
ve (10) nolu denklemde (11b) sınır şartı ve (13) nolu eşitlik yerine yazılırsa
( 0 − a)
03
02
0 = EI zz y = R A
+ MA
−F
+ 0 + c2
6
2
6
3
c2 = 0
(14)
bulunur. (5, 7, 13 ve 14) nolu eşitlikler (9 ve 10) nolu denklemlerde yerine konulursa eğim
denklemi
( x − a)
dy F b 2
x 2 F a b2
(
)
EI zz
= 3 3a + b
−
x−F
2
dx
2
2
L
L
2
( 0 ≤ x < L)
(15)
( 0 ≤ x < L)
(16)
ve sehim denklemi
( x − a)
F b2
x 3 F a b2 x 2
EI zz y = 3 ( 3a + b)
−
−
F
6
2
6
L
L2
3
şeklini alır.
•
ALTERNATİF ÇÖZÜM :
Bu problemin ikinci çözümü MACAULAY METODU doğrudan tatbik edilerek elde edilebilir.
Bu amaçla, A noktasını referans alan eğilme moment denklemi
M ( x ) = EI zz
d2y
= R A x + M A − F ( x − a)
dx 2
( 0 ≤ x < L)
(1)
( 0 ≤ x < L)
(2)
( 0 ≤ x < L)
(3)
eğim denklemi
( x − a)
dy
x2
EI zz
= RA
+ MAx − F
+ c1
dx
2
2
2
sehim denklemi
( x − a)
x3
x2
+ MA
−F
+ c1 x + c2
6
2
6
3
EI zz y = R A
şeklinde yazılabilir. Şekil 3 den sınır şartları
x = 0 da
dy
= 0 ve y = 0
dx
(4a,b)
olacaktır. (2) nolu denkleme (4a) sınır şartı uygulanırsa
MKV2-014-3
Sayfa = 4
ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
0 = EI zz
06. HAZİRAN. 1996
( 0 − a)
dy
0
= RA
+ MA0− F
+ c1
dx
2
2
2
2
c1 = 0
(5)
ve (3) nolu denklemde (4b) sınır şartı yerine yazılırsa
( 0 − a)
03
02
0 = EI zz y = R A
+ MA
−F
+ 0 + c2
6
2
6
3
c2 = 0
(6)
bulunur. (5 ve 6) nolu eţitlikler (2 ve 3) nolu denklemlerde yerine konulursa eğim denklemi
( x − a)
dy
x2
EI zz
= RA
+ MAx − F
dx
2
2
2
( 0 ≤ x < L)
(7)
( 0 ≤ x < L)
(8)
sehim denklemi
( x − a)
x3
x2
EI zz y = R A
+ MA
−F
6
2
6
3
şeklini alır. Ancak burada RA ve MA reaksiyonlarının tespit edilmesi gerekmektedir. Bu amaçla
x = L de
dy
= 0 ve y = 0
dx
(9a,b)
sınır şartları sırasıyla (7 ve 8) nolu denklemlerde yerine yazılırsa
( L − a)
dy
L2
0 = EI zz
= RA
+ MAL − F
dx
2
2
RA L + 2 M A =
2
L2
b2
⇒ RA
+ MAL = F
2
2
F b2
L
( L − a)
L3
L2
0 = EI zz y = R A
+ MA
−F
6
2
6
(10)
3
⇒ RA
L3
L2
b3
+ MA
=F
6
2
6
F b3
RA L + 3 M A = 2
L
(11)
bulunur. (11) nolu denklemden (10) nolu denklemi çıkartırsak
2
F b3 F ( L − a)
F b2
F b2
MA = 2 −
= 2 ( b − L) = 2 ( − a )
L
L
L
L
MA = −
F b2 a
L2
(12)
bulunur. (12) nolu ifade (10) nolu ifadede yerine konulursa
MKV2-014-3
Sayfa = 5
ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
06. HAZİRAN. 1996
Fab Fb
=
RA L + 2 −
L
L2
2
2
F ab
Fb
+2
L
L2
2
⇒ RA L =
2
F b2
F b2
(
)
R A L = 2 L + 2a = 2 ( a + b + 2a )
L
L
RA =
F b2
( 3a + b)
L3
(13)
bulunur. (12 ve 13) nolu denklemler (7 ve 8) nolu denklemlerde yerine konulursa eğim denklemi
EI zz
( x − a)
dy F b 2
x 2 F a b2
= 3 ( 3a + b)
−
x−F
2
dx
2
2
L
L
2
( 0 ≤ x < L)
(14)
( 0 ≤ x < L)
(15)
ve sehim denklemi
( x − a)
F b2
x 3 F a b2 x 2
(
)
EI zz y = 3 3a + b
−
−F
2
6
2
6
L
L
3
şeklini alır. (14 ve 15) nolu denklemler B noktasını içermemektedir. İlaveten MB ve RB
reaksiyonları bilinmemektedir. Bu amaçla, B noktası referans alınarak eğilme moment denklemi
M ( x ) = EI zz
d2y
= R B x + M B − F ( x − b)
dx 2
( 0 ≤ x < L)
(16)
( 0 ≤ x < L)
(17)
( 0 ≤ x < L)
(18)
eğim denklemi
( x − b)
dy
x2
EI zz
= RB
+ MBx − F
+ c3
dx
2
2
2
sehim denklemi
( x − b)
x3
x2
EI zz y = RB
+ MB
−F
+ c3 x + c4
6
2
6
3
şeklinde yazılabilir. Şekil 3 den sınır şartları
x = 0 da
dy
= 0 ve y = 0
dx
(19a,b)
olacaktır. (17) nolu denkleme (19a) sınır şartı uygulanırsa
( 0 − b)
dy
02
0 = EI zz
= RB
+ MB0 − F
+ c3
dx
2
2
2
c3 = 0
(20)
ve (18) nolu denklemde (19b) sınır şartı yerine yazılırsa
( 0 − b)
03
02
0 = EI zz y = R B
+ MB
−F
+ 0 + c4
6
2
6
3
MKV2-014-3
Sayfa = 6
ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
06. HAZİRAN. 1996
c4 = 0
(21)
bulunur. (20 ve 21) nolu eşitlikler (17 ve 18) nolu denklemlerde yerine konulursa eğim denklemi
( x − b)
dy
x2
EI zz
= RB
+ MBx − F
dx
2
2
2
( 0 ≤ x < L)
(22)
( 0 ≤ x < L)
(23)
sehim denklemi
( x − b)
x3
x2
EI zz y = RB
+ MB
−F
6
2
6
3
şeklini alır. Ancak burada RB ve MB reaksiyonlarını tespit edebilmek için
x = L de
dy
= 0 ve y = 0
dx
(24a,b)
sınır şartları sırasıyla (22 ve 23) nolu denklemlerde yerine yazılırsa
( L − b)
dy
L2
0 = EI zz
= RB
+ MB L − F
dx
2
2
RB L + 2 M B =
L2
a2
⇒ RB
+ MB L = F
2
2
F a2
L
(25)
( L − b)
L3
L2
0 = EI zz y = RB
+ MB
−F
6
2
6
RB L + 3 M B =
2
3
L3
L2
a3
⇒ RB
+ MB
=F
6
2
6
F a3
L2
(26)
bulunur. (26) nolu denklemden (25) nolu denklemi çıkartırsak
2
F a2
Fa 3 F a 2 F a 2
Fa 3 F ( L − b)
(
)
MB = 2 −
= 2 −
= 2 a − L = 2 ( a − a − b)
L
L
L
L
L
L
F a2 b
MB = −
L2
(27)
bulunur. (27) nolu ifade (25) nolu ifadede yerine konulursa
F a 2 b F a 2
=
RB L + 2 −
L
L2
⇒ RB L =
F a 2 b
F a2
+2
L
L2
F a2
F a2
RB L = 2 ( L + 2b) = 2 ( a + b + 2b)
L
L
RB =
F a2
( a + 3b)
L3
(28)
bulunur. (27 ve 28) nolu denklemler (22 ve 23) nolu denklemlerde yerine konulursa eğim
denklemi
MKV2-014-3
Sayfa = 7
ERCİYES ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
MUKAVEMET - II ( A,B GRUBU VE İKİLİ EĞİTİM ) II. VİZE CEVAPLARI
( x − b)
Fa b
dy F a
x
= 3 ( a + 3b)
−
x−F
2
dx
2
2
L
L
2
EI zz
2
2
06. HAZİRAN. 1996
2
( 0 ≤ x < L)
(29)
( 0 ≤ x < L)
(30)
sehim denklemi
EI zz
( x − b)
dy F a 2
x3 F a2 b x2
= 3 ( a + 3b)
−
−F
2
dx
6
2
6
L
L
3
şeklini alır.
MKV2-014-3
Sayfa = 8
