deu endustrı muh

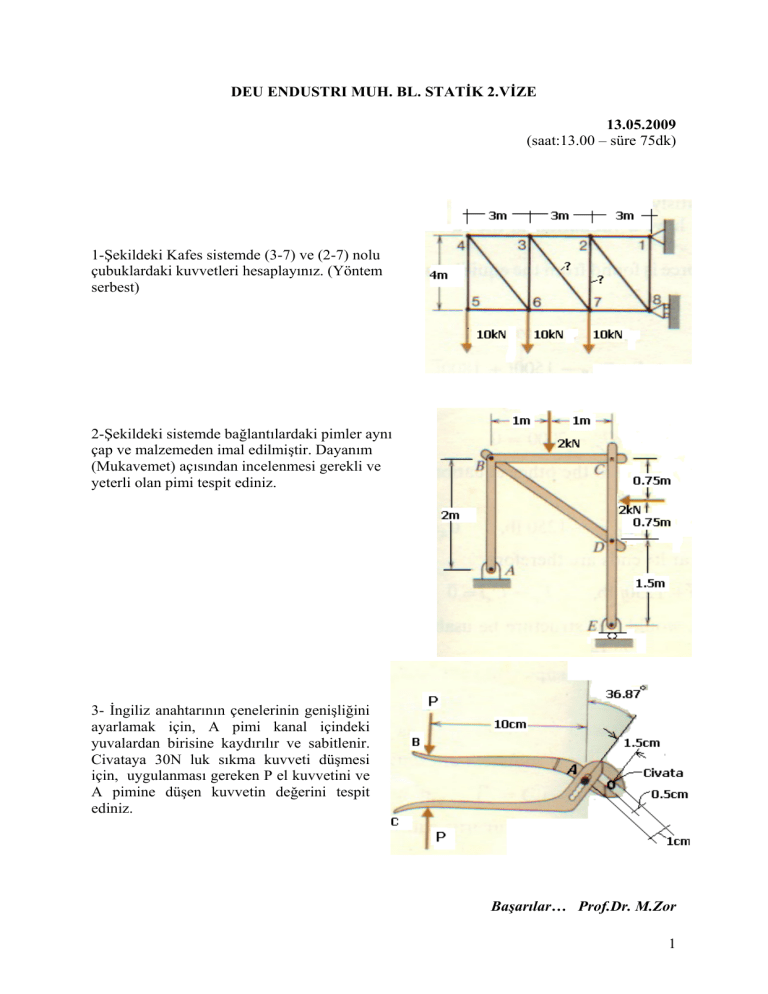
DEU ENDUSTRI MUH. BL. STATİK 2.VİZE
13.05.2009
(saat:13.00 – süre 75dk)
1-Şekildeki Kafes sistemde (3-7) ve (2-7) nolu
çubuklardaki kuvvetleri hesaplayınız. (Yöntem
serbest)
2-Şekildeki sistemde bağlantılardaki pimler aynı
çap ve malzemeden imal edilmiştir. Dayanım
(Mukavemet) açısından incelenmesi gerekli ve
yeterli olan pimi tespit ediniz.
3- İngiliz anahtarının çenelerinin genişliğini
ayarlamak için, A pimi kanal içindeki
yuvalardan birisine kaydırılır ve sabitlenir.
Civataya 30N luk sıkma kuvveti düşmesi
için, uygulanması gereken P el kuvvetini ve
A pimine düşen kuvvetin değerini tespit
ediniz.
Başarılar… Prof.Dr. M.Zor
1
DEU ENDUSTRI MUH. BL. STATİK 2.VİZE ÇÖZÜMLERİ
CEVAP 1:
∑M A = 0
II. Kesim
10 * 9 + 10 * 6 + 10 * 3 − B x * 4 = 0
Bx = 45 kN
∑F
A
Ax
=0
x
Ay
Ax − B x = 0 ⇒ Ax − 45 = 0
Ax = 45 kN
Bx
B
∑ Fy = 0
B
Ay − 10 − 10 − 10 = 0
A y = 30 kN
I. KESİM:
∑ Fy = 0
F23
− F27 + 30 = 0
F27 = 30 kN : 2-7 nolu çubuğa gelen çeki kuvveti
∑M
8
45 kN
A
30 kN
F27
=0
F87
F23 * 4 + F27 * 3 − 45 * 4 = 0
45 kN
B
4 F23 + 30 * 3 − 45 * 4 = 0
F23 = 22.5 kN
II. KESİM
3
4
cos α = = 0.6 sin α = = 0.8
5
5
∑M8 = 0
22.5 * 4 − (F73 sin α ) * 3 + 10 * 3 − 45 * 4 = 0
F73 = −25 kN : 3-7 nolu çubuğa gelen bası kuvveti
22.5 kN
45 kN
A
F73
F76
30 kN
α
45 kN
B
CEVAP 2:
∑MA = 0
− 2 * 1 + 2 * 1.25 − E y * 2 = 0
E y = 0.25 kN : E pimine gelen kuvvet
∑F
x
=0
Ax − 2 = 0
Ax = 2 kN
∑F
y
=0
Ay − 2 − 0.25 = 0
Ay = 2.25 kN
FA = 2 2 + 2.252
FA = 3.01 kN : A pimine gelen kuvvet
Ax
A
Ay
Ey
2
ABC elemanı
BD elemanı
EDC elemanı
Cy
Cx
α
FBD
Cx
FBD
Cy
B
FBD
A
2 kN
C
cosα=0.8
sinα=0.6
2.25 kN
α
α
D
D
FBD
ABC elemanına ait SCD dan:
∑MC = 0
E
2 * 2 − 2.25 * 2 − FBD sin α * 2 + 2 *1 = 0
FBD = 1.25 kN : B ve D pimlerine gelen kuvvet
0.25 kN
∑M
B
=0
2 * 2 − 2 *1 − C y * 2 = 0
C y = 1 kN
∑F
x
=0
2 − C x − FBD cos α = 0 ⇒ C x = 2 − 1.25 * 0.8
C x = 1 kN
FC = 12 + 12 ⇒ FC = 1.41 kN : C pimine gelen kuvvet
Pimlere gelen kuvvetler hesaplandığında maksimum kuvvetin A piminde oldu görülür.
Dolayısıyla A pimi incelenmelidir.
CEVAP 3:
∑M
A
=0
P *10 − 30 *1.5 = 0
P = 4.5 N
∑F
y
=0
− P − 30 * cos 36.87 + Ay = 0 ⇒ Ay = 4.5 + 30 * 0.8
Ay = 28.5 N
∑F
x
=0
30 N
Ax
Ay
Ax − 30 * sin 36.87 = 0 ⇒ Ax = 30 * 0.6
Ax = 18 N
FA = 28.5 2 + 18 2 ⇒ FA = 33.71 N
3