Fall 2006

Name:
Spring 2011
11 June 2011
ME-210 Applied Math for ME
Std ID:
Final Examination
Grade:
Closed book and notes
Show all your calculation steps. No calculators.
Use the back side of the same sheet to continue solving a problem.
Duration: 130 minutes
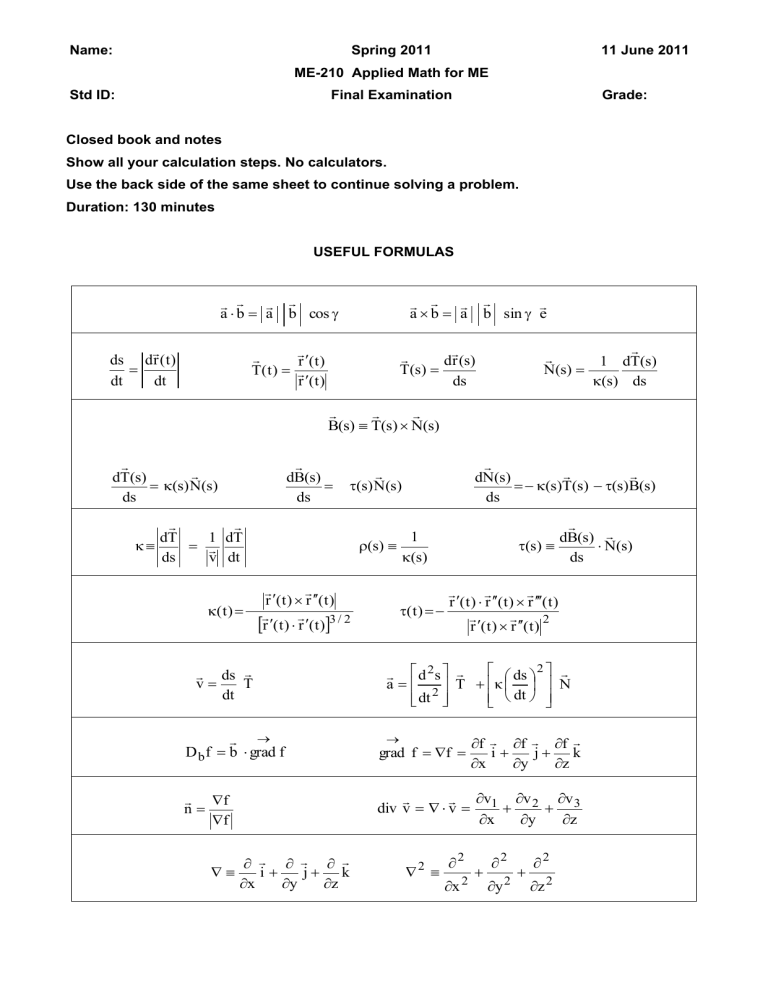
USEFUL FORMULAS
  
ab  a

ds d r ( t )

dt
dt
  
ab  a

b cos 


b sin  e


1 dT(s)
N(s) 
(s) ds


d r (s)
T(s) 
ds


r ( t )
T( t )  
r ( t )



B(s)  T(s)  N(s)


dT(s)
 (s) N(s)
ds

dB(s)

ds



dN(s)
  (s)T(s)  (s)B(s)
ds

(s) N(s)


dT
1 dT

 
ds
v dt


r ( t )  r ( t )
( t )  
r (t )  r (t )3 / 2
 ds 
v
T
dt

dB(s) 
(s) 
 N(s)
ds
1
(s) 
(s)



r ( t )  r ( t )  r ( t )
( t )  


2
r ( t )  r ( t )
  ds  2  
  d 2s  
κ    N
a
T


  dt  
 dt 2 
 
D b f  b  grad f
grad f  f 
 f
n
f
v
v

 v
div v    v  1  2  3
x
y
z

     
i
j k
x
y
z

2 
2
x 2
f  f  f 
i
j k
x
y
z

2
y 2

2
z 2
v    v
 v
v   v
v  


curl v    v   3  2  i   1  3  j   2  1 k
z   z
x   x
y 
 y


 div (v)  0
t
curl (f )  0
n
If [C]  [A][B]
det([A]) 
n
 (1)
j k
k 1
c jk   a jib ik
then
i 1
n
det([A])   (1) j  k a jk M jk
a jk M jk
j 1
where j  1, 2, ..., or n
where k  1, 2, ..., or n
[A] - 1 =
xi = Di / D
Adj[A]
det[A]
Adj[A] = [C i j ] T
e i  = cos + i sin
(cos  + i sin) n = cos(n) + i sin(n)
[A] [x] =  [x]
    2k 
   2k  
z n  r n cos 
  i sin 
  ,k = 0,1,2, … ,n -1
 n 
  n 
1
ez = e(x
1
+ iy )
= ex eiy
ln(z) = ln |z| + i arg(z)
cosh(z) = ( e z + e – z ) / 2
sinh(z) = ( e z – e – z ) / 2
cos(z) = ( e i z + e – i z ) / 2
sin(z) = ( e i z – e – i z ) / 2i
df
 f (z o  z)  f (z o ) 
 lim 

dz z zo z0 
z

w = f(z) = f(x + iy) = u(x,y) + i v(x,y)
ux = vy
df
  u x  i vx
dz z zo
u y = -v x
∯( ⃗ ̂)
∬( ⃗ ̂)
∭(
∬[ ⃗ ( (
∬⃗ ̂
∫ ⃗ ( ⃗)
) (
∬(
⃗
⃗)
)) ⃗⃗]
) (
⃗) ̂
∫ ⃗ ( ⃗( ))
⃗

z  z0
QUESTION 1 (20 points)
Find all the possible solutions for the following system of equations using Gauss Elimination and back
substitution:
2w  3x  2y  7
3w  y  z  7
2x  y  z  1
SOLUTION
Matrix representation of the system of equations:
w
2 3 2 0    7
3 0 1 1  x   7

y  
0 2 1 1     1
z
The augmented matrix:
2 3 2 0
3 0 1 1

0 2 1 1
7
7

1
Gauss elimination:
1
2 *   2  2  3  1
3 
2 3 2 0
0 9 4 2

0 2 1 1
7
7

1 
2 3 2 0
0 9 4 2

0 0
1 5
7  1
7  2

5  3 *   9  3   2  2
Back substitution:
y - 5 z = 5 => y = 5 + 5 z
-9 x + 4 y - 2 z = -9 x + 20 + 20 z - 2 z = -9 x + 20 + 18 z = -7 => x = 3 + 2 z
2 w + 3 x - 2 y = 2 w + 9 + 6 z - 10 - 10 z = 2 w - 1 - 4 z = 7 => w = 4 + 2 z
 4 2
 5  5 
All possible solutions:   +   z , where z is arbitrary.
3 2
   
0  1
QUESTION 2 (20 points)
Find the eigenvalues and eigenvectors of
1 0 0 
M  1 0 1 .


1 1 0 
Check your results by multiplying [M] with the eigenvectors you found.
SOLUTION
Characteristic polynomial:
1  0
0
M   I  1  1  1    2  1  0
1
1 
Eigenvalues: 1    2  1  0  1,2  1 , 3  1.
Eigenvectors corresponding to eigenvalue 1,2  1 :
1  1 0 0   x1 
0



1 1 x 2  0 
 
 
 1 1 1 x3 3 0
 x1   x2 1   x3 1
M  1I  1

c1  c2 
 1
 1
 c2 
0
 1
 x1 1   x2 1   x3 1  0
 x 1   c1   c1  1  c2 0 , where c1 and c2 are arbitrary.


 
 
1 0 0  c1+c2  c1+c2 
Check: 1 0 -1  c1  =  c1  

 
 

1 -1 0   c2   c2 
Eigenvectors corresponding to eigenvalue 3  1 :
1  1 0 0   x1 
0
 x13  0




M   1I 1 1 1 x2  0 

 
 
 x2 3   x3 3
 1 1 1  x3 3 0
0
0




 x 3  c3  c3 1 , where c3 is arbitrary.
 
 
c3 
 1
1 0 0   0   0 
Check: 1 0 -1 c3  = -c3  = 
    
1 -1 0  c3  -c3 
0
c  
 3
c3 
QUESTION 3 (10+10 points)
a) Evaluate
sin    i 
and express the result in Cartesian form, i.e., find the real and imaginary parts.
2i
b) Find (all possible values for) z when zz  z  1  i .
SOLUTION
sin π - i ei π-i - e-i π-i
e1+iπ - e-1-iπ
e1 cos  π + i sin π - e-1 cos -π + i sin-π
=
=
=
2+i
2 i  2 + i
2 -1 + i 2
2 -1 + i 2

a)
=



- e + e-1
- e + e-1
-1 - i 2
e - e-1 1 + i 2 e2 - 1
e2 - 1
=
=
=
+
i
-1 + i 2 -1 - i 2
2 -1 + i 2
2
2 1 + 22
10 e
5e
b) Let z = x + iy  z z + z =  x + i y  x - i y + x + i y = x2 + y2 + x + i y = 1 + i .
Real part: x2  y2  x  1
2
  x  1 x  1
Imaginary part: y  1 
 x2  x  x  x  1  0
 x  0 or x  1
 Roots: z1  i , z2  1  i
QUESTION 4 (10×2 points)
Let f  x,y,z = x2 - y z and v  x,y,z  v1  x,y,z i  v2  x,y,z j  v3  x,y,z k  x2 i  y z j . State whether the
following expressions make sense and evaluate them if possible:
a) f
b)   f
d)  v
c)  f
e)   v f)  v
g)  f
h) f
i)   v
SOLUTION
a) f 
f
f
f
i
j
k  2 x i z j y k.
x
y
z
b)   f : Divergence of a scalar function is not defined.
c)  f : Curl of a scalar function is not defined.
d)  v : Gradient of a vector function is not defined.
e)   v 
v1 v2 v3   2  f
f



x    y z   0   2 x  z .
x y z x
y
z
 v v 
 v v 
 v v 
f)   v   3  2  i   1  3  j   2  1  k .
 z x 
 y z 
 x y 









  0    yz i    x2   0 j    yz   x2  k  y i .
z
x 
y
z
y

x




j
g)   f   i 

x

y

z





k   2 x i  z j  y k   2x    z    y   2 .

x

y

z

h)   f  0 , because curl of the gradient of a scalar function is always zero.
i)     v :   v  2 x  z is a scalar function and curl of a scalar function is not defined.



j
j)     v   i 
y
z
 x


k    y i   y   0 .
x

j)   v
QUESTION 5 (20 points)
Evaluate
 1  x  dA , where the surface S is the cylinder x
2
+ y2 = 1 between z = 0 and z = 1 + x.
S
Hint: Let x = cos(θ), and find the parametric representation of the surface S as r  ,z
dA 
r r

dz d
 z
SOLUTION
Let x  cos   y  1  x2  sin  . Then, a parametrization for S is: r ,z  cos  i  sin j  z k .
r
r
  sin  i  cos  j ,
k 

z
 1  x  dA 
S
2  1 cos 
 
0
2

0
i
j
k
r r

  sin  cos  0  cos  i  sin  j  cos2   sin2   1
 z
0
0
1
2
2
1  cos  r  r dz d   1  cos 2 d   1  2cos   cos2  d
 z
0
0
 2 
cos2  1
sin2 

3
0 1  2 cos   2  d   2   2 sin  4  0  3