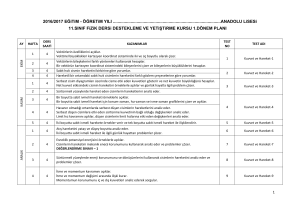
TEKNOLOJİNİN BİLİMSEL İLKELERİ
Bölüm-6
DÜZGÜN CİSİMLERİN AĞIRLIK
MERKEZLERİ
6.1. Ağırlık Merkezinin Tanımı
Bütün cisimler arzın merkezine doğru çekilirler. Bu çekim
kuvvetine yer çekimi kuvveti denir.
Cismi meydana getiren partiküllerin tümünün hareket yönü arzın
merkezine doğrudur.
Cisimlerin kütleciklerinin (maddesel noktalarının) ağırlıklarının
meydana getirdiği kuvvetlerin bileşkesinin tatbik noktasına o cismin
ağırlık merkezi denir.
Şekil 6.1. Cisimlerin Ağırlıkları Arzın Merkezine Doğrudur
Özellikle cisimlerin dengeli olarak yerleştirilmeleri için cisimlerin
kararlı bir yapıda olması ve ağırlık merkezlerinin zemine yakın olması
gerekir. Yarış arabalarının zemine yakın şekilde üretilmelerinin temel
nedeni ağırlık merkezlerinin yere yakın olması nedeni yüksek süratte
devrilmemeleri, yani dengeli bir yapıya sahip olmalarıdır.
34
TEKNOLOJİNİN BİLİMSEL İLKELERİ
Cisimler için 3 çeşit denge durumu vardır:
1) Kararlı Denge Şekil 6.2
2) Kararsız Denge Şekil 6.3
3) Nötr Denge Şekil 6.4
6.2. Kararlı, Kararsız ve Doğal Denge
1- Kararlı Denge = Durumu değiştirilmeye zorlanan cisim
uygulanan kuvvet kalktığında ilk orijinal konumuna döner. Cismin ağırlık
merkezi mümkün olan en alt noktadır.
Şekil 6.2.
2- Kararsız Denge= Uygulanacak küçük bir kuvvet ile dengesi
bozulan ve ilk konumuna dönemeyen cisimlerin denge durumudur.
Cismin ağırlık merkezi mümkün olan en üst konumdadır.
Şekil 6.3.
35
TEKNOLOJİNİN BİLİMSEL İLKELERİ
3- Doğal (Nötral) Denge= Durumu değiştirilmeye çalışılan cisim,
her zaman aynı konumunu korur. Bu tür denge durumuna sahip
cisimlerde ağırlık merkezi daima aynı yüksekliktedir.
Şekil 6.4.
6.3. Bazı Cisimlerin Ağırlık Merkezleri
En çok bilinen geometrik şekillerden kare veya dikdörtgenin ağırlık
merkezi köşegenlerin kesim noktasıdır (Şekil 6.5.a).
Dairesel kesitli parçaların ağırlık merkezi eksenlerinin kesim
noktasıdır (Şekil 6.5.b). Üçgenin ağırlık merkezi ise kenar ortayların
kesim noktasıdır (Şekil 6.5.c).
Şekil 6.5. Bazı Cisimlerin Ağırlık Merkezleri
36
TEKNOLOJİNİN BİLİMSEL İLKELERİ
6.4.
Düzgün Şekilli Cisimlerin Ağırlık Merkezlerinin
Bulunması
Düzgün şekilli cisimlerin ağırlık merkezlerinin bulunması için şekil
düzgün şekillerde parçalara ayrılır. Her parçanın ağırlık merkezinin
koordinat merkezine olan uzaklıkları ve alanları bulunur. İlave edilmiş
parçalar artı, çıkarılmış parçalar ise eksi olarak değerlendirilir.
Şekil 6.6. Cisimlerin Ağırlık Merkezinin Bulunması
X=
X1A 1 + X 2 A 2 + ..... + X n A n
A 2 + A 2 +...... + A n
Y=
Y1A 1 + Y2 A 2 ... + Y 3 A 3
A 2 + A 2 + .... + A n
Soru 6.1. Şekil 6.7’de görülen malzemenin ağırlık merkezinin
koordinatlarını hesaplayınız?
Şekil 6.7
37
TEKNOLOJİNİN BİLİMSEL İLKELERİ
Parça iki düzgün parçaya ayrılarak birinci I, ikincisi ise II ile
isimlendirilir. Parçaların alanları ve ağırlık merkezinin koordinat eksenine
olan mesafeleri belirlenir.
X
Y
A
I
2
4
2,8
II
2
1,5
3,6
X=
X1A 1 + X 2 A 2
A 2 +A 2
X=
2 x 2,8 + 3 x 3,6
=
2,8 + 3,6
Y=
Y1A 1 + Y2 A 2
A 2 +A 2
Y=
4 x 2,8 + 1,5 x 3,6
= 2,3 cm
2,8 + 3,6
2 cm
6.5. Bölüm – 6 (Ağırlık Merkezi) Soruları
1. Şekil 6.8’deki parçanın ağırlık merkezini hesaplayınız?
Şekil 6.8.
38
TEKNOLOJİNİN BİLİMSEL İLKELERİ
2. Şekil 6.9’deki parçanın ağırlık merkezini hesaplayınız?
Şekil 6.9.
Şekil 6.10.’daki parçanın ağırlık merkezini hesaplayınız?
Şekil 6.10.
39