The uniform distribution is a probability distrib% ution that has equal

Probability Distributions for Continuous Random Variables:
The Uniform Distribution (Sabit Olas¬l¬kl¬Da¼
g¬l¬m)
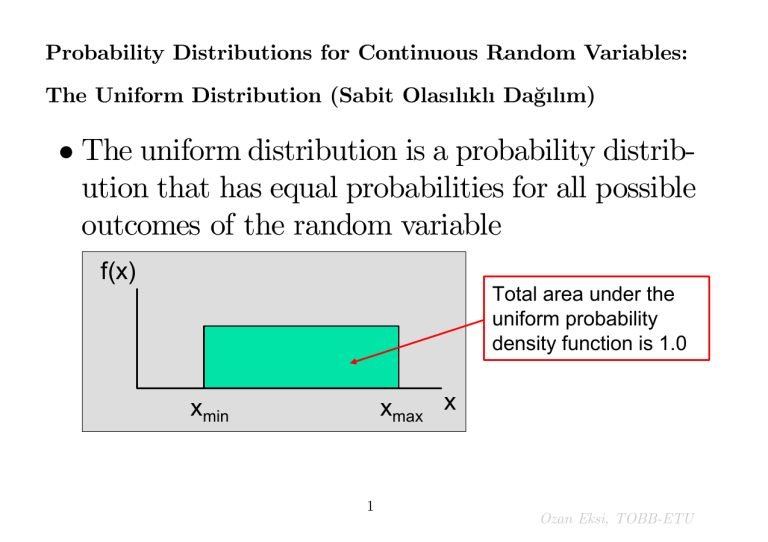
The uniform distribution is a probability distribution that has equal probabilities for all possible
outcomes of the random variable
f(x)
Total area under the
uniform probability
density function is 1.0
xmax x
xmin
1
Ozan Eksi, TOBB-ETU
It has propability density function of
9
8
1
<
for xmin < x < xmax =
f (x) = xmax xmin
;
:
0
elsewhere
–Its mean is
= E(X) =
Z xmax
xmin
2
xmax + xmin
xf (x)dx =
2
Ozan Eksi, TOBB-ETU
It has propability density function of
9
8
1
<
for xmin < x < xmax =
f (x) = xmax xmin
;
:
0
elsewhere
–Its variance is
2 = E[(X
Z xmax
=
xmin
)2 ]
(x
1
2
) f (x)dx = (xmax
12
3
xmin)2
Ozan Eksi, TOBB-ETU
Ex: 2 x 6 aras¬nda tan¬mlanm¬ş sabit olas¬l¬kl¬
da¼
g¬l¬m düşünelim. Bunun olas¬l¬k fonksiyonu
1
2 x 6 için f (x) =
= 0:25
6 2
ki şu şekilde gösterilebilir
f(x)
.25
2
6
4
x
Ozan Eksi, TOBB-ETU
Ortalamas¬:
xmax + xmin 2 + 6
=
=
=4
2
2
Varyasyonu:
2 = 1 (x
max
12
1
2
xmin) = (6
12
5
2)2 = 1:333
Ozan Eksi, TOBB-ETU
The Normal Distribution (Normal Da¼
g¬l¬m)
The normal distribution is the most important
distribution in the statistical theory
–It is bell-shaped
–It is symmetrical around the mean
–Its mean, median and mode are equal
–Location is determined by the mean,
–Spread is determined by the standard deviation,
6
Ozan Eksi, TOBB-ETU
–The random variable has an in…nite theoretical range: 1 to +1
f(x)
s
µ
x
Mean
= Median
= Mode
By varying the parameters µ and s , we obtain
different normal distributions
7
Ozan Eksi, TOBB-ETU
8
Ozan Eksi, TOBB-ETU
A (normal) random variable is the one having
normal distribution where the probability density function is
1x
(
)2
1
f (x) = p e 2
for 1 < x < 1; > 0
2
The normal distribution closely approximates the
probability distributions of a wide range of random variables
9
Ozan Eksi, TOBB-ETU
Computations of probabilities are direct and elegant
Distributions of sample means approach a normal distribution given a “large”sample size*
If random variable X has a normal distribution
with and variance 2 , then it is shown as
X
N ( ; 2)
10
Ozan Eksi, TOBB-ETU
Cumulative Normal Distribution: When X
N ( ; 2), cumulative distribution function is
Z x0
F (x0) = P (X x0) =
f (x)dx
1
f(x)
0
x
x0
11
Ozan Eksi, TOBB-ETU
The probability for a range of values is measured
by the area under the curve
P (a < X < b) = F (b)
a
µ
12
b
F (a)
x
Ozan Eksi, TOBB-ETU
The total area under the curve is 1.0, and the
curve is symmetric, so half is above the mean,
half is below
f(X) P( −∞ < X < μ) = 0.5
0.5
P(μ < X < ∞ ) = 0.5
0.5
µ
X
P(−∞ < X < ∞) = 1.0
13
Ozan Eksi, TOBB-ETU
The Standardized Normal (Standart Normal Da¼
g¬l¬m)
Any normal distribution (with any mean and
variance combination) can be transformed into
the standardized normal distribution (Z), with
mean 0 and variance 1
14
Ozan Eksi, TOBB-ETU
This need to transform X units into Z units by
subtracting the mean of X and dividing by its
standard deviation
X
Z=
It obtains the following
f(Z)
Z ~ N(0,1)
1
0
15
Z
Ozan Eksi, TOBB-ETU
Ex: E¼
ger X ortalamas¬100, standart sapmas¬50
olan rassal bir de¼
gişken ise, X = 200 de¼
gerinin Z
karş¬l¬g¼¬şudur
X
200 100
Z=
=
=2
50
Buna göre X = 200 de¼
geri X de¼
gişkeninin ortalamas¬olan 100’den 2 standart sapma yüksektedir.
Böylece X=200 de¼
gerinin, X’in alabilece¼
gi tüm
de¼
gerlere için göreli yerini bulmuş oluruz
16
Ozan Eksi, TOBB-ETU
Note that the distribution is the same, only the
scale is standardized
b −μ
 a −μ
P(a < X < b) = P
<Z<

σ
σ


 b −μ  a −μ
= F
 − F

 σ   σ 
f(x)
a
µ
b
x
a −μ
σ
0
b −μ
σ
Z
17
Ozan Eksi, TOBB-ETU
The Standardized Normal Table gives probability for any value of z
–Normal da¼
g¬l¬ma sahip bir X rassal de¼
gişkeni
için P(a < X < b) de¼
gerini bulal¬m
Önce X’in a ve b’ye eşit oldu¼
gu de¼
gerleri
Z’ye çevirebilir, sonra da kümülatif normal
tablosunu kullanabiliriz
–Ex: X ortalamas¬8.0, standart sapmas¬5 olan
normal da¼
g¬l¬ma sahip bir rassal de¼
gişken olsun (yani X N (8; 25)). P(X < 8.6) de¼
gerini
18
Ozan Eksi, TOBB-ETU
bulal¬m
X
Z=
=
8:6
8
5
= 0:12, P (Z < 0:12) = 0:547
µ=8
s = 10
8 8.6
µ=0
s =1
X
P(X < 8.6)
0 0.12
Z
P(Z < 0.12)
–Yani X rassal de¼
gişkeninin alabilece¼
gi de¼
gerlerin %54.78’i 8.6’n¬n alt¬ndad¬r
19
Ozan Eksi, TOBB-ETU
20
Ozan Eksi, TOBB-ETU
For upper tail (üst kuyruk) properties
–Ex: P (Z > 2:00) =?
P (Z < 2:00) = 0:9772
)
P (Z > 2:00) = 1
21
0:9772 = 0:0228
Ozan Eksi, TOBB-ETU
For negative Z-values, use the fact that it is symmetric distribution
Ex: P (Z <
)
2:00) =?
P (Z < 2:00) = 0:9772
P (Z < 2:00) = 1 0:9772 = 0:0228
.9772
.9772
.0228
.0228
Z
22
Z
Ozan Eksi, TOBB-ETU
Ex: Finding the X value for a Known Probability
–X
N (8; 25) ise X’in hangi de¼
geri X’in alabilece¼
gi tüm de¼
gerlerin %20’sinin üstündedir?
.80
.20
?
8.0
-0.84 0
23
Ozan Eksi, TOBB-ETU
Z de¼
geri için bahsi geçen de¼
gerin 0.84 oldu¼
gunu
standart normal tablosundan biliyoruz. O halde
X
Z=
)
X=
+ Z = 8 + ( 0:84)5 = 3:8
24
Ozan Eksi, TOBB-ETU
Ex: Araba yedek parças¬üreten bir şirketin üretti¼
gi bir ürünün dayan¬m süresi normal da¼
g¬l¬ma
sahiptir ve ortalamas¬1,250 hafta, standart sapmas¬ da 250 haftad¬r. Bu ürünlerden rastgele
seçilen bir tanesinin 900 ila 1,300 hafta aras¬nda
dayanma olas¬l¬g¼¬nedir?
25
Ozan Eksi, TOBB-ETU
P (900 < X < 1300) = P (
900
<Z<
1300
900
1250
1300 1250
= P(
<Z<
)
250
250
= P ( 1:2 < Z < 0:2)
= F (0:2) F ( 1:2)
= 0:5793 (1 0:8643)
= 0:44
26
Ozan Eksi, TOBB-ETU
)
Assessing Normality: Not all continuous random
variables are normally distributed. It is important to evaluate how well the data is approximated by a normal distribution. However, there
are tests that can be applied, for instance, by the
use of statistical programs
27
Ozan Eksi, TOBB-ETU