Kovaryans Analizi
(Analysis of Covariance)
Deney Tasarımındaki analiz Lineer Model çerçevesinde ele alındığında, etkenler
sınıflama düzeyinde ölçülen birer açıklayıcı değişken olarak düşünülmektedir. Deney
Tasarımına genel olarak Varyans Analizi de denmektedir. Bazı durumlarda oranlama veya
aralık düzeyinde (üçüncü ölçme düzeyinde) ölçülen açıklayıcı değişkenlerin Deney
Tasarımına katılması analizi iyileştirmektedir. Örneğin, bir ilâcın beş farklı dozunun ilâcın
etki süresine (Y) etkisi, araştırılmak istendiğinde ve bloklama etkeni (yardımcı etken) olarak
yaş alındığında, bunu; çocuk, genç, orta yaşlı ve yaşlı olarak dört grupta (düzeyde) analize
katmak yerine, doğrudan yıl olarak analize katabiliriz. Đlâcın her dozu 10 hasta üzerinde birer
kez denendiğinde ve etki süresi (Y) ile yaş (Z) arasında doğrusal bir ilişki olduğu
düşünüldüğünde,
i = 1, 2, 3, 4,5
, εij ∼ BND(0, σε2 )
Yij = µ + αi + γ Z ij + εij ,
j = 1, 2,...,10
veya
i = 1, 2,3, 4, 5
Yij = µ + αi + γi Z ij + εij ,
, εij ∼ BND(0, σε2 )
j = 1, 2,...,10
gibi bir model yazılabilir. Bu modelde sınıflama düzeyinde ölçülen açıklayıcı değişken
yanında üçüncü ölçme düzeyinde ölçülen açıklayıcı değişken de bulunmaktadır. Bir Deney
Tasarımında sadece sınıflama düzeyinde etkenler (açıklayıcı değişkenler) bulunduğunda bu
Deney Tasarımına Varyans Analizi, sınıflama düzeyinde ölçülen etkenler yanında üçüncü
ölçme düzeyinde ölçülen açıklayıcı değişkenler de bulunduğunda Kovaryans Analizi
denmektedir. Üçüncü ölçme düzeyindeki açıklayıcı değişkenlere eş-değişkenler (kovaryetler,
covariates, concominant variables, supplementary variables) denmektedir. Bir Kovaryans
Analizi Modeli,
Y = X β + Zγ + ε
biçimindedir. X matrisi Varyans Analizindeki tasarım matrisidir. Z matrisi kovaryetlerin
gözlem matrisidir. Đstatistiksel sonuç çıkarım (parametre tahmini ve hipotez testi) bu model
üzerinde yürütülebilir. Teorisini vermeksizin, Minitab paket programını kullanarak bazı
örnek problemler üzerinde istatistiksel sonuç çıkarım yapmaya çalışalım.
Örnek 1 Ege Üniversitesi Ziraat Fakültesi Đvesi koyun sürüsünde bir mevsimde doğan
kuzular üç gruptan birine alınmış ve 1. gruptakiler bir ay, 2. gruptakiler iki ay, 3. gruptakiler
üç ay emzirilmiş ve üç aylık canlı ağırlıkları (Y, kg) ölçülmüştür. Emzirmenin ağırlık
üzerindeki etkisi araştırılmak istenmektedir. Başlangıçta her grupta 7 kuzu varken, 1. gruptan
iki kuzu üç aya erişmeden ölmüştür. Her gruptaki kuzuları doğum ağırlığı bakımından eşit
yapma imkânı olmadığından ve doğum ağırlığının (Z) etkisi de göz ardı edilmek
istenmediğinden,
Yij = µ + αi + γ Z ij + εij
i = 1, 2,3
j = 1, 2,..., n
i
n1 = 5, n2 = n3 = 7
εijk ~BND (0, σε2 )
gibi bir model çerçevesinde,
H 0 : α1 = α2 = α3 = 0
H1 : α1 ≠ α2 veya α1 ≠ α3 veya α2 ≠ α3
hipotezi test edilecektir.
Gözlemler (Düzgüneş...(1991), sayfa 233, Tablo 12.2) :
1 ay emenler
Y1 j
Z1 j
2 ay emenler
3 ay emenler
Y2 j
Z2 j
Y3 j
Z3 j
12.8
11.0
12.6
11.5
12.0
16.1
19.1
19.6
20.0
18.0
11.5
16.6
4.3
3.4
4.6
3.8
4.0
Minitab Verisi:
Y Grup
12,8 1
11,0 1
12,6 1
11,5 1
12,0 1
16,1 2
19,1 2
19,6 2
20,0 2
18,0 2
11,5 2
16,6 2
19,0 3
19,8 3
16,6 3
17,0 3
18,6 3
16,9 3
19,3 3
Z
4,3
3,4
4,6
3,8
4,0
3,2
4,8
4,9
5,1
5,0
3,4
4,4
4,2
5,1
4,3
4,3
4,6
3,8
4,7
3.2
4.8
4.9
5.1
5.0
3.4
4.4
19.0
19.8
16.6
17.0
18.6
16.9
19.3
4.2
5.1
4.3
4.3
4.6
3.8
4.7
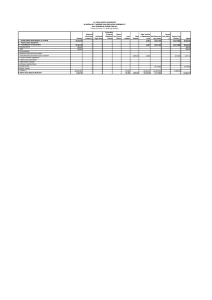
General Linear Model: Y versus Grup, covariate Z
Factor
grup
Type Levels
fixed
3
Values
1 2 3
Analysis of Variance for Y
Source
Z
grup
Error
Total
Term
Constant
Z
DF
1
2
15
18
Seq SS
90,354
75,086
23,218
188,658
Coef
4,178
2,7153
Adj SS
41,158
75,086
23,218
SE Coef
2,274
0,5266
Adj MS
41,158
37,543
1,548
T
1,84
5,16
F
26,59
24,25
P
0,000
0,000
P
0,086
0,000
Kovaryet kullanmadan yapılan analiz:
One-way ANOVA: Y versus Grup
Analysis of Variance for C8
Source
DF
SS
MS
grup
2
93,52
46,76
Error
16
36,46
2,28
Total
18
129,98
Level
1
2
3
N
5
7
7
Pooled StDev =
Mean
3,994
8,770
9,251
1,510
StDev
0,294
2,135
1,208
F
20,52
P
0,000
Individual 95% CIs For Mean
Based on Pooled StDev
----------+---------+---------+-----(-----*-----)
(----*----)
(----*----)
----------+---------+---------+-----5,0
7,5
10,0