MT 131 F˙INAL Ç ÖZÜMLER 1. (a) f(x) = tanx, b = , a = 0 olsun. f ′(x

MT 131 FİNAL ÇÖZÜMLER
1. (a) f (x) = tan x, b = 31 , a = 0 olsun. f ′ (x) = sec2 x,
f ′′ (x) = 2 sec2 x tan x, f ′′′ (x) = 2 sec4 x + 4 sec2 x tan2 x
f (0) = 0, f ′ (0) = 1, f ′′ (0) = 0, f ′′′ (0) = 2 olduğundan P3 (x) = x +
1
ve tan 31 ≈ P3 ( 13 ) = 13 + 81
= 28
81 bulunur.
x3
3
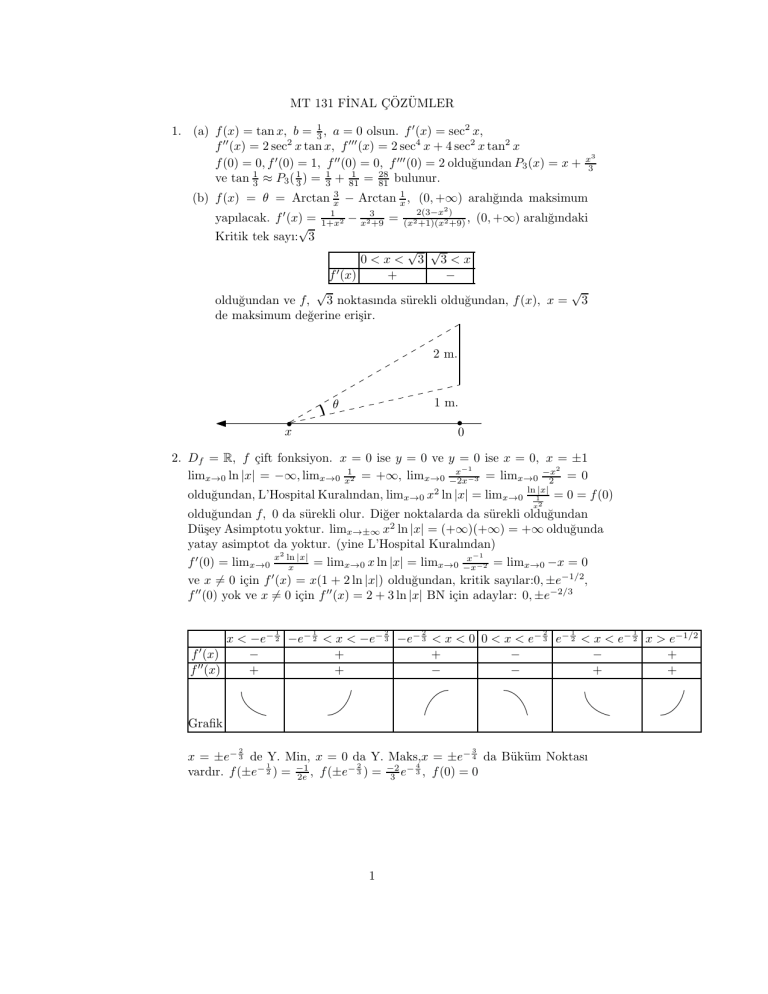
(b) f (x) = θ = Arctan x3 − Arctan x1 , (0, +∞) aralığında maksimum
yapılacak. f ′ (x) =
√
Kritik tek sayı: 3
1
1+x2
− x23+9 =
2(3−x2 )
(x2 +1)(x2 +9) ,
0<x<
f ′ (x)
+
(0, +∞) aralığındaki
√ √
3 3<x
−
√
√
olduğundan ve f, 3 noktasında sürekli olduğundan, f (x), x = 3
de maksimum değerine erişir.
2 m.
1 m.
θ
x
0
2. Df = R, f çift fonksiyon. x = 0 ise y = 0 ve y = 0 ise x = 0, x = ±1
x−1
−x2
limx→0 ln |x| = −∞, limx→0 x12 = +∞, limx→0 −2x
−3 = limx→0
2 = 0
olduğundan, L’Hospital Kuralından, limx→0 x2 ln |x| = limx→0
ln |x|
1
x2
= 0 = f (0)
olduğundan f, 0 da sürekli olur. Diğer noktalarda da sürekli olduğundan
Düşey Asimptotu yoktur. limx→±∞ x2 ln |x| = (+∞)(+∞) = +∞ olduğunda
yatay asimptot da yoktur. (yine L’Hospital Kuralından)
2
|x|
x−1
f ′ (0) = limx→0 x ln
= limx→0 x ln |x| = limx→0 −x
−2 = limx→0 −x = 0
x
′
ve x 6= 0 için f (x) = x(1 + 2 ln |x|) olduğundan, kritik sayılar:0, ±e−1/2,
f ′′ (0) yok ve x 6= 0 için f ′′ (x) = 2 + 3 ln |x| BN için adaylar: 0, ±e−2/3
1
1
2
2
2
1
1
x < −e− 2 −e− 2 < x < −e− 3 −e− 3 < x < 0 0 < x < e− 3 e− 2 < x < e− 2 x > e−1/2
′
f (x)
−
+
+
−
−
+
f ′′ (x)
+
+
−
−
+
+
Grafik
2
3
x = ±e− 3 de Y. Min, x = 0 da Y. Maks,x = ±e− 4 da Büküm Noktası
1
− 23
− 43
vardır. f (±e− 2 ) = −1
) = −2
, f (0) = 0
2e , f (±e
3 e
1
2
y=x ln |x |
-1/2
-e
-1
-2/3
-e
-2/3
e
e
-1/2
1
ln(1 − cos 2x) ∞
∞ belirsizliği var.
ln x
2 sin 2x
2x sin 2x
2x sin 2x(1 + cos 2x)
2x(1 + cos 2x)
1−cos 2x
=
=
=
=
1
2
1
−
cos
2x
sin 2x
sin 2x
x
x(1 + cos 2x)
x
(1 + cos 2x)
, lim
= 2, L’Hospital Kuralından,
sin x cos x x→0 sin x
cos x
ln(1−cos 2x)
ln(1 − cos 2x)
1
= 2 olur. (1 − cos 2x) ln x = e ln x
lim
ve ex , 2 de
x→0
ln x
1
sürekli olduğundan bileşkenin limiti teoreminden lim (1 − cos 2x) ln x = e2
1
3. (a) y = (1 − cos 2x) ln x olsun ln y =
x→0
(b) ex in (x → +∞ iken) düşey olmayan bir asimptotu ise lim (ex − P (x)) = 0
x→+∞
x
e − P (x)
0
olur, Dolayısıyla lim
=
= 0 olur. Buradan da
x→+∞
ex
+∞
P (x)
P (x)
lim
1− x
= 0 bunun sonucu olarak lim
= 1 elde
x→+∞
x→+∞ ex
e
edilir.
ey + e−y
4. (a) y = coth−1 x olsun. coth y = x, x = y
,
e − e−y
(ey − e−y )x = ey + e−y
ey (x − 1) = e−y (x + 1)
x+1
(x − 1)e2y = x + 1
e2y =
x −1
x+1
x+1
1
2y = ln
y = 2 ln
x−1
x−1
(b) |x| ≥ 1 için y = Arcsec x olsun. x = sec y ve 0 ≤ y ≤ π, (y 6= π2 )
olur. cos y = x1 ve 0 ≤ y ≤ π olduğundan y = Arccos x1 olur.
1
, (b = f (a))
f ′ (a)
5
olur. x + 2x = 3 denkleminin tek çözümü x = 1 olduğundan
g ′ (3) = f ′1(1) = 17 olur.
1
(b) Ters FonksiyonunTürevlenebilmesi Teoreminden g ′ (x) = ′
f (g(x))
olur. Her iki tarafın türevi alınırsa
−f ′′ (g(x))g ′ (x)
−f ′′ (g(x))
g ′′ (x) =
=
(f ′ (g(x)))2
(f ′ (g(x)))3
5. (a) Ters FonksiyonunTürevlenebilmesi Teoreminden g ′ (b) =
olur. f ′′ (g(x)) > 0 ve f ′ (g(x)) > 0 olduğundan g ′′ (x) < 0 olur.
2