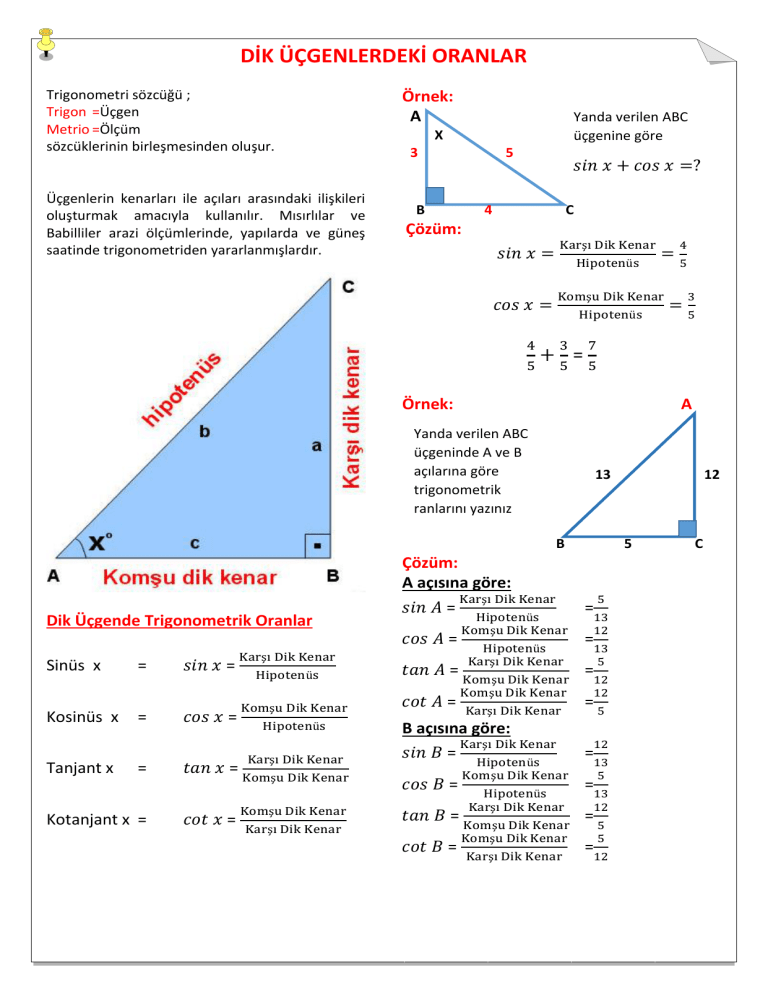
DİK ÜÇGENLERDEKİ ORANLAR
Trigonometri sözcüğü ;
Trigon =Üçgen
Metrio =Ölçüm
sözcüklerinin birleşmesinden oluşur.
Üçgenlerin kenarları ile açıları arasındaki ilişkileri
oluşturmak amacıyla kullanılır. Mısırlılar ve
Babilliler arazi ölçümlerinde, yapılarda ve güneş
saatinde trigonometriden yararlanmışlardır.
Örnek:
A
Yanda verilen ABC
üçgenine göre
X
3
B
5
.
𝑠𝑖𝑛 𝑥 + 𝑐𝑜𝑠 𝑥 =?
4
C
Çözüm:
𝑠𝑖𝑛 𝑥 =
Karşı Dik Kenar
𝑐𝑜𝑠 𝑥 =
Komşu Dik Kenar
4
5
Hipotenüs
Hipotenüs
3
7
5
5
+ =
Örnek:
Sinüs x
=
𝑠𝑖𝑛 𝑥 =
Kosinüs x
=
𝑐𝑜𝑠 𝑥 =
Komşu Dik Kenar
𝑡𝑎𝑛 𝑥 =
Karşı Dik Kenar
Tanjant x
=
Kotanjant x =
𝑐𝑜𝑡 𝑥 =
Hipotenüs
Hipotenüs
Komşu Dik Kenar
Komşu Dik Kenar
Karşı Dik Kenar
=
𝑐𝑜𝑠 𝐴 =
=
𝑐𝑜𝑡 𝐴 =
Hipotenüs
Komşu Dik Kenar
Hipotenüs
Karşı Dik Kenar
Komşu Dik Kenar
Komşu Dik Kenar
Karşı Dik Kenar
13
5
=
12
12
=
=
𝑐𝑜𝑠 𝐵 =
=
𝑐𝑜𝑡 𝐵 =
Hipotenüs
Komşu Dik Kenar
Hipotenüs
Karşı Dik Kenar
Komşu Dik Kenar
Komşu Dik Kenar
Karşı Dik Kenar
5
13
12
B açısına göre:
Karşı Dik Kenar
𝑠𝑖𝑛 𝐵 =
𝑡𝑎𝑛 𝐵 =
=
3
5
12
5
Çözüm:
A açısına göre:
Karşı Dik Kenar
𝑠𝑖𝑛 𝐴 =
𝑡𝑎𝑛 𝐴 =
5
13
B
Karşı Dik Kenar
4
A
Yanda verilen ABC
üçgeninde A ve B
açılarına göre
trigonometrik
ranlarını yazınız
Dik Üçgende Trigonometrik Oranlar
=
5
12
13
5
13
12
=
=
5
5
12
.C
KURAL
Birbirilerini 900 ye tamamlayan açıların ;
Sinüsleri ile kosinüsleri
Tanjantları ile kotanjantları eşittir.
𝟑𝟎𝟎 − 𝟒𝟓𝟎 − 𝟔𝟎𝟎
𝐓𝐫𝐢𝐠𝐨𝐧𝐨𝐦𝐞𝐭𝐫𝐢𝐤 𝐎𝐫𝐚𝐧𝐥𝐚𝐫ı
Örnek:
sin30° = cos60°
cos30° = sin60°
tan30° = cot60°
cot30° = tan60°
Tümler iki açıdan birinin sinüsü
diğerinin kosinüsüne, birinin tanjantı
diğerinin kotanjantına eşittir.
KURAL
0 < X < 900 iken x artttıkça
Sin x ve tan x; x artarken artar, x
azalırken azalır.
Cos x ve cot x; x artarken azalır, x
azalırken artar.
𝑠𝑖𝑛 00 < 𝑠𝑖𝑛 10 < 𝑠𝑖𝑛 20
𝑐𝑜𝑠 00 > 𝑐𝑜𝑠 10 > 𝑐𝑜𝑠 20
𝑡𝑎𝑛 00 < 𝑡𝑎𝑛 10 < 𝑡𝑎𝑛 20
𝑐𝑜𝑡 00 > 𝑐𝑜𝑡 10 > 𝑐𝑜𝑡 20
Örnek:
a = cos15°
b = sin71°
c = sin56°
d = cos87°
Çözüm:
Olduğuna göre
a,b,c,d yi
sıralayınız
Sıralama yapmak için verilen açıların
trigonometrik oranları aynı türden olmalıdır.
Buna göre;
a = cos15° = sin75°
b = sin71°
c = sin56°
d = cos87° = sin3°
dir. O halde;
a > b > c > d olur.
Örnek: 𝑠𝑖𝑛 300 . tan 450 + cos 600 =?
Çözüm:
𝑠𝑖𝑛 300 . tan 450 + cos 600 =?
1
1 2
.1 + = = 1
2
2 2
Örnek:
𝑐𝑜𝑠 300 . 𝑐𝑜𝑠 450
𝑐𝑜𝑠 600 . 𝑠𝑖𝑛 600
√3 √2
.
2 2 =
1 √3
2. 2
KURAL
=?
√6
4 = √6 . 4 = √6 = √2
4 √3 √3
√3
4
sin 𝑥
𝑡𝑎𝑛 𝑥 = cos 𝑥
cos 𝑥
𝑡𝑎𝑛 𝑥. cot 𝑥 = 1
𝑐𝑜𝑡 𝑥 = sin 𝑥
𝑠𝑖𝑛2 𝑥 + 𝑐𝑜𝑠 2 𝑥 = 1
Örnek:(𝑡𝑎𝑛 𝑥
sin 𝑥
𝑡𝑎𝑛 𝑥 = cos 𝑥
𝑡𝑎𝑛 𝑥 𝑦𝑒𝑟𝑖𝑛𝑒
1
+ cos 𝑥 ) ÷
sin 𝑥
olduğunu biliyoruz.
sin 𝑥
cos 𝑥
𝑘𝑜𝑦𝑢𝑦𝑜𝑟𝑢𝑧.
1
sin 𝑥
sin 𝑥+1
(cos 𝑥 + cos 𝑥 ) ÷
sin 𝑥+1
sin 𝑥
=?
=?
Bir Trigonometrik Oranı Verilen Açının Diğer
Trigonometrik Oranını Bulma
Dik üçgen çizerek diğer trigonometrik oranlarını
bulabiliriz.
Örnek: sin 𝑥 =
Çözüm:
A
6
sin 𝑥+1
cos 𝑥
sin 𝑥+1
cos 𝑥
÷
sin 𝑥+1
sin 𝑥
B
. sin 𝑥+1 =?
cos 𝑥
olur.
3
Örnek: sin 𝑥 + cos 𝑥 = 𝑖𝑠𝑒
2
sin 𝑥 . cos 𝑥 =?
Çözüm:
3
sin 𝑥 + cos 𝑥 =
2
Her iki tarafın karesini alırsak;
3
𝑠𝑖𝑛2 𝑥 + 2 sin 𝑥 cos 𝑥 + 𝑐𝑜𝑠 2 𝑥 = ( )2
2
𝑠𝑖𝑛2 𝑥 + 𝑐𝑜𝑠 2 𝑥 = 1
2 sin 𝑥 . cos 𝑥 =
2 sin 𝑥 . cos 𝑥 =
sin 𝑥 . cos 𝑥 =
sin 𝑥 . cos 𝑥 =
sin 𝑥 . cos 𝑥 =
5
4
5
4
5
8
9
4
5
x
.
8
8
-1
4
÷2
÷2
C
cos 𝑥 =
6
6
10
𝟑𝟎𝟎 − 𝟒𝟓𝟎 − 𝟔𝟎𝟎
𝑫𝚤ş𝚤𝒏𝒅𝒂 𝑩𝒊𝒓 𝑨ç𝚤 𝑽𝒆𝒓𝒊𝒍𝒊𝒓𝒔𝒆….
Örnek:
A
Yanda verilen ABC
üçgeninde verilenlere
göre lACl nedir?
12
X
sin 𝟐𝟒𝟎 = 0,4
𝟐𝟒𝟎
B
Çözüm:
4
0,4 =
10
sin 𝟐𝟒𝟎 =
4
9
10
tan 𝑥 =
= tan 𝑥
1+2 sin 𝑥 . cos 𝑥 =
𝑖𝑠𝑒 𝑡𝑎𝑛𝑥 𝑣𝑒 cos 𝑥 𝑛𝑒𝑑𝑖𝑟
5
=?
sin 𝑥
sin 𝑥
8
lACl 4
=
içler dışlar çarpımı yaparsak
12 10
lACl. 10 = 12.4
lACl. 10 = 48
lACl =
48
10
.C
=4,8 olur
