MAT 1009 Matematik I 0/ 1

Fonksiyonun Limiti
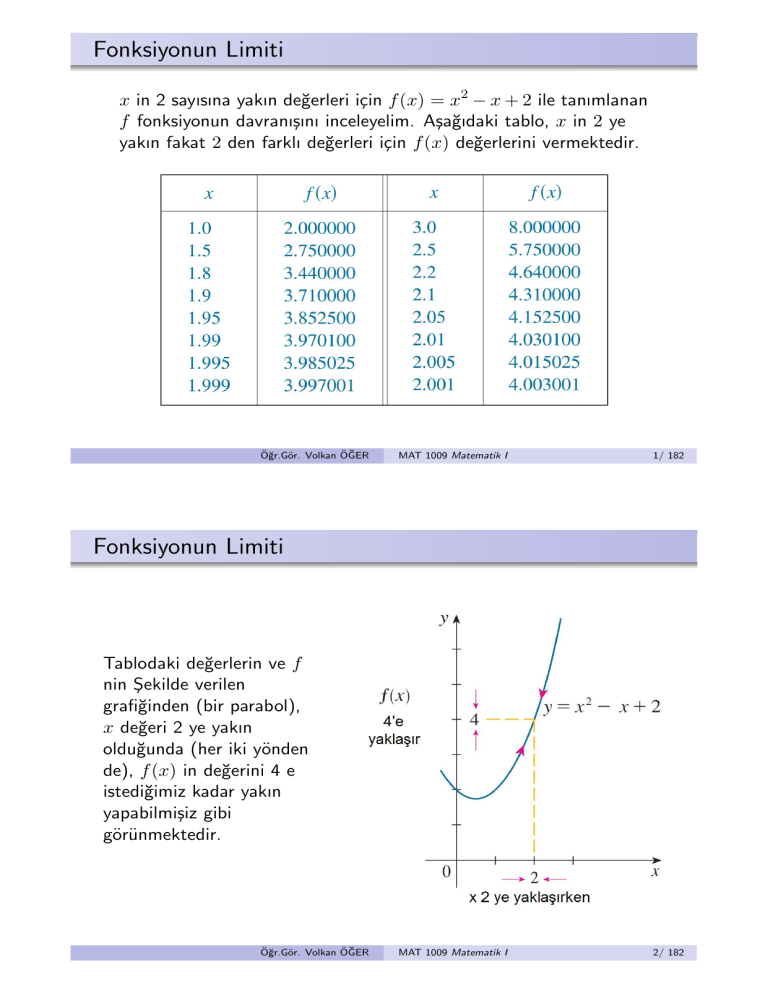
x in 2 sayısına yakın değerleri için f (x) = x2 − x + 2 ile tanımlanan
f fonksiyonun davranışını inceleyelim. Aşağıdaki tablo, x in 2 ye
yakın fakat 2 den farklı değerleri için f (x) değerlerini vermektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
1/ 182
MAT 1009 Matematik I
2/ 182
Fonksiyonun Limiti
Tablodaki değerlerin ve f
nin Şekilde verilen
grafiğinden (bir parabol),
x değeri 2 ye yakın
olduğunda (her iki yönden
de), f (x) in değerini 4 e
istediğimiz kadar yakın
yapabilmişiz gibi
görünmektedir.
Öğr.Gör. Volkan ÖĞER
Fonksiyonun Limiti
Bunu ”x, 2 ye yaklaşırken, f (x) = x2 − x + 2 fonksiyonunun limiti
4 e eşittir” diyerek ifade ederiz. Bu ifadenin gösterimi
lim (x2 − x + 2) = 4
x→2
şeklindedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
3/ 182
Fonksiyonun Limiti
Genelde aşağıdaki gösterimi kullanırız.
Tanım 1: x değerlerini a sayısına yeteri kadar yakın (her iki
yönden de) ancak a dan farklı alarak, f (x) değerini L sayısına
istediğimiz kadar yaklaştırabiliyorsak, “x değişkeni a sayısına
yaklaşırken, f (x) in limiti L dir” der ve
lim f (x) = L
x→a
yazarız.
Kabaca bu, x değişkeni, a sayısına x 6= a olacak şekilde (her iki
yönden) yaklaşırken, f (x) değerinin giderek L sayısına daha yakın
değerler alması anlamına gelir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
4/ 182
Fonksiyonun Limiti
lim f (x) = L
x→a
limiti için diğer bir gösterim şekli
x → a iken f (x) → L
dir ve “x değişkeni a sayısına yaklaşırken, f (x) değerleri L ye
yaklaşır” şeklinde okunur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
5/ 182
Fonksiyonun Limiti
Limit tanımındaki “x 6= a” ifadesine dikkat ediniz.
Bu, x değişkeni a sayısına yaklaşırken f (x) in limitini bulmak için,
x = a değerini hiç düşünmediğimiz anlamına gelir.
Aslında f (x) fonksiyonu, x = a noktasında tanımlı bile olmayabilir.
Önemli olan, yalnızca f (x) fonksiyonunun a nın yakınında nasıl
tanımlandığıdır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
6/ 182
Fonksiyonun Limiti
Şekil 1:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
7/ 182
Fonksiyonun Limiti
Şekil 2:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
8/ 182
Fonksiyonun Limiti
Şekil 3:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
9/ 182
Fonksiyonun Limiti
Şekillerde üç fonksiyonun grafiği verilmiştir. (3) de f (a) tanımlı
değildir ve (2) de f (a) 6= L dir. Ancak tüm durumlarda, a da ne
olduğundan bağımsız olarak lim f (x) = L dir.
x→a
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
10/ 182
Örnek
sin x
limitini bulunuz.
x→0 x
Örnek: lim
Çözüm: Yine f (x) = sin x/x fonksiyonu x = 0 noktasında tanımlı
değildir.
Bir hesap makinesi
kullanarak (ve x ∈ R için
sin x in radyan ölçümü x
olan açının sinüsü
olduğunu anımsayarak),
virgülden sonra sekizinci
basamağa kadar doğru
olan değerlerle yandaki
tabloyu oluştururuz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
11/ 182
Örnek...
Şekil 4:
Tablodan ve Şekil 4 daki grafikten
sin x
=1
x→0 x
lim
olduğunu tahmin ederiz. Bu tahmin gerçekten de doğrudur ve
bunu ileride geometrik bir akıl yürütmeyle kanıtlayacağız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
12/ 182
Örnek
Örnek: lim sin
x→0
π
limitini bulunuz.
x
Çözüm: Burada da f (x) = sin( πx ) fonksiyonu sıfır noktasında
tanımlı değildir.Bazı küçük x değerleri için fonksiyonun değerlerini
hesaplarsak
f (1) = sin π = 0
f ( 12 ) = sin 2π = 0
f ( 13 ) = sin 3π = 0
f ( 14 ) = sin 4π = 0
(1)
f (0.1) = sin 10π = 0 f (0.01) = sin 100π = 0
elde ederiz. Benzer biçimde f (0.001) = f (0.0001) = 0 olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
13/ 182
Örnek...
Bu bilgiler ışığında
π
=0
x→0
x
tahminini yapmak çekici gelsede, bu kez tahmin doğru değildir.
lim sin
Her n tamsayısı için f (1/n) = sin nπ = 0 olmasına rağmen, x in
sıfıra yaklaşan sonsuz tane değeri için f (x) = 1 olduğu da
doğrudur.
[Aslında,
π
π
= + 2nπ
x
2
olduğu zaman, sin(π/x) = 1 dir ve buradan x i çözerek
x = 2/(4n + 1) buluruz.]
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
14/ 182
Örnek...
f nin grafiği şekil 5 de verilmiştir.
Şekil 5:
Grafikteki kesik çizgiler, x sıfıra yaklaşırken sin(π/x) değerlerinin
−1 ile 1 arasında sonsuz kez gidip geldiğine işaret etmektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
15/ 182
Örnek...
x sıfıra yaklaşırken f (x) değerleri belli bir sayıya yaklaşmadığından
lim sin
x→0
π
x
limiti yoktur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
16/ 182
Örnek
1
limitini (varsa) bulunuz.
x→0 x2
Örnek: lim
Çözüm: x değişkeni 0 a yakın olduğunda, x2 de 0 a yakın olur, ve
1/x2 çok büyük olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
17/ 182
Örnek...
Şekil 6:
Aslında, Şekil 6 de gösterilen f (x) = 1/x2 fonksiyonunun
grafiğinden, x değerleri 0 a yeteri kadar yakın alınarak, f (x) in
değerlerinin istenildiği kadar büyük yapılabileceği görülmektedir.
Bu nedenle f (x) in değerleri herhangi bir sayıya yaklaşmaz ve
1
dolayısıyla lim 2 limiti yoktur.
x→0 x
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
18/ 182
Örnek
Örnek: Heaviside fonksiyonu H,
0, t < 0
H(t) =
1, t ≥ 0
olarak tanımlanır. [Bu fonksiyon adını elektrik mühendisi Oliver
Heaviside(1850-1925) den almıştır ve t = 0 anında şalteri indirilen
devredeki elektrik akımını ifade etmek için kullanılabilir.] Grafiği
Şekil 7 de verilmiştir.
Şekil 7:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
19/ 182
Örnek...
t değişkeni 0 a soldan sağdan yaklaştığında H(t), 0 a yaklaşır.
t, 0’a sağdan yaklaştığında, H(t) bu kez 1 e yaklaşır. Bu nedenle t
sıfıra yaklaşırken, H(t) nin yaklaştığı tek bir değer olmadığından
lim H(t) yoktur.
x→0
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
20/ 182
Tek Yönlü Limitler
Bir önceki örnekte H(t) değerinin, t, 0 a sağdan yaklaşırken 0 a, t
nin 0 a soldan yaklaşması durumunda 1 e yaklaştığını gözledik.
Bunu simgesel olarak
lim H(t) = 0
t→0−
ve
lim H(t) = 1
t→0+
ile gösteririz. t → 0− sembolü t nin yalnızca 0 dan küçük
değerlerini düşündüğümüzü gösterir. Aynı şekilde t → 0+ , t nin
yalnızca 0 dan büyük değerlerini düşündüğümüzü gösterir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
21/ 182
Tek Yönlü Limitler
Tanım 2: x değişkeni a dan küçük olacak şekilde a ya yeterince
yakın yakın alınarak, f (x) değerleri L sayısına istenildiği kadar
yakın yapılabiliyorsa, x değişkeni a ya yaklaşırken f (x) in soldan
limiti [veya x değişkeni a ya soldan yaklaşırken f (x) in limiti] L
dir deriz ve
lim f (x) = L
x→a−
yazarız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
22/ 182
Tek Yönlü Limitler
Tanım 2 nin Tanım 1 den tek farkının, x değişkeninin a dan küçük
olması koşulu olduğuna dikkat ediniz.
Benzer biçimde, x değişkeninin a dan büyük olması koşulunu
getirirsek, x değişkeni a ya yaklaşırken f (x) in sağdan limiti L
dir denir ve
lim f (x) = L
x→a+
yazarız. Dolayısıyla, x → a+ sembolü, yalnızca x > a değerlerini
düşündüğümüz anlamına gelir. Bu tanımlar Şekil 8 da
örneklenmiştir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
23/ 182
Tek Yönlü Limitler
Şekil 8:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
24/ 182
Tek Yönlü Limitler
Tanım 1 ile tek yönlü limitlerin tanımlarını karşılaştırırsak,
aşağıdakinin doğru olduğunu görürüz.
lim f (x) = L
x→a
olması için yeterli ve gerekli koşul
lim f (x) = L ve
x→a+
Öğr.Gör. Volkan ÖĞER
lim f (x) = L dir.
x→a−
MAT 1009 Matematik I
25/ 182
Örnek
Örnek: Bir g fonksiyonunun grafiği Şekil 9 da verilmiştir. Bunu
kullanarak (eğer varsa) aşağıdaki limitlerin değerini bulunuz.
a) lim g(x)
x→2−
b) lim g(x)
x→2+
c) lim g(x)
x→2
d) lim g(x)
x→5−
e) lim g(x)
x→5+
Şekil 9:
f ) lim g(x)
x→5
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
26/ 182
Örnek...
Çözüm:
Grafikten x değişkeni 2 ye soldan yaklaşırken, g(x) in 3 e
yaklaştığını, buna karşılık x değişkeni 2 ye sağdan yaklaşırken g(x)
in 1 e yaklaştığını görürüz. Dolayısıyla
a) lim g(x) = 3 ve b) lim g(x) = 1 olur.
x→2−
Öğr.Gör. Volkan ÖĞER
x→2+
MAT 1009 Matematik I
27/ 182
Örnek...
c) Sağ ve sol limitler farklı olduğu için, lim g(x) olmadığı sonucuna
x→2
varırız.
Grafikten ayrıca
d) lim g(x) = 2 ve e) lim g(x) = 2
x→5−
x→5+
olduğu görülmektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
28/ 182
Örnek...
f) Bu kez sağ ve sol limitler aynıdır ve dolayısıyla,
lim g(x) = 2
x→2
elde ederiz. Buna rağmen g(5) 6= 2 dir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
29/ 182
Limit Kurallarını Kullanarak Limit Almak
Limit Kuralları: c sabit bir sayı ve
lim f (x) ve lim g(x)
x→a
x→a
limitleri varsa,
1.
2.
3.
4.
lim [f (x) + g(x)] = lim f (x) + lim g(x)
x→a
x→a
x→a
lim [f (x) − g(x)] = lim f (x) − lim g(x)
x→a
x→a
x→a
lim [c.f (x)] = c. lim f (x)
x→a
x→a
lim [f (x).g(x)] = lim f (x). lim g(x)
x→a
x→a
x→a
lim f (x)
f (x)
x→a
5. Eğer; lim g(x) 6= 0 ise lim
=
dir.
x→a
x→a g(x)
lim g(x)
x→a
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
30/ 182
Örnek
Örnek: Limit kurallarını ve f ile g nin Şekil 10 de verilen
grafiklerini kullanarak (varsa) aşağıdaki limitleri bulunuz.
a) lim [f (x) + 5g(x)]
x→−2
b) lim [f (x)g(x)]
x→1
f (x)
x→2 g(x)
c) lim
Şekil 10:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
31/ 182
Örnek...
Çözüm:
a) f ve g nin grafiklerinden
lim f (x) = 1 ve
x→−2
lim g(x) = −1
x→−2
olduğunu görüyoruz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
32/ 182
Örnek...
Dolayısıyla
lim [f (x) + 5g(x)] = lim f (x) + lim [5g(x)] Kural 1 ile
x→−2
x→−2
x→−2
= lim f (x) + 5 lim g(x)
Kural 3 ile
= 1 + 5(−1) = −4
dür.
x→−2
Öğr.Gör. Volkan ÖĞER
x→−2
MAT 1009 Matematik I
33/ 182
Örnek...
b) lim f (x) = 2 olduğunu görüyoruz. Ancak lim g(x) limiti yoktur
x→1
x→1
çünkü sağ ve sol limitler farklıdır:
lim g(x) = −2
x→1−
lim g(x) = −1
x→1+
Dolayısıyla Kural 4 ü kullanamayız. Sol limit sağ limite eşit
olmadığı için, verilen limit yoktur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
34/ 182
Örnek...
c) Grafik yardımı ile
lim f (x) ≈ 1.4 ve
x→2
lim g(x) = 0
x→2
buluruz. Ancak bölenin limiti 0 olduğundan, Kural 5 i
kullanamayız. Pay sıfırdan farklı bir sayıya yaklaşırken, payda 0 a
yaklaştığından limiti yoktur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
35/ 182
Limit Kurallarını Kullanarak Limit Almak
6.
7.
8.
n pozitif tamsayı olduğunda lim [f (x)]n = [ lim f (x)]n dir.
x→a
x→a
lim c = c
x→a
lim x = a
x→a
9. n pozitif tamsayı olmak üzere lim xn = an dir.
x→a
10.
n pozitif tamsayı olmak üzere lim
x→a
√
n
x=
√
n
a dır.
(n çift ise, a > 0 varsayarız.)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
36/ 182
Örnek
Örnek: Her adımı açıklayarak, aşağıdaki limiti bulunuz.
lim (2x2 − 3x + 4)
x→5
Çözüm:
lim (2x2 − 3x + 4) = lim (2x2 ) − lim (3x) + lim 4 (kural 1 ve 2)
x→5
x→5
x→5
x→5
= 2 lim x2 − 3 lim x + lim 4
(kural 3)
= 2(52 ) − 3(5) + 4
(kural 7, 8 ve 9)
x→5
x→5
x→5
= 39
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
37/ 182
Örnek
Ancak aşağıdaki örneklerin sergilediği gibi, doğrudan yerine koyma
yöntemi ile tüm limit değerleri bulunamaz.
x2 − 1
Örnek: lim
limitini bulunuz.
x→1 x − 1
Çözüm: f (x) = (x2 − 1)/(x − 1) olsun. f (1) değeri tanımlı
olmadığı için limiti x = 1 koyarak bulamayız. Paydanın limiti 0
olduğu için Bölüm kuralını da kullanamayız. Bunun yerine cebir
bilgimizi kullanmalıyız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
38/ 182
Örnek...
x2 − 1
(x − 1)(x + 1)
=
x−1
x−1
olarak çarpanlara ayıralım. Buradan x − 1 in pay ve paydanın ortak
çarpanı olduğunu görürüz. x değişkeni 1 e giderken limit
alındığında x 6= 1 olduğundan x − 1 6= 0 dır. Dolayısı ile
sadeleştirme yapabiliriz. Böylece limiti
x2 − 1
lim
x→1 x − 1
(x − 1)(x + 1)
x→1
x−1
= lim
= lim (x + 1)
x→1
=1+1=2
olarak buluruz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
39/ 182
Örnek
(3 + h)2 − 9
Örnek: lim
limitini bulunuz.
h→0
h
(3 + h)2 − 9
Çözüm: F (h) =
olarak tanımlayalım. F (0) tanımlı
h
olmadığından, lim F (h) limitini h = 0 değerini yerine koyarak
h→0
hesaplayamayız. Fakat F (h) yi cebirsel olarak sadeleştirirsek,
(h2 + 6h + 9) − 9
h2 + 6h
F (h) =
=
=6+h
h
h
buluruz. (h değişkeni 0 a yaklaşırken, yalnızca h 6= 0 değerlerini
düşündüğümüzü hatırlayınız.) Dolayısıyla
(3 + h)2 − 9
lim
= lim (6 + h) = 6
h→0
h→0
h
olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
40/ 182
Örnek
√
Örnek: lim
t→0
t2 + 9 − 3
limitini bulunuz.
t2
Çözüm: Paydanın limiti 0 olduğundan Bölüm kuralını doğrudan
kullanamayız. Buradaki cebirsel işlem, paydadaki kare kökten
kurtulmaktır:
√
lim
t→0
t2 + 9 − 3
t2
√
= lim
t→0
√
t2 + 9 − 3 t2 + 9 + 3
.√
t2
t2 + 9 + 3
(t2 + 9) − 9
t2
= lim √
= lim √
t→0 t2 ( t2 + 9 + 3)
t→0 t2 ( t2 + 9 + 3)
1
1
=q
t→0
t2 + 9 + 3
lim(t2 + 9) + 3
t→0
1
1
=
=
3+3
6
= lim √
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
41/ 182
Limit Kurallarını Kullanarak Limit Almak
Bazı limitleri almak için en iyi yöntem önce sağ ve sol limitleri
almaktır. Aşağıdaki teorem limitin varlığı için yeterli ve gerek
koşulun sağ ve sol limitlerin varlığı ve eşitliği olduğunu ifade
etmektedir.
Teorem: lim f (x) = L için gerekli ve yeterli koşul
x→a
lim f (x) = L = lim f (x) dir.
x→a+
x→a−
Tek yönlü (sağ ve sol) limitleri alırken Limit Kurallarının bu tür
limitler için de geçerli olduğu gerçeğini kullanırız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
42/ 182
Örnek
Örnek: lim |x| = 0 olduğunu gösteriniz.
x→0
Çözüm: Mutlak değer fonksiyonunun
x,
x≥0
|x| =
−x, x < 0
olarak tanımlandığını hatırlayınız. 0 < x için |x| = x olduğundan,
lim |x| = lim x = 0
x→0+
x→0+
elde ederiz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
43/ 182
Örnek
x < 0 için |x| = −x dir ve dolayısıyla
lim |x| = lim (−x) = 0
x→0−
x→0−
dir. Teorem gereğince
lim |x| = 0
x→0
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
44/ 182
Örnek
|x|
limitinin olmadığını kanıtlayınız.
x→0 x
Örnek: lim
Çözüm:
lim
x→0+
lim
x→0−
|x|
x
= lim
= lim 1 = 1
x
x→0+ x
x→0+
|x|
−x
= lim
= lim (−1) = −1
x
x→0− x
x→0−
Sağ ve sol limitler farklı olduklarından, Teorem gereğince aranılan
limit yoktur. f (x) = |x|/x fonksiyonunun grafiği Şekil 4 de
verilmiştir ve yanıtımızı desteklemektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
45/ 182
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
46/ 182
Örnek...
Limit Kurallarını Kullanarak Limit Almak
Teorem : x in a ya yakın (x = a dışında) değerleri için
f (x) ≤ g(x) ise
ve x değişkeni, a ya yaklaşırken f (x) ve g(x) in limitleri varsa
lim f (x) ≤ lim g(x)
x→a
x→a
olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
47/ 182
Limit Kurallarını Kullanarak Limit Almak
Sıkıştırma Teoremi : x in a ya yakın (x = a dışında) değerleri için
f (x) ≤ g(x) ≤ h(x)
ve
lim f (x) = lim h(x) = L
x→a
x→a
lim g(x) = L
x→a
Öğr.Gör. Volkan ÖĞER
ise
dir.
MAT 1009 Matematik I
48/ 182
Sıkıştırma Teoremi
Kimi zaman Sandviç Teoremi olarak da anılan Sıkıştırma
Teoreminin anlamı Şekil 11 da açıklanmıştır.
Şekil 11:
Bu teorem, g(x) fonksiyonu a yakınında f (x) ve h(x) arasında
sıkışmışsa, ve a sayısında f ve h fonksiyonlarının limitleri var ve L
ye eşitse, zorunlu olarak g fonksiyonunun da a daki limitinin L
olduğunu söyler.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
49/ 182
Örnek
Örnek : lim x2 sin
x→0
1
=?
x
Çözüm : Önce, lim sin
x→0
1
limiti olmadığından,
x
lim x2 sin
x→0
1
1
= lim x2 · lim sin
x→0
x x→0
x
eşitliğini kullanamayacağımıza dikkat edin.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
50/ 182
Örnek...
Bununla birlikte,
1
≤1
x
olduğundan, Şekil 12 de gösterildiği gibi
1
−x2 ≤ x2 sin ≤ x2
x
elde ederiz.
−1 ≤ sin
Şekil 12:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
51/ 182
Örnek...
lim x2 = 0 ve lim (−x2 ) = 0 olduğunu biliyoruz.
x→0
x→0
Sıkıştırma teoreminde
f (x) = −x2 ,
g(x) = x2 sin
alarak
lim x2 sin
x→0
1
x
ve
h(x) = x2
1
=0
x
buluruz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
52/ 182
Süreklilik
Bazı örneklerde x değişkeni a ya yaklaşırken f fonksiyonunun
limitinin fonksiyonun a noktasındaki değeri olarak
hesaplanabildiğini fark etmiştik.
Bu özelliğe sahip fonksiyonlara a noktasında süreklidir denir.
Sürekliliğin matematiksel tanımının, bu kelimenin günlük anlamına
oldukça yakın olduğunu ileride göreceğiz. (Sürekli bir olay,
kesintiye ve ani değişikliğe uğramadan devam eder.)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
53/ 182
Süreklilik
Tanım:
f fonksiyonun a sayısındaki sürekliğiği
lim f (x) = f (a)
x→a
eşitliğini sağlamasıdır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
54/ 182
Süreklilik
a noktasında sürekli olmayan bir f fonksiyonuna a noktasında
süreksizdir denir.
Tanıma göre, açıkça belirtilmemiş olsa da, bir fonksiyonun a
noktasındaki sürekliliği üç koşulun sağlanmasını gerektirmektedir:
1.
2.
3.
f (a) tanımlıdır (a sayısı f nin tanım kümesindedir).
lim f (x) limiti vardır.
x→a
lim f (x) = f (a) dır.
x→a
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
55/ 182
Süreklilik
Tanım, f nin a noktasına yaklaşırken, f (x) in f (a) değerine
yaklaşması olarak ifade eder.
Dolayısıyla sürekli fonksiyonların, değişken x deki küçük bir
değişikliğin, f (x) de de küçük bir değişikliği gerekli kılma özelliği
vardır.
Aslında x deki değişikliği yeterince küçük tutarak, f (x) deki
değişim istenildiği kadar küçük tutulabilir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
56/ 182
Süreklilik
Geometrik olarak, bir aralıktaki her noktada sürekli olan bir
fonksiyonu, grafiği kesintisiz bir fonksiyon olarak düşünebilirsiniz.
Bu, kalemle grafiği takip ettiğinizde, kalemi kaldırmadan grafiği
izleyebilmeniz demektir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
57/ 182
Örnek
Örnek : Grafiği Şekil ?? de verilen fonksiyonun sürekli olmadığı
noktaları bularak, nedenlerini açıklayınız.
Şekil 13:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
58/ 182
Örnek...
Çözüm : a = 1 noktasında fonksiyonun grafiğinde bir kesinti
olduğundan, fonksiyon bu noktada süreksiz görünmektedir. Bunu
matematiksel olarak, f (1) değeri tanımsız olduğundan fonksiyonun
1 noktasında süreksiz olduğu şeklinde açıklarız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
59/ 182
Örnek...
Grafik a = 3 noktasında da kesintiye uğramaktadır. Ancak,
buradaki süreksizliğin nedeni farklıdır. Burada f (3) tanımlıdır.
Ancak, sağ ve sol limitler farklı olduklarından lim f (x) limiti
x→3
yoktur ve bundan dolayı f , 3 noktasında sürekli değildir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
60/ 182
Örnek...
a = 5 noktası fonksiyon için nasıl bir noktadır? Bu noktada f (5)
tanımlıdır ve lim f (x) limiti vardır (sağ ve sol limitler eşittir).
x→5
Ancak
lim f (x) 6= f (5)
x→5
olduğundan, f fonksiyonu 5 noktasında sürekli değildir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
61/ 182
Örnek
Örnek : Aşağıdaki fonksiyonların sürekli olmadığı noktaları
bulunuz.
 1

 2 , x 6= 0
x2 − x − 2
x
(a) f (x) =
(b) f (x) =

x−2

1,
x=0
 2
x −x−2



, x 6= 2
x
−
2
(c) f (x) =
(d) f (x) = [|x|]



1,
x=2
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
62/ 182
Örnek...
Çözüm :
x2 − x − 2
(a) f (x) =
x−2
f (2) tanımlı olmadığından, f fonksiyonu 2 noktasında sürekli
değildir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
63/ 182
Örnek...
 1

 2 , x 6= 0
x
(b) f (x) =


1,
x=0
Burada f (0) = 1 tanımlıdır. Ancak
1
x→0 x2
lim f (x) = lim
x→0
limit yoktur. Bu nedenle, f fonksiyonu 0 noktasında sürekili
değildir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
64/ 182
Örnek...
 2
x −x−2



, x 6= 2
x
−
2
(c) f (x) =



1,
x=2
Bu örnekte f (2) = 1 tanımlıdır ve
x2 − x − 2
(x − 2)(x + 1)
lim f (x) = lim
= lim
= lim (x+1) = 3
x→2
x→2
x→2
x→2
x−2
x−2
vardır.
lim f (x) 6= f (2)
x→2
olduğundan, f fonksiyonu 2 noktasında sürekli değildir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
65/ 182
Örnek...
(d) Tam değer fonksiyonu f (x) = [|x|] tam sayılarda süreksizdir
çünkü n bir tam sayı ise, lim [|x|] limiti yoktur.
x→n
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
66/ 182
Örnek...
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
67/ 182
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
68/ 182
Örnek...
Süreksizlik Çeşitleri
Şekillerde, örnekte çalışılan fonksiyonların grafiklerini vermektedir.
Örneklerin tümünde grafik bir kalem ile izlenirse, var olan bir delik
veya kesinti veya atlama nedeniyle kalem kaldırılmadan grafiğin
çizilmesi olası değildir.
(a) ve (c) örneklerindeki süreksizliklere giderilebilir süreksizlikler
denir. Çünkü yalnız 2 noktasında f fonksiyonunu yeniden
tanımlayarak süreksizliği giderebiliriz. [g(x) = x + 1 fonksiyonu
süreklidir.]
(b) deki süreksizlik türüne sonsuz süreksizlik denir.
(d) deki süreksizlik türüne ise, fonksiyon bir değerden diğerine
sıçradığından, sıçrama tipi süreksizlik adı verilir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
69/ 182
Sağdan/Soldan Süreklilik
f fonksiyonunun a da sağdan sürekli olması
lim f (x) = f (a)
x→a+
eşitliğini sağlaması; a da soldan sürekli olması ise
lim f (x) = f (a)
x→a−
eşitliğini sağlaması olarak tanımlanır.
Bir aralığın tüm noktalarında sürekli olan fonksiyona o aralıkta
süreklidir denir. (Fonksiyon, aralığın uç noktalarının yalnızca bir
tarafında tanımlanmış ise bu noktalarda süreklilik, sağdan veya
soldan süreklilik anlamındadır.)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
70/ 182
Süreklilik
Teorem : c bir sabit, f ve g fonksiyonları a sayısında sürekli
fonksiyonlarsa, aşağıdaki fonksiyonlar da a noktasında süreklidir:
1.
f +g
2. f − g
4.
fg
5.
f
,
g
3. cf
g(a) 6= 0 ise
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
71/ 182
Süreklilik
Teorem :
(a) Her polinom gerçel sayıların tümünde, R = (−∞, ∞) da
süreklidir.
(b) Her rasyonel (kesirli) fonksiyon tanım kümesinde süreklidir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
72/ 182
Süreklilik
Bu teoremin bir uygulaması olarak, bir kürenin hacminin,
yarıçapına göre sürekli bir biçimde değiştiğini söyleyebiliriz. Bunun
nedeni V (r) = 43 πr3 ün yarıçap r nin bir polinomu olmasıdır.
Benzer biçimde, dik olarak 50 ft/sn hızla havaya fırlatılan bir topun
t saniye sonraki yüksekliğini veren h = 50t − 16t2 fonksiyonu da,
polinom olduğundan, süreklidir. Dolayısıyla topun yüksekliği
zamana göre sürekli bir biçimde değişir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
73/ 182
Örnek
x3 + 2x2 − 1
Örnek : lim
limitini bulunuz..
x→−2
5 − 3x
x3 + 2x2 − 1
fonksiyonu rasyonel bir
5 − 3x
fonksiyondur ve teorem gereğince, tanım kümesi olan
{x ∈ R|x 6= 53 } kümesinde süreklidir. Bu nedenle
Çözüm : f (x) =
x3 + 2x2 − 1
x→−2
5 − 3x
lim
= lim f (x) = f (−2)
x→−2
=
(−2)3 + 2(−2)2 − 1
1
=−
5 − 3(−2)
11
dir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
74/ 182
Süreklilik
f −1 fonksiyonunun grafiği f nin grafiğinin y = x doğrusuna göre
yansıması olduğundan, f sürekli bir fonksiyonsa, f −1 fonksiyonu da
süreklidir. (f fonksiyonunun grafiğinde kesinti yoksa, y = x
doğrusuna göre yansımasında da kesinti yoktur.)
Teorem : Aşağıdaki fonksiyonlar tanım kümelerinde sürekli
fonksiyonlardır:
Polinomlar
Trigonometrik fonksiyonlar
Üstel fonksiyonlar
Kök fonksiyonları
Öğr.Gör. Volkan ÖĞER
Rasyonel fonksiyonlar
Ters trigonometrik fonksiyonlar
Logaritmik fonksiyonlar
MAT 1009 Matematik I
75/ 182
Örnek
Örnek : lim
x→π
sin x
limitini bulunuz.
2 + cos x
Çözüm : y = sin x fonksiyonu, teoremden dolayı süreklidir.
Paydadaki y = 2 + cos x fonksiyonu, iki sürekli fonksiyonun
toplamı olduğundan, süreklidir. Bu fonksiyon hiç bir zaman 0
değildir çünkü her x için cos x ≥ −1 olduğundan, her yerde
2 + cos x > 0 dır. Böylece,
f (x) =
sin x
2 + cos x
fonksiyonu her yerde süreklidir. Dolayısıyla, sürekli fonksiyonun
tanımından,
lim
x→π
sin x
sin π
0
= lim f (x) = f (π) =
=
=0
2 + cos x x→π
2 + cos π
2−1
olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
76/ 182
Süreklilik
Teorem : f fonksiyonu b de sürekli ve lim g(x) = b ise,
x→a
lim f (g(x)) = f (b)
x→a
dir. Başka bir deyişle,
lim f (g(x)) = f lim g(x)
x→a
x→a
dir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
77/ 182
Örnek
Örnek : lim arcsin
x→1
√ 1− x
limitini bulunuz.
1−x
Çözüm : arcsin sürekli bir fonksiyon olduğundan, teoremi
uygulayabiliriz:
√ √ 1− x
1− x
lim arcsin
= arcsin lim
x→1 1 − x
x→1
1−x
√
1− x
√
√
= arcsin lim
x→1 (1 − x)(1 + x)
1
√
= arcsin lim
x→1 1 + x
= arcsin
Öğr.Gör. Volkan ÖĞER
1
π
=
2
6
MAT 1009 Matematik I
78/ 182
Süreklilik
Teorem : g fonksiyonu a da, f fonsiyonu da g(a) sürekli ise,
(f ◦ g)(x) = f (g(x)) olarak verilen f ◦ g bileşke fonksiyonu a
noktasında süreklidir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
79/ 182
Örnek
Örnek : Aşağıdaki fonksiyonların sürekli olduğu yerleri bulunuz:
(a) h(x) = sin(x2 )
(b) F (x) = ln(1 + cos x)
Çözüm : (a) g(x) = x2 ve f (x) = sin x olmak üzere
h(x) = f (g(x))
dir. Bir polinom olduğu için, g fonksiyonu R de süreklidir. f
fonksiyonu da her yerde süreklidir.
Böylece, teoremden, h = f ◦ g fonksiyonu R de süreklidir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
80/ 182
Örnek...
(b) Teoremden, f (x) = ln x ve (y = 1 ve y = cos x her yerde
sürekli olduklarından) g(x) = 1 + cos x süreklidir.
Dolayısıyla, teoremden, F (x) = f (g(x)) fonksiyonu tanımlı olduğu
her yerde süreklidir.
ln(1 + cos x) fonksiyonunun tanımlı olması için 1 + cos x > 0
olmalıdır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
81/ 182
Örnek...
Dolayısıyla, cos x = −1 olduğu zaman tanımlı değildir, ve bu
durum x = ±π, ±3π, . . . olduğunda gerçekleşir.
Böylece, F fonksiyonu π nin tek katlarında süreksizdir ve bu
değerlerin arasındaki aralıklarda süreklidir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
82/ 182
Süreklilik
Ara Değer Teoremi : f fonksiyonu kapalı [a, b] aralığında sürekli,
N sayısı f (a) ile f (b) arasında herhangi bir sayı olsun. (a, b)
aralığında, f (c) = N eşitliğini sağlayan bir c sayısı vardır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
83/ 182
Süreklilik
Şekil 14:
Ara değer teoremi, sürekli bir fonksiyonun f (a) ile f (b) arasındaki
her değeri aldığını söyler. Bu özellik, Şekil 14 de gösterilmiştir. N
değeri [(a) da olduğu gibi] bir kez veya [(b) de olduğu gibi] bir kaç
kez alınabilir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
84/ 182
Örnek
Ara değer teoreminin bir uygulaması, aşağıdaki örnekte olduğu
gibi, denklemlerin köklerinin yerlerinin belirlenmesidir.
Örnek : 4x3 − 6x2 + 3x − 2 = 0 denkleminin 1 ile 2 arasında bir
kökü olduğunu gösteriniz.
Çözüm : f (x) = 4x3 − 6x2 + 3x − 2 olsun. Verilen denklemin bir
çözümünü, diğer bir deyişle, 1 ile 2 arasında f (c) = 0 olacak
şekilde bir c sayısı arıyoruz. Dolayısıyla, teoremde a = 1, b = 2 ve
N = 0 alalım.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
85/ 182
Örnek...
f (1) = 4 − 6 + 3 − 2 = −1 < 0
ve
f (2) = 32 − 24 + 6 − 2 = 12 > 0
ve böylelikle f (1) < 0 < f (2) elde ederiz. Bu, N = 0 sayısının
f (1) ile f (2) arasında olduğunu verir. f fonksiyonu bir polinom
olduğundan her yerde süreklidir. Dolayısıyla, ara değer teoremi ile 1
ve 2 arasındaki bir c sayısı için f (c) = 0 olmalıdır. Bu da verilen
denklemin 1 ile 2 arasında bir kökü olması demektir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
86/ 182
Sonsuzluk İçeren Limitler
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
87/ 182
Sonsuz Limitler
y = 1/x2 fonksiyonunun değerler tablosunu ve şekildeki grafiğini
inceleyerek
1
lim 2
x→0 x
limitinin olmadığı, ve x i 0 a yeterince yakın alarak, 1/x2
değerlerinin istenildiği kadar büyük yapılabileceği sonucuna
varmıştık.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
88/ 182
Sonsuz Limitler
Dolayısıyla f (x) in değerleri sonlu bir sayıya yaklaşmaz ve
lim (1/x2 ) limiti yoktur.
x→0
Bu tür davranışı betimlemek için
1
=∞
x→0 x2
lim
gösterimini kullanırız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
89/ 182
Sonsuz Limitler
Bu ∞ işaretini bir sayı olarak düşündüğümüz anlamına gelmediği
gibi, limitin var olduğu anlamına da gelmez.
Bu yalnızca limitin olmamasının nedeninin ifadesidir: x değişkeni 0
a yeterince yakın alınarak, 1/x2 istenildiği kadar büyütülebilir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
90/ 182
Sonsuz Limitler
Genellikle, x değişkeni a ya yaklaşırken f (x) in değerlerinin giderek
büyüdüğünü (veya “sınırsız olarak arttığını”) göstermek için,
simgesel olarak
lim f (x) = ∞
x→a
yazarız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
91/ 182
Sonsuz Limitler
lim f (x) = ∞
x→a
gösterimi, x değişkeni a ya yeterince yakın (sağından veya
solundan) ama a dan farklı alınarak, f (x) değerlerinin istenildiği
kadar büyük yapılabilineceği anlamına gelir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
92/ 182
Sonsuz Limitler
lim f (x) = −∞ gösterimi “x değişkeni a ya yaklaşırken f (x) in
x→a
limiti eksi sonsuz” ya da “ x değişkeni a ya yaklaşırken, f (x)
sınırsız olarak azalır” olarak okunabilir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
93/ 182
Sonsuz Limitler
Örnek olarak
1
lim − 2 = −∞
x→0
x
verilebilir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
94/ 182
Sonsuz Limitler
Benzer tanımlar “x → a− ” gösteriminin yalnız a dan küçük x
değerlerini ve benzer biçimde “x → a+ ” gösteriminin yalnız x > a
değerlerini düşündüğümüz anlamına geldiği anımsanarak tek yönlü
limitler için de verilebilir.
lim f (x) = ∞
x→a−
lim f (x) = −∞
x→a−
lim f (x) = ∞
x→a+
lim f (x) = −∞
x→a+
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
95/ 182
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
96/ 182
Sonsuz Limitler
Sonsuz Limitler
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
97/ 182
Düşey Asimptot
Tanım :
Aşağıdakilerin en az birinin doğru olması durumunda, x = a
doğrusuna, y = f (x) eğrisinin düşey asimptotu denir.
lim f (x) = ∞
x→a
lim f (x) = −∞
x→a
lim f (x) = ∞
x→a−
lim f (x) = −∞
x→a−
Öğr.Gör. Volkan ÖĞER
lim f (x) = ∞
x→a+
lim f (x) = −∞
x→a+
MAT 1009 Matematik I
98/ 182
Örnek
Örnek : lim
x→3+
2x
2x
ve lim
limitlerini bulunuz.
x−3
x→3− x − 3
Çözüm : x’in değeri, 3’ten büyük ve 3’e yakın ise, payda x − 3
küçük ve pozitif bir sayı ve pay 2x de 6’ya yakın olacağından,
2x/(x − 3) oranı büyük bir pozitif sayı olacaktır. Buradan sezgisel
olarak
2x
=∞
lim
x→3+ x − 3
olduğunu görürüz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
99/ 182
Örnek...
Benzer biçimde, x’in 3’ten küçük ve 3’e yakın değerleri için x − 3
negatif ve küçük bir sayıdır, ama 2x yine pozitif bir sayıdır(6’ya
yakın). Dolayısıyla 2x/(x − 3) sayısal değeri büyük negatif bir sayı
olur. Böylece
2x
lim
= −∞
x→3− x − 3
elde ederiz.
y = 2x/(x − 3) eğrisinin
grafiği şekilde verilmiştir.
x = 3 düşey bir
asimptotdur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
100/ 182
Düşey Asimptot
Tanıdık y = tan x ve y = ln x fonksiyonlarının grafiklerinde de
düşey asimptotlar vardır.
Grafiğe bakarak
lim ln x = −∞
x→0+
olduğunu görürüz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
101/ 182
Düşey Asimptot
Şekilden
lim
x→(π/2)−
tan x = +∞
olduğu görülür. Aslında, n tamsayı olmak üzere x = (2n + 1)π/2
doğrularının herbiri y = tan x eğrisinin düşey asimptotudur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
102/ 182
Sonsuzdaki Limitler
f fonksiyonu (0, ∞) aralığında tanımlı olsun.
lim f (x) = L
x→∞
ifadesi, x’in değeri yeterince büyük seçilerek, f (x) değerinin L’ye
istenildiği kadar yakın yapılabileceği anlamını taşır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
103/ 182
MAT 1009 Matematik I
104/ 182
Sonsuzdaki Limitler
Tanımın geometrik açıklaması
şekillerde verilmiştir. Bir f
fonksiyonunun (yatay asimptot
denilen) y = L doğrusuna
yaklaşmasının bir çok yolu
olduğuna dikkat ediniz.
Öğr.Gör. Volkan ÖĞER
Örnek
x2 − 1
Örnek : f (x) = 2
x +1
Şekil 15:
x2 − 1
=1
x→∞ x2 + 1
lim
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
105/ 182
Sonsuzdaki Limitler
Şekil 15’e dönersek, x’in sayısal olarak büyük negatif değerleri için
f (x) değerlerinin 1’e yaklaştığını görürüz.
x’i negatif sayılardan sınırsız olarak küçülterek, f (x) değerini 1’e
istediğimiz kadar yakın yapabiliriz. Bu,
x2 − 1
lim
=1
x→−∞ x2 + 1
olarak ifade edilir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
106/ 182
Sonsuzdaki Limitler
Genel olarak, Şekil 16’da görüldüğü gibi,
lim f (x) = L
x→−∞
gösterimi, x negatif sayılardan yeteri kadar küçülterek, f (x)
değerlerinin L saysına istenildiği kadar yakın yapılabileceğini ifade
eder.
Şekil 16:
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
107/ 182
Sonsuzdaki Limitler
Burada da −∞ bir sayı değildir, ancak sıklıkla lim f (x) = L
x→−∞
ifadesi,
”x eksi sonsuza giderken, f (x)’in limiti L’dir”
olarak okunur.
Tanım :
Eğer lim f (x) = L veya lim f (x) = L ise, y = L doğrusuna
x→∞
x→−∞
y = f (x) eğrisinin yatay asimptotu denir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
108/ 182
Sonsuzdaki Limitler
Örneğin,
x2 − 1
lim
=1
x→−∞ x2 + 1
olduğundan y = 1 doğrusu, Şekil 15’deki eğrinin yatay
asimptotudur. İki yatay asimptotu olan bir eğri örneği
y = tan−1 x’dir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
109/ 182
Örnek
lim tan−1 x = −
x→−∞
π
2
lim tan−1 x =
x→∞
π
2
(2)
olduğundan, y = −π/2 ve y = π/2 doğrularının her ikisi de yatay
asimptotlardır. (Bu, x = ±π/2 doğrularının tanjant eğrisi
grafiğinin düşey asimptotu olanlarındandır.)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
110/ 182
Örnek
1
1
ve lim
limitlerini bulunuz.
x→∞ x
x→−∞ x
Örnek : lim
Çözüm : x büyükken 1/x’in küçük olduğunu gözlemleyiniz.
Örneğin,
1
= 0, 01
100
1
= 0, 0001
10.000
1
= 0, 000001
1.000.000
dir. Gerçekten x’i yeterince büyük seçerek 1/x’i 0’a istediğimiz
kadar yakın yapabiliriz. Tanım gereğince
1
=0
x→∞ x
lim
elde ederiz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
111/ 182
Örnek...
Benzer şekilde x’in negatif büyük değerleri için 1/x negatif ve
küçük olur. Böylece
1
=0
lim
x→−∞ x
buluruz. Buradan, y = 0 doğrusunun (x-ekseni) y = 1/x eğrisi için
yatay asimptot olduğu sonucuna ulaşırız.(Eğri şekilde verilen
hiperboldür.)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
112/ 182
Sonsuzdaki Limitler
Daha önce verilen Limit Kuralları’nın çoğu sonsuzdaki limitlerde de
geçerlidir. Verilen Limit Kuralları’nın (Kural 9 ve 10 dışında)
”x → a” yerine ”x → ∞” veya ”x → −∞” konduğunda da geçerli
olduğu kanıtlanabilir.
Özel olarak, n pozitif bir tamsayı olmak üzere
1
= 0,
x→−∞ xn
lim
Öğr.Gör. Volkan ÖĞER
1
= 0’dır.
x→∞ xn
lim
MAT 1009 Matematik I
113/ 182
Örnek
3x2 − x − 2
Örnek : lim
limitini bulunuz.
x→∞ 5x2 + 4x + 1
Çözüm : Kesirli bir fonksiyonun sonsuzdaki limitini bulmak için
önce pay ve paydayı, paydadaki x’in en büyük kuvvetine böleriz.
(Yalnızca x’in büyük değerleri ile ilgilendiğimizden, x 6= 0
varsayabiliriz.) Bu örnekte paydadaki x’in en büyük kuvveti x2
olduğundan limit kurallarından
3x2 − x − 2
lim
x→∞ 5x2 + 4x + 1
=
=
Öğr.Gör. Volkan ÖĞER
3x2 −x−2
x2
lim 5x2 +4x+1
x→∞
x2
lim
x→∞
3−
5+
1
x
4
x
MAT 1009 Matematik I
−
+
2
x2
1
x2
114/ 182
Örnek...
=
lim (3 −
1
x
−
lim (5 +
4
x
+
x→∞
x→∞
1
2
x
x→∞
4 limx→∞ x1 lim x12
x→∞
1
x
x→∞
lim 3 − lim
=
x→∞
lim 5 +
x→∞
2
)
x2
1
)
x2
− 2 lim
=
3−0−0
3
=
5+0+0
5
buluruz. Benzer bir hesaplama x → −∞ iken alınan limitin yine
3/5 olduğunu verir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
115/ 182
Örnek...
Şekilde verilen kesirli fonksiyonun y = 3/5 yatay asimptotuna
yaklaşmasını göstererk bu hesaplamaların sonucunu sergilemektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
116/ 182
Örnek
y = 0 (x-ekseni), y = ex doğal üstel fonksiyonunun grafiği için
yatay bir asimptottur.
lim ex = 0.
x→−∞
Öğr.Gör. Volkan ÖĞER
(3)
MAT 1009 Matematik I
117/ 182
Örnek
Örnek : lim e1/x limitini bulunuz.
x→0−
Çözüm : t = 1/x değişkeni için, x → 0− iken t → −∞ olduğunu
biliyoruz. Böylece (3)’den
lim e1/x = lim et = 0
x→0−
t→−∞
olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
118/ 182
Örnek
Örnek : lim sin x limitini bulunuz.
x→∞
Çözüm : x artarken, sin x değerleri −1 ile 1 arasında sonsuz kez
salınır. Bu nedenle lim sin x limiti yoktur.
x→∞
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
119/ 182
Sonsuzdaki Sonsuz Limitler
lim = ∞
x→∞
gösterimi, x büyürken f (x) değerlerinin de büyüdüğünü ifade eder.
Aşağıdaki gösterimlerin de anlamları benzerdir:
lim = ∞
x→−∞
lim = −∞
x→∞
Öğr.Gör. Volkan ÖĞER
lim = −∞
x→−∞
MAT 1009 Matematik I
120/ 182
Sonsuzdaki Sonsuz Limitler
lim ex = ∞
x→∞
lim x3 = ∞
x→∞
Öğr.Gör. Volkan ÖĞER
lim x3 = −∞
x→−∞
MAT 1009 Matematik I
121/ 182
Sonsuzdaki Sonsuz Limitler
x → ∞ iken y = ex , y = x3 ’den çok daha hızlı büyümektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
122/ 182
Örnek
Örnek : lim (x2 − x) limitini bulunuz.
x→∞
Çözüm :
lim (x2 − x) = lim x2 − lim x = ∞ − ∞
x→∞
x→∞
x→∞
yazılamayacağına dikkat ediniz. Limit Kuralları ∞ bir sayı
olmadığından sonsuz limitlerde kullanılmazlar. (∞ − ∞
tanımlanamaz.) Ancak hem x hem de x − 1 sınırsız olarak
büyüdüğünden
lim (x2 − x) = lim x(x − 1) = ∞
x→∞
x→∞
yazabiliriz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
123/ 182
Örnek
x2 + x
Örnek : lim
limitini bulunuz.
x→∞ 3 − x
Çözüm : Pay ve paydayı(paydadaki polinomun en yüksek kuvveti
olan) x ile bölerek, x → ∞ iken x + 1 → ∞ ve 3/x − 1 → −1
olduğundan,
x2 + x
x+1
lim
= lim 3
= −∞
x→∞ 3 − x
x→∞
−
1
x
buluruz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
124/ 182
Teğetler, Hızlar ve Diğer Değişim Hızları
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
125/ 182
Teğetler
Bir C eğrisi, y = f (x) denklemi ile verilmiş olsun. C eğrisinin
P (a, f (a)) noktasındaki teğetini bulmak istersek, P ’nin yakınındaki
x 6= a, koşulunu sağlayan bir Q(x, f (x)) noktasını alarak P Q kiriş
doğrusunun eğimini hesaplarız:
mP Q =
f (x) − f (a)
x−a
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
126/ 182
Teğetler
x değeri a’ya yaklaştıkça, Q noktası da eğri üzerinden P noktasına
yaklaşacaktır. Eğer mP Q bir m sayısına yaklaşırsa, t teğetini P ’den
geçen ve eğimi m olan doğru olarak tanımlarız. (BU, teğet
doğrusunun, Q noktası ve P ’ye yaklaşırken P Q kiriş doğrularının
limit durumu olduğunu söylemek demektir.)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
127/ 182
Teğet Doğrusu
Tanım :
Eğer aşağıdaki limit varsa, y = f (x) eğrisinin P (a, f (a))
noktasındaki teğet doğrusu, P (a, f (a)) noktasından geçen ve
eğimi
f (x) − f (a)
m = lim
x→a
x−a
olan doğrudur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
128/ 182
Örnek
Örnek : y = x2 parabolünün P (1, 1) noktasındaki teğet
doğrusunun denklemini bulunuz.
Çözüm : a = 1 ve f (x) = x2 olduğundan, eğim
x2 − 1
f (x) − f (1)
= lim
m = lim
x→1 x − 1
x→1
x−1
(x − 1)(x + 1)
= lim
x→1
x−1
= lim (x + 1) = 1 + 1 = 2
x→1
dir. Doğru denkleminin nokta-eğim biçimini kullanarak, (1, 1)
noktasındaki teğet doğrusunun denkleminin
y − 1 = 2(x − 1) ya da y = 2x − 1 olduğunu buluruz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
129/ 182
Teğet Doğrusu
Bir eğrinin bir noktasındaki teğetinin eğimini, eğrinin o noktadaki
eğimi olarak da adlandırırız.
Bunun ardındaki fikir, eğrinin üzerindeki noktaya yeterince
odaklanıldığında eğrinin adeta bir doğru gibi görünmesidir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
130/ 182
Teğet Doğrusu
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
131/ 182
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
132/ 182
Teğet Doğrusu
Teğet Doğrusu
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
133/ 182
Teğet Doğrusu
Şekillerde bu işlemi, y = x2 eğrisi için göstermektedir.
Ne kadar çok odaklanılırsa, parabol o denli bir doğruya
benzemektedir.
Başka bir deyişle, eğri adeta teğet doğrusundan ayırt edilemez hale
gelmektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
134/ 182
Teğet Doğrusu
Teğet doğrusunun eğimi için, bazı durumlarda kullanımı daha kolay
olan bir başka ifade vardır.
h=x−a
olsun, o zaman
x=a+h
olur. Dolayısıyla, P Q kiriş doğrusunun eğimi
mP Q =
f (a + h) − f (a)
h
olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
135/ 182
Teğet Doğrusu
(Şekilde, h > 0 durumu gözterilmiştir ve Q, P ’nin sağındadır.
h < 0 durumunda Q, P ’nin solunda olmalıdır.)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
136/ 182
Teğet Doğrusu
x, a’ya yaklaştıkça, h’nin de 0’a yaklaştığına dikkat ediniz (çünkü
h = x − a’dır). Dolayısıyla, tanımdaki teğet doğrusunun eğiminin
ifadesi
f (a + h) − f (a)
m = lim
(4)
h→0
h
biçimine dönüşür.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
137/ 182
Örnek
Örnek : y = 3/x hiprbolünün (3, 1) noktasındaki teğet
doğrusunun denklemini bulunuz.
Çözüm : f (x) = 3/x olsun. O halde (3, 1) noktasındaki teğetin
eğimi
f (3 + h) − f (3)
h→0
h
3−(3+h)
3
3+h − 1
= lim
= lim 3+h
h→0
h→0
h
h
−h
1
1
= lim
= lim −
=−
h→0 h(3 + h)
h→0 3 + h
3
m =
lim
olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
138/ 182
Örnek...
Dolayısıyla, (3, 1) noktasındaki teğetin bir denklemi
1
y − 1 = − (x − 3)
3
olur ve
x + 3y − 6 = 0
biçiminde sadeleşir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
139/ 182
Örnek...
Hiperbol ve teğeti şekilde gösterilmektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
140/ 182
Hızlar
s = f (t), hareket denklemi uyarınca bir doğru boyunca hareket
eden bir cisim düşünelim.
Burada s, cismin başlangıç noktasından başlayarak (yönü de
dikkate alan) yer değiştirmesini göstersin.
Hareketi tanımlayan f fonksiyonuna cismin konum fonksiyonu
denir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
141/ 182
Hızlar
t = a ile t = a + h arasındaki zaman aralığında konumdaki değişim,
f (a + h) − f (a) olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
142/ 182
Hızlar
Bu zaman aralığındaki ortalama hız
f (a + h) − f (a)
yer değiştirme
=
ortalama hız =
zaman
h
ile ifade edilir ve şekildeki P Q kiriş doğrusunun eğimi ile aynıdır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
143/ 182
Hızlar
Şimdi ortalama hızları, daha da kısa [a, a + h] zaman aralıklarında
hesapladığımızı varsayalım. Başka bir deyişle, h sıfıra yaklaşsın.
t = a anındaki v(a) hızını (ya da anlık hızı) bu ortalama hızların
limiti olarak tanımlarız:
f (a + h) − f (a)
h→0
h
v(a) = lim
(5)
Bu, t = a anındaki hızın, P ’deki teğet doğrusunun eğimine eşit
olduğu anlamına gelir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
144/ 182
Türevler
Daha önce y = f (x) denklemi ile ifade edilen bir eğrinin x = a
noktasındaki teğetinin eğimini
f (a + h) − f (a)
h→0
h
m = lim
(6)
olarak tanımladık.
Aynı zamanda konum fonksiyonu s = f (t) ile verilen bir cismin
t = a anındaki hızının
f (a + h) − f (a)
h→0
h
v(a) = lim
olduğunu gördük.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
145/ 182
Türevler
Aslında herhangi bir bilim ya da mühendislik dalında ne zaman bir
değişim hızı hesaplasak yukarıdaki gibi limitler ortaya çıkar. Bu
biçimdeki limitlerle çok yaygın olarak karşılaşıldığından, bunlar için
özel bir isim ve gösterim kullanılır.
Tanım :
Eğer varsa, aşağıdaki limite, f fonksiyonunun a sayısındaki türevi
denir ve f 0 (a) ile gösterilir:
f (a + h) − f (a)
h→0
h
f 0 (a) = lim
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
146/ 182
Türevler
f (a + h) − f (a)
h→0
h
f 0 (a) = lim
Eğer x = a + h yazarsak, h = x − a olur ve h’nin 0’a yaklaşması
için gerekli ve yeter koşul x’in a’ya yaklaşmasıdır. Dolayısıyla, teğet
doğrularını bulurken gördüğümüz gibi, türevin tanımını ifade
etmenin eşdeğer bir yolu şudur:
f (x) − f (a)
x→a
x−a
f 0 (a) = lim
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
(7)
147/ 182
Örnek
Örnek : f (x) = x2 − 8x + 9 fonksiyonunun a noktasındaki
türevini bulunuz.
Çözüm : Tanımdan,
f 0 (a) =
=
f (a + h) − f (a)
h→0
h
lim
[(a + h)2 − 8(a + h) + 9] − [a2 − 8a + 9]
h→0
h
lim
a2 + 2ah + h2 − 8a − 8h + 9 − a2 + 8a − 9
= lim
h→0
h
2ah + h2 − 8h
= lim
= lim (2a + h − 8) = 2a − 8
h→0
h→0
h
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
148/ 182
Fonksiyon Olarak Türev
Önceki bölümde bir f fonksiyonunun sabit bir a sayısındaki türevi
üzerinde durduk:
f (a + h) − f (a)
h→0
h
f 0 (a) = lim
(8)
Burada bakış açımızı değiştirelim ve a nın değişken olduğunu
varsayalım.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
149/ 182
Fonksiyon Olarak Türev
Denklem 8 de, a nın yerine bir x değişkeni koyarsak,
f (x + h) − f (x)
h→0
h
f 0 (x) = lim
(9)
elde ederiz. Bu limitin var olduğu her x sayısına bir f 0 (x) sayısı
karşıgelir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
150/ 182
Fonksiyon Olarak Türev
Dolayısıyla, f 0 f nin türevi olarak adlandırılan ve denklem 9 ile
tanımlanan yeni bir fonksiyon olarak ele alınabilir.
x deki f 0 (x) değerinin, geometrik olarak f nin grafiğinin (x, f (x))
noktasındaki teğet doğrusunun eğimi olarak yorumlanabileceğini
biliyoruz.
f 0 fonksiyonu f nin türevi olarak adlandırılır çünkü f den denklem
9 deki limit işlemi ile ”türetilmiştir”.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
151/ 182
Örnek
Örnek: f (x) = x3 − x ise, f 0 (x) için bir formül bulunuz.
Çözüm: Türevi hesaplamak için denklem 9 yi kullandığımız
zaman, h nin değişken olduğunu ve limit hesabı yapılırken x in
sabit olarak değerlendirildiğini hatırlamalıyız.
f 0 (x)
[(x + h)3 − (x + h)] − [x3 − x]
f (x + h) − f (x)
= lim
= lim
h→0
h→0
h
h
x3 + 3x2 h + 3xh2 + h3 − x − h − x3 + x
= lim
h→0
h
3x2 h + 3xh2 + h3 − h
= lim
h→0
h
= lim (3x2 + 3xh + h2 − 1) = 3x2 − 1
h→0
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
152/ 182
Örnek
√
Örnek: f (x) = x ise, f 0 türevini bulunuz. f 0 nün tanım
kümesini bulunuz.
Çözüm:
f (x + h) − f (x)
h→0
h
√
√
x+h− x
= lim
h→0
h
√
√
√
√
x+h− x
x+h+ x
·√
= lim
√
h→0
h
x+h+ x
f 0 (x) = lim
(x + h) − x
1
1
√
√ = √
√ =√
h→0 h( x + h + x)
x+ x
2 x
= lim
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
153/ 182
Örnek...
1
f 0 (x) = √
2 x
x > 0 ise, f 0 (x) vardır, bu nedenle f 0 nün tanım kümesi (0, ∞)
olur.
Bu küme, f nin tanım kümesi olan [0, ∞) kümesinden küçüktür.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
154/ 182
Diğer Gösterimler
Bağımsız değişkenin x, bağımlı değişkenin y olduğu geleneksel
y = f (x) gösterimini kullanırsak, türev için kullanılan bazı yaygın
gösterimler aşağıdaki gibidir.
f 0 (x) = y 0 =
df
d
dy
=
=
f (x) = Df (x)
dx
dx
dx
D ve d/dx sembolleri türev alma işlemini ifade ettiğinden türev
alma operatörleri olarak adlandırılır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
155/ 182
Diğer Gösterimler
Leibniz tarafından ortaya konulan dy/dx sembolü (şimdilik) bir
oran olarak değerlendirilmemelidir; yalnızca f 0 (x) ile eşanlamlıdır.
Buna karşın, özellikle değişim gösterimi ile birlikte kullanıldığında
çok yararlı ve anlamlı bir gösterimdir.
Türevin tanımını Leibniz gösterimi ile,
dy
∆y
= lim
dx ∆x→0 ∆x
şeklinde yazabiliriz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
156/ 182
Diğer Gösterimler
dy/dx türevinin bir a sayısındaki değerini, Leibniz gösterimi ile,
dy dy
ya da
dx x=a
dx x=a
olarak ifade ederiz ve bu gösterim ile f 0 (a) eşanlamlıdır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
157/ 182
Türevlenebilirlik
Tanım :
Eğer f 0 (a) varsa, f fonksiyonuna a da türevlenebilirdir denir.
Eğer f bir (a, b) [ya da (a, ∞) ya da (−∞, a) ya da (−∞, ∞)]
açık aralığındaki her sayıda türevlenebilirse, f fonksiyonu (a, b)
açık aralığında türevlenebilirdir denir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
158/ 182
Örnek
Örnek: f (x) = |x| fonksiyonu nerede türevlenebilirdir?
Çözüm: Eğer x > 0 ise, |x| = x olur ve h yi, x + h > 0 koşulunu
sağlayacak kadar küçük seçebiliriz ve bu nedenle |x + h| = x + h
olur. Dolayısıyla x > 0 için
|x + h| − |x|
h→0
h
f 0 (x) = lim
(x + h) − x
h
= lim = lim 1 = 1
h→0 h
h→0
h→0
h
= lim
elde ederiz ve bu nedenle x > 0 için f türevlenebilirdir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
159/ 182
Örnek...
Aynı şekilde, eğer x < 0 ise, |x| = −x olur ve h yi, x + h < 0
koşulunu sağlayacak kadar küçük seçebiliriz. ve bu nedenle
x + h < 0 ve dolayısıyla |x + h| = −(x + h) olur. Dolayısıyla,
x < 0 için
|x + h| − |x|
h→0
h
f 0 (x) = lim
−(x + h) − (−x)
−h
= lim
= lim −1 = −1
h→0
h→0 h
h→0
h
= lim
elde ederiz ve bu yüzden x < 0 için f türevlenebilirdir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
160/ 182
Örnek...
x = 0 için şunu incelemeliyiz;
f (0 + h) − f (0)
h→0
h
f 0 (0) = lim
|h|
|0 + h| − |0|
= lim
h→0 h
h→0
h
= lim
Öğr.Gör. Volkan ÖĞER
(limit var ise)
MAT 1009 Matematik I
161/ 182
Örnek...
Sağ ve sol limitleri ayrı ayrı hesaplayalım:
lim
h→0+
|0 + h| − |0|
|h|
h
= lim
= lim
= lim 1 = 1
h
h→0+ h
h→0+ h
h→0+
ve
lim
h→0−
|0 + h| − |0|
|h|
−h
= lim
= lim
= lim (−1) = −1.
h
h→0− h
h→0− h
h→0−
Bu limitler farklı olduğundan, f 0 (0) yoktur. Dolayısıyla f, 0
dışındaki her noktada türevlenebilirdir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
162/ 182
Örnek...
f 0 nün formülünü
f 0 (x) =
1 ,
−1 ,
x > 0 ise
x < 0 ise
olarak verebiliriz ve grafiği Şekil(b) deki gibidir. f 0 (0) ın var
olmaması gerçeği, geometrik olarak y = |x| in (0, 0) noktasında
teğet doğrusunun olmaması olgusunda yansıtılmaktadır. (Bkz.
Şekil(a).)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
163/ 182
Süreklilik ve Türevlenebilirlik
Süreklilik ve türevlenebilirliğin her ikisi de, bir fonksiyon için sahip
olması istenilir özelliklerdir. Aşağıdaki teorem bu özelliklerin nasıl
ilişkili olduklarını göstermektedir.
Teorem :
Eğer f, a sayısında türevlenebilirse f, a sayısında süreklidir.
Not: Teoremin tersi yanlıştır; bir başka deyişle, sürekli fakat
türevlenebilir olmayan fonksiyonlar vardır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
164/ 182
Süreklilik ve Türevlenebilirlik
Örneğin, f (x) = |x| fonksiyonu,
lim f (x) = lim |x| = 0 = f (0)
x→0
x→0
olduğundan 0 da süreklidir.
Fakat, bir önceki örnekte f nin 0 da türevlenebilir olmadığını
gösterdik.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
165/ 182
Bir Fonksiyon Nasıl Türevlenebilir Olmayabilir?
Eğer f fonksiyonunun grafiğinde ”köşe” veya ”kırılma” varsa, f nin
grafiğinin o noktada teğeti yoktur ve f, o noktada türevlenebilir
değildir. (f 0 (a) değerini hesaplamaya çalıştığımızda, sağ ve sol
limitlerinin farklı olduğunu görürüz.)
En son verdiğimiz teorem, bir fonksiyonun türevi olmamasının bir
başka yolunu verir. Eğer f, a sayısında sürekli değilse, f nin a da
türevlenebilir olmadığını söyler. Bu nedenle, f süreksiz olduğu
noktada (örneğin, sıçrama biçimindeki süreksizlerde) türevlenebilir
değildir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
166/ 182
Bir Fonksiyon Nasıl Türevlenebilir Olmayabilir?
Üçüncü bir olasılık ise, eğrinin x = a da düşey bir teğet
doğrusuna sahip olmasıdır. Bir başka ifadeyle, f a da sürekli ve
lim |f 0 (x)| = ∞
x→a
olmalıdır. Bu, x → a ya yaklaştıkça, teğet doğrularının dikleşmesi
demektir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
167/ 182
Bir Fonksiyon Nasıl Türevlenebilir Olmayabilir?
Şekil ele aldığımız üç olasılığı da göstermektedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
168/ 182
İkinci Türev
f türevlenebilir bir fonksiyonsa, f 0 de bir fonksiyondur, dolayısıyla
f 0 nün kendisininde (f 0 )0 = f 00 ile gösterilen bir türevi olabilir.
Bu yeni f 00 fonksiyonu, f nin ikinci türevi olarak adlandırılır,
çünkü f nin türevinin türevidir.
Leibniz gösterimini kullanarak, y = f (x) fonksiyonunun ikinci
türevini aşağıdaki gibi yazarız.
d dy
d2 y
= 2
dx dx
dx
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
169/ 182
Örnek
Örnek: f (x) = x3 − x ise, f 00 (x) i bulunuz.
Çözüm: Daha önce, f 0 (x) = 3x2 − 1 olduğunu bulmuştuk.
Dolayısıyla, ikinci türev
f 0 (x + h) − f 0 (x)
h→0
h
f 00 (x) = lim
[3(x + h)2 − 1] − [3x2 − 1]
= lim
h→0
h
3x2 + 6xh + 3h2 − 1 − 3x2 + 1
= lim
h→0
h
= lim (6x + 3h) = 6x
h→0
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
170/ 182
İkinci Türev - İvme
Genel olarak, ikinci türevin anlamınıdeğişim hızının değişim hızı
olarak açıklayabiliriz. Bunun en bilinen örneği aşağıda
tanımlayacağımız ivme dir.
Doğru boyunca hareket eden bir cismin konum fonksiyonu s = f (t)
ise, bu fonksiyonun birinci türevinin, cismin hızını zamanın bir
fonksiyonu olarak gösterdiğini biliyoruz:
v(t) = f 0 (t) =
df
dt
Hızdaki zamana göre anlık değişim hızı olan a(t), nesnenin ivmesi
olarak adlandırılır.
Öyleyse, ivme fonksiyonu hız fonksiyonunun türevidir ve bu nedenle
konum fonksiyonunun ikinci türevidir:
a(t) = v 0 (t) = f 00 (t)
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
171/ 182
Yüksek Mertebeden Türevler
Genelleştirirsek, f nin n inci türevi f (n) ile gösterilir ve f
fonksiyonunun n kez türevinin alınmasıyla elde edilir. y = f (x) ise,
y
(n)
=f
(n)
dn y
= n
dx
yazarız.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
172/ 182
Doğrusal Yaklaştırımlar
Bir eğrinin, teğet noktasının çevresinde, o noktadaki teğet
doğrusuna çok yakın olduğunu görmüştük.
Aslında, türevlenebilir bir fonksiyonungrafiğindeki bir noktaya
doğru odaklandıkça, grafiğin o noktadaki teğet doğrusuna daha
çok benzediğine dikkat etmiştik.
Bu gözlem, fonkiyonlar için yaklaşık değerler bulma yöntemlerinden
birinin temelini oluşturur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
173/ 182
Doğrusal Yaklaştırımlar
Fikir şudur: Bazen bir fonksiyonun f (a) değerini hesaplamak kolay
olabilirken, f nin buna yakın değerlerini hesaplamak zor (dahası,
olanaksız) olabilir. Bu nedenle, grafiği f nin (a, f (a)) noktasındaki
teğet doğrusu olan L doğrusal fonksiyonunun kolay hesaplanan
değeriyle yetiniriz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
174/ 182
Doğrusal Yaklaştırımlar
Genelde, (a, f (a)) noktasındaki teğet doğrusunu, x sayısı a ya
yakınken y = f (x) eğrisinin yaklaştırımı olarak kullanırız. Bu teğet
doğrusunun denklemi
y = f (a) + f 0 (a)(x − a)
dır
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
175/ 182
Doğrusal Yaklaştırımlar
ve
f (x) ≈ f (a) + f 0 (a)(x − a)
yaklaştırımına f nin a daki doğrusal yaklaştırımı ya da teğet
doğrusu yaklatırımı denir.
Grafiği teğet doğrusu olan
L(x) = f (a) + f 0 (a)(x − a)
doğrusal fonksiyonu, f nin a daki doğrusallaştırılması olarak
adlandırılır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
176/ 182
Örnek
√
Örnek: f (x) = x fonksiyonunun a = 1 √
deki doğrusal
√
√
yaklaştırımını bulunuz. Daha sonra bunu 0.99, 1.01 ve 1.05
sayılarının yaklaşık değerlerini bulmak için kullanırız. Bulduğunuz
değerler sayıların gerçek değerlerinden fazla mı, yoksa az mıdır?
√
Çözüm: Öncelikle, y = x fonksiyonunun x = 1 deki teğet
doğrusunun eğimi olan f 0 (1) değerini bulmalıyız. Daha önceki
örneklerde
1
f 0 (x) = √
2 x
olarak bulmuştuk.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
177/ 182
Örnek...
1
Dolayısıyla, f 0 (1) = olur ve (1, 1) noktasındaki teğet doğrusunun
2
denklemi
1
y − 1 = (x − 1)
2
ya da
1
1
y = x+
2
2
ve doğrusal yaklaştırım
√
1
1
x ≈ L(x) = x +
2
2
olur.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
178/ 182
Örnek...
Özel olarak,
√
√
√
0.99 ≈ L(0.99) = 12 (0.99) +
1
2
= 0.995
1.01 ≈ L(1.01) = 12 (1.01) +
1
2
= 1.005
1.05 ≈ L(1.05) = 12 (1.05) +
1
2
= 1.025
elde ederiz.
√
0.99 = 0.994987,
√
1.01 = 1.00499,
Öğr.Gör. Volkan ÖĞER
√
1.05 = 1.0247
MAT 1009 Matematik I
179/ 182
Örnek...
√
Şekilde y = x fonksiyonu ve onun doğrusal yaklaştırımı
L(x) = 12 x + 21 fonksiyonunun grafikleri çizilmiştir.
Yaklaşık değerlerimizin gerçek değerlerden fazla olduğunu
görmekteyiz, çünkü teğet doğrusu eğrinin üzerindedir.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
180/ 182
Örnek...
Aşağıdaki tabloda doğrusal yaklaştırımdan elde edilen değerler,
gerçek değerlerle yaklaştırılmaktadır.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
181/ 182
Örnek...
Tablo ve Şekilde, teğet doğrusu yaklaştırımının, x değişkeni 1 e
yakınken iyi yaklaşık değerler verdiğine, fakat x değişkeni 1 den
uzaklaştıkça elde edilen değerlerin gerçek değerlere yakınlıklarının
azaldığına dikkat ediniz.
Öğr.Gör. Volkan ÖĞER
MAT 1009 Matematik I
182/ 182

Download

MAT 1009 Matematik I 0/ 1

Products

Support

MAT 1009 Matematik I 0/ 1

Add this document to collection(s)

Add this document to saved

Suggest us how to improve StudyLib