15.02.2016
SAKARYA
ÜNİVERSİTESİ
KAVRAMALAR
SAKARYA ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE ELEMANLARI-II DERS NOTU
Doç.Dr. Akın Oğuz KAPTI
SAKARYA
ÜNİVERSİTESİ
Kavramalar
2 / 42
Kavramaların temel görevi iki mili birbirine bağlamaktır. Bu temel görevin
yanında şu fonksiyonları da yerine getirebilir:
Uzun millerin parçalı yapılarak kavramayla birleştirilmesi,
Eksenleri çakışmayan millerde kaçıklığın giderilmesi,
Gerektiğinde miller arası bağlantının kesilmesi,
Bir mildeki darbe ve titreşimlerin diğer mile geçmesinin önlenmesi,
Sigorta görevi görmesi.
1
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Kavrama Çeşitleri
3 / 42
1. Rijit kavramalar
2. Dengeleme kavramaları
Mekanizma hareketli kavramalar (Oldham)
Elastik kavramalar
3. Çözülebilen kavramalar (Debriyaj)
4. Emniyet kavramaları
5. Özel kavramalar (Amaca göre imal edilen)
SAKARYA
ÜNİVERSİTESİ
Rijit Kavramalar
4 / 42
Eksenleri aynı doğrultuda olan iki mili bağlamakta
kullanılan kavramalar rijit kavramalar olarak anılır.
Bağlanan miller yekpare bir mil gibi davranır. Rijit
kavramaların şu çeşitleri vardır:
Bilezikli zarflı kavramalar.
Cıvatalı zarflı kavramalar.
Kasnaklı (flanşlı) kavramalar.
2
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Bilezikli Zarflı Kavrama
5 / 42
İki taraftan hafif olarak konik torna edilmiş manşonlar
üzerine aynı koniklikte bilezikler çakılarak kavrama için
gerekli basınç sağlanır. Çözülüp takılması kolaydır. Kirli,
pis ortamlarda çevre hızları düşük olan durumlarda
kullanılırlar.
SAKARYA
ÜNİVERSİTESİ
Yağ Kanallı Bilezikli Kavrama
6 / 42
Bileziğin çakılmasını kolaylaştırmak amacıyla bileziğe yağ
kanalları açılmıştır. Bu yağ kanallarından basınçlı yağ
gönderilerek iki yüzey arasında yağ filmi oluşturulur.
Bileziğin çakılması ve çıkarılması kolaylaşır.
3
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Bilezikli Zarflı Kavrama
7 / 42
Bilezikli Zarflı Kavrama
8 / 42
Mil ile kavrama arasındaki toplam sürtünme kuvveti:
Fs
L
. .d . p.
2
Sürtünme momenti:
d .d 2
M s Fs .
. p..L
2
4
Döndürme momentinin iletilebilmesi için:
M s k .M d
Bileziğin çakma kuvveti (b: manşon genişliği):
Fç .d 1 .b. p a .(tan )
4
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Cıvatalı Zarflı Kavrama
9 / 42
Burada bilezikler
yerine cıvatalar
kullanılmıştır.
Momentin kuvvet
bağı ile iletildiği
kabul edilerek
bilezikli
kavramalardaki
gibi hesaplar
yapılır.
SAKARYA
ÜNİVERSİTESİ
Cıvatalı Zarflı Kavrama
10 / 42
5
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Cıvatalı Zarflı Kavrama
11 / 42
Mil ve zarf arasında oluşan basınç p ise sürtünme
momenti
.d 2
Ms
.L. p.
4
Burada cıvatalara verilen ön gerilme kuvveti Fön
ve n adet cıvata varsa
n.Fön .d .L. p
Fön
SAKARYA
ÜNİVERSİTESİ
1
. .d .L. p
n
Kasnaklı Kavrama
12 / 42
Moment iletimi iki kasnak arasında oluşan sürtünmeyle
sağlanır. Kasnaklardan birinde silindirik çıkıntı ve diğerinde
ise karşılığı vardır. Böylece iki milin merkezlenmesi sağlanır.
İki kasnak uygun sayıda cıvata ile birbirine bağlanır.
6
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Kasnaklı Kavrama
13 / 42
Kasnaklı Kavrama
14 / 42
7
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Kasnaklı Kavrama
15 / 42
Şekilde görüldüğü gibi dr
kalınlığında birim eleman
alınırsa buradaki normal kuvvet:
Fn 2. .r.dr. p
Sürtünme kuvveti ve momenti:
Fs Fn .
M s Fs .r
Kasnaklı kavramada
oluşan sürtünme yüzeyi
SAKARYA
ÜNİVERSİTESİ
Kasnaklı Kavrama
16 / 42
Burada tüm sürtünme alanındaki toplam sürtünme
momentini hesaplamak için integral alınarak:
D/2
Ms
2. .r.dr. p..r 2. . p.
d2 / 2
D/2
r
d2 / 2
2
.dr M s
1
. . . p.( D 3 d 23 )
12
Burada (n) sayıda cıvata için oluşacak basınç:
p
FN
n.Fön
A
.( D 2 d 22 )
4
Bu ifadeyi sürtünme momenti denkleminde yerine
yazılarak:
D 3 d 23
n
M s .Fön . . 2
3
D d 22
8
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Oldham Kavraması
17 / 42
Eksenleri arasında mesafe bulunan paralel milleri
birbirine bağlar ve aradaki kaçıklığı dengeler.
SAKARYA
ÜNİVERSİTESİ
Oldham Kavraması
18 / 42
9
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Oldham Kavraması
19 / 42
Oldham Kavraması
20 / 42
Şekilde C diskinin üzerinde, radyal doğrultuda, birbirine dik iki
kanal vardır. Kuvvetin düşük olması için, C diski hafif bir
malzemeden yapılmalı ve eksenler arası mesafe az olmalıdır.
I ve II millerine bağlı olan özdeş A ve B diskleri üzerindeki
çıkıntılar, C diskindeki kanallara oturmaktadır.
A ve B diskleri dairesel hareket yaparken, C diski bu kanallar
arasında eksantrik bir dönme yapar.
10
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Oldham Kavraması
21 / 42
C diskinin M merkezi, O1 ve O2 merkezlerini çap kabul
eden bir daire çizer. Bu yüzden A ve B disklerine göre iki
kat hızda döner.
Yani A ve B diskleri φ açısı ile döndüğünde C diskinin M
merkezi bu daire etrafında ψ = 2.φ açısıyla döner.
ψM = 2.φA = 2.φB
SAKARYA
ÜNİVERSİTESİ
Oldham Kavraması
22 / 42
M merkezinde oluşan kuvvet:
FM m.(2 ) 2 .
a
2
Bir φ açısı ile dönme olduğunda millere etkiyen
kuvvetler:
F1 m.( 2 ) 2 .a. cos
F2 m.(2 ) 2 .a. sin
11
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Kardan Kavraması
23 / 42
Eksenleri arasında açı olan milleri bağlar. Bu
kavramada, eksenleri dik iki mafsal bulunduğundan
istavroz kavraması da denir. Sistem üç serbestlik
derecelidir.
tan OK OK . cos
tan tan . cos
tan OK
OK
SAKARYA
ÜNİVERSİTESİ
Kardan Kavraması
24 / 42
12
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Kardan Kavraması
25 / 42
Kardan Kavraması
26 / 42
13
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Hidrodinamik Kavrama
27 / 42
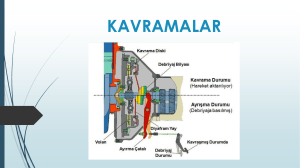
Çözülebilen Kavramalar
28 / 42
Çözülebilen kavramalar, moment ve hareket iletiminin, en
az iki yüzeyin birbiri üzerinde çalışmasıyla oluşan
sürtünme
momentiyle
iletildiği
sürtünme
yüzeyli
kavramalardır. Diskli, lamelli ve dişli olarak tasarlanırlar.
a) Diskli Kavrama: Moment iletimi iki yüzey arasındaki
sürtünme momentiyle gerçekleşir.
14
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Diskli Çözülebilen Kavramalar
29 / 42
Diskli Çözülebilen Kavramalar
30 / 42
15
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Diskli Çözülebilen Kavramalar
31 / 42
Diskli Çözülebilen Kavramalar
32 / 42
Yüzey basıncı:
p
Fk
( rd2 ri2 ).
Kavrama momenti:
rd
M k 2. . p.. r 2 .dr
ri
2.
. p. .(rd3 ri3 )
3
Denklemde p değeri yerine konursa:
r3 r3
2
M k .Fk .. d2 i2
3
rd ri
2 r3 r3
rm . d2 i2
3 rd ri
n adet sürtünme yüzeyi için kavrama momenti:
M k n.Fk . .rm
16
15.02.2016
SAKARYA
ÜNİVERSİTESİ
Lamelli Çözülebilen Kavramalar
33 / 42
Çok sayıda sürtünme yüzeyi olan, kullanım alanı
oldukça geniş bir kavrama türüdür.
a
Fk Fh .
Düşey kuvvet ve eksenel kuvvet ilişkisi:
b
Sürtünme yüzeyi sayısı, iç lamel adedinin iki katı olarak
alınır.
SAKARYA
ÜNİVERSİTESİ
Dişli Çözülebilen Kavramalar
34 / 42
Dişli kavramalarda sistem devreye girerken iki milin
eşit hızda olması gerekeceğinden sistem durdurulur,
dişliler birbirine geçtikten sonra çalıştırılır. Devreden
çıkışta ise sistemin durdurulması gerekmez.
17
15.02.2016
SAKARYA
ÜNİVERSİTESİ
SAKARYA
ÜNİVERSİTESİ
Dişli Çözülebilen Kavramalar
35 / 42
Kavramalarda yük altında devreye girme
36 / 42
I mili, ω1 hızında Md1
momentini iletiyor.
Başlangıçta durmakta
olan II mili, kavramanın
devreye girmesiyle
dönmeye başlıyor ve ω2
hızında Md2 momentini
iletiyor.
Kavrama devreye girerken
moment ve hız değişimi
grafikte gösterilmiştir.
18