İntegral Uygulamaları

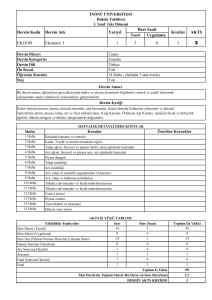
İntegral Uygulamaları
ÜNİTE
12
Yazar
Prof.Dr. Vakıf CAFEROV
Amaçlar
Bu üniteyi çalıştıktan sonra;
• düzlemsel alan ve dönel cisimlerin hacimlerinin belirli integral
yardımı ile hesaplanabileceğini,
• küre, koni ve kesik koninin hacim formüllerinin belirli integral
yardımıyla nasıl kolayca bulunabileceğini göreceksiniz.
İçindekiler
• Giriş
309
• Alan Hesabı
309
• Hacim Hesabı
315
• Değerlendirme Soruları
319
Çalışma Önerileri
• Ünite içinde çözülmüş örneklerin çözümlerini iyice inceleyiniz
• Yanlış sonuçlar çıkmaması için alan hesaplarken fonksiyonun
hangi aralıkta pozitif, hangi aralıkta negatif olduğunu belirlemeye çalışınız
• Çok sayıda fonksiyon örnekleri alıp fonksiyonların grafikleri
ile x-ekseni arasındaki; iki fonksiyonun grafikleri arasındaki
alanları hesaplamaya çalışınız
• Dönel cisimlerin hacimleri ile ilgili de çok sayıda örnek çözmeye çalışınız.
ANADOLU ÜNİVERSİTESİ
İNTEGRAL UYGULAMALARI
309
1. Giriş
Geçen ünitede, bir fonksiyonun grafiği ile x-ekseni arasındaki düzlemsel bir bölgenin alanının bulunması probleminin bizi matematiğin ikinci ana kavramı olan integral kavramına nasıl getirdiğini gördük.
İntegralin çeşitli bilim dallarında (mühendislik, fizik, ekonomi...) çok sayıda uygulamaları vardır. Bir ünitede bu uygulamaların hepsinden bahsetmek imkansızdır.
Bu ünitede belirli integralin basit uygulamalarından olan düzlemsel alan ve dönel
cisimlerin hacmi konularını ele alacağız.
2. Alan Hesabı
Geçen ünitede bir [a, b] aralığında sürekli ve negatif olmayan y = f(x) fonksiyonu
için y = f(x) eğrisi, x-ekseni, x = a, x = b doğruları arasındaki alanın
b
a
f(x) dx
belirli integrali olduğu ispatlanmıştı. Eğer y = f(x) fonksiyonu [a, b] aralığında negatif ise o zaman sözü edilen alan
-
b
a
f(x) dx integraline eşittir.
Eğer c ∈ (a, b) olmak üzere, f(x) fonksiyonu (a, c) aralığında negatif, (c, b) aralığında pozitif ise, o zaman y = f(x) eğrisi, x-ekseni, x = a, x = b doğruları arasındaki
toplam alan
-
c
a
b
f(x) dx +
c
f(x) dx ,
eğer fonksiyon (a, c) aralığında pozitif, (c, b) de negatif ise o zaman sözü edilen alan
c
a
f(x) dx -
b
c
f(x) dx
olur.
Aşağıdaki şekilleri inceleyerek yukarıdaki formülleri anlamaya çalışınız.
AÇIKÖĞRETİM FAKÜLTESİ
310
İNTEGRAL UYGULAMALARI
y = f(x)
y = f(x)
a
b
a
●
●
●
●
●
c
b
●
a
●
b
●
c
y = f(x)
f(x) < 0
Şekil 12.1
Bu durumlar A=
b
a
f(x) dx formülü ile birleştirilebilir.
Örnek: 1) y = x2 - 3x - 4 parabolü ile x-ekseni arasındaki
2) y = (x - 1)3 eğrisi, x-ekseni, x = -1, x = 2 doğruları arasındaki
3) y = 1 - x3 eğrisi, x-ekseni, x = 0, x = 3 doğruları arasındaki
alanları hesaplayalım.
Çözüm: Aşağıda verilen grafikleri gözönünde tutalım.
1)
Şekil 12.2
x2 - 3x - 4 = 0 ⇒ x = -1, x = 4 .
Parabol, apsis eksenini x = -1 ve x = 4 noktalarında keser ve (-1, 4) aralığında x2
- 3x - 4 fonksiyonu negatiftir. Buna göre sözü edilen S alanı aşağıdaki gibi hesaplanır:
S = -
4
3
2
(x2 - 3x - 4)dx = - x - 3x - 4x
-1
3
2
= 125 ≅ 20.83 .
6
ANADOLU ÜNİVERSİTESİ
4
-1
= - 64 - 24 - 16 - - 1 - 3 + 4
3
3 2
İNTEGRAL UYGULAMALARI
311
2)
Şekil 12.3
x değişkeni [-1, 2] aralığında değişirken x ∈ (-1, 1) ise (x -1)3 fonksiyonu
negatif, x ∈ (1, 2) ise pozitiftir. Buna göre sözü edilen S alanı
S = = -
1
-1
1
-1
(x - 1) 3 dx +
2
1
(x - 1) 3 dx
2
(x3 - 3x2 + 3x - 1)dx + (x3 - 3x2 + 3x - 1)dx
4
2
= - x - x3 + 3x - x
4
2
1
1
-1
4
2
+ x - x3 + 3x - x
4
2
2
= 4,25
1
olur.
3)
Şekil 12.4
1 - x3 = 0 ⇒ x3 = 1 ⇒ x = 1 .
Buna göre, y = 1 - x3 fonksiyonu x = 1 noktasında işaret değiştirmektedir.
x in 0 ile 3 arasında olması gerektiğini hatırlarsak x ∈ (0, 1) iken 1 - x3 fonksiyonu pozitif, x ∈ (1, 3) iken ise negatiftir. Buna göre bulmak istediğimiz alan,
AÇIKÖĞRETİM FAKÜLTESİ
İNTEGRAL UYGULAMALARI
312
S =
1
0
(1 - x3 )dx -
3
4
(1 - x3 )dx = x - x
1
4
= 1 - 1 - 0 - 3 - 81 - 1 - 1
4
4
4
1
0
4
- x -x
4
3
=
1
= 3 + 69 + 3 = 75 = 18.75
4
4
4
4
dır.
[a, b] aralığında verilmiş y = f(x) eğrisi ile x-ekseni arasındaki alanı bulma işleminde ilk adım f(x) in bu aralıkta işaretinin incelenmesidir.
?
1)
2)
3)
4)
y = x2 - 4x eğrisi ile x-ekseni arasındaki,
y = 9 - x2 eğrisi ile x-ekseni arasındaki,
y = x3 eğrisi, x-ekseni, x = -1, x = 2 doğruları arasındaki,
y = sinx eğrisi, x-ekseni, x = π/4, x = 3π/2 doğruları arasındaki alanları
hesaplayınız.
Cevaplarınız 10 2 , 36 , 4 1 , ve 4 + 2 olmalıdır.
3
4
2
[a, b] aralığı üzerinde tanımlı, sürekli y = f(x) ve y = g(x) fonksiyonları verilsin ve
her bir x ∈ [a, b] için
f(x) ≥ g(x)
eşitsizliği sağlansın ( f(x) ve g(x) sabit işaretli olmayabilir, şekil 12.5 e bakınız). O zaman y = f(x), y = g(x) eğrileri, x = a, x = b doğruları arasında kalan alan
S=
b
a
[f(x) - g(x)] dx
formülü ile hesaplanır.
Şekil 12.5
Örnek: 1) y = 2x - x2 eğrisi ve y = x doğrusu arasında
2) y = x2 ve y = x eğrileri arasında
kalan alanları bulalım.
ANADOLU ÜNİVERSİTESİ
İNTEGRAL UYGULAMALARI
313
Çözüm: 1)
Şekil 12.6
y = 2x - x2 parabolü ile y = x doğrusunun kesişim noktalarını bulalım.
2x - x2 = x ⇒ x2 - x = 0 ⇒ x(x - 1) = 0 ⇒ x = 0 ve x = 1 .
Grafikler x = 0 ve x = 1 apsisli noktalarda kesişiyorlar. x değişkeni 0 ile 1 arasında
iken parabol doğrudan yukarıda kalır. Buna göre istediğimiz alan aşağıdaki gibidir:
S =
1
0
(2x - x2 - x)dx =
1
2
3
(x - x2 )dx = x - x
0
2 3
1
0
=1 .
6
2)
Şekil 12.7
y = x2 ile y = x eğrilerinin kesişim noktalarını bulalım.
x2 = x ⇒ x4 = x ⇒ x(x3 - 1) = 0 ⇒ x = 0 , x = 1 .
x ∈ [0, 1] iken x ≥ x2 olduğundan arada kalan alan
1
S = ( x - x2 )dx =
0
1
1
3
3
(x2 - x2 )dx = 2 x2 - x
0
3
3
olur.
AÇIKÖĞRETİM FAKÜLTESİ
1
0
= 2 - 1 - 0 =1
3 3
3
314
İNTEGRAL UYGULAMALARI
Eğer [a, b] aralığının tüm noktalarında f(x) ≥ g(x) eşitsizliği sağlanmıyorsa, örneğin, c
∈ (a, b) olmak üzere, her x ∈ (a, c) için f(x) ≥ g(x) ve her x ∈ (c, b) için f(x)
≤ g(x) ise y = f(x), y = g(x) eğrileri ve x = a, x = b doğruları arasındaki alan
S =
c
a
[f(x) - g(x)] dx +
b
c
[g(x) - f(x)] dx
olur.
Örnek: y = x3, y = x eğrileri arasında kalan bölgenin x = 0 dan x = 2 ye kadar
olan kısmının alanını bulunuz.
Şekil 12.8
Çözüm: x ∈ (0, 1) ise x > x3 ; x ∈ (1, 2) ise x3 > x olduğundan sözü edilen alan
S =
1
0
x - x3 dx +
2
1
3
4
x3 - x dx = 2 x2 - x
3
4
3
1
3
4
+ x - 2 x2
4
3
0
2
=
1
3
= 2 - 1 + 16 - 2 22 - 1 - 2 = 29 - 2 22 ≅ 2,95
3 4
4
3
4 3
6
3
dir.
Genel olarak [a, b] üzerinde sürekli y = f(x) ve y = g(x) grafik eğrileri arasındaki
bölgenin x = a dan x = b ye kadar olan kısmının alanı
S=
formülü ile hesaplanır.
ANADOLU ÜNİVERSİTESİ
b
a
f(x) - g(x) dx
İNTEGRAL UYGULAMALARI
2
1) y = x
2
315
eğrisi ve y = 4 - x doğrusu arasındaki alanı bulunuz.
2) y = sinx , y = cos x eğrileri arasındaki bölgenin x = - π den x = π ye kadar2
2
ki kısmının alanını bulunuz.
Cevaplarınız 18 ve 2 2 olmalıdır.
3. Hacim Hesabı
Bu bölümde dönel cisimlerin hacimlerinin integral yardımı ile hesaplanmasını ele
alacağız. [a, b] aralığında sürekli y = f(x) fonksiyonunun grafiğini ele alalım.
Şekil 12.9
ABCD düzlem parçasını x - ekseni etrafında döndürdüğümüzde tabanları paralel
daireler olan üç boyutlu bir cisim elde edilir. Bu cisme dönel cisim denir. Bu cismin
hacmi
V=π
b
a
f2 (x) dx
formülü ile hesaplanır.
Örnek: 1) y = x eğrisi, x-ekseni, x = 1 ve x = 4 doğruları ile sınırlı,
2) y = ex eğrisi, x - ekseni, x = -1 ve x = 1 doğruları ile sınırlı
bölgelerin x - ekseni etrafında dönmesiyle oluşan dönel cisimlerin hacimlerini bulalım.
AÇIKÖĞRETİM FAKÜLTESİ
?
İNTEGRAL UYGULAMALARI
316
Çözüm: 1) V = π
2) V = π
4
1
1
-1
x 2 dx = π
2
ex dx = π
4
2
x dx = πx
1
2
1
4
1
= π 8 - 1 = 15 π ≅ 23,55 .
2
2
e2x dx = π 1 e2x
-1
2
1
-1
= π e2 - e-2 ≅ 11,4 .
2
Şekil 12.10
Örnek: y = x2 - 2x parabolü, x = 1 ve x = 3 doğruları ile sınırlı bölgenin x ekseni etrafında dönmesiyle oluşan dönel cismin hacmini bulalım.
Çözüm: V = π
3
1
2
x2 - 2x dx = π
3
1
5
x4 - 4x3 + 4x2 dx = π x - x4 + 4 x3
5
3
3
1
= π 18 - 23 + 1 = π 54 - 23 + 15 = 46 π ≅ 9,63 .
5
15
15
15
Şekil 12.11
?
y = 1 eğrisi, x - ekseni x = 2, x = 3 doğruları ile sınırlı bölgenin x - ekseni
x
etrafında dönmesinden meydana gelen hacmi bulunuz.
Cevabınız π olmalıdır.
6
ANADOLU ÜNİVERSİTESİ
İNTEGRAL UYGULAMALARI
317
Geometriden bilindiği gibi yarıçapı R, yüksekliği h olan dairesel dik koninin hacmi;
taban yarıçapları R ve r, yüksekliği h olan kesik koninin hacmi; yarıçapı R olan kürenin hacmi sırasıyla aşağıdaki formüllerle verilir:
V = 1 π R2 h,
3
V = 1 π h R 2 + Rr + r2 ,
3
V = 4 π R3 .
3
Şimdi bu formüllerin dönel cisimlerin hacimleri formulünden nasıl elde edilebileceğini görelim.
Dairesel Dik Koninin Hacmi
Dairesel dik koniyi ve koordinat sistemini şekildeki gibi alalım.
A
R
α
●
B
●
h
0
Şekil 12.12
|AB| = R, |OB| = h
olur. Bu durumda koni , [OA] doğru parçasının x - ekseni etrafında dönmesiyle elde edilen dönel cisimden başka bir şey değildir. Dönel cismin hacim formülünü uygulayabilmemiz için OA doğru parçasının denklemini y = f(x) şeklinde ifade etmemiz gerekiyor.
OA nın denklemi y = mx şeklindedir.
m = tanα =
m eğimi tanα ya eşit olduğundan
AB R
= ; OA nın denklemi y =R x olarak bulunur.
OB h
h
Buradan, dönel cismin hacim formülüne göre koninin hacmi
V =π
h
0
f2 (x) dx = π
2
3
= π. R .x
2
3
h
h
0
h
=π
0
olur.
AÇIKÖĞRETİM FAKÜLTESİ
R x 2 dx = π
h
2
. R2
h
h
0
R 2 x2 dx
h2
3
. h = 1 π R2 . h
3
3
318
İNTEGRAL UYGULAMALARI
Kesik Koninin Hacmi
Şekil 12.13
Kesik koniyi ve koordinat sistemini şekildeki gibi alalım.
|OA| = r,
|BC| = R,
|OC| = h
olur. Kesik koni, [AB] doğru parçasının x - ekseni etrafında dönmesinden meydana gelir. AB nin denklemini bulalım. Doğrunun denklemi y = mx + n gibidir ve m, n
sabitleri bulunmalıdır.
m = tanα ,
BD
=R-r
AD
h
n = r, tanα =
olduğundan AB nin denklemi
y = R-r x + r
h
olur. Buna göre kesik koninin hacmi olarak,
V =π
h
0
R - r x + r 2 dx = π
h
= π R-r
h
2
= π R-r
h
2
= π
h
0
R-r
h
2
x2 +
x3 + 2r (R - r) x2 + r2 x
h
3
2
2r (R - r)
x + r2 dx
h
h
0
h 3 + 2r (R - r) h 2 + r2 h
h
3
2
R-r2h
+ rh (R - r) + r2 h
3
= π h R 2 - 2Rr + r2 + 3Rr - 3r2 + 3r2
3
bulunur.
ANADOLU ÜNİVERSİTESİ
= π h R 2 + Rr + r2
3
İNTEGRAL UYGULAMALARI
319
Kürenin Hacmi
Şekil 12.14
Koordinat sistemini şekildeki gibi kürenin merkezinde seçelim. O zaman küre, ABC
yarım çemberinin x - ekseni etrafında dönmesinden meydana gelen bir dönel cisimdir. Buna göre ABC eğrisinin y = f(x) şeklindeki denklemini bulmamız gerekiyor.
Merkezi koordinat başlangıcında, yarıçapı R olan çemberin denklemi x2 + y2 = R2
dir. Buna göre ABC yarım çemberinin denklemi
y=
R 2 - x2
-R ≤ x ≤ R
dir. Buna göre kürenin hacmi,
V =π
R
-R
f 2 (x) dx = π
3
= π R2 x - x
3
R
-R
R
-R
R 2 - x2
2
dx = π
R
-R
R 2 - x2 dx
3
3
= π R 3 - R - -R 3 + R
3
3
3
3
= π 2R 3 - 2 R 3 = π 4R = 4 π R
3
3
3
olarak bulunur.
Değerlendirme Soruları
1.
f: [-1, 2] → IR, f(x) = |x| fonksiyonunun grafiği ile x-ekseni arasındaki
alan kaç birimkaredir?
A. 3
B. 5/2
C. 2
D. 3/2
E. 1
AÇIKÖĞRETİM FAKÜLTESİ
320
İNTEGRAL UYGULAMALARI
2.
f: [0, π] → IR, f(x) = cosx eğrisi, x = 0, x = π doğruları ve x-ekseni tarafından sınırlanan alan kaç birimkaredir?
A. 0
B. 1
C. 3/2
D. 2
E. π
3.
y = ex eğrisi, x = 0, x = 1 doğruları ve x-ekseni tarafından sınırlanan alan
kaç birimkaredir?
A. e
B. e /2
C. e - 1
D. e + 1
E. 2e
4.
f: [1, ∞] → IR, f(x) = lnx eğrisi, x-ekseni ve x = e doğrusu tarafından sınırlanan alan kaç birimkaredir?
A. e
B. e /2
C. 1
D. 2/e
E. 1/e
5.
y = x2 + 2x - 3 parabolu ile x-ekseni arasında kalan alan kaç birimkaredir?
A. 32/3
B. 9
C. 9/2
D. 4
E. 5/3
6.
y = lnx eğrisi, x = 1 doğrusu ve x-ekseni tarafından sınırlanan alan kaç
e
birimkaredir?
A. 1 - 2
e
2
B.
e
C. 1
e
D. 1
E. e
ANADOLU ÜNİVERSİTESİ
İNTEGRAL UYGULAMALARI
7.
y = x2 - 1 eğrisi ile y = x - 1 doğrusu tarafından sınırlanan alan kaç birimkaredir?
A. 1/6
B. 1/3
C. 1/2
D. 5/6
E. 1
8.
f: [0, 2π] → IR, f(x) = sinx eğrisi ile x-ekseni tarafından sınırlanan alan kaç
birimkaredir?
A. 1/2
B. 1
C. 3/2
D. 2
E. 4
9.
y = 3x, y = 0, x = 2 tarafından sınırlanan bölgenin x-ekseni etrafında dönmesiyle oluşan dönel cismin hacmi kaç birimküptür?
A. 6π
B. 12π
C. 24π
D. 36π
E. 72π
10. y = 1 - |x| eğrisi ile x-ekseni arasında kalan bölgenin x-ekseni etrafında
dönmesiyle oluşan dönel cismin hacmi kaç birimküptür?
A. 2 π
3
B. 1 π
3
C. 4 π
3
D. π
E. 2π
11. y =
4 - x2 eğrisi ile x-ekseni arasında kalan alanın x-eksenin etrafında
dönmesiyle oluşan dönel cismin hacmi kaç birimküptür?
A. 24π
B. 32 π
3
C. 8π
D. 4π
E. 2π
AÇIKÖĞRETİM FAKÜLTESİ
321
322
İNTEGRAL UYGULAMALARI
12. y = x3 eğrisi, x = -1 , x = 1 doğruları ve x-ekseni tarafından sınırlanan
alanın x-ekseni etrafında dönmesiyle oluşan dönel cismin hacmi kaç birimküptür?
π
A.
7
2π
B.
7
3π
C.
7
4π
7
E. π
D.
Değerlendirme Sorularının Yanıtları
1. B
2. D
3. C
4. C
5. A
ANADOLU ÜNİVERSİTESİ
6. A
7. A
8. E
9. C
10. A
11. B
12. B