ıntegral

Alan ve Uzaklık
Alan Problemi
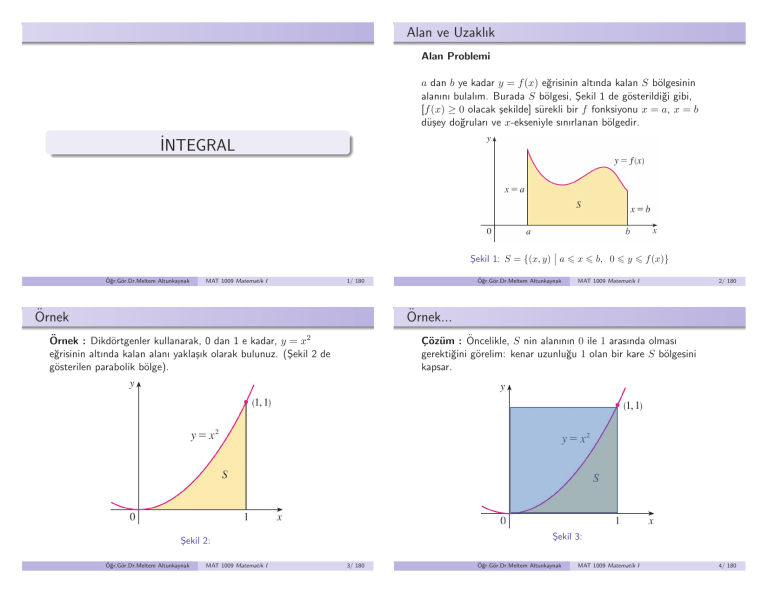
a dan b ye kadar y = f (x) eğrisinin altında kalan S bölgesinin
alanını bulalım. Burada S bölgesi, Şekil 1 de gösterildiği gibi,
[f (x) ≥ 0 olacak şekilde] sürekli bir f fonksiyonu x = a, x = b
düşey doğruları ve x-ekseniyle sınırlanan bölgedir.
İNTEGRAL
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Şekil 1: S = {(x, y) a 6 x 6 b, 0 6 y 6 f (x)}
Öğr.Gör.Dr.Meltem Altunkaynak
1/ 180
Örnek
MAT 1009 Matematik I
2/ 180
Örnek...
Örnek : Dikdörtgenler kullanarak, 0 dan 1 e kadar, y = x2
eğrisinin altında kalan alanı yaklaşık olarak bulunuz. (Şekil 2 de
gösterilen parabolik bölge).
Çözüm : Öncelikle, S nin alanının 0 ile 1 arasında olması
gerektiğini görelim: kenar uzunluğu 1 olan bir kare S bölgesini
kapsar.
Şekil 3:
Şekil 2:
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
3/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
4/ 180
Örnek...
Örnek...
1
Ancak bundan daha iyisini yapabiliriz. Şekil 4(a) daki gibi x = ,
4
3
1
x = , x = düşey doğrularını çizerek S yi S1 , S2 , S3 ve S4
2
4
şeritlerine ayıralım.
Bu şeritlerin her birinin tabanı kendi tabanına eşit, yüksekliği ise
şeridin sağ kenar uzunluğuna eşit olan bir dikdörtgen gibi
düşünebiliriz [Bkz. Şekil 5(b)].
Şekil 5: (b)
Şekil 4: (a)
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
5/ 180
Örnek...
MAT 1009 Matematik I
6/ 180
Örnek...
Her dikdörtgenin genişliği
1
ve yükseklikleri, sırasıyla
4
2 2 2
1
1
3
,
,
ve 12 dir.
4
2
4
Bu dikdörtgenlerinin alanlarının toplamını R4 ile gösterirsek
1
R4 = ·
4
Diğer bir deyişle, bu dikdörtgenlerin yüksekliği, f (x) = x2
1
1 1
1 3
3
fonksiyonunun sırasıyla 0, ,
, ,
, ,
,1
4
4 2
2 4
4
2
2
2
1
1
1
15
1
1
3
+ ·
+ ·
+ · 12 =
= 0.46875
4
4
2
4
4
4
32
elde ederiz.
alt aralıklarının sağ uç noktalarındaki değerleridir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
7/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
8/ 180
Örnek...
Örnek...
Şekil 5(b) deki dikdörtgenlerin yerine Şekil 6 deki küçük
dikdörtgenleri kullanırsak,
Şekilden, S nin alanının(A), R4 den küçük olduğunu görüyoruz,
dolayısıyla
A < 0.46875
Şekil 6:
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
9/ 180
Örnek...
MAT 1009 Matematik I
10/ 180
Örnek...
bu dikdörtgenlerin yüksekliklerini, f yi alt aralıkların sol uç
noktalarında hesaplayarak dikdörtgenlerin toplam alanı
1
1
L4 = · 02 + ·
4
4
2
2
2
1
1
7
1
1
3
+ ·
+ ·
=
= 0.21875
4
4
2
4
4
32
olur.
S nin alanının L4 den büyük olduğunu görüyoruz, dolayısıyla A için
0.21875 < A < 0.46875
alt ve üst sınırlarını elde ederiz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
11/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
12/ 180
Örnek...
Örnek...
Bu işlemleri daha fazla sayıda dikdörtgen kullanarak yineleyebiliriz.
Şekil 7, S bölgesinin genişlikleri eşit uzunlukta olan sekiz
dikdörtgene bölüşünü gösteriyor.
Küçük dikdörtgenlerin (L8 ) alanları toplamını ve büyük
dikdörtgenlerin (R8 ) alanları toplamını hesaplayarak, A için
öncekinden daha iyi alt ve üst sınır elde ederiz:
0.2734375 < A < 0.3984375
Dolayısıyla, soruya verilebilecek olası bir yanıt, S nin gerçek
alanının 0.2734375 ile 0.3984375 arasında bir değer olduğudur.
Şekil 7: R8 ve L8
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
13/ 180
Örnek...
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
14/ 180
Alan Problemi
Bölgelerin sayısını arttırarak daha iyi sınırlar bulabiliriz. Tablo, n
tane dikdörtgen için yapılan benzer hesaplarla, yüksekliklerin sol uç
noktalarda hesaplandığı (Ln ) ve sağ uç noktalarda hesaplandığı
(Rn ) değerlerini gösterir.
n
10
Ln
0.2850000
Rn
0.3850000
30
0.3168519
0.3501852
50
0.324000
0.3434000
100
0.3283500
0.3383500
1000
0.3328335
0.3338335
1
Tablodaki değerler, n arttıkça Rn nin e yaklaştığını
3
düşündürür.Bir sonraki örnek bunun doğruluğunu gösterir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Şekil 1 deki daha genel bir S bölgesinin alanını bulalım. Önce Şekil
8 da görüldüğü gibi, S yi genişlikleri eşit olan n tane
S1 , S2 , . . . , Sn şeritlerine ayıralım.
Şekil 8:
15/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
16/ 180
Alan Problemi
Alan Problemi
Si yi, genişliği ∆x, yüksekliği f (xi ) olan bir dikdörtgen gibi
düşünelim (Bkz. Şekil 9).
[a, b] aralığının uzunluğu b − a dır. Dolayısıyla her bir şeridin
genişliği
b−a
∆x =
n
olur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Şekil 9:
Dikdörtgenin alanı f (xi )∆x dir.
Öğr.Gör.Dr.Meltem Altunkaynak
17/ 180
Alan Problemi
MAT 1009 Matematik I
18/ 180
Alan Problemi
S nin alanını yaklaşık olarak, dikdörtgenlerin alanlarını toplayarak
bulabiliriz, bu da
Tanım : Sürekli bir f fonksiyonunun grafiği altında kalan bölgenin
A alanı, yaklaştırım dikdörtgenlerinin toplam alanının limitidir:
Rn = f (x1 )∆x + f (x2 )∆x + . . . + f (xn )∆x
A = lim Rn = lim [f (x1 )∆x + f (x2 )∆x + . . . + f (xn )∆x] (1)
n→∞
n→∞
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
19/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
20/ 180
Alan Problemi
Alan Problemi
f sürekli olduğundan, tanımdaki limitin her zaman var olduğu
kanıtlanabilir.
Aslında i inci dikdörtgenin yüksekliğini, sol ya da sağ uç noktalar
yerine, f nin, [xi−1 , xi ] alt aralığındaki herhangi bir x∗i deki değeri
olarak alabilirdik.
Sol uç noktaları kullandığımızda sonucun değişmeyeceği de
gösterilebilir:
x∗1 , x∗2 , . . . , x∗n sayılarına örnek noktalar denir.
A = lim Ln = lim [f (x0 )∆x+f (x1 )∆x+. . .+f (xn−1 )∆x] (2)
n→∞
n→∞
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
21/ 180
Alan Problemi
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
22/ 180
Alan Problemi
Şekil 10, örnek noktaların uç noktalar olarak alınmadığı
dikdörtgenlerle yaklaşımı göstermektedir.
Dolayısıyla S nin alanı daha genel olarak
A = lim [f (x∗1 )∆x + f (x∗2 )∆x + . . . + f (x∗n )∆x]
n→∞
(3)
şeklinde ifade edilir.
Şekil 10:
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
23/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
24/ 180
Alan Problemi
Alan Problemi
Dolayısıyla, Denklem (1), (2) ve (3) deki alan ifadeleri
A = lim
Terim sayısı fazla olan toplamları kısaca göstermek için çoğunlukla
sigma gösterimini kullanırız. Örneğin,
n
X
n→∞
A = lim
f (xi )∆x = f (x1 )∆x + f (x2 )∆x + . . . + f (xn )∆x
n→∞
i=1
A = lim
n→∞
n
X
f (xi )∆x
n
X
f (xi−1 )∆x
n
X
f (x∗i )∆x
i=1
i=1
i=1
olarak yazılabilir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
25/ 180
Belirli İntegral
MAT 1009 Matematik I
26/ 180
Belirli İntegral
NOT 1 :
Belirli İntegralin Tanımı f fonksiyonu a ≤ x ≤ b aralığında
tanımlı ve sürekli olsun, [a, b] kapalı aralığını ∆x = (b − a)/n eşit
uzunluğunda n alt aralığa ayıralım. Alt aralıkların uç noktaları
x0 (= a), x1 , x2 , . . . , xn (= b) olsun ve her alt aralıktan, x∗i noktası
[xi−1 , xi ] de olacak şekilde x∗1 , x∗2 , x∗3 , . . . , x∗n , örnek noktalarını
seçelim.
f (x)dx = lim
n→∞
a
n
X
f (x)dx gösteriminde f (x), integrali alınan
Zb
f (x)dx belirli integrali bir sayıdır; x değişkenine
a
fonksiyon, a, b integralin sınırları; a alt sınır, b üst sınır olarak
adlandırılır. İntegrali hesaplama sürecine de integral almak denir.
NOT 2 :
Bu durumda, a dan b ye f nin belirli integrali
Zb
Zb
a
bağlı değildir.
Aslında x yerine istediğimiz harfi koyabiliriz, integralin değeri
değişmez:
Zb
Zb
Zb
f (x)dx = f (t)dt = f (r)dr
f (x∗i )∆x
i=1
olarak tanımlanır.
a
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
27/ 180
a
Öğr.Gör.Dr.Meltem Altunkaynak
a
MAT 1009 Matematik I
28/ 180
Belirli İntegral
Belirli İntegral
NOT 4 :
NOT 3 : Karşılaştığımız fonksiyonların çoğunun sürekli olmasına
karşın, tanımdaki limit, f nin sonlu sayıda giderilebilir ya da
sıçrama tipi süreksizliği olduğunda da vardır. Dolayısıyla, bu tip
fonksiyonların da belirli integralini tanımlayabiliriz.
Tanımda karşılaştığımız
n
X
f (x∗i )∆x
i=1
toplamına Riemann toplamı denir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
29/ 180
Belirli İntegral
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
30/ 180
Belirli İntegral
Eğer f pozitifse, Riemann toplamını, yaklaştırım dikdörtgenlerinin
toplam alanı olarak yorumlayabileceğimizi biliyoruz (Bkz. Şekil 11).
Buradaki tanım ile alan tanımını karşılaştırırsak,
Zb
f (x)dx belirli
a
integralinin a dan b ye kadar, y = f (x) eğrisinin altında kalan alan
olduğunu görürüz. (Bkz. Şekil 12)
Şekil 11:
Şekil 12:
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
31/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
32/ 180
Belirli İntegral
Belirli İntegral
Bu tip Riemann toplamlarının limiti, 14 de gösterilen durumu
ortaya çıkarır. Belirli integral, alanların farkı olan net alan olarak
yorumlanabilir:
Z b
f (x)dx = A1 − A2
Eğer f , Şekil 13 teki gibi hem pozitif hem de negatif değerler
alıyorsa, Riemann toplamı x-ekseninin üstünde kalan
dikdörtgenlerin toplam alanı ile, x-ekseni altında kalan
dikdörtgenlerinin toplam alanının farkıdır.
a
Burada A1 , x-ekseninin üstünde ve f nin grafiğinin altında kalan,
A2 ise x-ekseninin altında ve f nin grafiğinin üstünde kalan alını
gösterir.
Şekil 13:
Şekil 14:
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Belirli İntegrallerin Özellikleri
1. c bir sabit sayı olmak üzere
Zb
a
2.
Za
f (x)dx = −
Za
f (x)dx = 0
b
3.
Zb
4.
a
MAT 1009 Matematik I
c dx = c(b − a)
5. c bir sabit olmak üzere
Zb
cf (x)dx = c
a
6.
Zb
a
7.
[f (x) + g(x)]dx =
f (x)dx +
a
Öğr.Gör.Dr.Meltem Altunkaynak
Zb
Zc
a
[f (x) − g(x)]dx =
f (x)dx +
Zb
c
Zb
a
f (x)dx −
f (x)dx =
Zb
f (x)dx
a
a
f (x)dx
Zb
34/ 180
Belirli İntegrallerin Özellikleri
a
Zb
Öğr.Gör.Dr.Meltem Altunkaynak
33/ 180
Zb
Zb
g(x)dx
a
f (x)dx
a
g(x)dx
a
MAT 1009 Matematik I
35/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
36/ 180
İntegralleri Karşılaştırma Özellikleri
8. a ≤ x ≤ b iken f (x) ≥ 0 ise
Zb
a
9. a ≤ x ≤ b iken f (x) ≥ g(x) ise
Örnek
f (x)dx ≥ 0 dır.
Zb
a
f (x)dx ≥
Zb
g(x)dx dır.
Örnek :
a
m(b − a) ≤
a
2
e−x dx integraline alt ve üst
0
sınır bulunuz.
10. a ≤ x ≤ b iken m ≤ f (x) ≤ M ise
Zb
Özellik 10 u kullanarak
Z1
f (x)dx ≤ M (b − a)
dır.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
37/ 180
Örnek...
MAT 1009 Matematik I
38/ 180
Örnek...
2
Çözüm : f (x) = e−x fonksiyonu [0, 1] aralığında azalan bir
fonksiyon olduğundan, mutlak maksimum değeri M = f (0) = 1,
mutlak minimum değeri ise m = f (1) = e−1 dir. Özellik 10 dan
e
−1
(1 − 0) ≤
Z1
0
e−1 ≈ 0.3679 olduğundan
2
e−x dx ≤ 1(1 − 0)
0.367 ≤
ya da
e−1 ≤
Z1
0
Z1
0
2
e−x dx ≤ 1
yazabiliriz. Bu örneğin sonucu Şekil ?? de gösterilmiştir.
e
−x2
dx ≤ 1
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
39/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
40/ 180
Belirli İntegrallerin Hesaplanması
Belirli İntegrallerin Hesaplanması
Değer Bulma Teoremi
Örneğin, f (x) = x2 nin bir ilkelinin F (x) = 13 x3 olduğunu
biliyoruz. Değer Bulma Teoremi bize
f fonksiyonu [a, b] aralığında sürekliyse, f fonksiyonunun herhangi
bir F ilkeli, başka bir deyişle F ′ = f için
Zb
a
f (x)dx = F (b) − F (a)
Öğr.Gör.Dr.Meltem Altunkaynak
Z1
0
dir.
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
41/ 180
a
Örnek :
= F (b) − F (a)
f (x)dx = F (x)
a
Z3
ex dx integralini hesaplayınız.
Çözüm: f (x) = ex fonksiyonunun bir ilkeli F (x) = ex
olduğundan Değer Bulma Teoremi’ni kullanarak
ib
Z3
a
MAT 1009 Matematik I
ex dx = ex
1
b
h
ib
yazılabilir. Sıkça kullanılan diğer gösterimler F (x) ve F (x)
a
a
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
42/ 180
1
gösterimini kullanarak F ′ = f olmak üzere
Zb
MAT 1009 Matematik I
Örnek
Değer Bulma Teoremi’ni uygularken
F (x)
1 3 1 3 1
·1 − ·0 =
3
3
3
olduğunu söyler.
Belirli İntegrallerin Hesaplanması
ib
x2 dx = F (1) − F (0) =
i3
1
= e3 − e
elde ederiz.
43/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
44/ 180
Örnek
Örnek...
Özel olarak b = π/2 alırsak, 0 dan π/2 ye kadar kosinüs eğrisinin
altında kalan alanın, sin(π/2) = 1 olduğunu kanıtlamış oluruz.
Örnek : 0 ≤ b ≤ π/2 olmak üzere x = 0 dan x = b ye kadar
kosinüs eğrisinin altında kalan alanı bulunuz.
Çözüm: f (x) = cos x fonksiyonunun bir ilkeli F (x) = sin x
olduğundan
A=
Zb
cos x dx = sin x
0
ib
0
= sin b − sin 0 = sin b
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Belirsiz İntegraller
f (x)dx = F (x),
46/ 180
Belirli ve belirsiz integralin arasındaki ayrıma dikkat etmelisiniz.
Zb
Z
f (x)dx belirli integrali bir sayı,
f (x)dx belirsiz integrali ise
f (x)dx gösterimi kullanılır. Dolayısıyla,
Z
MAT 1009 Matematik I
Belirsiz İntegraller
İlkeller ile integraller arasındaki ilişkiden dolayı f nin ilkelini
göstermek için
Z geleneksel olarak belirsiz integral olarak
adlandırılan
Öğr.Gör.Dr.Meltem Altunkaynak
45/ 180
a
F ′ (x) = f (x)
bir fonksiyondur.
anlamına gelir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
47/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
48/ 180
Belirsiz İntegraller
Belirsiz İntegraller Tablosu
Z
f fonksiyonunun I aralığındaki bir ilkeli F ise f nin bu aralıktaki en
genel ilkelinin, C herhangi bir sabit olmak üzere F (x) + C şeklinde
olduğunu anımsayınız.
Örneğin,
Z
[f (x) + g(x)]dx =
Z
1
dx = ln |x| + C
x
1
d
ln |x| =
dx
x
gösterimi f nin herhangi bir ilkelini ya da (her C için bir tane
olmak üzere), bütün ilkeller ailesini de gösterebilir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
49/ 180
Belirsiz İntegraller Tablosu
Z
ax dx =
xn dx =
f (x)dx +
Z
g(x)dx
f (x)dx
xn+1
+C
n+1
Z
1
dx = ln |x| + C
x
Z
ex dx = ex + C
Öğr.Gör.Dr.Meltem Altunkaynak
Z
(n 6= 1)
MAT 1009 Matematik I
50/ 180
Belirsiz İntegraller Tablosu
ax
+C
ln a
Z
sin xdx = cos x + C
Z
cos xdx = sin x + C
Z
sec2 xdx = tan x + C
Z
csc2 xdx = − cot x + C
Öğr.Gör.Dr.Meltem Altunkaynak
cf (x)dx = c
Z
formülü (0 içermeyen her aralıkta) doğrudur, çünkü
Z
MAT 1009 Matematik I
Z
sec x tan xdx = sec x + C
Z
csc x cot xdx = − csc x + C
Z
Z
51/ 180
√
x2
1
dx = tan−1 x + C
+1
1
dx = sin−1 x + C
1 − x2
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
52/ 180
Örnek
Örnek
Örnek :
Örnek : Gösterim konusundaki uzlaşmamızı ve belirsiz
integraller tablosunu kullanarak
Z
Z
Z
4
2
4
(10x − 2 sec x)dx = 10 x dx − 2 sec2 xdx
= 10
Z3
0
Değer Bulma Teoremi’nden
Çözüm :
Z3
x5
− 2 tan x + C
5
0
(x3 − 6x)dx integralini hesaplayınız.
3
(x − 6x)dx =
x2
x4
−6
4
2
3
0
1
1
= ( · 34 − 3 · 32 ) − ( · 04 − 3 · 02 )
4
4
= 2x5 − 2 tan x + C
elde ederiz. Yanıtın türevini alarak doğruluğunu kontrol etmelisiniz.
=
81
− 27 − 0 + 0 = −6.75
4
elde ederiz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Örnek
MAT 1009 Matematik I
54/ 180
Örnek
Z2 Örnek :
0
3
2x − 6x + 2
x +1
3
Değer Bulma Teoremi’nden
Z2 3
2x − 6x + 2
x +1
3
Çözüm : Önce integrali alınan fonksiyonu bölme yaparak
sadeleştirmemiz gerekir:
Z9
1
dir. Bu, integralin kesin değeridir.
MAT 1009 Matematik I
√
2t2 + t2 t − 1
dt integralini hesaplayınız.
t2
1
2
x4
x2
−1
dx = 2 − 6 + 3 tan x
4
2
0
2
1 4
x − 3x2 + 3 tan−1 x
=
2
0
1 4
(2 ) − 3(22 ) + 3 tan−1 2 − 0
=
2
= −4 + 3 tan−1 2
Öğr.Gör.Dr.Meltem Altunkaynak
Z9
Örnek :
dx integralini bulunuz.
Çözüm:
0
Öğr.Gör.Dr.Meltem Altunkaynak
53/ 180
55/ 180
√
Z9
2t2 + t2 t − 1
(2 + t1/2 − t−2 )dt
dt =
t2
1
t3/2 t−1 9
= 2t + 3 −
−1 1
2
2 3/2 1 9
= 2t + t +
3
t 1
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
56/ 180
Örnek...
Z9
1
Yerine Koyma Kuralı
√
2
2
1
2
1
2t2 + t t − 1
dt = [2 · 9 + (9)3/2 + ] − (2 · 1 + · 13/2 + )
2
t
3
9
3
1
= 18 + 18 +
Öğr.Gör.Dr.Meltem Altunkaynak
2
4
1
− 2 − − 1 = 32
9
3
9
MAT 1009 Matematik I
olur.
57/ 180
Örnek
Örnek :
u = g(x) değer kümesi I aralığı olan türevlenebilir bir fonksiyon ve
f fonksiyonu I aralığında sürekliyse,
Z
Z
f (g(x)) g ′ (x) dx = f (u) du
(4)
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
58/ 180
Yerine Koyma Kuralı
Z
x3 cos(x4 + 2) dx integralini bulunuz.
Çözüm : du = 4x3 dx diferansiyeli, 4 çarpanı dışında, integralin
içinde yer aldığından, u = x4 + 2 değişken değişikliğini yaparız. Bu
yüzden, x3 dx = du/4 ve Yerine Koyma Kuralı’ndan
Z
Z
Z
1
1
3
4
cos u du
x cos(x + 2) dx = cos u · du =
4
4
=
1
sin u + C
4
=
1
sin(x4 + 2) + C
4
Yerine Koyma Kuralının temel fikri, karmaşık bir integrali daha
basit bir hale dönüştürmektir. Bu başlangıçtaki x değişkeninden, x
e bağlı bir fonksiyon olan u ya geçilerek yapılır.
olur. Son aşamada başlangıçtaki x değişkenine dönmemiz
gerektiğine dikkat ediniz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
59/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
60/ 180
Örnek
Örnek :
Örnek...
Z
√
2x + 1dx integralini hesaplayınız.
√
Çözüm 2: Olası bir başka değişken değişikliği de u = 2x + 1 dir.
dx
Bu durumda du = √
bundan dolayı
2x + 1
√
dx = 2x + 1 du = u du olur. (Ya da u2 = 2x + 1, ve bundan
dolayı 2u du = 2 dx olduğunu gözlemleyiniz.) Böylece
Z
Z
Z
√
2x + 1 dx = u · u du = u2 du
Çözüm 1: Bu durumda u = 2x + 1 olsun. du = 2dx, ve
dx = du/2 olur. Dolayısıyla, Yerine Koyma Kuralı
Z
Z
Z
√
√ du
1
2x + 1 dx =
u
=
u1/2 du
2
2
=
1
1 u3/2
·
+ C = u3/2 + C
2 3/2
3
=
1
= (2x + 1)3/2 + C
3
u3
1
+ C = (2x + 1)3/2 + C
3
3
elde edilir.
verir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Örnek
Örnek:
MAT 1009 Matematik I
62/ 180
Örnek
Z
√
x
dx integralini bulunuz.
1 − 4x2
Örnek :
Çözüm: u = 1 − 4x2 olsun. Dolayısıyla du = −8x dx buradan
x dx = − 81 du olur ve
Z
Z
Z
1
1
1
x
√
√ du = −
dx = −
u−1/2 du
8
8
u
1 − 4x2
=−
bulunur.
Öğr.Gör.Dr.Meltem Altunkaynak
61/ 180
MAT 1009 Matematik I
e5x dx integralini hesaplayınız.
Çözüm : u = 5x alırsak, du = 5 dx, buradan dx = 51 du olur.
Bundan dolayı
Z
Z
1
1
1
eu du = eu + C = e5x + C
e5x dx =
5
5
5
1p
1 √ 2 u +C =−
1 − 4x2 + C
8
4
Öğr.Gör.Dr.Meltem Altunkaynak
Z
dir.
63/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
64/ 180
Örnek
Örnek :
Örnek...
Z
tan x dx integralini hesaplayınız.
Çözüm : Önce tanjantı, sinüs ve cosinüs cinsinden yazalım:
Z
Z
sin x
dx
tan x dx =
cos x
− ln | cos x| = ln | cos x|−1 = ln (1/| cos x|) = ln | sec x|
olduğundan, sonuç
Z
tan x dx = ln | sec x| + C
Bu, du = − sin x dx ve buradan sin x dx = −du olduğundan
u = cos x seçmemiz gerektiğini gösterir:
Z
Z
Z
1
sin x
dx = −
du
tan x dx =
cos x
u
biçiminde de yazılabilir.
= − ln |u| + C = − ln | cos x| + C
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
65/ 180
MAT 1009 Matematik I
66/ 180
Örnek
Belirli İntegraller İçin Yerine Koyma Kuralı
Örnek : 5 i kullanarak
Z4
√
2x + 1 dx integralini hesaplayınız.
0
g ′ fonksiyonu [a, b] aralığında, f fonksiyonu u = g(x) in değer
kümesinde sürekliyse,
Zb
a
Zg(b)
f (u) du
f (g(x))g (x) dx =
′
Çözüm : u = 2x + 1 ise dx = du/2 olur. İntegralin yeni sınırlarını
belirlemek için
x = 0, ⇒ u = 2 · 0 + 1 = 1
(5)
ve
x = 4, ⇒ u = 2 · 4 + 1 = 9
olduğuna dikkat edelim. Dolayısıyla
g(a)
√
olur.
2x + 1 dx =
Z9
1
1√
1 2
u du = · u3/2
2
2 3
9
1
1
26
= (93/2 − 13/2 ) =
3
3
olur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
67/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
68/ 180
Örnek...
Örnek
Örnek :
Z2
1
dx
integralini hesaplayınız.
(3 − 5x)2
Çözüm : u = 3 − 5x olsun. du = −5dx buradan da dx = −du/5
olur. x = 1 iken u = −2, x = 2 iken u = −7 dir. Böylece
5 i kullandığımızda, integrali aldıktan sonra x değişkenine
dönmediğimizi gözlemleyelim. Diğer bir deyişle u cinsinden bir
ifadeyi u nun uygun değerleri arasında hesaplıyoruz.
Z2
1
dx
(3 − 5x)2
1
=−
5
Z−7
du
u2
−2
1 −7
1 −7
1
=
=− −
5
u −2
5u −2
1
=
5
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Örnek
Örnek :
Öğr.Gör.Dr.Meltem Altunkaynak
69/ 180
1 1
− +
7 2
=
1
14
MAT 1009 Matematik I
70/ 180
Simetrik Fonksiyonların İntegralleri
Ze
ln x
dx integralini bulunuz.
x
f fonksiyonunun [−a, a] aralığında sürekli olduğunu varsayalım.
Za
Za
(a) f çift fonksiyonsa [f (−x) = f (x)],
f (x) dx = 2 f (x) dx
1
Çözüm : du = dx/x integralde göründüğünden u = ln x alırız.
x = 1 iken u = ln 1 = 0; x = e iken u = ln e = 1 dir. Buradan
Ze
1
ln x
dx =
x
Z1
0
Öğr.Gör.Dr.Meltem Altunkaynak
u du =
2 1
u
2
0
=
(b) f tek fonksiyonsa [f (−x) = −f (x)],
1
2
MAT 1009 Matematik I
0
−a
dir.
Za
f (x) dx = 0 dır.
−a
71/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
72/ 180
Örnek
Örnek
Örnek : f (x) = x6 + 1 fonksiyonu, f (−x) = f (x) eşitliğini
sağladığından çifttir, dolayısıyla
Z2
6
(x + 1) dx = 2
Z2
Örnek : f (x) =
eşitliğini sağladığından tektir, dolayısıyla
6
(x + 1) dx
Z1
0
−2
tan x
fonksiyonu, f (−x) = −f (x),
1 + x2 + x4
1
= 2 x7 + x
7
2
=
0
128
+2
7
=
284
7
tan x
dx = 0
1 + x2 + x4
−1
olur.
olur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
73/ 180
Örnek :
f (x)g ′ (x) dx = f (x)g(x) −
Z
g(x)f ′ (x) dx
(6)
Anımsanması daha kolay gösterim için u = f (x), v = g(x) olsun.
Diferansiyelleri dv = g ′ (x)dx ve du = f ′ (x)dx dir, dolayısıyla
Yerine Koyma Kuralı’na göre kısmi integral alma formülü
Z
Z
udv = uv − vdu
(7)
MAT 1009 Matematik I
Z
x sin x dx integralini bulunuz.
Çözüm : u = x, dv = sin xdx ise du = dx, v = − cos x olur,
dolayısıyla
Z
Z
x sin x dx = x(− cos x) − (− cos x) dx
formülü kısmi integral formülü olarak adlandırılır.
Öğr.Gör.Dr.Meltem Altunkaynak
74/ 180
Örnek
Kısmi İntegral Alma
Z
MAT 1009 Matematik I
= −x cos x +
Z
cos x dx
= −x cos x + sin x + C olur.
75/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
76/ 180
Örnek
Örnek :
Örnek
Z
ln x dx integralini hesaplayınız.
Örnek :
1
Çözüm : Burada u = ln x, dv = dx ise du = dx, v = x dir.
x
Kısmi integral alarak,
Z
Z
dx
ln x dx = x ln x − x
x
Z
= x ln x − dx
Z
x2 ex dx integralini bulunuz.
Çözüm : x2 nin türevi alındığında basitleştiğine dikkat ediniz. Bu
yüzden u = x2 , dv = ex dx seçeriz. Buradan du = 2xdx, v = ex
olur. Kısmi integral alma yöntemi,
Z
Z
2 x
2 x
x e dx = x e − 2 xex dx
verir.
= x ln x − x + C elde ederiz.
Bu örnekte f (x) = ln x türevi f den daha basit olduğundan kısmi
integral alma etkili olmuştur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
77/ 180
Örnek...
MAT 1009 Matematik I
78/ 180
Örnek
R
Elde ettiğimiz xex dx integrali, başlangıçtaki integralden daha
basittir ama hala apaçık ortada değildir. Bunun için
u = x, dv = ex dx alarak kısmi integrali bir kez daha kullanırız.
du = dx, v = ex olduğundan
Z
Z
x
x
xe dx = xe − ex dx = xex − ex + C
dir. Bunu yukarıdaki denklemde yerine koyarak,
Z
Z
2 x
2 x
x e dx = x e −2 xex dx = x2 ex −2xex +2ex +C1
Örnek :
(C1 = −2C)
Z
ex sin x dx integralini hesaplayınız.
Çözüm : Türevi alınınca ne ex ne de sin x fonksiyonu basitleşir.
u = ex , dv = sin x dx seçelim. O zaman, du = ex dx ve
v = − cos x polur, dolayısıyla, kısmi integral
Z
Z
x
x
e sin x dx = −e cos x dx + ex cos x dx
(8)
verir.
elde ederiz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
79/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
80/ 180
Örnek...
Örnek...
R
Elde ettiğimiz ex cos x dx integrali için tekrardan kısmi integrali
uygulayalım. Bu kez, u = ex ve dv = cos x dx alalım. Buradan
du = ex dx ve v = sin x olur ve
Z
Z
ex cos x dx = e′ x sin x − ex sin x dx
(9)
İki yana
R
ex sin x dx eklersek
Z
2 ex sin x dx = −ex cos x + ex sin x
elde ederiz. Denklemi sadeleştirip, integral sabitini eklersek
Z
1
ex sin x dx = ex (sin x + cos x) + C
2
dir. Denklem 9 i denklem 8 te yerine koyarsak
Z
Z
x
x
x
e sin x dx = −e cos x + e sin x + ex sin x dx
buluruz.
elde ederiz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
81/ 180
MAT 1009 Matematik I
82/ 180
Örnek
Kısmi integrasyon ve Değer bulma teoremi
Örnek :
Z1
tan−1 x dx integralini hesaplayınız.
0
Kısmi integral formülünü, Değer Bulma Teoremi’yle birleştirirsek,
belirli integralleri, kısmi integrallerle hesaplayabiliriz. f’ ve g’ nün
sürekli olduğunu varsayarak ve Değer Bulma Teoremi’ni kullanarak,
a dan b ye kadar denklem 6 in her iki yanını da hesapladığımızda
Zb
f (x)g ′ (x) dx = f (x)g(x)
a
ib
a
−
Zb
g(x)f ′ (x) dx
Çözüm : u = tan−1 x, dv = dx ise du =
Denklem 10
Z1
i1 Z1
−1
−1
tan x dx = x tan x −
0
(10)
x
dx
1 + x2
0
0
a
= 1 · tan
elde ederiz.
dx
, v = x olur.
1 + x2
=
π
−
4
−1
Z1
1 − 0 · tan
−1
0−
Z1
x
dx
1 + x2
0
x
dx
1 + x2
0
verir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
83/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
84/ 180
Örnek...
Trigonometrik İntegraller
Bu integrali hesaplamak için, t = 1 + x2 değişken değişikliğini
yapalım. Bu durumda, dt = 2x dx, dolayısıyla x dx = dt/2 olur.
x = 0 iken t = 1; x = 1 iken t = 2 olduğundan,
Z1
x
1
dx =
1 + x2
2
0
Z2
1
1
dt
= ln |t|
2
2
Trigonometrik integraller, altı temel trigonometrik fonksiyonun
cebirsel kombinasyonunu içeren integrallerdir.
2
Örneğin,
1
Z
1
1
= (ln 2 − ln 1) = ln 2
2
2
tan−1 x dx =
0
2
3
cos x sin x dx,
Z
tan4 x dx
Genel fikir, bulmak istediğimiz karmaşık trigonometrik integralleri,
trigonometrik özdeşlikler kullanarak daha kolay çözümlenebilen
integrallere dönüştürebilmektir.
dir. Dolayısıyla
Z1
sec x dx,
Z
π ln 2
−
4
2
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
85/ 180
Sinüs ve Kosinüs Çarpımları
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
86/ 180
Sinüs ve Kosinüs Çarpımları : Durum 1
m tek ise , m yi 2k + 1 olarak yazar ve
m ve n negatif olmayan tamsayılar olmak üzere
Z
sinm x cosn x dx
sinm x = sin2k+1 x = (sin2 x)k sin x = (1 − cos2 x)k sin x
eşitliğini kulanırız.
formundaki integraller.
Öğr.Gör.Dr.Meltem Altunkaynak
Sonra tek kalan sin x i integraldeki dx ile birleştirerek sin x dx
yerine −d(cos x) yazarız.
MAT 1009 Matematik I
87/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
88/ 180
Örnek
Örnek :
Sinüs ve Kosinüs Çarpımları : Durum 2
R
sin3 x cos2 x dx integralini hesaplayınız.
Çözüm :
Z
Z
3
2
sin x cos x dx =
sin2 x cos2 x sin x dx
Z
=
(1 − cos2 x) cos2 x [−d(cos x)]
Z
(1 − u2 )(u2 )(−du)
=
Z
=
(u4 − u2 ) du
=
=
m çift ve n tek ise, n yi 2k + 1 olarak yazar ve
cosn x = cos2k+1 x = (cos2 x)k cos x = (1 − sin2 x)k cos x
eşitliğini kullanırız. Sonra tek kalan cos x i integraldeki dx ile
birleştirerek cos x dx yerine d(sin x) yazarız.
u5 u3
−
+C
5
3
cos5 x cos3 x
−
+C
5
3
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
89/ 180
Örnek
Örnek :
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
90/ 180
Sinüs ve Kosinüs Çarpımları : Durum 3
R
Çözüm :
Z
cos5 x dx integralini hesaplayınız.
cos5 x dx =
=
=
=
Z
Z
Z
Z
cos4 x cos x dx
2
m ve n çift ise
2
(1 − sin x) d(sin x)
sin2 x =
(1 − u2 )2 du
1 − cos 2x
,
2
cos2 x =
1 + cos 2x
2
trigonometrik özdeşliklerini kullanırız.
(1 − 2u2 + u4 ) du
2
1
= u − u3 + u5 + C
3
5
1
2
= sin x − sin3 x + sin5 x + C
3
5
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
91/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
92/ 180
Örnek
Örnek...
Örnek :
Çözüm :
Z
2
R
sin2 x cos4 x dx integralini hesaplayınız.
4
sin x cos x dx =
=
=
=
Z 1 − cos 2x
2
1 + cos 2x
2
2
dx
1
(1 − cos 2x)(1 + 2 cos 2x + cos2 2x) dx
8
Z
1
(1 + cos 2x − cos2 2x − cos3 2x) dx
8
1
1
x + C1 + sin 2x + C2
8
2
Z
2
3
− (cos 2x + cos 2x) dx
Z
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
cos2 2x terimini içeren integrali şu şekilde çözümleriz:
Z
Z
1
2
cos 2x dx =
(1 + cos 4x) dx
2
1
1
=
x + sin 4x + C3
2
4
Öğr.Gör.Dr.Meltem Altunkaynak
93/ 180
Örnek...
MAT 1009 Matematik I
94/ 180
Örnek...
Çözümlediğimiz bu integralleri kullanarak
Z
1
1
2
4
x + C1 + sin 2x + C2
sin x cos x dx =
8
2
Z
2
3
− (cos 2x + cos 2x) dx
cos3 2x terimini içeren integrali ise şu şekilde çözümleriz:
Z
Z
3
cos 2x dx =
(1 − sin2 2x) cos 2x dx
Z
1
=
(1 − u2 ) du
2
1
1
3
sin 2x − sin 2x + C4
=
2
3
=
1
1
1
1
x + C1 + sin 2x + C2 −
x + sin 4x
8
2
2
4
i
1
1
sin 2x − sin3 2x − C4
−C3 −
2
3
1
=
16
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
95/ 180
1
1
3
x − sin 4x + sin 2x + C
4
3
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
96/ 180
Örnek...
Kareköklerden Kurtulmak
Örnek :
π/4
R √
Böylelikle
1 + cos 4x dx integralini hesaplayınız.
Z
0
Çözüm : Karekökten kurtulmak için
cos2 θ =
1 + cos 2θ
2
π/4 √
1 + cos 4x dx =
0
=
veya 1 + cos 2θ = 2 cos2 θ
=
özdeşliğini kullanırız.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
=
0
√ Z
2
√
Z
π/4
0
| cos 2x| dx =
sin 2x
2
2
π/4
0
√
π/4 √
√
2 cos2 2x dx
0
√ Z
2
π/4
cos 2x dx
0
√
2
2
=
(1 − 0) =
2
2
MAT 1009 Matematik I
98/ 180
R
tan4 x dx integralini hesaplayınız.
Çözüm :
Z
Z
Z
4
2
2
tan x dx =
tan x · tan x dx = tan2 x · (sec2 x − 1) dx
Z
Z
2
2
=
tan x sec x dx − tan2 x dx
Z
Z
2
2
=
tan x sec x dx − (sec2 x − 1) dx
Z
Z
Z
2
2
2
=
tan x sec x dx − sec x dx +
dx
tan x, sec x ve karelerinin integrallerini ve
tan2 x = sec2 x − 1
sec2 x = 1 + tan2 x
özdeşliklerini kullanarak tanjant ve sekant fonksiyonlarının
kuvvetlerini içeren integralleri hesaplayabiliriz.
MAT 1009 Matematik I
2 cos2 2x dx
Örnek
Örnek :
Öğr.Gör.Dr.Meltem Altunkaynak
π/4 √
Öğr.Gör.Dr.Meltem Altunkaynak
97/ 180
tan x ve sec x Kuvvetlerinin İntegralleri
Z
99/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
100/ 180
Örnek
Sinüs ve Kosinüslerin Çarpımları
ilk integralde u = tan x dönüşümünü yaparak, ikinci ve üçüncü
integralde ise bildiğimiz integralleri kullanarak
Z
1
tan4 x dx = tan3 x − tan x + x + C
3
Uygulamada karşılaştığımız
Z
sin mx sin nx dx,
Z
sin mx cos nx dx,
Z
cos mx cos nx dx
sonucunu elde ederiz.
trigonometrik integrallerini hesaplamak için
=
Z
tan2 x sec2 x dx −
Öğr.Gör.Dr.Meltem Altunkaynak
Z
sec2 x dx +
Z
dx
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
101/ 180
Örnek :
şu özdeşikleri kullanırız:
1
sin mx cos nx = [sin(m − n)x + sin(m + n)x]
2
1
cos mx cos nx = [cos(m − n)x + cos(m + n)x]
2
102/ 180
Örnek
Sinüs ve Kosinüslerin Çarpımları
1
sin mx sin nx = [cos(m − n)x − cos(m + n)x]
2
MAT 1009 Matematik I
R
sin 3x cos 5x dx integralini hesaplayınız.
Çözüm : m = 3 ve n = 5 ile (12) eşitliğinden
Z
Z
1
[sin(−2x) + sin 8x] dx
sin 3x cos 5x dx =
2
Z
1
(sin 8x − sin 2x) dx
=
2
cos 8x cos 2x
= −
+
+C
16
4
(11)
(12)
(13)
elde edilir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
103/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
104/ 180
Trigonometrik Dönüşümler
Trigonometrik Dönüşümler - Durum 1
√
a bir reel sayı olmak üzere
p
a2 + x2
p
x2 − a2
p
a2 − x2
x = a tan θ
dönüşümü kullanılır. Böylelikle
a2 + x2
ifadelerini içeren integralleri hesaplamak için trigonometrik
dönüşümler kullanırız.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
a2 + x2 ifadesinin olduğu integrallerde
ve
dx
ifadeleri
105/ 180
Trigonometrik Dönüşümler - Durum 1
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
106/ 180
Trigonometrik Dönüşümler - Durum 1
x = a tan θ dönüşümünde ilk değişken θ ya geri dönüş yapabilmek
için, x = a tan θ dönüşümünün tersinir olmasını bekleriz.
sırasıyla
a2 + x2 = a2 + a2 tan2 θ = a2 (1 + tan2 θ) = a2 sec2 θ
Dolayısıyla tan−1 fonksiyonunun tanımlı olmasını kullanarak,
x
π
π
θ = tan−1
,
− <θ<
a
2
2
ve
dx = a sec2 θ dθ
ifadelerine dönüşür.
Öğr.Gör.Dr.Meltem Altunkaynak
ters dönüşümünü yaparız.
MAT 1009 Matematik I
107/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
108/ 180
Örnek
Örnek :
Örnek...
Z
ifadelerini kullanarak
Z
Z
dx
√
=
4 + x2
Z
=
Z
=
dx
√
integralini hesaplayınız.
4 + x2
Çözüm : x = 2 tan θ dönüşümünü yaparız. Böylelikle
4 + x2 = 4 + 4 tan2 θ = 4(1 + tan2 θ) = 4 sec2 θ
dx = 2 sec2 θ dθ
elde ederiz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
√
ve
| sec θ| = sec θ
olur)
= ln | sec θ + tan θ| + C
√
4 + x2 x + +C
= ln 2
2
MAT 1009 Matematik I
110/ 180
x2 − a2 = a2 sec2 θ − a2 = a2 (sec2 θ − 1) = a2 tan2 θ
trigonometrik dönüşümünü kullanırız. Böylece
x −a
π
π
< θ < olduğu için
2
2
sırasıyla
x = a sec θ
2
(−
Trigonometrik Dönüşümler - Durum 2
x2 − a2 ifadesini içeren integralleri hesaplamada
2
sec θ dθ
Öğr.Gör.Dr.Meltem Altunkaynak
109/ 180
Trigonometrik Dönüşümler - Durum 2
2 sec2 θ dθ
√
4 sec2 θ
sec2 θ dθ
| sec θ|
dx = a sec θ tan θ dθ
dx
ifadelerine dönüşür.
ifadeleri
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
111/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
112/ 180
Örnek
Trigonometrik Dönüşümler - Durum 2
2
Örnek : x > iken
5
İntegrali almaya başladığımız ilk değişken θ ya geri dönüş
yapabilmek için dönüşümümüzün tersinir olmasını bekleriz.
Z
√
dx
integralini hesaplayınız.
25x2 − 4
Çözüm : Öncelikle paydadaki ifadeyi daha açık yazalım:
s
s 2
p
4
2
2
2
2
=5 x −
25x − 4 = 25 x −
25
5
Dolayısıyla sec−1 fonksiyonunun tanımından, x = a sec θ
dönüşümünün ters dönüşümü

 0 ≤ θ < π , x ≥ 1;
x
a
2
,
θ = sec−1
π
x

a
< θ ≤ π, a ≤ −1.
2
x>
2
olduğu için dönüşümü
5
x=
olur.
2
sec θ,
5
dx =
2
sec θ tan θ dθ,
5
0<θ<
π
2
olarak yaparız.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
113/ 180
MAT 1009 Matematik I
114/ 180
Örnek...
Bu dönüşümleri integralde yerine koyarak
Z
Z
Z
dx
dx
(2/5) sec θ tan θ dθ
√
p
=
=
2
2
5(2/5) tan θ
25x − 4
5 x − (4/25)
Z
1
1
=
sec θ dθ = ln | sec θ + tan θ| + C
5
5
√
1 5x
25x2 − 4 ln +
=
+C
5 2
2
Böylelikle
2
4
4
4
4
2
=
sec2 θ −
= (sec2 θ − 1) =
tan2 θ
x −
5
25
25
25
25
2
ve 0 < θ <
π
2
için tan θ > 0 olduğundan
s
x2
2
2
2
2
= | tan θ| = tan θ
−
5
5
5
elde ederiz.
bulunur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
115/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
116/ 180
Trigonometrik Dönüşümler - Durum 3
√
Trigonometrik Dönüşümler - Durum 3
a2 − x2 ifadesini içeren integralleri çözmek için
sırasıyla
x = a sin θ
a2 − x2 = a2 − a2 sin2 θ = a2 (1 − sin2 θ) = a2 cos2 θ
trigonometrik dönüşümünü kullanırız. Böylece
a2 − x2
ve
dx = a cos θ dθ
dx
ifadelerine dönüşür.
ifadeleri
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
117/ 180
MAT 1009 Matematik I
118/ 180
Örnek
Trigonometrik Dönüşümler - Durum 3
Örnek :
İntegrali hesaplamayı sonuçlandırmak için orjinal değişken x e geri
dönmemiz gerekir. Bunun için x = a sin θ dönüşümünün tersinir
olmasını bekleriz. sin−1 fonksiyonun tanımından, ters dönüşüm
x
−π
π
,
≤θ≤
θ = sin−1
a
2
2
Z
x2 dx
√
integralini hesaplayınız.
9 − x2
Çözüm :
x = 3 sin θ,
dx = 3 cos θ dθ,
−
π
π
<θ<
2
2
9 − x2 = 9 − 9 sin2 θ = 9(1 − sin2 θ) = 9 cos2 θ
olur.
dönüşümü ile
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
119/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
120/ 180
Örnek...
Örnek...
Z
x2 dx
√
9 − x2
9 sin2 θ · 3 cos θ dθ
|3 cos θ|
Z
=
= 9
Z
=
=
sin2 θ dθ
1 − cos 2θ
dθ
2
sin 2θ
9
θ−
+C
2
2
= 9
=
Z
=
=
elde edilir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
+C
9
(θ − sin θ cos θ) + C
2
!
#
√
2
x
x
9
9
−
x
sin−1 − ·
+C
2
3
3
3
9
x xp
sin−1 −
9 − x2 + C
2
3
2
MAT 1009 Matematik I
cos x = 2 cos2
x
1
x
= sec2 =
1 + tan
2
2
cos2 (x/2)
özdeşliğini ve cos2
2
cos2
sin 2θ
θ−
2
122/ 180
z = tan(x/2) Dönüşümü
Bu trigonometrik dönüşüm, sinüs ve kosinüs fonksiyonlarının
bölümleri olduğunda kullanılır. Trigonometrik özdeşlikler yardımıyla
cos x, sin x ve dx için kullanılacak ifadeleri şu şekilde bulabiliriz:
özdeşliğinden
Öğr.Gör.Dr.Meltem Altunkaynak
121/ 180
z = tan(x/2) Dönüşümü
9
2
x
1
=
yi kullanarak
2
1 + z2
cos x = 2
x
1
=
2
1 + z2
x
−1
2
1 − z2
1
−
1
=
1 + z2
1 + z2
elde edilir.
bulunur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
123/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
124/ 180
z = tan(x/2) Dönüşümü
z = tan(x/2) Dönüşümü
Diğer taraftan
cos x = 1 − 2 sin2
özdeşliğinden ve cos x =
sin2
Bu kez
x
2
sin x = 2 sin
1 − z2
den
1 + z2
1 − cos x
x
=
=
2
2
1−
x
x
cos
2
2
1
z2
x
2 x
=
ve
sin
=
den
2
1 + z2
2
1 + z2
r
r
2z
z2
1
sin x = 2
=
1 + z2 1 + z2
1 + z2
özdeşliğinden, cos2
1 − z2
2
1 + z2 = z
2
1 + z2
elde edilir.
bulunur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
z = tan(x/2) Dönüşümü
126/ 180
Özetle, z = tan x2 trigonometrik dönüşümünü yaptığımızda
1
x
1
x
1
dz = sec2 dx =
1 + tan2
dx = (1 + z 2 )dx
2
2
2
2
2
dx =
MAT 1009 Matematik I
z = tan(x/2) Dönüşümü
z = tan x2 de türev alarak da
bulunur. Böylelikle
Öğr.Gör.Dr.Meltem Altunkaynak
125/ 180
cos x =
2
dz
1 + z2
1 − z2
,
1 + z2
sin x =
2z
,
1 + z2
dx =
2
dz
1 + z2
eşitliklerini kullanırız.
olur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
127/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
128/ 180
Örnek
Örnek :
Örnek...
Z
dx
integralini hesaplayınız.
1 + sin x + cos x
Z
Çözüm : İntegral, sinüs ve kosinüs bölümlerini içerdiği için
z = tan x2 dönüşümünü uygularız. Böylece
x
z = tan ,
2
cos x =
1 − z2
,
1 + z2
dx =
2dz
1 + z2
sin x =
2dz
1 + z2
1 − z2
2z
+
1+
1 + z2 1 + z2
Z
dz
2
dz =
=
2
2
1 + z + 2z + 1 − z
z+1
x
= ln |z + 1| + C = ln 1 + tan + C
2
2z
1 + z2
buluruz.
MAT 1009 Matematik I
=
Z
Z
ifadelerini kullanarak
Öğr.Gör.Dr.Meltem Altunkaynak
dx
1 + sin x + cos x
Öğr.Gör.Dr.Meltem Altunkaynak
129/ 180
MAT 1009 Matematik I
130/ 180
Örnek
Kısmi Kesirler
Örnek :
Z
5x − 4
dx integralini bulunuz.
+x−1
2x2
Çözüm : Paydanın doğrusal çarpanlara ayrıldığına dikkat ediniz:
Rasyonel fonksiyonların (polinomların oranının) integralini almak
için onları, kısmi kesirler olarak adlandırılan, integrallerinin nasıl
alınacağını bildiğimiz, daha basit kesirlerin toplamı olarak yazarız.
5x − 4
5x − 4
=
+x−1
(x + 1)(2x − 1)
2x2
Payın derecesinin paydanın derecesinden küçük olduğu böyle bir
durumda, verilen rasyonel fonksiyonu, A ve B sabit olmak üzere,
kısmi türevlerin toplamı olarak yazabiliriz:
A
B
5x − 4
=
+
(x + 1)(2x − 1)
x + 1 2x − 1
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
131/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
132/ 180
Örnek...
Örnek...
2A + B = 5
ve − A + B = −4
5x − 4
A
B
=
+
(x + 1)(2x − 1)
x + 1 2x − 1
Bu doğrusal denklemleri A ve B için çözerek A = 3 ve B = −1
elde ederiz. Buradan
5x − 4 = A(2x − 1) + B(x + 1)
5x − 4 = (2A + B)x + (−A + B)
bulunur. Bu kısmi kesirlerin her birinin integralini (sırasıyla
u = x + 1 ve u = 2x − 1 değişken değişikliğini kullanarak) almak
kolaydır. Böylece
Z
Z 5x − 4
1
3
dx
dx =
−
2x2 + x − 1
x + 1 2x − 1
A ve B değerlerini bulmak için denkemin iki yanını da
(x + 1)(2x − 1) ile çarparız ve
3
1
5x − 4
=
−
(x + 1)(2x − 1)
x + 1 2x − 1
elde ederiz. x in katsayıları ile sabit terimler eşit olmalıdır.
Dolayısıyla
2A + B = 5 ve − A + B = −4
tür.
= 3 ln |x + 1| −
1
ln |2x − 1| + C
2
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
133/ 180
NOT 1
MAT 1009 Matematik I
134/ 180
NOT 2
Paydada ikiden fazla doğrusal çarpan varsa, her çarpan için bir
terim eklememiz gerekir. Örneğin,
Örnekte payın derecesi paydanınkine eşit veya daha büyük olsaydı
ilk önce bölmemiz gerekirdi. Örneğin,
x+6
A
B
C
= +
+
x(x − 3)(4x + 5)
x
x − 3 4x + 5
2x3 − 11x2 − 2x + 2
5x − 4
=x−6+
2x2 + x − 2
(x + 1)(2x − 1)
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Burada A, B ve C sabitleri, A, B ve C bilinmeyenlerini içeren üç
denklemden oluşan sistemi çözerek belirlenir.
135/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
136/ 180
NOT 3
NOT 4
Paydayı olabildiğince çarpanlarına ayırırken, b2 − 4ac diskriminantı
negatif olan, indirgenemeyen ikinci dereceden a x2 + b x + c
çarpanını elde edebiliriz. Buna karşılık gelen kısmi kesir, A ve B
belirlenecek sabitler olmak üzere
Doğrusal çarpanlardan biri tekrarlanıyorsa kısmi kesire fazladan
terimler eklememiz gerekir. Örneğin :
Ax + B
a x2 + b x + c
x
A
B
C
=
+
+
2
2
(x + 2) (x − 1)
x + 2 (x + 2)
x−1
dir. Bu terimin integralini, kareye tamamlayarak ve
Z
dx
1
−1 x
+C
=
tan
x2 + a2
a
a
(14)
formülünü kullanarak hesaplarız.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Örnek
Örnek :
Öğr.Gör.Dr.Meltem Altunkaynak
137/ 180
MAT 1009 Matematik I
138/ 180
Örnek...
Z
2x2 − x + 4
dx integralini hesaplayıız.
x3 + 4x
2x2 − x + 4 = (A + B)x2 + Cx + 4A
Çözüm : x3 + 4x = x(x2 + 4) daha fazla çarpanlarına
ayrılamadığından,
Katsayıları eşitlediğimizde
2x2 − x + 4
A Bx + C
= + 2
2
x(x + 4)
x
x +4
A+B =2
C = −1
4A = 4
elde ederiz. Buradan A = 1, B = 1 ve C = −1 buluruz ve
Z Z
1
x−1
2x2 − x + 4
dx
dx =
+
x3 + 4x
x x2 + 4
yazarız. x(x2 + 4) ile çarparsak,
2x2 − x + 4 = A(x2 + 4) + (Bx + C)x
olur.
= (A + B)x2 + Cx + 4A
elde ederiz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
139/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
140/ 180
Örnek...
Örnek...
Z
2x2 − x + 4
dx =
x3 + 4x
Z 1
x−1
+
x x2 + 4
İkinci integrali, a = 2 alarak Formül (14) den hesaplarız:
Z
Z
Z
Z
1
x
1
2x2 − x + 4
dx =
dx +
dx −
2
2
2
x(x + 4)
x
x +4
x +4
dx
İkinci terimin integralini almak için integralini ikiye ayırırız:
Z
Z
Z
x
1
x−1
dx =
dx −
dx
2
2
4
x +4
x +4
x +4
= ln |x| +
1
1
ln(x2 + 4) − tan−1 (x/2) + K
2
2
Birinci integralde, u = x2 + 4 değişken değişikliğini yaparız ve
du = 2x dx olur.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Has Olmayan İntegraller
Zb
Öğr.Gör.Dr.Meltem Altunkaynak
141/ 180
MAT 1009 Matematik I
142/ 180
1. Tip: Sonsuz Aralıklar
1. Tipten Has Olmayan İntegrallerin Tanımı
Zt
f (x) dx integrali, her t ≥ a sayısı için varsa, limitin (sonlu
(a)
f (x) dx belirli integralini tanımlarken, [a, b] sınırlı aralığında
a
tanımlı olan bir f fonksiyonu aldık ve bu aralıkta f nin sonsuz
süreksizliliğinin olmadığını varsaydık.
0
bir sayı olarak) var olduğu durumlarda
Bu bölümde, belirli integral kavramını, aralığın sonsuz olduğu ve f
nin [a, b] üzerinde sonsuz süreksizliği olduğu durumlara
genişleteceğiz.
Z∞
f (x) dx = lim
a
Her iki durumda da integrale has olmayan integral denir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
t→∞
Zt
f (x) dx
a
dir.
143/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
144/ 180
1. Tip: Sonsuz Aralıklar
(b)
Zb
t
1. Tip: Sonsuz Aralıklar
f (x) dx integrali, her t ≤ b için varsa, limitin (sonlu
Z∞
bir sayı olarak) var olduğu durumlarda
Zb
f (x) dx = lim
t→−∞
Zb
f (x) dx ve
a
Zb
f (x) dx has olmayan integralleri,
−∞
söz konusu limitler varsa yakınsak, limitler yoksa ıraksak olarak
adlandırılır.
f (x) dx
t
−∞
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
(c)
f (x) dx ve
a
Za
1
belirleyiniz.
f (x) dx integrallerinin her ikisi de
−∞
−∞
146/ 180
Z∞
Örnek : (1/x) dx integralinin yakınsak ya da ıraksak olduğunu
Çözüm : Tanımın (a) şıkkından,
yakınsaksa,
Z∞
MAT 1009 Matematik I
Örnek
1. Tip: Sonsuz Aralıklar
Z∞
Öğr.Gör.Dr.Meltem Altunkaynak
145/ 180
f (x) dx =
Za
−∞
f (x) dx +
Z∞
Z∞
f (x) dx
1
dx = lim
t→∞
x
1
a
Zt
1
it
1
dx = lim ln |x|
t→∞
x
1
= lim (ln t − ln 1) = lim ln t = ∞
olarak tanımlarız. (c) şıkkında herhangi bir a gerçel sayısı
kullanılabilir.
t→∞
t→∞
Z∞
dur. Limit sonlu bir sayı olmadığında (1/x) dx ıraksaktır.
1
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
147/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
148/ 180
Örnek
Örnek :
Örnek...
Z0
x ex dx integralini hesaplayınız.
−∞
Z0
Çözüm : Tanımın (b) şıkkından
t
Z0
x ex dx = lim
t→∞
Z0
t → −∞ iken et → 0 olduğunu biliyoruz. L’Hospital Kuralı’ndan
x ex dx
lim t et = lim
t
−∞
x ex dx = x ex
t
i0
t
−
Öğr.Gör.Dr.Meltem Altunkaynak
Z0
t
1
t→−∞ −e−t
= lim
= lim (−et ) = 0
t→−∞
dır.
ex dx = −t et − 1 + et
MAT 1009 Matematik I
t
t→−∞ e−t
t→−∞
olur. u = x ve dv = ex dx seçerek kısmi integral alırsak du = dx
ve v = ex olur.
Z0
x ex dx = −t et − 1 + et
Öğr.Gör.Dr.Meltem Altunkaynak
149/ 180
Örnek...
MAT 1009 Matematik I
150/ 180
Örnek
Örnek :
Dolayısıyla,
Z∞
1
dx integralini hesaplayınız.
1 + x2
−∞
Z0
Çözüm : Tanımın (c) şıkkında a = 0 seçmek işimizi
kolaylaştıracaktır:
x ex dx = lim (−t et − 1 + et )
t→−∞
−∞
Z∞
= −0 − 1 + 0 = −1
olur.
−∞
1
dx =
1 + x2
Z0
1
dx +
1 + x2
∞
Z∞
1
dx
1 + x2
0
Sağdaki integralleri ayrı ayrı hesaplamalıyız:
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
151/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
152/ 180
Örnek...
Z∞
Örnek...
1
dx = lim
t→∞
1 + x2
0
Zt
dx
= lim tan−1 x
1 + x2 t→∞
0
Z0
it
1
dx = lim
t→−∞
1 + x2
−∞
0
MAT 1009 Matematik I
t
i0
dx
−1
dx
=
lim
tan
x
t→−∞
1 + x2
t
= lim (tan−1 0 − tan−1 t)
π
= lim (tan−1 t + tan−1 0) = lim tan−1 t =
t→∞
t→∞
2
Öğr.Gör.Dr.Meltem Altunkaynak
Z0
t→−∞
π π
=
=0− −
2
2
Öğr.Gör.Dr.Meltem Altunkaynak
153/ 180
Örnek...
MAT 1009 Matematik I
154/ 180
Örnek
Örnek : Hangi p değeri için
Z∞
Her iki integral de yakınsak olduğundan verilen integral de
yakınsaktır ve
Z∞
π π
1
dx = + = π
2
1+x
2
2
1
dx
xp
1
integrali yakınsaktır?
−∞
Çözüm : İlk örnekten, p = 1 olduğunda integralin ıraksak
olduğunu biliyoruz, dolayısıyla p 6= 1 varsayalım. Bu durumda
dir.
Z∞
1/(1 + x2 ) > 0 olduğundan verilen has olmayan integral
y = 1/(1 + x2 ) eğrisinin altında x ekseninin üstünde kalan sonsuz
bölgenin alanı olarak yorumlanabilir.
1
1
dx = lim
t→∞
xp
Zt
1
x−p+1
1
dx
=
lim
t→∞ −p + 1
xp
x=t
x=1
1
1
= lim
−1
t→∞ 1 − p tp−1
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
155/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
156/ 180
Örnek...
Örnek...
Eğer p < 1 ise p − 1 < 0 ve
p > 1 ise p − 1 > 0 dır ve t → ∞ iken tp−1 → ∞ ve 1/tp−1 → 0
dır. Dolayısıyla
p>1
için
Z∞
1
t→∞
1
1
dx =
p
x
p−1
Z∞
1
MAT 1009 Matematik I
= t1−p → ∞
1
dx integrali, p > 1 ise yakınsak, p ≤ 1 ise ıraksaktır.
xp
Öğr.Gör.Dr.Meltem Altunkaynak
157/ 180
2. Tip: Sürekli Olmayan Fonksiyonların İntegrali
MAT 1009 Matematik I
158/ 180
2. Tip: Sürekli Olmayan Fonksiyonların İntegrali
(b) f fonksiyonu (a, b] aralığında sürekli ve a noktasında
süreksizse, limitin (sonlu bir sayı olarak) var olduğu
durumlarda
Zb
Zb
f (x) dx
f (x) dx = lim
2. Tipten Has Olmayan İntegralin Tanımı
(a) f fonksiyonu [a, b) aralığında sürekli ve b noktasında
süreksizse, limitin (sonlu bir sayı olarak) var olduğu
durumlarda
Zb
Zt
f (x) dx = lim
f (x) dx
t→a+
a
t
dir.
t→b−
a
1
tp−1
olur, dolayısıyla integral ıraksaktır.
olur ve integral yakındaktır.
Öğr.Gör.Dr.Meltem Altunkaynak
iken
Zb
a
dir.
f (x) dx has olmayan integraline, söz konusu limit varsa
a
yakınsak, yoksa ıraksak denir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
159/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
160/ 180
Örnek
2. Tip: Sürekli Olmayan Fonksiyonların İntegrali
(c) f fonksiyonu, a < c < b olan bir c noktasında süreksiz ve
Zc
Zb
f (x) dx,
f (x) dx integrallerinin her ikisi de yakınsaksa,
a
Örnek :
c
Zb
f (x) dx =
a
Zc
f (x) dx +
a
Zb
Z5
√
2
1
dx integralini bulunuz.
x−2
√
Çözüm : Önce, verilen integralin, f (x) = 1/ x − 2 nin x = 2 de
düşey asimptotu olduğundan, has olmadığına dikkat ediniz.
f (x) dx
c
olarak tanımlarız.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
161/ 180
Örnek...
MAT 1009 Matematik I
162/ 180
Örnek
Süreksizlik, [2, 5] aralığının sol uç noktasında olduğundan tanımın
(b) şıkkını kullanarak:
Z5
2
dx
√
x−2
= lim
t→2+
Z5
t
√
Zπ/2
Örnek :
sec x dx integralinin yakınsak ya da ıraksak olduğuna
i5
√
dx
= lim 2 x − 2
t
x − 2 t→2+
0
karar veriniz.
√
√
= lim 2( 3 − t − 2)
Çözüm : Verilen integral,
t→2+
lim
x→(π/2)−
sec x = ∞ olduğundan, has
değildir.
√
=2 3
buluruz. Dolayısıyla verilen integral yakınsaktır.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
163/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
164/ 180
Örnek...
Örnek
Tanımın (a) şıkkını kullanarak t → (π/2)− iken sec t → ∞ ve
tan t → ∞ olduğundan
Zπ/2
sec x dx =
lim
t→(π/2)−
0
=
=
Zt
Örnek : Olanaklı ise
0
sec x dx
t→(π/2)−
lim
t→(π/2)−
ln | sec x + tan x|
dx
integralini hesaplayınız.
x−1
Çözüm : x = 1 doğrusu, integrali alınan fonksiyonun düşey
asimptotudur. Bu nokta [0, 3] aralığının içinde olduğundan,
tanımın (c) şıkkında c = 1 alarak:
0
lim
Z3
it
0
Z3
[ln(sec t + tan t) − ln 1]
0
=∞
dx
=
x−1
Z1
0
dx
+
x−1
Z3
1
dx
x−1
yazarız
dur. Dolayısıyla verilen integral ıraksaktır.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
165/ 180
Örnek...
MAT 1009 Matematik I
166/ 180
Örnek...
ve t → 1− iken 1 − t → 0+ olduğundan
Z1
0
dx
x−1
= lim
t→1−
Zt
0
Dolayısıyla
it
dx
= lim ln |x − 1|
x − 1 t→1−
0
Z1
0
dx/(x − 1) ıraksaktır. Bu,
de ıraksak olmasını gerektirir.
= lim (ln |t − 1| − ln | − 1|)
t→1−
[
= lim ln(1 − t) = −∞
Z3
0
t→1−
Z3
1
dx/(x − 1) integralinin
dx/(x − 1) integralini hesaplamamıza gerek kalmaz.]
buluruz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
167/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
168/ 180
Uyarı
Uyarı
Yukarıdaki örnekte, x = 1 asimptotunu fark etmeseydik ve integrali
alınan fonksiyonu sıradan bir integralle karıştırsaydık, aşağıdaki gibi
hatalı bir hesap yapabilirdik:
Z3
0
Bundan böyle
Zb
f (x) dx işaretini gördüğümüzde, [a, b] üzerinde f
a
i3
dx
= ln |x − 1| = ln 2 − ln 1 = ln 2
x−1
0
ye bakarak integralin sıradan bir belirli integral mi yoksa has
olmayan bir integral mi olduğuna karar vermemiz gerekmektedir.
Bu yanlıştır, integral has olmadığından limitler cinsinden
hesaplanmalıdır.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Örnek
Örnek :
Öğr.Gör.Dr.Meltem Altunkaynak
169/ 180
MAT 1009 Matematik I
170/ 180
Örnek...
Z1
ln x dx integralini hesaplayınız.
u = ln x ve dv = dx ile kısmi integral alırsak, du = dx/x ve v = x
olur.
Z1
i1 Z1
ln x dx = x ln x − dx
0
Çözüm : limx→0+ ln x = −∞ olduğundan, f (x) = ln x
fonksiyonunun 0 da düşey asimptotu olduğunu biliyoruz.
Dolayısıyla verilen integral has değildir ve
Z1
ln x dx = lim
0
t→0+
Z1
t
t
t
= 1 ln 1 − t ln t − (1 − t)
= −t ln t − 1 + t
ln x dx
elde ederiz.
t
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
171/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
172/ 180
Örnek...
Has Olmayan İntegraller İçin Karşılaştırma Testi
Birinci terimin limitini almak için L’Hospital Kuralını kullanırız:
lim t ln t = lim
t→0+
t→0+
ln t
1/t
= lim
+
1/t t→0 −1/t2
= lim (−t) = 0
Bazen has olmayan bir integralin kesin değerini bulmak olanaklı
değildir ancak yine de yakınsak mı, ıraksak mı olduğunu bilmek
önemlidir.
t→0+
Dolayısıyla
Z1
0
ln x dx = lim (−t ln t − 1 + t)
t→0+
= −0 − 1 + 0 = −1
dir.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Has Olmayan İntegraller İçin Karşılaştırma Testi
(b)
a
g(x) dx ıraksaksa,
Z∞
Z∞
g(x) dx yakınsaksa,
ve
Z∞
a
f (x) dx ıraksaktır.
MAT 1009 Matematik I
175/ 180
Z∞
f (x) dx yakınsak da olabilir ıraksak da
a
a
a
Öğr.Gör.Dr.Meltem Altunkaynak
174/ 180
Tersi doğru olmayabilir:
a
0
MAT 1009 Matematik I
Has Olmayan İntegraller İçin Karşılaştırma Testi
Karşılaştırma Teoremi: f ve g nin x ≥ a için f (x) ≥ g(x) ≥ 0
olan sürekli fonksiyonlar olduğunu varsayalım.
Z∞
Z∞
(a)
f (x) dx yakınsaksa,
g(x) dx de yakınsaktır.
Z∞
Öğr.Gör.Dr.Meltem Altunkaynak
173/ 180
f (x) dx ıraksaksa,
Z∞
g(x) dx ıraksak da olabilir yakınsak da.
a
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
176/ 180
Örnek
Örnek...
Örnek :
Z∞
Z∞
2
e−x dx integralinin yakınsak olduğunu gösteriniz.
0
e
−x2
dx =
0
2
e
−x2
dx =
0
Z1
e
−x2
dx +
0
Z∞
e
−x2
dx +
0
Z∞
2
e−x dx
1
İkinci integral için,x ≥ 1 iken,
Çözüm : e−x nin ilkeli temel fonksiyon olmadığından, integrali
doğrudan hesaplayamayız.
Z∞
Z1
x2 ≥ x
ve
2
e−x dx
−x2 ≤ −x
1
olduğunu kullanarak
yazar ve sağdaki ilk integralin sıradan bir belirli integral olduğunu
gözlemleriz.
2
e−x ≤ e−x
olduğunu görürüz.
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr.Meltem Altunkaynak
177/ 180
Örnek...
MAT 1009 Matematik I
178/ 180
Örnek
e−x fonksiyonunun integralini hesaplamak kolaydır:
Z∞
e
−x
dx = lim
t→∞
Zt
1
1
e−x dx = lim (e−1 − e−t ) = e−1
1 + e−x
1
Örnek :
> ve
x
x
t→∞
Z∞
(1/x) dx ıraksak olduğundan,
1
e−x
2
e−x
Böylece Karşılaştırma Teoremi’nde f (x) =
ve g(x) =
Z∞
2
alırsak,
e−x dx integralinin yakınsak olduğunu görürüz. Bunun
Karşılaştırma Teoremi’nden
Z∞
1 + e−x
dx integrali de ıraksaktır.
x
1
1
sonucu olarak
Z∞
2
e−x dx yakınsaktır.
0
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
179/ 180
Öğr.Gör.Dr.Meltem Altunkaynak
MAT 1009 Matematik I
180/ 180

Download

ıntegral

Products

Support

ıntegral

Add this document to collection(s)

Add this document to saved

Suggest us how to improve StudyLib