matlab/sımulınk`e başlangıç

 MATLAB/SIMULINK’E BAŞLANGIÇ Hazırlayan: YUSUF ONUR KOÇBERBER Yokocbeber(at)etu‐edu‐tr TOBB EKONOMİ VE TEKNOLOJİ ÜNİVERSİTESİ
ELEKTRİK VE ELEKTRONİK MÜHENDİSLİĞİ
01.01.2008 v1.
25.02.2009 v2.
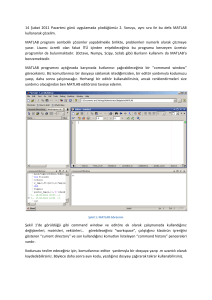
İçindekiler Matlab’a Başlangıç .................................................................................................................................. 3 Vektörler .............................................................................................................................................. 4 Matrisler .............................................................................................................................................. 6 Çizgeler ................................................................................................................................................ 9 Polinomlar ......................................................................................................................................... 12 Transfer Fonksiyonu ve Durum Uzayı Gösterimi ............................................................................... 14 Analiz ................................................................................................................................................. 17 Simulink ................................................................................................................................................. 20 2 Matlab’a Başlangıç langıç Yeni M‐File Simulink Workspace Çalışma Klasörü Command Window Komut Geçmişi Kılavuz boyunca sık kullanılacak Matlab elemanları yukarıda işaretlenmiştir. Çalışma klasörü olarak belirtilen “Current Directory” aksi belirtilmedikçe yapılan tüm çalışmaların kaydedildiği klasördür. Birbirine bağlı m‐dosyaları çalıştırılacaksa tüm dosyaların bu klasörde olması gerekmektedir aksi takdirde m‐dosyası içinde dosyanın bilgisayardaki konumu tam olarak belirtilmelidir. Çalışmalar sırasında yararlı bir kaç komut: •
•
•
•
•
clc: Command window’u temizlemektedir. whos: Workspace’deki değişkenlerle ilgili bilgileri göstermektedir (özellikle iki değişkenin boyutu uyuşmadığında kontrol etmek amacıyla kullanılır) clear Değişkenİsmi: İlgili değişkeni workspace’den siler. help Fonksiyonİsmi: İlgili fonksiyon hakkında özet bir yardım gösterir. syms Değişkenİsmi: ilgili değeri değişken yapar (türev , integral gibi sembollerin kullanıldığı işlemler için). 3 Vektörler Vektörler 1xn boyutlu matrislerdir. Bir vektör tanımlamak için: “Command Window” ’a >> a = [1 2 3 4 5 6 9 8 7] komutunu giriniz. Böylece aşağıdaki sonuç elde edilir. Görüldüğü üzere a değeri “Workspace” penceresinde yerini almıştır. Bu pencereden işlemler sırasında kullanılan tüm parametreler ve onlarla ilgili çeşitli bilgiler (boyutu, en büyük değeri , en küçük değeri , boyu vs.) görülebilir. Benzer şekilde 0 ile 100 arasında eşit dağılmış 5 elemanlı bir vektör yaratmak için >> a=0:20:100
Sonuç: a =
0
20
40
60
80
100
a=0:20:100 gösterimi 0’dan başlayarak 100’e kadar her adımda bir sonraki elemana 20 eklemektedir. a vektörünün ilk elemanına ulaşmak istenildiğinde a(1) komutu kullanılmaktadır. >> a(1)
ans =
0
Not: Çoğu programlama dillerinin aksine MATLAB dizilerin ilk elemanını 0 değil 1 olarak indekslemektedir. Bu sebepten dolayı ilk elemana ulaşmak için a(1) komutu kullanılmıştır. 4 Çarpım A vektörünü ile birlikte ikinci bir b vektörü yaratalım. >> b= a - 5
b =
-5
15
35
55
75
95
A ile b vektörünü çarpıp c adlı yeni bir matrise atamak istiyoruz. Bu durumda “c= a * b “ komutunu kullanırsak; >> c= a * b
??? Error using ==> mtimes
Inner matrix dimensions must agree.
Yukarıdaki hata ile karşılaşılır. Bunun nedeni “*” işleci matris çarpımı yapmaktadır yani iki tane 1xn boyutundaki matrisi çarpmak mümkün değildir. Burada vektör çarpımı yapılması gerekmektedir. Vektör Çarpımı işleci “ .* “ şeklindedir. >> c= a .* b
c =
0
300
1400
3300
6000
9500
Görüldüğü üzere a ve b vektörlerinde konum itibariyle karşılıklı elemanlar birbirleriyle çarpılmıştır. Not: Benzer şekilde kuvvet işleçi de (^) vektör işlemleri için .^ şeklinde kullanılmalıdır. 5 Matrisler Matrisin tanımlanması: Matrisler tanımlanırken değişik yollar bulunmaktadır. En genel yol yeni bir satır için “;” kullanılmasıdır. >> a=[1 2 ; 3 4]
a =
1
2
3
4
Bir başka yol ise: >> b = [ 1 2
3 4 ]
b =
1
2
3
4
Matris değerleri girilirken workspace’deki değer isimleri veya sanal sayılar kullanılabilir. Sanal sayılar için “i” veya “j” kullanılabilir. Not: Eğer i veya j değişkenine daha önce başka değer atamışsanız bu değişkeni sqrt(‐1)’e eşitlemeniz yeterlidir. Matrisin Transpozu Daha önceden tanımlanan b matrisinin transpozunu almak için ; >> b'
ans =
1
3
2
4
6 Matrisin Tersi Daha önceden tanımlanan b matrisinin tersini almak için ; >> inv(b)
ans =
-2.0000
1.0000
1.5000
-0.5000
Matrisin Özdeğeri Daha önceden tanımlanan b matrisinin özdeğerlerini bulmak için ; >> eig(b)
ans =
-0.3723
5.3723
Vektör veya matris tanımlarken, kolaylık amacıyla tüm elemanları 0 tanımlamak için “zeros” , tüm elemanları 1 tanımlamak için ” ones” , tüm elemanları rastgele sayılardan oluşturmak için “rand” fonkisyonu kullanılabilir. >> zeros (5,1)
ans =
0
0
0
0
0
Dizilere uygulanan fonkisyonlar •
length(a): a dizisinin eleman sayısı yani uzunluğu •
size(a): a dizisinin boyutu •
sum(a): a matrisinin sütun başına eleman toplamı (eğer sadece sütün veya satır matrisiyse tüm elemanların toplamını verir) •
kd(n): kd dizisinin n. eleman değeri A(n,:): A matrisinin sadece n. satırı A(:,n): A matrisinin sadece n. sütunu •
•
7 •
A‘: A matrisinin transpozu yani devriği •
det(A): A matrisinin determinantı •
inv(A) : A matrisinin tersi •
diag(A): A matrisinin ana diagonel (çapraz) elemanları •
[v,d]=eig(A): A matrisinin özvektörleri ve özdeğerleri •
Elemanter işlemler: Eleman eleman işlem demektir ve . (nokta) işleci kullanılır: Çarpma: .* , Bölme: ./ , Üs alma: .^ 8 Çizgeler Matlab’daki en önemli fonksiyonlardan biri “plot” fonksiyonudur. Plot(x,y) şeklinde belirtilen bu komutta x değerleri çizgenin yatay eksenine, y değerleri çizgenin düşey eksenine çizilecektir. Örneğin; >> t=0:0.1:5 şeklinde zaman değerlerimizi belirleyelim, >> y=sin(2*pi*t) >>plot (t,y) Bu noktadan sonraki komutları m dosyasına yazmak daha yararlı olacaktır çünkü bir çok komutu arkaya tek satırlık komut penceresine yazmak zaman kaybettirmektedir. Yeni bir m dosyası açmak için File>New>M‐File Gelen editörün içine yeni değerleri tanımlayınız : t=0:0.1:10;
y= 2.^(10-t);
plot (t,y,'r:')
title ('çizge 1')
xlabel (' x ekseni')
ylabel ('y ekseni')
Dosyayı kaydedip Debug>Run dosyaismi veya kısayol olarak F5 tuşuna basınız . 9 Örnekte görüldüğü üzere plot fonksiyonuna eklenen ‘r:’ terimi grafiği kırmızı ve noktalı yapmıştır. Başka renkler için “g ,b,c,m,y,k,w” gibi belirteçleri , değişik şekiller için “. , o , x, ^, + , * ‐. , ‐‐“ belirteçleri deneyebilirsiniz. Örneğin “ g ‐‐ “ grafiği yeşil ve çizgili “ b*” mavi ve yıldızlı göstermektedir. Xlabel ve Ylabel fonksiyonları ile x ve y eksenine ‘eksen ismi’ formatında istenilen isimler verilebilir. Aynı m‐dosyasının en sonuna “ axis tight” komutunu ekleyip m dosyasını tekrar çalıştırınız. Görüldüğü üzere grafiğin eksenleri çizdirilen fonksiyonun minimum ve maksimum değerlerine göre ayarlanmıştır. “Axis” komutu grafiklerin daha anlaşılır olması için önemli bir araçtır ve her zaman plot’tan sonra kullanılır. Bu komutun bir diğer kullanımı ise “ axis([xmin, xmax, ymin, ymax]) “ şeklindedir. Bu sayede görmek istediğimiz grafiğin eksenlerinin en küçük ve en büyük değerleri ayarlanabilir. Birden Çok Grafiği Yönetmek Birden fazla grafiği (aynı x‐ekseni baz olmak üzere) üst üste çizmek için; Örneğin: x,y1,y2,….yn için; 1.yol: plot(x,y1,x,y2,..x,yn) 2.yol: plot(x,y1), hold on, plot(x,y2,..x,yn) •
Çoklu grafiği etiketlemek için: 1.yol: Grafik üzerinde metin ekleme yapılır. 2.yol: legend(‘1.grafikmetin’,’2.grafikmetin’….) fonksiyonu kullanılır. •
Birden fazla grafiği farklı pencerelerde (aynı veya farklı x‐ekseni baz olmak üzere) çizmek için subplot(m,n,p) fonksiyonu kullanılır. Bu fonksiyon matris düzeninde çizim alanı açar ve grafikler yine plot fonksiyonu ile çizilir. 10 Örnek: Hold on komutu ile grafiklerin üst üste çizilmesi t = 0:0.01:1;
x= 0:0.1:10;
y = x.^(t);
plot(t,y,'b:')
hold on
z = sin(2*pi*t);
plot(t,z,'r+')
w = y.*z;
plot(t,w,'g--')
legend('x^{t}','sin(2*\pi*t)','x^{t}sin(2*\pi*t)')
axis tight
grid on
Örnek: Aynı grafiklerin subplot komutu ile ayrı ayrı pencerelerde çizilmesi; subplot (3,1,1)
t = 0:0.01:1;
x= 0:0.1:10;
y = x.^(t);
plot(t,y,'b:')
title ('x^{t}')
legend('x^{t}')
grid on
subplot (3,1,2)
z = sin(2*pi*t);
plot(t,z,'r+')
legend ('sin(2*\pi*t)')
title ('sin(2*\pi*t)')
grid on
11 subplot (3,1,3)
w = y.*z;
plot(t,w,'g--')
legend('x^{t}sin(2*\pi*t)')
title ('x^{t}sin(2*\pi*t)')
grid on
Polinomlar Matlab polinomları bir vektör ile tanımlar. Örnek olarak ; 3s4+6s3‐3s2+10s+1 Polinomu aşağıdaki vektör ile tanımlanır. >> A=[ 3 6 -3 10 1]
A =
3
6
-3
10
1
Eğer arada eksik katsayılar varsa bu katsayılar 0 ile gösterilir. Örnek olarak; 7s4+10 >> A=[7 0 0 0 10]
A =
7
0
0
0
10
12 Polinomun değerini bulmak için “polyval” fonksiyonu kullanılabilir. Örneğin a=[7 0 0 0 10] polinomunun s=3’teki değerini bulmak için ; >> polyval([7 0 0 0 10] ,3)
ans =
577
Aynı yöntemi kullanarak polinom çizdirilebilir. Örnek: t=-5:0.1:3
A=[1 2 -10 -7 4]
plot(t,polyval(A,t))
200
150
100
50
0
-50
-5
-4
-3
-2
-1
0
1
2
3
Görüldüğü üzere grafik y=0 eksenini 4 kere kesmektedir. Köklerin tam yeri “roots” komutu ile tespit edilebilir. >> roots (A)
ans =
-4.0000
2.6180
-1.0000
0.3820
13 Transfer Fonksiyonu ve Durum Uzayı Gösterimi Transfer fonksiyonunu belirtmek için öncelikle pay ve paydayı tanımlamak gerekmektedir. Bunun için >> num=[1]
num =
1
>> den=[1 14 56 160]
den =
1
14
56
160
>> tf(num,den)
Transfer function:
1
------------------------s^3 + 14 s^2 + 56 s + 160
Aynı şekilde bu transfer fonksiyonun durum uzayı gösterimlerinden biri aşağıdaki gibidir. y= Bu gösterimi Matlab’a aktarmak için ss(a,b,c,d) şeklinde bir gösterim kullanılmalıdır. >> a=[0 1 0 ; 0 0 1; -160 -56 -14]
a =
0
1
0
0
0
1
-160
-56
-14
>> b=[0 ;1 ; -14 ]
>> c=[1 0 0 ]
>> d=[0]
a,b,c,d matrisleri tanımlandıktan sonra “ss” komutu ile gösterim tamamlanır. 14 >> ss(a,b,c,d)
a =
x1
x2
x3
x1
0
1
0
x2
0
0
1
x3
-160
-56
-14
b =
u1
x1
0
x2
1
x3
-14
c =
y1
x1
x2
x3
1
0
0
d =
u1
y1
0
Transfer fonksiyonundan durum uzayı gösterimi veya durum uzayı gösteriminden transfer fonksiyonu elde edilebilir. Daha önceki örnekte transfer fonksiyonu “num “ ve “den” isimleri ile tanımlanmıştı. Durum uzayı gösterimini A,B,C,D matrislerine aktarmak için ; >> [A,B,C,D]=tf2ss(num,den)
A =
-14
-56
-160
1
0
0
0
1
0
0
1
B =
1
0
0
C =
0
D =
0
15 Aynı şekilde durum uzayı gösteriminden transfer fonksiyonu çıkarılabilir. Bunun için ss2tf komutu kullanılır. Yukarıdaki örneklerde kullandığımız a,b,c,d matrislerini kullanırsak; >> [pay,payda]=ss2tf(a,b,c,d)
pay =
0
0.0000
1.0000
0.0000
1.0000
14.0000
56.0000
160.0000
payda =
16 Analiz Elde edilen gösterimleri analiz etmek için •
•
•
•
Bode çizgesi Adım cevabı Dürtü cevabı Kutuplar ve sıfırlar bulunabilir. Daha önceden elde ettiğimiz pay ve payda değişkenlerini “ sistemin_transfer_fonksiyonu ” isimli bir değişkene atayalım. >> sistemin_transfer_fonksiyonu=tf(num,den) Transfer function:
1
------------------------s^3 + 14 s^2 + 56 s + 160
Bode çizgesi için; >>bode(sistemin_transfer_fonksiyonu) Bode Diagram
-40
Magnitude (dB)
-60
-80
-100
Phase (deg)
-120
0
-90
-180
-270
-1
10
0
1
10
10
Frequency (rad/sec)
Grafikte istenilen noktalara tıklanarak ilgili değerler alınabilir. 17 2
10
Adım cevabı için ; >>step(sistemin_transfer_fonksiyonu)
-3
8
Step Response
x 10
7
6
Amplitude
5
4
3
2
1
0
0
0.5
1
1.5
2
2.5
3
Time (sec)
Yüzde aşım , yükselme zamanı,tepe değeri gibi değerler grafikte ilgili yerlere tıklanarak ölçülebilir fakat 2007 ve sonrası sürümlerde stepinfo komutu bulunmaktadır. >> stepinfo(sistemin_transfer_fonksiyonu)
ans =
RiseTime: 0.4526
SettlingTime: 2.0948
SettlingMin: 0.0060
SettlingMax: 0.0072
Overshoot: 14.7300
Undershoot: 0
Peak: 0.0072
PeakTime: 1.0067
18 Dürtü cevabı için; >> impulse(sistemin_transfer_fonksiyonu)
-3
14
Impulse Response
x 10
12
10
8
Amplitude
6
4
2
0
-2
-4
0
0.5
1
1.5
2
Time (sec)
Sistemin kutupları pole komutu ile bulunur. >> pole(sistemin_transfer_fonksiyonu)
ans =
-10.0000
-2.0000 + 3.4641i
-2.0000 - 3.4641i
Sistemin sıfırları tzero komutu ile bulunur. >> tzero(sistemin_transfer_fonksiyonu)
ans =
Empty matrix: 0-by-1
Bu örnekte sistemin sıfırı olmadığından boş matris çıkmıştır. 19 2.5
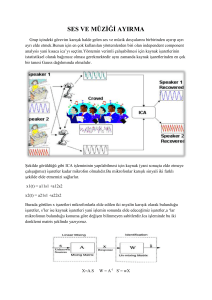
3
3.5
Simulink Simulink modelleme ve benzetim için geliştirilmiş grafiksel ara yüze sahip bir Matlab uzantısıdır.Simulinkte sistemler ekran üzerine blok diyagramlar halinde çizilmektedir.Transfer fonksiyonu blokları, toplayıcılar gibi blokların dışında osiloskop , fonksiyon üreteci gibi sanal giriş/çıkış cihazları da bulunmaktadır. Simulink , Matlab içinde çalışan bir program olduğundan iki program arasında rahatlıkla veri transferi yapılabilir. Bu kılavuzda her bloğun tek tek tanıtılmasından ziyade örnekler üzerinden gidilecektir. Programın başlatılması; Matlab içerisinde command window’a simulink yazılmalıdır. >>simulink
“Simulink Library Browser” penceresi açıldıktan sonra File>New>Model seçilerek blokların ekleneceği boş ekran elde edilir. Simulink Library Browser penceresinden bloklar sürükle bırak şeklinde açılan boş model sayfasına eklenmelidir. 20 Örnek 1: Öncelikle •
•
•
•
Simulink>sources kütüphanesinden “step” bloğunu Simulink>continuous kütüphanesinden “derivative” bloğunu Simulink>math Operations kütüphanesinden “add” ve “gain” bloğunu Simulink>commonly used blocks kütüphanesinden “scope” bloğunu tasarım ekranına ekleyiniz. Blokların girişlerinden farenin tuşuna basılı tutarak sonraki bloğun girişine gittiğiniz takdirde bloklar bağlanır fakat kısa yol olarak ilk bloğu seçtikten sonra ctrl tuşuna basılı tutarak hedef blok üzerine tıklandığı takdirde bloklar kendiliğinden bağlanır. Scope bloğu üzerine iki tıklayarak, parameters sekmesinden, Scope Parametreleri 3 farklı veriyi aynı anda gözlemek amacıyla, “number of axes” alanını 3 yapınız. Bloklar bağlanıldığında aşağıdaki şekildeki gibi bir görüntü oluşması gerekmektedir. 21 Simülasyon ayarlarını yapmak için , Simulation > Configuration Parameters penceresini açınız. Sistemi sabit adım ile çözmek için gelen pencereden, “Solver options‐Type” seçeneğini “Fixed‐Step” olarak seçiniz. “Fixed‐step size” olarak sırasıyla ”1” , “0.01” ve “auto” değerleri kullanılacaktır. Şekilde görülen “Simulation Stop Time” alanına benzetimin kaç saniye süreceği girilmelidir. Simülasyon süresini 2 olarak girdikten sonra şekilde görülen “start simulation” tuşuna tıklayarak veya kısayol olarak “ctrl+t” ile benzetimi başlatınız. Adım aralığı : 1 Adım aralığı : 0.01 22 Adım aralığı : auto Örnek 2: Öncelikle •
•
•
Simulink>sources kütüphanesinden “step” bloğunu Simulink>continuous kütüphanesinden “transfer fcn” bloğunu Simulink>commonly used blocks kütüphanesinden “scope” bloğunu tasarım ekranına ekleyiniz. Adım cevabı bulunacak transfer fonksiyonu aşağıdaki gibidir Transfer Fcn bloğunun değerlerini değiştirmek için üzerine iki tıklayınız , “numerator coefficient” ve “denominator coefficient” alanları ile sırasıyla pay ve paydanın değerleri vektör şeklinde tanımlanmaktadır. 23 Scope bloğuna iki kere tıklayarak sonucu görüntüleyiniz. Sonucun tam olarak görüntülenmesi için şekilde görülen autoscale butonuna tıklayınız. Örnek 3: PID ve Subsystem Oluşturma Öncelikle şekilde görülen blok şemayı kurunuz. Kazançların değerlerini P terimi için Kp, I terimi için Ki ve D terimi için Kd şeklinde değiştirildiğine dikkat ediniz. Daha sonra şema üzerindeki tüm elemanları seçtikten sonra sağ tıklayıp “create subsystem” seçeneğini seçiniz. 24 Subsystem haline dönüşen blok üzerine tekrar sağ tıklayarak “mask subsystem” seçeneğini seçiniz. Gelen pencerenin “Parameters” sekmesinden Add butonu ile yeni parametreler ekleyiniz. “Variable” alanına daha önce ismi değiştirilen blokların ismini girmeniz gerekmektedir. Aksi takdirde ilgili bloğun değerine dışarıdan erişilemeyecektir. Add Butonu Elde edilen “subsystem” adlı bloğun ismini “PID” olarak değiştiriniz ve aşağıdaki blok şemayı kurunuz. 25 PID bloğuna tıkladığınızda Kp , Kd ve Ki değerlerini girebildiğinizi göreceksiniz.Farklı Kp, Kd, Ki değerleri ile bu terimlerin sisteme etkisini gözleyebilirsiniz. Scope bloğundan çıkan grafiğin yükselme zamanı, yüzde aşımı gibi değerleri “zoom to y‐axis” yakınlaştırma butonları ile ölçebileceğiniz gibi grafiğin değerlerini Matlab’ın “workspace” bölümüne göndererek daha önce anlatılan stepinfo komutunu kullanabilirsiniz. Scope Parametreleri Yakınlaştırma butonları
Grafik verisini “workspace” alanına aktarmak için şekilde gösterildiği gibi “scope parameters” butonuna tıklayıp “data history” sekmesini seçmek gerekmektedir.”Save data to workspace” seçeneği işaretlenerek gönderilecek olan verinin “workspace”de hangi değişken ismi ile tanımlanacağını belirtmek gerekir bu isim varsayılan şekilde “ScopeData” olarak belirlenmiştir. Format kısmından “Array” seçilerek değişkenin nx2’lik bir matris şeklinde belirtilmesi sağlanmalıdır. Bu değişkenin n uzunluğundaki satır kısmı benzetim uzunluğu ile doğru orantılıdır. 1.kolonu zaman değerleri yani x ekseni, 2.kolonu ise bu zaman karşılığında alınan değerleri belirtmektedir yani y eksenidir. Stepinfo(Y ekseni,X ekseni) şeklinde kullandığından doğru sonuç almak için aşağıdaki şekilde kullanılmalıdır. 26 >> stepinfo(ScopeData(:,2),ScopeData(:,1))
ans =
RiseTime: 0.6484
SettlingTime: 3.1281
SettlingMin: 0.9185
SettlingMax: 1.0682
Overshoot: 6.8172
Undershoot: 0
Peak: 1.0682
PeakTime: 1.5505
Örnek 4: Aşağıdaki blok şemayı kurunuz. Daha önceki örnekte olduğu gibi “scope parameters” penceresine gidilerek “axes” alanı 3 yapılmalıdır. Bu sayede scope penceresi 3’e bölünecektir. Eğer grafikleri üst üste çizdirmek istiyorsanız “mux” elemanını kullanabilirsiniz. Tellerin üzerine çift tıklayarak isimlendirebilirsiniz, bu sayede “scope” ekranındaki grafikleri tespit etmek daha kolay olmaktadır. “Simulation time” alanını 20 yaparak benzetimi başlatınız. Görüldüğü üzere scope ekranı 3 farklı pencereye bölünmüş ve hepsinin başlığı bulunmaktadır. 27 28