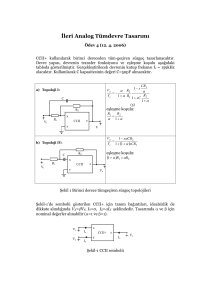
5. CMOS AKIM TAùIYICI
Akım taúıyıcı, akımın çok farklı empedans seviyelerindeki iki kapı arasında
taúındı÷ı üç kapılı aktif bir devre olarak tanımlanabilir. ølk akım taúıyıcı olan birinci
kuúak akım taúıyıcı (CCI) 1968 yılında Smith ve Sedra tarafından ortaya atılmıútır.
1970 yılında Smith ve Sedra daha kullanıúlı bir akım taúıyıcı devresi olan ikinci
kuúak akım taúıyıcı devresini (CCII) geliútirmiúlerdir. Günümüzde, akım taúıyıcı
denildi÷inde, ikinci kuúak akım taúıyıcı (CCII) anlaúılmaktadır. Aktif eleman olarak
akım taúıyıcının kullanılmasıyla çeúitli türden aktif devre yapılarını gerçekleútirmek
mümkündür. Bu yapılara örnek olarak, aktif süzgeç ve osilatör devreleri verilebilir.
v
Y
iZ
Y
CCII +
vX
X
Z
vY
CCII -
vX
i
X
iZ
Y
Z
X
i
X
(a)
(b)
ùekil-5.1. Evirmeyen (CCII+) ve eviren (CCII-) türden ikinci kuúak akım taúıyıcıların devre
sembolleri : a) evirmeyen türden akım taúıyıcı , b) eviren türden akım taúıyıcı.
Evirmeyen (CCII+) ve eviren (CCII-) türden ikinci kuúak akım taúıyıcıların
devre sembolleri ùekil-5.1’de görülmektedir. CCII, aúa÷ıda verilen ba÷ıntılarla
tanımlanan üç uçlu bir devredir.
v X = vY
iY = 0
iZ = # i X
(5.1)
Bu ba÷ıntılarda vY, vX büyüklükleri Y ve X uçlarındaki gerilimlerin, iY, iX ve iZ
büyüklükleri de Y, X ve Z uçlarına iliúkin akımların toplam ani de÷erini
göstermektedir.
iZ = iX ise CCII pozitif akım taúıyıcı adını alır ve CCII+ sembolü ile
gösterilir. iZ = -iX ise CCII negatif akım taúıyıcı olarak isimlendirilir ve CCIIsembolü ile belirtilir. (5.1) ba÷ıntısından anlaúılaca÷ı gibi, Y ve Z için küçük iúaret
uç empedansları büyük, x için ise küçük olmalıdır.
5.2
CCII'nin gerçekleútirilmesi için iúlemsel kuvvetlendiriciler ve bipolar
tranzistorlarla devre kurulmasına dayanan tasarım yöntemleri bulunmaktadır. Bu
yöntemler, ilkesel olarak tümleútirilmeye elveriúli olsalar bile, özellikle iúlemsel
kuvvetlendiricilerden yararlanılmasına yönelik olanlar, gerçekleútirilme açısından
ekonomik de÷ildirler. Bunun baúlıca nedeni, her iúlemsel kuvvetlendirici için kırmık
üzerinde ayrı bir alana gereksinme duyulmasıdır. Karmaúık yapıdaki sistemlerin
küçük boyutta gerçekleútirilmesini sa÷layan CMOS teknolojisinin hızlı geliúimi
sonucunda, son yıllarda, analog fonksiyonları gerçekleútiren ve akım taúıyıcıları da
kapsayan CMOS devrelerin geniú çapta tümleútirilebilmesi mümkün kılınmıútır. Bu
bölümde, CMOS tekni÷i ile gerçekleútirilebilen iki ayrı akım taúıyıcı yapısı ele
alınacaktır.
5.1. CMOS CCII+ devresi
T3
T4
+VDD
T5
T6
T2
T1
iZ
iX
+vY
+vZ
vX
RX
I1
T7
I2
T8
-VSS
ùekil-5.2. Pozitif (evirmeyen) türden akım taúıyıcı yapısı.
CMOS tekni÷i ile gerçekleútirilen bir pozitif akım taúıyıcı devresi ùekil5.2'de verilmiútir. T3-T6 PMOS tranzistorları ile T7-T8 NMOS tranzistorları akım
aynası olarak görev yapmaktadır. I1 akım kayna÷ı devre için gerekli olan kutuplama
akımını sa÷lar. Tranzistorların eú, akım aynalarının birim kazançlı oldukları ve tüm
tranzistorların doyma bölgesinde çalıútıkları varsayılsın. Devrenin çalıúması
aúa÷ıdaki biçimde açıklanabilir:
5.3
T3-T4 tranzistorları T1 ve T2 tranzistorlarından birbirine eú akımların
akmasını sa÷larlar. Böylece VGS1 = VGS2 olur ki, bu da vY = vX olmasını sa÷lar. RX
direncinden akan iX akımı T2 tranzistorundan ve T3-T4 akım aynasından da akar. VX
> 0 olması durumunda iX = vX/RX akımı x ucundan dıúarıya do÷ru akacak,
dolayısıyla T3-T4 akım kayna÷ının akımı I1 + iX olacaktır. Bu akım, T5 tranzistoru ve
T7-T8 akım aynası ile Y ucuna yansıtılarak T1 tranzistorunun kaynak akımındaki
de÷iúimi kompanze eder, böylece iy daima sıfır olur. Aynı zamanda, T6 tranzistoru I1
+ ix akımını Z ucuna yansıtacaktır. Bu durumda, I1 = I2 yapılırsa, Z ucundan dıúarıya
do÷ru iZ = iX akımı akar. Fark edilebilece÷i gibi, iZ akımının yönü iX akımı ile
aynıdır. Bu nedenle, devre, pozitif (evirmeyen türden) akım taúıyıcı (CCII+)
olarak isimlendirilir.
5.2. Negatif akım taúıyıcı (CCII-)
T3
T4
T1
+vY
T5
+VDD
T6
I2
T2
iX
iZ
vX
+vZ
I1
T7
T8
T9
T10
-VSS
ùekil-5.3. Negatif (faz döndüren türden) akım taúıyıcı yapısı.
Negatif akım taúıyıcı yapısı ùekil-5.3'de verilmiútir. Bu devre, ùekil5.2'deki devreden türetilmiútir. Yapıda, T9 ve T10 tranzistorları I1 + iX akımını Z
ucuna yansıtırlar. I2 = I1 yapılması durumunda, z ucundan içeriye do÷ru bir iZ = iX
akımı akar.
5.3. Akım taúıyıcının performansı
Buraya kadar yapılan incelemelerde bütün tranzistorların eú oldukları ve
doyma bölgesinde çalıútıkları varsayılmıútır. Pratikte ise, tranzistorların birbirine
5.4
tam olarak eú olmamalarından ileri gelen bir hatanın ortaya çıkaca÷ı ve bu hatanın,
yapının performansında ideal performansa göre bazı sapmalara neden olaca÷ı
açıktır.
ùekil-5.2'deki devre ele alınsın. I1 akım kayna÷ının çıkıú direnci sonsuz
kabul edilsin. Bu durumda, küçük iúaretler için vy ve vx arasındaki iliúki
H1 =
R x gm 2 ( gm 4 gd 1 - gm 3 gd 4 )
R x gm 2 gm 3 gd 4 + gm 2 gd 2 + gm 3 gd 4
(5.2)
olmak üzere
v x = v y .(1 - H 1 )
(5.3)
biçiminde yazılabilir. (5.2) ba÷ıntısında gmi ve gdi büyüklükleri sırasıyla Ti (i =...)
tranzistorunun geçiú iletkenli÷ini ve savak iletkenli÷ini , RX ise X ucuna ba÷lanan
direnci göstermektedir. H1 << 1 ise Y ucundaki gerilim X ucuna yüksek do÷rulukta
aktarılacaktır, baúka bir deyiúle X ucundaki gerilim Y ucundaki gerilimi iyi bir
úekilde izleyecektir. Örnek olarak, RX = 1k, gm2 = 2.51 x 10-4 A/V, gm3 = 1.93 x 104
A/V, gd1 = gd2= 1.01 x 10-7 A/V ise H1 =0.05% olur.
X ucundan içeriye do÷ru bakıldı÷ında görülen küçük iúaret direnci
aúa÷ıdaki biçimde yazılabilir:
rx =
1 § gm 4 gd 5 + gm 8 gd 1 ·
.¨
¸
g m2 © g m 4 .( g m 8 + g d 5 ) ¹
(5.4)
Sayısal bir örnek verilirse, gm8 =2.52x10-4 A/V, gd5 = 1.02 x 10-7 A/V de÷erleri için
rx = 3.7 : bulunur ki, bu direncin de÷eri istenen özellikleri sa÷layacak kadar
küçüktür.
Y ucundaki küçük iúaret direnci hesaplanırsa
gd
1+ 1
g m3
(5.5)
ry =
g d7
ba÷ıntısı elde edilir. gd7 = 1.02 x 10-7 A/V için ry = 9.8 M: bulunur ki, bu da yeteri
kadar büyük bir direnç de÷eridir ve bu ucun gösterece÷i giriú direnci sonsuz kabul
edilebilir.
Z ucundaki uç direnci yaklaúık olarak T3-T6 akım aynasının çıkıú direnciyle
I2 akım kayna÷ının çıkıú direncinin paralel eúde÷erine eúittir ve
rz =
gd 6
1
+ g dI 2
(5.6)
5.5
biçiminde ifade edilebilir. (5.6) ba÷ıntısındaki gdI2 büyüklü÷ü I2 akım kayna÷ının
savak iletkenli÷idir. rz direncinin de÷eri tipik olarak birkaç M: mertebesindedir. Bu
direnç Wilson akım aynası yahut kaskod akım kayna÷ı kullanılarak arttırılabilir.
Devrenin yüksek frekanslardaki davranıúını inceleyelim. Yüksek
frekanslarda baskın kutup x ucuna ba÷lanan eúde÷er direnç ve kapasitelerden ileri
gelir. Bu kutup
f
x
=
R x gm 2 gm 4
2S ( R x g m 3 C1 + C 3 )
(5.7)
biçiminde ifade edilebilir. Bu ba÷ıntıdaki C3 ve C1 kapasiteleri
C 3 = ( C gs 3 + C gs 4 + C gs 5 + C gs 6 ) ve C1 = C gs 1
úeklinde tanımlanmıúlardır.
økinci kutup T3-T6 akım aynasından ileri gelmekte ve
fm =
gm 3
(5.9)
2S C 3
ba÷ıntısıyla verilmektedir. Bu kutup frekansı, yukarıdaki sayısal de÷erler için 5
MHz civarında olur.
Vx ve Vy gerilimleri arasındaki dengesizlik de
1/2
2( E 1 - E 2 ) § I 1 ·
¸
.¨
V OS = ( V T 1 V T 2 ) E 1 + E 2 ¨© E 1 + E 2 ¸¹
(5.9)
ba÷ıntısı ile verilebilir. (5.9) ba÷ıntısında VTi ve Ei büyüklükleri, sırasıyla, Ti
tranzistorunun eúik gerilimini ve geçiú iletkenli÷i parametresini göstermektedir. VOS
dengesizlik geriliminde birinci terim T1 ve T2 tranzistorlarının eúik gerilimlerinin
farklı olmasından ileri gelmektedir. Modern CMOS prosesinde bu bileúen birkaç
mV mertebesinde olur. økinci bileúen ise geometrideki sapmalardan ileri gelir.
Ba÷ıntıdan fark edilebilece÷i gibi, bu bileúeni azaltmak için W/L oranı azaltılabilir,
yahut I1 akım küçültülebilir.
5.6
IX
RX1
RX2
RX3
VY
RX3 >RX2 > RX1
ùekil-5.4a. Farklı RX de÷erleri için DC geçiú e÷risi (lineer de÷iúim bölgesi gösterilmiútir.)
RX3 >RX2 > RX1
VX/VY
1
RX3
RX2
RX1
Frekans, log
ùekil-5.4b. Farklı RX de÷erleri için frekans e÷rileri.
CCII’nin farklı RX de÷erleri için elde edilen DC geçiú karakteristi÷i ve
frekans e÷risi ùekil-5.4a ve ùekil-5.4b'de gösterilmiútir. ùekil-5.4'den görülebilece÷i
gibi, devre, verilen bir gerilimi geniú bir aralık içerisinde pozitif ve negatif akımlara
yüksek bir do÷rulukla çevirebilmektedir.
CCII+ ve CCII- devrelerini farklı topolojilerle gerçekleútirmek
mümkündür. CMOS tekni÷i ile gerçekleútirilen üç farklı devre topolojisi ùekil-5.5,
ùekil-5.6 ve ùekil-5.7’de görülmektedir.
5.7
T5
T6
T3
T4
T10
T9
iz = ix
x
Y
T2
I
X
v
y
I
B
Z
i
x
Rz
Rx
B
I
B
T13
T7
V
DD
T12
M11
v
T1
V
bias1
T14
T15
T8
V
bias 2
V
T16
SS
V
DD
T5
T6
T9
T3
T4
T10
T17
T21
T12
T18
T22
T11
I
v
B
i
x
i
z
x
Z
T1
T2
Y
X
R
v
I
y
I
B
Rz
x
B
I
V
V
B1
T7
B2
T8
T13
B
T14
T19
T23
T16
T20
T24
T15
-V
SS
ùekil-5.5. CMOS tekni÷i ile gerçekleútirilen CCII+ ve CCII- yapıları, Örnek-1.
5.8
T5
T14
T15
T7
T12
T8
T10
M9
T13
VDD
T16
T11
iz = ix
Z
I
X
bias
R
R
x
in +
in -
i
T1
Y
T2
Rz
x
Cc
bias
T3
T6
T4
T17
T18
VSS
VDD
T5
T7
T14
T12
T15
M16
T21
T19
T8
T10
T9
T11
I
bias
T13
i =-ix
z
Z
X
in -
T1
T2
in +
Y
Rz
R
R
x
i
x
Cc
bias
T3
T4
T6
T17
T18
T20
T22
VSS
ùekil-5.6. CMOS tekni÷i ile gerçekleútirilen CCII+ ve CCII- yapıları, Örnek-2.
5.9
V
DD
T4
T3
T1
T5
T6
iz = ix
M2
ix
M17
Z
vx
X
Rz
v
y
Y
T12
T9
Rx
T18
T11
T10
T8
T7
T16
T13
T15
T14
V
SS
ùekil-5.7. CMOS tekni÷i ile gerçekleútirilen CCII+ ve CCII- yapıları, Örnek-3.
5.10
5.4. Elektronik olarak kontrol edilebilen akım taúıyıcı (ECCII)
+VDD
T4
I1
T5 T5'
I1
IO
T4'
I2
I2
I2
Vref
T3
T3'
IB+i
IB-i
T2'
T6
T1
T2
IA
T6'
T8
T7
T1'
-VSS
ùekil-5.8. Elektronik olarak kontrol edilebilen akım taúıyıcı hücresi.
Elektronik olarak kontrol edilebilen akım taúıyıcı yapısı, akım transfer oranı
bir akım ya da bir gerilimle de÷iútirilebilen bir akım taúıyıcı düzenidir. ECCII'nin
tanım ba÷ıntıları
iY = 0
v X = vY
i Z = r h32 i X
(5.10)
biçimindedir. (5.10) ba÷ıntısındaki h32 büyüklü÷ü, de÷eri elektronik yoldan kontrol
edilebilen akım transfer oranıdır. ECCII yapısı ùekil-5.8'de verilmiútir. Bu devrede
T1, T2 ve T3 tranzistorlarından oluúan yapı grubu ile T1', T2' ve T3' den oluúan yapı
grubu, kare alan birer devre olarak davranırlar. T7, T8 tranzistorları ve IA akım
kayna÷ı, T3 ve T3' tranzistorlarına kutuplama gerilimi sa÷layan akım kontrollu bir
gerilim referansı devresi oluútururlar. Bütün tranzistorların doymada çalıútıkları ve
T5 ile T5' dıúındaki tranzistorların tümünün eúit W/L oranlarına sahip oldukları kabul
edilsin. Bu úart altında
5.11
2
I1
= 2IA+
( I B +i )
8IA
( I B - i )2
8IA
| I B | + |i| d 4 I A
I2= 2 I A+
olmak üzere, devrenin çıkıú akımı
§n IB·
¸.i
io = ¨
©2 I A¹
(5.11)
biçiminde ifade edilebilir. (5.11) ba÷ıntısından fark edilebilece÷i gibi, küçük iúaret
akımı, de÷eri elektronik yoldan de÷iútirilebilen bir k çarpanıyla çarpılarak çıkıúa
yansımaktadır. (5.11) ba÷ıntısı, aynı zamanda, n büyüklü÷ünün kazancın de÷iúim
aralı÷ını da belirleyen bir faktör oldu÷unu göstermektedir.
| I B | + |i| d 4 I A
úartı uyarınca, kazancı arttırmak üzere IB büyüklü÷ü istenildi÷i kadar büyütülemez.
Örne÷in, n=1 için k çarpanının maksimum de÷eri 2 ile sınırlanır. Buna göre kmaks <
2n yazılabilir. Devrenin tümü ùekil-5.9'da verilmiútir. Bu yapıda T9'dan T13'e kadar
olan tranzistorlar gerilimden akıma dönüútürücü olarak çalıúırlar. Bu yapıda T9-T10,
T11-T12, T17, T18, T15-T20 tranzistorlarının eú, akım kaynaklarının yansıtma
oranlarının 1 olduklarını ve tüm tranzistorların doymada çalıútıklarını kabul edelim.
MOS tranzistorların giriú direnci çok yüksek oldu÷undan, iy akımı iy = 0 alınabilir.
T9'dan T12'ye kadar olan tranzistorlar ve IC akım kayna÷ı birlikte bir gerilim izleyici
oluútururlar ve X ucundaki gerilimin Y ucundaki gerilimi izlemesini sa÷larlar. T13
tranzistoru, akım izleyici iúlevinin yerine getirilmesinin yanısıra, X ucunun düúük
empedanslı olmasını da sa÷lar.
X ucundan küçük bir i akımının akması durumunda, akım izleyici T13
tranzistorunun savak akımını IB + i de÷erine kadar arttırır. T15 tranzistoru, bu akımı
akım kuvvetlendiricisinin A ucuna yansıtırken, T16 tranzistoru da aynı akımı T17-T20
tranzistorlarından oluúan akım kayna÷ının giriúine getirir. 2IB sabit akım kayna÷ı
nedeniyle T17 ve T19 tranzistorlarının savak akımları (IB - i) de÷erini alırlar. Bu akım
da, akım kuvvetlendiricisinin B ucuna yansıtılır. Böylece, z ucundan dıúarıya do÷ru
bir iz = k.i çıkıú akımı akar. iz akımı ix akımı ile aynı yönde oldu÷undan, bu devre
5.12
ECCII+ olarak isimlendirilmektedir. T15 tranzistorunun B ucuna, T20 tranzistorunun
da A ucuna ba÷lanması durumunda ECCII- elde edilebilece÷i gösterilebilir.
+V DD
T11
T12
T14
T15
T13
Y
VY
T9
T10
X
IC
T16
IB+iX
VX
T17
T18
T19
T20
IB-iX
2IB
IX
-VSS
+VDD
IB
Z
IA
IZ
VZ
Vref
B
A
-VSS
ùekil-5.9. Elektronik olarak kontrol edilebilen akım taúıyıcı yapısı.
Devrenin ideal davranıúından sapmasının baúlıca nedenleri, tranzistorların
gm geçiú iletkenliklerinin sonlu olması ve tranzistorlar arasındaki dengesizliklerdir.
Akım kaynaklarının çıkıú dirençleri sonsuz kabul edilirse, devredeki gerilim-akım
çeviricinin geçiú iletkenli÷i hatası
' gm
gm
|
g d 10 + g d 12
g m 10
.100
(5.12)
biçiminde yüzde olarak ifade edilebilir. Bu ba÷ıntıdan hareketle gm10 = 2.51 x 10-4
A/V, gd10 = gd12 = 1.02 x 10-7 A/V de÷erleri için geçiú iletkenli÷i hatası hesaplanırsa
'gm/gm =%0.08 bulunur. x ve y uçlarından içeriye do÷ru bakıldı÷ında görülen giriú
empedansları
5.13
rx =
( g m 9 + g m 10 ).( g d 10 + g d 12 )
g m 9 g m 10 g m 13
(5.13)
rz =
1
gd 5 + gd 6
(5.14)
biçiminde ifade edilebilirler. gm6 = gm10 = 2.51 x 10-4 A/V ve gm3 = 3.3x10-4 A/V için
rx = 4.9 Ohm bulunur. Yine, gd5 = gd6 = 1.02 x 10-7 A/v için rz = 4.9 MOhm elde
edilir. Wilson veya kaskod akım kaynaklarının kullanılmasıyla bu son de÷er daha
da büyütülebilir. x ucundaki dengesizlik gerilimi
1/2
V OS = ( V T 9
§
·
E 9 - E 10 ¨¨ I D 9 + I D 10 ¸¸
.
- V T 10 ) E 9 + E 10 ¨ ( E 9 + E 10 ) ¸
¨
¸
4
©
¹
(5.15)
ba÷ıntısıyla ifade edilebilir. (5.15) ba÷ıntısındaki birinci terim eúik gerilimlerinin
farklı olmasından ileri gelir. økinci dengesizlik bileúeni ise geometrideki
sapmalardan kaynaklanır.
Farklı n de÷erleri için ız/ix akım kazancının IB/IA oranıyla ne úekilde
de÷iúece÷i ùekil-5.10'da gösterilmiútir.
iz/ix
n=5
n=3
n=1
IB/IA
ùekil-5.10. Farklı n de÷erleri için (iz/ix) akım transfer oranının (IB/IA) oranına ba÷ımlılı÷ı.
5.14
5.5. Akım taúıyıcılarda ideal olmama etkilerinin modellenmesi
ødeal bir akım taúıyıcıda, giriú ve çıkıú empedansları sonsuz, band geniúli÷i
sonsuz, X ucundan içeriye do÷ru bakıldı÷ında görülen empedans sıfırdır. X ucundan
akacak akımla X ve Z uçlarındaki gerilimler için herhangi bir dalgalanma sınırı söz
konusu de÷ildir. Gerçek bir akım taúıyıcıda, ideal akım taúıyıcıdan farklı olarak,
giriú (Y) ve çıkıú (Z) empedansları sonlu, X ucundan görülen empedans sıfırdan
büyük, vx/vy ve iz/ix geçiú fonksiyonlarının band geniúli÷i sonlu olmaktadır. Bunun
yanısıra, X ucundaki akım ve gerilim
I X min i X (t ) I Xmaks
V X min v X (t ) V Xmaks
sınırları arasında, Z ucundaki gerilim de
VZ min v Z (t ) VZmaks
sınırları arasında de÷iúmekte, bu sınırlar zorlandı÷ında, devre karakteristiklerinde
doyma bölgesi ortaya çıkmaktadır.
Bu bölümde, söz konusu idealsizlikleri modellemek üzere, basit yapılı ve
yüksek do÷ruluklu bir akım taúıyıcı makromodeli verilecektir.
Makromodel
h .I
VOFF
+
R C1 V C1
D6
+VDD
-
X
-
+V Y
R
+VZ
CO
CY
RO
IZ
-V
SS
IX
+VX
L
D
D1
RC1
R E1
-
VE1
2
RP
D5
P
D
CP
R E1 V
r X1
E1 r
X2
+
3
k VrX1
+
3
1 Y
+
k V
4 rX1
+
-VSS
k V
D4
-
VC1
+
-
+VDD
+
k 2 VX
ùekil-5.11. Akım taúıyıcı makromodeli.
+
5.15
Akım taúıyıcının lineer ve lineer olmayan davranıúını modelleyen makromodel
ùekil-5.11’de görülmektedir. Makromodel oluúturulurken, akım taúıyıcının giriúçıkıú karakteristiklerinden ve frekans e÷rilerinden yararlanılmıú, model bu
karakteristikleri aslına uygun bir biçimde verecek ve az sayıda lineer olmayan
eleman içerecek biçimde düzenlenmiútir. Bunun için VX-VY ve VZ-VY gerilim
geçiú e÷rilerinin, IX-VY ve IZ-VY akım geçiú e÷rilerinin, X, Y ve Z uçlarından içeriye
do÷ru bakıldı÷ında görülen ZX, ZY ve ZO empedanslarının frekansla de÷iúim
e÷rilerinin ölçü yoluyla yahut simülasyonla çıkartılması gerekmektedir. Model
parametreleri, yukarıda de÷inilen karakteristiklerden yararlanılarak kolayca
bulunabilmektedir. Kurulan lineer olmayan eúde÷er devre dokuz R elemanı, üç C
elemanı, bir L elemanı, beú ba÷ımlı kaynak, beú ba÷ımsız gerilim kayna÷ı ve 6 diyot
elemanı içermektedir. Bu elemanlar yardımıyla yapının gerilim ve akım izleme
karakteristikleri, giriú ve çıkıú empedansları, akım ve gerilim sınırlama özellikleri
yeteri kadar do÷ru olarak modellenebilmektedir. Y ucuna iliúkin özellikleri temsil
etmek için bir ba÷ımsız gerilim kayna÷ı, bir R ve bir de C elemanı kullanılmıútır. X
ucuna iliúkin giriú empedansının, akım ve gerilim sınırlama özelliklerinin
modellenmesi için beú R elemanı, bir C elemanı, bir L elemanı, iki ba÷ımlı gerilim
kayna÷ı, dört ba÷ımsız gerilim kayna÷ı ve dört de diyot elemanı öngörülmüútür. X
ucundan içeriye do÷ru bakıldı÷ında, ikinci dereceden bir empedans fonksiyonu ile
ifade edilebilen bir empedans karakteristi÷i elde edilir. Rezonans karakteristi÷i
biçimindeki bu davranıúı modellemek üzere, eúde÷er devreye L elemanı eklenmiútir.
Z ucuna iliúkin çıkıú empedansı ve gerilim sınırlama özelliklerinin temsil edilmesi
için de bir ba÷ımlı akım kayna÷ı, üç R elemanı, bir C elemanı, iki ba÷ımsız gerilim
kayna÷ı ve iki diyot elemanı kullanılmıútır.
Gerçek akım taúıyıcı ve makromodel karakteristikleri
Makromodelin do÷rulu÷unu göstermek üzere, ùekil-5.5’de verilen CMOS
akım taúıyıcı için SPICE 2. DÜZEY MOS modeli kullanılarak gerçek devre için
elde edilen simülasyon sonuçlarıyla önerilen makromodel ile elde edilen SPICE
simülasyonu sonuçları karúılaútırılmıútır. Örnek olarak seçilen CMOS akım
taúıyıcıya iliúkin makromodel parametreleri Tablo-5.1’de verilmiútir.
5.16
Tablo-5.1. Makromodel parametreleri.
Eleman
Eleman de÷eri
Eleman
RY
CY
rX1
rx2
CX
LP
RP
k1
k2
RO
RC1
VC1
RE1
VE1
RC2
1E12 Ohm
0.0489 pF
327 Ohm
400 Ohm
0.1 pF
40 PH
32kOhm
1
1
620 kOhm
10 kOhm
5.72 V
10 kOhm
1.1 V
1860 Ohm
k3
k4
IS1
IS2
IS3
Is4
IS5
IS6
VOFF
CO
VC2
RE2
VE2
h
-
Eleman
de÷eri
-9
-2.2
1E-14A
1E-14A
1E-14A
1E-14A
1E-14A
1E-14A
-63 mV
.5 pF
3.3 V
3 kOhm
1.2 V
1
-
Z ucu açık devre, RX =1k iken elde edilen VX-VY ve VZ-VY gerilim geçiú
e÷rileri ùekil-5.12’de görülmektedir. ùekil-5.13’de RX = 0 için eleman modeli ve
makromodelle elde edilen IX - VY de÷iúimleri , baúka bir deyiúle X ucundaki
akımının VY ile de÷iúimi yer almaktadır.
X ucunun açık devre edilmesi durumunda bu uçtaki VX geriliminin VY
gerilimi ile ne úekilde de÷iúece÷i eleman modeli ve makromodel ile hesaplanmıú,
sonuçlar ùekil-5.14’de gösterilmiútir.
X ucundan içeriye do÷ru akıldı÷ında görülen ZX empedansının frekansla
de÷iúim e÷risi ùekil-5.15’de , Z ucundan içeriye do÷ru bakıldı÷ında görülen ZO
empedansının de÷iúim e÷risi de ùekil-5.16’da verilmiútir. vX/vY ve vZ /vY gerilim
geçiú e÷rilerinin frekansla de÷iúimleri ùekil-5.17’de gösterilmiútir. ùekillerden
kolaylıkla fark edilebilece÷i gibi, verilen model, akım taúıyıcının lineer ve lineer
olmayan davranıúını aslına uygun bir biçimde modellemektedir. Makromodel
yardımıyla elde edilen sonuçlar, eleman modelleri yardımıyla elde edilen sonuçlarla
iyi bir uyum sa÷lamaktadır.
5.17
ùekil-5.12. RX = 5k, RZ = oo için eleman modeli ve makromodel yardımıyla elde edilen VXVY ve VZ-VY de÷iúimleri.
ùekil-5.13. X ucundan içeriye ve dıúarıya do÷ru akıtılan akımın sınırları.
5.18
r.
ùekil-5.14. RX = f için VX - VY de÷iúimi.
ùekil-5.15. X ucundan görülen ZX empedansının frekansla de÷iúimi için makromodel ve
eleman modeli yardımıyla elde edilen simülasyon sonuçları.
5.19
ùekil-5.16. Z ucundan görülen ZO empedansının frekansla de÷iúimi için makromodel ve
eleman modeli yardımıyla elde edilen simülasyon sonuçları.
ùekil-5.17. vx/vy ve vz/vy gerilim transfer oranlarının frekansla de÷iúimi için makromodel ve
eleman modeli yardımıyla elde edilen simülasyon sonuçları.
5.20
KAYNAKLAR
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
K.C. Smith, A. Sedra, The current conveyor - a new circuit building block, IEEE
Proc., 56, pp.1368-1369, 1968.
A. Sedra, K.C.Smith, A second generation current conveyor and its applications,
IEEE Trans. on Circuit Theory, CT-17, pp.132-134, 1970.
S.-I. Liu, H.-W. Tsao, J. Wu, T.-K.Lin, MOSFET capacitor filters using unity
gain CMOS current conveyors, Electronics Letters, 26, pp.1430-1431, 1990.
M.C. Chang, C. Toumazou, 3V MOS current conveyor for VLSI technology,
Electronics Letters, 29, 317-318, 1993.
A.S. Sedra, G.W. Roberts, F.Gohh, The current conveyor: History, Progress and
New Results, IEEE Proc., 137, 78-77, 1990.
W.S. Amptorn, V. Riewruja, F. Cheevasuvit, Integrible CMOS-base realization of
current conveyors, Int.J. Electronics , 71, 793-798, 1991.
H. Sedef, Akım taúıyıcı kullanarak aktif devre sentezinde yeni olanaklar, Doktora
tezi, YTÜ FBE, Elektronik ve Haberleúme Mühendisli÷i ABD. Ocak 1994.
C.M. Chang, P.-C.Chen, Realization of current-mode transfer function using
second-generation current conveyors, Int. J. Electronics, 71, 809-815, 1991.
B. Yenen, CMOS akım taúıyıcıların makromodellerinin oluúturulması ve akım
taúıyıcılı süzgeçlerin analizi, Yüksek Lisans Tezi, øTÜ FBE, Elektronik ve
Haberleúme Mühendisli÷i ABD. Ocak 1995.
B. Yenen, N. Tarım, H. Kuntman, Aktif süzgeç simülasyonuna yönelik bir akım
taúıyıcı makromodeli, Elektrik Müh. 6. Ulusal Kongresi Bildiri Kitabı, Cilt 3,
1023-1026, Uluda÷ Üniversitesi, Bursa, 11-17 Eylül 1995.
N. Tarım, B. Yenen and H. Kuntman, Simple and accurate nonlinear currentconveyor macromodel,
Melecon 96, Proceedings of 8th Mediterranean
Electrotechnical Conference, Vol.1, pp.447-450, Bari, Italy, May 13-16, 1996.
H. Tek, F. Anday, Voltage transfer function synthesis using current conveyors,
Electronics Letters, 25, 1552-1553, 1989.