ELE222 ELEKTRONİĞE GİRİŞ (CRN: 11248, 11249, 11250)
Yarıyılsonu Sınavı 8 Ocak 2009 9.00-11.00
Rıza Can TARCAN / Metin YAZGI / İnci ÇİLESİZ
Bu sınavda çözüm için kullandığınız kağıtların yanında SADECE hesap makinası ve kendi el yazınız ile hazırlanmış A4 boyutlu 2
adet (arkalı-önlü) "kopya kağıdı" kullanma hakkınız var. Sınav sonunda kağıtlar toplanırken "kopya kağıdı"nızı sınav kağıtları
ile beraber veriniz. Bulduğunuz sonuçların birimlerini yazmayı ve birim uyumuna dikkat etmeyi unutmayınız.
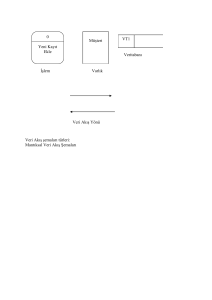
Soru-1 Şekil-1’de işlemsel kuvvetlendirici kullanılarak
tasarlanmış bir kuvvetlendirici devresi görülmektedir.
a) Şekil-1’deki devrede Vout1 gerilimini Vin’e bağlı olarak
bulunuz. (10)
b) Şekil-1’deki işlemsel kuvvetlendirici +10V ve -10V luk
kaynaklarla beslenmektedir. Devrenin girişine Vin = 2V’luk
giriş gerilimi uygulanırsa çıkışta Vout1’in değeri ne olur? (10)
c) Şekil-1’deki devrede görülen İ.K.’nın pozitif girişindeki
0,2V’luk gerilimin etkisini giderip toplam olarak
Vout/Vin=+15’lik kazanç elde edecek şekilde, çıkışa kaskat
bağlanacak işlemsel kuvvetlendiricili bir kat tasarlayınız. (10)
Şekil-1
Not: Direnç değerlerini kΩ mertebesinde olmak şartıyla
(belirtilen kazancı sağlayacak şekilde) istediğiniz gibi
seçebilirsiniz.
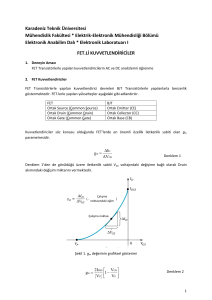
VDD = +5V
R1
RD1
ro
RS2
vo
Rg
M1
vg
R2
RS1
ri
VSS = -5V
M2
Ry
4k
Soru-2 Şekil-2’de verilen MOS’lu devre için
β1/2=Kn1 = 0,5 µn Cox (W/L) = 500 µA/V2,
β2/2=KP2 = 0,5 µP Cox (W/L) = 200 µA/V2,
Vt1 = -Vt2 = 1,2 V; VA1 = VA2 = ∞ ve Rg = 4k olarak verilmiş
olsun.
a) DC çalışma noktasında ID1 = 0,2 mA, ID2=0,5 mA,
VDS1 = 2 V, VDS2 = -6 V ve ri = 100k olacak şekilde direnç
değerlerini bulunuz. (20)
b) vo/vg kazancını ve devrenin çıkış direncini bulunuz. (20)
Şekil-2
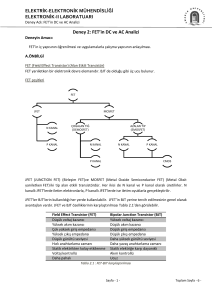
Soru 3- Şekil-3a’da kullanılan tranzistorlar için
hFE= βF = 250, |VBE| = 0,6V, VT = 25mV ve
VA = ∞ değerleri verilmiştir.
a) VE4 gerilimi 0V olacak şekilde R8 direncini
hesaplayıp, ri giriş ve ro çıkış dirençlerini
bulunuz. (10)
b) Kv = Vo/Vi küçük işaret gerilim kazancını
bulunuz ve fark kuvvetlendiricisinin CMRR
katsayısını bulunuz. (10)
c) Devrenin doğru akım kutuplama şartlarını
değiştirmeden Kv = Vo/Vi gerilim kazancının
hangi direnç ile belirlenebileceğini
Şekil-3a
belirtikten sonra |Kv| = 1000 olacak şekilde
bu direncin yeni değerini hesaplayınız. (10)
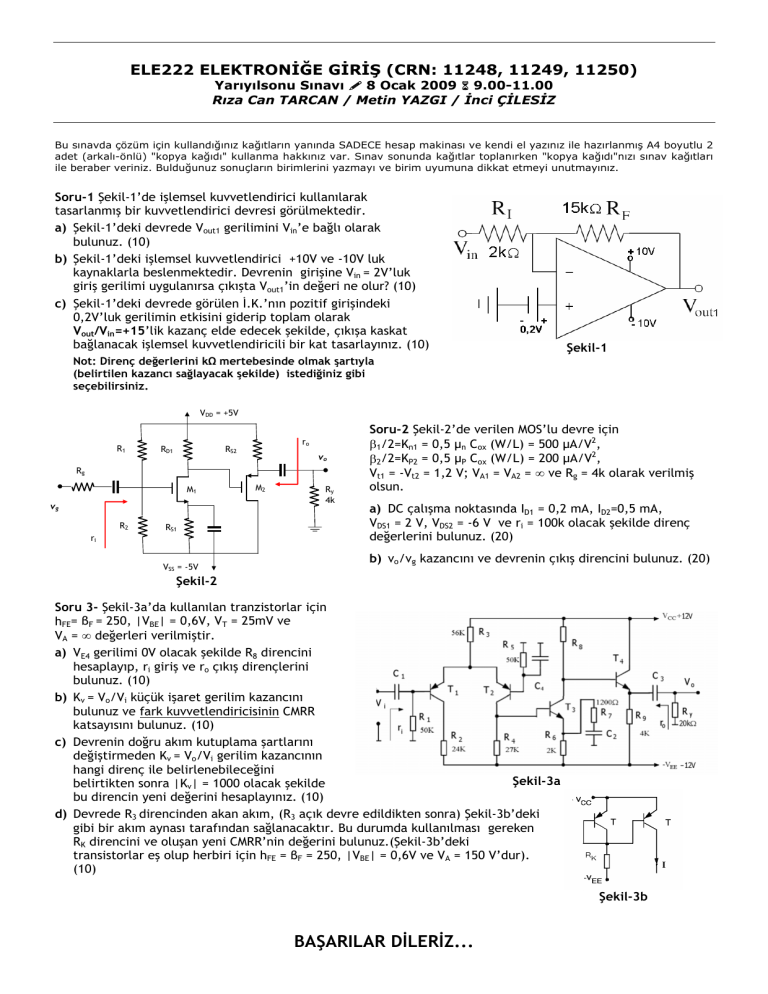
d) Devrede R3 direncinden akan akım, (R3 açık devre edildikten sonra) Şekil-3b’deki
gibi bir akım aynası tarafından sağlanacaktır. Bu durumda kullanılması gereken
RK direncini ve oluşan yeni CMRR’nin değerini bulunuz.(Şekil-3b’deki
transistorlar eş olup herbiri için hFE = βF = 250, |VBE| = 0,6V ve VA = 150 V’dur).
(10)
Şekil-3b
BAŞARILAR DİLERİZ...
Ç Ö Z Ü M L E R
1. PROBLEM
a) İ.K.’ya negatif geribesleme (çıkışı ile negatif girişi direnç (RF) ile bağlanmış) olduğundan VP=VN (1) yazılabilir.
Tabi bu durum çıkış kaynakların belirlediği sınır değerlere ulaşmadığı sürece geçerlidir. (1) ifadesi ve İK’nin
girişlerinden akım çekmeyeceği bilgisi yardımıyla akım ve gerilim denklemleri yazılırsa
Vin − V N V N − Vout1
V − 0.2V 0.2V − Vout1
=
⇒ in
=
RI
RF
2kΩ
15kΩ
(2) elde edilir.
⇒ Vout1 = 1.7V − 7.5Vin
b) İK’nin çıkış gerilimi kaynakların belirlediği sınırları aşamaz. − 10V ≤ Vout1 ≤ 10V (3) Buradan hareketle
Vin = 2V ⇒ Vout1 = 1.7V − 7.5Vin = −13.3V < −10V ⇒ Vouıu1 = −10V elde edilir. Yani Vout1 -10V’ta sınırlanır.
c) Toplam kazanç pozitif istendiğinden aynı konfigurasyona sahip devreden (faz çeviren kuvvetlendirici) bir tane
daha kullanılarak çözüme ulaşılabilir. Devre Şekil-4’de verilmektedir. İkinci kat için süperpozisyon ilkesi
uygulanırsa:
Vout = −
RF 2
R
Vout1 + (1 + F 2 )V2
RI 2
RI 2
15Vin = −
+ (1 +
RF 2
(1.7V − 7.5Vin )
RI 2
RF 2
)V2
RI 2
Şekil-4
sonucuna ulaşılır. Buradan Vin’li ifadelerle kendi aralarında diğer ifadelerde kendi aralarında eşitlenirse
15Vin = −
0=−
R
RF 2
( −7.5Vin ) ⇒ F 2 = 2
RI 2
RI 2
RF 2
R
3.4V
1.7V + (1 + F 2 )V2 ⇒ 0 = −2 x1.7V + (1 + 2)V2 ⇒ V2 =
≅ 1.13V
RI 2
RI 2
3
RF2=2kΩ
RI2=1kΩ alınabilir
2. PROBLEM
Probleme başlarken MOS devrelerde MOS transistörlerin doymada çalışması koşulunu sağlamaları gerektiğini
anımasayalım.
V DS 2 = VDD − VSS − I D 2 RS 2 = 5V − (−5V ) − 0,5mA ⋅ RS 2 = 6V denkleminden RS 2 = 8k olarak bulunduktan
⎡1
W⎤
(VGS 2 − Vt 2 ) ⇒ VGS 2 = ±
sonra I D 2 = ⎢ µ p C ox
L ⎥⎦ 2
⎡1
⎣2
2
uygun çözüm ( VGS 2 < Vt 2 olacak biçimde) VGS 2
I D2
+ Vt 2 = ±1,58V − 1,2V den PMOS için
W⎤
⎢⎣ 2 µ p C ox L ⎥⎦
2
= − 2,78V ya da VSG 2 = 2,78V
2/6
Ç Ö Z Ü M L E R
V S 2 = V SS + V DS 2 = 1V ⇒ VG 2 = V D1 = V S 2 − V SG 2 = 1V − 2,78V = − 1,78V olduğu için
RD1 =
VDD − VD1 5V + 1,78V
=
= 33k 9
I D1
0,2mA
Ayrıca
W⎤
⎡1
2
2
I D1 = ⎢ µ n C ox ⎥ (VGS1 − Vt1 ) = 0,5m(VGS1 − 1,2V ) = 0,2mA denkleminden
L ⎦1
⎣2
VGS1 = ±
I D1
W⎤
⎡1
C
µ
n
ox
⎢⎣ 2
L ⎥⎦ 1
+ Vt1 den NMOS için uygun çözüm olarak VGS 1 = 1,83V elde edilir.
VDS1 = V DD − VSS − I D1 ( RD1 + RS 1 ) = 5V − (−5V ) − 0,2mA ⋅ (33k 9 + RS1 ) = 2V denkleminden
RS 1 =
V S 1−VSS − 1,78V − 2V − (−5V )
=
= 6k1 bulunur.
I D1
0,2mA
W⎤
⎡1
2
2
I D1 = ⎢ µ n C ox ⎥ (VGS1 − Vt1 ) = 0,5m(VGS1 − 1,2V ) = 0,2mA denkleminden de
L ⎦1
⎣2
VGS1 = ±
I D1
W⎤
⎡1
⎢⎣ 2 µ n C ox L ⎥⎦
1
+ Vt1 den ( VGS 2 > Vt 2 olacak biçimde) uygun çözüm olarak VGS 1 = 1,83V elde edilir.
Burada ilginç bir durumla karşılaşıyoruz: Baz bölücü dirençler öyle alınmalı ki 1. MOS’un geçidinde
VG1 = VGS 1 + VS1 = 1,83V + (−1,78V − 2V ) = −1,95V sağlansın.
Geçitten içeri akım akmayacağına göre hem
VG = VDD +
R2
[VDD − VSS ] = VSS + R2 10 = −1,95V ⇒ R2 = − 1,95 + 5 = 0,305
R2 + R1
R2 + R1
R2 + R1
10
olacak hem de
ri = R1 || R2 =
1
1
1
+
R1 R2
=
R1 R2
= 100k olacak. Buradan kolaylıkla görürüz ki
R1 + R2
ri
R2
100k
=
=
= 0,305 ⇒ R1 = 328k ve
R1 R1 + R2
R1
1
1
1
1
1
1
=
+
=
=
+
⇒ R2 = 144k
ri R1 R2 100k 328k R2
3/6
Ç Ö Z Ü M L E R
Kazanç hesaplarına gelince
gm2vgs2
Rg
vo
vgs2
+
+
gm1vgs1
vg
R1||R2
vgs1
RD1
RS2
Ry
W⎤
⎡
g m1 = ⎢2µ n C ox ⎥ (VGS1 − Vt1 ) = 2 * 0,5m * (1,83V − 1,2V ) = 0,63mA / V
L ⎦1
⎣
W⎤
⎡
g m 2 = ⎢2µ p C ox ⎥ (VGS 2 − Vt 2 ) = 2 * 0,2m * (2,78V − 1,2V ) = 0,63mA / V
L ⎦2
⎣
v o = g m 2 v gs 2 ( RS 2 || R y ) = g m 2 ( RS 2 || R y )v gs 2
v gs 2 = − g m1v gs1 RD1 − vo = −( g m1v gs1 R D1 + v o )
v gs1 =
ri
R1 || R2
vg =
vg
R g + R1 || R2
R g + ri
[
v o = − g m 2 ( RS 2 || R y ) g m1v gs1 RD1 + v o
]
⎡
⎤
⎫⎪
⎧⎪ r
v o = − g m 2 ( RS 2 || R y ) ⎢ g m1 R D1 ⎨ i v g ⎬ + vo ⎥
⎪⎩ R g + ri ⎪⎭
⎢⎣
⎥⎦
g m1 g m 2 RD1 ( RS 2 || R y ) ⎛ ri
vo
⎜
=−
1 + g m 2 ( RS 2 || R y ) ⎜⎝ R g + ri
vg
⎞
⎟ = − 0,63 ⋅ 0,63 ⋅ 33k 9(8k || 4k ) ⎛⎜ 100k ⎞⎟ = − 12,87
⎟
1 + 0,63(8k || 4k )
⎝ 4k + 100k ⎠
⎠
ro = RS 2 = 8k olduğu ise küçük işaret devresinden açıkça görülmektedir.
4/6
Ç Ö Z Ü M L E R
3. PROBLEM
1 numaralı çevrimde
denklemerinden
I E = I E1 + I E 2 kabul ederek VCC = I E RE + VEB + I B1 R1 ve I B1 = I B 2 =
I E = 200µA ve re1 = re 2 = re =
2I E
βf
VT
= 250Ω bulunur.
I E1
1
3
2
2 numaralı çevrimden
I E3 =
I C 2 ≅ I E 2 kabulu ile ( I B 3 − I C 2 ) R 4 +VBE 3 + I E 3 R6 = 0 denkleminden
I C 2 R4 − VBE 3
≅ 1mA ve re 3 = 25Ω bulunur.
R4
+ R6
βf
VE 4 = 0V olduğuna göre VB 4 = 0,6V ve I E 4 =
3 numaralı çevreden ise
0 − (−VEE )
= 3mA ve re 4 = 8,33Ω bulunur.
R4
VCC − VB 4
I
= I C3 + E4
β f olacağından I C 3 ≅ I E 3 = 1mA olduğu düşünülürse
R8
R8 = 11k 265 bulunur.
Devrenin giriş direnci ri ' =
β f (re1 + re 2 || R3 ) ve ri = r i ' || R1 = 38k 6
Emetör çıkışlı devrenin çıkış direnci ro = R9 || (
R8
β f + re 4 ) = 44,5Ω
olarak bulunur.
b. şıkkı:
ri 3 = β f ( re 3 + R 6 || R 7 ) = 193 k
ri 4 = β f ( re 4 + R9 || R y ) = 835k
5/6
Ç Ö Z Ü M L E R
K v=
R9 || R y
v e1, 2
vo
v v
v
− R8 || ri 4
R || r
R 3 || re 2
olduğundan
= o ⋅ c3 ⋅ c 2 ⋅
=
⋅
⋅ 4 i3 ⋅
vi v c 3 vc 2 ve1, 2 vi
re 4 + R9 || R y re 3 + R6 || R7
re 2
re + R 3 || re 2
K v=
vo
= − 687 bulunur.
vi
Kazanç bulmak için bir başka yol da
K v=
R9 || R y
− R8 || ri 4
vo
v v v
R || r
= o ⋅ c3 ⋅ c 2 =
⋅
⋅ 4 i 3 olup sonuç yine aynı çıkar.
vi v c 3 v c 2 vi
re 4 + R9 || R y re 3 + R6 || R7
2re
CMRR = 20 log
2 RE + re
= 53dB
re
c. şıkkı:
Devrenin kazancı DC kutuplama koşulları değiştirilmeden (DC açıdan C2 ve C3 kapasiteleri tarafından
yalıtıldıklarından) R7 ve Ry dirençleri ile değiştirilebilir. R y → ∞ bile olsa son katın kazancı ancak 1 olacağından
toplam kazanç çok az değişir. Bu durumda kazanç R7 direnci ile değiştirilebilir.
K v=
R9 || R y
R4 || β f (re 3 + R6 || R7 )
− R8 || ri 4
vo
v v v
olduğundan
= o ⋅ c3 ⋅ c 2 =
⋅
⋅
vi v c 3 v c 2 vi
re 4 + R9 || R y re 3 + R6 || R7
2re
K v=
27k || 250(25Ω + R6 || R7 )
vo
− 11k115
= 0,998 ⋅
⋅
25Ω + R6 || R7
250Ω
vi
denkleminde
R7 → 0 yani R6 || R7 = 0 olursa K v = 0,998 ⋅
artmaktadır.
K v = −1000 = 0,998 ⋅
− 11k115 27 k || 250(25Ω )
= −9003 ’e kadar
⋅
25Ω
250Ω
27k || 250(25Ω + 2k || R7 )
− 11k115
⋅
sağlayan R7 = 640Ω olarak bulunur.
25Ω + 2k || R7
250Ω
d. şıkkı:
IE =
VCC − (−VEE ) − VEB
= 200µA sağlayacak R K = 117 k
RK
ro =
VA
150V
=
= 750k
I E 200 µA
CMRR = 20 log
2ro + re
= 75dB
re
6/6