Fizik 101: Ders 15 Ajanda

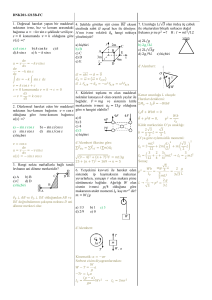
Fizik 101: Ders 15
Ajanda

İki boyutta elastik çarpışma

Örnekler (nükleer saçılma, bilardo)

Impulse ve ortalama kuvvet
İki boyutta 2 cismin elastik çarpışması
Öncesi
Sonrası
m1
v1,i
m1
KM
v1,f
KM
VKM
VKM
m2
v2,i
P korunduğundan VKM sabittir!!
m2
v2,f
Elastik Çarpışmada Enerji:
Önceki slayttan:
v *1,i  v *1,f
2
2
1 boyuttaki anlamı:
v*1,f = -v* 1,i
v*2,f = -v*2,i
2 yada 3 boyutta:
v *1,i  v *1,f
v * 2 ,i  v * 2 ,f
Elastik Çarpışma:

Görüyoruz ki:
KM çerçevesi:
v *1,i  v *1,f
v * 2 ,i  v * 2 ,f
v*1,f
v*1,i

v*2,i
KM
v*2,f
 = “çarpışma açısı”
Ders 15, Soru 1
Elastik Çarpışma

Aşağıda iki çarpışma verilmiştir. İlkinde bir golf topu V hızı
ile durgun olan bir bowling topuna çarpıyor ve ikincisinde V
hızı ilen gelen bowling topu duran bir golf topuna çarpıyor.

Hangi durumda golf topunun hızı çarpışmadan sonra daha fazladır?
(a) 1
(b) 2
V
1
(c) aynı
V
2
Ders 15, Soru 1
Çözüm


İki cismin elastik çarpışmadan önce birbirine yaklaşma hızı
ile çarpışmadan sonra birbirinden uzaklaşma hızı aynıdır.
Bowling topu golf topundan daha ağır olduğundan her iki çarpışmada da
hızı daha az değişecektir.
V
1
V
2
Ders 15, Soru 1
Çözüm


İlk durumda bowling topu hemen hemen durgun kalacak ve golf topu Vye
yakın bir hızla geri dönecek.
İkinci durumda bowling topu V hızına yakın bir hızda yoluna devam edecek
dolayısıyla golf topu 2V hızına yakın bir hızla geri tepecektir.
V
1
V
2V
2
2-Cismin 2 Boyutta Elastik Çarpışması



Çarpışma öncesi hızları bildiğimizi farz edelim.
Çarpışmadan sonra cisimlerin hareketleri hakkında bilgi
elde etmek istiyoruz.
 Yani: v1x,f , v1y,f , v2x,f , v2y,f
Başka ne biliyoruz :
 Elastik bir çarpışmada kinetik enerji ve momentum
korunur. Bunlardan 3 denklem elde ederiz:
Ef = Ei
 Px,f = Px,i
 Py,f = Py,i


(Burada Px = p1x + p2x = m1v1x + m2v2x vs)
3 denklem ve 4 bilinmeyen var:
 Başka bilgilere ihtiyacımız var (çarpışma açısı,
kütleler).
2 Boyutta Elastik Çarpışması:
Nükleer Çarpışma

Kütlesi M bilinmeyen bir parçacık başlangıçta
durgundur. Kütlesi m olan başka bir parçacık pi
momentumu ile çarpar. Çarpışmadan sonra, çarpan
parçacığın momentumu pf olarak ölçülüyor.

Verilenler pi , pf ve m cinsinden M’yi bulun.
durgun
m
M
pi
P
M
m
pf
önce
sonra
2 Boyutta Elastik Çarpışması:
Nükleer Çarpışma
Bilinenler:
pi, pf, m
durgun
y
Arananlar:
Px, Py, M
x
Elde var 3 denklem:
m pi
M
önce
1) x yönünde momentumun korunumu
2) y yönünde momentumun korunumu
P
3) enerjinin korunumu
3 bilinmeyen 3 denklem! Çözüm MÜMKÜN!
pf
sonra
Kinetik Enerji

Kinetik Enerji :
K = 1/2mv2
Kinetik enerjiyi momentum cinsinden
ifade etmek mümkün:
K = ½ mv 2
m 2v 2

2m
( m v )2

2m
p2
K=
2m
2 Boyutta Elastik Çarpışması:
Nükleer Çarpışma


Momentumun korunumu: pi = pf + P
  P2 = (pi -pf )2
pf
P
pi
Kinetik enerji korunumu:
p i2
2m

pf2
2m
+
2
P
2M
Mom. Korun. P 2  (p i - p f )2
P2
 p i2
pf2 
 2M 

 2m 2m 
 (p i - p f )2 
M  m 2

2
 p i p f 
2 Boyutta Elastik Çarpışması:
Nükleer Çarpışma
 (pi - pf )
M  m 2
2
 p i - p f
2



pf
P

Sonuç:

Eğer pi ve pf ölçer ve m biliniyorsa M değeri
bulunur.


pi
Görmediğimiz bir şey hakkında bir şeyler öğrenebiliriz!
Atomik, nükleer ve parçacık fiziğinde yapılan
onca işin arkasındaki temel fikir budur.
Rutherford Saçılması

Enerjisi, Ei bilinen helyum çekirdeği ( parçacıkları)
ile bilinmeyen bir örnek dövülür. Gelen parçacıklara
göre çarpışmadan ~180o ile geri dönen parçacıkların
enerjisi Ef ölçülür.
Ei
Ef
detektör
(enerji ölçer)
Bilinmeyen
madde
Rutherford Saçılması
pf
 (pi - pf )2 
M  m 2

2
 p i - p f 

P
pi
180o durumunda çok daha basit:
 (p i + pf )2 
(v i + v f )(v i + v f )


M m 2
m
2 
(v i + v f )(v i - v f )
p f 
 p i
M
(v i
m
(v i
+ vf )
- vf )
1 mv f 2  M - m  2
Ef

 2
 
2
M + m
1 mv
Ei
i
2
vf  vi
(M - m )
(M + m )
M çözülürse


m1 + Ef 
Ei 

M

Ef 
1 
E
i 

Rutherford Saçılması

Enerjisi, Ei bilinen helyum çekirdeği ( parçaçıkları)
ile bilinmeyen bir örnek dövülür. Gelen parçacıklara
göre çarpışmadan ~180o ile geri dönen parçacıkların
enerjisi Ef ölçülür.
Ei
Ef


Bilinmeyen
m1 + Ef 
Ei 

madde
M

Ef 
1

Ei 

detektör
(enerji ölçer)
Bu sayede bilinmeyen maddenin çekirdek kütlesini
öğreniriz.
(Hangi maddeden yapıldığını çıkartırız.).
Rutherford Saçılması

Örneğin: Çarpan  parçacıklarının başlangıç
enerjileri Ei = 2 MeV olsun ve bilinmeyen
maddeden saçıldıktan sonra geri dönen 
parçacıklarının enerjisi Ef = 1.1 MeV olsun.
Bilinmeyen maddenin ağırlığı nedir?
 m() = 4
(2 proton, 2 netron)


m1 + Ef 
Ei 

 M 

Ef 
1 
E
i 

M = 27
(

(1 -
)
1.1 )
2
4 1 + 1.1
2
Aliminyum!! (13 proton,
14 neutron)
2 Boyutta Elastik Çarpışması:
Bilardo

Eğer sadece ıstaka topunun ilk hızını biliyorsak
çarpışmadan sonraki durum hakkında yeteri bilgimiz
yok ama buna rağmen bazı şeyler öğrenebiliriz.
Bilardo.

Topun birinin durgun olduğu duruma bakalım:
pf
pi
vkm
Pf
F
önce
sonra
Kırmızı topun son durumdaki yönü nereden
çarpıldığına bağlı.
Bilardo.

Momentum korunur: pi = pf + Pf
pi2 = (pf + Pf )2 = pf2 + Pf2 + 2 pf  Pf

Kinetik enerji korunur:
p 2i
pf2 Pf 2

+
2m 2m 2m
pf  Pf = 0

İki denklemin karşılaştırılmasından:
Dolayısıyla, Pf ve pf dik olmalıdır!
p 2i  pf2 + Pf 2
Pf
pf
pi
Bilardo.

Çarpışmadan sonra 90o derece birbirinden ayrılır.
pf
pi
vcm
Pf
F
önce
sonra
Bilardo.

Bu şekilde beyaz topu tutarak kırmızı topu deliğe
gönderebiliriz.
Bilardo.


Bu şekilde beyaz topu tutarak kırmızı topu deliğe
gönderebiliriz.
Yada yanından geçebilir. Bildiğimiz tek şey toplar
çarpıştıktan sonraki açısı 90o.
Bilardo.

Topların ikisini de nasıl deliğe gönderebilirsiniz?
!
Ders 15, Soru 2
2 Boyutta Elastik Çarpışma

Şekilde görüldüğü gibi hareketli bir top duran topa vuruyor.
Çarpışma elastiktir.
 Çarpışmadan sonra topların olası yolları nedir?
(a)
(b)
(c)
Ders 15, Soru 2
Çözüm

İlk çözümde toplar arasındaki aç 90o değildir.

İkinci çözümde y yönünde net bir katkı olacaktır.
Ders 15, Soru 2
Çözüm


Üçüncü durumda y yönünde net momentum sıfırdır ve
çarpışmadan sonra momentumlar arasındaki açı 90o dir.
Sonuç olarak 3. durum momentumun ve enerjinin korunmasını
sağlayan tek durumdur.
Çarpışma “zaman skalası”

Çarpışma etkileşmeyi içerir ki bu etkileşme oldukça
çabuktur (kısa sürelidir).
vf
vi
Vf
F
önce
sonra
Toplar kısa bir zaman
birbirine dokunur
Çarpışma “zaman skalası”

Kısa çarpışma zamanında kuvvet büyük olabilir.
t
t1
p1
t2
p2
t3
p3 = 0
F2
t4
p4
F4
F3
t5
p5
Kuvvet ve İmpuls

Aşağıdaki diyagram tipik bir çarpışmada kuvvet zaman
değişimini göstermektedir. İmpuls, I, kuvvetin zamana
göre integrali.
F
I  t if F dt
t
İtme(Impuls) I = eğrinin altındaki alan!
Impuls birimi Ns.
t
t
ti
tf
Kuvvet ve İmpuls
F
dP
dt
kullanarak
impulsu yazarsak:
dP
dt
dt
 tt dP  Pf - Pi  ΔP
I  tt F dt  tt
f
i
F
f
i
f
i
I  P
impuls = momentum değişimi!
t
t
ti
tf
Kuvvet ve İmpuls

İmpuls çarpışmanın doğasıdan çok
değişimine bağlı olduğundan farklı
çarpışma aynı impulsu verebilir.
momentum
iki
F
alan aynı
F
ti
t
t büyük, F küçük
tf
t
t
tf
ti
t küçük, F büyük
t
Kuvvet ve İmpuls
Yumşak yay
F
F
Sert yay
ti
t
t büyük, F küçük
t
tf
t
tf
ti
t küçük, F büyük
t
Ders 15, Soru 3
Kuvvet & Impuls

Biri hafif diğeri ağır 2 kutu başlangıçta sürtünmesiz bir
yüzeyde durgun iken aynı büyüklükte sabit bir F kuvveti
her iki kutuya 1 saniye uygulanır.

Kuvvetten sonra hangi kutunun momentumu daha fazladır?
(a) ağır
F
(b)
hafif
hafif
(c) aynı
F
ağır
Ders 15, Soru 3
Çözüm
Biliyoruz ki Fort  Δp
Δt
yani
Δp  Fort Δt
Burada F ve t her iki kutu içinde aynıdır!
Kutuların son momentumları aynıdır.
F
hafif
F
ağır
Kuvvet ve İmpuls

Ortalama kuvveti tanımlamak için impulsu kullanabiliriz.
t = tf - ti zaman aralığında bir
kuvvetin zaman ortalaması:
F
tf
1
I
Fort   F dt 
Δt ti
Δt
yada:
Fav 
ΔP
Δt
Fav
t
t
ti
tf
Kuvvet ve İmpuls
Yumşak yay
F
Fort
F
Sert yay
Fort
ti
t
t büyük, F küçük
t
tf
t
tf
ti
t küçük, F büyük
t
Özet



2 boyutta elastik çarpışma.
Örnekler (nükleer çarpışma, bilardo).
İmpuls ve ortalama kuvvet.