10 = 1 x = ± -∞ 1.5

Örnek: Newton Yöntemini kullanarak f  x   x3  3x  2 fonksiyonunun   102 hassasiyet ile
yaklaşık kökünü bulunuz.
Çözüm:
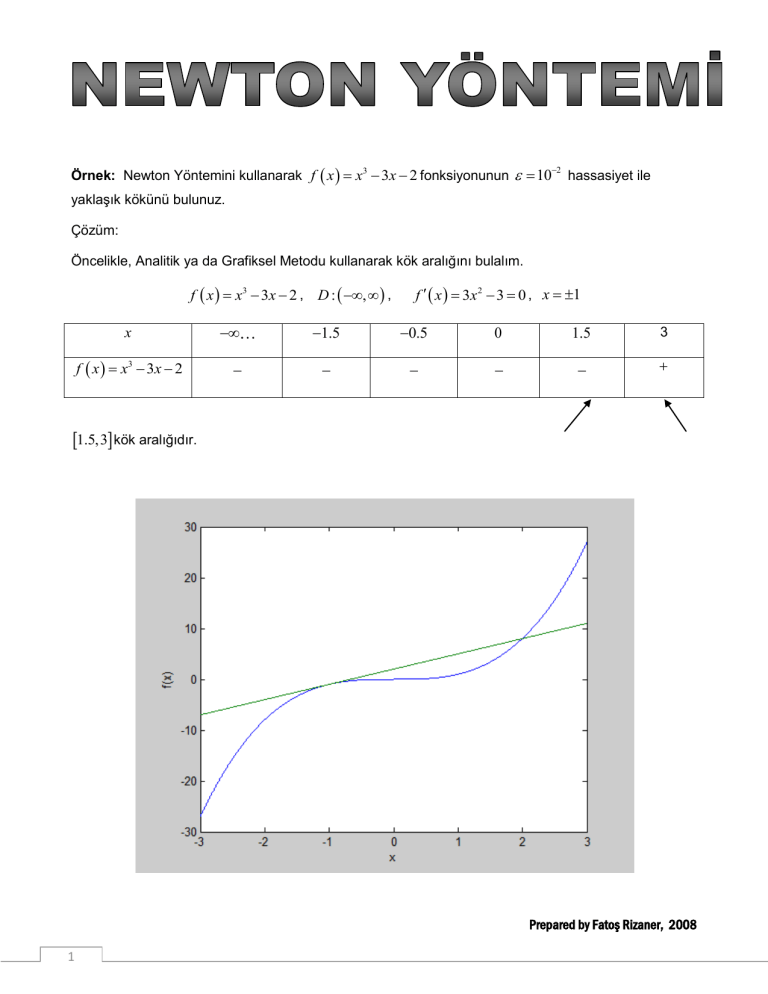
Öncelikle, Analitik ya da Grafiksel Metodu kullanarak kök aralığını bulalım.
f  x   x3  3x  2 , D :  ,   ,
x
f  x   x 3  3x  2


f   x   3x 2  3  0 , x  1
1.5
0.5
0
1.5
3





1.5,3 kök aralığıdır.
Prepared by Fatoş Rizaner, 2008
1
Newton Yöntemi Pn 1  Pn 
f  Pn 
.
f   Pn 
Başlama noktasını seçerken 2 yöntemimiz vardır.
1. Eğer f  a  f   x   0 , P0  a .
2. Eğer f  b  f   x   0 , P0  b .
f  x   x3  3x  2 , f   x   3x 2  3 , f   x   6 x
f 1.5 f   x    3.125 6 x   18.75x  0 ,
f  3 f   x   16  6 x   96 x  0
Böylece başlama noktası P0  3 .
P0  3
P1  P0 
f  P0 
f  3
16
 3
 3
 2.3333 ,
f   P0 
f   3
24
P2  P1 
f  P1 
f  2.3333
 2.3333 
 2.0556 ,
f   P1 
f   2.3333
P2  P1  2.0556  2.3333  0.2777
P3  P2 
f  P2 
f  2.0556 
 2.0556 
 2.0019 ,
f   P2 
f   2.0556 
P3  P2  2.0019  2.0556  0.0537
P4  P3 
f  P3 
f  2.0019 
 2.0019 
 2,
f   P3 
f   2.0019 
P4  P3  2  2.0019  0.0019  102 , STOP here.
P1  P0  2.3333  3  0.6667
n
Pn
f  Pn 
Pn1  Pn
0
3
f  3  16
-----------
1
2.3333
f  2.3333  3.7033
P1  P0  2.3333  3  0.6667
2
2.0556
f  2.0556  0.5191
P2  P1  2.0556  2.3333  0.2777
3
2.0019
f  2.0019  0.0171
P3  P2  2.0019  2.0556  0.0537
4
2
f  2  0
P4  P3  2  2.0019  0.0019
Yaklaşık kök x  2
Prepared by Fatoş Rizaner, 2008
2
Sabit Nokta Bulma Yöntemi ile karşılaştırabilmek için başlama noktasını P0  2.5 alalım.
P0  2.5
P1  P0 
f  P0 
f  2.5
 2.5 
 2.1111 ,
f   P0 
f   2.5
P1  P0  2.1111  2.5  0.3889
P2  P1 
f  P1 
f  2.1111
 2.1111 
 2.0074 ,
f   P1 
f   2.1111
P2  P1  2.0556  2.3333  0.1037
P3  P2 
f  P2 
f  2.0074 
 2.0074 
 2,
f   P2 
f   2.0074 
P3  P2  2  2.0074  0.0074  102 , STOP here.
n
Pn
f  Pn 
Pn1  Pn
0
2.5
f  3  6.125
-----------
1
2.1111
f  2.1111  1.0753
P1  P0  2.1111  2.5  0.3889
2
2.0074
f  2.0074  0.0669
P2  P1  2.0556  2.3333  0.1037
3
2
f  2  0
P3  P2  2  2.0074  0.0074
Yaklaşık kök x  2 .
Newton Yöntemi Sabit Nokta Bulma Yönteminden daha hızlıdır.
Prepared by Fatoş Rizaner, 2008
3