Ortaöğretim 9. Sınıf

Ortaöğretim
MATEMATİK
9. Sınıf
2. Kitap
Yazarlar
Komisyon
DEVLET KİTAPLARI
BİRİNCİ BASKI
……………………,2013
MİLLÎ EĞİTİM BAKANLI ĞI YAYINLARI.................................................................................. : 5891
DERS K İTAPLARI D İZİSİ............................................................................................................ : 1621
13.06.Y.0002.4361
Bu kitap Millî Eğitim Bakanlığı, Bilim, Sanayi ve Teknoloji Bakanlığı ile TÜBİTAK arasında imzalanan
“Eğitimde İşbirliği” protokolü kapsamında hazırlanmıştır.
Kitabın her hakkı saklıdır ve Millî Eğitim Bakanlığı’na aittir. Kitabın düzeni, metni, soru ve şekilleri
kısmen de olsa hiçbir şekilde alınıp yayımlanamaz.
EĞİTİM MATERYALLLERİ GELİŞTİRME EDİTÖRLERİ (Alfabetik sırada)
Dr. Ayhan Kürşat ERBAŞ
Dr. Bülent ÇETİNKAYA
Dr. Bülent GÜVEN
Dr. İlhan KARATAŞ
Dr. Zübeyir ÇINKIR
EĞİTİM MATERYALLLERİ GELİŞTİRME GRUBU (Alfabetik sırada)
Dr. Ali BOZKURT
Öğrt. Gör. Özkan GÜNER
Öğretmen Celal KARATAŞ
Dr. Enver TATAR
Arş. Gör. Avni YILDIZ
Öğretmen Faruk DÜŞÜNCELİ
Dr. Fatih KARAKUŞ
Arş. Gör. Erdem ÇEKMEZ
Öğretmen Kadir İLHAN
Dr. Hasan ATİK
Arş. Gör. Mahmut KERTİL
Öğretmen Mehmet AYDIN
Dr. Muharrem AKTÜMEN
Arş. Gör. Murat KOL
Öğretmen Orhan ÇİFTÇİ
Dr. Rahmet SAVAŞ EREN
Öğretmen Abdullah Aydın ÜNLÜ
Öğretmen Salih BEKTAŞ
Dr. Serkan ÖZEL
Öğretmen Adem KOCABAŞ
Uzman Yrd. Halil İbrahim TAŞOVA
Dr. Temel KÖSA
Öğretmen Arif ORUÇ
Uzman Yrd. Ramazan ALKAN
Dr. Tolga KABACA
Öğretmen Barış YAYLI
DİL UZMANI
Dr. Mehmet Akif ÇEÇEN
GÖRSEL TASARIM UZMANI
Semih Volkan PİŞKİN
PROGRAM GELİŞTİRME UZMANI
Dr. Selçuk ÖZDEMİR
ÖLÇME DEĞERLENDİRME UZMANLARI
Dr. Burcu ATAR
Dr. Bengü BÖRKAN
REHBERLİK VE PSİKOLOJİK DANIŞMANLIK UZMANI
Dr. Yasin ÖZTÜRK
ISBN: 978-975-11-3772-2
Millî Eğitim Bakanlığı, Talim ve Terbiye Kurulunun 31.07.2013 gün ve 100 sayılı kararı ile
ders kitabı olarak kabul edilmiş, Destek Hizmetleri Genel Müdürlüğünün 07.08.2013 gün
ve 2036478 sayılı yazısı ile birinci defa 222.000 adet basılmıştır.
Korkma, sönmez bu şafaklarda yüzen al sancak;
Sönmeden yurdumun üstünde tüten en son ocak.
O benim milletimin yıldızıdır, parlayacak;
O benimdir, o benim milletimindir ancak.
Bastığın yerleri toprak diyerek geçme, tanı:
Düşün altındaki binlerce kefensiz yatanı.
Sen şehit oğlusun, incitme, yazıktır, atanı:
Verme, dünyaları alsan da bu cennet vatanı.
Çatma, kurban olayım, çehreni ey nazlı hilâl!
Kahraman ırkıma bir gül! Ne bu şiddet, bu celâl?
Sana olmaz dökülen kanlarımız sonra helâl.
Hakkıdır Hakk’a tapan milletimin istiklâl.
Kim bu cennet vatanın uğruna olmaz ki feda?
Şüheda fışkıracak toprağı sıksan, şüheda!
Cânı, cânânı, bütün varımı alsın da Huda,
Etmesin tek vatanımdan beni dünyada cüda.
Ben ezelden beridir hür yaşadım, hür yaşarım.
Hangi çılgın bana zincir vuracakmış? Şaşarım!
Kükremiş sel gibiyim, bendimi çiğner, aşarım.
Yırtarım dağları, enginlere sığmam, taşarım.
Ruhumun senden İlâhî, şudur ancak emeli:
Değmesin mabedimin göğsüne nâmahrem eli.
Bu ezanlar -ki şehadetleri dinin temeliEbedî yurdumun üstünde benim inlemeli.
Garbın âfâkını sarmışsa çelik zırhlı duvar,
Benim iman dolu göğsüm gibi serhaddim var.
Ulusun, korkma! Nasıl böyle bir imanı boğar,
Medeniyyet dediğin tek dişi kalmış canavar?
O zaman vecd ile bin secde eder -varsa- taşım,
Her cerîhamdan İlâhî, boşanıp kanlı yaşım,
Fışkırır ruh-ı mücerret gibi yerden na’şım;
O zaman yükselerek arşa değer belki başım.
Arkadaş, yurduma alçakları uğratma sakın;
Siper et gövdeni, dursun bu hayâsızca akın.
Doğacaktır sana va’dettiği günler Hakk’ın;
Kim bilir, belki yarın, belki yarından da yakın
Dalgalan sen de şafaklar gibi ey şanlı hilâl!
Olsun artık dökülen kanlarımın hepsi helâl.
Ebediyyen sana yok, ırkıma yok izmihlâl;
Hakkıdır hür yaşamış bayrağımın hürriyyet;
Hakkıdır Hakk’a tapan milletimin istiklâl!
Mehmet Âkif Ersoy
GENÇLİĞE HİTABE
Ey Türk gençliği! Birinci vazifen, Türk istiklâlini, Türk Cumhuriyetini,
ilelebet muhafaza ve müdafaa etmektir.
Mevcudiyetinin ve istikbalinin yegâne temeli budur. Bu temel, senin en
kıymetli hazinendir. İstikbalde dahi, seni bu hazineden mahrum etmek
isteyecek dâhilî ve hâricî bedhahların olacaktır. Bir gün, istiklâl ve cumhuriyeti
müdafaa mecburiyetine düşersen, vazifeye atılmak için, içinde bulunacağın
vaziyetin imkân ve şeraitini düşünmeyeceksin! Bu imkân ve şerait, çok
namüsait bir mahiyette tezahür edebilir. İstiklâl ve cumhuriyetine kastedecek
düşmanlar, bütün dünyada emsali görülmemiş bir galibiyetin mümessili
olabilirler. Cebren ve hile ile aziz vatanın bütün kaleleri zapt edilmiş, bütün
tersanelerine girilmiş, bütün orduları dağıtılmış ve memleketin her köşesi bilfiil
işgal edilmiş olabilir. Bütün bu şeraitten daha elîm ve daha vahim olmak üzere,
memleketin dâhilinde iktidara sahip olanlar gaflet ve dalâlet ve hattâ hıyanet
içinde bulunabilirler. Hattâ bu iktidar sahipleri şahsî menfaatlerini,
müstevlîlerin siyasî emelleriyle tevhit edebilirler. Millet, fakr u zaruret içinde
harap ve bîtap düşmüş olabilir.
Ey Türk istikbalinin evlâdı! İşte, bu ahval ve şerait içinde dahi vazifen,
Türk istiklâl ve cumhuriyetini kurtarmaktır. Muhtaç olduğun kudret,
damarlarındaki asil kanda mevcuttur.
Mustafa Kemal Atatürk
Sembol ve Gösterimler
Kitabımızı Tanıyalım
Ön Söz
İÇİNDEKİLER
VIII
IX
X
3. ÜNİTE: FONKSİYONLAR
Bölüm 3.1. Fonksiyon Kavramı ve Gösterimi
437
3.1.1. Fonksiyon Kavramı
440
3.1.2. Birim, Sabit ve Doğrusal Fonksiyonlar
465
Bölüm Değerlendirme
486
Bölüm 3.2. Fonksiyonların Grafikleri
491
3.2.1. Fonksiyon Grafiklerini Okuma ve Yorumlama
494
3.2.2. f(x) =
xn
Biçimindeki Fonksiyonların Grafikleri
525
3.2.3. Doğrusal Fonksiyonlarla İlgili Uygulamalar
537
3.2.4. y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
551
3.2.5. Parçalı Tanımlı Fonksiyonlar ve Grafikleri
564
3.2.6. Bire Bir ve Örten Fonksiyonlar
582
Bölüm Değerlendirme
601
Ünite Değerlendirme
609
4. ÜNİTE: ÜÇGENLERDE EŞLİK VE BENZERLİK
Bölüm 4.1. Eşlik
633
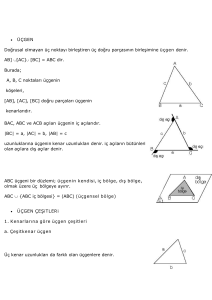
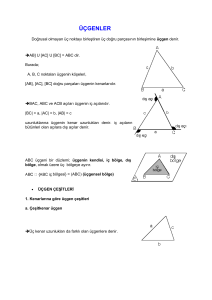
4.1.1. Üçgende Açılar
636
4.1.2. Üçgenlerin Eşliği
652
4.1.3. İkizkenar ve Eşkenar Üçgen
674
4.1.4. Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
686
Bölüm Değerlendirme
709
Bölüm 4.2. Benzerlik
713
4.2.1. Üçgende Orantılı Doğru Parçaları
716
4.2.2. Üçgenlerin Benzerliği
728
4.2.3. Üçgenlerin Benzerliğini Problem Çözme ve Modellemede Kullanma
760
Bölüm Değerlendirme
769
Bölüm 4.3. Üçgenin Yardımcı Elemanları
773
4.3.1. Açıortay
776
4.3.2. Üçgende Kenarortay
802
4.3.3. Üçgenin Kenar Orta Dikme ve Yükseklikleri
814
Bölüm Değerlendirme
828
Ünite Değerlendirme
833
CEVAP ANAHTARI
SÖZLÜK
VII
Sembol ve Gösterimler
∧
ve
Q’
irrasyonel sayılar kümesi
f(x) = mx + n Doğrusal fonksiyon
∨
veya
R
gerçek sayılar kümesi
f(x) = 0
⇒
ise, gerektirme
R ×R
Kartezyen koordinat sistemi
⇔
çift gerektirme
(ancak ve ancak)
Kökü f fonksiyonun
x-eksenini kestiği noktayı
veren denklem
f(x) = |x|
Mutlak değer fonksiyonu
=
eşittir
≠
eşit değildir
≡
denktir
∈
elemanıdır
∉
elemanı değildir
⊂
alt küme
⊄
alt küme değil
∪
birleşim
∩
kesişim
karekök
∅ , { } boş küme
[a, b]
a, b kapalı aralığı
(a, b)
a, b açık aralığı
[a, b)
a’dan kapalı, b’den açık aralık
(a, b]
a’dan açık, b’den kapalı aralık
A×B
A ve B kümelerinin kartezyen
çarpımı
A – B , A/B
a|b
A ve B kümelerinin farkı;
A fark B
b sayısı, a sayısını (tam) böler
a ≡ b (mod m) modül m ye göre
a ve b sayıları denktir
a
a’nın denklik sınıfı
Z/m
m modülüne göre kalan
sınıflarının kümesi
Z
Z
Q
küçük veya eşittir
>
büyüktür
≥
büyük veya eşittir
1-1
bire bir
|x|
x’in mutlak değeri
//
paralellik
br
birim
^
diklik
cm
santimetre
∼
benzer
m
metre
≈
yaklaşık
km
kilometre
≅
eş
dk.
dakika
[AB]
AB doğru parçası
sn.
saniye
|AB|
AB doğru parçasının
uzunluğu
sa
saat
AB ışını
L
litre
[AB
%
ABC
%
m (ABC)
°
derece
mL
mililitre
a
a:b ,
a’nın b’ye oranı
b
a
c
=
orantı
b
d
%
yüzde
ABC açısı
ABC açısının ölçüsü
W
A
$
AB
AB yayı
A açısı
X
aritmetik ortalama
K. A. K.
kenar-açı-kenar
S
standart sapma
A. K. A.
açı-kenar-açı
Q1
Alt çeyrek
K. K. K.
kenar-kenar-kenar
Q2
Ortanca
Q3
Üst çeyrek
D
ABC
D
A (ABC)
D
ABC üçgeni
ABC üçgeninin alanı
A açısının açıortayı
f(x)
x değişkenine bağlı f fonksiyonu
vA
A kenarının kenarortayı
hA
A kenarının yüksekliği
sin
sinüs
pozitif tam sayılar kümesi
Grafik (f ) Koordinat düzleminde f
fonksi yonu sağlayan noktaların
kümesi
cos
kosinüs
negatif tam sayılar kümesi
I(x)
tan
tanjant
rasyonel sayılar kümesi
f(x) = c
cot
kotanjant
sayma sayılar kümesi
tam sayılar kümesi
–
≤
]Z] g (x) , x ≤ a
]
f (x) = [] h (x) , a < x < b
]]
k (x) , x ≥ b
\
Parçalı tanımlı fonksiyon
nA
doğal sayılar kümesi
+
küçüktür
ABC üçgeninin alanı
N
Z
<
Ç(ABC)
sayma sayıları kümesi
+
n. dereceden kök
f: A → B A kümesinden B kümesine
tanımlı f fonksiyonu
S
N
n
VIII
Birim fonksiyon
Sabit fonksiyon
KİTABIMIZI TANIYALIM
Neler Öğreneceğiz?
Anahtar Terimler
İlgili başlık altında öğrenilmesi amaçlanan temel konu ve
kavramlar
Konuyla ilişkili temel
kavram ve terimler
Sembol ve Gösterimler
Dikkat
Konuyla ilişkili temel
sembol ve gösterimler
Konuyla ilişki dikkat edilmesi gereken uyarılar
Anahtar Bilgi
Konu içinde geçen kavramlarla ilgili temel ilişki
ve bilgiler
Bunu biliyor muydunuz
Konuyla ilişkili gerçek
hayattan merak uyandıracak ilginç bilgiler
MATEMATİK ATÖLYESİ
Konuyu keşfederek öğrenmenizi sağlayacak şekilde, adım adım yapılandırılmış, kimi zaman bilgi iletişim teknolojilerinin de entegre edildiği etkinlikler.
Konu ve kavramların daha iyi anlaşılmasını sağlayacak temel alıştırma ve uygulamalarla bunların
çözümleri
Konu Adı
KENDİMİZİ SINAYALIM
İnceleyelim
Konu içinde geçen kavramlarla ilişkili bilgileri
geliştirmek için internet
vb. kaynakları kullanarak araştırma yapmayı
gerektirecek durum ve
görevler
Matematik Tarihi
Konuyla ilişkili matematik tarihinden kişi
ve olaylar
Konu bittikten sonra konuyu pekiştirecek
türde kavram yoklama ve muhakeme,
alıştırma, uygulama ve problem çözme
türünden sorular
BÖLÜM ÖZETİ
İlgili bölümde geçen temel kavram, ilişki ve bilgilerin bir özeti
Bölüm Numarası Bölüm Adı
HAZIR MIYIZ?
Konuya başlamadan önce konuyla
ilişkili hazır bulunuşluğu belirlemek
için hazırlanmış sorular
Başlarken
Bölüm Numarası Bölüm Adı
BÖLÜM DEĞERLENDİRME
İlgili bölümde işlenen konuları birbirleriyle ilişkilendirerek pekiştirmeyi amaçlayan sorular
Ünite Numarası Ünite Adı
ÜNİTE DEĞERLENDİRME
Konuyla ilgili günlük hayatta karşılaşılabilecek örnek
durumlar
İlgili ünitedeki tüm bölümleri ve konu/
kavramları içerecek şekilde klasik ve/
veya test türünde sorular
IX
ÖN SÖZ
Değerli Öğrenciler ve Öğretmenler,
Toplumsal değişim ve gelişimin giderek ivme kazandığı, bilgi ve iletişim teknolojilerinin insan hayatının her anını etkilediği bir çağda yaşamaktayız. Yeni bilgiler, fırsatlar ve araçlar matematiğe bakış açımızı, matematikten beklentilerimizi, matematiği kullanma biçimimizi ve hepsinden önemlisi matematik öğrenme ve öğretme süreçlerimizi yeniden
şekillendirmektedir. Teknolojik gelişmelerle birlikte, daha önceki kuşakların karşılaşmadığı yeni problemlerle karşılaşılan günümüz dünyasında, matematiğe değer veren, matematiksel düşünme gücü gelişmiş, matematiği modelleme
ve problem çözmede kullanabilen bireylere her zamankinden daha çok ihtiyaç duyulmaktadır.
Ortaöğretim Matematik Dersi (9, 10, 11 ve 12. Sınıflar) Öğretim Programı’na uygun olarak hazırlanan bu kitap, öğrencileri sosyal ve mesleki hayata hazırlamayı ve yüksek öğrenimde gerekli olan temel matematiksel bilgi ve becerilerle
donatmayı amaçlamaktadır. Ancak, bunun gerçekleşmesi öncelikle matematiği “yararlı, uğraşmaya değer” bulma ve
“özenle ve sebat ederek çalışmayla” mümkündür.
Kitabın içeriğinde, konular ele alınırken, kavramsal anlamanın yanı sıra işlemsel akıcılığın kazandırılması; öğrenilen bilgilerin matematiksel iletişimde, problem durumlarını modelleme ve çözmede etkin kullanımına önem verilmektedir.
Konu ve kavramların öğrenciler tarafından yapılandırılması sürecine eşlik etmek ve öğrencilerin güçlü matematiksel
anlamlar geliştirmelerine yardımcı olmak için kitapta aşağıdaki türden deneyim ve ögelere yer verilmiştir:
•
Merak, sebep-sonuç dahilinde sorgulama ve keşfetme.
•
Değişkenler arasındaki ilişkileri gözlemleme.
•
Özel durumlardan hareketle genellemelere ulaşma.
•
Matematiksel yapıların ortak özelliklerinden yola çıkarak soyutlama yapma.
•
Verileri sınıflandırma, analiz etme ve yorumlama.
•
Matematiği, modelleme ve problem çözme sürecinde aktif olarak kullanma.
•
Yeni bilgileri mevcut bilgilerle ve farklı disiplinlerle ilişkilendirme.
•
Ulaşılan sonuçları matematiksel dilde ifade etme, gerekçelendirme ve paylaşma.
•
Bilgi ve iletişim teknolojilerinden aktif olarak yararlanma.
•
Bir insan ürünü olarak matematiğin konu ve kavramlarının tarihsel gelişimi ve bu bağlamda öne çıkan matematikçileri tanıma.
Bu kitabın içeriği, öğrencilerin aşağıdaki hedeflere ulaşmalarını sağlayacak şekilde yapılandırılmıştır:
Sayılar ve Cebir
•
Küme kavramını örneklerle açıklama, kümeler üzerinde yapılan işlemleri anlama, kümelerin temel özelliklerini belirleme ve gerçek/gerçekçi durumların modellemesini içeren problemlerin çözümünde kümelerden yararlanma
•
Sayı kavramını gerçek sayıları oluşturacak şekilde genişletme; birinci dereceden denklem ve eşitsizliklerin çözüm kümelerini bulma; denklem, yüzde, oran-orantı ve bir sayının kuvveti kavramlarını kullanarak sözel problemleri çözme
•
Fonksiyonu; bağımlı, bağımsız değişkenler arasındaki ilişki olarak açıklama ve ilgili problem durumlarını fonksiyonların tablo, grafik ve cebirsel gösterimlerinden yararlanarak inceleme
X
Geometri
•
Üçgenin temel elemanları, yardımcı elemanları ve bunlar arasındaki ilişkileri neden-sonuç ilişkisi içerisinde açıklama
•
Dik üçgende dar açıların trigonometrik değerlerini belirleme ve bu oranları problem çözme sürecinde kullanma
•
Sinüs ve kosinüs teoremlerini anlama ve bunların uygulamalarını bağlamsal bir yaklaşım çerçevesinde yapma
•
İki üçgenin eş veya benzer olmasını sağlayan asgari koşulları belirleme ve üçgenlerin eşliğini ve benzerliğini gerçek yaşam problemlerinin çözümünde aktif olarak kullanma
•
Farklı problem durumlarında kullanılabilecek en uygun üçgen alan bağıntısının hangisi olduğuna karar verme ve
üçgenin alan bağıntılarını problem çözme sürecinde kullanma
•
Dik üçgendeki temel uzunluk ilişkilerini problem çözme sürecinde kullanma
•
Vektörler aracılığı ile koordinat düzleminde geometri yapmak için yeni bir bakış açısı geliştirme
Veri, Sayma ve Olasılık
•
Verileri uygun grafiklerle temsil etme
•
Birden fazla veri grubunu karşılaştırma ve yorumlamada merkezi eğilim ve yayılım ölçülerini ve grafikleri kullanma
•
Olasılıkla ilgili temel kavramları açıklama ve eş olasılıklı olayların olasılık değerlerini hesaplama
Kitaptaki kavram ve konular ele alınırken Ortaöğretim Matematik Dersi Öğretim Programı’nın 9. sınıfta öğrencilerde
geliştirmeyi hedeflediği beceriler aşağıdaki gibi ilişkilendirilmektedir.
Modelleme / Problem Çözme
•
Kümeleri, denklem-eşitsizlikleri, fonksiyonları, üçgenlerde benzerliği ve dik üçgende trigonometrik oranları gerçek/gerçekçi hayat durumlarını modelleme ve problem çözmede kullanma
•
Kümeleri, denklem-eşitsizlikleri, fonksiyonları, üçgenlerde benzerliği ve dik
üçgende trigonometrik oranları gerçek/gerçekçi hayat durumlarını modelleme ve problem çözmede kullanma
Matematiksel Süreç
Becerileri
Modelleme / Problem çözme
•
İspat, orantısal akıl yürütme ve olasılıklı düşünme becerisi kazanma
•
Üçgenin özelliklerini neden-sonuç bağlamında inceleme
•
Kümeler, denklem ve eşitsizlikler, fonksiyonlar, üçgen, vektör, veri ve olasılığa
özgü terim ve sembolleri matematiksel düşünceleri ifade etmede kullanma
•
Küme, denklem, eşitsizlik ve fonksiyon kavramlarının birbirleriyle olan ilişkilerini açıklama; bu kavramlar arasındaki cebirsel ve geometrik temsil ilişkilerini
fark etme
•
Üçgenin temel ve yardımcı elemanları arasındaki ilişkileri açıklama
Akıl Yürütme
Matematiksel İletişim
İlişkilendirme
•
Bilgi ve İletişim Teknolojileri
•
Bir fonksiyonun cebirsel gösterimi ile grafik gösterimi arasındaki ilişkileri belirleme,
Geometrik ilişkileri keşfetme
vb. amacıyla bilgi ve iletişim teknolojilerinden yararlanma
Bu kitabın öğretmen ve öğrencilerimiz için önemli bir kaynak ve öğretim materyali olacağı ümidindeyiz.
Eğitim Materyalleri Geliştirme Editörleri
XI
Ünite
3
FONKSİYONLAR
Bölüm 3.1. Fonksiyon
Kavramı ve Gösterimi
Bu Bölümde Neler Öğreneceğiz?
•
Fonksiyon kavramını
•
Gerçek sayılar üzerinde tanımlanmış fonksiyon örneklerini
•
Gerçek/gerçekçi hayat durumlarının fonksiyon olarak modellenebileceğini
•
Verilen bir fonksiyona ait değerler tablosu oluşturmayı
•
Bir fonksiyonun şema ve grafik yardımıyla gösterimlerini
•
Birim, sabit ve doğrusal fonksiyonları
•
İki fonksiyonun eşitliği kavramını
Neden Öğreneceğiz?
Fonksiyonlar matematiğin en temel konularından biridir ve matematiğin günlük hayatta en fazla kullanılan konularındandır. Bu nedenlerle fonksiyon kavramının iyi anlaşılması ve fonksiyonlarla ilgili temel
cebirsel işlem becerilerinin kazanılması gerekmektedir.
Fonksiyonların kullanımını içeren veya fonksiyonlarla modellenebilen gerçek/gerçekçi hayat durumlarına verilebilecek örneklerden bazıları şunlardır:
•
Zamana bağlı yer kabuğu hareketlerini gösteren sismografik ölçümler
•
Farklı dövizlerin, altın ve petrolün zamana bağlı değişim değerlerinin belirtildiği grafiksel gösterimler
•
Simülasyonların oluşturulması
•
Uzaydaki gezegen ve yıldız gibi cisimlerin konumlarının zamana bağlı belirlenmesi
•
Uzaya gönderilen uydu ve uzay araçlarının yapım ve kullanımı için gerekli olan bilimsel çalışmalar
Bölüm 3.1. Fonksiyon Kavramı ve Gösterimi
HAZIR MIYIZ?
1.
Aşağıda verilen sayılar arasındaki ilişkiye
8.
Ardışık iki doğal sayının karelerinin farkı
7 olduğuna göre, bu iki sayının toplamı
kaçtır?
9.
x = 1 ve y = –1 için,
uygun birer kural oluşturunuz.
2.
3.
a. 2 4 6 8 …
b. 1 3
5
c. 4 7 10 13 ….
ç. 1 4
9 16 ….
7 …
(x + 1, 6) = (5, y – 4) eşitliğini sağlayan x ve
(5x – 3y) – [(x – 3y) – (y – (x – y))]
y değerlerini bulunuz.
işleminin sonucu kaçtır?
(a2 – b2 , 6) = (48, a + b) olduğuna göre,
a · b kaçtır?
4.
A = {1, 2, 3} ve B = {5, 8} kümeleri için
A x B kümesini yazınız. Şema ve grafikle
gösteriniz.
10. (3a – 2b) + 4(4a + 2b) – (a + 2b)
işleminin sonucu nedir?
11. “Bir sayının 3 katına 7 eklenip sonucu 2 ile
bölünüp 4 eklendiğinde 12 bulunuyorsa bu
sayı kaçtır?” sorusunun çözümünü sağlayan
denklemi yazınız.
5.
A x B = {(1,3), (1,5), (1,7), (4,3), (4,5), (4,7)}
olduğuna göre, A ve B kümelerini bulunuz
ve A x B yi grafikle gösteriniz.
12. “Hangi sayının yarısının 7 katı aynı sayının 3
katının 3 fazlasına eşittir?” sorusunun çözü-
6.
A = {1, 2, 3} ve B = {4, 5, 6} kümeleri için
münü sağlayan denklemi yazınız.
A x B kümesinin kaç alt kümesinde A kümesinin tüm elemanları birer kez kullanılır?
13. 2x + y = 12 doğrusu veriliyor. Aşağıda verilen
7.
438
x ve y tam sayı olmak üzere 3x + 2y = 17 koşulunu sağlayan beş tane (x, y) ikilisi yazınız.
Ünite 3. Fonksiyonlar
noktalardan hangileri bu doğrunun üzerindedir? Bulunuz.
a. (1,10)
b. (2,8)
c. (3,5)
ç. (7,–2)
d. (9,–6)
e. (3,7)
Bölüm 3.1. Fonksiyon Kavramı ve Gösterimi
HAZIR MIYIZ?
14. Tablolardaki a ve b değerleri arasındaki
kurallar tabloların altında belirtilmiştir. Bu
kurallara uygun olarak tabloları doldurunuz.
a.
b.
a
b
a
16. Bir fabrikada bir ham madde işletilerek elde
edilen ürün ham maddenin değerinin dört
katına satılmaktadır. Bu fabrikada bir günde
1000 TL lik ham madde işlenebilmektedir.
b
1
1
Fabrikada 10 günde ne kadarlık ham madde
2
2
işlenir? İşlenen ham maddeden elde edilen
3
3
ürünün değeri kaç TL olur?
4
4
5
5
b=a–3
b = 7a
c.
a
b
17. Yetişkin bir ağacın 26 otomobilden yayılan
3
karbondioksiti emme kapasitesine sahip
5
7
olduğu iddia edilmektedir. Buna göre;
9
Bulunduğunuz şehirdeki tahmini otomobil
11
sayısına göre en az kaç ağaca ihtiyaç vardır?
b = 3a + 2
15. Tablolardaki x ve y değerleri arasındaki ilişkiye uygun bir kural bulunuz.
a.
b.
x
y
x
y
1
4
1
7
2
7
2
13
3
10
3
19
4
13
4
25
5
16
5
31
18. y = x – 2 denkleminde, x değişkeninin alacağı değerlere karşılık olarak y değişkeninin
alabileceği değerlerin oluşturduğu ikilileri
grafik üzerinde gösteriniz.
c.
x
y
3
1
5
5
7
9
9
13
11
17
19.
3a + 5b = 17
2 denklem sistemini sağlayan
2a – 3b = –14
(a, b) ikilisi bulunuz.
Ünite 3. Fonksiyonlar
439
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
3.1.1. Fonksiyon Kavramı
Neler Öğreneceğiz?
•
Fonksiyon kavramını
•
Bir fonksiyonun tanım ve değer
kümelerini
•
Bir fonksiyon için değerler tablosu oluşturmayı
•
Bağımlı–bağımsız değişkenler
arasındaki ilişki olarak fonksiyonları
•
İki fonksiyonun eşit olma durumunu
Başlarken
Günlük hayatta karşılaştığımız birçok durumda,
aralarında ilişkilendirme olan iki çokluktan birinin
diğerine bağımlı olarak değiştiğini görürüz.
Örneğin, her hafta tartılan bir bebek için kilonun
zamana bağlı değişimi söz konusudur.
Hareket halindeki bir araba için alınan yolun
zamana bağlı değişiminden bahsedebiliriz. Benzer
şekilde bir fabrikadaki üretilen ürün miktarının işçi
sayısına bağlı değişimini de örnek verebiliriz. Bu
örneklerdeki ve benzeri durumları fonksiyon kavramını kullanarak matematiksel olarak çalışabiliriz.
Kümeler konusunda soyut ve somut nesne topluluklarını ve bu toplulukların genel
özelliklerini kümelerde işlemleri kullanarak incelemiştik. Bu ünitede ise iki kümenin
elemanları arasındaki belirli türdeki ilişkilendirmeleri yani fonksiyonları inceleyeceğiz. Sınıftaki öğrencilere birer öğrenci numarası vermek, bu sınıftaki öğrenciler
kümesi ile bu sınıf için kullanılacak öğrenci numaralarının kümesi arasında bir fonksiyon belirttiği gibi, bir şirketin günlük kar veya zararı, bir ağacın boyunun günlere
göre değişimi, gökyüzüne doğru attığımız bir topun zamana bağlı yüksekliği, güneş
ile dünya arasındaki mesafenin zamana bağlı büyüklüğü de birer fonksiyon belirtmektedir.
Anahtar Terimler
•
Fonksiyon
•
Tanım kümesi
•
Değer kümesi
•
Görüntü kümesi
•
Bağımlı değişken
•
Bağımsız değişken
•
Eşit fonksiyon
Matematikte öğrendiğimiz birçok şey fonksiyon olarak görülebilir. Örneğin, aritmetikteki toplama ve çarpma işlemleri sayı ikililerini sayılara eşleyen birer fonksiyondur. Benzer şekilde, geometrideki öteleme ve döndürme işlemleri geometrik
şekiller arasındaki bir fonksiyondur. Olasılık konusunda olayları, olma olasılıklarıyla
eşleme de bir fonksiyon örneğidir. Fonksiyonlar, trigonometri, limit, türev ve integral gibi daha sonraki yıllarda göreceğimiz birçok matematik konusu için de temel
bir kavramdır.
Sembol ve Gösterimler
•
•
f:A → B
Fonksiyonlar konusunu öğrenmekle günlük hayatta karşılaşabileceğimiz birçok
problemi kolaylıkla çözebileceğimiz gibi kainatın işleyişi hakkındaki düşüncelerimiz
de derinlik kazanacaktır. Kainattaki varlıklar hakkındaki bilgilerin ve kainatta gözlemlenen olayların matematiksel olarak incelenebilmesinde anahtar bir rolü olan
fonksiyonların kullanımı sadece matematikle sınırlı değildir. Fizik gibi doğa bilimlerinde fonksiyonların çok etkin ve yaygın bir kullanımı vardır. Günümüzde fonksiyonlar konusu, mühendislikten ekonomiye, eğitim bilimlerinden tıpa kadar birçok
alanda başarıyla kullanılmaktadır.
f(x)
440
Ünite 3. Fonksiyonlar
Fonksiyon Kavramı
Bir akaryakıt istasyonunda alınan benzin miktarı değiştikçe ödenecek tutar da değişir. Bu iki değişken arasındaki ilişkiyi bir örnekle inceleyelim.
Benzinin litresinin 5 TL olduğunu varsayalım. Farklı miktarlardaki benzin için ödenecek tutarları bir tabloyla aşağıdaki gibi gösterebiliriz. Örneğin 5 litre benzin alan biri
25 TL ödemelidir.
Akaryakıt istasyonlarında, alınan benzin miktarı ile ödenecek tutar arasındaki ilişkiyi gaz pompa makinasındaki ek1
5
randan daha iyi izleyebiliriz. Şöyle ki, öncelikle “Litre Fiyatı”
2
10
girilerek makine kullanıma hazır hale getirilir. Sonrasında
3
15
benzin aldıkça miktarını “Litre” ekranından, ödenecek tuta4
20
rı da “Satış Tutarı” ekranından takip edebiliriz. Bu şekilde iki
5
25
çokluk arasındaki ilişkiyi gözlemleriz. Diğer bir ifadeyle, TL
cinsinden ödenecek tutarın litre cinsinden benzin miktarı6
30
na bağlı değişimini ekrandan izleyebiliriz. Farklı örneklerle
7
35
ilgili kullanışlı genellemeler yapabilmek için bu durumu
biraz daha irdeleyelim. Gaz pompa makinası, alınan benzin miktarını okudukça ödenecek tutarı göstermektedir. Bu durumu bir şema ile gösterebiliriz:
Miktar(L)
Tutar (TL)
Benzin miktarı
girdi
Makine
çıktı
Ödenecek tutar
Makinenin okuduğu değerlere “girdi”, hesapladığı tutara “çıktı” diyelim.
Örneğin, aşağıdaki şema 4 litre benzine karşılık 20 TL ödeme yapılması gerektiğini belirtiyor. Ayrıca makinenin hesaplama yapmak için kullandığı kuralı da görebiliyoruz:
4
girdi
Makine
5 katı
çıktı
20
Burada şu iki duruma dikkat edelim:
1.
Her girdi için bir çıktı hesaplanmakta
2.
Her bir girdi için yalnızca bir çıktı bildirilmekte
Fonksiyonun matematiksel tarifine geçmeden, fonksiyonun iki çokluk arasında bu iki
şartı sağlayan ilişkilendirmeler olduğunu belirtelim.
Ünite 3. Fonksiyonlar
441
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
Bu makinede alınan benzin miktarı değiştikçe ödenmesi gereken tutar da değiştiğinden ikisi de değişken olarak isimlendirilebilir. Tutarın değişmesi miktara bağımlıdır. Bu
Bunu biliyor muydunuz
durumda tutara bağımlı değişken, miktara ise bağımsız değişken denilebilir. Miktarı
Değişken, bir problem ya
da bir dizi işlemler bağlamında değişen bir değerdir.
Sabit ise değişmeden kalan
değerdir. Örneğin, y = 2x + 5
ifadesinde x ve y değişkenler,
2 ve 5 sabitlerdir.
x, tutarı y ile isimlendirdiğimizde y, x e bağımlı bir değişken olur. Yukarıdaki şekilsel
gösterimi miktarın her durumu için ayrı ayrı yapmaktansa, bağımlı ve bağımsız değişkenleri kullanarak şu şekilde genel bir anlatım yapabiliriz:
x
girdi
Makine
Bağımsız
değişken
Matematik Tarihi
5x
5 katı
çıktı
y
Bağımlı
değişken
Bu örnekteki x ve y arasındaki ilişkiyi y = 5x ifadesiyle belirtebileceğimize dikkat edelim.
Johann Bernoulli
Şimdi başka bir makine örneği üzerinde bağımlı ve bağımsız değişken kavramlarını
biraz daha açalım.
1
(1667-1748)
5 4 3 2 1
1718'de Johann Bernoulli
“bir değişken ve sabit sayılarla ifade edilen herhangi
bir ifade”yi fonksiyon
olarak ele almıştır.
20 16 12 8 4
4 katı
y = 4x
Girdi (x)
Çıktı (y)
1
4
2
8
3
12
4
16
5
20
x
4x
Makineye giren değerler (bağımsız değişkenler) ile çıkan değerler (bağımlı değişkenler) arasındaki ilişki:
"Çıktı" = 4 · "Girdi"
şeklindedir. Örneğin, makineye sırasıyla 1 girince 4; 2 girince 8 çıkıyor. Diğer örnekler
makine ve tablo üzerinde gösterilmiştir.
G
442
Ç
• 1
• 4
• 2
• 8
• 3
• 12
• 4
• 16
• 5
• 20
Ünite 3. Fonksiyonlar
Girdileri bir küme ve çıktıları başka bir küme olarak
da düşünebiliriz. Bu durumda her bir girdiye karşılık
gelen çıktı eşlenir.
Şimdi kümeler arasındaki ilişki bağlamında fonksiyonun matematiksel tanımını verelim.
Fonksiyon Kavramı
İnceleyelim
A ve B boş olmayan iki küme olsun. A kümesinin her bir elemanını B kümesinin
bir ve yalnız bir elemanına eşleyen ilişkiye A dan B ye tanımlı fonksiyon denir.
A dan A ya tanımlı bir fonksiyona kısaca A da tanımlı fonksiyon da denir. Fonksiyonlar genellikle f, g, h, F, G, H gibi sembollerle gösterilir.
Tanım Kümesi Değer Kümesi
•
Bir A kümesinden B kümesine tanımlı f fonksiyonu kısaca şu şekilde gösterilir:
f:A→B
Burada A ya fonksiyonun tanım kümesi, B ye ise fonksiyonun değer kümesi
denir.
a •
•
•
x •
•
• f(a)
• f(x)
Bağımsız değişkenler bağımlı
değişkenlerde bir değişime
neden olmak için manipüle
edilen değişkenlerdir.
Eğer f fonksiyonu A kümesinden alınan bir x elemanını, B kümesindeki bir y
elemanı ile ilişkilendiriyor ise y, x in f altındaki görüntüsü veya f in x teki
değeri y dir denir ve bu durum y = f(x) şeklinde ifade edilir. Tanım kümesindeki
elemanların fonksiyon altındaki görüntülerinin oluşturduğu kümeye fonksiyonun görüntü kümesi denir ve f(A) ile gösterilir. Görüntü kümesi ortak özellik
yöntemiyle şu şekilde gösterilir:
f(A) = { f(x) : x ∈ A }
Yapmış olduğumuz fonksiyon tanımındaki şu iki özelliği vurgulayalım:
1.
Tanım kümesindeki her bir eleman değer kümesinden bir elemanla mutlaka
ilişkilendirilmiştir,
ve
2.
Tanım kümesindeki herhangi bir eleman değer kümesinden en fazla bir elemanla ilişkilendirilmiştir.
Bunu biliyor muydunuz
f : A → B olması bu iki şartın aynı anda sağlanması anlamına gelmektedir. Şimdi bu
durumu tersinden okuyalım:
Fonksiyon kavramı, teknolojik gelişmelerin sonucu
olarak da ortaya çıkan ve
gerçek dünyadaki birçok
girdi-çıktı durumlarını temsil
eden matematiksel ilişkiler
bağlamında da kullanılmaktadır.
Yukarıdaki şartlardan en az biri sağlanmıyorsa f : A → B bir fonksiyon belirtmez.
Daha net bir ifadeyle,
1.
Tanım kümesinde, değer kümesinden bir elemanla ilişkilendirilmeyen en az bir
eleman var ise (çıktısı olmayan girdi varsa)
veya
2.
Tanım kümesinde, değer kümesinden birden fazla elemanla ilişkilendirilen en az
bir eleman var ise (birden fazla çıktısı olan girdi varsa)
f fonksiyon belirtmez.
Ünite 3. Fonksiyonlar
443
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
f
A
Dikkat edilecek olursa bir fonksiyo-
B
nun görüntü kümesi, değer kümesi-
•
•
Görüntü Kümesi
•
Matematik Tarihi
•
Gottfried Wilhelm Leibniz
•
dir. Bu durum yandaki gibi bir şekille
•
açıklanabilir.
•
•
nin bir alt kümesidir, yani f(A) ⊂ B
•
Tanım Kümesi
Değer Kümesi
Yukarıdaki örneklerdeki makine benzetmesine tekrar geri dönecek olursak, f fonksiyonu x girdisini alıp f(x) çıktısına götüren bir makine şeklinde düşünülebilir.
(1646-1716)
x
Fonksiyonu “bir çokluğun
bir başkasına bağlı olarak
değişmesi” olarak tanımlamıştır.
girdi
f
Bağımsız
değişken
çıktı
f(x)
Bağımlı
değişken
2
A = {1, 3, 5, t, u} ve B = {4, 10, 12, 20, 4p, 4t, 4u} kümeleri için f : A → B fonksiyonu A kümesindeki her elemanı, bu elemanların 4 katı olan ve B kümesinde yer alan elemanlarla
ilişkilendirsin. Bu durumu temsilen aşağıdaki makine modellemesini kullanabiliriz.
1, 3, 5, t, u
4, 12, 20, 4t, 4u
4 katı
f(x) = 4x
A
• 1
B
• 4
• 10
• 3
• 12
• 5
• 20
• t
• 4p
• u
444
f
• 4t
• 4u
Ünite 3. Fonksiyonlar
Girdi
Çıktı
1
f(1) = 4
3
f(3) = 12
5
f(5) = 20
t
f(t) = 4t
u
f(u) = 4u
A kümesinden alınan girdi değerlerine karşılık gelen
çıktı değerleri hem yaptığımız makine modellemesinde hem de oluşturduğumuz tabloda gösterilmiştir. Bu fonksiyon için tanım kümesi A, değer kümesi
B ve görüntü kümesi f(A) = {4, 12, 20, 4t, 4u} dur.
Görüntü kümesinin değer kümesinin bir alt kümesi
olduğunu, yani f(A) ⊂ B olduğunu biliyorduk. Bu
örnekte f(A) ≠ B olabileceğini, yani görüntü ve
değer kümelerinin farklı kümeler olabileceğini
gözlemliyoruz.
Fonksiyon Kavramı
Burada, f(1) = 4 olması durumunu, "1 in f altındaki görüntüsü 4 tür" veya f nin "1 deki
değeri 4 tür" şeklinde de belirtebiliriz. Benzer şekilde, bu örneğimizde 3 ün f altındaki
görüntüsünün 12 ve f nin 5 teki değerinin 20 olduğunu söyleyebiliriz.
Matematik Tarihi
Leonhard Euler
Fonksiyon herhangi bir girdiye karşılık girdinin 4 katı olan bir çıktı verdiğinden, x değişkenini kullanarak fonksiyonun yaptığı ilişkilendirmeyi kısaca
f(x) = 4x
şeklinde ifade edebiliriz. Tanım kümesinden herhangi bir elemanı temsil eden x değişkenini girdi kabul ettiğimizde çıktıyı göstermek için birbirine denk olan birkaç seçeneğimiz vardır : 4x, f(x) veya y.
(1707-1783)
Fonksiyonu harflerle
göstermek için çalışmalar
yapmıştır. Bu çalışmalar
matematiksel bir ifade
olarak fonksiyonun oluşmasını sağlamıştır. Euler
yaptığı tanımlamada, f
fonksiyonunu göstermek
amacıyla, y = f(x) bağıntısını yazmıştır.
Şöyle ki;
•
Fonksiyonun ilişkilendirme kuralını kullanırsak, çıktıyı 4x ile gösterebiliriz.
•
x e karşılık gelen çıktının, x in f altındaki görüntüsü olduğunu kullanırsak, çıktıyı
f(x) ile gösterebiliriz.
•
Bağımsız değişken olan x girdisine karşılık, çıktının bağımlı bir değişken belirteceğinden, çıktıyı y değişkeni ile gösterebiliriz.
Dolayısıyla, f(x) = 4x, y = f(x) veya y = 4x ifadeleri aynı ilişkiyi belirtmektedir.
EULER'in yukarıdaki resmi
Jakob Emanuel Handmann
tarafından çizilmiş yağlı
boya tablosudur.
Herhangi bir anlam karmaşasına meydan vermemek için yaptığımız sembol kullanımlarını ve tanımlamaları bu örnek üzerinde detaylı bir şekilde açıkladık. Fonksiyonlarla
ilgili birkaç örnek üzerinde daha çalıştığımızda bu tanımlama ve sembolleri daha rahat
kullanıyor olacağız.
3
f : R → R fonksiyonu "verilen bir gerçek sayıyı 2
katının 3 fazlasıyla eşleştiriyor" şeklinde tanımlansın. Bu fonksiyonun makina modellemesini şekildeki gibi yapabiliriz.
x
2 katının
3 fazlası
2x + 3
Gerçek sayılar sonsuz bir küme olduğundan bütün
gerçek sayıların f altındaki görüntülerini tek tek yaf(x) = 2x + 3
zamayız. Bir x değişkenini kullanarak f fonksiyonunun yaptığı ilişkilendirmeyi f(x) = 2x + 3 şeklinde
belirtebiliriz. İstenildiği zaman da, verilen herhangi bir gerçek sayının f altındaki görüntüsünü bulabiliriz. Örneğin, x in alabileceği bazı değerler ve bu değerlerin f altındaki
görüntüleri aşağıda verilmiştir:
Ünite 3. Fonksiyonlar
445
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
x = – 4 ise f(– 4) = 2·(– 4) + 3 = – 5 tir.
Bunu biliyor muydunuz
5
5
5
x = – 2 ise f ` – 2 j = 2 · ` – 2 j + 3 = – 5 + 3 = – 2 dir.
x = – 1 ise f(–1) = 2(–1) + 3 =1 dir.
x = 0 ise f(0) = 2 ·0 + 3 = 3 tür.
7
7
7
7
19
x = 8 ise f ` 8 j = 2· ` 8 j + 3 = 4 + 3 = 4 tür.
x = 1 ise f(1) = 2·1 + 3 = 5 tir.
Dünyanın etrafında binlerce
uydu birer yörüngede dönmektedirler. Bu uyduların
hızları bulundukları yörüngenin dünyaya uzaklığına
göre değişiklik göstermektedir. Yani, uyduların hızları
dünyaya olan uzaklıklarının
bir fonksiyonudur.
x = a ise f(a) = 2a + 3 tür.
x = a + 1 ise f(a + 1) = 2(a + 1) + 3 = 2a + 5 tir.
x = t2 ise f(t2) = 2t2 + 3 tür.
Bunları, daha kolay anlaşılır olması için bir tablo halinde verebiliriz:
x
–4
5
–2
–1
0
7
8
1
f(x)
–5
–2
1
3
19
4
5
a
a+1
2a + 3 2a + 5
t2
2t2 + 3
Bir takım x girdi değerlerine karşılık f(x) çıktı değerlerinin verildiği tabloya f nin
değerler tablosu denilmektedir.
Şimdiye kadar verdiğimiz örneklerde fonksiyon için hep cebirsel ifadeler kullandık. Ancak, fonksiyonların tanım ve değer kümeleri arasında yaptıkları ilişkilendirmelerin cebirsel bir ifadeyle açıklanabilecek bir kuralı olmak zorunda değildir. Şimdi buna bir örnek
verelim.
4
A = {a, b, c} ve B = {2, 3, 4, 5, 6} kümeleri için f : A → B fonksiyonunun değer tablosu
şu şekilde verilsin:
x
a
b
c
f(x)
3
5
4
Bu durumda f(a) = 3, f(b) = 5 ve f(c) = 4 olduğunu görüyoruz. Yani a, b ve c nin f altındaki görüntüleri sırasıyla 3, 5
ve 4 tür. A kümesi f nin tanım kümesi, B kümesi f nin değer kümesi ve f(A) = {3 ,4, 5} de f nin görüntü kümesidir.
f nin fonksiyon tanımında verdiğimiz şartları sağlayan bir ilişkilendirme olduğuna dikkat edelim:
446
Ünite 3. Fonksiyonlar
Fonksiyon Kavramı
1.
2.
A da, f nin B den bir elemanla ilişkilendirmediği boşta eleman yok. Yani A daki
her elemanın B kümesinde olan bir görüntüsü var.
A da, f altında görüntüsü birden fazla olan eleman yok. Yani A daki elemanların f
altında yalnız birer görüntüleri var.
Bu örnekten de anlaşılacağı gibi değer kümesinde, tanım kümesinden bir elemanla
eşleşmeyen eleman olması fonksiyon olmaya engel değildir.
A, B ve f(A) kümelerinin Venn şemalarını kulB
f
lanarak f fonksiyonunun yaptığı ilişkilendir• 2
meyi şekildeki gibi gösterebiliriz.
A
• a
• 3
• b
• 4
• c
• 5
f(A)
• 6
Sonlu bir A kümesi ile herhangi bir f : A → B
fonksiyonu verildiğinde f(A) görüntü kümesinde en az 1, en fazla s(A) kadar eleman
olacağını görebiliriz.
Şimdi fonksiyon belirtmeyen ilişkilendirmelere örnekler verelim:
5
A = {a, b, c} ve B = {2, 3, 4, 5, 6} kümeleri için aşağıdaki ilişkilendirmeler bir fonksiyon
belirtmez:
a.
A
B
Bu ilişkilendirmede A kümesindeki c elemanı B
• 2
kümesinden herhangi bir elemanla eşleşme-
• a
• 3
miştir. Dolayısıyla bu bir fonksiyon belirtmez.
• b
• 4
• c
• 5
• 6
b.
A
B
• 2
• a
• 3
• b
• 4
• c
• 5
Bu ilişkilendirmede A kümesindeki a elemanı B
kümesinden birden fazla, elemanla eşleşmiştir.
Dolayısıyla bu bir fonksiyon belirtmez.
• 6
c.
A
B
• 2
• a
• 3
• b
• 4
• c
• 5
Burada A kümesindeki b elemanı B kümesinden
herhangi bir elemanla eşleşmemiştir. Üstelik c
elemanı B kümesinden birden fazla elemanla
eşleşmiştir. Bu iki nedenden dolayı bu ilişkilendirme bir fonksiyon belirtmez.
• 6
Ünite 3. Fonksiyonlar
447
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
6
Aşağıda verilen durumların fonksiyon belirtip belirtmeyeceğini bulalım.
a.
Alfabedeki her harfin kendisiyle başlayan günle ilişkilendirilmesi
b.
Sınıftaki öğrencilerin doğum günleri ile ilişkilendirilmesi
c.
Ülkemizdeki vatandaşların Türkiye Cumhuriyeti kimlik numaralarıyla ilişkilendirilmesi
a.
Alfabedeki harfler = {a, b, c, ç, … , z}, günlerin baş harfleri = {p, s, ç, c} olduğundan
her harfin eşleşeceği bir günün baş harfi yoktur. Bu durum bir fonksiyon belirtmez.
b.
Sınıftaki her bir öğrencinin yalnız bir doğum günü olduğundan bu durum sınıftaki
öğrenciler kümesinden sınıftaki öğrencilerin doğum günlerini kapsayan herhangi
bir doğum günleri kümesine tanımlı bir fonksiyon belirtir.
c.
Her bir vatandaşlarımız için yalnız bir Türkiye Cumhuriyeti kimlik numarası olduğundan bu durum bir fonksiyon belirtir.
7
2
f : $ 0, 3, 5, 3 , – 4,
sini bulalım.
2 . → R ve f(x) = 3x – 4 ile verilen fonksiyonun görüntü küme-
Tanım kümesindeki her elemanın görüntüsünü bulalım.
x
f(x)
–4
f(–4) = 3·(–4) – 4 = –16
0
f(0) = 3·0 – 4 = –4
2
3
2
2
f` 3 j = 3 $ 3 – 4 = – 2
2
f^ 2 h = 3 2 – 4
3
f(3) = 3·3 – 4 = 5
5
f(5) = 3·5 – 4 = 11
Buna göre görüntü kümesi " - 16, - 4, - 2, 3 2 - 4, 5, 11 , dir.
448
Ünite 3. Fonksiyonlar
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında fonksiyon kavramını ve bir kümenin (tanım kümesi) her bir elemanını başka bir kümenin
(değer kümesi) bir ve yalnız bir elemanına eşleyen ilişki olarak fonksiyon tanımını inceleyeceğiz.
“Aklından bir sayı tut” diyerek başlayan sorularla karşılaşmışsınızdır. Bizde bu ifadeden hareketle bir örnekle başlayalım.
Adım 1
Aklınızdan bir doğal sayı tutunuz.
Adım 2
Bu sayıyı 4 ile çarpınız.
Sayı
Sonuç
1
…
2
…
3
…
x
…
Adım 3
Elde ettiğiniz sayıya 2 ekleyiniz.
Adım 4
Bulduğunuz sayıyı 2 ye bölünüz.
Adım 5
Elde ettiğiniz sonucu söyleyiniz.
Adım 6
Bu aşamalara göre tabloyu doldurunuz.
Adım 7
Tuttuğunuz sayı ile çıkan sonuç arasındaki ilişkiyi matematiksel olarak ifade ediniz. Bu ilişki bir fonksiyon mudur?
Neden?
Adım 8
Şimdi de, yukarıda verilen adımları sondan başa doğru uygulayarak yandaki tabloyu
doldurunuz.
Sayı
Sonuç
…
21
…
35
…
43
Ünite 3. Fonksiyonlar
449
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
8
Bir f : Z → Z fonksiyonu “Her bir tam sayıyı, karesinin 2 katının 4 eksiğine götürüyor.”
şeklinde tanımlanıyor. Buna göre, 2, 5 ve 2k (k ∈ Z) sayılarının görüntülerini bulalım.
Bizden f(2), f(5) ve f(2k) ifadelerin değerlerini bulmamız isteniyor. Önce fonksiyonun
verilen kuralını cebirsel bir ifadeye dönüştürmemiz tekrar eden benzer işlemler için
bize kolaylık sağlayacaktır.
Herhangi bir n tam sayısının karesi n2 dir. Dolayısıyla n sayısının karesinin 2 katı 2n2
dir. Buradan n tam sayısının karesinin 2 katının 4 eksiğinin 2n2 – 4 olduğu sonucuna
ulaşırız. Bu durumda, fonksiyonun kuralını f(n) = 2n2 – 4 şeklinde verebiliriz (bu fonksiyonun kuralını f(x) = 2x2 – 4 olarak da verebiliriz, çünkü hem n hem x değerleri tanım
kümesinden alınan bir değişkeni belirtmektedir). Buna göre,
f(2) = 2 · 22 – 4 = 2 · 4 – 4 = 4
f(5) = 2 · 52 – 4 = 2 · 25 – 4 = 46
f(2k) = 2 · (2k)2 – 4 = 2 · 4k2 – 4 = 8k2 – 4
olur. Böylece, 2 nin f altındaki görüntüsü 4, 5 in görüntüsü 46 ve 2k nın görüntüsü
8k2 – 4'tür.
9
A = {1, 3, 5, 7} ve B = {1, 2, 3, 4, 5, 6, 7, 8} kümeleri veriliyor. f : A → B fonksiyonu
f (x) = 8 – x ile veriliyor. Bu fonksiyonun görüntü kümesini bulalım.
Fonksiyonun kuralını kullanarak tanım kümesindeki elemanların görüntülerini bulalım.
f (1) = 8 – 1 = 7
f (3) = 8 – 3 = 5
f (5) = 8 – 5 = 3
f (7) = 8 – 7 = 1 olur.
Bu nedenle, görüntü kümesi f (A) = {1, 3, 5, 7} olur.
450
Ünite 3. Fonksiyonlar
Fonksiyon Kavramı
10
f : A → B , f (x) = x + 5 ile verilen bir fonksiyon için tanım, değer ve görüntü kümeleri
hakkında B = {4, 6, 8}, f(A) = B ve s(A) = 3 olduğu biliniyor. Buna göre A kümesini
bulalım.
s(A) = 3 olduğundan a ≤ b ≤ c olmak üzere A = {a, b, c} olsun. Şimdi a, b ve c değerlerini
bulalım.
Bu durumda {4, 6, 8} = f(A) = {f(a), f(b), f(c)} = {a + 5, b + 5, c + 5} olur.
Buradan a + 5 = 4, b + 5 = 6 ve c + 5 = 8 eşitliklerinden A = { –1, 1, 3} olarak bulunur.
11
f : (1, 7] → R ve f(x) = 4x + 2 ile verilen f fonksiyonun görüntü kümesini bulalım.
Bu fonksiyonun tanım kümesi (1,7] aralığı olduğundan, tanım kümesindeki herhangi
bir x elemanı 1 < x ≤ 7 eşitsizliklerini sağlar. Bu aralıktaki her bir sayının görüntüsünü
bulmak yerine şimdi bu tür x ler için f(x) in sağladığı eşitsizlikleri bulalım.
x ∈ (1, 7] ⇒ 1 < x ≤ 7
⇒ 4 · 1 < 4x ≤ 4 · 7
⇒ 4 < 4x ≤ 28
⇒ 4 + 2 < 4x + 2 ≤ 28 + 2
⇒ 6 < 4x + 2 ≤ 30
⇒ 6 < f(x) ≤ 30
⇒ f(x) ∈ (6, 30]
Tekrar edecek olursak, x ∈ (1, 7] iken f(x) ∈ (6, 30] olmaktadır.
Bu nedenle, f((1, 7]) ⊂ (6, 30] olur.
Şimdi herhangi bir y ∈ (6, 30] değerinin tanım kümesi olan (1,7] aralığından bir elemanın görüntüsü olup olmadığına bakalım.
f(x) = y ⇒ 4x + 2 = y
y-2
⇒x=
olur.
4
Ünite 3. Fonksiyonlar
451
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
Diğer taraftan,
6 < y ≤ 30 ⇒ 4 < y – 2 ≤ 28
y-2
⇒1<
≤7
4
⇒ 1 < x ≤ 7 olur.
Yani f(x) = y ve y ∈(6, 30] ise 1 < x ≤ 7 olmalıdır. Buradan (6, 30] ⊂ f((1, 7]) sonucunu
elde etmiş oluruz.
f((1,7]) ⊂ (6, 30] ve (6, 30] ⊂ f((1, 7]) olduğundan f((1,7]) = (6, 30] sonucunu elde
ederiz.
Fonksiyonların grafikleri ve doğrusal fonksiyon konularını öğrendikten sonra bu problemin daha kısa çözümlerini de yapabiliyor olacağız.
12
Bir f fonksiyonu f : R → R ve f(x) = x2 olarak tanımlanıyor. Buna göre aşağıdakileri
ifadelerin değerlerini bulalım.
a.
f(x + 5)
b.
f(x – 6)
a.
f(x) = x2 eşitliğinde x gördüğümüz yere x + 5 yazalım:
Anahtar Bilgi
f(x + 5) = ( x + 5)2 = x2 +10x + 25 olarak bulunur.
(a + b)2 = a2 + 2ab + b2
(a –
b)2
=
a2
– 2ab +
b.
Benzer şekilde f(x – 6) = (x – 6)2
b2
= x2 – 2 ·x ·6 + 62
= x2 – 12x + 36 dır
13
f : R → R fonksiyonu f (x) =
değerini bulalım.
a. f(0)
452
b. f(–1)
Ünite 3. Fonksiyonlar
x +2
kuralı ile veriliyor. Buna göre aşağıdaki ifadelerin
x2 + 1
c. f(2x)
ç. f(x + 1)
d. f(a + b)
Fonksiyon Kavramı
Bu ifadeler sırasıyla 0, –1, 2x, x + 1 ve a + b nin f altındaki görüntüleridir. f nin kuralında x yerine bu değerleri yazarak görüntülerini bulabiliriz.
0 +2
=2
02 + 1
a.
f (0) =
b.
f (- 1) =
c.
f (2x) =
ç.
f (x + 1) =
(x + 1) + 2
x+3
= 2
(x + 1) 2 + 1
x + 2x + 2
d.
f (a + b) =
(a + b) + 2
a+b+2
= 2
(a + b) 2 + 1
a + 2ab + b 2 + 1
1
-1 + 2
= 2
(- 1) 2 + 1
2x + 2
2x + 2
= 2
(2x) 2 + 1
4x + 1
14
f : R → R fonksiyonu f(x) = x2 – x + 1 kuralı ile veriliyor. Buna göre aşağıdaki ifadelerin
değerini bulalım.
a.
f(–1)
b.
f(2)
c.
f(x2)
ç.
f(x + 1)
d.
x ≠ 1 iken
f (x) - f (1)
x-1
e.
x ≠ a iken
f (x) - f (a)
x-a
a.
f(–1) = (–1)2 – (–1) + 1 = 1 + 1 + 1 = 3
b.
f(2) = (2)2 – 2 + 1 = 4 – 2 + 1 = 3
Ünite 3. Fonksiyonlar
453
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
c.
f(x2) = (x2)2 – x2 + 1 = x4 – x2 + 1
ç.
f(x + 1) = (x + 1)2 – (x + 1) + 1 = x2 + 2x + 1 – x – 1 + 1 = x2 + x + 1
d.
f (x) - f (1)
x 2 - x + 1 - (1 2 - 1 + 1)
x (x - 1)
x2 - x
=
= x - 1 = x - 1 = x , bu sadeleştirme
x-1
x-1
işlemini x ≠ 1 koşulu altında çalıştığımızdan yapabildiğimize dikkat edelim.
e.
f (x) - f (a)
x 2 - x + 1 - ( a 2 - a + 1)
x 2 - a 2 - (x - a)
=
x-a =
x-a
x-a
(x + a) (x - a) - (x - a)
(x - a) (x + a - 1)
=
= x+a-1
=
x-a
x-a
yine buradaki sadeleştirme işlemini x ≠ a koşulu altında çalıştığımızdan yapabiliyoruz.
15
Bir f fonksiyonu f : R → R ve f(x) = 2x +1 olarak tanımlanıyor. Buna göre
f(2) + f(–1) + f(5) = f(m + 1) + 6
eşitliğini sağlayan m değerini bulalım.
Öncelikle eşitlikteki her bir ifadenin değerini bulmalıyız:
f (2) = 2 $ 2 + 1 = 5
f (- 1) = 2 $ (- 1) + 1 = - 1
f (5) = 2 $ 5 + 1 = 11
f (m + 1) = 2 $ (m + 1) + 1 = 2m + 3
bulunur ve verilen eşitlik 5 + (–1) + 11 = 2m + 3 + 6 şeklinde olur. Buradan
15 = 2m + 9 ve m = 3 olarak bulunur.
454
Ünite 3. Fonksiyonlar
Fonksiyon Kavramı
16
f : R → R olmak üzere f(x + 3) = 9x – 11 olarak tanımlanan f fonksiyonu için aşağıdaki
ifadelerin değerini bulalım.
a.
f(4)
b.
f(0)
1. Yol
a.
f(4) ün değerini bulmak için f(x + 3) = 9x – 11 eşitliğinin sol tarafını f(4) yapan x
değerini bulmalıyız.
x + 3 = 4 ⇒ x = 1 olduğundan
x =1 için f(x + 3) = 9x – 11 ⇒ f(1 + 3) = 9·1 – 11 olur.
⇒ f(4) = – 2 olur.
b.
Benzer şekilde,
x + 3 = 0 ⇒ x = – 3 olduğundan
x = – 3 için f(x + 3) = 9x – 11 ⇒ f(–3 + 3) = 9·(–3) – 11 olur.
⇒ f(0) = –38 olur.
2. Yol
Öncelikle verilen eşitliği kullanarak f(x) in ifadesini bulalım.
x + 3 te x yerine x – 3 yazarsak x elde edileceğinden
f(x – 3 + 3) = 9(x – 3) – 11 ⇒ f(x) = 9x – 38
Buradan
a.
f(4) = 9 · 4 – 38 = –2
b.
f(0) = 9 · 0 – 38 = –38
olarak bulunur.
Ünite 3. Fonksiyonlar
455
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
17
Rüzgâr türbininin rüzgâr enerjisinden ürettiği elektrik, rüzgâr türbininin verimliliğine, havanın yoğunluğuna, rüzgârın
dik olarak geçmekte olduğu alana ve en önemlisi rüzgârın
hızına bağlıdır. Rüzgâr gücü, rüzgâr enerjisinden üretilen
elektriğin miktarını belirtmek için kullanılan bir tabirdir. Bir
rüzgâr türbininde havanın yoğunluğu 1,225 kg/m3 iken rüzgâr gücünü P(v) (Watt) rüzgârın hızı v (m/s) cinsinden veren
fonksiyon şu şekilde olsun:
kg
P (v) = v 3 0, 1 m
Buna göre rüzgârın hızı 10 m/s ve 20 m/s iken bu rüzgâr
türbininin üreteceği gücün kaç Watt olduğunu hesaplayakg.m 2
lım. ( Watt =
eşitliğini kullanalım.)
s3
Rüzgâr hızı iki katına çıkınca bu rüzgâr türbininin üreteceği gücün kaç katına çıkacağını bulalım (v ≠ 0).
Rüzgârın hızı 10 m/s iken v =10 m/s olacağından bu rüzgâr türbininin rüzgâr gücü
kg
P(10) = 103 (m/s) 3· 0,1 m
kg.m 2
= 100
= 100 Watt olacaktır.
s3
Rüzgârın hızı 20 m/s iken v=20 m/s olacağından bu rüzgâr türbininin rüzgâr gücü
kg
P(20)= 203 (m/s)3· 0,1 m
= 800
kg.m 2
= 800 Watt olacaktır.
s3
kg
Rüzgâr hızı v m/s iken bu rüzgâr türbininin rüzgâr gücü P(v) = v3 0,1 m idi.
kg
Rüzgâr hızı 2v m/s iken bu rüzgâr türbininin rüzgâr gücü P(2v) = 8v3 0,1 m olacağından, P(2v) = 8 · P(v) olur. Bu nedenle rüzgâr hızı 2 katına çıkarken rüzgâr gücü 8 katına
çıkmaktadır.
456
Ünite 3. Fonksiyonlar
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında, bir elektronik tablolama programı yardımıyla bağımsız ve bağımlı değişken arasındaki
ilişkiyi ve bu ilişkinin grafiksel gösterimini inceleyeceğiz.
Araç ve Gereçler: Bir elektronik tablolama programı.
•
Bir elektronik tablolama programını (Excel vb.) açıp x ve y sütunları oluşturunuz.
•
x sütununa istediğiniz kadar değer girişi yapınız. y sütunundaki değerleri y = 3x + 1 kuralına uygun olarak bulunuz.
Bunun için;
•
y sütununun ilk hücresine çift tıkladıktan sonra = (3* A2 + 1) yazıp enter tuşuna basınız. A2 x sütunundaki ilk
hücreyi temsil etmektedir. Hücrenin kendisine tıklandığında formüle hücrenin kodu otomatik eklenir.
•
Hücrenin sağ alt köşesindeki noktaya tıklayıp aşağıya x sütunu kadar çekip bırakınız. Program benzer formülü x
deki tüm değerler için uygulayacaktır.
Şekil 1
Şekil 2
Şekil 3
•
Verileri seçip grafik menüsünden grafiğini çiziniz.
•
y = f(x) = 3x + 1 fonksiyonu için f(7), f(100) değerlerini bulunuz.
•
f(a) = 37 ise a değerini bulunuz.
•
A = {19, 27, 71, 87, 91} için f(A) görüntü kümesini bulunuz.
•
A = {0, 12, 2, 4, 7, 567, 13, 234, 543} kümesi için f(A) görüntü kümesini bulunuz.
•
Benzer şekilde yine elektronik tablolama programını kullanarak aşağıda istenenleri yapınız.
f(x) = 5x – 7, g(x) = – x + 9, y =
bulunuz.
2x - 1
fonksiyonlarının belirlediğiniz tanım kümeleri için görüntü kümelerini
5
Ünite 3. Fonksiyonlar
457
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
18
a pozitif bir tam sayı olmak üzere bir kenar uzunluğu a birim olan bir karenin kenar
uzunluğuyla alanı arasındaki ilişkinin bir fonksiyon olup olmayacağını inceleyelim.
Kenar uzunluğu (br)
ALAN (br2)
1
1
2
4
3
9
4
16
5
25
…
…
2
a
a
Bir kenarının uzunluğu a br olan karenin alanı a2 br2 dir. Burada kenar uzunlukları kümesinin her bir elemanı, alan kümesinde bir ve
yalnız bir elemana karşılık gelmektedir.
f : {1, 2, 3, ...} → {1, 4, 9, ...}
f(a) = a2 olur.
Buradan kenar uzunlukları verilen karelerin kenar uzunluklarıyla alanları arasındaki eşleme fonksiyon belirtir.
İki Fonksiyonun Eşitliği
Fonksiyonların eşitliğini tanımlamadan önce bir örnek üzerinde duralım.
x 2 + 2x - 3
cebirsel ifadesini sadeleştirirsek x+3 cebirsel ifadesini elde ederiz.
x-1
Şöyle ki,
(x + 3) (x - 1)
x 2 + 2x - 3
=
= x+3
x-1
(x - 1)
olur. Ancak x + 3 ifadesi x in alacağı bütün gerçek sayılar için bir gerçek sayı belirtse de
x 2 + 2x - 3
ifadesi x = 1 de tanımsız olmakta ve bu değer haricindeki x gerçek sayıları
x-1
için bir gerçek sayı olmaktadır. Dolayısıyla, şu soruyu sorabiliriz.
Kuralları f (x) =
x 2 + 2x - 3
ve g(x) = x + 3 ile verilen f ve g fonksiyonlarının tanım
x-1
ve değer kümeleri ile eşit fonksiyonlar olup olmadıkları hakkında neler söyleyebiliriz?
458
Ünite 3. Fonksiyonlar
Fonksiyon Kavramı
Bu soruların cevapları fonksiyonun tanımında yer almaktadır. Fonksiyonun tanımı gereği bir tanım ve bir görüntü kümesi vardır. Şimdi verdiğimiz örnekteki fonksiyonların
tanım ve görüntü kümelerinin neler olabileceğini bulalım.
f (x) =
x 2 + 2x - 3
ifadesi x = 1 de tanımsızdır. Ama x in alacağı diğer gerçek sayılarda
x-1
tanımlıdır. Dolayısıyla f fonksiyonunun tanım kümesi 1 haricindeki herhangi bir gerçek
sayıyı içeren bir küme olabilir.
g(x) = x + 3 ifadesi herhangi bir değer için tanımlı olduğundan g fonksiyonunun tanım
kümesi herhangi bir gerçek sayıyı içeren bir küme olabilir.
Ayrıca, x gerçek sayısı 1 den farklı ise f(x) = g(x) olacağına dikkat edelim.
Örneğin, f fonksiyonu f : R – {1} → R ve g fonksiyonu g : R → R şeklinde olabilir.
Böyle olması durumunda f ve g fonksiyonları farklı fonksiyonlar belirtecektir çünkü,
tanım kümeleri farklı olacaktır.
Başka bir seçenek olarak f fonksiyonu f : R – {1} → R ve g fonksiyonu g : R – {1} → R şeklinde olabilir. Bu durumda f ve g fonksiyonlarının tanım ve değer kümeleri aynı olduğu
gibi yapacakları ilişkilendirmeler de aynı olacaktır. Yani tanım kümesindeki herhangi bir
x için f(x) = g(x) olacaktır. Bu nedenle, bu seçenekte f ve g fonksiyonları eşit fonksiyonlar
olacaktır.
Fonksiyonların eşit olması için iki önemli hususa dikkat etmemiz gerekir:
1.
Fonksiyonların eşit olması için tanım ve görüntü kümelerinin eşit olması
2. Tanım kümesinin her bir elemanı için fonksiyonların görüntülerinin aynı olması
O halde tanımımızı şu şekilde yapabiliriz:
f : A → B ve g : C → D fonksiyonları verilsin. Eğer
1.
A=C
(tanım kümelerinin eşitliği)
2.
B=D
(görüntü kümelerinin eşitliği)
3.
Her bir x ∈ A = C için f(x) = g(x)
(tanım kümesindeki elemanlara karşılık gelen görüntünün eşitliği)
şartları sağlanırsa, f ile g fonksiyonlarına eşit fonksiyonlar denir ve f = g biçiminde gösterilir.
Ünite 3. Fonksiyonlar
459
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
19
A = {–1, 4} , B = {–1, 14} olmak üzere,
f : A → B, f(x) = x2 – 2 ve g : A → B, g(x) = 3x + 2 ile tanımlanan f ve g fonksiyonlarının
eşit fonksiyonlar olup olmadığını bulalım.
f ve g fonksiyonlarının tanım ve değer kümeleri aynıdır. Şimdi bu fonksiyonların yaptığı
ilişkilendirmelere bakalım.
x = –1 için f(–1) = (–1)2 – 2 = –1
x = 4 için f(4) = 42 – 2 = 14
x = –1 için g(1) = 3 ·(–1) + 2 = –1
x = 4 için g(4) = 3·4 + 2 = 14
olduğundan f(–1) = g(–1) ve f(4) = g(4), yani tanım kümesindeki her bir elemanın
f ve g altındaki görüntüleri eşittir. Bu nedenle bu fonksiyonlar eşittir yani f = g dir.
20
Aşağıdaki fonksiyonların eşit olup olmadıklarını inceleyelim.
x
3
4
5
6
11
15
f(x)
7
8
9
10
15
19
f, g : {3, 4, 5, 6, 11, 15} → {7, 8, 9, 10, 15, 19}, g(x) = x + 4
g(x) fonksiyonun değerler tablosunu oluşturduğumuzda f(x) ile aynı değerler tablosu
elde edilir. Ayrıca f ve g nin tanım ve değer kümeleri de aynıdır. Bu durumda f = g dir.
21
Aşağıda verilen f ve g fonksiyonlarının eşit olup olmadığını belirleyelim.
f : {1, 3, 5, 6, 8} → {7, 9, 11, 12, 14, 15}, f(x) = x + 6
g : {1, 3, 5, 6, 9} →{7, 9, 11, 12, 14, 15}, g(x) = x + 6
f ve g fonksiyonlarının tanım kümeleri eşit değildir. Aynı kurala sahip olsalar da f ve g
eşit fonksiyonlar değildir. Yani f ≠ g dir.
460
Ünite 3. Fonksiyonlar
Fonksiyon Kavramı
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
Aşağıdaki ifadelerde verilen boşluklara uygun
sözcükler yazınız.
a.
A ve B kümeleri boş kümeden farklı iki küme olmak
üzere A nın her elemanının, B nin yalnız bir elema-
4.
nı ile ilişkilendirilmesine A dan B ye bir …………
denir.
b.
Aşağıdaki kümeler arasındaki eşlemelerin fonksiyon belirtip belirtmediğini açıklayınız.
A
B
A
B
–2
9
3
1
–1
7
6
0
3
9
3
0
12
A kümesinden B kümesine tanımlanan bir fonksiyon verilsin. A kümesine bu fonksiyonun
A
ç.
3.
4
5
2
f : A → B olmak üzere f(A) kümesine f fonksiyonunun ………………….. denir.
4
3
6
8
f : A → B ve y = f(x) olarak tanımladığımız fonksiyonumuzda x değerine ……………… değişken,
y değerine ise x in aldığı değerlere bağlı olarak
değiştiği için ……………… değişken denir.
2.
3
B
……………. B kümesine de …………. denir.
c.
2
Fonksiyon kavramını kendi cümlelerinizle açıklayınız.
Tanım kümesi, değer kümesi, görüntü kümesi
kavramlarını açıklayınız.
5.
Aşağıda verilen şemalardan kaç tanesinin A dan B
ye bir fonksiyon olduğunu bulunuz.
A
B
A
B
• a
• 1
• a
• 1
• b
• 2
• b
• 2
• c
• 3
• c
• 3
A
B
A
B
• a
• 1
• a
• 1
• b
• 2
• b
• 2
• c
• 3
• c
• 3
• d
• 4
B
A
B
• 1
• a
• 2
• b
• 3
• c
• 4
• d
A
• a
• b
• c
Ünite 3. Fonksiyonlar
• 1
461
Fonksiyon Kavramı
KENDİMİZİ SINAYALIM
Alıştırmalar
1.
2.
3.
f : A → R bir fonksiyon A = {– 4, – 3, – 2, – 1} ve
f(x) = 1 – 2x ise bu fonksiyonun görüntü kümesini
bulunuz.
f : {6, 8, 10, 12} → Z fonksiyonu için değerler
tablosu
x
6
8
10
12
f(x)
2
–3
1
–4
A= {1,3,5,7,9} olmak üzere f : A → Z fonksiyonunun değerler tablosu şu şekildedir.
x
1
3
5
7
9
f(x)
–1
0
1
2
3
Verilenlere göre
nedir?
5.
6.
462
Bir f: R → R fonksiyonu "Her bir gerçek sayıyı, 5
fazlasının 3 katına eşliyor." şeklinde tanımlanıyor.
Buna göre, (–5) in ve 7 nin görüntülerini bulunuz.
8.
Bir f: R → Z fonksiyonu "Her bir doğal sayıyı, sekiz
katının 12 fazlasına eşliyor." şeklinde tanımlanıyor.
Buna göre, 3 ün ve 6 nın görüntülerini bulunuz.
9.
f: R → R fonksiyonu f(x) = 3x – 6 olarak tanımlanıyor. Buna göre aşağıdakileri bulunuz.
a.
f(x+1)
f : A → R bir fonksiyon, A = {–2, –1, 0, 1, 2} ve
f(x) = 7x – 6 ise bu fonksiyonun görüntü kümesini
bulunuz.
f (6) - f (8)
olarak verilmiştir. Verilenlere göre f (10) + f (12)
ifadesinin eşiti nedir?
4.
7.
f (9) + f (5) - f (7)
ifadesinin eşiti
f (3) - f (1)
f: R → R ve f (x) = 3x + 8 ile verilen f fonksiyonu
için f ((2,6]) kümesini bulunuz.
f: R → R ve f (x) = –2x +1 ile verilen f fonksiyonu
için f ([1,4)) kümesini bulunuz.
Ünite 3. Fonksiyonlar
b. f(7 – 2x)
ç. f(2x2+11)
c. f(9x – 6)
10. f: R → R fonksiyonu f(x) = 2x2 –4x+ 1 olarak tanımlanıyor. Buna göre aşağıdakileri bulunuz.
a.
f(x+1)
b. f(3x – 1)
c.
f( – x)
d.
f(x2)
11. f: R → R fonksiyonu f(x) = x2 + 1 olarak tanımlanıyor. Buna göre aşağıdakileri bulunuz.
a.
f(x+3)
b. f(x – 1)
c.
f(6 – x)
d. f(x2 + 1)
12. f: R → R fonksiyonu f(x) = x2 – 5 olarak tanımlanıyor. Buna göre aşağıdakileri bulunuz.
a.
f(2x)
b. f(1 – x)
c.
f(4 x+6)
ç. f(x2–1)
13. f: R → R ve f (x) = 5x – 4 ile verilen f fonksiyonu
için f ([–3, 9]) kümesini bulunuz.
Fonksiyon Kavramı
KENDİMİZİ SINAYALIM
14. f: R → R olmak üzere f(x) = 4x + 2 fonksiyonu
olarak tanımlanıyor.
f(3) + f(–2) + f(1) = f(a + 2) + 2 ise a değerini bulunuz.
15. f: R → R olmak üzere f(x) = 2x – 6 fonksiyonu
olarak tanımlanıyor.
4·f(3) + 5· f(–2) = 3·f(c+1) – 4 ise c değerini bulunuz.
16. f: R → R fonksiyonu f(x–8) = 3x – 1 olarak tanımlanıyor. Buna göre aşağıdakileri bulunuz
a.
f(7)
b. f(–5)
c.
f(2)
ç. f(– 6)
17. A = {2} , B = {–2,–1,0,1,2} olmak üzere,
f : A → B, f(x) = 3x – 8
20. f: R → R, f(x) = 4x fonksiyonu için aşağıdaki değerleri bulunuz.
1
a. f(3)
b. f(100)
c. f c m
2
ç. f(–5)
d. f ^ 2 h
e. f(r)
21. Aşağıdaki tablolarda verilen y bağımlı değişkenini
x bağımsız değişkeni cinsinden ifade edilebilecek
bir kural bulunuz. Bulduğunuz kuralı elektronik
tablolama programı yardımında oluşturarak kontrol ediniz.
x
1
2
3
4
5
y
8
9
10
11
12
I
x
1
2
3
4
5
y
–3
–2
–1
0
1
II
x
1
2
3
4
5
y
2
4
6
8
10
x
1
2
3
4
5
III
y
–2
1
4
7
10
IV
g : A → B, g(x) = 5x – 12
ile tanımlanan f ve g fonksiyonlarının eşit fonksiyonlar olup olmadığını bulunuz.
18. A = {–6, 3} , B = {–3, 0, 3, 6, 9} olmak üzere,
f : A → B, f(x) = x2 + 4x – 12
22. Aşağıda tanım kümesi ve kuralı verilen fonksiyonların değer kümeleri gerçek sayılar ise bu fonksiyonların görüntü kümelerini bulunuz.
Tanım Kümesi
Kural
Görüntü Kümesi
A = {1, 5, 7, 2}
f(x) = x–8
B = {–8, –15, –17,2} f(x) = 6x+4
g : A → B, g(x) = x + 6
ile tanımlanan f ve g fonksiyonlarının eşit olup
olmadığını bulunuz.
19. A = {–3, 0, 3} , B = {–27, –5, 0, 5, 27} olmak üzere,
f (3) – f (4)
x–3
fonksiyonu için
23. f: R → R, f(x) =
5
2
değerini bulunuz.
f : A → B, f(x) = x3 ve
24. f: R → R, f(x) = 4x – 3 ise f(a), f(b+1), f(c–2), f(2d),
f(3k + 1) değerlerini bulunuz.
g : A → B, g(x) = 9x ile tanımlanan f ve g fonksiyonlarının eşit olup olmadığını bulunuz.
25. A={–1,0,1}, B={–1,1} kümeleri veriliyor. f: A → B,
f(x) = x2 – x – 1 fonksiyonunun grafiğini çiziniz.
Ünite 3. Fonksiyonlar
463
Fonksiyon Kavramı
KENDİMİZİ SINAYALIM
x 2 –4
x–2
26.
g : R " R, g (x) = x + 2
f: R – {2} " R, f (x) =
33. (EĞLENCELİ MATEMATİK) Tüm sınıf arkadaşlarınızla beraber bu oyunu oynayabileceğiniz gibi bir
arkadaşınızla da kendi aranızda oynayabilirsiniz.
Bu oyunun kuralı çok basit: oyunculardan birisi
bir kural belirler ve bu kurala uygun iki sayı söyler;
fonksiyonlarının eşit olup olmadığını bulunuz.
Nedenini açıklayınız.
diğer oyuncular bu iki sayı arasındaki kuralı (ilişkiyi)
bulmaya çalışırlar. Bu oyun için kağıt ve kalem
yeterlidir. Oyunun detaylarını örneklerle anlatalım.
27. f: R → R, f(x) = 3x – 6 ve f(a) = 6 ise a değerini
bulunuz.
Size iki sayı söyleyeceğim. Bu sayılardan ilkine
bazı matematiksel işlemler uyguladığımda ikinci
sayıyı elde ederim. Size, bu matematiksel işlemleri
tahmin edene kadar sayı çiftleri vermeye devam
edeceğim. Örneğin; (3, 10) – Kuralı bilemezseniz
size yeni sayı çiftini vereceğim.
28. C = {–1, 0, 1} kümesi veriliyor.
m: C " C, m (t) = t 3 ve n: C " C, n (z) = z fonksiyonları eşit midir? Neden?
(7, 18) – Kuralı tahmin ettiyseniz (İlk sayının iki
x
29. f: R → R, f(x)= –4 fonksiyonu için f(x + 1), f(x – 1),
3
x
f(2x), f(3x – 1), f a k , f(x2) değerlerini bulunuz.
2
katından dört fazlası) emin olmak için siz kuralı
söylemeden size bir sayı verip ikinci sayının ne
olması gerektiğini soracağım. Eğer bilirseniz kuralı
açıklayabilirsiniz. Aksi taktirde oyun devam eder.
30. Aşağıdaki tablodaki verilere göre y bağımlı değişkeni ve x bağımsız değişkeni arasındaki ilişki ne
olabilir?
x
1
2
3
4
5
y
–1
1
3
5
7
31. f: R → R f(x)=
bulunuz.
32. f: R → R f(x)=
a.
Kuralı bulmak için nasıl bir düşünce yolu izledim?
b.
Sıralı ikililerin birinci bileşenleri ve ikinci bileşenleri
nasıl kümeler oluştururlar?
c.
Her kural için verdiğim sayıya karşılık bir başka sayı
bulabilir miyim?
bx + 3
ve f(–1) = 7 ise b değerini
2
x
+ 5 ve f(3) = 9 ise d değerini
d
bulunuz.
464
Bu oyunu oynadıktan sonra şu sorulara cevap
arayınız:
Ünite 3. Fonksiyonlar
Birim, Sabit ve Doğrusal Fonksiyonlar
3.1.2. Birim, Sabit ve Doğrusal Fonksiyonlar
Neler Öğreneceğiz?
•
Bir fonksiyonun grafiksel gösterimini
•
Birim fonksiyonu
•
Sabit fonksiyonu
•
Doğrusal fonksiyonu
Başlarken
90 km/sa sabit hızla giden bir tren düşünelim. Bu
trenin hızını zamana bağlı olarak veren fonksiyon
için neler söyleyebilirsiniz? Aynı trenin aldığı yolu
zamana bağlı olarak veren fonksiyon hakkında neler söyleyebilirsiniz?
Anahtar Terimler
Daha önce bir fonksiyonun yaptığı ilişkilendirmenin bir kural, değerler tablosu veya
tanım ve değer kümelerinin Venn şemaları üzerinden verilebildiğini gördük. Ayrıca
kümeler konusunda iki kümenin kartezyen çarpımının grafiksel gösterimini öğrendik.
Bununla beraber kartezyen düzlemi de öğrenerek cebirsel bir yapı olan R x R kartezyen çarpım kümesinin geometrik bir yapı olan kartezyen düzlemle temsil edilebileceğini öğrendik. Şimdi ise bu temsilden kartezyen çarpımların bazı alt kümeleri için de
yararlanarak fonksiyonların grafiksel gösterimini öğreneceğiz.
Fonksiyon grafiği
•
Birim fonksiyon
•
Sabit fonksiyon
•
Doğrusal fonksiyon
Sembol ve Gösterimler
A ve B boş olmayan iki küme ve f: A →B bir fonksiyon olsun. Tanım kümesinden
aldığımız her bir x ∈ A ile x in görüntüsü olan f(x) ∈ B elemanlarından oluşturduğumuz (x, f(x)) ikililerinden oluşan kümeye f nin grafik noktaları kümesi deriz
ve Grafik(f) ile gösteririz. Bu ikililer kümesini ortak özellik yöntemiyle şu şekilde
gösterebiliriz:
Grafik(f) = {(x,f(x)) : x ∈ A} = {(x,y) : x ∈ A ve y = f(x)}
Dikkat edersek bu kümeyi tanım kümesindeki x ler ile f altındaki görüntülerini birlikte düşünüp ikililer oluşturarak elde ettik. Grafik(f ) kümesindeki ikililerin birinci
bileşenlerinin kümesi f in tanım kümesini, ikinci bileşenlerinin kümesi ise f nin görüntü kümesini verir. Dolayısıyla bir f fonksiyonunu tanımlamak için Grafik(f ) kümesi ile f in değer kümesini vermek yeterlidir.
Bu kümeyle ilgilenmekteki nedenimiz kümenin f fonksiyonunun grafiksel gösteriminde temel bir araç olmasıdır. Şöyle ki,
Grafik(f) ⊂ A x B
dir. Bu durumda AxB nin grafiksel gösterimini yaptığımız gibi bu sefer sadece
Grafik(f ) de bulunan ikileri aynı grafik üzerinde göstereceğiz. Bu da bize f fonksiyonunun grafiğini yani grafiksel gösterimini vermiş olacaktır. Şimdi daha özel bir
durumu düşünelim. Eğer A 1 R ve B 1 R ise A x B 1 R x R olduğundan
Grafik(f) 1 R x R
olur. Bu durumda f fonksiyonunun grafiği kartezyen düzlemin bir alt kümesi olarak
gösterilir ve kartezyen düzleme ait özellikleri kullanarak fonksiyonun grafiği üzerinde incelemeler yapabiliriz.
Ünite 3. Fonksiyonlar
•
465
•
Grafik (f )
•
I(x) = x
•
f(x) = c
•
f(x) = mx + n
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
Şimdi fonksiyonların grafiksel gösterimlerine örnekler verelim:
1
Değer kümesi R olan bir f fonksiyonu için
1
Grafik (f) = 'c –1, m , (0, 1), (1, 1), (2, 2), (3, –1) 1 olarak veriliyor. Buna göre,
2
a. bu fonksiyonun tanım ve görüntü kümelerini bulalım.
b.
Bu fonksiyonun grafiğini koordinat sisteminde gösterelim.
Fonksiyonun tanım kümesini A ile gösterelim. Grafik(f ) kümesinin ilk bileşenlerinin
kümesi {–1, 0, 1, 2, 3} olduğundan A = {–1, 0, 1, 2, 3} dır. Benzer şekilde Grafik(f ) kü1
mesinin ikinci bileşenlerinin kümesi ' –1, , 1, 2 1 olduğundan f nin görüntü kümesi
2
f (A) = ' –1,
1
, 1, 2 1 olur.
2
y
Tanım kümesini x-ekseninde, değer kümesini
y-ekseninde belirterek Grafik(f ) kümesinde
verilen ikilileri yandaki şekilde gösterebiliriz.
Bu bize f fonksiyonunun grafiğini verir.
2
–1
1 1
2
0
3
1
2
x
–1
2
A = {a, b, c} ve B = {2, 3, 4, 5, 6} kümeleri için f: A → B fonksiyonunun değer tablosu şu
şekilde veriliyor:
x
a
b
c
f(x)
3
5
4
Buna göre f fonksiyonunu grafikle gösterelim.
466
Ünite 3. Fonksiyonlar
Birim, Sabit ve Doğrusal Fonksiyonlar
B
6
5
4
3
2
Bunu biliyor muydunuz
1
0
a
b
A
c
Bazı Fransız matematikçilerin oluşturduğu Bourbaki ekolüne göre bir A
kümesinden B kümesine
tanımlı f fonksiyonu A x B
kümesinin belli özelliklerini
sağlayan alt kümesi şeklinde
tanımlanmaktadır. Bu yaklaşımı tamamen takip etmiş
olsaydık bizim bu kitapta
Grafik(f ) ile gösterdiğimiz
kümeyi de f ile göstermemiz
gerekirdi. Bu kitapta “bağıntı”
kavramını ele almadığımızdan ve fonksiyon kavramını
bağıntı kavramını kullanarak tanımlamadığımızdan
dolayı biz birçok kaynakta da
geçen Grafik(f ) sembolünün
kullanımını uygun gördük.
Böylece fonksiyon için
kullanılan sembole yüklenen
farklı anlamlardan dolayı oluşabilecek yanılgıların önüne
geçmeyi hedefledik.
3
f: A → Z ve f(x) = x2 – x +1 ile verilen fonksiyonun tanım kümesi A = {–1, 0, 1, 2} dir.
Buna göre, f fonksiyonunun grafiksel gösterimini yapalım.
Bu fonksiyonun önce görüntü kümesini sonra da Grafik(f ) kümesini bulalım.
f(–1)=(–1)2 – (–1) +1 = 3
f(0) = (0)2 – (0) +1 = 1
f(1) = (1)2 – (1) +1 = 1
f(2) = (2)2 – (2) +1 = 3
Dolayısıyla, görüntü kümesi f(A) = {1, 3} ve Grafik (f ) = {(–1,3), (0,1), (1,1), (2,3)} olarak
bulunur. Bu bilgileri kullanarak fonksiyonun grafiğini şu şekilde gösterebiliriz:
y
3
2
1
–1
0
1
2
3
x
Ünite 3. Fonksiyonlar
467
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
Birim Fonksiyon
4
A = {a, b, c} ve B = {a, b, c, d} kümeleri için f: A → B fonksiyonunun değer tablosu şu
şekilde veriliyor:
x
a
b
c
f(x)
a
b
c
Buna göre f fonksiyonunu grafikle gösterilim.
y
c
b
a
a
b
c
x
Bu örnekte tanım kümesindeki her bir elemanın görüntüsü de kendisidir. Bu durumun
neticesi olarak A = f(A) ve A ⊂ B olur. Şimdi bu şekildeki özel tip fonksiyonların tanımını
yapalım:
Tanım kümesindeki her değeri kendisiyle eşleyen fonksiyona birim fonksiyon
denir. Birim fonksiyon genellikle I ile gösterilir ve birim fonksiyonun kuralı I(x) = x
olarak belirtilir.
5
f: {1, 2, 3, 4, 5} → {1, 2, 3, 4, 5}, f(x) = x olarak verilen bu birim fonksiyonu şema ve grafikle gösterelim.
f: {1, 2, 3, 4, 5} → {1, 2, 3, 4, 5}, f(x) = x fonksiyonunun şema gösterimi şu şekildedir:
468
Ünite 3. Fonksiyonlar
Birim, Sabit ve Doğrusal Fonksiyonlar
f
A
B
• 1
• 1
• 2
• 2
• 3
• 3
• 4
• 4
• 5
• 5
Bu fonksiyonu için Grafik(f ) = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)} tir. Bu nedenle bu fonksiyonun grafiksel gösterimi ise aşağıdaki gibidir:
B
5
4
3
2
1
0
1
2
3
4
A
5
6
Anahtar Bilgi
f: Z → R , f(x) = x olarak verilen birim fonksiyonun tanım kümesini –4 ile 4 arasındaki
değerleri için grafiksel gösterimi şu şekildedir:
A ve B boş olmayan kümeler
olmak üzere f: A → B, f(x)
= x ise bu fonksiyona birim
fonksiyon denir. Burada
y
f(x) = x
4
A = f(A) ⊂ B olmaktadır.
3
2
(1,1)
1
–4
–3
–2
–1
(0,0) 1
–1
2
3
4
x
–2
–3
–4
Ünite 3. Fonksiyonlar
469
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
Bundan sonraki örneklerimize geçmeden önce doğruların grafiklerinin çizimiyle ilgili
bir hatırlatma yapalım:
Herhangi bir a ve b sabitleri ve x, y ∈ R için, y = ax + b denklemi bir doğru belirtir.
Farklı iki noktadan yalnız ve yalnız bir doğru geçtiğinden, bir doğrunun grafiğini kartezyen düzlemde çizmek için doğrunun üzerinde iki nokta tespit edip bu noktalardan
geçen doğruyu düz bir şekilde çizmemiz yeterlidir. Diğer bir ifade ile y = ax + b denklemini sağlayan herhangi iki farklı (x, y) ikilisi bulup bu ikilileri koordinatları kabul eden
iki noktayı kartezyen düzlemde belirledikten sonra bu noktaları düz bir çizgiyle birleştirirsek istediğimiz doğru grafiğini elde etmiş oluruz.
7
f: R → R , f(x) = x birim fonksiyonunun grafiksel gösterimini yapalım.
Bu fonksiyon herhangi bir gerçek sayıyı kendisine eşliyor. Bu fonksiyonun grafiğini de
önce grafik(f) kümesini oluşturup bu kümeyi kartezyen düzlemde gösterebiliriz. Ancak
görüntüler için y bağımlı değişkenini kullanırsak y = f(x) eşitliğimiz bu fonksiyon için y = x
şeklinde olur. y = x ifadesi bir doğru denklemi belirtir. O halde fonksiyonumuzun grafiği bu
doğrunun grafiğidir. Bu durumda grafiği çizmek için iki nokta belirleyelim.
x = 0 ise y = 0 ve de x = 1 ise y = 1 olacağından doğrumuz (0, 0) noktasından yani orijinden ve (1,1) noktasından geçer. Bu noktaları kartezyen düzlemde gösterip düz bir
şekilde birlertirerek fonksiyonumuzun grafiğini elde etmiş oluruz:
y
f(x) = x
4
3
2
1
–4 –3
–2
–1
(0,0)1
–1
–2
–3
–4
470
Ünite 3. Fonksiyonlar
2
3
4
x
Birim, Sabit ve Doğrusal Fonksiyonlar
8
f: R → R ve f(x) = (2n – 3)x + m – 2 ile verilen fonksiyon birim fonksiyon olduğuna göre
n ve m değerlerini bulalım.
f birim fonksiyon olduğundan tanım kümesindeki her değeri kendisiyle eşlemesi gerekir. Yani bütün x gerçek sayıları için f(x) = x, yani x = (2n – 3)x + m – 2 olmalıdır. Bu
eşitliği x = 0 ve x = 1 için yazarsak 0 = m – 2 ve 1 = (2n – 3) + m – 2 eşitlikleri elde edilir.
Birinci eşitlikten m = 2 ve bu değerin ikinci eşitlikte yerine yazılmasıyla 1 = 2n – 3 yani
n = 2 elde edilir.
9
f: R → R ve f (x) = (a – 4) x2 + (b + 7)x + c – b ile verilen fonksiyon birim fonksiyon olduğuna göre a, b ve c değerlerini bulalım.
f birim fonksiyon olduğundan bütün x gerçek sayıları için f (x) = x olmalıdır. Elimizde a,
b ve c gibi üç bilinmeyen var ve bu bilinmeyenleri bulmak için eşitlikler elde etmeliyiz:
x = 0 için, f(0) = 0, buradan (a – 4)02 + (b + 7) 0 + c – b = 0 ve de b = c sonucu elde edilir.
Bu durumda fonksiyonumuz f(x) = (a – 4)x2 + (b + 7) x kuralını sağlar.
x = –1 için f(–1)= –1, buradan (a – 4) (–1)2 + (b + 7) (–1) = –1 yani (a – 4) – (b + 7) = –1
elde edilir. Benzer şekilde, x = 1 için f(1) = 1, buradan (a – 4) + (b + 7) = 1 elde edilir.
Bulduğumuz bu eşitlikleri taraf tarafa toplayınca 2(a – 4) = 0, ve de a = 4 elde edilir.
Bulduğumuz bu değeri eşitliklerimizden birinde yerine yazarak b + 7 = 1 ve de b = –6
sonucunu elde ederiz. Bu durumda b = c olduğundan c = –6 olarak bulunur.
Sabit Fonksiyon
Şimdi iki farklı örnek üzerinde bir sabit fonksiyonun nasıl bir fonksiyon olduğunu gözlemleyip sabit fonksiyonun tanımını vereceğiz.
Ebrar ve Serkan bir mağazadan alışveriş yapmış ve ödeme yapmak için kasaya gitmişlerdir. Serkan kampanyadan her birinin fiyatı 14,99 TL olan sıfır yaka T–shirt, klasik bir
gömlek, 3’lü çorap takımı ve dokuma bir şal seçmiştir. Ebrar'ın aldığı desenli gömlek,
T–shirt, bluz, mini şemsiye ve kemerin her birinin fiyatı 19,99 TL dir. Ebrar ve Serkan’ın
aldığı ürünler ve fiyatları arasındaki ilişkiyi göstermek için kümeler oluşturup her biri
için birer fonksiyon tanımlayalım.
Ünite 3. Fonksiyonlar
471
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
B
C
A
C
¨ 9,99
¨ 9,99
¨ 14,99
¨ 14,99
¨ 19,99
¨ 19,99
¨ 29,99
¨ 29,99
Alışverişlerinde Serkan sadece 14,99 TL lik ürünler satın alırken Ebrar sadece 19.99 luk
ürünler almıştır. Bir başka ifadeyle her iki fonksiyondaki tanım kümeleri değer kümesindeki tek bir elemanla eşleşmiştir. Bu durumda her iki fonksiyon için de görüntü kümeleri birer elemanlıdır.
Şimdi başka bir örnek verelim:
10 000 TL paramız olsun ve bu parayı bankada tutmak istediğimizi varsayalım. Parayı
bankaya vadesiz hesaptan yatırdığımızı, bu hesap üzerinde hiçbir işlem yapmadığımızı
ve bankanın herhangi bir kesinti yapmadığını varsayalım. Bu durumda zamana bağlı
olarak hesaptaki paranın miktarını veren tablo şöyle olacaktır:
Zaman (Ay)
1
2
3
…
20
Bakiye (1000 TL)
10
10
10
…
10
Tablodaki bu değerlerin grafiksel gösterimi ise şöyledir:
Hesaptaki para
miktarı (1000 TL)
10
5
0
5
10
15
20
Zaman (ay)
Bu iki örnekteki ortak nokta fonksiyonların görüntü kümelerinin bir elemanlı bir küme
olmasıdır. Şimdi bu tür fonksiyonların tanımını yapalım:
f : A → B ile verilen bir f fonksiyonu A kümesinin bütün elemanlarını B kümesinden yalnızca bir eleman ile eşliyorsa bu fonksiyona sabit fonksiyon denir. Eşleme
yapılan elemanı c ile gösterirsek f sabit fonksiyonunun kuralı f(x) = c şeklindedir.
Tanımdan ve örneklerden de anlaşılacağı gibi sabit bir fonksiyonun görüntü kümesi bir
elemanlı olmalıdır ve görüntü kümesi bir elemanlı olanfonksiyonlar sabit fonksiyonlardır.
472
Ünite 3. Fonksiyonlar
Birim, Sabit ve Doğrusal Fonksiyonlar
10
A = {1, 2, 3} ve B = {a, b, c} kümeleri ile f : A → B ve f(A) = {c} şeklinde bir sabit fonksiyon
veriliyor. Bu fonksiyonu küme şemasında ve grafiksel olarak gösterelim.
A
f
B
• 1
• a
• 2
• b
• 3
• c
B
c
b
a
1
2
3
A
11
f: R → R ve f(x) = 4 ile verilen fonksiyonun grafiğini çizelim.
f(x) = 4 kuralını y = 4 şeklinde ele alabiliriz. Bu durumda herhangi bir x değeri için y
değerleri daima 4 olacaktır. Bu durumda grafiğimiz şu şekildedir:
y
Anahtar Bilgi
6
5
4
3
2
1
–6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6
–1
A ve B boş olmayan kümeler
ve c ∈ B olmak üzere
f: A → B, fonksiyonu verilsin.
Her x ∈ A için f(x) = c oluyorsa bu fonksiyona sabit
fonksiyon denir.
x
İkinci bir yaklaşım olarak hatırlayalım ki, y = 4 denkleminde x olmadığından bu denkleme karşılık gelen doğru x-eksenine paralel olacaktır. Bu durumda (0, 4) noktasının
doğru üzerinde olduğunu bilmemiz, bu fonksiyonun grafiğini çizmek için yeterlidir.
Ünite 3. Fonksiyonlar
473
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
12
f: R → R ve f(x) = (m – 2)x + m + 1 ile verilen f fonksiyonu sabit bir fonksiyondur.
Buna göre
a.
m
b.
f(1250)
değerini bulalım.
a. f sabit bir fonksiyon olduğundan fonksiyonun kuralı değişkenden bağımsız olmalıdır. Dolayısı ile f(x) ifadesindeki x in katsayısı 0 olacağından m–2=0 dır.
İkinci bir yaklaşım olarak, sabit fonksiyon için görüntü tek elemanlı olacağından tanım
kümesinden alacağımız herhangi iki değerin görüntüsü de aynıdır. Örneğin, f(0)=f(1)
olmalıdır.
f(0) = m + 1 ve f(1) = (m–2)+m+1=2m–1 olduğundan m+1=2m–1 ve de m=2 elde edilir.
b.
m=2 olduğundan f(x)=3 tür. Bu nedenle f(1250)=3 olur.
13
(m–1) x + 2
ile verilen f fonksiyonu sabit bir fonksiyon ise m
x–2
sayısını ve f(x) ifadesini bulalım.
f: R –{2} → R ve f(x)=
f sabit bir fonksiyon ise tanım kümesindeki her elemanın f altındaki görüntüsü aynıdır.
Bu durumda x = 0 ve x = 1 için f(0) = f(1) yani
(m - 1) · 0 + 2
(m - 1) · 1 + 2
=
0-2
1-2
–x + 2
olur. Ancak dikkat edilirx–2
se iki fonksiyonun eşitliği konusunda öğrendiğimiz gibi f fonksiyonu ile g: R – {2} → R
ve g(x) = –1 ile verilen g fonksiyonu eşit fonksiyonlardır. Dolayısıyla f(x) = –1 dir.
olmalıdır. Buradan m=0 elde edilir. Bu durumda f (x) =
474
Ünite 3. Fonksiyonlar
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında farklı değerler için elde edilen bir grafiğin hangi fonksiyon türüne ait olduğunu inceleyeceğiz.
Araç ve Gereçler:
• Cetvel (20–30 cm)
• Yay
• Kalem veya çubuk
• Ufak bir kap (kağıttan yapabilirsiniz)
• Bozuk para
Yandaki gibi bir düzenek kurun.
Adım 1
Kabımıza koyduğumuz bozuk paraya göre kabımızın alt kısmı cetvel üzerinde hangi değeri gösterir?
Adım 2
Bu sorunu cevabını bulabilmek için aşağıdaki işlemleri farklı bozuk para değerleri için tekrar edin.
Adım 3
Bozuk parayı kaba yerleştirin ve kabın alt kısmının cetvel üzerindeki değeri not edin. (Burada kaba eklenen her bozuk
para için yayın esnemesinin arttığını varsayıyoruz. Dolayısıyla yay seçimi buna göre yapılmalı.)
Adım 4
Bulduğunuz değerler için grafik çizin.
Adım 5
Ne çeşit bir grafik elde ettiniz?
Adım 6
Grafiğinizin başlangıç noktası neresidir?
Adım 7
Deney yapmadan 3 tane 25 kuruşun kabınızın alt kısmını cetvelin hangi seviyesine getireceğini söyleyin. Cevabınızı ve
yönteminizi arkadaşlarınızla tartışınız.
Ünite 3. Fonksiyonlar
475
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
Doğrusal Fonksiyon
a ∈ R , a ≠ 0 ve b ∈ R şeklindeki a ve b sabitleri verilsin. Bir f: R → R fonksiyonunun kuralı f(x) = ax + b biçiminde ise bu fonksiyona doğrusal fonksiyon denir.
14
f: R → R ve f(x) = 3x + 1 ile verilen doğrusal fonksiyon verilsin. A = {0, 1, 2, 3, 4} kümesindeki elemanların f altındaki görüntülerini bulalım ve bunları bir tabloda gösterelim.
f(0) = 3 · 0 + 1 = 1 ve benzer şekilde f(1) = 4, f(2) = 7, f(3) = 10, f(3) = 13 olur. Dikkat
edersek A kümesindeki elemanlar 1 er 1 er artarken f altındaki görüntüleri 3 er 3 er
artmakta. Bulduğumuz değerleri tabloda gösterelim:
x
0
1
2
3
4
f(x)
1
4
7
10
13
15
f: R → R ve f(x) = 2x + 1 ile verilen doğrusal fonksiyonun tanım, değer ve görüntü kümelerini belirtelim ve bu fonksiyonun grafiğini çizelim.
Bu fonksiyonun tanım kümesi R, yani tüm gerçek sayılardır. Bu fonksiyonun değer
kümesi de R olarak verilmiş. Görüntü kümesinin değer kümesinin bir alt kümesi olduğunu yani f(R) ⊂ R olduğunu biliyoruz. Şimdi değer ve görüntü kümelerinin eşit
olup olmadığına yani f(R) = R eşitliğinin sağlanıp sağlanmadığına bakalım. Bunun için
R ⊂ f(R) olmasın yeterli (bunun neden yeterli olduğunu belirtiniz). Dolayısıyla, değer
kümesinden aldığımız bir b değerinin tanım kümesinden bir elemanın görüntüsü olup
olmadığına bakacağız. b = f(a) ise b = 2a + 1 ve buradan a = (b – 1) / 2 olur ki b bir gerçek sayı olduğundan a da bir gerçek sayı olur. Böylece değer ve görüntü kümelerinin
eşit olduğunu sonucuna ulaştık.
Bu fonksiyonun grafiğini çizerken tanım kümesi R olduğundan tüm x-ekseni tanım kümesini temsil edecektir. Benzer şekilde görüntü ve değer kümeleri R olduğundan tüm
y-ekseni de bu kümeleri temsil edecektir. Ayrıca hatırlayacağımız üzere y = f(x) veya
y = 2x + 1 olması bu denklemin grafiğinin bir doğru olduğunu göstermektedir. Daha
önce de belirttiğimiz gibi doğru grafiği için iki noktanın bulunması yeterli olacaktır. Bu
noktaları tespit etmek için x e değerler verip görüntülerini bulabiliriz. Örneğin,
x
-
1
2
0
f(x)
0
1
1
, 0 m ve (0, 1) noktaları grafik üzerinde olacaktır çünkü doğrunun eşitliğini sağ2
layan x ve y ikililerinden oluşmaktadır. Şimdi bu noktaları grafik üzerinde gösterip bu
noktalardan geçen doğruyu çizebiliriz.
c-
476
Ünite 3. Fonksiyonlar
Birim, Sabit ve Doğrusal Fonksiyonlar
B
y = 2x + 1
Anahtar Bilgi
2
a ile b birer gerçek sayı ve
a ≠ 0 olmak üzere, gerçek
sayılar üzerinde tanımlı bir
f fonksiyonu f(x) = ax + b
kuralı ile verilirse bu fonksiyon bir doğrusal fonksiyonu
belirtir.
1
–2
–1 - 1 0
2
1
2
A
Bu örnekte izlediğimiz yol bütün doğrusal fonksiyonların grafikleri çiziminde uygulanabilir. Benzer şekilde herhangi bir f: R → R ve f(x) = ax + b doğrusal fonksiyonu için
tanım, değer ve görüntü kümelerinin R olduğu gösterilebilir.
16
f: R → R ve f (x) = 2x – 2 doğrusal fonksiyonunun grafiğini çiziniz.
Verilen fonksiyonun tanım, değer ve görüntü kümelerinin R olduğunu ve de grafiğini
çizmek için grafiğin üzerindeki en az iki noktaya ihtiyacımız olduğunu biliyoruz. Bu
noktaların bir önceki örnekte olduğu gibi grafiğin x ve y eksenlerini kestiği noktalar
alabiliriz. y = 2x – 2 eşitliğinde x = 0 için y = –2 olur ve bu bize (0, –2) noktasını verir.
Benzer şekilde y = 0 için 0 = 2x – 2 den x = 1 olur ve bu bize (1,0) noktasını verir. (0, –2)
noktasının grafiğin y-eksenini kestiği nokta ve (1, 0) noktasının grafiğin x-eksenini kestiği nokta olduğuna dikkat edelim. Bu durumda f: R → R ve f (x) = 2x – 2 fonksiyonunun grafiği (0, –2) ve (1, 0) noktalarından geçen bir doğrudur.
y
y = 2x – 2
2
1
0
–1
0
1
2
3
x
–1
–2
Ünite 3. Fonksiyonlar
477
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
17
f, R de tanımlı doğrusal bir fonksiyon olarak veriliyor. f(2) = 2 ve f(4) = 12 ise f fonksiyonunun kuralını bulalım.
f , de tanımlı doğrusal bir fonksiyon olduğundan ve f (x) = ax +b şeklindedir.
f(2) = 2 ve f(4) = 12 olduğundan f(2) = 2a + b = 2 olur ve 2a + b = 2 elde edilir.
Diğer taraftan f(4) = 4a + b = 12 ⇒ 4a + b = 12 dir. Buradan,
–2a – b = – 2
+
4a + b = 12
taraf tarafa toplarsak
2a = 10 ve a = 5 bulunur.
Bulduğumuz a = 5 değerini 2a + b = 2 de yerine yazarsak 2 · 5 + b = 2 olur ve b = –8
olarak bulunur.
Buna göre f(x) doğrusal fonksiyonunun kuralı f(x)= 5x – 8 dir.
18
f, R de tanımlı doğrusal bir fonksiyon olarak veriliyor. f(3) = 9 ve f(6) = 15 ise f(4) değerini bulalım.
f(x) doğrusal bir fonksiyon olduğundan bu fonksiyonun kuralı f(x) = ax+b şeklindedir.
Verilenleri kullanarak 9 = f(3) = 3a+b ve 15 = f(6) = 6a+b elde edilir. Bu durumda
3a+b = 9
6a+b = 15
olur. a ve b bilinmeyenlerini bu doğrusal denklem sistemini için çözerek bulabiliriz.
Birinci eşitliği ikinci eşitlikten çıkardığımızda b bilinmeyenini yok ederek, 3a=6 ve buradan a=2 elde edilir. Bulduğumuz bu değeri ilk eşitlikte yerine yazarsak 3 · 2 + b = 9
ve de b=3 olur.
Buna göre f(x) doğrusal fonksiyonunun kuralı f(x)= 2x + 3 olur.
Buradan f(4) = 2 · 4 + 3 = 11 olarak bulunur.
478
Ünite 3. Fonksiyonlar
Birim, Sabit ve Doğrusal Fonksiyonlar
19
f: R → R ve f (x) = (a – b – 3)x3 + (2a – b – 7)x2 + (a–1)x + (a + b) fonksiyonu doğrusal bir
fonksiyon ise bu fonksiyonun kuralını bulalım.
Birinci yol:
f doğrusal bir fonksiyon olduğundan, sıfırdan farklı bir m ve herhangi bir n sabit gerçek
sayıları için f (x) = mx + n şeklinde olmalıdır. Buradan f(–1) = n – m, f(0) = n, f(1)=m+n
ve f(2) = 2m + n olacaktır. Buradan
f(2) – 2f(1) + f(0) = 0 ve
f(–1) + f(1) – 2f(0) = 0
eşitlikleri elde edilir.
Diğer taraftan f için bize verilen kuralı kullanırsak
f(–1) = –(a – b – 3) + (2a – b – 7) – (a – 1) + (a + b) = a + b – 3
f(0) = a + b
f(1) = a – b – 3 + 2a – b – 7 + a – 1 + a + b = 5a – b – 11
f(2) = (a – b – 3) 8 + (2a – b – 7) 4 + (a – 1) 2 + a + b = 19a – 11b – t54
olur. Buradan
f(2) – 2f(1) + f(0) = 19a – 11b – 54 – 2(5a – b – 11) + (a + b) = 10a – 8b – 32
f(–1) + f(1) – 2f(0) = (a + b – 3) + (5a – b – 11) – 2(a + b) = 4a – 2b – 14
bulunur.
Bu durumda
10a – 8b – 32 = 0
4a – 2b – 14 = 0
doğrusal denklem sistemini elde ederiz. Bu eşitlikleri 2 ye bölüp düzenlersek
5a – 4b = 16
2a – b = 7
Anahtar Bilgi
elde edilir. İkinci denklemi 4 ile çarpıp ilk denklemi çıkartırsak 3a = 12 ve de a = 4 bulunur. Bunu ikinci denklemde yerine yazarsak 8 – b = 7 ve de b = 1 elde edilir. Buradan
"f: R → R " ifadesi yerine
"R de tanımlı f fonksiyonu"
ifadesi de kullanılmaktadır.
n = f(0) = a + b = 5 ve m = f(1)–f(0) = 5a – b – 11 – (a + b) = 4a – 2b – 11 = 4.4 – 2.1 – 11 = 3
olur. Bu durumda f(x) = 3x + 5 olarak bulunur.
Ünite 3. Fonksiyonlar
479
Bölüm
3.1
Fonksiyon Kavramı ve Gösterimi
İkinci Yol:
f doğrusal bir fonksiyon olduğundan, x3 ve x2 nin katsayıları sıfır olmalıdır (bunun nedeni üzerinde düşünüp arkadaşlarınızla tartışınız). Buradan
a–b–3 = 0
•
Bunu biliyor muydunuz
ise
a–b = 3
2a –b–7 = 0 ise 2a–b = 7 olur. Bu denklemlerin çözersek a=4 ve b=1 olarak
bulunur. Buna göre f (x) = (4–1)x +(4+1) = 3x+5 olmalıdır.
Gerçek yaşam durumlarında doğrusal fonksiyon
örnekleri ile karşılaşabiliriz.
Örneğin 50 km/sa sabit
hızla giden bir arabanın
aldığı yolun zamana bağlı
değişimi,
20
f, R de tanımlı doğrusal bir fonksiyon olarak veriliyor. 2. f(x)+ f(x+2)=9x+18 ise f fonksiyonunun kuralını belirleyelim.
x: zaman (sa)
y: yol (km)
•
için y = 50x
Cep telefonu operatörlerinin kampanyalarında
dakikaya göre ücret
tarifeleri. Örneğin,
f doğrusal bir fonksiyon olduğundan f(x) = ax+b şeklindedir. Buradan
f(x+2) = a(x+2)+b = ax+2a+b olur. Bu nedenle
25 TL ödemeli, dakika
sınırı aşınca dakikası 0,12
TL şeklindeki bir tarife
2 · f(x)+f(x+2) = 2(ax+b)+ax+2a+b = 3ax+2a+3b olur. Verilenleri kullanarak
y: ücret (TL)
eşitliğini elde ederiz. Bu eşitliğin herhangi bir x gerçek sayısı için sağlanacağını biliyoruz. Dolayısıyla buradan sonra a ve b değerlerini iki yolla bulabiliriz.
3ax+2a+3b = 9x+18
x: dakika sınırını aşan
konuşma süresi (dakika)
için y = 25 + 0,12x dir.
Birinci yol:
Farklı x değerleri için eşitliği kullanıp a ve b değerlerini bulabiliriz.
x = 0 için 3a · 0+2a+3b = 9 · 0+18 yani 2a+3b = 18 olur.
x = 1 için 3a · 1+2a+3b = 9 · 1+18 yani 5a+3b = 27 olur.
İkinci denklemden birinci denklemi çıkartırsak 3a = 9 ve de a = 3 elde edilir. Bunu ilk
eşitlikte kullanırsak 2 · 3+3b = 18 ve de b = 4 sonucuna ulaşırız.
İkinci yol:
Herhangi bir x ∈ R için 3ax+2a+3b = 9x+18 eşitliği sağlandığından 3a = 9 ve 2a+3b = 18
olmalıdır (nedeni üzerinde düşünüp arkadaşlarınızla tartışınız). Buradan da a = 3 ve b = 4
sonucuna ulaşılabiliriz.
Sonuç olarak f(x) = 3x + 4 kuralını elde ederiz.
480
Ünite 3. Fonksiyonlar
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında verilen şeklin değişme kuralını ve bu kurala bağlı olarak istenilen herhangi bir adımda
şeklin görüntüsünü ve içerdiği kare sayısını hesaplamayı öğreneceğiz.
1. adım
2. adım
İlk iki adımı verilmiş yukarıdaki şekil düzenli bir şekilde değişmektedir.
Adım 1
Birinci adım ve ikinci adım arasındaki farkı bulunuz.
Adım 2
İki adım arasındaki farkı dikkate alırsanız üçüncü adım sizce nasıl olmalıdır?
Adım 3
Birinci, ikinci ve üçüncü adımların her birinde kaçar kare bulunmaktadır?
Adım 4
Dördüncü adımdaki kare sayısını bu adımı çizmeden tahmin etmeye çalışın.
Adım 5
Dördüncü adım için tahmininizi bu adımı çizerek kontrol edin.
Adım 6
Yedinci adımda sizce kaç kare olmalıdır?
Adım 7
Şekillerin değişim kuralını genel olarak nasıl ifade edebilirsiniz?
Adım 8
Bulduğunuz kuralı diğer arkadaşlarınızla karşılaştırınız ve kuralınızın 10, 20 ve 30. adımlar için kare sayılarını doğru
şekilde bulup bulamadığını kontrol ediniz. (Bu adımdaki kuralınızı test etmek için GeoGebra gibi bir dinamik geometri
yazılımı kullanabilirsiniz).
Adım 9
Bu kuralı bir fonksiyon olarak yazmak isterseniz bu fonksiyon ne olacaktır?
Ünite 3. Fonksiyonlar
481
Birim, Sabit ve Doğrusal Fonksiyonlar
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
Aşağıdaki ifadelerde noktalı olan yerleri doldurunuz.
a.
f : A → A tanımlanan f fonksiyonunda A kümesinin her elemanını tekrar kendisine eşliyorsa, f fonksiyonuna
.........................
denir. Birim fonksiyon . . . . . . . . . . . . . . . . . . . . . . . . . biçiminde gösterilir.
b.
f : A → B tanımlanan f fonksiyonunda A kümesinin bütün elemanları, B kümesinin yalızca bir elemanı ile eşleyen
f fonksiyonuna . . . . . . . . . . . . . . . . . . . . . . . . . denir.
c.
Doğrusal fonksiyonların grafiği kartezyen düzlemde bir . . . . . . . . . . . . . . . . . . . . . . . . . dur.
2.
Aşağıda fonksiyon kavramıyla ile ilgili bazı bilgiler verilmiştir. Bunlardan doğru olanların yanına “D” , yanlış olanların yanına “Y” yazınız.
(…)
Denklemler ve fonksiyonlar kavramsal olarak birbirinden farklıdır.
(…)
Bazı denklemler aynı zamanda bir fonksiyon belirtir.
(…)
Fonksiyonlarda bağımlı ve bağımsız değişkenler vardır.
(…)
Fonksiyonlarda tanım ve değer kümelerinden söz edilirken, denklemlerde çözüm kümesi söz konusudur.
(…)
Kavramsal olarak denklemler ve fonksiyonlar aynı anlamı ifade ederler.
(…)
Fonksiyonlar bir dönüşüm tanımlarlar.
3.
Gerçek sayılar kümesinde tanımlı aşağıdaki ifadelerden hangileri bağımsız ve bağımlı değişken bağlamında bir
fonksiyon belirtir? Cevabınızın nedenini açıklayınız.
a.
2x + 3 = –1
b.
x + 2y = 5
c.
x2 + 4x + 3
ç.
y = x2 + e
d.
x2 + y2 = 4
e.
g(x) = x1/2
f.
x = ay, a ∈ R
482
Ünite 3. Fonksiyonlar
Birim, Sabit ve Doğrusal Fonksiyonlar
KENDİMİZİ SINAYALIM
4.
5.
Tabloda verilen ilişkilerden hangisi/hangileri fonksiyondur?
Tanım bölgesi
İlişki
Değer bölgesi
1
2012 yılında tüm illerimizin
belediye başkanları
Yılın belediye başkanı seçimi
2012 yılında tüm illerimizin belediye
başkanlarının sırası
2
2013 yılında üretilen otomobil markaları
Arabanın markası – satış
adedi
2013 yılında üretilen otomobil markalarının her birinin satış adedi
3
Türkiye’deki 2012 araba yarışı
pilotları
Pilot – kazandığı yarış
2012 deki tüm araba yarışları
x sütunu tanım, y sütunu ise değer kümesinin elemanlarını göstermek üzere f ve g fonksiyonlarından hangisi
doğrusal bir fonksiyondur? Neden?
f
g
x
y
x
y
1
5
10
1
2
10
20
3
3
15
30
7
4
20
40
13
5
25
50
21
6
30
60
31
7
35
70
43
8
40
80
57
6.
Sabit fonksiyon, birim fonksiyon, doğrusal fonksiyon kavramlarını kendi cümlelerinizle açıklayınız.
7.
f: R → R, f(x) = ax + b fonksiyonun birim fonksiyon belirtmesi için a ve b değerleri ne olmalıdır?
8.
f: R → R, f(x) = (a – 2)x + 6 fonksiyonun sabit fonksiyon belirtmesi için a ne olmalıdır?
9.
f: R → R, f (x) = (n + 5)x + n + 6 fonksiyonu sabit fonksiyon olduğuna göre f(1) kaçtır?
Ünite 3. Fonksiyonlar
483
Birim, Sabit ve Doğrusal Fonksiyonlar
KENDİMİZİ SINAYALIM
10. f: R → R, g(x) = (a–2) x2+(b+2)x–a.b fonksiyonu sabit bir fonksiyon ise g(2015) kaçtır?
11. f: R → R, f (x) = a.x + b – 4.x + 8 fonksiyonun birim fonksiyon olduğuna göre 2 · a +3 · b değerlerini bulunuz.
12. f: R → R, ve f(x)=ax+b olmak üzere; f(1) = 9 ve f(2) = 17 olduğuna göre, f(11) kaçtır?
13. Tanımlı olduğu kümede, f(x)=
k . x – 20
sabit fonksiyon ise k – f(–8) kaçtır?
x–5
14. g: R → R, g(x)=(2m–4)x3–m fonksiyonu sabit bir fonksiyon ise m nin alabileceği değerler toplamı kaçtır?
15. Tanım ve görüntü kümeleri aşağıdaki tablolarla belirtilen fonksiyonların birim, sabit veya doğrusal fonksiyon
olarak isimlendiriniz.
x
y
3
12
8
32
11
44
17
68
21
84
16. f: R – {3} → R, f(x) =
x
3
8
11
17
21
y
7
7
7
7
7
x
y
3
3
8
8
11
11
17
17
21
21
(m–2) x + 3
fonksiyonu sabit bir fonksiyon ise m sayısı kaçtır?
2x–6
17. f: R → R, f (x) = (2a + b – 2)x3 + (3a – b – 8)x2 + (a – 5)x + (a – b) fonksiyonu doğrusal bir fonksiyon ise aşağıda
istenenleri bulunuz.
a.
f(x) fonksiyonunun kuralını
18. Gerçek sayılarda tanımlı f (x) =
b. f (5)
c. f (–8)
ç. f (x+1)
ax + b
a
b
sabit fonksiyonu ise
olmalıdır. Neden?
=
cx + d
c
d
19. Bir arabanın aldığı yolla harcadığı benzin arasında doğrusal ilişki vardır. (Örneğin;10 km gittiğinde 1 lt benzin
20 km gittiğinde 2 lt benzin gibi) arabanın aldığı yolla benzin arasındaki ilişkinin grafiğini çiziniz? Çizdiğiniz
grafiğin fonksiyon olması için tanım ve değer kümeleri nasıl olmalıdır? Bu grafiğin denklemini yazınız.
484
Ünite 3. Fonksiyonlar
Fonksiyon Kavramı ve Gösterimi
BÖLÜM ÖZETİ
Fonksiyon: A ve B boş olmayan iki küme olsun. A kümesinin her bir elemanını B kümesinin bir ve yalnız bir
elemanına eşleyen ilişkiye A’dan B’ye tanımlı fonksiyon
denir ve f: A → B şeklinde gösterilir.
Eşit fonksiyonlar: f : A → B ve g: C → D fonksiyonları için
A ve B kümelerinin elemanları arasında yapılan bir ilişkilendirmenin fonksiyon olabilmesi için;
3. Tanım kümesindeki her x için, f(x) = g(x) olmalıdır.
•
A ≠ ∅ ve B ≠ ∅ olmalıdır.
•
A kümesinde eşlenmeyen eleman olmamalıdır.
•
A kümesinin elemanlarından bir tanesi, B kümesinin
elemanlarından birden fazlası ile eşlenmemelidir.
Burada A tanım kümesi, B ise değer kümesi olarak tanımlanır. B kümesinin her elemanının A kümesinin elemanı olması gerekmez. A kümesinin elemanlarının B
kümesinden eşlendiği elemanlara görüntü kümesi denir. Görüntü kümesi, değer kümesinin boş olmayan bir
alt kümesidir. Görüntü kümesi f(A) ile gösterilir ve ortak
özellik yöntemiyle f(A) = {f(x) : x ∈ A} şeklinde gösterilir.
y = f(x) olarak tanımladığımız fonksiyonumuzda x değerine bağımsız değişken, y değerine ise x’in aldığı değerlere bağlı olarak değiştiği için bağımlı değişken denir.
x
girdi
f
çıktı
bağımsız
değişken
f(x)
bağımlı
değişken
Şemada görüldüğü gibi f fonksiyonu bir makineye de
benzetilebilir. Makinenin girdileri olarak tanım kümesindeki her elemanına karşılık değer kümesindeki yalnızca
bir elemanı çıktı olarak vermektedir.
Bir f : A →B fonksiyonu ile a ∈ A ve b ∈B için b = f (a) ise
•
a nın f altındaki görüntüsü b dir.
•
f in a daki değeri b dir.
•
f fonksiyonu a yı görüntü kümesinden b ile ilişkilendirmiştir.
1. Tanım kümeleri eşit olmalıdır.
2. Değer kümeleri eşit olmalıdır.
koşulları sağlanıyorsa f ve g fonksiyonlarına eşit fonksiyonlar denir ve f = g şeklinde gösterilir.
Bir f: A → B fonksiyonu için. Tanım kümesinden aldığımız
her bir x ∈ A ile x in görüntüsü olan f(x) ∈ B elemanlarından oluşturduğumuz (x, f(x)) ikililerinden oluşan kümeye
f in grafik noktaları kümesi deriz ve Grafik(f) ile gösteririz. Bu ikililer kümesini ortak özellik yöntemiyle şu şekilde
gösterebiliriz:
Grafik(f)={(x,f(x)) : x ∈ A } = {(x,y) : x ∈ A ve y=f(x)}
Grafik(f) ⊂ AxB dir. Bu nedenle Grafik(f ) kümesini AxB
kümesinin grafiksel gösterimine benzer şekilde grafiksel
olarak ifade edebiliriz. Bu f fonksiyonunun grafiksel gösterimini verir.
Tanım kümesindeki her değeri kendisiyle eşleyen fonksiyona birim fonksiyon denir. f bir birim fonksiyon ise
kuralı f(x) = x şeklindedir.
Tanım kümesindeki her elemanı sabit bir değerle eşleyen fonksiyona sabit fonksiyon denir. f bir sabit fonksiyon ve görüntü kümesi {c} ise kuralı f(x) = c şeklindedir.
f: R→R ve f(x) = c sabit fonksiyonunun grafiği (0,c) noktasından geçen ve x-eksenine paralel olan bir doğrudur.
a ve b sabitleri a ∈ R , a ≠ 0 ve b ∈ R şeklinde verilsin.
Bir f: R→R fonksiyonunun kuralı f(x) = ax+b biçiminde
ise bu fonksiyona doğrusal fonksiyon denir. f: R→R
ve f(x) = ax+b doğrusal fonksiyonunun grafiği (0, b) ve
(–b/a, 0) noktalarından geçen bir doğrudur. Bu doğru xeksenini (–b/a, 0) ve y-eksenini de (0, b) noktasında keser.
Ünite 3. Fonksiyonlar
485
3. 1. Fonksiyon Kavramı ve Gösterimi
BÖLÜM DEĞERLENDİRME
Uygulama Soruları
1.
f: R → R f(x) = 2x2 –3 fonksiyonu için
a.
f(–2)
b.
f(0)
c.
f(2)
ç.
f(a+1)
d.
f(x2)
e.
f(x2+1)
5.
Bu durumu cebirsel bir fonksiyon olarak ifade
ediniz.
6.
f: A → B, f(x) = 2x + 1 fonksiyonunun görüntü
kümesi, B = {–2, 3, 6} olduğuna göre A kümesini
bulunuz.
7.
f: R – {a} → R, f (x) =
8.
A = {–1, 1}, B = {–1, 1} olmak üzere,
değerlerini bulunuz.
2.
Bir f fonksiyonu “Her bir pozitif tam sayıyı kendisi ile çarpımsal tersinin toplamına götürüyor.”
şeklinde tanımlanmıştır. Bu fonksiyonu ve f(4)’ün
değerini bulunuz.
3.
Bir g fonksiyonu “Her bir negatif gerçek sayıyı tam
sayıyı kendisi ile çarpımsal tersinin toplamına
götürüyor.” şeklinde tanımlanmıştır. Bu fonksiyonu
ve f(1/4)’ün değerini bulunuz.
4.
Bir kişinin deniz seviyesinden yüksekliğin karekökü
ile orantılı olarak yatay uzaklığı görebildiğini kabul
edelim. Buna göre eğer deniz seviyesinden 25
metre yükseklikte ise 30 kilometreye kadar uzaklığı
görebiliyorsa
a.
Eğer deniz seviyesinden 64 m yükseklikte ise ne kadar uzağı görebilir?
b.
Bir kişinin 24 kilometreye uzaklığı görebilmesi için
deniz seviyesinden kaç metre yükseklikte olması
gerekir?
486
Ünite 3. Fonksiyonlar
x2 + 3
x–5
ifadesi bir fonksiyon belirttiğine göre a değeri
kaçtır?
f : A → B, f(x) = x2 – 2 ve g : A → B, g(x) = x – 2 ile
tanımlanan f ve g fonksiyonlarının eşit fonksiyonlar
olup olmadığını bulunuz.
9.
Aşağıda verilen f ve g fonksiyonlarının eşit olup
olmadığını belirleyiniz.
f: {1, 2, 3, 4, 5} → {3, 5, 7, 9, 11, 13} , f(x) = 2x + 1
g: {1, 2, 3, 4, 5} → {3, 5, 7, 9, 11, 13, 15} , g(x) = 2x + 1
3. 1. Fonksiyon Kavramı ve Gösterimi
BÖLÜM DEĞERLENDİRME
10. f: N → R f (x) =
x2 - 4
x+2
g: N → R g(x) = x – 2 olsun.
16. f: R→R,
6x–a
fonksiyonu için f(2) = 3 ise a sayısını
f (x) =
5
bulunuz.
f ve g fonksiyonlarının eşit olup olmadığını belirleyiniz.
11. A = {–1, 0, 1} ve B = {1, 3, 5} kümeleri veriliyor.
g: A → B, g(t) = t3 – t + 1 ise g fonksiyonu sabit bir
fonksiyon mudur? Neden?
17. C = {0, 1, 2} ve D = {–1, 0, 1, 2, 3, 4} kümeleri veriliyor.
g: C → D , g(x) = 1 – x ve h: C → D, h(x) = x – 1
fonksiyonları eşit midir? Neden?
12. f: R → R, f(x) = (4a – 8)x + a + 6 fonksiyonu sabit
fonksiyon olduğuna göre f(19) değerini bulunuz.
18. f doğrusal fonksiyon olmak üzere,
f(2) = 3, f(4) = 4 ise f(2023) değerini bulunuz.
13. f: R→R, f (x) = (a–7)x2 + (a–b) x +(3a+2b) fonksiyonunun sabit fonksiyon olduğuna göre, f (20)
değerini bulunuz.
14. f: R → R,
f (x) = (3a–9)x3 + (a–b) x2 – (a+2c) x +(a+b–c)
fonksiyonunun sabit fonksiyon olduğuna göre, f
(8) değerini bulunuz.
4x + 8
sabit fonksi15. Tanımlı olduğu kümede, f (x) =
x+n
yon ise n+f(1) kaçtır? Bulunuz.
19. f(x) = (2a + 6)x + b – 11 fonksiyonun birim fonksiyon olduğuna göre a + b değerlerini bulunuz.
20. f (x) = (m + 5)x2 + (n + 8) x + n – k + 2 fonksiyonun
birim fonksiyon olduğuna göre m + n + k değerlerini bulunuz.
21. f: R → R, f (x) = 3x – 5 fonksiyonunun grafiğini
çiziniz.
Ünite 3. Fonksiyonlar
487
3. 1. Fonksiyon Kavramı ve Gösterimi
BÖLÜM DEĞERLENDİRME
22. f: R→R, f (x) = 5 – 3x fonksiyonunun grafiğini
çiziniz.
27. Gerçek sayılar kümesinde tanımlı f(x) = ax + b doğrusal, g(x) = (3 – a)x + 4 sabit fonksiyonlardır.
g(3) = f(5) ise f(7) kaçtır?
23. f: R→R,
f (x) = (4a + 2b – 10)x3 + (8a – 4b – 12)x2 + (a + 4)x + (b)
Araştırma Soruları
fonksiyonu doğrusal bir fonksiyon ise aşağıda
istenenleri bulunuz.
a.
f(x)
b.
f(2)
c.
f(x + 2)
ç.
f(x2)
d.
f(x2 – 2)
e.
f(x2 – 2x + 1)
24. f gerçek sayılarda tanımlı doğrusal bir fonksiyondur.
1.
f bir doğrusal fonksiyon ise f(x – y) = f(x) – f(y)
midir? Açıklayınız.
2.
f(x) = mx + n doğrusal fonksiyonunun m ≠ 0 durumunda neden bir kökü vardır? Açıklayınız.
3.
Aynı doğru üzerinde yer alan üç noktadan geçen
bir grafik her zaman doğrusal bir fonksiyonun
grafiği midir? Neden?
f(1) = 5 ve f(3) = 1 ise f(19) değerini bulunuz.
25. f gerçek sayılarda tanımlı doğrusal bir fonksiyondur.
f(2) = 9 ve f(4) = 19 ise f(x) kuralını bulunuz.
f(x – 8)‘i bulunuz.
26. f ; gerçek sayılar kümesinde tanımlı bir fonksiyondur. 3 · f(x) + f(2x) = 10x + 20 ise f(x) fonksiyonun
kuralını belirleyiniz.
488
Ünite 3. Fonksiyonlar
3. 1. Fonksiyon Kavramı ve Gösterimi
BÖLÜM DEĞERLENDİRME
Eğlenceli Matematik soruları
1.
Aşağıdaki bulmacada boş yerleri uygun şekilde doldurunuz.
1
2
3
4
5
6
8
7
9
10
11
12
13
14
SAĞDAN SOLA
SOLDAN SAĞA
1.
y = f(x) fonksiyonunun kuralında y'ye verilen ad.
2.
4.
A ve B kümeleri boş kümeden farklı iki küme olmak
üzere A'nın her elemanının B'nin yalnız bir elemana
eşlenmesi
A kümesinden B kümesine tanımlanan bir fonksiyonda A kümesine verilen ad
3.
Doğrusal fonksiyon grafiğine verilen ad
5.
A kümesinin bütün elemanları, B kümesinin yalnızca bir elemanı ile eşleyen f fonksiyona verilen ad
7.
Fonksiyonların grafik üzerinde x-eksenine paralel
çizilen doğrularla bire-bir ve örten olduğunu inceleme testine verilen ad
8.
A kümesinin her elemanını tekrar kendisine eşliyen
fonksiyonuna verilen ad
6.
A kümesinin her bir öğesi
9.
A kümesinden B kümesine tanımlanan bir fonksiyonda B kümesine verilen ad
10. A kümesinden B kümesine tanımlanan fonksiyonda
f(A) kümesine verilen ad
13. y = f(x) = ax + b şeklindeki fonksiyonumuzda x
değişkenie verilen ad
14. f(x) = ax + b şeklindeki fonksiyonlara verilen ad
11. f(x) = ax2 biçiminde verilen fonksiyonların grafiğine
verilen ad
12. y = f(x) olarak tanımladığımız fonksiyonumuzda y
değişkenine verilen ad.
Ünite 3. Fonksiyonlar
489
3. 1. Fonksiyon Kavramı ve Gösterimi
BÖLÜM DEĞERLENDİRME
N
U
C
E
Y
Q
D
J
U
R
U
L
Y
W
V
B
I
R
I
M
H
S
Z
N
V
O
X
C
C
V
H
V
X
N
H
X
O
Q
I
Y
R
S
K
A
U
N
W
N
Y
X
H
T
D
C
I
D
L
G
E
F
K
T
N
L
H
F
Z
U
M
H
T
E
O
G
F
X
F
R
C
X
E
L
O
S
I
A
Y
T
J
W
X
U
A
D
Y
C
O
Y
C
W
T
T
H
R
M
Ğ
V
L
B
U
S
N
E
Z
B
B
A
Ğ
I
M
L
I
I
M
N
O
A
L
E
W
E
L
M
U
A
Q
J
C
I
D
M
A
X
L
K
P
G
S
G
N
Z
N
M
L
F
R
A
I
R
K
R
E
I
S
L
D
L
W
Y
X
O
E
K
C
S
O
I
C
E
O
K
S
O
Ğ
U
Z
A
I
M
S
F
H
N
B
U
W
C
N
N
E
V
M
S
M
C
Ü
U
C
O
W
C
D
P
I
O
O
J
H
B
U
H
G
O
B
T
P
K
M
A
T
M
R
Y
D
J
W
M
O
Ğ
H
T
S
T
A
O
T
G
F
I
V
O
Ü
R
N
K
E
Ğ
G
R
I
A
Y
C
A
U
L
I
R
A
D
T
Y
R
Y
U
P
M
P
W
A
S
O
H
J
K
J
O
L
B
H
I
E
B
V
S
Y
I
G
T
O
M
E
T
S
V
I
D
O
B
R
N
A
K
Z
M
K
D
D
A
R
Y
X
A
O
H
J
S
U
E
G
Ö
R
Ü
N
T
Ü
K
Ü
M
E
S
İ
H
K
S
F
U
E
I
B
K
I
H
R
F
Ü
F
V
J
D
J
N
Z
U
C
Y
A
T
A
Y
D
O
Ğ
R
U
U
B
Y
D
J
T
T
B
T
M
X
B
T
M
N
N
O
G
D
K
J
W
X
R
P
W
S
G
P
A
M
K
I
X
Q
K
Z
E
Ü
W
M
U
J
H
Y
I
I
O
H
I
Aşağıda harfleri karışık olarak verilen kavramları düzeltiniz ve yukarıdaki tabloda bu kavramları bulunuz.
(Örneğin NİNOSKYFO: FONKSİYON)
NİNOSKYFO
AENEML
KÜTSMIENAM
EĞIÜEKMSEDR
ÖTGRÜÜN
NÜGKSÜMÖIRTEÜ
MZSBAIĞI
MIAIĞLB
IMBIR
AITBS
RASUDLOĞ
AOBARLP
YDARYTAOUĞ
ĞRDUO
1.
Aşağıda istenenleri yapınız.
•
Aklınızdan bir sayı tutunuz.
•
Bu sayıya ardışığı olan sayıyı ekleyiniz.
•
Bulduğunuz sayıya 9 ekleyiniz.
•
Çıkan sayıyı 2 ye bölünüz.
•
Bulduğunuz bu sayıdan da ilk başta tuttuğunuz sayıyı çıkarınız.
•
Sonuç kaç çıktı?
Farklı tam sayı değerleri için bu bu adımları tekrar ediniz. Bulduğunuz sonuçları karşılaştırınız.
Tuttuğunuz sayı ile çıkan sonuç arasındaki ilişkiyi matematiksel olarak ifade ediniz. Bu ilişki bir hangi fonksiyon türüne
örnek olabilir? Neden?
490
Ünite 3. Fonksiyonlar
Ünite
FONKSİYONLAR
Bölüm 3.2.
3
Fonksiyonların Grafikleri
•
Bu Bölümde Neler
Öğreneceğiz?
•
•
•
Fonksiyonların grafiğini okumayı ve yorumlamayı
f(x) = xn ( n d Z ) biçimindeki fonksiyonların
grafiklerini
•
•
Doğrusal fonksiyonların grafikleriyle ilgili
uygulamaları
y = f(x) fonksiyonun grafiği ile f(x) = 0
denkleminin köklerinin ilişkisi
Parçalı tanımlı şekilde verilen fonksiyonları
ve grafiklerini
Bire bir fonksiyonları ve örten fonksiyonları
200
150
105
100
50
537
0
50
100
150 200
250 300
350 400 450
500
550 600
650
700 750
800 850 900
950 1000 1050 1100
Neden Öğreneceğiz?
Matematikte birçok bilgi için farklı temsil biçimleri kullanılır. Bu sayede, problem çözümlerinde matematiksel temsiller arasından uygun olanları seçmek, uygulamak ve aralarında dönüşümler yapmak; matematiksel, fiziksel, toplumsal olayları yorumlamak ve modellemek için temsiller kullanmak mümkün olmaktadır.
Bu çerçevede fonksiyonların özellikle de farklı temsil ve gösterimlerinin anlaşılması önemlidir. Bir fonksiyonun grafiksel gösterimi, fonksiyon hakkındaki birçok bilgiyi görsel ve anlaşılması kolay bir şekilde sunduğu
gibi, cebir ile geometriyi bir arada kullanmamıza imkan verir.
Diğer taraftan, günlük hayatımızdaki bazı verilerin kolay anlaşılmasını sağlamak ve akılda kalıcılığını arttırmak için bu verilerin sunumunu sayısal ve sözel ifade etme, şekillere dökme gibi yöntemler yardımıyla
yaparız. Örneğin, bir işyeri veya şirket sahibi aylık kar zarar durumlarını geçmişle de kıyaslayarak görmek
için görsel sunumlar isteyebilir. Fonksiyon grafikleri bu gibi birçok durum için etkin bir sunum yöntemidir.
Boğaziçi Köprüsü’nün temeli 20 Şubat 1970 tarihinde atılmış ve 29 Ekim 1973 tarihinde hizmete açılmıştır.
Köprünün kule yüksekliği yaklaşık olarak 105 metre, ara açıklığı ise 1074 metredir. Köprünün sağlam dur92 2 184
masını sağlayan çelik halatların pozisyonu bir fonksiyonla ifade edilebilir: f(x) =
x x + 105
537
537
Köprüye dikkatli bakacak olursanız yol kısmı da yere paralel değildir. Bunun amacı köprünün direncini
artırmak ve daha sağlam olmasını sağlamaktır. Köprünün yol kısmının pozisyonu da bir fonksiyon grafiği
şeklinde olup g(x) = -
9
537
2
18
2
x +
x
537
fonksiyonu ile ifade edilebilir.
Bölüm 3.2. Fonksiyonların Grafikleri
HAZIR MIYIZ?
1.
Kartezyen düzlemde x–ekseni üzerinde orijinden
önce sağa 5 birim, sonra aşağı yönde 2 birim ilerlendiği zaman gelinen noktanın koordinatları (5,–2)
olmaktadır. Benzer şekilde,
a.
Orijinden y ekseni boyunca 2 birim yukarı çıktıktan
sonra 3 birim sağa A noktasına
y
0
5
x
2
b.
Orijinden y ekseni boyunca 2 birim aşağı indikten
sonra 3 birim sağa B noktasına
c.
Orijinden x ekseni boyunca 3 birim sola gittikten
sonra 3 birim yukarı C noktasına
ç.
Orijinden x ekseni boyunca 2 birim sola gittikten
sonra 2 birim aşağı D noktasına ulaşılmaktadır.
Buna göre A, B, C ve D noktalarının koordinatlarını kartezyen düzlemde gösteriniz.
2.
Kartezyen düzlemdeki bir A noktasından 2 birim sağa 3 birim aşağı yönde ilerlenildiğinde (0,0) noktasına geliniyor. Buna göre A noktasının koordinatları nedir?
3.
(1, 1), (2, 3), (3, 4), (4, 6) ve (5, 7) noktalarını Kartezyen düzlemde gösteriniz. Bu noktaların dizilişi ile
ilgili neler söylenebilir?
4.
Herhangi bir fonksiyonun grafiğini alarak bu grafiği x–eksenine dikey doğrularla tarayınız.
Çizdiğiniz her bir dikey doğru fonksiyon grafiğini kaç noktada kesti?
5.
Herhangi bir fonksiyonun grafiğini alarak bu grafiği x–eksenine paralel doğrularla tarayınız.
Çizdiğiniz her bir paralel doğru fonksiyon grafiğini kaç noktada kesti?
492
6.
x2 = 4 eşitliğini sağlayan x değerlerini bulunuz.
7.
x2 + 4x + 4 = 0 eşitliğini sağlayan x değerlerini bulunuz.
8.
f(x) = x – 4 fonksiyonunun grafiğinin x–eksenini kestiği nokta ile x – 4 = 0 denkleminin kökünü
karşılaştırınız.
Ünite 3. Fonksiyonlar
Bölüm 3.2. Fonksiyonların Grafikleri
HAZIR MIYIZ?
9.
R de tanımlı f fonksiyonu f(x) = 2x – 9 ile veriliyor. Bu fonksiyonun grafiği olan doğrunun
eğimini bulunuz.
10. f(x) = x + 3 fonksiyonun grafiğini x < –1 ve g(x) = –x + 1 fonksiyonunun grafiğini x > –1
için çiziniz. Bu grafikleri aynı kartezyen düzlemde gösteriniz.
11. Aşağıda verilen doğrusal denklemlerin grafiklerini çiziniz.
a.
b. y = 2x – 1
y=x–1
c. y = x + 2
12. y = 3 – x denklemi için x ! " 1 , 2 , 5 , 8 , ise y değerlerinin kümesini yazınız.
13. y = 3x + 1 denklemi için y ! 61 , 10@ ise x hangi aralıkta değerler alabilir?
14. Aşağıda grafiği verilen doğruların eğimlerini bulunuz.
y
6
y = 2x + 4
y = –2x + 4 5
y = –x + 1
y = 3x – 6
4
3
2
1
–7 –6 –5 –4 –3 –2 –1
–1
x
0 1
2
3
4
5
6
7
–2
–3
–4
–5
–6
Ünite 3. Fonksiyonlar
493
Bölüm
3.2
Fonksiyonların Grafikleri
3.2.1. Fonksiyon Grafiklerini Okuma ve Yorumlama
Neler Öğreneceğiz?
•
Dikey doğru testini
•
fonksiyonların grafiğinden
Başlarken:
Yandaki grafikte, ülkemizdeki nüfus
artış hızının yıllara göre binde kaç azaldığını (değiştiğini) görüyoruz. Bu grafikten ne gibi çıkarımlar yapabiliriz?
Örneğin, şu sorulara cevap bulabilir
miyiz?
– tanım ve görüntü kümelerini
– tanım kümesindeki bir elemanın görüntüsünü
– görüntü kümesindeki bir
elemanın ters görüntülerini
– tanım kümesinin bir alt
kümesinin görüntüsünü
Verilen bir yıldaki nüfus artış hızını başka bir yıldaki nüfus artış hızıyla kıyaslayabilir miyiz?
– görüntü kümesinin bir alt
kümesinin ters görüntüsünü
bulmayı
Nüfus artış hızı (binde)
35
30
25
20
15
10
5
0
Yıllar
1955 1960 1970 1980 2000 2008
1955 ile 2008 yılları arasında nüfus artış
hızının en fazla olduğu yıl hangi yıldır?
Nüfus artış hızının azalıp artma bakımından seyri nasıldır?
Anahtar Terimler
•
Fonksiyonun grafiği
•
Tanım kümesinin alt
kümesinin görüntüsü
•
Değer kümesinin alt kümesinin ters görüntüsü
•
Dikey doğru testi
Bu örnekte olduğu gibi verilerin grafiksel sunumu sizce ne gibi faydalar sağlamaktadır?
Benzer şekilde gazete ve dergilerin
ekonomi sayfalarına baktığımızda borsa, enflasyon gibi birçok konuda grafiklerin sıklıkla kullanıldığını görürüz.
•
Sembol ve Gösterimler
Karmaşık verileri daha iyi analiz edebilmek için verileri görsel hale getirmek iyi
bir çözümdür. Fonksiyon grafiklerinin
kullanımı verileri görsel hale getirip anlaşılmasını kolaylaştırdığı gibi fonksiyonların özelliklerini kullanarak eldeki verilerden yeni bilgilere ulaşmamıza da imkan
sağlar.
f | A " B ve
K 1 A için f ^ K h
Fonksiyon grafiklerinin yorumlarına
geçmeden önce çizimlerini örneklerle
hatırlayalım.
2000 – 2012 BENZİN FİYATLARI
494
Ünite 3. Fonksiyonlar
Ülkemizdeki 2000 ve 2012 yıllarına ait
benzin fiyatları yanda verilmiştir. Bu
değerleri tablo ve grafik yardımıyla
gösterelim.
Fonksiyon Grafiklerini Okuma ve Yorumlama
Yıl
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
Fiyat
0,59
1,24
1,62
1,74
2,29
2,57
2,75
3,06
2,78
3,38
3,87
4,19
4,20
Tablodaki değerleri (yıl, fiyat) sıralı ikilisi olarak x–y koordinat sistemi üzerinde gösterelim.
Benzin fiyatı (TL)
4,20
4,19
3,87
3,38
3,06
2,78
2,75
2,57
2,29
Anahtar Bilgi
1,74
1,62
y = f(x) fonksiyonunda
girdiler x ekseninde çıktılar y
ekseninde gösterilir.
1,24
0,59
y
12
Çıktı
20
11
20
10
09
20
08
20
20
07
20
06
05
20
04
20
03
20
02
20
20
01
20
20
00
Yıllar
Grafiğe bakarak kolay bir şekilde yıllar geçtikçe benzin fiyatlarının nasıl değiştiğini görebiliriz. Örneğin, benzin fiyatlarının genel eğilimi yıllar geçtikçe artmasıdır. Fakat 2008
yılında fiyatların iniş eğiliminde olduğunu görmekteyiz.
Girdi
1
f : R → R ve f(x) = x + 1 ile verilen bir doğrusal fonksiyon olsun.
A = {–3, –2, 1, 2, 4} ve B = {–1, 0, 1, 5} kümeleri veriliyor. Buna göre
a.
Tanım kümesinin bir alt kümesi olan A kümesindeki elemanların f altındaki görüntülerini bulalım.
b.
Görüntü kümesinin bir alt kümesi olan B kümesindeki elemanların, tanım kümesindeki hangi elemanların f altındaki görüntüleri olduğunu bulalım.
c.
Bu doğrusal fonksiyonun grafiğini, grafiğin x ve y eksenlerini kestiği iki noktayı
kullanarak çizelim.
d.
Çizdiğiniz grafik üzerinde koordinatları, A kümesindeki elemanlar ve bu elemanların f altındaki görüntüleri olan noktaları gösterelim.
Ünite 3. Fonksiyonlar
495
x
Bölüm
3.2
Fonksiyonların Grafikleri
a.
f nin A kümesinin elemanlarındaki değerlerini bulalım.
f(–3) = –3 + 1 = –2,
f(–2) = –2 + 1 = –1,
f(2) = 2 + 1 = 3
b.
f(1) = 1 + 1 = 2,
f(4) = 4 + 1 = 5
Öncelikle f nin tanım kümesi R dir.
Bu durumda, görüntüsü –1 olan a ! R şeklindeki a değerini bulalım.
f(a) = –1 den a + 1 = –1 ve de a = –2 bulunur. Bu durumda görüntüsü –1 olan
tanım kümesinin elemanı –2 dir. Bu durum, “–1 in f altındaki ters görüntüsü –2”
dir şeklinde de ifade edilmektedir.
Benzer şekilde, f(b) = 0 ise b + 1 = 0 ve b = –1; f(c) = 1 ise c + 1 = 1 ve c = 0;
f(d) = 5 ise d + 1 = 5 ve d = 4 olur. Bu durumda 0, 1 ve 5 sırasıyla –1, 0 ve 4 ün f
altındaki görüntüleridir.
c.
f nin grafiği, y = x + 1 denklemiyle belirtilen doğrudur. Bu doğrunun x eksenini
kestiği noktanın y bileşeni 0 olacağından, 0 = x + 1 eşitliğinden x = –1, bulunur.
Bu nedenle, (–1, 0) noktası grafiğin x eksenini kestiği noktadır.
y ekseniyle grafiğin kesişme noktasında x bileşeni 0 olacağından y = 0 + 1 ve
y = 1 olur. Dolayısıyla, (0, 1) noktası grafiğin y eksenini kestiği noktadır.
Böylece f in grafiği (–1, 0) ve (0, 1) noktalarından geçen doğrunun grafiği olarak
şu şekildedir:
y
5
4
3
2
(–1, 0)
–3
496
Ünite 3. Fonksiyonlar
–2
–1
1 (0, 1)
0
1
2
3
4
x
Fonksiyon Grafiklerini Okuma ve Yorumlama
d.
A kümesinde bulunan elemanların f altındaki görüntülerini bulmuştuk. Bunlara karşılık gelen noktaların koordinatları (–3, –2), (–2, –1), (1, 2), (2, 3), (4, 5) dir.
Bu noktaların x ve y bileşenleri fonksiyonun kuralı olan y = f(x) yani y = x + 1
eşitliğini sağladığından bu noktalar f nin grafiği üzerindedir ve şu şekilde grafikle
gösterilirler:
y
5
(4, 5)
4
3
(2, 3)
2
(1, 2)
1
–3
–2
–1
0
1
2
3
4
x
–1
(–2, –1)
–2
(–3, –2)
Doğrusal fonksiyon için yaptığımız bu işlemlerde herhangi bir fonksiyon için doğru olan şu bilgiyi kullandık:
Bir (a, b) sıralı ikilisini oluşturan bileşenler bir f fonksiyonunun kuralı olan y = f(x)
eşitliğini b = f(a) şeklinde sağlarsa koordinatları (a, b) olan nokta f fonksiyonunun
grafiği üzerindedir.
Bunun tersi de doğrudur. Şöyle ki, eğer y = f(x) ile verilen fonksiyonun grafiği üzerindeki bir noktanın koordinatları (a, b) ise a ile b arasında b = f(a) ilişkisi vardır.
Hatırlayacağımız gibi, a tanım kümesinden bir eleman ve b = f(a) ise b görüntü
kümesine ait bir eleman olmalıdır. Bu durumda b, a nın f altındaki görüntüsüdür
veya f nin a daki değeri b dir deriz.
b görüntü kümesinden bir eleman ise b = f(a) eşitliğini sağlayan ve tanım kümesinin elemanı olan bir a vardır. Ancak, b = f(a) eşitliğini sağlayan a değerleri birden
fazla olabilir ve hepsinin tanım kümesinde bir eleman olma zorunluluğu yoktur.
b değer kümesinden bir eleman, b = f(a) ve a tanım kümesinin bir elemanı ise b nin
f altındaki bir ters görüntüsü a dır deriz.
Ünite 3. Fonksiyonlar
497
Bölüm
3.2
Fonksiyonların Grafikleri
Şu ana kadar bir fonksiyonun tanım kümesini, görüntü kümesini ve tanım kümesindeki elemanların fonksiyon altındaki görüntülerini bulmayı, fonksiyonun değerler tablosunu
veya fonksiyonun kuralını kullanarak öğrendik. Şimdi ise fonksiyonun grafiğini kullanarak
da bunların bulunabileceğini göreceğiz. Önce belirttiğimiz ilişkileri, fonksiyonun grafiği, tanım kümesi ve görüntü kümesi açısından yeni bir açıklamayla tekrar edip detaylandıralım.
f fonksiyonunun grafiği üzerindeki bir noktadan x eksenine çizdiğimiz dik doğrunun
x eksenini kestiği noktanın x bileşeni, f in tanım kümesinin elemanıdır. Benzer şekilde
fonksiyonun grafiği üzerinden alınan bir noktadan y eksenine çizdiğimiz dik doğrunun
y eksenini kestiği noktanın y bileşeni, f in değer kümesinin elemanıdır. Bu işlemi fonksiyonun grafiği üzerindeki her bir nokta için yaparak, fonksiyonun tanım kümesini ve
görüntü kümesini bulabiliriz.
Bir fonksiyonun grafiği verildiğinde tanım kümesindeki herhangi bir a değerinin bu
fonksiyon altındaki görüntüsünü bulabiliriz. Bunun için x ekseni üzerinde a değeri ile
belirtilen noktayı buluruz. Bu noktadan x–eksenine dik bir doğru çizerek bu doğrunun
fonksiyonun grafiğini kestiği noktayı buluruz. Grafik üzerinde bulduğumuz bu noktadan y eksenine dik bir doğru çizeriz. Bu doğru aynı zamanda da x eksenine paraleldir.
Bu doğrunun y eksenini kestiği noktaya karşılık gelen b değeri, a nın f altındaki görüntüsü olur. Örneğin bu işlemler bir grafik üzerinde aşağıdaki gibi belirtilebilir:
y
y
b
x
a
x
Diğer taraftan, bir fonksiyonun grafiği verildiğinde değer kümesindeki herhangi bir b
değerinin varsa bu fonksiyon altındaki ters görüntülerini bulabiliriz. Bunun için y ekseni üzerinde b değeri ile belirtilen noktayı buluruz. Bu noktadan y–eksenine dik bir
doğru çizerek bu doğrunun fonksiyonun grafiğini kestiği noktaları buluruz. Bu noktalar
en az bir tanedir. Grafik üzerinde bulduğumuz bu noktalardan x eksenine dik doğrular
çizeriz. Bu doğrular aynı zamanda da y eksenine paraleldir. Bu doğruların x eksenini
kestiği noktalara karşılık gelen değerler, b nin f altındaki ters görüntüleridir. Örneğin,
aşağıdaki grafik üzerindeki b için bunları yaparsak b nin ters görüntüleri a ve c olur ve
şu şekilde gösterilebilir:
y
b
c
498
Ünite 3. Fonksiyonlar
a
x
Fonksiyon Grafiklerini Okuma ve Yorumlama
2
g fonksiyonunun grafiği şu şekildedir:
y
Buna göre, bu fonksiyonun
5
a. Tanım kümesini
4
b. Görüntü kümesini
3
c. Tanım kümesindeki –2, 0 ve 3 ün g altındaki
görüntülerini
2
1
–2
–1
0
1
a.
2
3
4
5
x
ç. Görüntü kümesindeki 1, 3 ve 4 ün g altındaki
ters görüntülerini bulalım.
2
Fonksiyonun grafiği üzerindeki her bir
noktadan x eksenine çizdiğimiz dik
doğrular x eksenini tanım kümesinin
elemanlarına karşılık gelen noktalarda
kesecektir. Bu dik doğruların x eksenini
kestiği noktalar yandaki grafikte yeşil ile
1
gösterilmiştir. O halde g nin tanım kümesi
y
5
4
3
–2
–1
0
1
2
3
4
5
x
y
b.
Fonksiyonun grafiğinin her bir noktasından y eksenine dik doğrular çizdiğimizde
bu doğruların y eksenini kestiği noktalara
karşılık gelen değerler görüntü kümesini
verecektir. Bu noktalar yandaki grafikte
mavi ile gösterilmiştir. Dolayısıyla g nin
görüntü kümesi [1, 4] olarak bulunur.
5
4
3
2
1
–2
–1
0
6- 2 , 1@ , " 2, 3, 4 , olur.
1
2
3
4
5
x
Bu durumda fonksiyonumuz g | 6- 2, 1@ , " 2, 3, 4 , $ B şeklinde olacaktır. Bura-
da B kümesi g nin değer kümesi ve g ^6- 2, 1@ , " 2, 3, 4 ,h = 61, 4@ kümesi de g nin
görüntü kümesidir. Grafikteki bilgilerden B hakkında söyleyebileceğimiz tek şey
[1, 4] 1 B olduğudur.
Ünite 3. Fonksiyonlar
499
Bölüm
3.2
Fonksiyonların Grafikleri
c.
y
5
4
3
2
1
–2
–1
0
ç.
1
2
3
4
5
x
y
5
4
3
2
1
–2
–1
0
1
2
3
4
5
x
x ekseni üzerinde –2, 0 ve 3 noktalarını
bulup bu noktalardan geçen ve x eksenine dik olan doğrular g nin grafiğini
yandaki şekilde belirtilen (–2, 1), (0, 3) ve
(3, 4) noktalarında keser. Bu noktalardan y
eksenine çizdiğimiz dik doğrular da y
eksenini yine yandaki şekilde belirtilen
noktalarda kesecektir. Bu nedenle –2, 0 ve
3 ün g altındaki görüntüleri sırasıyla 1, 3
ve 4 tür. Yani g(–2) = 1, g(0) = 3
ve g(3) = 4’tür.
y ekseninde 1, 3 ve 4 noktalarını bulalım.
Bu noktalardan x eksenine paralel doğrular çizelim. Bu doğruların g nin grafiğini
kestiği noktalar yandaki şekilde belirtilen
noktalarda keser. Bu noktalardan x eksenine çizdiğimiz dik doğrular da x eksenini
yine yandaki şekilde görüldüğü gibi –2, 0,
1, 2, 3, 4 noktalarında kesecektir.
Bu nedenle
1 in g altındaki ters görüntüsü –2, yani g(–2) = 1,
3 ün g altındaki ters görüntüsü 0, yani g(0) = 3
4 ün g altındaki ters görüntüleri 1, 2, 3 ve 4 tür. Yani g(1) = g(2) = g(3) = g(4) = 4
tür. 4 ün birden fazla ters görüntüsünün olduğuna dikkat edelim.
500
Ünite 3. Fonksiyonlar
Fonksiyon Grafiklerini Okuma ve Yorumlama
3
Bunu biliyor muydunuz
f fonksiyonunun grafiği şekildeki gibidir. Buna göre;
y
a.
f in tanım ve görüntü kümelerini
bulalım.
3
5
2
2 5
3
1
–3
c.
–2– 3 –1
2
0
–1
–3
2
b.
3
2 2
3
1
x
f in tanım kümesinden alınan
-3
3
- 3,
, 0, 1, , 2 ve 3 ’ün f altındaki
2
2
görüntülerini bulalım.
Kule ayakları arasındaki orta
açıklığı 1090 metre ve temelden itibaren kule yüksekliği
111 metre olan Fatih Sultan
Mehmet Köprüsü 3 Temmuz
1988’de işletmeye açıldı. Bir
kuleden x metre uzaklıktaki halatların yüksekliğini
yaklaşık olarak hesaplamak
için, kuralı
110
h (x) =
(x - 542) 2 + 5
542
f(x) = y
–2
Görüntü kümesindeki elemanlardan hangilerinin f altındaki ters görüntüsünün
tanım kümesinden birer, ikişer veya üçer elemandan oluştuğunu bulalım.
-3
3
, 0E ve ;1 , E aralıklarında yer alan elemanların f altındaki görüntülerinin
2
2
oluşturdukları kümeleri bulalım.
;
ç.
a.
olan gerçek sayılarda tanımlı
h fonksiyonundan yararlanabiliriz.
Tanım kümesini grafikten x eksenine çizdiğimiz dik doğrularla aşağıdaki grafikte yeşille belirtildiği gibi [–3, 3] şeklinde buluruz. Görüntü kümesini grafikten
y eksenine çizdiğimiz dik doğrularla aşağıdaki şekilde maviyle belirtildiği gibi
;
- 3 5 şeklinde buluruz.
, E
2 2
y
3
5
2
2 5
3
1
–3
–2– 3 –1
2
3
2 2
1
–1
–3
2
–2
3
x
f(x) = y
Ünite 3. Fonksiyonlar
501
Bölüm
3.2
Fonksiyonların Grafikleri
b.
- 3,
3
-3
, 0, 1, , 2 ve 3 noktalarının f altındaki görüntüleri sırasıyla
2
2
-3
5
5
dir.
, 0, , 2, 0, - 1 ve
2
3
2
c.
y = 2 doğrusu grafiği iki noktada kesmektedir ki bunlardan birinin koordinatları
(1, 2) dir. Benzer şekilde y = 0 doğrusu yani x ekseni, grafiği iki noktada kesmek-3
3
, 0 m ve c , 0 m dır. Bu nedenle, görüntü
tedir ki bu noktaların koordinatları c
2
2
kümesindeki 0 ve 2 nin f altındaki ters görüntüleri ikişer elemandır.
y ekseninde 0 ile 2 nin arasında yer alan herhangi bir yerden x eksenine paralel
bir doğru çizersek grafiği üç noktada keser. Bu nedenle, görüntü kümesindeki
elemanlardan (0, 2) aralığında olanların f altındaki ters görüntüleri üçer elemandır.
-3
5
, 0 n , c 2 , E kümesindeki
Görüntü kümesindeki diğer elemanların, yani =
2
2
elemanların f altındaki ters görüntüleri birer tanedir.
ç.
-3
, 0E aralığında yer alan elemanların görüntülerinin
2
5
3
oluşturduğu küme ;0, E tür. Benzer şekilde ;1, E aralığında yer alan elemanla3
2
rın görüntülerinin oluşturduğu küme [0, 2] dir.
Tanım kümesinde olup ;
Şimdi görüntü olan elemanlar ile ters görüntü olan elemanların oluşturduğu
kümeler için kullanacağımız sembolik gösterimleri tanımlayalım.
A ve B kümeleri ile f | A $ B fonksiyonu verilsin. Herhangi bir C ve D kümeleri
C 1 A ve D 1 f ^Ah olsun. Bu durumda tanım kümesinin bir alt kümesi olan C kü-
mesindeki elemanların f altındaki görüntülerinin oluşturduğu kümeye kısaca C nin
f altındaki görüntüsü denir ve f(C) ile gösterilir. Bu küme ortak özellik yöntemiyle
f(C) = {f(x) : x ∈ C}
şeklinde belirtilir.
Benzer şekilde görüntü kümesinin bir alt kümesi olan D kümesindeki elemanların
f altındaki ters görüntülerinin oluşturduğu kümeye D kümesinin f altındaki ters
görüntüsü deriz ve bu kümeyi ortak özellik yöntemiyle
D nin f altındaki ters görüntüsü = {x ∈ A : f(x) ∈ D}
şeklinde gösteririz.
502
Ünite 3. Fonksiyonlar
Fonksiyon Grafiklerini Okuma ve Yorumlama
4
f : R → R ve f(x) = ax + b doğrusal fonksiyonu ile c < d ve n < m şartlarını taşıyan c, d,
n, m gerçek sayıları için
a.
[c, d] nin f altındaki görüntüsü
b.
[n, m] nin f altındaki ters görüntüsü
kümelerini bulalım.
Burada olduğu gibi herhangi bir f doğrusal fonksiyonunun grafiğine bakacak olursak, f
doğrusal fonksiyonu x eksenindeki bir kapalı (açık) aralıktaki elemanları y eksenindeki
bir kapalı (açık) aralıktaki elemanlarla eşlemektedir. f in grafiğinin bu eşlemeye karşılık
gelen kısmı ise bir doğru parçasıdır. Bu doğru parçasının uç noktalarının koordinatlarını, kapalı aralıkların uç noktaları ve f altındaki görüntüleri oluşturmaktadır. Bu nedenle
çözüme aşağıdaki gibi devam edebiliriz.
a.
[c, d] nin f altındaki görüntüsü f([c, d]) dir. f(c) = ac + b ve f(d) = ad + b dir. Burada, a>0 iken f(c) < f(d) olduğundan, f([c,d]) = [f(c),f(d)] = [ac + b, ad + b] olacaktır.
Eğer a<0 ise f(c) > f(d) olduğundan f([c,d]) = [f(d), f(c)] = [ad + b, ac + b]
İkinci bir yol olarak, a>0 iken f ^6c, d@h 1 6f ^ c h , f ^dh@ ve 6f ^ c h , f ^dh@ 1 f ^6c, d@h
olduğu gösterilerek f ^6c, d@h ve 6f ^ c h , f ^dh@ kümelerinin eşitliği gösterilebilir.
a<0 iken de benzer bir yol izlenebilir.
Grafikteki ilgili doğru parçasının uç noktaları ise (c,ac + b) ve (d,ad + b) noktalarıdır.
b.
Görüntü kümesinde yer alan n ve m elemanlarının f altındaki ters görüntüleri
sırasıyla u ve v olsun. Bu durumda f(u) = n ve f(v) = m dir. Buradan au + b = n ve
av + b = m olur. Dolayısıyla, u =
^n - bh
a
,v =
^m - bh
a
rumda, [n, m] nin f altındaki ters görüntüsü a > 0 iken ;
^m - bh ^n - bh
olarak bulunur. Bu du^n - bh ^m - bh
a
,
a
E ve a<0
E aralığıdır. Grafikteki ilgili doğru parçasının uç noktaları
a
n–b
m–b
ise c
, n m ve c
, m m noktalarıdır.
a
a
iken ;
a
,
Ünite 3. Fonksiyonlar
503
Fonksiyonların Grafikleri
5
5
4
3
2
Yanda g fonksiyonunun grafiği verilmiştir. Buna göre,
y
a. Fonksiyonun tanım, değer ve görüntü kümelerini
bulalım.
b. Tanım kümesinin bir alt kümesi olan (1,2] ün g altındaki görüntüsünü bulalım.
1
x
–2 –1 0 1 2 3
–1
y = –2x + 4
–2
c.
Görüntü kümesinin bir alt kümesi olan [0,4] ün g altındaki ters görüntüsünü bulalım.
–3
a.
Tanım kümesinin R olduğu grafikten anlaşılmaktadır. Benzer şekilde, görüntü
kümesinin R olduğu grafikten anlaşılmaktadır. Bu durumda değer kümesi de
görüntü kümesine eşit olarak R olacaktır.
b.
(1, 2] nin g altındaki görüntüsü g((1, 2]) dir. Ayrıca, g(1) = 2 ve g(2) = 0 dır. Dolayısıyla, bir önceki örnektekine benzer olarak g((1, 2]) = [g(2), g(1)) = [0,2) olur.
c.
[0, 4] ün g altındaki ters görüntüsü [0, 2] dir.
6
h | 6- 1, 2@ → R fonksiyonunun kuralı h(x) = –3x + 1 olarak veriliyor. Bu fonksiyonun
görüntü kümesini bulalım ve grafiğini çizelim.
Bu fonksiyonun tanım kümesi [–1, 2] ve değer kümesi
de R olarak verilmiştir.
y
5
4
3
2
1
x
Tanım kümesi
–2 –1
Değer kümesi
Bölüm
3.2
0 1
–1
2
3
4
–2
–3
–4
–5
504
Ünite 3. Fonksiyonlar
Bu fonksiyonun grafiğini çizmek için doğrusal fonksiyonların çiziminde izlediğimiz yoldan faydalanabiliriz.
Çünkü h nin tanım kümesi R olsaydı bir doğrusal fonksiyon olurdu ve doğrusal fonksiyonların bir önceki örnekte belirtilen özelliklerini h için de kullanabiliriz.
O halde h nin grafiği, [–1, 2] aralığındaki elemanları [h(–1),
h(2)] yani [–5, 4] aralığındaki elemanlarla eşlemektedir.
Diğer bir ifadeyle, h nin görüntü kümesi [–5, 4] tür. Ayrıca h nin grafiği, uç noktaları (–1, 4) ve (2, –5) olan doğru
parçasıdır. Bu bilgiler doğrultusunda h fonksiyonunun
grafiği yandaki şekildedir.
Fonksiyon Grafiklerini Okuma ve Yorumlama
7
Bir fidanın dikildiği andan itibaren yıllara göre büyüme grafiğinin aşağıdaki gibi olduğunu varsayalım.
y
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1 2 3 4 5 6 7 8 9 10 11
x
Buna göre;
a.
3, 6 ve 7. yıllarda fidanın boyunu bulalım.
b.
Kaçıncı yılda fidanın boyunun 4 metre ve kaçıncı yılda 14 metre olduğunu bulalım.
c.
Fidanın boyunun 4 metreden 14 metreye çıkana kadar geçen zaman aralığını
grafikte zamanın belirtildiği eksen üzerinde gösterelim.
ç.
Fidanın boyu 4 metre iken kaç yıl sonra fidanın boyu 14 metre olduğunu bulalım.
a.
Grafiği bir f fonksiyonunun grafiği olarak düşünelim. Örneğin, verilen grafik ,
f: [0, 9] $ [2, 15] şeklinde bir fonksiyonun grafiği olarak düşünülebilir. Bu durumda 3, 6, 7. yıllardaki fidanın boyu sırasıyla f(3), f(6), f(7) değerleridir. Grafikten
f(3) = 10, f(6) = 12, f(7) = 13 olduğu görülmektedir. Öyleyse fidanın boyu 3. yılda
10 metre, 6. yılda 12 metre, 7. yılda 13 metre olur.
Ünite 3. Fonksiyonlar
505
Fonksiyonların Grafikleri
b.
Fidanın boyunun 4 ve 14 metre
olduğu yıllar f(x) = 4 ve f(t) = 14
eşitliğini sağlayan x ve t
değerleridir. Diğer bir ifadeyle
bu değerler, f in görüntü
kümesindeki 4 ve 14 elemanlarının f altındaki ters görüntüleridir. Ters görüntüleri bulmak
için grafik üzerinde yapacağımız işlem yandaki grafik
üzerinde şekilde belirtilmiştir.
y
Fidanın boyu (m)
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1 2 3 4 5 6 7 8 9 10 11
x
Zaman (yıl)
Böylece, 4 ün ters görüntüsü 1, 14 ün ters görüntüsü 8 olduğundan fidanın boyunun 4
metre olduğu yıl 1. yıldır. Benzer şekilde fidanın boyunun 14 metre olduğu yıl 8. yıl olur.
c.
Fidanın boyunun 4 m den 14 m
ye çıktığı süreci grafik üzerinde
yandaki gibi belirtebiliriz.
Boydaki değişim aralığını dikey
eksende mavi ve buna karşılık
gelen zaman aralığını da yatay
eksende yeşil ile gösterdik.
Bu soruyu f fonksiyonu için
şu şekilde de ifade edebiliriz:
f in görüntü kümesinin bir alt
kümesi olan [4,14] aralığının f
altındaki ters görüntüsü nedir?
Grafikten de anlaşılacağı üzere
bu soruya cevabımız [1, 8]
şeklindedir.
ç.
Fidanın boyu (m)
Bölüm
3.2
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
y
x
1 2 3 4 5 6 7 8 9 10 11
Zaman (yıl)
Zaman aralığındaki değişim süresi 8–1 = 7 yıldır. Diğer bir ifadeyle, fidanın boyu
4 metre iken 7 yıl sonra fidanın boyu 14 metre olur.
506
Ünite 3. Fonksiyonlar
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında bir fonksiyonun tanım ve değer kümesi değiştiğinde grafiğinde oluşan değişiklikleri inceleyeceğiz.
f(x) = 2x + 1 fonksiyon kuralı veriliyor. Buna göre bu fonksiyonun;
Adım 1
Tanım kümesi A = {–2, –1, 0, 1, 2} değer kümesi B = {–4, –3, –1, 0, 1, 2, 3, 4, 5} olacak şekilde grafiğini çiziniz.
Adım 2
Tanım kümesi A = {–2, –1, 0, 1, 2} değer kümesi B = {–5, –3, –1, 1, 3, 4, 5} olacak şekilde grafiğini çiziniz.
Adım 3
Tanım ve değer kümesi doğal sayılar olacak şekilde grafiğini çiziniz.
Adım 4
Tanım ve değer kümesi tamsayılar olacak şekilde grafiğini çiziniz.
Adım 5
Tanım kümesi tamsayılar değer kümesi reel sayılar olacak şekilde grafiğini çiziniz.
Çizdiğiniz bu grafiklerden yola çıkarak;
Adım 6
Değer kümesindeki değişimin grafiği nasıl etkilediğini belirtiniz.
Adım 7
Tanım kümesindeki değişimin grafiği nasıl etkilediğini belirtiniz.
Ünite 3. Fonksiyonlar
507
Bölüm
3.2
Fonksiyonların Grafikleri
8
y
–2
–1
2
Yandaki grafiğe göre aşağıda istenenleri
yapalım.
1
a. Grafiği verilen fonksiyonun tanım ve
değer kümelerini bulalım.
0
x
b. Grafiğin koyu kısmı grafiği olan
fonksiyonun tanım ve görüntü
kümelerini bulalım.
a.
Tanım ve değer kümeleri gerçek sayılar kümesi olabilir.
b.
Grafikte mavi çizgiyle verilen kısmın üzerindeki noktalara karşılık gelen x–eksenindeki değerler [–2, –1] aralığındadır. Yine grafikteki bu noktalara karşılık gelen
y–eksenindeki değerler [0,1] aralığındadır. Dolayısıyla grafikte belirtilen kısım,
tanım kümesindeki [–2, –1] aralığındaki elemanların görüntü kümesindeki [0, 1]
elemanları ile ilişkilendirilmesi ile elde edilmiştir.
y
y
–2
508
–1
Ünite 3. Fonksiyonlar
2
2
1
1
0
x
–2
–1
0
x
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında verilen bir grafiğin fonksiyon grafiği olup olmadığını belirlemeye çalışacağız.
Aşağıdaki grafikleri inceleyiniz.
f :R
y
g:R
y
R
6
h: R
y
R
R
g
f
3
x
0
0
4
k : 6–4, 3 h
y
2
−4
0
−5
9
0
4
x
h
x
R
k
x
l : " a, b, c, d , " " a, b, c, d ,
y
d
c
b
a
a
b c d
m: R
y
R
5
4
3
2
1
x
−2
5 4 3 2 1−1 1 2 3 4 5
−2
−3
−4
−5
x
Adım 1
Her bir grafik için tanım ve değer kümelerini belirleyiniz.
Adım 2
Her bir grafikte grafiğe dikey doğrular (y–eksenine paralel doğrular) çiziniz.
Adım 3
Çizdiğiniz her bir dikey doğrunun grafiği kestiği nokta/noktalar ile x–eksenini kestiği noktayı işaretleyiniz.
Adım 4
Grafiğe çizilen dikey doğruların x eksenini kestiği noktaların tanım kümesinin elemanları olduğunu düşünerek tanım
kümesinden bir eleman değer kümesinden kaç elemanla eşleştiğini verilen grafikler için belirleyiniz.
Adım 5
Elde ettiğiniz sonuca göre yukarıdaki grafiklerden hangileri fonksiyon grafiğidir?
Ünite 3. Fonksiyonlar
509
Bölüm
3.2
Fonksiyonların Grafikleri
f fonksiyonu A 1 R kümesinden B 1 R kümesine tanımlı bir fonksiyon olsun. Fonksiyonların grafiksel gösterimleriyle ilgili açıklamalarımızdan anlaşılacağı üzere, koordinatları f in yaptığı ilişkilendirmelerle belirlenen ikililer olan noktaların kartezyen düzlemde gösterilmesi f in grafiğini vermektedir. Bu nedenle, daha önce de belirttiğimiz
gibi f in grafiği R x R nin bir alt kümesi olmaktadır. Şimdi bunun tersinin doğru olup
olmadığını düşünelim:
Bunu biliyor muydunuz
R x R nin herhangi bir alt kümesi, bir fonksiyonun grafiği şeklinde düşünülebilir mi?
Bu soruya, fonksiyon grafikleriyle ilgili bazı bilgileri hatırlatarak ve bazı örnekleri göz
önünde bulundurarak cevap arayalım. Bir fonksiyon grafiğinin üzerindeki noktalardan
x eksenine dik doğrular (dikey doğrular) çizildiğinde bu doğruların x–eksenini kestiği
noktaların x bileşenleri tanım kümesinin elemanlarıdır. Diğer taraftan, x ekseni üzerinde olup tanım kümesinde yer alan bir elemana karşılık gelen bir noktadan geçen ve x
eksenine dik olan bir doğru çizdiğimizde, bu doğru fonksiyonun grafiğini mutlaka bir
noktada kesmeli ve birden fazla noktada da kesmemelidir.
Bir bilgisayar klavyesindeki
her bir tuşun bir görevi (bir
fonksiyonu) vardır. Belirli bir
harfi veya karakteri yazmak
için o tuşa basarız. Bir tuş
birden fazla karakteri yazmak
için kullanılmaz. Zaten bundan dolayı da bazı karakter
ve sembollerin yazılması için
birkaç tuş kombinasyonu
kullanılarak yeni tuşlar elde
edilmiştir.
Bahsettiğimiz durumlara birer örnek verelim:
y
1.
x–eksenini x = a noktasında kesen dikey doğru,
verilen grafiği kesmiyorsa bu grafik tanım kümesinde a yı eleman olarak bulunduran bir fonksiyona ait
olamaz. Çünkü, a değerine karşılık değer kümesinde
a ile eşlenen bir eleman olmayacaktır; bu da fonksia
x
yon olma kuralına aykırıdır. Grafiğin, bu tür a
elemanlarını dışlayarak oluşturduğumuz tanım
kümesine sahip bir fonksiyon grafiği olabileceği ayrıca düşünülmelidir.
2.
x eksenini x = a noktasında kesen dikey doğru
grafiği bir noktada kesiyor olsun. Bu durumda tanım
kümesindeki a değeri, değer kümesinden bir
elemanla eşlenmiştir. Eğer x ekseni üzerinde
belirlediğimiz bir tanım kümesine karşılık gelen
noktalardan çizilen tüm dikey doğrular grafiği yalnız
a
x
bir noktada kesiyorsa tanım kümesindeki her bir
eleman değer kümesinden yalnız bir elemanla
eşlenmiş demektir. Öyleyse bu durumda, grafik belirlediğimiz tanım kümesine
sahip bir fonksiyonun grafiğidir.
3.
y
y
a
510
Ünite 3. Fonksiyonlar
x
x–eksenini x = a noktasında kesen doğru grafiği
birden fazla noktada kesiyorsa, bu grafik tanım
kümesinde a yı eleman olarak bulunduran bir
fonksiyona ait olamaz. Çünkü, a elemanı değer
kümesinden birden fazla elemanla eşlenmiştir, bu
da fonksiyon olma kuralına aykırıdır. Bu durumda
grafik herhangi bir fonksiyon grafiği olamaz.
Fonksiyon Grafiklerini Okuma ve Yorumlama
9
Dikkat
Aşağıdaki seçeneklerdeki grafiklerin, tanımlandıkları kümelerde bir fonksiyonun grafiği olup olmayacağını bulunuz.
b. f | 6- a, a@ $ 6- b, b@
a. f : R → R
y
y
2
b
1
−1
0
x
1
−a
a
0
Verilerin grafiksel gösterimi
her zaman bir fonksiyon grafiği şeklinde değildir. Benzer
şekilde çizdiğimiz bir grafik
her zaman bir fonksiyon
grafiği olmayabilir.
x
–b
d. h | " - 2, - 1, 0, 1, 2 , $ " 0, 1 , 2, 3, 4 ,
c. f : R → R
y
y
(–2, 4)
4
(2, 4)
3
1
2
(–1, 1)
−1
1
0
x
Anahtar Bilgi
(1, 1)
1
−3
−2 −1
0
Bir grafiğe dikey doğrular
çizerek bir grafiğin fonksiyon
grafiği olup olmadığını anlama yöntemine dikey doğru
testi denir.
x
(0, 0)
1
2
3
−1
Dikey eksen değer kümesi,
yatay eksen tanım kümesi
olmak üzere grafiği kesecek
şekilde çizilen dikey doğrular;
a.
y
1
x
−1
Grafikte x ekseni boyunca çizilen her
dikey doğru grafiği yalnız bir noktada
kestiğinden verilen tanım kümesi olan R
deki her eleman değer kümesinden
yalnız bir elemanla eşleşmiştir. Bu yüzden
bu grafik f : R → R şeklindeki bir
fonksiyonun grafiği olabilir.
0
Ünite 3. Fonksiyonlar
511
•
grafiği her zaman birer
noktada kesiyorsa grafik
fonksiyon grafiğidir.
•
grafiği birden fazla
noktada kesiyorsa grafik
fonksiyon grafiği değildir.
Bölüm
3.2
Fonksiyonların Grafikleri
b.
y
b
x
–a
a
x ekseni üzerindeki (–a, a) aralığında
çizilen her dikey doğru verilen grafiği iki
noktada kesmektedir. Bu yüzden bu
grafik, önerilen f: [–a, a] → [–b, b] şeklindeki bir fonksiyonun grafiği olamayacağı
gibi, başka tür bir fonksiyonun da grafiği
olamaz.
–b
c.
x eksenindeki dikey doğrulardan x = a
haricindekiler grafiği bir noktada kesmiştir. Sadece a noktasında fonksiyonun
değeri yoktur. Önerilen fonksiyon
y
x
a
–b
Ancak, bu verilen grafiğin
g | R - " a , $ R şeklinde bir fonksiyonun grafiği olabileceğine dikkat edelim.
y
ç.
3
Tanım kümesindeki her noktadan
geçecek şekilde dik doğrular çizdiğimizde bu doğrular grafiği yalnızca bir
noktada keser. Bu durumda verilen grafik
2
h: {–2, –1, 0, 1, 2}$ {0, 1, 2, 3, 4} fonksi-
4
(–2, 4)
(2, 4)
1
(–1, 0)
yonunun grafiğidir. Benzer şekilde,
(1, 1)
x
(0, 0)
−2
f : R → R şeklinde ve tanım kümesi
R olduğundan, verilen grafik f gibi bir
fonksiyonun grafiği değildir.
−1
h:{−2, −1, 0, 1, 2}
0
1
2
" 0, 1, 2, 3, 4 , 1 B için
g | " - 2, - 1, 0, 1, 2 , $ B şeklindeki bir
fonksiyonun da grafiği olabilir.
{0, 1, 2,3,4}
Ancak verilen grafik, " - 2, - 1, 0, 1, 2 , 1 A 1 R ve " - 2, - 1, 0, 1, 2 , ! A şeklindeki bir A
kümesi için f | A $ R olan bir fonksiyonun grafiği değildir.
512
Ünite 3. Fonksiyonlar
Fonksiyon Grafiklerini Okuma ve Yorumlama
10
Aşağıda verilen grafiklerin, ilgili tanım kümelerine uygun bir fonksiyon grafiği olup olmayacağını bulunuz.
y
a. f | 6- 2, 3h $ R
b. g | 60, 3h $ R
y
c. h : R $ R
y
h
f
x
0
-2
0
x
g
x
0
Dikey doğru testini, belirtilen fonksiyonların tanım kümelerini dikkate alarak verilen
grafiklerde uygulayalım.
y
a. f | 6- 2, 3h $ R
b. g | 60, 3h $ R
y
f
-2
a.
b.
c.
0
x
0
x
c. h : R $ R
y
h
0
x
Verilen grafik f | 6- 2, 3h $ R şeklindeki bir fonksiyonun grafiğidir. Çünkü,
6- 2, 3h aralığındaki dikey doğrular verilen grafiği hep birer noktada kesmektedir.
Verilen grafik g | 60, 3h $ R şeklindeki bir fonksiyonun grafiği olmadığı gibi
y = f(x) şeklindeki herhangi başka bir f fonksiyonunun da grafiği değildir. Çünkü
tanım kümesi olan ^0, 3h aralığındaki her hangi bir dikey doğru grafiği iki noktada kesmektedir.
Verilen grafik h | R $ R şeklindeki bir fonksiyonun grafiği olmadığı gibi
y = f(x) şeklindeki herhangi başka bir f fonksiyonunun da grafiği değildir. Çünkü
bazı dikey doğrular grafiği iki noktada kesmektedir.
Ünite 3. Fonksiyonlar
513
Bölüm
3.2
Fonksiyonların Grafikleri
11
y
1
f fonksiyonunun grafiği verilmiştir. Buna göre,
0,5
x
(–1, 0)
−3 −2,5 −2 −1,5 −1 −0,5 0 0,5
−0,5
–1
f
a. f in tanım ve görüntü kümelerini bulunuz.
1
b. f([ –
(0, −1)
−1,5
13
, 0]) ifadesinin eşitini bulunuz.
10
c. [–3,0] kümesinin f altındaki ters görüntüsünü bulunuz.
–2
−2,5
(–2, -3)
–3
1
y
0,5
x
(–1, 0)
−3 −2,5 −2 −1,5 −1 −0,5 0 0,5
−0,5
–1
1
(0, −1)
−1,5
f
13
,0] ile [–1,0] aralıklarının
10
f altındaki görüntülerinin aynı olduğuna
b. Öncelikle [ –
–2
−2,5
(–2, -3)
–3
1
dikkat edelim. [–1,0] in f altındaki görüntüsü yandaki grafikte mavi doğru parçası ile
gösterilmiştir. Dolayısıyla,
- 13
f([
, 0 ]) = f([–1, 0]) = [–1, 0] dır.
10
y
0,5
x
(–1, 0)
−3 −2,5 −2 −1,5 −1 −0,5 0 0,5
−0,5
–1
f
(0, −1)
−1,5
–2
−2,5
(–2, -3)
514
a. Aşağıdaki şekilde grafiğin tanım kümesi x
ekseni üzerinde yeşil doğru parçası ile
görüntü kümesi de y ekseni üzerinde mavi
doğru parçası ile gösterilmiştir. Dolayısıyla
tanım kümesi [–2, 0], görüntü kümesi ise
[–3, 0] dır.
–3
Ünite 3. Fonksiyonlar
1
c. f nin görüntü kümesinin [–3, 0] aralığı olduğunu bulmuştuk. Herhangi bir fonksiyonda,
görüntü kümesinin fonksiyon altındaki ters
görüntüsü tanım kümesidir. Ayrıca, bu fonksiyonun tanım kümesi [–2, 0] olarak bulunmuştur. Dolayısıyla [–3, 0] ın f altındaki ters
görüntüsü [–2, 0] dır.
Fonksiyon Grafiklerini Okuma ve Yorumlama
12
Bir h fonksiyonunun grafiği yanda verilmiştir.
Buna göre,
a. h nin tanım ve görüntü kümelerini bulunuz.
b. [–1, 1] in h altındaki görüntüsünü bulunuz.
c. (–1, 3] ün in h altındaki görüntüsünü bulunuz.
ç. 0’ın h altındaki görüntüsünü ve 2’nin h altındaki ters görüntüsünü bulunuz.
d. [–1, 1] kümesinin f altındaki ters görüntüsünü bulunuz.
y
3
(1 -
h
(−1, 2)
2
(3, 2)
3 , 1)
1
(1 +
−2
−1
0
1
2
3
3 , 1)
x
4
−1
−2
(1,- 2)
−3
y
3
a.
h fonksiyonunun grafiğinde tanım kümesi
yeşil doğru, görüntü kümesi de mavi yarı
doğru ile belirtilmiştir. Dolayısıyla h nin
tanım kümesi (–∞, ∞) ve görüntü kümesi
[–2, ∞) dur.
b.
h fonksiyonunun grafiğinde belirtilen mavi
doğru parçası h([–1, 1]) dir. Dolayısıyla,
h([–1, 1]) = [–2, 2] dir.
c.
Benzer şekilde verilen grafikten anlaşılacağı
üzere h((–1, 3]) = [–2, 2] dir.
h
2
1
x
−2 −1 0 1
−1
−2
2
3
4
(1,- 2)
−3
y
3
2
1
x
−2 −1 0 1
−1
−2
2
3
(1,- 2)
y
−3
3
(1 -
3 , 1)
2
1
(1 +
−2 −1 0 1
−1
−2
−3
(1,- 2)
2 3
3 , 1)
x
ç.
Verilen grafikten h(0) = –1, h(–1) = h(3) = 2
olduğu görülür. Bu durumda, 0 nin görüntüsü –1’dir. 2 nin ters görüntüleri –1 ve 3’tür.
d.
[–1,1] kümesinin h altındaki ters görüntüsü yandaki grafikte yeşil doğru parçalarıyla belirlenmiştir. Dolayısıyla, cevap
61 - 3 , 0@ , 62, 1 + 3 @ dir.
Ünite 3. Fonksiyonlar
515
Bölüm
3.2
Fonksiyonların Grafikleri
13
g fonksiyonunun grafiği yanda
verilmiştir. Buna göre,
a.
g nin tanım ve görüntü kümelerini bulunuz.
b.
[2, 4] in g altındaki ters görüntüsünü bulunuz.
y
y = g(x)
5
4
3
2
1
–4 –3 –2 –1
a.
–1
x
0 1
2
3
4
g nin tanım kümesi R ve görüntü kümesi 60, 3h dur.
y
g
5
4
3
2
1
–4 –3 –2 –1
b.
–1
x
0 1
2
3
4
Aşağıda belirtilen grafiklerden anlaşılacağı üzere [2, 4] ün g altındaki ters görüntüsü 6- 4, - 2@ , 62, 4@ tür.
y
y
g
5
4
3
3
2
2
1
–5 –4 –3 –2 –1
516
5
4
1
x
0
1
Ünite 3. Fonksiyonlar
2
3
4
5
g
–5 –4 –3 –2 –1
x
0
1
2
3
4
5
Fonksiyon Grafiklerini Okuma ve Yorumlama
KENDİMİZİ SINAYALIM
Kavram Yoklama ve Muhakeme
1.
Aşağıda boş bırakılan yerlere uygun ifadeleri
yazınız.
a.
Bir fonksiyonun grafiğinde girdiler . . . . . . . . . . . . . . . . . . . . . . .
ekseninde çıktılar ise . . . . . . . . . . . . . . . . . . . . . . . . . . ekseninde
gösterilir.
b.
Bir fonksiyonun kartezyen düzlemde gösterilmesine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . gösterim denir.
c.
Fonksiyonun grafiğinin girdilerinin kümesine
. . . . . . . . . . . . . . . . çıktılarının kümesine . . . . . . . . . . . . . . . . kümesi
denir.
2.
Aşağıdaki verilen olaylarla ilgili grafiklerin hangisi/
hangileri bir fonksiyon belirtmez?
a.
Bir bardağa bir musluktan su doldurulurken bardaktaki su yüksekliğinin zamana bağlı değişimi.
b.
Bir maçtaki atılan gol sayısının zamana bağlı değişimi.
c.
Bir çaydanlık su ısıtıldığında suyun sıcaklığının
zamana bağlı değişimi.
ç.
Uygulama Soruları
1.
A = {1, 3, 4} ve f: A→R fonksiyonunun kuralı
f(x) = 2x + 4 olduğuna göre, f(A) görüntü kümesini
bulunuz.
2.
g: A → R, g(x) = 4 – 2x fonksiyonu için g(A)= [–4,2]
ise A kümesini bulunuz.
3.
Gerçek sayılarda tanımlı f fonksiyonunun grafiği
aşağıda verilmiştir. Buna göre, [2,9] kümesinin f
altındaki görüntü kümesi nedir?
y
Bir şehirdeki insanları sahip oldukları kredi kartlarına eşleme ilişkisi.
0
–6 –5 –4 –3 –2 –1
7
6
5
4
3
2
1
1 2
–1
x
3 4 5 6 7 8 9
Ünite 3. Fonksiyonlar
517
Fonksiyon Grafiklerini Okuma ve Yorumlama
KENDİMİZİ SINAYALIM
4.
Gerçek sayılar kümesi üzerinde tanımlı aşağıda grafiği verilen fonksiyon için B = [1,8] kümesinin ters
görüntü kümesi nedir?
7.
f(3) + f(0) – f(–2) değeri kaçtır?
y
8
7
6
5
4
3
2
1
–2
5.
y
–2 –1
01
2
–1
2
f fonksiyonunun verilen grafiğine göre
2
4
3
2
1
0
1 2 3
f
x
x
Aşağıdaki grafikler f ve g fonksiyonlarının grafikleri
g (6) - f (0)
olduğuna göre
değeri kaçtır?
f (6) - f (3)
8.
Bir f fonksiyonunun grafiği aşağıdaki gibidir.
f(a) = 6, f(b) = 3, f(c) = 0 ise a + b – c değeri kaçtır?
y
y
9
8
7
6
5
4
3
2
1
f
0
1 2 3 4 5
–5 –4 –3 –2 –1
x
x
Bir doğrusal fonksiyon grafiği aşağıdaki gibidir. Bu
grafikte verilen k değeri kaçtır?
y
9.
Şekilde bir f fonksiyonunun grafiği verilmiştir. Buna
göre f(0) = a, f(a) = b ve f(b) = c ise c kaçtır?
y
k
4
x
01 2
518
(5, 0)
0 1 2 3 4 5 6 7 8 9 10
–6 –5 –4 –3 –2 –1
6.
(0, 3)
g
6
5
4
3
2
1
Ünite 3. Fonksiyonlar
5
(3, 5)
4
(2, 3)
3
(0, 2) 2
1
x
0
1 2 3
Fonksiyon Grafiklerini Okuma ve Yorumlama
KENDİMİZİ SINAYALIM
10. Grafiği verilen f fonksiyon için f(x-1)=4 ise x in
alabileceği değerler toplamı kaçtır?
y
4
y
3
8
7
6
5
4
3
2
1
2
(2, 3)
1
(–1, 0)
f
–3
–2
–1
(0, 1)
0
–1
1
x
2
3
–2
x
01 2 3 4
–4 –3 –2 –1
12.
–3
Yukarıda bir f fonksiyonunun grafiği verilmiştir.
Buna göre;
11. Aşağıda grafiği verilen fonksiyonların tanım ve
görüntü kümelerini belirleyiniz.
y
a.
3
1
B(–3,1)
–4
–3
–2
–1
b.
0
–1
f in tanım ve görüntü kümelerini bulunuz.
b.
A = {-1, 0, 1, 2} kümesinin f altındaki görüntüsünü
bulunuz.
c.
A = {x | -1 ≤ x ≤ 2} kümesinin f altındaki görüntüsünü bulunuz.
ç.
B = {0, 1, 3} kümesinin f altındaki ters görüntüsünü
bulunuz.
d.
B = {0, 3} kümesinin f altındaki ters görüntüsünü
bulunuz.
A(2,3)
2
f
a.
1
2
3
4
x
y
A(–1,3)
3
g
2
1
C(2,0)
–2
–1
0
1
2
3
x
–1
Ünite 3. Fonksiyonlar
519
Fonksiyon Grafiklerini Okuma ve Yorumlama
KENDİMİZİ SINAYALIM
13.
15. f: R " R , f (x) = –4x – 7 fonksiyonu veriliyor.
y
4
a.
3
2
b. [0, 5] aralığının f altındaki görüntüsünü bulunuz ve grafikte gösteriniz.
1
c.
x
–5
–4
–3
–2
–1
0
f fonksiyonun grafiğini çiziniz.
–1
1
2
Görüntüsü -19 olan elemanın f altındaki ters
görüntüsünü bulup grafikte gösteriniz.
3
Yukarıda bir g fonksiyonunun grafiği verilmiştir.
Buna göre;
16.
y
a.
g nin tanım ve değer kümelerini bulunuz.
4
b.
A = {-5, -4, -1, 0, 1, 2} kümesinin g altındaki görüntüsünü bulunuz.
3
c.
A = {x | -3 ≤ x ≤ 2} kümesinin g altındaki görüntüsünü bulunuz.
ç.
B = {x | 0 ≤ x ≤ 4} kümesinin g altındaki ters görüntüsünü bulunuz.
d.
2
1
x
–2
B = {0, 1, 3, 4} kümesinin g altındaki ters görüntüsünü bulunuz.
–1
0
–1
1
2
–2
–3
14. A= {–2, –1, 0, 1, 2} ve f: A " R fonksiyonunun kuralı
–2
f (x) =
x + 0, 25 ile veriliyor.
3
a.
f fonksiyonunun değerler tablosunu oluşturunuz.
b. f fonksiyonun grafiğini çiziniz.
Tanım, değer ve görüntü kümelerini grafik üzerinde gösteriniz.
520
Ünite 3. Fonksiyonlar
Grafiği verilen f fonksiyonu için;
a.
tanım, değer ve görüntü kümelerini bulunuz.
b. x = 0 ve x = –1 elemanlarının f altındaki görüntülerini bulunuz.
c.
y = 1 ve y = –1 çıktılarının f altındaki ters görüntülerini bulunuz.
Fonksiyon Grafiklerini Okuma ve Yorumlama
KENDİMİZİ SINAYALIM
17.
19. Aşağıdaki grafiklerin hangileri bir fonksiyon grafiği
olabilir? Nedenini çıklayınız.
y
3
2
–1 –1
–2
a.
0
2
1
y
x
–4
–5
–6
–7 –6 –5 –4 –3 –2 –1
–10
Grafiği verilen fonksiyon için;
b.
a) x=-1, x=0, x=1 ve x=2 elemanlarının bu
fonksiyon altındaki görüntülerini bulunuz.
y
b) y=-1, y=0 ve y=-5 çıktılarının bu fonksiyon altındaki ters görüntülerini bulunuz.
0
y
–2
c.
4
x
1
–2
0
3
y
x
x
0
5
4
3
2
1
1
–4
y
y
4
–1
x
y
7
8
6
5
4
3
2
1
–6 –5 –4 –3 –2 –1–1 1 2 3 4 5 6
18. Aşağıdaki verilen grafiklerin y = f(x) şeklinde bir
fonksiyon grafiği olup olmadığını bulunuz.
0
x
0
–1
–2
–8
y
6
5
4
3
2
11 2 3 4 5 6 7
x
x
–4
0
–7 –6 –5 –4 –3 –2 –1–1 1 2 3 4 5 6 7 8
x
–2
Ünite 3. Fonksiyonlar
521
Fonksiyon Grafiklerini Okuma ve Yorumlama
KENDİMİZİ SINAYALIM
f.
ç.
y
y
0
–5 –4 –3 –2 –1
–1
–2
5
4
3
2
1
0
x
–4 –3 –2 –1
–1
–2
–3
–4
–5
1 2 3 4 5
5
4
3
2
1
x
1 2 3 4 5
d.
g.
y
0
–3 –2 –1
–1
y
6
5
4
3
2
1
x
1 2 3 4 5 6
e.
0
–4 –3 –2 –1
–1
–2
–3
–4
522
y
4
3
2
1
1 2 3 4 5
Ünite 3. Fonksiyonlar
x
0
–4 –3 –2 –1–1
–2
–3
–4
4
3
2
1
1 2 3 4 5 6
x
MATEMATİK ATÖLYESİ
Bu atölye çalışmasının amacı, f(x) = xn (n ∈ Z) biçimindeki fonksiyonların davranışlarının bilgi ve iletişim teknolojilerinden yararlanılarak incelenmesidir.
Araç ve Gereçler: Elektronik tablolama, grafik hesap makinesi, bilgisayar cebir sistemi, dinamik matematik/geometri
yazılımı vb. grafik çizimi yapılabilen bir araç/yazılım
Adım 1
Grafik çizimi yapabilen bir araç/yazılım kullanarak;
n = 2, 4, 6, 8, 10 değerleri için y = xn fonksiyonlarının grafiklerini çiziniz.
Adım 5
n = 1, 3, 5, 7, 9 değerleri için y = xn fonksiyonlarının grafiklerini farklı renklerde aynı koordinat düzlemi üzerinde
çizdirin. Bu tür grafiklerin ortak özellikleri için neler söylenebilir? Açıklayınız.
Adım 2
n = 2, 4, 6, 8, 10 değerleri için y = xn fonksiyonlarının grafiklerini farklı renklerde aynı koordinat düzlemi üzerinde
çiziniz. Bu tür grafiklerin ortak özellikleri için neler söylenebilir? Açıklayınız.
Adım 6
n = -1, -3, -5, -7, -9 değerleri için y = xn fonksiyonlarının
grafiklerini aynı koordinat düzlemi üzerinde çizdirin. Bu
tür grafiklerin ortak özellikleri için neler söylenebilir?
Açıklayınız.
Adım 3
n = -2, -4, -6, -8, -10 değerleri için y = xn fonksiyonlarının
grafiklerini aynı eksen üzerinde çiziniz. Bu tür grafiklerin
ortak özellikleri için neler söylenebilir? Açıklayınız.
Adım 7
n nin çift olmayan bir negatif veya pozitif tamsayı olması
durumunda y = xn şeklindeki fonksiyonların grafiklerinin
nasıl değiştiğini açıklayınız.
Adım 4
n nin çift bir negatif veya pozitif tamsayı olması durumunda y = xn şeklindeki fonksiyonların grafiklerinin nasıl
değiştiğini açıklayınız.
Adım 8
n nin tek veya çift bir pozitif tamsayı olması durumunda
y = xn şeklindeki fonksiyonların görüntü kümelerinin nasıl değiştiğini açıklayınız.
Yukarıdaki adımları, örneğin, bir dinamik matematik/geometri yazılımı olan GeoGebra kullanarak aşağıdaki şekilde yapabilirsiniz. (Geogebra yazılımını http://www.geogebra.org veya http://www.geocebir.org adreslerinden
ücretsiz indirebilir ve kullanabilirsiniz.)
Ünite 3. Fonksiyonlar
523
MATEMATİK ATÖLYESİ
Geogebra kurulu bir bilgisayarda, geogebrayı açalım. Öncelikle bir sürgü oluşturalım:
Araç çubuğundan Sürgü aracını
sol tuşu ile tıklayın.
seçin ve ekranın neresinde sürgüyü oluşturmak istiyorsanız oraya farenizin
Karşınıza Sürgü aracı ile ilgili özelliklerin olduğu bir pencere gelecektir:
Program sürgüye ilk değer olarak a ismini vermektedir. Sürgünün adını n olarak değiştirelim. Ayrıca sürgünün minimum ve maksimum değerleri ve artış miktarını da yukarıdaki
şekilde görüntülendiği gibi belirledikten sonra Uygula tuşuna basınız.
Ekranda beliren sürgüyü hareket ettirdiğinizde n değeri de
belirlediğiniz aralıkta belirlediğiniz artış miktarı ile değişecektir.
GeoGebra ekranının sol alt köşesindeki Giriş ekranını kullanarak fonksiyonumuzu tanımlayacağız.
^ sembolü üst anlamına gelip x^n ifadesi matematiksel olarak xn anlamına gelmektedir. Fonksiyonu girdikten sonra
klavyeden Enter/Return tuşuna basıldığında fonksiyon n sürgüsüne bağlı olarak oluşacaktır.
Şimdi n değerini değiştirerek fonksiyonun nasıl değiştiğini gözlemleyiniz. Aşağıda n = –1 ve n = 2 değerleri için oluşan grafiğe yer verilmiştir.
y
y
3
y =f(x)
n=2
2
n = –1
y =f(x)
2
1
1
–4
–3
–2
0
–1
1
–1
–2
524
Ünite 3. Fonksiyonlar
2
3
x
–3
–2
0
–1
–1
–2
–3
1
2
3
4
x
Fonksiyon Grafiklerini Okuma ve Yorumlama
Neler Öğreneceğiz?
3.2.2. f(x) = xn Biçimindeki Fonksiyonların Grafikleri
•
Başlarken
f(x) = xn biçimindeki fonksiyonların grafiklerini
Bazı fonksiyonların grafiklerine veya benzerlerine mimaride, teknolojik araçlarda ve
doğada rastlanmaktadır. Örneğin, fotoğraflarda görülen uzay araştırmalarında kullanılan
radyo teleskopun/antenin, asma köprülerin ve
kıvrımlı bir nehrin şeklini f(x) = xn, n ∈ Z biçimindeki fonksiyonların grafiklerini kullanarak
ifade edebiliriz.
Anahtar Terimler
•
Ele aldığımız bir şeklin fonksiyon grafiği olarak
modellenebilmesinin faydaları sizce neler
olabilir?
Sembol ve Gösterimler
•
x br
x br
Fonksiyon grafiği
Bir kenar uzunluğu x br
olan bir karenin alanını kenar uzunluğuna bağlı olarak değişen ve A(x) ile belirtilen bir çokluk olarak
düşündüğümüzde
A: R+ → R+ ve A(x) = x2
şeklinde bir fonksiyonla
karşılaşırız. Benzer şekilde, bir kenar uzunluğu x br olan bir küpün hacmini kenar uzunluğuna bağlı olarak değişen ve V(x) ile belirtilen bir çokluk olarak düşündüğümüzde
V: R+ → R+ ve V(x) = x3 şeklinde bir fonksiyon elde ederiz. Bu fonksiyonların grafikleri
kare ve küpte kenar uzunluk değiştikçe alan ve hacmin değişimini daha iyi görmemizi
sağlar. Dikkat edersek bu cebirsel kurallara sahip fonksiyonların 0 da ve negatif gerçek
sayılarda da tanımlanabileceğini görebiliriz. Bu fonksiyonlar birçok durum için temel
örnek niteliğindedir. Bu fonksiyonların grafiklerini bilmemiz bir gereklilik olduğu gibi,
bunlardan daha karmaşık kurala sahip fonksiyonların grafiklerinin anlaşılmasında bir
avantajdır.
Ünite 3. Fonksiyonlar
525
f(x) = xn , n ! Z
Bölüm
3.2
Fonksiyonların Grafikleri
Bu kısımda göreceğimiz fonksiyonlar, n negatif bir tam sayı iken f: R – {0} → R ve n nin
diğer tam sayı durumları için f: R → R şeklindeki olup aşağıdaki cebirsel kurallara sahip
fonksiyonlardır:
n = 0 için f(x) = 1
Anahtar Bilgi
f(x) = xn biçimindeki fonksiyonların grafikleri çizilirken;
1
x
1
n = –2 için f(x) = 2
x
1
n = –3 için f(x) = 3
x
n = –1 için f(x) =
1. Fonksiyona ait bir değerler
tablosu oluşturulur.
2. Fonksiyonun grafiği üzerinde yer alan ve koordinatları değerler tablosu ile
verilen noktalar kartezyen
düzlemde gösterilir.
3. Düzlemde gösterilen
noktalardan geçen bir eğri
kabaca çizilir.
n = 1 için f(x) = x
n = 2 için f(x) = x2
n = 3 için f(x) = x3
Bunlar kısaca n ∈ Z olmak üzere f(x) = xn şeklinde de ifade edilebilir. Şimdi n nin bazı
değerleri için bu tür fonksiyonların grafiklerini, fonksiyona ait değerler tablosunu, yani
fonksiyonun grafiği üzerindeki bazı noktaların koordinatlarını bularak çizmeye çalışalım.
4. Bu işlem nokta sayısını
artırarak tekrar edilirse
hata payı daha az olan bir
grafik elde edilmiş olur.
1
n = 0 için f: R → R, f(x) = xn fonksiyonunun grafiğini çizelim.
5. Çoğu durumda grafiğin
genel yapısı göreceli
olarak az sayıda noktanın
grafiksel gösterimi yapılarak tespit edilebilmektedir.
y
2
f(x) = 1
1
0
–2
–1
1
2
n = 0 için f(x) = xn = x0 = 1 olacağından, f fonksiyonu bir sabit fonksiyondur. Daha önce gördüğümüz gibi bu fonksiyonun grafiği y ekseninde 1 den geçen ve x eksenine paralel olan
bir doğrudur.
2
n = 1 için f: R → R, f(x) = xn fonksiyonunun grafiğini çizelim.
n = 1 için f(x) = xn = x1 = x olacağından f fonksiyonu bir birim fonksiyondur. Yine daha
önce ele aldığımız gibi bu fonksiyonun grafiği (0,0) orijin ve (1,1) noktalarından geçen
bir doğrudur. Şimdi bu doğrunun grafiğini hemen çizmek yerine, bundan sonraki örneklerde kullanacağımız bir yöntemi anlatmak için ikiden fazla nokta kullanarak çizelim.
Önce grafik üzerindeki bazı noktaların koordinatlarını belirlemek için fonksiyona ait
bir değerler tablosu oluşturalım. Sonra bu noktaları kartezyen düzlemde gösterelim.
526
Ünite 3. Fonksiyonlar
f(x) = xn Biçimindeki Fonksiyonların Grafikleri
x
y
0
0
1
1
2
2
3
3
–1
–1
–2
–2
–3
–3
–3
...
...
x(∈ R)
x
–4
–5
5
y
4
3
2
1
–5 –4 –3 –2 –1 0 1
–1
–2
2
3
4
5 x
3
4
5 x
3
4
5 x
1. Grafiksel Gösterim
Grafikte gösterilen noktaların doğrusal
olduğunu gözlemleyebiliyoruz. Ama
fonksiyon grafiğimiz olan doğrumuzu
tam olarak elde etmiş değiliz. Şimdi yaptığımız işlemleri, grafik üzerinde yer alan
daha fazla noktayı belirleyerek tekrar
edelim. Bu durumda grafik 2. Grafiksel
Gösterimdeki gibi olacaktır.
y
5
4
3
2
1
–5 –4 –3 –2 –1 0 1
–1
–2
2
–3
–4
–5
2. Grafiksel Gösterim
Bu grafik elde etmek istediğimiz doğru
grafiğine daha çok benziyor değil mi? Bu
işlemleri her seferinde artırarak devam
ettiğimizde f: R → R, f(x) = x fonksiyonun grafiği, 3. Grafiksel Gösterimdekine
daha çok yaklaşmış olacaktır.
y
5
4
3
2
1
–5 –4 –3 –2 –1 0 1
–1
–2
2
–3
–4
–5
3. Grafiksel Gösterim
Ünite 3. Fonksiyonlar
527
Bölüm
3.2
Fonksiyonların Grafikleri
3
n = 2 için f: R → R, f(x) = xn fonksiyonunun grafiğini çizelim.
n = 2 için f(x) = xn = x2 dir. Bu fonksiyona ait bir değerler tablosu ve bu değerlere karşılık
gelen noktaların grafiksel gösterimi şu şekildedir:
y
x
y
9
0
0
1
1
8
7
2
4
3
9
–1
1
–2
4
–3
9
6
5
4
3
2
1
–4 –3 –2 –1 0 1
–1
y
9
3
4 x
Bu fonksiyon tanım kümesindeki her elemanı, kendisinin karesiyle eşlenmektedir. Dolayısıyla grafik
üzerindeki noktaların ordinatları, apsislerden daha
hızlı büyümektedir. Ayrıca tanım kümesindeki her
eleman hiçbir zaman negatif bir sayı ile eşlenmemektedir.
8
7
6
5
4
3
2
1
–4 –3 –2 –1 0 1
–1
2
2
3
4 x
Benzer şekilde grafik üzerindeki nokta sayısını artırırsak bu durumda grafik yandaki gibi olacaktır.
y
9
Yaptığımız işlemlere nokta sayısını artırarak devam ettiğimizde ve tanım kümesinin tüm gerçek sayılar olduğu düşünüldüğünde;
f: R → R, f(x) = x2 fonksiyonunun grafiğinin yandaki gibi olacağı anlaşılacaktır.
8
7
6
5
4
3
2
1
–4 –3 –2 –1 0 1
–1
528
Ünite 3. Fonksiyonlar
2
3
4 x
f(x) = xn Biçimindeki Fonksiyonların Grafikleri
Şimdi başka bir fonsiyonun grafiğini aynı yöntemle elde edelim.
4
n = 3 için f: R → R, f(x) = xn fonksiyonunun grafiğini çizelim.
n = 3 için f(x) = xn = x3 olur. Bu fonksiyon için bir değerler tablosu ve buna karşılık gelen
noktaların grafiği 1. Grafiksel gösterimdeki gibi olacaktır.
x
y = f(x)
–2
–8
–1
–1
0
0
1
1
2
8
f: R → R, f(x) = x3 fonksiyonunda tanım kümesindeki her eleman değer kümesinden kendisinin küpüyle eşlenmektedir.
Dolayısıyla grafiğin üzerindeki noktaların koordinatlarının apsislere göre büyümesi daha önce incelediğimiz f(x) = x2 fonksiyonundakinden çok daha hızlıdır. Değerler tablosuna yeni değerler eklediğimizde, yani grafiksel gösterimini yaptığımız
noktası sayısını arttırdığımızda grafik 2. Grafiksel Gösterimdeki
gibi olacaktır.
Fonksiyonun tanım kümesinin tüm gerçek sayılar olduğu düşünüldüğünde f: R → R,
f(x) = x3 fonksiyonunun grafiği 3. Grafiksel gösterimdeki gibi olacaktır.
y
y
y
8
7
8
7
8
7
6
5
6
5
6
5
4
4
4
3
2
3
2
3
2
1
1
1
–3 –2 –1 0 1
–1
–2
2
3 x
–3 –2 –1 0 1
–1
–2
2
3 x
–3 –2 –1 0 1
–1
–2
–3
–4
–3
–4
–3
–4
–5
–6
–5
–6
–5
–6
–7
–8
–7
–8
–7
–8
1. Grafiksel Gösterim
2. Grafiksel Gösterim
2
3 x
3. Grafiksel Gösterim
Ünite 3. Fonksiyonlar
529
Bölüm
3.2
Fonksiyonların Grafikleri
5
Bunu biliyor muydunuz
n = –1 için: R − 0 → R, f(x) = xn fonksiyonunun grafiğini çizelim.
Bilgisayar cebir sistemleri ile
dinamik matematik/geometri
yazılımları fonksiyon grafiklerinin
çizimini yaparken, temelde bizim
bu kısımda uyguladığımız yönteme
benzeyen metodları kullanırlar.
Şöyle ki, çizilecek grafik üzerinde
belli sayıdaki noktayı belirli aralıklardan seçer, bu noktaları grafik
üzerinde gösterir ve bu noktaları
ikişer ikişer birleştiren doğrular çizerler. Nokta seçimlerini ise burada
belirtemeyeceğimiz matematiksel
bilgi ve teknikleri kullanarak akıllı
bir şekilde yaparlar.
1
n = –1 için f(x) = x–1 = dir. Bazı x değerleri için f fonksiyonunun aldığı değerler tablosu
x
şu şekildedir:
x
Örneğin
f: ;-
–2
–1
y =f(x) - 1 - 1 - 1
2
3
4
–1
–20
grafiğin 25 noktasını kullanarak
çizdirirsek
10
1
x
2
y
grafiğin nokta sayısı seçimini belirtmeden çizdirirsek
3
4
4
3
2
1
1
2
1
3
1
4
Tanım kümesi olan sıfır hariç tüm gerçek
sayılar düşünüldüğünde f: R − {0} → R,
1
fonksiyonunun grafiğinin şöyle
f(x) =
x
olacağını görebiliriz:
y
5
4
3
2
20
10
–6 –5 –4 –3 –2 –1
1
2
6
5
4
–20
–1
1
x değerleri negatif değerlerle küçüldükçe veya pozitif değerlerle büyüdükçe fonksiyonun değerleri (y) 0’a yaklaşmaktadır.
–10
–2
–4
1
2
•
Şimdi koordinatları tabloda verilen (x,y)
ikilileri olan noktaları grafik üzerinde
gösterelim:
20
–1
–3
1
3
(0,1) aralığında x değerleri sıfıra yaklaştıkça fonksiyonun değerleri (y) pozitif değerler alarak büyümektedir ve x değeri sıfıra yaklaştıkça y değerleri daha da büyümektedir.
x
2
–10
–2
–2
1
4
•
10
1
1
1
1
2
4
3
(-1,0) aralığında x değerleri sıfıra yaklaştıkça fonksiyonun değeri (y) negatif değerler alarak küçülmektedir ve x değeri sıfıra yaklaştıkça y değerleri daha da küçülmektedir.
20
0
-
•
f(x) = x5 – 3x3 ile verilen
fonksiyonun grafiğini Mathematica
programında grafiğin 10 noktasını
kullanarak çizdirirsek
–1
–3
Tablodaki değerler incelendiğinde;
22 22
, E " [- 20, 20] ve
10 10
–2
–4
3
2
1
0 1
–1
x
2
2
3
4
5
6 x
–5 –4 –3 –2 –1
1
–10
–2
0 1
–1
–20
–3
–2
–4
–3
grafiklerini elde ederiz
–5
–6
530
Ünite 3. Fonksiyonlar
–4
–5
2
3
4
5 x
f(x) = xn Biçimindeki Fonksiyonların Grafikleri
Şu ana kadar bu kısımda gördüğümüz fonksiyon grafiklerini bir arada görelim:
n ∈ {1, 2, 3, –1} için f(x) = xn in grafikleri
4
y
f(x) = x
3
2
y
4
f(x)=x2
3
2
1
1
–4 –3 –2 –1 0 1
–1
2
3
–4 –3 –2 –1 0 1
–1
4 x
2
3
4 x
–2
–2
y=f(x)=xn, n=2
y=f(x)=xn, n=1
y
4
5
4
y
f(x)=x3
3
2
3
2
1
–5 –4 –3 –2 –1
–4 –3 –2 –1 0 1
–1
2
3
4 x
f (x) =
1
x
3
4
1
0 1
–1
–2
–2
–3
–3
–4
–4
2
5 x
–5
y=f(x)=xn, n=3
y=f(x)=xn, n=–1
Benzer işlemler n = 2, 4, 6 için de izlendiğinde f: R → R, f(x) = xn fonksiyonunun grafiği n = 2, 4, 6 için şu şekilde elde edilecektir:
y
g(x) = x4
h(x) = x6
f(x) = x2
1
–1
0
1
Bu grafiklerde n değerleri bir pozitif çift tamsayı
olarak alınmıştır. Bu grafiklerde şu bilgileri gözlemleyebiliriz: y = xn nin grafiğinin kolları y-eksenine göre simetriktir. n değeri büyüdükçe –1 < x < 1
iken y = xn in grafiğinin kolları y–ekseninden
uzaklaşırken, x > 1 ve x < –1 iken fonksiyonun değerleri çok daha hızlı büyüdüğünden grafiğin
kolları y-eksenine yaklaşır.
x
Yine, benzer işlemler n = 3, 5, 7 için de izlendiğinde, f: R → R, f(x) = xn fonksiyonunun
grafiğinin n = 3, 5, 7 değerleri için şu şekilde olduğu görülecektir:
Ünite 3. Fonksiyonlar
531
Bölüm
3.2
Fonksiyonların Grafikleri
h(x) = x7
g(x) = x5
f(x) = x3
1
–1
1
Bu grafiklerde n değerleri bir pozitif tek tamsayı
olarak alınmıştır. Bu grafiklerde şu bilgileri gözlemleyebiliriz: y = xn in grafiğinin kolları orijine
göre simetriktir. n değeri büyüdükçe –1 < x < 1
iken y = xn in grafiğinin kolları y-ekseninden
uzaklaşırken, x > 1 ve x < –1 iken fonksiyonun değerleri çok daha hızlı büyüdüğünden grafiğin
kolları y-eksenine yaklaşır.
–1
En son yaptığımız işlemler n nin negatif değerleriyle tekrarlandığında elde edeceğimiz grafikleri görelim:
n = –2, –4, –6 için f: R −
{0}, R, f(x) = xn fonksiyonunun grafiğin bir negatif çift tamsayı olmak
üzere, y = xn in grafiğinin
kolları y-eksenine göre
simetriktir.
y
f (x) =
g (x) =
1
0
–1
h (x) =
1
x2
1
x4
1
x6
x
1
y
n = –3, –5, –7 için
f (x) =
g (x) =
1
–1
h (x) =
0
–1
532
Ünite 3. Fonksiyonlar
1
1
x3
1
x5
1
x7
x
f: R – {0} → R, f(x) = xn
fonksiyonunun grafiğin
bir negatif tek tamsayı
olmak üzere, y = xn in
grafiğinin kolları orijine
göre simetriktir.
f(x) = xn Biçimindeki Fonksiyonların Grafikleri
KENDİMİZİ SINAYALIM
1.
f, g, h, k: R → R, x → xn fonksiyonlarının grafikleri verilmiştir. Bu grafikleri benzerliklerine göre sınıflandırınız. Bu
sınıflandırmayı nasıl yaptığınızı açıklayınız.
9
8
7
6
5
4
3
2
1
y
9
8
7
6
5
4
3
2
1
y=f(x)
x
0
–6 –5 –4 –3 –2 –1
–1 1 2 3 4 5 6
–5 –4 –3 –2 –1
y
5
4
y=g(x)
3
2
2
3
4
y=k(x)
3
2
1
0 1
–1
y=h(x)
x
0
–6 –5 –4 –3 –2 –1
–1 1 2 3 4 5 6
y
5
4
y
5 x
–5 –4 –3 –2 –1
1
0 1
–1
–2
–2
–3
–3
–4
–4
–5
–5
2
3
4
5 x
Grafikleri verilen f, g ve h fonksiyonlarının kuralı x8 xn, n ∈ Z şeklindedir.
Buna göre, bu fonksiyonları, kurallarındaki n değerinin büyüklüğüne göre
sıralayınız.
2.
y
y = f(x)
y = g(x)
y = h(x)
1
–1
0
1
x
Ünite 3. Fonksiyonlar
533
f(x) = xn Biçimindeki Fonksiyonların Grafikleri
KENDİMİZİ SINAYALIM
3.
Gerçek sayılar kümesinde tanımlı f(x)=x fonksiyonu
için aşağıdaki soruları cevaplayınız.
5.
Gerçek sayılar kümesinde tanımlı h(x) = x3 fonksiyonları için aşağıdaki soruları cevaplayınız.
a.
f(–5), f(1), f(5) değerlerini bulunuz.
a.
h(–1), h(0), h(2) değerlerini bulunuz.
b.
f(a) = –4, f(b) = 9, f(c) = –1 eşitliklerini sağlayan a, b
ve c değerlerini bulunuz.
b.
h(a) = –8, h(b) = 1, h(c) = 27 eşitliklerini sağlayan a,
b ve c değerlerini bulunuz.
c.
f fonksiyonunun tanım kümesinin bir alt kümesi
olan [1, 4] kümesinin fonksiyon altındaki görüntüsünü bulunuz.
c.
h fonksiyonunun tanım kümesinin bir alt kümesi
olan [–2, 2] kümesinin fonksiyon altındaki görüntüsünü bulunuz.
ç.
f fonksiyonunun değer kümesinin bir alt kümesi
olan [–2, 6] kümesinin fonksiyon altındaki ters görüntüsünü bulunuz.
ç.
h fonksiyonunun değer kümesinin bir alt kümesi
olan [–1, 8] kümesinin fonksiyon altındaki ters görüntüsünü bulunuz.
4.
Gerçek sayılar kümesinde tanımlı g(x) = x2 fonksiyonu için aşağıdaki soruları cevaplayınız.
6.
a.
g(–2), g(0), g(2) değerlerini bulunuz.
b.
g(a) = –2, g(b) = 0, g(c) = 1 eşitliklerini sağlayan varsa a, b ve c değerlerini bulunuz.
c.
ç.
534
g fonksiyonunun tanım kümesinin bir alt kümesi
olan [-1, 4] kümesinin fonksiyon altındaki görüntüsünü bulunuz.
g fonksiyonunun değer kümesinin bir alt kümesi
olan [1, 9] kümesinin fonksiyon altındaki ters görüntüsünü bulunuz.
Ünite 3. Fonksiyonlar
a.
1
fonksiyonun;
x
f(–3), f(–1), f(1), f(3), f(4) değerlerini bulunuz.
f: R – {0} → R, f(x) =
b.
f(a) = 1, f(b) = 0 eşitliklerini sağlayan varsa a ve b
değerlerini bulunuz.
c.
f fonksiyonunun tanım kümesinin bir alt kümesi
olan [1,2] kümesinin fonksiyon altındaki görüntüsünü bulunuz.
ç.
f fonksiyonunun değer kümesinin bir alt kümesi
olan [-2, -1] kümesinin fonksiyon altındaki ters görüntüsünü bulunuz.
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında grafik çizme özelliği bulunan bir dinamik matematik/geometri
yazılımı yardımıyla doğrusal fonksiyonlarda bağımlı değişkenin değişim hızı ile fonksiyonun grafiği olan doğrunun eğimi arasındaki ilişkiyi inceleyeceğiz.
Araç ve Gereçler: Grafik çizme özelliği bulunan bir dinamik matematik/geometri yazılımı
Adım 1
g: R → R ve g(x) = 2x + n olmak üzere; n = −2, –1, 0, 1, 2
değerleri için g doğrusal fonksiyonunun grafiğini (aynı
kartezyen düzlemde) çiziniz. Grafiklerde nelerin değiştiğini nelerin sabit kaldığını inceleyiniz.
Adım 2
n ∈ R olmak üzere n’nin farklı değerleri için g = R → R
ve g(x) = 2x + n ile verilen fonksiyonun grafiğinin nasıl
değiştiğini açıklayınız.
Adım 6
f : R → R ve y = f(x)= mx +n fonksiyonu veriliyor. m
ve n sabitleri için birer değer seçerek (örneğin m = −2,
n = 1) bu fonksiyona ait bir değerler tablosu oluşturunuz. Örneğin,
x
y=f(x)
1
a
...
f(1)=?
f(a)=?
...
Oluşturduğunuz tablodaki değerleri kullanarak ardışık
iki y değeri farkının bunlara karşılık gelen x değerleri farf (a) - f (1)
kına oranını belirleyiniz. Örneğin,
a-1
Adım 3
h: R → R ve h(x) = mx + 1 olmak üzere; m = −2, −1, 0, 1,
2 değerleri için doğrusal bir fonksiyon olan h nin grafiğini (aynı kartezyen düzlemde) çiziniz. Grafiklerde nelerin
değiştiğini nelerin sabit kaldığını inceleyiniz.
Adım 4
Bulduğunuz oranlarla belirlediğiniz m değeri arasında
nasıl bir ilişki olduğunu açıklayınız.
Belirlediğiniz m değeri için farklı n değerleri alarak benzer oranlar oluşturunuz. Elde ettiğiniz oranlar ile m değeri arasındaki ilişkinin n değerlerinden nasıl etkilendiğini açıklayınız.
m ∈ R olmak üzere m’nin farklı değerleri için h : R → R
ve h(x) = mx + 1 ile verilen fonksiyonun grafiğinin nasıl
değiştiğini açıklayınız.
Adım 5
f: R → R ve y = f(x)= mx + n şeklindeki bir doğrusal fonksiyon için m ve n sabitlerini değiştirmenin fonksiyonun
grafiğine nasıl bir etki yaptığını açıklayınız.
Adım 7
f: R → R ve y = f(x) = mx +n fonksiyonunun grafiği ile
mx +n = 0 denkleminin çözüm kümesi arasında nasıl bir
ilişki olduğunu açıklayınız.
Ünite 3. Fonksiyonlar
535
Bölüm
3.2
Fonksiyonların Grafikleri
3.2.3. Doğrusal Fonksiyonlarla İlgili Uygulamalar
Neler Öğreneceğiz?
•
Ortalama değişim oranını (hızı)
•
Doğrusal fonksiyonlar ve değişim oranını (hızı)
Başlarken:
Günlük hayattaki birçok durumda iki
nicelik arasındaki ilişkiler bir doğrusal
fonksiyonla modellenebilir. Bu tür modeller, ilişkileri anlama, olayları analiz
etme ve tahminlerde bulunmada sıklıkla kullanılır.
Örneğin, bir GSM şirketinin STANDART
HAT abonelerinin aylık fatura tutarlarını
t dakika konuşma için;
Anahtar Terimler
•
Doğrusal fonksiyon
•
Değişim oranı (hızı)
•
Ortalama değişim oranı
(hızı)
•
Sabit değişim oranı (hızı)
F(t) = 5,95 + 0,16 . t
fonksiyonuna göre hesapladığını varsayalım. Bu fonksiyonun grafiği nasıl bir
grafiktir? Bu fonksiyonun tanım kümesi
nedir? Fonksiyonun kuralındaki 5,95 ne
anlama gelmektedir? Fonksiyonun kuralındaki 0,16 değerinin anlamı nedir?
Fatura tutarı 34,75 TL olan bir abone
kaç dakika konuşmuştur?
•
Sembol ve Gösterimler
f(x) = ax + b
Bu ve benzeri soruların cevaplarını
daha iyi verebilmek için doğrusal fonksiyonların grafiklerini daha detaylı inceleyip uygulamalarına yer vereceğiz.
536
Ünite 3. Fonksiyonlar
x
Tahmin
?
t
Doğrusal Fonksiyonlarla İlgili Uygulamalar
Değişim Oranı (Hızı)
Dünya Bankası Dünya Gelişim Göstergelerine göre
Türkiye ve Almanya’nın 2000 ve 2011 yıllarına ait nüfusları tabloda gösterilmektedir.
Yıllar
2000
2011
Almanya
82.211.508
81.797.673
Türkiye
63.627.862
73.639.596
Ülkeler
Kaynak: http://data.worldbank.org
Buna göre 2000-2011 yılları arasında her iki ülkenin nüfuslarındaki değişimi bularak
yorumlayalım.
2000’den 2011’e kadar geçen 11 yıllık süreçte Almanya’nın nüfusundaki değişim
81.797.673 – 82.211.508 = –413.835 kişi;
Türkiye’ninki ise 73.639.596 – 63.627.862 = 10.011.734 kişidir. Ancak bu bilgiler bize
nüfusun ne kadar hızlı bir şekilde arttığı veya azaldığını söylememektedir. Bu değerleri
2000 ve 2011 arasındaki zaman farkına bölerek yıllık bazda ortalama değişimi bulalım:
Almanya :
- 413 835
nüfustaki değişim
=
. - 37621 kişi/yıl
zamandaki değişim
11
Buna göre 2000-2011 yılları arasındaki 11 yıllık süreçte Almanya’nın nüfusu her yıl ortalama 37.621 kişi azalmıştır.
Türkiye:
10 011734
nüfustaki değ isim
ş
=
. 910158 kisi
ş /yıl
11
zamandaki de ğisim
ş
Buna göre 2000-2011 yılları arasındaki 11 yıllık süreçte Türkiye’nin nüfusu, yılda ortalama 910.158 kişi artmıştır.
Yukarıdaki örnekte iki değişken vardır; zaman ve nüfus. Buradaki ortalama değişme
oranı (hızı), nüfusun zamana bağlı olarak ne kadar bir hızla değiştiğini göstermektedir.
Her iki ülkenin verilerini nokta çiftleri olarak grafikle gösterip bu noktaları birer doğru
ile birleştirelim.
Ünite 3. Fonksiyonlar
537
Bölüm
3.2
Fonksiyonların Grafikleri
Nüfus (milyon kişi)
85
80
75
70
Almanya
Türkiye
65
60
1999
2001
2003
2007
2005
2009
2011
Zaman (yıl)
2000-2011 yılları arasında nüfus artışı veya azalışının ortalama olarak bu oranda (hızda)
olduğunu varsayarak, aradaki yıllar için nüfus miktarlarını yaklaşık olarak bulabiliriz.
Bunun için, ilgili doğruların denklemlerini (x yıl, y nüfus) kullanabiliriz. Ancak, 20002011 aralığının herhangi bir parçasında ve bu aralığın dışında kalan geçmiş veya gelecek yıllar için nüfus artış oranları bilinmediğinden yaptığımız varsayım bize doğru
sonuçlar vermeyebilir.
Anahtar Bilgi
Değişim oranı (hızı) veya ortalama değişim oranı (hızı) bir niceliğin değerindeki değişiminin başka bir nicelikteki değişime kıyasla ortalama ne kadar olacağını
gösteren bir orandır.
Doğrusal fonksiyonlarda değişim oranı (hızı) sabit olup,
fonksiyonun grafiği olan
doğrunun eğimine eşittir.
Diğer bir ifadeyle,
x bağımsız, y de x e bağımlı bir değişken olmak üzere, bu değişkenlere ait (x1, y1) ve
(x2, y2) değerleri verilsin. (x1, y1) değerlerinden (x2, y2) değerlerine geçişte yaşanan
y = f(x) = mx + b
fonksiyonu için değişim
oranı (hızı) m değeridir.
değişim oranı (hızı) =
y değerlerindeki değişim y2 − y1
=
,
x değerlerindeki değişim x2 − x1
şeklinde ifade edilir.
y
y = f(x)
y2
y1
0
538
Ünite 3. Fonksiyonlar
(x2, y2)
(x1, y1)
x1
x2
x
(x1 ≠ x2)
Doğrusal Fonksiyonlarla İlgili Uygulamalar
Bir doğru üzerinde alınacak herhangi iki nokta çifti için değişim oranı aynı olacaktır.
Bu nedenle, hatırlayacağınız gibi bir doğrunun eğimi, doğru üzerindeki herhangi iki
nokta arasındaki dikey değişimin yatay değişime oranı olarak tanımlanmaktaydı. Dikkat edilirse yukarıda tanımladığımız (x1, y1) değerlerinden (x2, y2) değerlerine geçişte
yaşanan (ortalama) değişim oranı (hızı) ile (x1, y1) ve (x2, y2) ile belirtilen noktalardan
geçen doğrunun eğimi aynı değerdir.
y = f(x) = mx + b şeklindeki bir doğrusal fonksiyonun değişim oranı (hızı), bu fonksiyonun grafiği üzerinden alınacak herhangi iki nokta çifti için olan değişim oranıdır, yani
bu fonksiyonun grafiği olan doğrunun eğimidir. Şimdi bununla ilgili bir örnek verelim.
1
Gerçek sayılarda tanımlı f(x) = x + 1, g(x) = –2x + 1, h(x) = 3x – 2 ve k(x) = x – 3 fonksiyonlarının değişim oranlarını (hızını) bularak yorumlayalım.
Verilen fonksiyonların değişim oranlarını (hızını) bulmak için öncelikle bu fonksiyonların bazı gerçek sayılarda aldığı değerleri bulalım. Örneğin, f, g, h ve k fonksiyonlarının
x = -5, -1, 0, 2, 3, 7 için aldığı değerler aşağıda verilen tablolardaki gibidir. Bu tablolarda
ardışık sıradaki iki x değeri farkı, x değerindeki değişimi; bunlara karşılık gelen y değerleri farkı da fonksiyonun değerindeki değişimi göstermektedir. Bu iki farkın oranı
ise fonksiyonun değişim oranını (hızını) göstermektedir.
x
f(x)
–5
–4
–1
0
2
3
7
0
1
3
4
8
x değerindeki
değişim
(x2 – x1)
f(x) değerindeki
değişim
f(x2) – f(x1)
Değişim oranı (hızı)
f(x2) – f(x1)
__________
x2 – x1
–1 – (-5) = 4
0 – (–1) = 1
2–0=2
3–2=1
7–3=4
0–(–4) = 4
1–0=1
3–1=2
4–3=1
8–4=4
4/4 = 1
1/1 = 1
2/2 = 1
1/1 = 1
4/4 = 1
Ünite 3. Fonksiyonlar
539
Bölüm
3.2
Fonksiyonların Grafikleri
x değerindeki
değişim
(x2 – x1)
g(x) değerindeki değişim
g(x2) – g(x1)
Değişim oranı (hızı)
g(x2) – g(x1)
__________
x2 – x1
3
1
–3
–5
–13
–1 – (–5) = 4
0 – (–1) = 1
2–0=2
3–2=1
7–3=4
3 – 11 = –8
1 – 3 = –2
–3 – 1 = –4
–5 – (–3) = –2
–13 – (–5) = –8
–8/4 = –2
–2/1 = –2
–4/2 = –2
–2/1 = –2
–8/4 = –2
x
h(x)
-5
-17
x değerindeki
değişim
(x2 – x1)
h(x) değerindeki değişim
h(x2) – h(x1)
Değişim oranı (hızı)
h(x2) – h(x1)
__________
x2 – x1
–1
0
2
3
7
–5
–2
4
7
19
–1 – (–5) = 4
0 – (–1) = 1
2–0=2
3–2=1
7–3=4
–5 – (–17) = 12
–2 – (–5) = 3
4 – (–2) = 6
7–4=3
19 – 7 = 12
12/4 = 3
3/1 = 3
6/2 = 3
3/1 = 3
12/4 = 3
x
k(x)
–5
–8
x değerindeki
değişim
(x2 – x1)
k(x) değerindeki
değişim
k(x2) – k(x1)
Değişim oranı (hızı)
k(x2) – k(x1)
__________
x2 – x1
–1
0
2
3
7
–4
–3
–1
0
4
–1 – (–5) = 4
0 – (–1) = 1
2–0=2
3–2=1
7–3=4
–4 – (–8) = 4
–3 – (–4) = 1
–1 – (–3) = 2
0 – (–1) = 1
4–0=4
4/4 = 1
1/1 = 1
2/2 = 1
1/1 = 1
4/4 = 1
x
g(x)
–5
11
–1
0
2
3
7
f(x) = x + 1, g(x) = –2x + 1, h(x) = 3x – 2 ve k(x) = x – 3 fonksiyonları için bu fonksiyonların değişim oranları (hızı) sabit değerler olup sırasıyla 1, –2, 3 ve 1 dir. Tablolarda değişimler ardışık iki x değeri ve fonksiyonun bunlara karşılık gelen ardışık değerleri için
hesaplanmıştır. Ancak, ardışık olmayan (herhangi iki) x değeri ve fonksiyonun bunlara
karşılık gelen değerleri için de hesaplansaydı değişen bir şey olmazdı. Örneğin x = –5
ve x = 3 için f(–5) = –4 ve f(3) = 4 olduğundan, f fonksiyonu için değişim oranı (hızı)
f (3) - f (- 5)
4 - (- 4)
8
=
= = 1 olarak bulunur.
3 - (- 5)
3+5
8
Dikkat edilirse bu doğrusal fonksiyonların değişim oranları (hızı) grafikleri birer doğru
olan bu fonksiyonların eğimidir. Bu durumu fonksiyonların grafikleri üzerinde de gözlemleyebiliriz.
540
Ünite 3. Fonksiyonlar
Doğrusal Fonksiyonlarla İlgili Uygulamalar
y
g
6
5
h
4
f
3
2
k
1
–4
–3
–2
–1
x
1
2
3
4
5
6
–1
–2
–3
–4
–5
Görüldüğü gibi kuralları farklı olan f ve k fonksiyonlarının değişim oranları (hızları) aynıdır. Bu durum, her iki fonksiyonun grafiklerinin birbirine paralel yani eğimleri aynı olan
iki doğru olmasından da açıkça görülmektedir.
Eğimin değerinin pozitif veya negatif olması değişim oranının yönünü göstermektedir. Pozitif eğim değerleri değişimin artış; negatif eğim değerleri de değişimin azalış (düşüş) şeklinde olduğunu göstermektedir. Eğimin mutlak değeri arttıkça/azaldıkça değişim oranı (hızı) da artacak/azalacaktır.
Örnekler üzerinde gözlemlediklerimizin herhangi bir doğrusal fonksiyon için de geçerli olduğunu gösterelim.
2
m ve n birer gerçek sayı ve m ≠ 0 olmak üzere, f fonksiyonu f(x) = mx + n ile verilen bir
doğrusal fonksiyon olsun. Bu fonksiyonun değişim oranının (hızının) sabit olduğunu
gösterelim.
Ünite 3. Fonksiyonlar
541
Bölüm
3.2
Fonksiyonların Grafikleri
Anahtar Bilgi
Verilen f fonksiyonunun grafiği üzerinde yer alan iki farklı nokta alalım. Bu noktaların
koordinatları (x1, y1) ve (x2, y2) olsun. Noktalar farklı olduğundan x1 ≠ x2 olacağına
dikkat edelim. Bu durumda y1 = f(x1) ve y2 = f(x2) olacaktır. Diğer taraftan f(x1) = mx1 + n
ve f(x2) = mx2 + n dir. Bu durumda (x1, y1) değerlerinden (x2, y2) değerlerine geçişte
yaşanan
Bir doğrusal fonksiyonda
mutlak değerce büyük eğim
daha büyük bir değişim oranı
(hızı) demektir. Eğimin pozitif
bir sayı olması artışı, negatif
bir sayı olması azalmayı
(düşüşü) gösterir.
Değişim oranı =
=
y2 - y1
x2 - x1
f (x 2 ) - f (x 1 )
x2 - x1
=
mx 2 + n - ^mx 1 + nh
x2 - x1
=
m (x 2 - x 1 )
x2 - x1
= m olur.
Bulduğumuz sonuç x1, x2, y1 ve y2 değerlerinden herhangi birini içermemektedir. Dolayısıyla, f doğrusal fonksiyonunun grafiği üzerindeki herhangi iki nokta için elde edeceğimiz değişim oranı aynı olacaktır. Diğer taraftan, bu değişim oranı fonksiyonun grafiği
olan doğrunun eğimidir. Bu nedenle yaptıklarımız, f: R → R ve f(x) = mx + n ile verilen
fonksiyonun grafiği olan doğrunun eğiminin m değeri olduğunu göstermektedir.
3
Aşağıdaki tabloda bazı değerleri verilen f ve g fonksiyonlarından hangisinin bir doğrusal fonksiyon olabileceğini inceleyelim.
542
x
y = f(x)
x
y = g(x)
–3
0
4
7
15
50
6
3
–1
–4
–12
–47
–7
–1
0
2
3
5
36
–12
–13
–9
–4
12
Ünite 3. Fonksiyonlar
Doğrusal Fonksiyonlarla İlgili Uygulamalar
f ve g fonksiyonlarında ardışık x ve y değerlerindeki değişim ve bunların oranlarını inceleyelim.
x
f(x)
-3
0
4
7
15
50
6
3
–1
–4
–12
–47
x
gx)
–7
–1
0
2
3
5
36
–12
–13
–9
–4
12
x değerindeki
değişim
(x2 – x1)
f(x) değerindeki
değişim
f(x2) – f(x1)
Değişim oranı (hızı)
f(x2) – f(x1)
__________
x2 – x1
0 – (–3) = 3
4–0=4
7–4=3
15 – 7 = 8
50 – 15 = 35
3 – 6 = –3
–1 – 3 = –4
–4 – (–1) = –3
–12 – (–4) = –8
–47 – (–12) = –35
–3/3 = –1
–4/4 = –1
–3/3 = –1
–8/8 = –1
–35/35 = –1
x değerindeki
değişim
(x2 – x1)
g(x) değerindeki
değişim
g(x2) – g(x1)
Değişim oranı (hızı)
g(x2) – g(x1)
__________
x2 – x1
–1 – (–7) = 6
0 – (–1) = 1
2–0=2
3–2=1
5–3=2
–12 – 36 = –48
–13 – (–12) = –1
–9 – (–13) = 4
–4 – (–9) = 5
12 – (–4) = 16
–48/6 = –8
–1/1 = –1
4/2 = 2
5/1 = 5
16/2 = 8
Görüldüğü gibi f fonksiyonu için değişim oranı (hızı) sabit iken, g fonksiyonu için sabit
bir değişim oranından (hızından) bahsetmek mümkün değildir. Bu durumda f fonksiyonu bir doğrusal fonksiyon olabilir ancak g fonksiyonu bir doğrusal fonksiyon olamaz.
f fonksiyonunun bir doğrusal fonksiyon olduğunu düşünelim. Bu durumda, bu fonksiyon y = f(x) = mx + b şeklindedir. Değişim oranı (hızı) bu fonksiyonun eğimi olacağından
m = –1 olmalıdır. Bu durumda y = f(x) = –x + b yazılabilir. Verilen (x, f(x)) değer çiftlerinden herhangi biri fonksiyonun kuralını sağlamalıdır. Bu durumda, örneğin (0, 3) için
3 = –1 · 0 + b
3=b
bulunur. O halde f fonksiyonunun kuralı y = f(x) = –x + 3 olmalıdır.
Ünite 3. Fonksiyonlar
543
Fonksiyonların Grafikleri
4
Verilen ifadelerdeki bağımlı ve bağımsız değişkenleri belirleyerek verilen durumdaki
değişim oranını yorumlayalım ve grafiksel olarak gösterelim. Bunu aşağıdaki her bir şık
için ayrı ayrı yapalım.
Bir otomobilin şehir içi ortalama yakıt tüketimi 11,2 km/L dir.
b.
y tüketilen yakıt miktarını (litre) ve x alınan yolu (km) göstermek üzere y = 0,18x
c.
M fatura tutarı (TL) ve t konuşma süresini (dk) göstermek üzere M = 0,3t + 7
a.
Tüketilen yakıt miktarı bağımsız değişken, gidilen yol bağımlı değişkendir. Değişim oranı (hızı) 11,2 km/L dir. Bunun anlamı tüketilen her 1 litre yakıtla 11,2 km yol
gidilebileceğidir.
Gidilen toplam yol (km)
a.
100
90
80
70
60
50
40
30
20
10
0
1
2
3
4
5
6
7
8
9
Harcanan yakıt (litre)
b.
Alınan yol (x km) bağımsız değişken, tüketilen benzin (y litre) bağımlı değişkendir.
Değişim oranı (hızı) 0,18’dir. Bu ise girdi değerindeki 1 birimlik artışın çıktı değerinde 0,18 birimlik artışa neden olacağı anlamına gelir. Diğer bir deyişle gidilen her
km yol için 0,18 litre benzin tüketilmesi gerektiği anlamına gelmektedir.
1.6
Harcanan yakıt (litre)
Bölüm
3.2
1.4
1.2
1.0
0.8
0.6
0.4
0.2
0
2
4
6
Gidilen toplam yol (km)
544
Ünite 3. Fonksiyonlar
8
10
c.
Konuşma süresi (t dk) bağımsız değişken, fatura tutarı (M TL) bağımlı değişkendir.
Değişim oranı 0,3’tür. Bu ise girdi değerindeki 1 birimlik artışın, çıktı değerinde 0,3
birim artışa neden olacağı anlamına gelir. Diğer bir deyişle her 1 dakika konuşma,
fatura tutarında 0,3 TL artışa neden olacaktır.
Toplam fatura tutarı (TL)
Doğrusal Fonksiyonlarla İlgili Uygulamalar
10
9
8
7
6
5
4
3
2
1
0
2
6
4
8
10
Konuşma süresi (dk)
5
Aşağıda A, B, C ve D koşucularının konum-zaman grafiği verilmiştir. Buna göre koşucuların
konumlarının zamana bağlı değişimini bularak
yorumlayalım.
y Konum (km)
A
20
B
C
D
16
12
8
4
0
1
2
3
4
5
x Zaman (sa)
Ünite 3. Fonksiyonlar
545
Bölüm
3.2
Fonksiyonların Grafikleri
Koşucuların konumlarının zamana bağlı değişim oranı (hızı) koşucuların hızlarıyla (km/
sa) ilişkilidir. Zamana bağlı konumlar birer doğru ile gösterildiğinden koşucuların konumlarının zamana bağlı değişim oranı (hızı) bu doğruların eğimi olacaktır. Buna göre
A koşucusuna ait doğrunun eğimi,
20 - 0
mA =
= 10 km/sa
2-0
B koşucusuna ait doğrunun eğimi,
20 - 8
mB =
= 4 km/sa
3-0
C koşucusuna ait doğrunun eğimi,
12 - 0
mC =
= 6 km/sa
3-1
D koşucusuna ait doğrunun eğimi,
16 - 4
mD =
= 2, 4 km/sa bulunur.
5-0
Bu durumda koşucuların en hızlıdan yavaşa doğru sıralaması A, C, B, D biçiminde olur.
6
Bir firmanın zamana (x yıl) bağlı gelir (milyon TL) fonksiyonu f, gider fonksiyonu g dir.
f(x)= 12 – 2x ve g(x) = x + 3, 0 ≤ x ≤ 6
verildiğine göre aşağıda istenenleri yapalım.
546
a.
f ve g fonksiyonlarının grafiklerini aynı koordinat düzleminde çiziniz.
b.
Gelir ve giderin eşit olduğu zamanı ve eşitlik anındaki miktarını bulunuz.
c.
Kâr edilen ve zarar edilen bölgeleri ve en büyük kârı belirleyiniz.
Ünite 3. Fonksiyonlar
Doğrusal Fonksiyonlarla İlgili Uygulamalar
a.
Grafikte f ve g fonksiyonlarının sadece [0,6] aralığında çizildiğine dikkat ediniz.
y
12
11
f(x) = 12 – 2x
10
9
8
g(x) = x + 3
7
6
5
4
3
2
1
x
1
b.
2
3
4
5
6
7
8
Gelir ve giderin eşit olduğu x değeri grafikte de görüldüğü gibi iki doğrunun kesim noktası olan (3, 6) noktasıdır. Bunu cebirsel olarak da bulabiliriz. İki denklemin
eşit olduğu noktayı bulmak için denklemleri birlikte çözelim.
f(x) = g(x)
12 – 2x = x +3
x = 3 bulunur.
x = 3 için gider fonksiyonunun (g nin) değeri y = x + 3 ⇒ y = 3+3 = 6 dır. Diğer bir deyişle gelir ve gider 3. yılda eşit olup 6 milyon TL’dir.
c.
Kâr edilen bölgeler, gelirin (f değerlerinin) giderden (g değerlerinden) daha fazla
olduğu bölgelerdir. f fonksiyonu [0, 3] arasında azalarak 12 den 6 ya düşmüştür. Bu
noktadan sonra f fonksiyonunun aldığı değerler g fonksiyonunkilerden daha küçüktür. O halde kâr edilen bölge [0, 3] aralığı zarar edilen bölge ise [3, 6] aralığıdır.
Şirketin kârı x = 0 değerinden itibaren hep azalmakta ve x = 3 değerinden sonra zarara
dönüşmektedir. Bu durumda en büyük kâr x = 0 noktasında olur.
f(0) – g(0) = 12 – 3 = 9 milyon TL
Ünite 3. Fonksiyonlar
547
Doğrusal Fonksiyonlarla İlgili Uygulamalar
KENDİMİZİ SINAYALIM
1.
3.
Aşağıda gerçek sayılarda tanımlı f(x) = ax + 8 fonksiyonun grafiği verilmiştir. Buna göre a kaçtır?
y
Aşağıda grafikleri verilen doğruların eğimlerini
bulunuz.
a.
y
y
f(x) = ax + 8
y=x+2
2
4
3
–2
x
4
y = –—x + 4
3
x
–2
x
b.
y
2
y
y=x+2
4
3
–2
x
4
y = –—x + 4
3
x
2.
Aşağıda denklemleri verilen doğruların eğimlerini
bulunuz:
a.
y = 2x – 1
b.
ç.
x=3
d.
x
+1
3
y=1
y=
c.
c.
2x − 3y = 6
y
x = –3
0
x
–3
–4
ç.
y
0
x = –3
548
Ünite 3. Fonksiyonlar
y = –4
y
x
–3
–4
y = –4
y
0
x
0
x
Doğrusal Fonksiyonlarla İlgili Uygulamalar
KENDİMİZİ SINAYALIM
4.
Şekilde grafikleri verilen f, g, h, p, q fonksiyonlarının değişim oranlarını (hızlarını) küçükten
büyüğe doğru sıralayınız.
6.
Yükseklik (metre)
y = h(x)
10
1000
y = f(x)
8
900
6
y = p(x)
–10 –8
–6
–4
4
800
y = q(x)
2
–2
(0, 900)
(30, 600)
550
2
4
6
8
10
–2
0
–6
5
10
15
20
25
30
35
t
Zaman (saniye)
–4
Paraşütle atlayan bir kişinin düşme hızı 900 metre
yükseğe geldiğinde sabitleniyor. Bu andan sonraki
30. saniyede yerden yüksekliği 600 metre olduğuna göre;
y = g(x)
–8
–10
5.
Aşağıdaki doğrusal fonksiyonların hangisinin değişim oranı (hızı) en büyüktür?
a.
f(x) = x – 4
b.
c.
h(x) = 2x+4
ç.
d.
t(x) = -x + 4
a.
Yükseklikteki ortalama değişim oranını (hızını) bularak yorumlayınız.
b.
Bu kişinin 900. metreden itibaren, zamana bağlı yükseklik değişimini bir fonksiyon olarak ifade ediniz.
c.
b şıkkında bulduğunuz fonksiyonun grafiğinin eğimi kaçtır?
ç.
Bu kişi 900 metre yükseklikte olduğu andan kaç saniye sonra yere ulaşır?
g(x) = -3x-4
2
k(x) = x + 2
3
Ünite 3. Fonksiyonlar
549
Doğrusal Fonksiyonlarla İlgili Uygulamalar
KENDİMİZİ SINAYALIM
7.
Bilgisayar üreten bir firmanın günlük giderini
üretilen bilgisayar sayısına bağlı bir fonksiyon
olarak düşünelim. Bu fonksiyonun bir doğrusal
fonksiyon olduğunu varsayalım. Firmanın, günlük
2000 TL sabit gideri varsa ve bir günde 10 bilgisayar üretirse, o günkü toplam gideri 11.000 TL
oluyor. Firmanın günde x adet bilgisayar üretmesi
durumunda günlük toplam giderini g(x) ile
gösterelim. Buna göre;
a.
g fonksiyonunu bulunuz.
b.
Günde 15 bilgisayar üretilmesi durumunda toplam
gider nedir?
c.
0 ≤ x ≤ 10 için gider fonksiyonunun grafiğini çiziniz.
550
Ünite 3. Fonksiyonlar
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
3.2.4. y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
Neler Öğreneceğiz?
•
Bir fonksiyonun sıfırı
•
Fonksiyonların grafiklerinin
kesişim noktalarının cebirsel ve
geometrik yorumu
Başlarken
Alışageldiğimiz yollardan çözümüne ulaşmakta zorluk çektiğimiz birçok problemi farklı
zemin ve koşullarda ele almamız, problem
hakkında yeni bilgilere ulaşmamıza imkan
verebilir. Örneğin, görülebilir ışığın yanında
diğer ışınları da algılayabilen teleskoplar yardımıyla birçok keşifler yapılmaktadır. İlk resimdeki nebula bunlardan biridir. Benzer şekilde,
ısıya duyarlı kameralar kullanırsak çıplak gözle
algılayamadığımız birçok şeyi karanlıkta bile
olsa fark edebiliyoruz.
Matematiksel birçok problemin çözümünde,
problemi farklı tarzlarda ifade ederek veya
problemin denk olduğu problemleri tespit
ederek matematiğin farklı alanlarına ait bilgi,
yöntem ve tekniklerden faydalanırız. Bu nedenle, konular arasında geçiş yapmamıza imkan veren yaklaşımlar çok önemlidir.
Cebire ait bir konu olarak sunmaya başladığımız fonksiyonların kartezyen düzlemde
(koordinat sisteminde) grafiklerini çizmekle,
fonksiyonlarla ilgili problem çözümlerinde
geometrik bilgi ve yöntemlerimizi kullanma
imkanına kavuşuyoruz. Bunun bir örneği olarak, bu kısımda denklem ve denklem sistemlerinin çözümlerinde fonksiyon grafiklerinin
ve grafiklerin birbirleriyle kesişmelerinin nasıl
kullanılabileceğini öğreneceğiz.
Anahtar Terimler
Rosette Nebula (Chadwell 49)
•
Bir denklemin kökü
•
Bir fonksiyonun sıfırı
Sembol ve Gösterimler
Hareket halindeki bir grup arabanın
termal kamera altındaki görüntüsü
y = f(x) fonksiyonu, bir şirketin zamana (x) bağlı olarak mali durumunu (y) göstersin. Bu
fonksiyonun grafiğinde
a.
grafiğin x ekseninin üzerinde olduğu yerler şirketin kâr ettiği zamanları
b.
grafiğin x ekseninin altında olduğu yerler şirketin zarar ettiği zamanları
c.
grafiğin x eksenini kestiği yerler ise şirketin ne kâr ne de zarar ettiği zamanlarıgöstermektedir.
Çünkü, bu durumda
Ünite 3. Fonksiyonlar
551
•
y = f(x)
•
y = f(x) = 0
Bölüm
3.2
Fonksiyonların Grafikleri
Anahtar Bilgi
y = f(x) fonksiyonunun
grafiği için;
•
x ekseninin altında kalan
kısımda f(x) < 0
•
x ekseninin yukarısında
kalan kısımda f(x) > 0
•
x ekseni üzerinde kalan
kısımda ise f(x) = 0 olur.
-
y değeri pozitif ise şirket kâr etmektedir.
-
y değeri negatif ise şirket zarar etmektedir.
-
y değeri sıfır ise şirket ne kâr ne de zarar etmektedir.
Burada şirketin ne kâr ne de zararda olduğunu temsil eden y=f(x)=0 değeri fonksiyonun grafiksel gösteriminde grafiğin x eksenini kestiği noktadır.
Bu kısımda, herhangi bir y = f(x) fonksiyonunun grafiğiyle f(x)=0 denklemi arasındaki
ilişkiyi ele alacağız. Böylece bu ilişkiyi kullanarak denklem çözümlerinde grafik yorumlamalarından yararlanacağız.
Fonksiyonların Sıfırları
Bir denklemin çözümü olan denklemin kökleri, denklemi sağlayan (doğrulayan) değerlerdir.
5
Örneğin, 2x – 5 = 0 gibi bir doğrusal denklemde x yerine değerini yazdığımızda bu
2
5
değerin denklemi sağladığı görebiliriz. Bu nedenle
değeri denklemin bir köküdür.
2
Gerçekten de bu denklemin kökünü
2x – 5 = 0
2x = 5
5
x=
2
şeklinde bulabiliriz. Şimdi y = 2x – 5 eşitliğini iki bilinmeyenli doğrusal bir denklem
olarak ele alalım. Dikkat edersek bu denklemde y değerini 0 alırsak ilk denklemimiz
olan 0 = 2x – 5 i elde ediyoruz.
Anahtar Bilgi
Bir denklemin kökü, denklemi sağlayan (doğrulayan)
değerlerdir.
Diğer taraftan x ve y bilinmeyenlerini bağımlı ve bağımsız değişkenler olarak ele aldığımızda y = 2x – 5 eşitliği f(x) = 2x – 5 doğrusal fonksiyonuyla yakından ilişkili olmaktadır.
Şöyle ki, y = 2x – 5 denklemini sağlayan (x, y) şeklindeki ikililer, f(x) = 2x – 5 doğrusal
fonksiyonunun grafiği üzerindeki noktaların koordinatlarıdır.
Şimdi şu soruyu düşünelim: 2x – 5 = 0 denkleminin kökü ile f(x) = 2x – 5 doğrusal fonksiyonunun grafiği arasında nasıl bir ilişki vardır?
Hatırlayacağımız gibi koordinatları (x, 0) şeklinde olan bir nokta x ekseni üzerindedir ve
x ekseni üzerindeki herhangi bir noktanın da koordinatları (x,0) şeklindedir. Bu nedenle, koordinatları (x, 0) şeklinde olan bütün noktalar, x eksenini verecektir.
Dikkat edilirse koordinatları (x, 0) olan noktalar, y = 0 denkleminin iki bilinmeyenli
(x ve y bilinmeyenleri) bir denklem olarak ele alındığındaki çözümlerine karşılık gelmektedir. Dolayısıyla x ekseni, y = 0 doğrusal denklemiyle ifade edilebilir.
552
Ünite 3. Fonksiyonlar
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
Benzer şekilde (gerekçelerini açıklayınız), y ekseni, x = 0 doğrusal denklemiyle ifade
edilebilir.
Anahtar Bilgi
Şimdi, 2x – 5 = 0 denkleminin kökü ile f(x) = 2x – 5 doğrusal fonksiyonunun grafiği arasında nasıl bir ilişki olduğunu bu bilgiler ışığında bulmaya çalışalım.
a ∈ R için f(a) = 0 oluyorsa
a sayısına f fonksiyonunun
sıfırı denir.
2x – 5 = 0 denkleminin kökü, f(x) = 0 eşitliğini sağlayan x değeridir. f(x) = 0 eşitliğini
sağlayan x değeri ise f fonksiyonunun grafiği üzerinde olup ordinatı 0 olan noktanın
apsisidir. Bu nokta ise y = f(x) fonksiyonunun grafiği ile x ekseninin kesiştiği noktadır.
Dolayısıyla aradığımız ilişkiyi kısaca şu şekilde belirtebiliriz: 2x – 5 = 0 denkleminin
kökü, f(x)=2x – 5 doğrusal fonksiyonuna ait grafiğin x eksenini kestiği yerdir. Şimdi
f(x) = 2x – 5 fonksiyonunun grafiğini inceleyelim.
3
Görüldüğü gibi grafiğin x-eksenini kestiği nokta
y = f(x) = 2x –5
2x – 5 = 0 denkleminin çözüm kümesi (kökü) olan
5
2,5 yani dir.
2
Bu örnekte gözlemlediğimiz durum genelde de
geçerlidir. Şöyle ki, herhangi bir denklemin kökünü
ilişkili fonksiyonun grafiğini kullanarak da bulabiliriz.
2
1
–2 –1
–1
1
2
3
4
5
–2
–3
a ∈ R için f(a) = 0 oluyorsa a sayısına f fonksiyonunun sıfırı denir. Diğer bir
ifadeyle, bir f fonksiyonun sıfırları f(x) = 0 denkleminin kökleridir. Bu durumda f
fonksiyonun sıfırları fonksiyonun grafiğinin x-eksenini kestiği noktalardır.
Örneğin, mx + n = 0 doğrusal denkleminin kökü f(x) = mx + n doğrusal fonksiyonunun
sıfırıdır.
1
Aşağıda grafikleri verilen fonksiyonların sıfırlarını bulalım.
a.
b.
3
2
y = g(x)
1
–4 –3 –2 –1
–1
y = f(x)
–2
–3
4
3
2
1
2
1
–4 –3 –2 –1
–1
1
2
–2
Ünite 3. Fonksiyonlar
553
Bölüm
3.2
Fonksiyonların Grafikleri
c.
Anahtar Bilgi
d.
2
y = h(x)
Bir f fonksiyonunun grafiği
y = f(x) denkleminin
grafiğidir. Grafiğin (varsa),
x-eksenini kestiği noktalar
f(x) = 0 denkleminin gerçek
sayılardaki çözüm kümesidir. Grafik x-eksenini hiçbir
noktada kesmiyorsa f(x) = 0
denkleminin gerçek sayılarda
çözüm kümesi boş kümedir.
y = k(x)
1
–2
–1
–1
2
1
–2
2
1
–1
–1
1
2
–2
a.
f fonksiyonunun grafiği x-eksenini (–3, 0) noktasında kestiği için x = –3 değeri
f fonksiyonunun sıfırıdır. Diğer bir ifadeyle f(x) = 0 denkleminin çözüm kümesi
{–3} 'tür.
b.
g fonksiyonunun grafiği x-eksenini (–3, 0) ve (1, 0) noktalarında kestiği için x = –3
ve x = 1 değerleri g fonksiyonunun sıfırlarıdır. Diğer bir ifadeyle g(x) = 0 denkleminin çözüm kümesi {–3, 1} dir.
1
h fonksiyonunun grafiği x-eksenini (–2, 0), (–1, 0), (0, 0), ( , 0) ve (1, 0) noktala2
1
rında kestiği için x = –2, –1, 0, , 1 değerleri h fonksiyonunun sıfırlarıdır. Diğer
2
1
bir ifadeyle h(x) = 0 denkleminin çözüm kümesi {–2, –1, 0 , 1} dir.
2
k fonksiyonunun grafiği x-eksenini (-1, 0), (0, 0) ve (1, 0) noktalarında kestiği için
x = –1, 0, 1 değerleri k fonksiyonunun sıfırlarıdır. Diğer bir ifadeyle k(x) = 0 denkleminin çözüm kümesi {–1, 0, 1} dir.
c.
ç.
Bir f fonksiyonun sıfırları için kullandığımız akıl yürütmeyi genişleterek
f(x) = a (a ∈ R ) denkleminin çözüm kümesini f fonksiyonun grafiği üzerinden
bulabiliriz. Şöyle ki,
f(x) = a
denkleminin çözüm kümesi
y = f(x)
y=a
denklem sistemini sağlayan x değerleridir. Diğer bir ifadeyle,
f(x) = a
denkleminin çözüm kümesi f fonksiyonunun grafiği ile y eksenini a da kesen
yatay doğrunun kesiştiği noktanın apsisidir.
554
Ünite 3. Fonksiyonlar
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
Örneğin aşağıda grafiği verilen f fonksiyonu için f(x) = 3 denkleminin çözüm kümesi y = f(x) fonksiyonun grafiğinin y = 3 doğrusu ile kesişiminin apsisi olacaktır.
5
5
4
y = f(x)
–4 –3 –2
4
y = f(x)
3
3
2
2
1
1
–1
1
2
–4 –3 –2
–2
–1
1
2
–2
Bu durumda f(x) = 3 denkleminin çözüm kümesi {–4} tür.
2
g fonksiyonunun grafiği yanda verilmiştir. Buna göre
g(x) = 3 denkleminin çözüm kümesini bulalım.
4
g
3
2
1
–4 –3 –2 –1
–1
1
2
–2
(–2,3)
g
4
3
g fonksiyonun grafiği ile y = 3 doğrusunun kesişimi
(–2, 3) ve (0, 3) noktalarıdır. Dolayısıyla g(x) = 3 denkleminin çözümü x ∈ {–2, 0} dir.
(0,3)
2
1
–4 –3 –2 –1
–1
1
2
–2
Ünite 3. Fonksiyonlar
555
Bölüm
3.2
Fonksiyonların Grafikleri
3
Bir firmanın zamana (x yıl) bağlı gelir (milyon TL) fonksiyonu f, gider fonksiyonu g dir.
0 ≤ x ≤ 6 için f(x)= 12 – 2x ve g(x) = x + 3 olarak verildiğine göre aşağıda istenenleri
yapalım.
a.
f ve g fonksiyonlarının grafiklerini aynı koordinat düzleminde çizelim.
b.
Gelir ve giderin eşit olduğu zamanı ve bu andaki geliri bulalım.
c.
Kâr edilen ve zarar edilen bölgeler ile en büyük kârı belirleyelim.
a.
Grafikte f ve g fonksiyonlarının sadece [0,6]
aralığında çizildiğine dikkat ediniz.
y
12
f(x) = 12 – 2x
g(x) = x + 3
3
1 2 3 4 5 6 7 8
b.
x
Gelir ve giderin eşit olduğu x değeri grafikte de görüldüğü gibi iki doğrunun
kesim noktası olan (3, 6) noktasıdır. Bunu cebirsel olarak da bulabiliriz. İki denklemin eşit olduğu noktayı bulmak için denklemleri birlikte çözelim.
f(x) = g(x) ⇒ 12 – 2x = x + 3
⇒ x=3
bulunur. x = 3 için gider fonksiyonunun değeri g(3) = 3 + 3 = 6 dır. Böylelikle
gelir ve gider 3. yılda eşit olup 6 milyon TL’dir.
c.
Kâr edilen bölgeler, gelirin (f değerlerinin) giderden (g değerlerinden) daha fazla
olduğu bölgelerdir. f fonksiyonu [0, 3) arasında azalarak 12 den 6 ya düşmüştür.
Bu noktadan sonra f fonksiyonunun aldığı değerler g fonksiyonunkilerden daha
küçüktür. O halde kâr edilen bölge [0, 3) aralığı zarar edilen bölge ise (3, 6] aralığıdır.
Şirketin kârı x = 0 değerinden itibaren hep azalmakta ve x = 3 değerinden sonra
durum zarara dönüşmektedir. Bu nedenle, en büyük kâr x = 0 noktasında
f(0) – g(0) = 12 – 3 = 9 milyon TL olur.
556
Ünite 3. Fonksiyonlar
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
4
Gerçek sayılar kümesinde tanımlı f fonksiyonunun grafiği verilmiştir. Buna göre f(x)=0
denkleminin kökleri toplamını bulalım.
y
4
3
2
y = f(x)
1
–4 –3 –2 –1
–1
1
2
3
4
x
f(x) = 0 denkleminin kökleri y=f(x) fonksiyonunun grafiğinin x eksenini kestiği noktalardır. Bu durumda verilen f fonksiyonunun grafiği x eksenini x = –4, x = –2, x = 2 ve
x = 4 noktalarında kesmektedir. Buradan f(x) = 0 denkleminin kökleri toplamı
(–4) + (–2) + 2 + 4 = 0 olur.
5
y = f(x)
Gerçek sayılar kümesinde tanımlı f ve g fonksiyonlarının grafikleri verilmiştir. Buna göre;
y
4
y = g(x)
3
I. f fonksiyonunun sıfırlarını bulunuz.
2
II. g fonksiyonunun sıfırlarını bulunuz.
III. f(x) = g(x) eşitliğini sağlayan x değerini bulunuz.
1
–1
–
I.
II.
3
2
–1
1
3
2
x
f fonksiyonunun grafiğinin x eksenini kestiği nokta olan x=0 değeri f fonksiyonunun sıfırıdır.
3
3
g fonksiyonunun grafiğinin x eksenini kestiği noktalar olan x = - ve x =
2
2
değerleri g fonksiyonunun sıfırlarıdır.
f(x) = g(x) eşitliğini sağlayan x değeri f ve g fonksiyonlarının grafiklerinin kesiştiği noktanın apsisidir. Bu durumda istenilen cevap x = 1 dir.
Ünite 3. Fonksiyonlar
557
Bölüm
3.2
Fonksiyonların Grafikleri
6
Gerçek sayılarda tanımlı f fonksiyonu
f(x) = x5 – x4 – x3 – x2 – 2x ile veriliyor. Bu fonksiyonun grafiği şekildeki gibidir. x değerleri
–1 den küçük ve 2 den büyük değerler aldıkça grafiğin x ekseninden uzaklaştığı bilinmektedir. Buna göre f fonksiyonunun grafiğini kullanarak
y
6
5
f (x)
4
3
2
1
–4 –3 –2 –1
–1
1
2
–2
–3
–4
–5
–6
558
3
4
x
a. x5 – x4 – x3 – x2 – 2x = 0 denkleminin çözüm kümesini bulalım.
b. x5 – x4 – x3 – x2 – 2x = –3 denkleminin kaç
tane gerçek sayı çözümü olduğunu bulalım.
c.
x5 – x4 – x3 – x2 – 2x = 3 denkleminin kaç
tane gerçek sayı çözümü olduğunu ve
varsa bu çözümün veya çözümlerin hangi ardışık iki tam sayı(lar) arasında olduğunu bulalım.
a.
Verilen denklem f(x) = 0 dır. y = f(x) fonksiyonunun grafiğinde, grafiğin x eksenini
kestiği noktalar x = –1, x = 0 ve x = 2 olduğundan bu denklemin çözüm kümesi
{–1, 0, 2} dir.
b.
Dikkat edilirse x5 – x4 – x3 – x2 – 2x = –3 denklemi y = f(x), y = –3 denklem sisteminin çözümünden elde edilecek olan x değerleridir. Bunun grafiksel anlamı f
fonksiyonu ile y=-3 doğrusunun kesişim noktalarının apsisleridir. Verilen grafiği
y eksenini –3 te kesen bir yatay doğru çizdiğimizde bu yatay doğrunun grafiği
üç noktada kestiği görülecektir. Dolayısıyla, verilen denklemin de üç gerçek sayı
çözümü olacaktır.
Ünite 3. Fonksiyonlar
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
Dikkat edilirse verilen denklemin çözümleri
–3 ün f altındaki ters görüntüleridir.
y
6
5
f (x)
4
3
2
1
–4 –3 –2 –1
–1
1
2
3
4
x
–2
–3
–4
–5
–6
c.
Benzer şekilde grafiği üzerinde y eksenini 3 te kesen bir yatay doğru çizersek bu
yatay doğrunun verilen fonksiyon grafiğini sadece bir noktada kestiği görülecektir. Ayrıca bu kesişim noktasının apsisinin 2 ile 3 arasında olduğu grafikten
görülmektedir.
y
6
5
f (x)
4
3
2
1
–4 –3 –2 –1
–1
1
2
3
4
x
Bu nedenle x5 – x 4 – x3 – x2 – 2x = 3 denkleminin sadece bir gerçek sayı çözümü
olup bu çözüm de (2, 3) aralığındadır.
–2
–3
–4
–5
–6
Ünite 3. Fonksiyonlar
559
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
KENDİMİZİ SINAYALIM
1.
2.
a.
Gerçek sayılarda tanımlı f(x) = 5x – 4 ile
g(x) = 3x + 4 fonksiyonlarının grafiklerinin kesiştiği
noktayı bulunuz.
Aşağıdaki denklem sistemlerinin çözüm kümelerini
ilgili fonksiyonların grafiklerini kullanarak bulunuz.
–3x – y = 6
3
2x – y = –3
4.
Aşağıda grafikleri verilen fonksiyonlar için
a.
f(x) = 0
b.
g(x) = 0
c.
h(x) = 0
ç.
q(x) = 0
y
q(x)
g(x)
–6 –5 –4 –3 –2 –1
d.
h(x) = 3
e.
g(x) = –4
x + 2y – 1= 0
3
x – 3y + 6 = 0
b.
5
4
3
2
1
–1
–2
–3
–4
–5
–6
–7
–8
h(x)
f(x)
x
1 2 3 4
denklemlerinin çözüm kümelerini bulunuz.
3.
5.
y
(2,3)
3
x2 + 5x + 6 = 0 denkleminin köklerini bir grafik çizim aracından/yazılımından yararlanarak bulunuz.
g
f
–1
1
2
3
4
5
x
–1
Grafikte verilenlere göre f ve g fonksiyonlarının
denklemlerin bulunuz.
6.
y
b
f(x) = –2x + 6
0
1
2
3
4
x
Grafikte verilenlere göre b değeri kaçtır?
560
Ünite 3. Fonksiyonlar
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
KENDİMİZİ SINAYALIM
7.
Aşağıdaki denklemleri verilen doğruların eksenleri
kesitği noktaları bulunuz.
a.
c.
y = 2x – 1
x
y= +1
3
2x – 3y = 6
ç.
x=3
d.
y=1
b.
9.
y
4
3
2
1
–2
1
–1
2
3
4
y = h(x)
x
Grafiği verilen h fonksiyonunun sıfırlarını bulunuz?
10.
8.
y
y = g(x)
y
3
2
y = f(x)
1
y = f(x)
m
–4
–3
–2
–1
1
2
3
4
x
–1
1
x
f ve g fonksiyonlarının grafikleri verilmiştir. f fonksiyonunun grafiğinin x – eksenini kestiği nokta m dir.
m nin g fonksiyonu altındaki ters görüntüsü nedir?
Grafiği verilen f fonksiyonunun grafiği x – eksenini
c noktasında kesiyor ve f(c2) = 0 ise c kaçtır?
Ünite 3. Fonksiyonlar
561
y = f(x) Fonksiyonunun Grafiği ile f(x) = 0 Denklemi Arasındaki İlişki
KENDİMİZİ SINAYALIM
11.
y
y = f(x)
3
2
y = g(x)
–2
1
–1
1
2
3
4
x
f ve g fonksiyonlarının grafikleri verilmiştir. f(a) = 0
ve g(b) = 0 ise a + b kaçtır?
12.
y
3
y = f(x)
2
1
–2
–1
y = g(x)
1
2
3
4
5
x
–1
Grafiği verilen f ve g fonksiyonlarının ters görüntülerinin eşit olduğu değer a ise g(a +2) in değeri
kaçtır?
562
Ünite 3. Fonksiyonlar
MATEMATİK ATÖLYESİ
Bu atölye çalışmasının amacı, birden fazla kuralla tanımlanan fonksiyonları bir örnek üzerinde incelemektedir.
a
b
c
Şekilde verilen a, b ve c depoları üst üste konulmuş dik silindir şeklindeki bölümlerden oluşmaktadır. Bu depolar boş
iken, musluklardan sabit hızla akan su ile doldurulmaktadır.
Adım 1
Her bir depo için, depo içindeki suyun yüksekliğini zamana bağlı olarak gösteren fonksiyonların grafiğini çiziniz.
Adım 2
Depolarda suyun yüksekliğinin nasıl değiştiğini çizdiğiniz grafikleri kullanarak açıklayınız. Bu grafikleri karşılaştırarak,
birim zamanda suyun yüksekliğinin en hızlı değiştiği depoyu tespit ediniz? Cevabınızın gerekçelerini açıklayınız.
Adım 3
Her bir depo için, depo içindeki suyun hacimini zamana bağlı olarak gösteren fonksiyonların grafiğini çiziniz.
Adım 4
Depolarda suyun hacminin nasıl değiştiğini çizdiğiniz grafikleri kullanarak açıklayınız. Bu grafikleri karşılaştırarak, birim zamanda suyun hacminin en hızlı değiştiği depoyu tespit ediniz. Cevabınızın gerekçelerini açıklayınız.
Ünite 3. Fonksiyonlar
563
Bölüm
3.2
Fonksiyonların Grafikleri
3.2.5. Parçalı Tanımlı Fonksiyonlar ve Grafikleri
Neler Öğreneceğiz?
•
Parçalı tanımlı fonksiyonu
•
Bir parçalı tanımlı fonksiyonun
grafiğini
Başlarken
Havanın tamamen güneşli, parçalı bulutlu
veya devamlı yağmurlu olduğu günler olabileceği gibi bir gün içinde sırasıyla dört mevsimi de yaşayabiliriz.
Benzer şekilde, bir duruma tek düze bir tarif
yeterli olabileceği gibi birden çok tarife ihtiyaç da duyulabilir. Bu, fonksiyonlar için de geçerlidir. Tanım kümesinin belli bir bölümü için
verilen ilişkilendirme kuralı, tanım kümesinin
diğer kısımları için geçerli olmayabilir. Yani
bir fonksiyonun yaptığı ilişkilendirmeyi tarif
etmek için birden fazla cebirsel kurala ihtiyaç
duyulabilir.
Anahtar Bilgi
•
Parçalı tanımlı fonksiyon
•
Mutlak değer fonksiyonu
•
Mutlak değerli fonksiyon
Örneğin, piyasa ekonomisinde, arz-talep dengesi içinde bir malın fiyatındaki değişimler
sıkça karşılaşılan durumlardır. Şöyle ki, bir malın fiyatı bir süre doğrusal olarak artıp, daha
sonra 3 hafta boyunca sabit kalabilir ve sonrasında tekrar doğrusal olarak artmaya devam
edebilir.
Sembol ve Gösterimler
•
y =|x|
•
•
y = | g (x) |
Z g (x),
]
f (x) = [ h (x),
]
\ k (x),
x≤a
a <x <b
x ≥b
Buna göre bu malın fiyatının zamana bağlı
değişimini gösteren fonksiyon nasıl bir fonksiyondur? Bu fonksiyonun grafiğini çizmek istersek nasıl bir grafik elde ederiz?
Yaptığı ilişkilendirmenin belirtilmesinde birden fazla kurala ihtiyaç duyulan fonksiyon
kullanımını gerektiren bazı örnekler üzerinde duralım.
564
Ünite 3. Fonksiyonlar
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
1
Bunu biliyor muydunuz
Bir motosiklet yarışçısının antrenmanlarında önce
belli bir hıza ulaştığını ve bundan sonra turlarını saymaya başladığını düşünelim. Bu motosikletlinin birinci tur başındaki hızının 100 km/sa. ve motor maksimum hızına ulaşana kadar her tur sonundaki
hızının o tur başındaki hızından 28 km/sa. fazla olduğunu varsayalım. Buna göre aşağıda istenenleri
yapalım.
a.
Bu motosikletlinin ilk 4 tur sonundaki hızlarını bulup bir tabloda gösteriniz.
b.
Hız ile tur sayısı arasında bulduğunuz tablo değerlerine uyan bir kural bulunuz.
Kenan Sofuoğlu (1984- )
Kenan Sofuoğlu, Türk
motorsporları tarihinin en
başarılı sporcusu olarak anılmaktadır 2007, 2010 ve 2012
yıllarında Dünya Supersport
şampiyonasını kazanan Sofuoğlu'nun başarısının sırrı,
azimle hedeflerine yönelik
sıkı çalışmasıdır.
(c, ç ve d seçeneklerinde bundan sonraki sorularda motosikletlinin turlar sayılmaya başladıktan sonraki herhangi bir andaki hareketinin bulduğunuz kurala uygun
olduğunu ve motorun maksimum hızının 296 km/sa olduğunu varsayınız.)
c.
İlk olarak kaçıncı tur sonunda bu motosikletlinin hızı 238 km/sa’den fazla olur?
ç.
Kaçıncı turda maksimum hıza ulaşır?
d.
Motosikletlinin tur- hız grafiğini çiziniz.
a.
Hızının (V), tur sayısına (t) bağlı olarak fonksiyonumuzu oluşturmaya çalışalım.
Burada V’nin t. tur sonundaki hızı gösterdiğine göre, bu durumu t’ye bağlı V(t)
fonksiyonu olarak düşünebiliriz. Verilenleri bu gösterime uygun olarak şu şekilde
ifade edebiliriz:
V(0) = 100 ve motor maksimum hızına ulaşana kadar V(t + 1) = V(t) + 28 olacaktır.
Buradan, V(1) = V(0) + 28 = 100 + 28 = 128, V(2) = V(1) + 28 = 128 + 28 = 156
bulunur. Benzer şekilde aşağıdaki tablodaki değerleri elde ederiz:
t
V(t)
b.
1
2
3
4
100 + 28 = 128 128 + 28 = 156 156 + 28 = 184 184 + 28 = 212
İlk tur başlangıç hızı 100 km/sa ve her turda da motosikletlinin hızını 28 km/sa
arttırdığı biliyoruz. Tablodaki değerleri de kullanarak motor maksimum hızına
ulaşana kadar
V(t) = 100 + 28·t
motor maksimum hızına ulaştıktan sonra da
V(t)= maksimum hız
olarak fonksiyonumuzu yazabiliriz.
Ünite 3. Fonksiyonlar
565
Bölüm
3.2
Fonksiyonların Grafikleri
c.
V(t) > 238 olmalıdır. 238 < 296 olduğundan 100 + 28·t > 238 eşitsizliğini elde
ederiz ve buradan 28t > 138 olur ve t > 4,9 olup motosikletlinin 5. turda hızı
238 km/sa ten fazla olmaya başlar.
ç.
V(t) ≤ 296 olmasını istiyoruz. Bu durumda 100 + 28t ≤ 296, buradan 28t ≤ 196
ve de t ≤ 7 elde edilir. Bu nedenle, motosikletlinin 7 tur sonunda hızı 296 km/sa
olarak sabitlenir.
d.
t değeri 0 ile 7 arasında iken V(t) = 100 + 28t doğrusal fonksiyonunun; t değeri 7
den büyük olduğunda ise V(t) = 296 sabit fonksiyonunun grafiğini çizeceğiz. Bu
durumda grafik aşağıdaki gibi çizilir.
296
268
240
212
184
156
128
100
0
1
2
3
4
5
6
7
8
9
10 tur
Hız fonksiyonu V(t) için elde ettiklerimizi tekrar şu şekilde ifade edebiliriz:
t ∈ [0, 7) için V(t) = 28t + 100,
t ∈ [7, ∞) için V(t) = 296 dir.
Dikkat edersek V(t) fonksiyonunun kuralını tarif etmek için birden fazla koşula
ihtiyaç duyduk. Şimdi, bu örnekte karşılaştığımız durumlara benzer fonksiyonları
tanımlayalım.
Tanım kümesinin ayrık altkümelerinde farklı kurallarla tanımlı olan fonksiyonlara
parçalı tanımlı fonksiyonlar veya kısaca parçalı fonksiyonlar denir.
2
g: (–∞, –1) → R, g(x) = x + 2,
h: [–1, 1) → R, h(x) = 1,
k: (1, ∞) → R, k(x) = x2
fonksiyonları verilsin. Buna göre
566
a.
g, h ve k nın her birinin grafiklerini farklı renkler kullanarak, aynı kartezyen düzlemde çizelim.
b.
g, h ve k fonksiyonlarının grafiklerinin birleşiminden oluşan grafiği, tek bir fonksiyonun grafiği şeklinde nasıl ifade edebileceğimizi açıklayalım.
Ünite 3. Fonksiyonlar
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
a.
y
4
3
2
1
–3 –2
g
b.
–1
–1
1
2
3
x
g fonksiyonunun grafiğini kırmızı, h
fonksiyonunun grafiğini yeşil ve k
fonksiyonun grafiğini de mavi renkle
gösterelim. Daha önce öğrendiğimiz
fonksiyon grafiklerinin çizimleri hakkındaki bilgilerimizi kullanarak şekildeki
grafiği elde ederiz.
Dikkat edecek olursak verilen 3 fonksiyonun grafiklerinin birleşimi olan grafiği,
tüm gerçek sayılarda tanımlı tek bir fonksiyonun grafiği olarak düşünülebilir. Şekildeki bütünleştirilmiş grafik üzerinde dikey doğru testi uygulandığında bunun
bir fonksiyon grafiği olduğu anlaşılacaktır.
f: R → R fonksiyonunun kuralını parçalı olarak şu şekilde tanımlayalım:
x ∈ (–∞,-1) ise f(x) = g(x),
x ∈ [–1,1) ise f(x) = h(x),
x ∈ [1,∞) ise f(x) = k(x).
Bu durumda, f fonksiyonu aradığımız fonksiyondur. Parçalı tanımlı verilen f fonksiyonunun kuralını aşağıdaki gibi bir gösterimle ifade edebiliriz.
g (x), - 3 < x < - 1
f (x) = * h (x), - 1 ≤ x < 1
k (x),
1≤x<3
Bu gösterimde, g, h ve k fonksiyonları için verilen cebirsel kuralları kullanırsak
x + 2, - 3 < x < - 1
f (x) = * 1,
-1 ≤ x < 1
2
x,
1≤x<3
elde edilir. Bu gösterim ise şu şekilde okunur:
x değerleri, –∞ < x < –1 şartını sağlarsa f(x) = x + 2 kuralı uygulanmalıdır.
x değerleri, –1 ≤ x < 1 şartını sağlarsa f(x) = 1 kuralı geçerlidir.
1 ≤ x < ∞ şartını sağlayan x ler için ise f(x) = x2 kuralı uygulanmalıdır. Örneğin,
f(0) = 1 olur, çünkü –1 ≤ 0 < 1 şartı sağlanır,
f(–4) = –4 + 2 = –2 olur çünkü, –∞ < –4 < –1 şartı sağlanmaktadır,
f(5) = 52 = 25 dir çünkü, 1 ≤ 5 < ∞ olduğunu biliyoruz.
Ünite 3. Fonksiyonlar
567
Bölüm
3.2
Fonksiyonların Grafikleri
3
Bir otoparkın ücret tarifesi aşağıdaki gibidir.
Park Süresi
(saat)
Ücret (TL)
0<t≤1
1,00
1<t≤2
3,00
2<t≤4
6,50
4<t≤6
10,00
6 < t ≤ 12
12,00
Buna göre park ücretinin, parkta kalma süresine bağlı grafiğini çizelim.
t saat bir aracın otoparkta kaldığı süreyi göstermek üzere, aracın ödeyeceği ücret g(t)
TL olsun. g fonksiyonunun tanım kümesi bu otoparkın izin verdiği park süreleri kümesidir. Park edilen bir araç en fazla 12 saat kalabildiğinden g nin tanım kümesi (0, 12]
aralığıdır.
Verilen bilgilere göre, bir kişi aracını park ettikten sonra
a.
Bir saat içinde alırsa 1 TL ödeme yapmalıdır, yani t ∈ (0, 1] için g(t) = 1 dir
b.
1 saatten fazla olmak üzere 2 saat içinde alırsa 3 TL ödeme yapmalıdır, yani
t ∈ (1, 2] için g(t) = 3 tür.
c.
2 saatten fazla olmak üzere 4 saat içinde alırsa 6,5 TL ödeme yapmalıdır, yani
t ∈ (2, 4] için g(t) = 6,5 tir.
d.
4 saatten fazla olmak üzere 6 saat içinde alırsa 10 TL ödeme yapmalıdır, yani
t ∈ (4, 6] için g(t) = 10 dur.
e.
6 saatten fazla olmak üzere 12 saat içinde alırsa 12 TL ödeme yapmalıdır, yani
t ∈ için g(t) = 12 dir.
Yukarıda g fonksiyonun kuralının nasıl olacağını, olabilecek farklı durumlar için açıkladık. Ancak bu açıklamalarımızın aynısını aşağıdaki gibi bir gösterim tercihi yaparak
daha kısa bir şekilde ifade edebiliriz.
Z 1, 0 < t ≤ 1 ise
]
] 3, 1 < t ≤ 2 ise
]
g ^ t h = [ 6, 5, 2 < t ≤ 4 ise
]
]] 10, 4 < t ≤ 6 ise
\ 12, 6 < t ≤ 12 ise
Bu gösterimde önce g fonksiyonunun alacağı değerleri sonra da bu değerlerin hangi
koşul altında geçerli olduğunu belirtiriz. Bu gösterimi okurken ise koşullardan başlarız.
568
Ünite 3. Fonksiyonlar
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
Örneğin, t değeri 2 ile 4 arasında veya 4 e eşitse g(t) = 6,5 dir deriz. Burada, g fonksiyonunun kuralını kısım kısım vermiş oluyoruz. Dolayısıyla g bir parçalı tanımlı fonksiyondur.
Bu örnekte g fonksiyonun görüntü kümesi, ödenecek tüm olası ücret miktarlarının
oluşturduğu küme olan {1, 3, 6.5, 10, 12} dir.
Verilenlere göre g fonksiyonunun grafiğini çizmek için
12
Ücret (TL)
(0, 1] aralığında y = 1,
(1, 2] aralığında y = 3,
10
(2, 4] aralığında y = 6,5,
(4, 6] aralığında y = 10,
6,5
(6, 12] aralığında y = 12
3
1
1 2
4
Süre (saat)
12
6
doğrularını çizmeliyiz. Böylece g fonksiyonunun grafiği aşağıdaki gibi elde edilir.
4
Tanım kümesi tüm gerçek sayılar olan bir f fonksiyonu parçalı tanımlı olarak aşağıdaki
gibi veriliyor:
Z 3x - 2, - 3 < x < - 5
]]
x+1
f (x) = [ 2
, -5 ≤ x < 0
]] x + 1
0≤x<3
\ 2x + 4,
Buna göre aşağıda verilenleri bulalım.
a. f(–5)
b. f(–10)
c. f(x2)
a.
f ^- 5h =
b.
f(–10) = 3(–10) – 2 = –32
c.
Herhangi bir x gerçek sayısı için x2 ≥ 0 olduğundan, f(x2) = 2x2 + 4 olarak bulunur.
-5 + 1
^ - 5h2 + 1
=-
4
2
=25 + 1
13
Ünite 3. Fonksiyonlar
569
Bölüm
3.2
Fonksiyonların Grafikleri
5
Bir postanede mektup ve kargo göndermek için alınan gönderinin kütlesine bağlı olarak belirlenen ücret tarifesi aşağıda verilmiştir.
Mektup Gönderme Tarifesi:
20 Grama kadar: 1 TL
20 Gramdan 50 grama kadar: 1,5 TL
50 Gramdan 100 grama kadar: 2 TL
100 Gramdan 250 grama kadar: 2,5 TL
250 gram ve üstü: 2,5 TL ye her 100 g fazlalık için 50 kr.
Bu tarifeye uygun bir fonksiyon oluşturarak bu fonksiyonun tanım ve görüntü kümelerini bulalım. Ayrıca bu fonksiyonun kuralını yazalım ve grafiğini çizelim.
x gönderinin gram cinsiden kütlesi olmak üzere gönderme ücreti g(x) TL olsun.
g fonksiyonunun tanım kümesi pozitif gerçek sayılar yani (0, ∞) dir. Bu fonksiyonun görüntü kümesi ise alınabilecek ücretlerdir, yani 1 TL ve 1 TL den itibaren 50 kr. ekleyerek
elde edeceğimiz tüm sayılardır. Bu durumda görüntü kümesini ortak özellik yöntemiyle şu şekilde belirtebiliriz:
k
' : k ≥ 2 ve k bir pozitif tam sayı 1
2
Verilen bilgiler doğrultusunda g fonksiyonunun kuralı parçalı tanımlı olarak şu şekilZ 1,
dedir:
0 < x < 20 için
]
] 1, 5,
20 ≤ x < 50 için
]
50 ≤ x < 100 için
]] 2,
g ^ x h = [ 2, 5,
100 ≤ x < 250 için
]
250 ≤ x < 350 için
] 3,
] 3, 5
350 ≤ x < 450 için
]
h
\ h
Buna göre
x ∈ (0, 20) ⇒ y = g(x)=1
x ∈ [20, 50) ⇒ y = g(x) = 1,5
x ∈ [50, 100) ⇒ y = g(x) = 2
x ∈ [100, 250) ⇒ y = g(x) = 2,5
x ∈ [250, 350) ⇒ y = g(x) = 3
x ∈ [350, 450) ⇒ y = g(x) = 3,5
...
Bu durumda g fonksiyonunun grafiği aşağıdaki gibi olacaktır.
570
Ünite 3. Fonksiyonlar
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
Ücret
...
3,5
3
2,5
2
1,5
1
20
50
100
250
450 gönderinin
kütlesi
350
6
Z
] - 2x + 2 , x < 1 ise
2
]
1
k (x) = [
≤ x < 2 ise
,
]1
2
]
\ x - 1 , x ≥ 2 ise
fonksiyonunun grafiğini çizelim.
k(x) fonksiyonunun her bir parçasında verilen kurallara sahip f(x) = x – 1, g(x) = 1 ve
h(x) = –2x + 2 doğrusal fonksiyonların grafiklerini çizelim.
h(x) = –2x + 2
f(x) = x – 1
2
g(x) = 1
1
–2 –1
–1
1
2
–2
Bu grafiklerin k nın tanımında belirtilen kısımlarını alarak k fonksiyonunun grafiğini
elde edeceğiz. Bu durumda f in grafiği üzerindeki noktalardan apsisleri [2, ∞) aralığında
1
olanları, g nin grafiği üzerindeki noktalardan apsisleri ; , 2 m aralığında olanları, h nin
2
1
grafiği üzerindeki noktalardan apsisleri c - ∞, m aralığında olanları alarak k nın grafi2
ğini şekildeki gibi elde ederiz.
k
2
1
1 1
–2 –1
–1 2
2
Ünite 3. Fonksiyonlar
571
Bölüm
3.2
Fonksiyonların Grafikleri
7
Yanda verilen üst üste iki dik silindir şeklindeki bölümden oluşan boş depo sabit miktarda su akıtan
bir musluk ile doldurulmaktadır. Alttaki silindirin
taban yarıçapı 5 metre ve yüksekliği 8 metredir.
Üstteki silindirin ise taban yarıçapı 2 metre, yüksekliği 10 metredir. Buna göre aşağıda istenenleri
yapalım. (r yerine 3 alınız)
r=2 m
h2=10 m
H=18 m
R=5m
h1=8 m
a.
Alttaki silindirde suyun hacminin yüksekliğe bağlı olarak değişim oranı (hızı)
nedir?
b.
Üstteki silindirde suyun hacminin yüksekliğe bağlı değişim oranı (hızı) nedir?
c.
Deponun tamamı için suyun hacminin yüksekliğe bağlı değişimini gösteren
fonksiyonun grafiğini çiziniz.
a.
Suyun hacminin yüksekliğe bağlı değişimini bir
fonksiyon olarak düşünebiliriz. Bu fonksiyonda
hacim bağımlı değişken, yükseklik ise bağımsız
değişkendir. Burada hacim ile yükseklik birlikte
değişmektedir.
h1=8m
1m
1m
Öncelikle yüksekliği birer birim artırarak hacimin aldığı değerleri bulalım.
1m
Dikkat
Burada değişim oranının
birimi m3/m'dir. Bu ifadenin
1m
m3
= m2
m
şeklinde yazılamayacağına
dikkat ediniz.
sadeleştirerek
572
Yükseklik (h)
Hacim
(V = rr2h)
0
0
1
75
2
150
3
225
4
300
8
600
Ünite 3. Fonksiyonlar
75 m3
75 m3
Tabloda görüldüğü üzere suyun
yüksekliğindeki her 1 metre artışına karşılık, hacim 75 m3
artmaktadır. Yani değişimde 1’e
75 bir oran vardır. Yükseklik 1
metreden 2 metreye çıktığında
hacimdeki değişim oranını
(hızını)
V2 - V1
150 - 75
=
= 75m 3 /m
2-1
1
olarak hesaplayabiliriz.
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
Yani suyun yüksekliği 1 birim arttığında hacim bunun 75 katı kadar artmaktadır. Değişim oranı sabit olduğu için istenen fonksiyon bir doğrusal fonksiyondur. Bu durumda
alttaki silindir bölüm için aranan doğrusal fonksiyonun eğimi 75 olmalıdır.
Şimdi değişim oranını, değişim oranının sabit olduğu bilgisini kullanmadan ikinci bir
yoldan hesaplayalım. Bunun için belli yükseklik değerleri yerine genel olarak aldığımız
(h, V) ve değerleri için hesaplayalım.
V2 - V1
rr 2 h 2 - rr 2 h 1
=
h2 - h1
h2 - h1
=
rr 2 ^ h 2 - h 1 h
h2 - h1
= rr 2
= 3 · 5 2 m 3 /m
= 75 m 3 /m
V2 - V1
= rr 2 olduğunu gözlemledik.
h2 - h1
Dolayısıyla verilen şartlar altında silindirdeki suyun hacminin yüksekliğe bağlı değişim
oranı sadece silindirin yarı çapına bağlıdır.
Dikkat edilirse burada
b.
1. Yol:
(a) seçeneğinde alttaki silindir için yaptığımız işlemi üstteki silindir bölüm için
yapalım.
1m
1m
Yükseklik (h)
Hacim
(V = rr2h)
8
600
9
612
10
624
12
648
18
720
12 m3
12 m3
Tabloda görüldüğü üzere
yüksekliğin her 1 metre
artışına karşılık hacim
12 m3 artmaktadır. Örneğin, suyun 8 ve 10 metre
yükseklikte olduğu
durumlara karşılık gelen
hacim değerleri sırasıyla
600 m3 ve 624 m3 tür. Bu
aralıktaki değişim oranı,
624 - 600
24
=
= 12m 3 /m
10 - 8
2
olarak hesaplanır. Başka aralıklar için bu işlemin sonucu aynı olacaktır. Değişim
oranı burada da sabit olduğu için istenen fonksiyon bir doğrusal fonksiyondur.
Bu durumda üstteki silindir bölüm için aranan doğrusal fonksiyonun eğimi 12
olmalıdır.
Ünite 3. Fonksiyonlar
573
Bölüm
3.2
Fonksiyonların Grafikleri
2. Yol:
(a) da bulduklarımızdan dolayı değişim oranı
Anahtar Bilgi
rr2 = 3 · 22m2 = 12m3/m dir.
- x, x < 0 ise
y = f (x) = x = (
x, x ≥ 0 ise
fonksiyonu mutlak değer
fonksiyonu olarak bilinir.
Mutlak değerli ifade içeren
fonksiyonlar parçalı tanımlı
fonksiyonlara örnektir.
c.
Suyun hacminin yüksekliğe bağlı değişimi alttaki ve üstteki bölümler için eğimleri sırasıyla 75 ve 12 olan birer doğrusal fonksiyonla gösterilebilir. (a) ve (b) de
bulduklarımız değişim oranlarıydı.
Alttaki silindir bölme için yazılacak fonksiyonda x yükseklik (m), f(x) de bu yükseklikteki suyun hacmini (m3) göstermek üzere,
f(x) = 75x + c
olmalıdır. Suyun yüksekliği 0 olduğunda hacim 0’dır. Bu durumda
f(0) = 75 · 0 + c = 0 ⇒ c = 0
bulunur. O halde, alttaki silindir bölme yüksekliğe bağlı hacim fonksiyonu,
0 ≤ x < 8 için f(x) = 75x
bulunur. Üstteki silindir bölme için eğimin 12 olduğunu bulmuştuk. O halde
suyun yüksekliğine bağlı hacmini gösteren fonksiyon,
g(x) = 12x + k
olmalıdır. Burada k değeri bulmak için bilinen değerlerden yararlanabiliriz.
g(x) = 12x + k fonksiyonu üstteki silindire ait olduğu için, suyun yüksekliği 8
metreden büyük, deponun boyu olan (iki bölmenin toplam yüksekliği) 18 metreden küçük olduğu durum için geçerlidir. Yükseklik 8 olduğunda hacmin 600 m3
olduğunu biliyoruz. Bu durumda,
g(8) = 12 · 8 + k = 600 ⇒ k = 504
bulunur. O halde 8 < x ≤ 18 için g(x) = 12x + 504 olur.
Bu durumda deponun tamamı için suyun yüksekliğe bağlı hacim fonksiyonu v(x)
aşağıdaki gibi olmalıdır.
v^xh = (
75x
, 0 ≤ x ≤ 8 ise
12x + 504 , 8 < x ≤ 18 ise
Parçalı tanımlı v(x) fonksiyonunun grafiğini aşağıdaki gibi çizebiliriz.
y
y
800
800
600
600
y = vx
500
400
400
200
200
5
574
10
15
Ünite 3. Fonksiyonlar
x
2
4
6
8
10
x
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
8
Anahtar Bilgi
Gerçek sayılarda tanımlı y = f(x) = |x| fonksiyonun grafiğini çizelim.
Mutlak değerli fonksiyonların
grafikleri çizilirken mutlak
değerin içindeki ifadenin
grafiği çizilir. Daha sonra
grafiğin x-ekseninin altında
kalan kısmının x-eksenine
göre simetriği alınır. Böylece
istenilen mutlak değerli ifade
içeren grafik çizilmiş olur.
Örneğin,
Öncelikle pozitif x değerleri için |x| = x, negatif x değerleri için |x| = –x ve de |0| = 0
olduğundan y = |x| mutlak değer fonksiyonunu parçalı tanımlı fonksiyonlar için kullandığımız gösterim yoluyla ifade edebiliriz:
Z - x , x < 0 için
]
x = [ 0 , x = 0 için
]
\ x , x > 0 için
f(x) = |g(x)| ifadesi
Son iki koşulu birleştirdikten sonra koşul sıralarını yeniden düzenleyerek şu şekilde de
gösterebiliriz:
x, x ≥ 0
x =(
- x, x < 0
Dolayısıyla, y = f(x) = |x| in grafiği x < 0 için y = –x ve x ≥ 0 iken y = x doğrularının grafiklerinin ilgili kısımlarıdır.
f^xh = g^xh = )
g^xh , g^xh ≥ 0
- g^xh , g^xh < 0
olacak şekilde yazılabilir.
5
y = –x
2
–5
y=x
5
–5
5
Anahtar Bilgi
–2
Kuralında mutlak değerli
ifade içeren bir f fonksiyonunun grafiği çizilirken, mutlak
değerli ifadeyi 0 (sıfır) yapan
değerler kritik değerlerdir. Tanım kümesi bu kritik
değerlere göre parçalanarak,
fonksiyonun ilgili aralıklardaki kuralı fonksiyonunun o
bölgelerde negatif ve pozitif
olmasına göre grafiği çizilir.
–5
Grafikten de görüldüğü gibi f(x) = |x| fonksiyonunun tanım kümesinin dikey doğru testinden R, görüntü kümesinin ise grafikten [0, ∞) olduğu görülmektedir.
Ünite 3. Fonksiyonlar
575
Bölüm
3.2
Fonksiyonların Grafikleri
9
f: R → R, f(x) = |4 – x| fonksiyonunun kuralını parçalı tanımlı olarak ifade edip grafiğini
çizelim.
Mutlak değerin tanımı gereği
x ≥ 4 iken |4 – x| = –(4 – x) = x – 4
x < 4 iken |4 – x| = 4 – x olduğundan
f^xh = 4 - x = )
=(
- ^4 - xh, x ≥ 4 ise
4 - x, x < 4 ise
4 - x , x ≥ 4 ise
x - 4 , x < 4 ise
f fonksiyonunun grafiğini elde etmek için, y = x – 4 fonksiyonunun grafiği çizilip, grafiğin x < 4 için olan kısmı; y = 4 – x fonksiyonunun grafiğini x ≥ 4 için olan kısmı alınarak
birleştirilir. Bu şekilde elde ettiğimiz grafik şudur:
y
4
y
g(x) = 4 – x
4
h(x) = x – 4
3
3
2
2
1
1
–1
2
4
6
8 x
–1
–2
–2
–3
–3
–4
–4
y = f(x) = |4 – x|
2
4
6
8 x
Dikkat edilirse f(x)= |4 – x| in grafiğini elde etmek için y = 4 – x doğrusunun grafiği çizilir. x-ekseninin üstünde kalan kısmın tamamı, x-ekseninin altında kalan kısmın (yani
fonksiyonun negatif değer aldığı kısmın) ise x-eksenine göre simetriği alınır. Bu alınan
grafikler f fonksiyonunun grafiğini oluşturur. Bu örnek üzerinde yaptığımız gözlemi şu
şekilde genelleyebiliriz:
Mutlak değerli fonksiyonların grafikleri çizilirken mutlak değerin içindeki ifadeyi
kural olarak alan fonksiyonun grafiği çizilir. Daha sonra grafiğin x-ekseninin üstünde olan kısımlar alınır. x-ekseninin altında kalan kısımlar varsa bu kısımların da
x-eksenine göre simetriği alınır. Böylece istenilen mutlak değerli ifade içeren grafik
çizilmiş olur.
576
Ünite 3. Fonksiyonlar
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
Aşağıdaki örneklerde y = f(x) in grafiğinden y = |f(x)| in grafiğinin nasıl elde edildiğini
inceleyiniz:
y
y
f(x) = 2 – x
6
4
4
2
2
2 3 4 5
f(x) = |x – 2|
6
x
2 3 4 5
–2
x
–2
–4
y
y
g(x) = x2 – 1
6
6
4
4
2
2
–1 1
–2
x
–1 1
–2
y h(x) = x3 – x – 2
y
8
4
–2
–4
–6
x
h(x) = |x3 – x – 2|
6
2
–5
g(x) = |x2 – 1|
4
2
5 x
–5
–2
5 x
–8
10
Gerçek sayılarda tanımlı f(x) = |x – 2| + x – 1 fonksiyonunun grafiğini çizelim.
Ünite 3. Fonksiyonlar
577
Bölüm
3.2
Fonksiyonların Grafikleri
x ≥ 2 için x – 2 ≥ 0 ⇒ |x – 2| = x – 2 olduğundan f(x) = x – 2 + x – 1 = 2x – 3'tür.
x < 2 için x – 2 < 0 ⇒ |x – 2| = –(x – 2) olduğundan f(x) = –(x – 2) + x – 1 = 1'dir.
Bu durumda f fonksiyonu şu şekilde ifade edilebilir:
f^xh = (
2x - 3, x ≥ 2
1,
x<2
Buna göre f fonksiyonunun grafiği, aşağıda gösterildiği gibi x ≥ 2 için f(x) = 2x – 3 fonksiyonunun grafiği x < 2 için f(x) = 1 fonksiyonunun grafiği olmalıdır.
y
3
f (x)
2
1
–1
1
2
3
x
Grafikten de görüldüğü gibi f fonksiyonu, kuralında bulunan mutlak değerli ifadeyi 0
(sıfır) yapan değerlerin sağında ve solunda farklı cebirsel ifadelerle temsil edilmektedir.
Parçalı tanımlı verilen bir fonksiyonda, tanım kümesinden olup fonksiyonun kuralının değişiklik gösterdiği yerlere fonksiyonun kritik değerleri denir.
y = |f(x)| şeklindeki parçalı tanımlı fonksiyonlar için f(x) = 0 eşitliğini sağlayan yerler bu
parçalı tanımlı fonksiyonun kritik noktaları olacaktır. Örneğin, gerçek sayılarda tanımlı
f(x) = |2x – 6| fonksiyonunun kritik noktası, 2x – 6 = 0 dan x = 3 olarak bulunur.
578
Ünite 3. Fonksiyonlar
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
KENDİMİZİ SINAYALIM
1.
Gerçek sayılarda tanımlı aşağıdaki fonksiyonların
grafiklerini çiziniz.
a.
3,
x<0
f^xh = (
x + 1, x ≥ 0
b.
3 - x,
x <- 2
g(x) = * 2x, - 2 ≤ x ≤ 1
2,
x>1
c.
h(x) = |x + 1|
4.
m
2
1
–1
–1
1
2
3
4
5
x + a, x < 1
m ^ x h = * 2,
1 ≤ x ≤ 5 fonksiyonunun grafiği
x - b, x > 5
şekilde gösterilmektedir? Buna göre a ve b
değerlerini bulunuz.
2.
Gerçek sayılarda tanımlı aşağıdaki fonksiyonların
grafiklerini çiziniz.
a.
k(x) = |3 – 2x|
b.
n(x) = |x + 1|
c.
m(x) = |x + 1| – 2
x-2
t(x) =
4
ç.
5.
Bir yüzme havuzunun giriş ücreti bir saate kadar
25 TL, bir saatten sonraki her yarım saat için 10
TL’dir. Bu durumda;
3.
Gerçek sayılarda tanımlı aşağıdaki fonksiyonların
grafiklerini çiziniz.
a.
f(x) = |x – 1| + |x + 3|
b.
g(x) = |2 – x| – |x + 1|
c.
g(x) = |x| + |1 – x|
a.
Havuzda yüzmeye giden iki arkadaşın havuzu kullanacakları zamana (saat) göre ödeyeceği toplam
ücreti (TL) gösteren bir fonksiyon yazınız.
b.
a) seçeneğinde bulduğunuz fonksiyonun grafiğini
çiziniz.
Ünite 3. Fonksiyonlar
579
Parçalı Tanımlı Fonksiyonlar ve Grafikleri
KENDİMİZİ SINAYALIM
6.
Bir GSM şirketi kullanıcılarına aylık 25 TL sabit ücret
karşılığı her yöne 250 dakika konuşma hakkı veren
bir tarife sunmaktadır. Bu tarifeye göre 250 dakika
aşımı halinde, ilave her dakika konuşma için 33
kuruş ücretlendirme yapılmaktadır. Bu durumda;
a.
Ayda ortalama 550 dakika konuşan bir kişinin bu
tarifeye göre ne kadar ücret ödeyeceğini bulunuz.
b.
Konuşma süresine (dakika) bağlı ödenecek ücreti
gösteren bir fonksiyon bulunuz.
c.
Üstte bulduğunuz fonksiyonun grafiğini çizerek
yorumlayınız.
d.
Aynı GSM şirketi farklı bir tarifeye göre aylık sabit
ücreti 5 TL ve dakika ücreti 10 kuruş olan bir paket
sunmaktadır. Her iki tarifedeki ücretlendirmeleri
karşılaştırarak, bu tarifelerin müşteriler için hangi
durumlarda daha karlı olduğunu açıklayınız.
580
Ünite 3. Fonksiyonlar
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında tanım kümesindeki elemanların değer kümesindeki farklı elemanlarla ilişkilendirildiği
fonksiyonları inceleyeceğiz.
Adım 1
Adım 2
Her ilin farklı bir plaka kodu olduğunu trafikte gözlemlemişsinizdir. Aşağıda verilen haritada her ilin ismi ve
plaka numarası görülmektedir. Bulunduğunuz coğrafi
bölgedeki illerin kümesini A, bu illerin plaka kodlarının
kümesini B ile gösteriniz.
A ve B kümelerini Venn şeması ile göstererek il ve plaka
kodlarını eşleyiniz.
Adım 3
A kümesindeki şehirlerden B kümesinden aynı plaka koduyla eşleşen var mı? Cevabınızı nedenleriyle açıklayınız.
01 Adana
22 Edirne
43 Kütahya
64 Uşak
02 Adıyaman
23 Elazığ
44 Malatya
65 Van
03 Afyon
24 Erzincan
45 Manisa
66 Yozgat
04 Ağrı
25 Erzurum
46 K. Maraş
67 Zonguldak
05 Amasya
26 Eskişehir
47 Mardin
68 Aksaray
06 Ankara
27 Gaziantep
48 Muğla
69 Bayburt
07 Antalya
28 Giresun
49 Muş
70 Karaman
08 Artvin
29 Gümüşhane
50 Nevşehir
71 Kırıkkale
09 Aydın
30 Hakkari
51 Niğde
72 Batman
10 Balıkesir
31 Hatay
52 Ordu
73 Şırnak
11 Bilecik
32 Isparta
53 Rize
74 Bartın
12 Bingöl
33 İçel
54 Sakarya
75 Ardahan
13 Bitlis
34 İstanbul
55 Samsun
76 Iğdır
14 Bolu
35 İzmir
56 Siirt
77 Yalova
15 Burdur
36 Kars
57 Sinop
78 Karabük
16 Bursa
37 Kastamonu
58 Sivas
79 Kilis
17 Çanakkale
38 Kayseri
59 Tekirdağ
80 Osmaniye
18 Çankırı
39 Kırklareli
60 Tokat
81 Düzce
19 Çorum
40 Kırşehir
61 Trabzon
20 Denizli
41 Kocaeli
62 Tunceli
21 Diyarbakır
42 Konya
63 Şanlıurfa
Adım 4
Bu kümelerin elemanları arasında yapılan ilişkilendirmenin neden bir fonksiyon olduğunu açıklayınız.
Adım 5
Bu fonksiyonun A kümesindeki her bir elemanı B kümesindeki farklı elemanlara eşleyip eşlemediğini belirtiniz.
Görüntü kümesinden aldığınız elemanların bu fonksiyon altında kaçar tane ters görüntüsü olmaktadır.
Ünite 3. Fonksiyonlar
581
Bölüm
3.2
Fonksiyonların Grafikleri
3.2.6. Bire Bir ve Örten Fonksiyonlar
Neler Öğreneceğiz?
•
Bire bir fonksiyonu
•
Örten fonksiyonu
•
Yatay doğru testini
Başlarken
3.2.6. Bire Bir ve Örten Fonksiyonlar
Marketlerde satılan her ürün çeşidinin bir barkodu vardır. Herhangi bir ürün çeşidinin fiyatını
barkod okuyucu yardımıyla öğrenebiliriz. Her
ürün çeşidine bir barkod numarası verilmesinin
sağladığı birçok kolaylıklar vardır.
Bir marketteki ürün çeşitlerini barkodlarına
eşleyen fonksiyonu düşünelim.
Terimler
•
Bire bir fonksiyon
•
Örten fonksiyon
•
Yatay doğru testi
Bir ürüne barkod verilirken nelere dikkat
edilmelidir?
•
Bunlar ele aldığımız fonksiyon için ne anlama gelmektedir?
Bu örnektekine benzer fonksiyonların incelenmesinde bire bir fonksiyon kavramıyla karşılaşırız. Diğer önemli bir özellik de bir fonksiyonun
örten olup olmadığıdır. Bu kısımda, oldukça
işlevsel olan fonksiyonların bire bir, örten ve
hem bire bir hem örten olma durumlarını inceleyeceğiz.
Sembol ve Gösterimler
•
•
Bire Bir Fonksiyon
1–1
A
B
A
B
.a
.1
.a
.b
.2
.b
.c
.3
.c
A
B
.a
.1
.b
.c
.3
.1
.2
.3
.4
A
B
.a
.1
.b
.2
.c
.3
Fonksiyon konusuna girişte,
bir fonksiyonun tanım
kümesindeki her bir elemanı,
değer kümesinin bir ve yalnız
bir elemanı ile eşleştirdiğini
vurgulamıştık. Örneğin, A
kümesinden B kümesine
tanımlanan yandaki ilişkiler
birer fonsiyon belirtmektedir.
Buna göre,
•
İlk satırdaki fonksiyonların tanım kümesindeki her bir eleman değer kümesinde
farklı bir elemanla eşleşmiştir.
•
İkinci satırdaki fonksiyonların tanım kümesinin bazı elemanları değer kümesinde
aynı elemanla eşleşmiştir. Şöyle ki, her iki fonksiyonda da tanım kümesinin a ve b
elemanları değer kümesindeki 1 elemanı ile eşleşmiştir.
Şimdi bu örneklerde gözlemlediğimiz fonksiyon özelliklerine yönelik bir tanım yapalım:
582
Ünite 3. Fonksiyonlar
Bire Bir ve Örten Fonksiyonlar
Bir fonksiyonun tanım kümesindeki her bir elemanın görüntüsü diğer elemanların görüntülerinden farklı ise o fonksiyona bire bir fonksiyon denir. Bu tanımı daha
net ifade etmek için bire bir olma kavramının cebirsel olarak ne anlama geldiğini
belirtelim:
Anahtar Bilgi
f: A → B fonksiyonu bire bir
ise, A kümesinden alınan
herhangi iki farklı elemanın
görüntüleri aynı olamaz.
Bir f: A → B fonksiyonu verildiğinde, herhangi a ∈ A ve b ∈ A için
a ≠ b ⇒ f(a) ≠ f(b)
şartı sağlanıyorsa f fonksiyonuna bire bir fonksiyon denir. Bu tanımı şu şekilde de
ifade edebiliriz: herhangi a ∈ A ve b ∈ A için
f(a) = f(b) ⇒ a = b
şartı sağlanıyorsa f fonksiyonu bire bir fonksiyondur.
Anahtar Bilgi
Bir f fonksiyonunun bire bir olma durumu “f fonksiyonu 1-1 dir.” şeklinde ifade edilebilir.
Her a, b ∈ A ve f: A → B,
f(a) = f(b) olması sadece a = b
durumunda gerçekleşiyorsa f
fonksiyonuna bire bir fonksiyon denir.
Bu üç tanım birbirine denk olmakla beraber, verilen bir fonksiyonun bire bir olduğunu
göstereceksek üçüncü tanım daha kullanışlıdır. Diğer taraftan, verilen bir fonksiyonun
bire bir olmadığını göstereceksek genellikle ikinci tanım daha kullanışlıdır. Girişte verilen örnekteki, bir marketteki ürün çeşidini barkodlarına eşleyen fonksiyon, bire bir
fonksiyondur.
Aşağıda şekilde verilen f fonksiyonu bire bir bir fonksiyondur. Ancak g fonksiyonu bire
bir değildir.
A
Anahtar Bilgi
g
f
B
B
A
.a
.k
.a
.b
.l
.b
.l
.c
.m
.c
.m
f bire bir dir.
Bir f: A → B fonksiyonu için
f(a) = f(b) olup a ≠ b olan iki
a, b ∈ A bulunabilirse, f
fonksiyonu bire bir fonksiyon
değildir.
g bire bir değildir.
Çünkü f fonksiyonunda A kümesindeki her eleman B kümesinden farklı bir elemanla
eşleşmiştir. g fonksiyonunda ise A kümesinin a ve b elemanları B kümesinin aynı elemanıyla eşleşmiştir.
Ünite 3. Fonksiyonlar
583
Bölüm
3.2
Fonksiyonların Grafikleri
1
f: R → R, f(x) = 2x fonksiyonunun bire bir olup olmadığını inceleyelim.
a ve b gibi iki gerçek sayı için f(a) = 2a ve f(b) = 2b olur. f(a) = f(b) olduğunda a ve b
değerleri arasındaki ilişkiyi bulalım.
f(a) = f(b)
⇒ 2a = 2b
⇒ a = b olur.
Böylece, her a, b ∈ R için f(a) = f(b) olması durumunda a = b olduğunu göstermiş olduk.
Bu nedenle f fonksiyonu bire bir fonksiyondur.
Tanım kümesinden alacağımız herhangi iki farklı elemanın değer kümesinde aynı elemanla eşleştiğini gösterebilirsek fonksiyonun bire bir olmadığını söyleyebiliriz. Aksi
durumda ise fonksiyon bire bir olacaktır.
2
f: R → R, f(x) = x2 fonksiyonunun bire bir olup olmadığını inceleyelim.
1. Yol:
a ve b gibi iki gerçek sayı için f(a) = a2 ve f(b) = b2 olur. f(a) = f(b) olduğunda a ve b
değerleri arasındaki ilişkiyi bulalım.
f(a) = f(b)
⇒ a2 = b2
⇒ a = b veya a = –b olur.
Bu durumda f(a) = f(b) olması için a ≠ b de olabilir. Öyleyse f: R → R, f(x) = x2 fonksiyonu
bire bir fonksiyon değildir.
584
Ünite 3. Fonksiyonlar
Bire Bir ve Örten Fonksiyonlar
2. Yol:
2 ve –2 birer gerçek sayı olduğundan f fonksiyonunun kümesinin elemanıdır.
f(2) = 4 = f(–2) dir. Fakat 2 ≠ –2 olduğundan f fonksiyonu bire bir değildir.
Siz de, tanım kümesini pozitif gerçek sayılar alarak çözümde izlediğimiz basamakların
+
ve sonucun nasıl değişeceğini açıklayınız. Böylece f: R → R, f(x) = x2 fonksiyonunun
bire bir fonksiyon olup olmadığını bulmuş olacaksınız.
3
f: R → R, f(x) = x3 fonksiyonunun bire bir olup olmadığını cebirsel olarak gösterelim.
a ve b gibi iki gerçek sayı için f(a) = a3 ve f(b) = b3 olur. f(a) = f(b) olduğunda a ve b değerleri arasındaki ilişkiyi bulalım.
f(a) = f(b) ⇒ a3 = b3 ⇒ a = b
Böylece f(a) = f(b) ise a = b olduğunu göstermiş olduk. Bu durumda f: R → R, f(x) = x3
fonksiyonu bire bir fonksiyondur.
4
f: R → R, f(x) = 3x3 – 1 fonksiyonunun bire bir olma durumunu inceleyelim.
a, b ∈ R olmak üzere f(a) = f(b) olsun. f(a) = 3a3 – 1 ve f(b) = 3b3 – 1 olduğundan
3a3 – 1 = 3b3 – 1 ⇒ 3a3 = 3b3 ⇒ a3 = b3 ⇒ a = b
Bu nedenle f fonksiyonu bire birdir.
Ünite 3. Fonksiyonlar
585
Bölüm
3.2
Fonksiyonların Grafikleri
5
f: R → R, f(x) = |x + 1| fonksiyonunun bire bir olup olmadığını inceleyelim.
1. Yol:
a, b ∈ R olmak üzere f(a) = f(b) olsun. f(x) = |x + 1| olduğundan
f(a) = |a + 1| ve f(b) = |b + 1| dir. Dolayısıyla,
f(a) = f(b)
⇒ |a + 1| = |b + 1| dir. Buradan
a + 1 = b + 1 veya a + 1 = –(b + 1)
⇒ a = b veya a + 1 = –b – 1 ⇒ a = b – 2
elde edilir. Bu nedenle, f fonksiyonu bire bir değildir.
2. Yol:
f fonksiyonunun tanım kümesi R dir. –2 ve 0 gerçek sayıları için,
f(–2) = |–2 + 1| = |–1| = 1 ve f(0) = |0 + 1| = |1| = 1
olur. Fakat –2 ≠ 0 olduğu için f fonksiyonu bire bir değildir.
Bir fonksiyonun bire bir olup olmadığını, yukarıdaki örneklerde kullandığımız cebirsel
yaklaşımla tespit edebileceğimiz gibi fonksiyonun grafiğinden yararlanarak da belirleyebiliriz.
Bir fonksiyonun grafiği verildiğinde tanım kümesindeki herhangi bir a değerinin bu
fonksiyon altındaki görüntüsünü bulabildiğimizi belirtmiştik. a noktasından x-eksenine dik olarak çizilen bir doğrunun grafiği kestiği noktanın ordinatı olan b değeri, a nın
f altındaki görüntüsüdür.
Eğer tanım kümesindeki birden fazla eleman için x-ekseninden çizilen dik doğrunun
grafiği kestiği noktanın ordinatı aynı ise bu fonksiyon bire bir değildir. Çünkü bu durumda tanım kümesindeki birden fazla elemanın görüntüsü aynı olacaktır.
586
Ünite 3. Fonksiyonlar
Bire Bir ve Örten Fonksiyonlar
6
Anahtar Bilgi
f: R → R , f(x) = 2x fonksiyonunun bire bir olduğunu fonksiyonun grafiğini kullanarak
belirleyelim.
Bir fonksiyonun görüntü kümesinden x-eksenine paralel
olarak çizilen doğrulardan en
az biri fonksiyonun grafiğini
birden fazla noktada kesiyorsa bu fonksiyon 1-1 değildir.
f: R → R , f(x) = 2x fonksiyonunun grafiğini çizdikten sonra f altında görüntüleri aynı
olan gerçek sayılar olup olmadığını fonksiyonun grafiğini kullanarak belirleyelim.
Örneğin, f altında görüntüsü 4 olan kaç tane x
değeri olduğunu bulmak için y = 4 noktasından
yatay bir doğru çizelim.
y
6
5
Bu yatay doğru, grafiği yalnız (2, 4) noktasında
kesmektedir. Bu durumda görüntüsü 4 olan sadece bir nokta vardır o da x = 2’dir.
4
3
2
1
–3 1 –2
–
0
1
2
3
x
–1
–2
–3
–4
y
Farklı y değerleri için de yatay doğrular çizdiğimizde, her yatay doğrunun grafiği sadece bir
noktada kestiğini görebiliriz. Bu da bize f fonksiyonunun bire bir fonksiyon olduğunu göstermektedir.
6
5
4
3
Yandaki örnekte detaylandırdığımız yönteme
yatay doğru testi denilmektedir.
2
1
–3 1 –2
–
0
1
2
3
x
–1
–2
–3
–4
Ünite 3. Fonksiyonlar
587
Bölüm
3.2
Fonksiyonların Grafikleri
Bir fonksiyonun grafiği üzerinde, x-eksenine paralel çizilen her doğru grafiği en
fazla bir noktada kesiyorsa grafik 1-1 fonksiyon grafiğidir. Bu grafiği birden fazla
noktada kesen en az bir yatay doğru varsa bu fonksiyon 1-1 değildir. Bu yönteme
yatay doğru testi adı verilir.
Verilen bir fonksiyon grafiği üzerinde yatay doğru testini uygulayarak fonksiyonun bire
bir olup olmadığını örneklerle inceleyelim.
7
Şekilde grafiği verilen f: R → R, f(x) = x2 fonksiyonunun 1 – 1 olup olmadığını inceleyelim.
y
9
8
7
6
5
4
3
2
1
–3 –2
–1
0
–1
1
2
3
x
Grafikte yatay doğru testi uyguladığımızda, yatay doğrulardan grafiği iki noktada kesenler olduğunu görmekteyiz.
y
8
7
Bu durumda f: R → R, y = x2 fonksiyonu bire bir
değildir.
6
5
4
3
2
1
–3 –2
588
–1
0
1
2
Ünite 3. Fonksiyonlar
3
x
Bire Bir ve Örten Fonksiyonlar
8
f: R → R, y = x3 fonksiyonunun bire bir olup olmadığını yatay doğru testi yardımıyla
inceleyelim.
Fonksiyonun grafiğinde yatay doğru testini uyguladığımızda, her yatay doğrunun grafiği yalnızca bir
noktada kestiği görülmektedir. Bu durumda
f: R → R, y = x3 fonksiyonu bire birdir.
y
F
3
E
2
1 A
–3 –2
–1
–1
–2
0
B
1
2
3
x
C
–3 D
9
Grafiği verilen fonksiyonun bire bir olup olmadığını
yatay doğru testi kullanarak belirleyelim.
y
4
3
2
1
–3
–2 –1
0
1
2
3
x
–1
–2
–3
Grafik üzerinde çizilen yatay doğrulardan bazıları
grafiği birden fazla noktada kesmektedir. Örneğin,
y = 0 doğrusu grafiği x in –2, 1 ve 2 değerlerinde
kesmektedir. Bu durumda f fonksiyonu bire bir
değildir.
y
4
3
2
1
–3
–2 –1
0
1
2
3
x
–1
–2
–3
Ünite 3. Fonksiyonlar
589
Bölüm
3.2
Fonksiyonların Grafikleri
10
y
2
1
–6 –5
–4
–3
0
–2 –1
1
2
3
4
5
6
x
–1
–2
Grafiği verilen fonksiyonun bire bir olup olmadığını yatay doğru testi kullanarak belirleyelim.
Grafik üzerinde çizdiğimiz yatay doğru, grafiği birden fazla noktada kesebilmektedir.
Bu durumda f fonksiyonu bire bir değildir.
y
2
1
–6 –5
–4
–3
0
–2 –1
1
2
3
4
5
6
–1
–2
Örten Fonksiyon
Bire bir fonksiyona girişte verdiğimiz örneği tekrar ele alalım.
A
B
B
.a
.1
.a
.b
.2
.b
.c
.3
.c
A
B
.a
.1
.b
.c
590
A
Ünite 3. Fonksiyonlar
.3
.1
.2
.3
.4
A
B
.a
.1
.b
.2
.c
.3
x
Bire Bir ve Örten Fonksiyonlar
Buna göre,
•
İlk sütundaki fonksiyonların değer kümeleri ile görüntü kümeleri birbirine eşittir.
•
İkinci sütundaki fonksiyonların değer kümeleri ile görüntü kümeleri birbirine eşit
değildir.
Anahtar Bilgi
f: A → B, f(A) = B ise f fonksiyonuna örten fonksiyon
denir.
Benzer şekilde, f: {1, 2, 3, 4, 5} → {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ve f(x) = 2x fonksiyonunun değer kümesi ile görüntü kümesini karşılaştıralım. Önce fonksiyonunun görüntü kümesini bulalım.
Başka bir ifadeyle, her b ∈
B için b = f(a) olacak şekilde
f(1) = 2 · 1 = 2, f(2) = 2 · 2 = 4, f(3) = 2 · 3 = 6, f(4) = 2 · 4 = 8, f(5) = 2 · 5 = 10 olduğundan
f(A) = {2, 4, 6, 8, 10} olup bu küme f in görüntü kümesidir. Diğer taraftan f in değer kümesi B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} dir. Bu durumda f(A) ≠ B olup görüntü kümesi değer
kümesine eşit değildir.
bir a ∈ A varsa f fonksiyonu
örten fonksiyondur.
Eğer bir fonksiyonun değer kümesindeki her eleman, tanım kümesinden en az bir
eleman ile eşleşmiş ise bu fonksiyon örten fonksiyondur.
Bir başka ifadeyle, bir fonksiyonun görüntü kümesi ile değer kümesi birbirine eşitse fonksiyon örtendir.
Şimdi bu tanımları cebirsel olarak ifade edelim:
f: A → B fonksiyonu için f(A) = B ise f örtendir.
Bu tanımı aşağıdaki gibi belirtmek yaygın ve kullanışlıdır:
f: A → B fonksiyonu verilsin. Her b ∈ B için b = f(a) olacak şekilde en az bir a ∈ A
varsa f örten bir fonksiyondur.
g
f
A
B
•
•
C
D
•
•
•
•
•
•
•
•
•
•
•
f örten değildir.
g örtendir.
Çünkü f(A) ≠ B dir.
Çünkü g(A) = B dir.
1
f: {1, 2, 3, 4, 5} → {2, 4, 6, 8, 10}, f(x) = 2x fonksiyonunun örten olup olmadığını inceleyelim.
f(A) = {2, 4, 6, 8, 10} ve B = {2, 4, 6, 8, 10} olup f(A) = B olduğundan f fonksiyonu örtendir.
Ünite 3. Fonksiyonlar
591
Bölüm
3.2
Fonksiyonların Grafikleri
2
Aşağıda verilen fonksiyonların örten olup olmadıklarını inceleyelim.
f
A
.18
.3
.8
.11
.15
B
C
g
.1
.4
.15
.3
.8
.29
.4
.9
.21
.5
.12
.17
.7
.15
D
f fonksiyonun görüntü kümesi f(A) = {18, 15, 29, 21} ve değer kümesi B = {18, 15, 29, 21, 17}
dir. Bu durumda, f(A) ≠ B olduğundan f bir örten fonksiyon değildir. g fonksiyonunun
görüntü kümesi g(C) = {4, 8, 9, 12, 15} ve değer kümesi D = {4, 8, 9, 12, 15} dir. g(C) = D
olduğundan g bir örten fonksiyondur.
Bir fonksiyonun bire bir olma durumunu incelemek için kullandığımız yatay doğru
testini fonksiyonun örten olma durumunu incelemek için de kullanabiliriz. Şöyle
ki, değer kümesinin elemanlarından çizilen her yatay doğru fonksiyonun grafiğini
en az bir noktada kesiyorsa bu fonksiyon örten fonksiyondur.
3
y
Bir f: [1, 4] → [2, 8] fonksiyonunun grafiği
şekildeki gibidir. Bu fonksiyonun örten
olup olmadığını yatay doğru testi ile inceleyelim.
8
7
6
5
4
3
2
1
1
592
–2
–
0
–1
1
2
3
Ünite 3. Fonksiyonlar
4
5
x
Bire Bir ve Örten Fonksiyonlar
Fonksiyonun tanım ve değer kümeleri şekilde
kırmızı renklerle gösterilmiştir. Yatay doğru testi
uygulandığında, değer kümesindeki her elemanın f
fonksiyonu altında bir ters görüntüsünün olduğu
görülecektir. Bu nedenle, bu fonksiyon örtendir.
y
8
7
6
5
Sizce, g: [1, 4] → [0, 10] fonksiyonu bu örnekteki
aynı grafikle verilirse örten olur mu? Neden?
4
3
2
1
0
1
2
3
4
x
5
4
f: R → R, f(x) = x2 fonksiyonunun örten olup olmadığını belirleyelim.
1. Yol: Fonksiyonun cebirsel kuralını kullanarak.
Fonksiyonunun tanım ve değer kümeleri tüm gerçek sayılar olarak verilmiş. Amacımız,
her b ∈ R için b = f(a), yani b = a2 şartını sağlayan bir a ∈ R olup olmadığını belirlemektir. Eğer b = –1 alırsak, –1 = a2 eşitliğini sağlayan bir gerçek sayı olmadığından, f
fonksiyonu örten olma şartını sağlamaz, yani örten değildir.
2. Yol: Fonksiyonun grafiğini kullanarak.
f fonksiyonunun grafiğini çizmeyi daha önce öğrenmiştik. Çizdiğimiz grafikte fonksiyonun değer kümesi
mavi renkle belirtilmiştir. Grafik incelendiğinde değer
kümesindeki negatif değerlerle eşlenen x değerlerinin
olmadığı görülmektedir.
y
9
8
7
6
5
Bu durumda f fonksiyonu örten değildir.
4
+
Sizce f: R → R , f(x) = x2 fonksiyonu örten bir fonksiyon
mudur? Neden?
3
2
1
–3 –2
–1
0
–1
1
2
3
x
Ünite 3. Fonksiyonlar
593
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında, dinamik matematik/geometri yazılımları kullanarak grafikleri çizilen fonksiyonların 1-1
veya örten olup olmadıklarını yatay doğru testi yardımıyla inceleyeceğiz.
Araç ve Gereçler: Elektronik tablolalama, grafik hesap makinesi, dinamik geometri/matematik yazılımı vb. grafik çizimi yapılabilen bir araç/yazılım.
Adım 1
Grafik çizme özelliği olan bir dinamik matematik/geometri yazılımı kullanarak gerçek sayılarda tanımlı y = f(x) = 4x – 1
grafiğini çiziniz.
Adım 2
y-eksenine dik (veya x-eksenine paralel) doğrular çizerek yatay doğru testini uygulayınız ve fonksiyonun
•
bire bir fonksiyon
•
örten fonksiyon
olup olmadığını belirleyiniz.
Adım 3
Gerçek sayılarda tanımlı
•
y = h(x) = –3x + 2,
•
y = g(x) = 6x,
•
y = t(x) = x2 – 5,
y = F(x) = x3,
•
y = G(x) = 2x,
•
y = H(x) = x3 – 2x2 – 5x + 6
•
fonksiyonlarının grafiklerini çizdirerek her bir fonksiyonun
•
bire bir fonksiyon
•
örten fonksiyon
olup olmadığını belirleyiniz.
Adım 4
Hem 1-1, hem de örten olan fonksiyonların grafiklerinin ortak özelliklerini açıklayınız.
594
Ünite 3. Fonksiyonlar
Bire Bir ve Örten Fonksiyonlar
5
f: R → R, f(x) = 2x + 1 fonksiyonunun 1-1 ve örten olup olmadığını inceleyelim.
f fonksiyonunun bire bir olması için, her a, b ∈ R ve a ≠ b için f(a) ≠ f(b) olmalıdır.
f(a) = 2a + 1 ve f(b) = 2b + 1 olduğundan, 2a + 1 ≠ 2b + 1 olması a ≠ b anlamına gelmektedir. Bu nedenle, f fonksiyonu 1-1’dir.
f fonksiyonunun örten olması için, her b ∈ R için f(a) = b eşitliğini sağlayan en az bir
a ∈ R bulunabilmelidir. Verilen fonksiyon için f(a) = 2a + 1 olduğundan, amacımız, her
b ∈ R için 2a + 1 = b eşitliğini sağlayan bir a gerçek sayısının var olup olmadığını bulmaktır.
b- 1
! R dir. Dolayısıyla f fonksiyonu örtendir.
b ∈ R iken 2a + 1 = b ise a =
2
Bu durumda, f: R → R, f(x) = 2x + 1 fonksiyonu hem 1-1 hem de örtendir.
Sizce f: N → N, f(x) = 2x + 1 fonksiyonu örten bir fonksiyon mudur? 1-1 bir fonksiyon
mudur? Neden?
f: A → B, y = f(x) fonksiyonu hem bire bir hem de örten fonksiyon ise f fonksiyonuna, bire bir ve örten fonksiyon denir.
Sizce f: R → R, f(x) = x3 fonksiyonu bire bir ve örten fonksiyon mudur? Neden?
Ünite 3. Fonksiyonlar
595
Bire Bir ve Örten Fonksiyonlar
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme Soruları
b.
y
6
1.
Aşağıdaki kavramları kendi cümlelerinizle açıklayınız.
a.
Bire bir fonksiyon
b.
Örten fonksiyon
4
Yatay doğru testi
3
c.
5
g
2
2.
3.
f: R →R , f(x) = 3x – 4 fonksiyonu bire bir midir?
Cevabınızı fonksiyonun grafiğini çizmeden açıklayınız.
1
–4 –3 –2
–1
f: {2, 3, 4, 5} → {8, 12, 16, 20}, f(x) = 4x fonksiyonu
örten midir? Cevabınızın nedenini açıklayınız.
2.
Yatay doğru testini kullanarak aşağıda grafikleri
verilen fonksiyonların tanımlı oldukları kümelerde
c.
Bire bir ve örten olup olmadıklarını belirleyiniz.
3
y
h
2
6
f
–4 –3 –2
5
–1
1
4
0 1
–1
3
–2
2
–3
1
–4
0
–1
3
y
4
–1
2
x
g: R →R
Örten
–2
3
–4
f: R →R , f(x) = 2x + 3 fonksiyonunun grafiğini
çizerek 1-1 ve örten olduğunu yatay doğru testi
yardımıyla gösteriniz.
a.
2
–3
Bire bir
1
2
3
x
–2
–3
f: R →R
596
–1
1
–2
Alıştırmalar
1.
0
Ünite 3. Fonksiyonlar
h: R – {0} →R
4
x
Bire Bir ve Örten Fonksiyonlar
KENDİMİZİ SINAYALIM
ç.
4.
y
Gerçek sayılarda tanımlı h fonksiyonun grafiği
veriliyor.
6
y
5
k
4
h
3
2
0
x
5
1
0 1
–1
–3 –2 –1
2
3
x
Yatay doğru testini kullanarak aşağıdaki soruları
cevaplayınız.
–2
k: R →[–1, ∞)
3.
a.
h fonksiyonu 1-1 ve örten midir?
b.
g: (0, 5) → R, g(x) = h(x) şeklinde tanımlanan g
fonksiyonu 1-1 ve örten midir?
5.
Bir dinamik geometri yazılımı kullanarak gerçek
sayılarda tanımlı
Gerçek sayılarda tanımlı f fonksiyonun grafiği
veriliyor.
F(x) = –x + 1
G(x) = x2 – 3
y
H(x) = x3 + 1
f(x) = 3x
3
h(x) = x3 – 3x
y = f(x)
0
2
fonksiyonlarının grafiklerini çizdiriniz. Yatay doğru
testini kullanarak bu fonksiyonların 1-1 ve örten
olup olmadıklarını belirleyiniz.
x
–1
1
fonksiyonunun 1-1 ve
x
örten olup olmadığını cebirsel olarak gösteriniz.
Yatay doğru testini kullanarak aşağıdaki soruları
cevaplayınız.
6.
a.
f fonksiyonu 1-1 ve örten midir?
7.
b.
g: [0, 2]→[–1, 3], g(x) = f(x) şeklinde tanımlanan g
fonksiyonu 1-1 ve örten midir?
Aşağıdaki fonksiyonları; bire bir ve örten, bire bir
ama örten değil, bire bir değil ama örten, hem bire
bir değil hem örten değil şeklinde sınıflandırınız:
i.
f: R→R , f(x) = x4
f: R – {0}→R , f (x) =
Ünite 3. Fonksiyonlar
597
Bire Bir ve Örten Fonksiyonlar
KENDİMİZİ SINAYALIM
ii.
g: N→N , g(x) = 2
iii. h: {a, b}→{1, 2, 3} , h(a) = 2 , h(b) = 1
iv. k: [0, ∞)→R , k(x) = x5
şaka yapmak ister. Bir gün gizlice Hoca’nın taşları
büyüklüğünde bir avuç taşı çömleğe boşaltır. Sonra doğruca Hoca’nın yanına gider ve sorar:
vi. m: [0, ∞)→R , m(x) = x
— Hocam, bugün ramazanın yirmi dördü mü, yirmi
beşi mi? Arkadaşlarla bir karara varamadık. Bana Hoca’ya
git danış. O bilir, dediler.
vii. n: Z→[0, ∞) , n(x) = 2 – x
Hoca:
viii. o: [0, ∞)→[0, ∞) , o(x) = x2
— Olur, şu bizim çömleğe bir bakalım,
v.
t: R→R , t(x) = |x|
der. Hoca, çömleğin yanına gider. İçindeki taşları saymak
için boşaltır. Hayretler içinde kalır. Taşları sayar, tam 124
tane taş vardır. Kendi kendine:
Uygulama ve Problem Çözme
— Allah Allah! Hiç böyle şey olmaz!
1.
diye söylenir. Soru soran adamın yanına geri gelir:
EĞLENCELİ MATEMATİK
— Bugün ramazanın altmış ikisi der.
Adam:
— Aman Hocam! Hiç böyle şey olur mu? Hiç ay altmış
iki çeker mi?
Hoca:
— Sen gene şükret, ben insaflı davrandım da yarısını
söyledim. Benim çömleğin hesabına kalsaydı bugün ramazanın yüz yirmi dördü idi, der.
Eskiden takvim günümüzdeki kadar yaygın değildi.
Özellikle köylerde ancak önemli bazı olaylara göre
zaman belirlenirdi. O yüzden özellikle ramazanda
günleri şaşırmamak için bazı usuller uygulanırdı.
Nasreddin Hoca da zamanı belirlemek için bir çömlek alır bir yığın ufak taş toplar.
Akşam olduğu zaman bu taşlardan bir tanesini
çömleğe atardı. Ramazanın kaçı olduğunu öğrenmek isteyince çömlekteki taşları sayardı. Hoca’nın
bu usulünü bilen bir arkadaşı Hoca’ya küçük bir
598
Ünite 3. Fonksiyonlar
Nasrettin Hoca’nın eşleme hesabı doğru olsaydı yani ramazanın her bir gününe karşılık çömleğe bir taş atılmış
olsaydı bu durum aşağıdaki fonksiyon türlerinden hangilerine örnek olurdu?
I. Bire bir fonksiyon
II. Örten fonksiyon
III. Bire bir ve örten fonksiyon
Bire Bir ve Örten Fonksiyonlar
BÖLÜM ÖZETİ
Bir fonksiyonun grafiği çizilirken tanım kümesi yatay eksende, değer kümesi de dikey eksende gösterilir.
Bir (a,b ) sıralı ikilisini oluşturan bileşenler bir f fonksiyonunun kuralı olan y = f(x) eşitliğini b = f(a) şeklinde sağlarsa,
koordinatları (a, b) olan nokta f fonksiyonunun grafiği üzerindedir. Bunun tersi de doğrudur: y = f(x) fonksiyonunun
grafiği üzerindeki bir noktanın koordinatları (a,b) ise a ile b arasında b=f(a) ilişkisi vardır. Değer kümesinin bir elemanı
olan b ile tanım kümesinin bir elemanı olan a arasında b=f(a) ilişkisi varsa, b nin f altındaki bir ters görüntüsü a dır deriz.
A ve B kümeleri ile f : A → B fonksiyonu verilsin. Herhangi bir C ve D kümeleri C ⊂ A ve D ⊂ f(A) olsun. Bu durumda
tanım kümesinin bir alt kümesi olan C kümesindeki elemanların f altındaki görüntülerinin oluşturduğu kümeye
kısaca C nin f altındaki görüntüsü denir ve f(C) ile gösterilir. Bu küme ortak özellik yöntemiyle şu şekilde belirtilir:
f(C) = {f(x): x ∈ C}
Görüntü kümesinin bir alt kümesi olan D kümesindeki elemanların f altındaki ters görüntülerinin oluşturduğu kümeye, D kümesinin f altındaki ters görüntüsü denir ve bu küme ortak özellik yöntemiyle şu şekilde belirtilir:
D nin f altındaki ters görüntüsü = {x ∈ A : f(x) ∈ D}
Bir grafik fonksiyon grafiği ise, yatay eksende gösterilen tanım kümesinin elemanlarından geçen dikey doğrular
grafiği birer noktada keser. Herhangi bir dikey doğru grafiği birden fazla noktada kesiyorsa grafik fonksiyon grafiği
değildir. Bu şekilde verilen grafiğin bir fonksiyona ait olup olmadığını anlama yöntemine dikey doğru testi denir.
f(x) = xn (n ∈ Z) biçimindeki fonksiyonların grafikleri çizilirken önce değer tablosu oluşturulur. Değer tablosundaki
veriler koordinat düzleminde işaretlenir ve bu noktalar birleştirilerek grafik çizilir. Örneğin,
R de tanımlı f(x) = x2
fonksiyonunu grafiği
R de tanımlı f(x) = x3
fonksiyonunu grafiği
1
x
fonksiyonunun grafiği
f: R – {0} → R, f(x) =
y y y
5 5 5
4 4 4
3 3 3
3 3 3
3 3 3
2 2 2
2 2 2
2 2 2
1 1 1
1 1 1
–5–2
–4–1
–3–1
–2 –1
–5 –4
–5 –3
–4
–3
–2
1 1 1
0 10 21 0321 432 543 x54 x 5 x
–4 –4
–2
–4 –2
–1
–20 –1
10 120 231 34
2 x43 x 4 x
–3 –3
–3 –1
–1 –1 –1
–1 –1 –1
–2 –2 –2
–4 –4–3 –4
–3–2 –3
–2–1 –2
–1 0–101 102 12 3 23 4 34x x4 x
–2 –2 –2
–1 –1 –1
–3 –3 –3
–3 –3 –3
–4 –4 –4
–2 –2 –2
–4 –4 –4
–5 –5 –5
y y y
4 4 4
y y y
4 4 4
x bağımsız, y de x e bağımlı bir değişken olmak üzere, bu değişkenlere ait (x1, x2) ve (x2, y2) değerleri verilsin. (x1, x2)
değerlerinden (x2, y2) değerlerine geçişte yaşanan
y değerlerindeki değişim
y - y1
= 2
değişim oranı (hızı) =
x2 – x1
x değerlerindeki değişim
şeklinde ifade edilir.
Ünite 3. Fonksiyonlar
599
Bölüm
3.2
Fonksiyonların Grafikleri
y = f(x) = mx + b şeklindeki bir doğrusal fonksiyonun değişim oranı (hızı) sabittir ve bu değer bu fonksiyonla belirtilen
doğrunun eğimi olan m değeridir.
Bir f fonksiyonu için, a ∈ R iken f(x) = 0 oluyorsa a gerçek sayısına f fonksiyonunun sıfırı denir. Diğer bir ifadeyle, bir f
fonksiyonun sıfırları f(x) = 0 denkleminin kökleridir. Bu durumda, f fonksiyonun sıfırları fonksiyonun grafiğinin x-eksenini kestiği noktalardır.
x ekseni, y = 0 doğrusal denklemiyle; y ekseni de x = 0 doğrusal denklemiyle ifade edilir.
Bir f fonksiyonu ve b ∈ R için f(x) = b denkleminin çözüm kümesi, f fonksiyonunun grafiği ile y eksenini b de kesen
yatay doğrunun kesiştiği noktaların apsislerinden oluşur.
Tanım kümesinin ayrık alt kümelerinde farklı kurallarla tanımlı olan fonksiyonlara parçalı tanımlı fonksiyonlar veya kısaca parçalı fonksiyonlar denir.
y = f (x) = | x | = (
–x, x < 0 ise
x, x ≥ 0 ise
parçalı fonksiyonu mutlak değer fonksiyonudur ve grafiği şekildeki gibidir:
Bir fonksiyonun tanım kümesindeki her bir elemanın görüntüsü diğer elemanların görüntülerinden farklı ise o fonksiyona bire bir fonksiyon (veya 1-1) denir. Bir
f : A → B fonksiyonu bire bir ise şu şartları sağlar:
herhangi a ∈ A ve b ∈ A için a ≠ b ⇒ f(a) ≠ f(b)
herhangi a ∈ A ve b ∈ A için f(a) = f(b) ⇒ a = b
Bir fonksiyonun değer kümesindeki her eleman, tanım kümesinden en az bir eleman ile eşleşmiş ise bu fonksiyon örten
fonksiyondur. f: A → B fonksiyonu örten ise aşağıdaki şartları sağlar:
f(A) = B dir.
•
Her b ∈ B için b = f(a) olacak şekilde en az bir a ∈ A vardır.
•
f: A → B, y = f(x) fonksiyonu hem bire bir hem de örten fonksiyon ise f fonksiyonuna, bire bir ve örten fonksiyon
denir.
Bir fonksiyonun grafiği üzerinde, x-eksenine paralel çizilen her yatay doğru grafiği en fazla bir noktada kesiyorsa grafik
1-1 fonksiyon grafiğidir. Grafiği birden fazla noktada kesen en az bir yatay doğru varsa bu fonksiyon 1-1 değildir.
Değer kümesinin elemanlarından çizilen her yatay doğru fonksiyonun grafiğini en az bir noktada kesiyorsa bu fonksiyon örten fonksiyondur.
Bu şekilde bir fonksiyonun grafiğini kullanarak fonksiyonun 1-1 olma ve örten olma durumlarını tespit etme yöntemine
yatay doğru testi denir.
600
Ünite 3. Fonksiyonlar
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
1.
Aşağıda verilen ifadelerdeki boşlukları uygun şekilde doldurunuz.
a.
Bir fonksiyonun grafiğinde girdiler . . . . . . . . . . . . . . . . . . . . . ekseninde çıktılar da . . . . . . . . . . . . . . . . . . . . . ekseninde gösterilir.
b.
Bir fonksiyonun belirlediği ikililer kümesinin kartezyen düzlemde gösterilmesine fonksiyonun
. . . . . . . . . . . . . . . . . . . . . gösterimi denir.
c.
Bir fonksiyonun girdilerine . . . . . . . . . . . . . . . . . . . . . kümesi ve
çıktılarına . . . . . . . . . . . . . . . . . . . . . kümesi denir.
ç.
a değeri pozitif iken, y = ax şeklindeki bir fonksiyon
için a değeri . . . . . . . . . . . . . . . . . . . . . ise fonksiyonun grafiği a
değeri . . . . . . . . . . . . . . . . . . . . . . . . . . . . . yaklaşır.
d.
a değeri negatif iken, y = ax şeklindeki bir fonksiyon
için a değeri . . . . . . . . . . . . . . . . . . . . . . . ise fonksiyonun grafiği a
değeri . . . . . . . . . . . . . . . . . . . . . . . . . . . . yaklaşır.
e.
f.
g.
3.
4.
f: [–2, 4] → R, f(x) = 3x – 2 fonksiyonu veriliyor.
Buna göre;
a.
Bu fonksiyonun tanım, değer ve görüntü kümelerini belirtiniz.
b.
Fonksiyonun grafiği üzerindeki bazı noktaların koordinatlarını, fonksiyonun değerler tablosunu oluşturarak tespit ediniz ve fonksiyonun grafiğini çiziniz.
c.
{–8, –5, –1, 0, 1, 6, 9} kümesinin f altındaki ters görüntüsünü bulunuz.
5.
Aşağıdaki grafikleri verilen fonksiyonların tanım ve
görüntü kümelerini bulunuz.
a.
32
y = f(x) şeklindeki bir fonksiyonun grafiğinde x-eksenini kesen noktalar . . . . . . . . . . . . . . . . . denkleminin çözüm kümesi olur.
Kartezyen düzlemdeki bir grafiğin, herhangi bir
fonksiyonun grafiği olup olmadığını anlamak için
. . . . . . . . . . . . . . . . . . . . . dikey doğrular çizilir ve grafiği kesen
bu doğruların grafiği . . . . . . . . . . . . . . . . . . . . . noktada kesmesi
gerekir.
y-eksenine dik olarak çizilen her bir doğrunun bir
fonksiyonun grafiğini en fazla birer noktada kesmesi, o fonksiyonun . . . . . . . . . . . . . . . . . . . . . olduğunu gösterir.
A = " 1, 2, 3, 4, 5 , kümesi için f: A → B, f(x) = –2x –
3 fonksiyonu veriliyor. Buna göre f nin görüntü
kümesini bulunuz.
y
y = f(x)
4
1
8
b.
y
k
d
x
y = g(x)
a
b
cx
n
m
c.
y
y = h(x)
2.
f: A → B, f(x) = 3x – 3 ve A = {–1, 2, 4, 7} ise f(A)
kümesini bulunuz.
x
Ünite 3. Fonksiyonlar
601
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
6.
a.
Aşağıda verilen grafiklerden hangileri gerçek sayılarda tanımlı bir fonkiyona ait olabilir?
8.
f: R → R, f(x) = ax + b fonksiyonu için f(1) = 7, f(8) = 35
olduğuna göre f(3) kaçtır?
y
x
9.
y = f(x)
–1
b.
Grafiği verilen f
fonksiyonu için
y
f ^1h + f ^2h
ifadesif ^3h
1
1
y
2
x
nin değeri kaçtır?
x
c.
10. Gerçek sayılarda tanımlı aşağıdaki fonksiyonların
{–1, 0, 1, 2, 3} girdi değerleri için değerler tablosu
oluşturarak grafiklerini çiziniz. Bu fonksiyonların
grafiklerini bir grafik çizim yazılımı/aracı ile çizdirip
bunları kendi çizimleriniz ile karşılaştırınız.
y
x
ç.
y
a.
f(x) = 4
b.
c.
h(x) = 3x + 0,3
ç.
d.
l(x) = 0,25x + 1
e.
f.
n(x) = 3x2
g.
ğ.
p(x) = x2 – 9
h.
g(x) = –4x
x
k(x) = - - 4
2
m(x) = x2
2
o(x) = + 1
x
t(x) = 0,5x2 – 1
x
11. Aşağıdaki doğrusal fonksiyonların grafiklerini çizerek değişim oranlarını (hızını) belirtiniz.
7.
602
f: R → R, f(x) = mx + n fonksiyonu için f(4) = 5,
f(2) = 1 olduğuna göre m + n kaçtır?
Ünite 3. Fonksiyonlar
a.
y=x+1
b. y = –2x
c. y = 3x + 5
ç.
y=
3
x+2
4
d. y = –8
e. y = 7
f.
y = –4x + 1
g. y = –x
ğ. y =
h.
y=0·2+x
ı. y = –4 + 7x
i. y = –0 · 3x – 0 · 4
3
-x
4
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
12. Aşağıda verilen fonksiyonların tanım kümelerinin
bazı değerleri için değerler tablosu yaparak grafiklerini çiziniz. Bu fonksiyonların grafiklerini bir grafik
çizim yazılımı/aracı ile çizdirip bunları kendi çizimleriniz ile karşılaştırınız.
a.
f: [–5, 5] → R, f(x) = –2
b.
g: [–3, 3] → R, g(x) = –3x
c.
ç.
14. Aşağıdaki fonksiyonların bire-bir ve/veya örten
olup olmadığını inceleyiniz.
a.
3
2
1
–3 –2 –1
–1
1
2
x
k: [–2, 2] → R, k(x) = - - 4
2
b.
d.
l: R → R, l(x) = –0,25x –1
e.
m: [–5, 3] → R, m(x) = x2
f.
n: R → [0, 12], n(x) = 3x2
g.
o: R → R, o(x) =
ğ.
p: [–6, 4] → R, p(x) = x2 – 16
h.
t: R → R, t(x) = 0,5x2 – 1
ı.
s: R → R, s(x) = 2x3
i:
b: R → R, b(x) = x3 – 2
y = f(x)
1 2 3
x
–2
–3
h: R → R, h(x) = 3x -
13.
f: [0, ∞) → [0, ∞)
y
g: R → R
y
3
2
1
–3 –2 –1
–1
2
x+1
y = g(x)
1 2 3
x
–2
–3
c.
h: R → R
y
4
3
2
1
–3 –2 –1
–1
y = h(x) –2
Şekilde verilen f
fonksiyonunun
grafiğine göre;
y
p
n
l
x
–3
ç.
m
1 2 3
k: R → [0, ∞)
y
3
k
a
b
c
d
e
x
a.
f(a), f(b), f(e) değerlerini bulunuz.
b.
f(x) = m ise x kaçtır?
2
1
–3 –2 –1
–1
y = k(x)
1 2 3
x
–2
–3
Ünite 3. Fonksiyonlar
603
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
15. Aşağıda gerçek sayılada tanımlı g, h, f, k ve t fonksiyonlarının grafikleri verilmiştir.
6
5
4
3
2
1
y
6
5
4
3
2
1
y = g(x)
–5 –4 –3 –2 –1
–1
6
5
4
3
2
1
y
y = h(x)
–5 –4 –3 –2 –1
–1
–2
–3
–4
–5
1 2 3 4 5 6 x
–2
–3
–4
–5
6
5
4
3
2
1
–5 –4 –3 –2 –1–1
–2
–3
–4
–5
1 2 3 4 5 6 x
–2
–3
–4
–5
–2
–3
–4
–5
6
5
4
3
2
1
y = k(x)
–5 –4 –3 –2 –1
–1
1 2 3 4 5 6 x
–5 –4 –3 –2 –1–1
y
y
1 2 3 4 5 6 x
y = t(x)
Buna göre aşağıdaki denklemlerin çözüm kümelerini bulunuz.
y
a.
g(x) = 0
b. h(x) = 0
c. f(x) = 0
ç.
k(x) = 0
d. t(x) = 0
e. h(x) = 4
f.
f(x) = 2
g. k(x) = 5
h. k(x) = 5
ı.
h(x) = –5
1 2 3 4 5 6 x
y = f(x)
16. Gerçek sayılarda tanımlı f(x) = (
4x - 2, x > 2
2 - x, x ≤ 2
fonsiyonu için f(–2) + f(4) + f(2) değerini bulunuz.
604
Ünite 3. Fonksiyonlar
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
17.
Şekilde grafiği
verilen fonksiyonun denklemi
aşağıdakilerden
hangisidir?
y
3
2
1
–3 –2 –1
–1
1
2
3
21. f: A " R, f ^ x h = x 2 + 2x ve f ^A h = [8, 15] olduğuna göre, A kümesi aşağıdakilerden hangisidir?
x
A) [–4, 2] ∪ [–5, 3]
B) [–5, –4] ∪ [2, 3]
C) [–5, –4]
D) [2, 3]
E) [2, 3] ∪ [–5, ∞)
–2
–3
A) y = 3x + 2
x y
C) + = 2
2 3
B) f(x) = –3x – 5
3
D) y = 2
E) 3x + 2y – 6 = 0
22.
18. A = {–1, 0, 1, 2} olmak üzere f: A → B ve f(x) = 2x + 1
ile verilen fonksiyon örten bir fonksiyondur. Buna
göre, B kümesi aşağıdakilerden hangisidir?
A) {–3, –1, 1, 2}
B) {–1, 0, 1, 2}
D) {–1, 1, 3, 5}
C) {–2, –1, 0, 3}
E) {–3, 0, 1, 3}
19. Gerçek sayılarda tanımlı f(x) = –3x + 5 fonksiyonu
veriliyor. f((0, 3]) kümesi aşağıdakilerden hangisidir?
A) [–7, –5)
B) (–4, 5)
D) [2, 7)
C) [–4, 5)
E) (–4, 5]
20. f: A → B fonksiyonu, f(x) = –x2 – 1 kuralıyla tanımlanıyor. A = {–2, –1, 0, 1, 2} olduğuna göre, f(A)
kümesinin elemanları toplamı kaçtır?
A) –15
B) –16
D) 16
C) 15
E) –14
y
4
3
2
1
–5 –4 –3 –2 –1
–1
–2
1 2 3 4 5 6 x
Şekilde grafiği verilen fonksiyon aşağıdakilerden
hangisidir?
Z - x, x < 0
ise
]]
0 ≤ x < 3 ise
A) f ^ x h = [ 1,
]] 2 x,
x≥3
ise
\3
Z - x, x ≤ 0
ise
]]
1, 0 < x < 3 ise
B) f ^ x h = [
]] 2 x, x ≥ 3
ise
\3
Z - x, x < 0
ise
]]
0
3
x
,
x
ise
≤
<
C) f ^ x h = [
]] 2 x, x ≥ 3
ise
\3
- x,
D) f ^ x h = * 1,
2x,
Z x,
]]
- x,
E) f ^ x h = [
2
]] x,
\3
x<0
ise
0 ≤ x < 3 ise
x≥3
ise
x<0
ise
0 ≤ x < 3 ise
x≥3
ise
Ünite 3. Fonksiyonlar
605
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
23.
y
25. Gerçek sayılarda tanımlanan aşağıdaki fonksiyonların grafiklerini çiziniz.
5
4
3
2
a.
1
–5 –4 –3 –2 –1
1
–1
2
3
4
5
6
x
–2
–3
b.
Şekilde grafiği verilen fonksiyon aşağıdakilerden
hangisidir?
Z - x,
]
f ^ x h = ] 1,
[
]] 2x ,
\ 3
x<0
ise
0 ≤ x < 3 ise
x≥3
ise
c.
x - 2,
f ^ x h = * x 2 - 2,
- 3x + 4,
ç.
3,
f ^ x h = * x,
- 3,
2, - 5 < x < 0 ise
C) f ^ x h = * x - 2, - 2 ≤ x ≤ 2 ise
x - 1,
2 < x ≤ 6 ise
d.
2x,
x ≤ - 5 ise
f ^ x h = * 3x + 1, - 5 < x ≤ 1 ise
- 3,
x>1
ise
2, - 5 < x < 0 ise
D) f ^ x h = * x - 1, - 2 ≤ x ≤ 2 ise
x - 1,
2 < x ≤ 6 ise
e.
f^xh = (
- 2, - 5 < x < 0 ise
A) f ^ x h = * x - 2, - 2 ≤ x ≤ 2 ise
x - 1,
2 < x ≤ 6 ise
B) f ^ x h = *
2, - 5 ≤ x < - 2 ise
x - 2, - 2 ≤ x ≤ 2 ise
x - 1,
2 < x ≤ 6 ise
- 2, - 5 < x < 2 ise
E) f ^ x h = * x - 2, - 2 ≤ x ≤ 2 ise
x - 1, 2 < x ≤ 6 ise
24. Gerçek sayılarda tanımlanan aşağıdaki fonksiyonların grafiklerini çiziniz.
1
a. y = |–8x|
b. y = x 3
c.
y = |x + 2| – 2
ç. y = |x – 1| – 1
d.
y = 2|x + 2| – 2
e. y = |x + 2| + |x|
606
x + 3,
x ≤ - 2 ise
f^xh = *
3, - 2 < x ≤ 1 ise
- x 2,
1<x
ise
Ünite 3. Fonksiyonlar
26.
x>0
ise
- 2 ≤ x < 0 ise
x <- 2
ise
x≥1
ise
- 1 < x ≤ 1 ise
x ≤-1
ise
5x - 7, x < 3 ise
3x 2 - 5, x ≥ 3 ise
y = f(x)
1
–2 –1
–1
–2
–3
–4
1 2 3 4 5 6 x
Şekilde grafiği
verilen ve gerçek
sayılarda tanımlı
olan fonksiyon
aşağıdakilerden
hangisidir?
A) f(x) = |x – 3| – 3
B) f(x) = |x – 3| + 3
C) f(x) = |x + 3| – 3
D) f(x) = - 4 - x - 3
E) f (x) = x - 4 - 3
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
27.
29.
y
–3
y
4
1
3
3
x
1
0
–4 –3 –2 –1
Şekilde grafiği verilen ve gerçek sayılarda tanımlı
olan fonksiyon aşağıdakilerden hangisidir?
x
-1
3
C) f (x) = - 2
x
+1
3
E) f (x) = 2
28.
y = f(x)
2
–1
A) f(x) = –2
(2, 4)
B) f ^ x h = - 2
x
-1
2
D) f(x) = - 3
x
-1
2
x
-1
3
Bir f fonksiyonunun grafiği
şekildeki
gibidir.
y
7
6
5
–1
0 1
2
3
4
x
–2
–3
(–2, –4)
–4
Bir f fonksiyonun grafiği şekildeki gibidir.
a.
Bu fonksiyonun tanım ve görüntü kümelerini bulunuz.
b.
A = {–1, 0, 1} kümesinin f altındaki görüntüsünü bulunuz.
c.
B = {x | 0 ≤ x ≤ 2} kümesinin f altındaki görüntüsünü
bulunuz.
ç.
f(C) = {x | 0 ≤ x ≤ 4} kümesinin f altındaki ters görüntüsünü bulunuz.
d.
f(D) = {0, 1, –4} kümesinin f altındaki ters görüntüsünü bulunuz.
4
3
2
1
–2 –1
0
–1
0 1
2
3
4
5
x
–2
a.
f((0, 2]) kümesi nedir?
b.
A = {–1, 2, 3} kümesinin f altıdaki görüntüsü nedir?
c.
[1, 3] kümesinin f altındaki görüntüsü nedir?
ç.
[–1, 5] kümesinin f altıdaki ters görüntüsü nedir?
Ünite 3. Fonksiyonlar
607
Bölüm 3. 2. Fonksiyonların Grafikleri
BÖLÜM DEĞERLENDİRME
30. Denizlerdeki su basıncı derinlere inildikçe artar.
Öyle ki; her 10 metrede basınç, yaklaşık olarak santimetre kareye 1 kilogram kadarlık artış gösterir.
Buna göre x derinlik olmak üzere, x derinlikteki su
basıncı f(x) olacak şekilde bir f fonksiyonu verilsin.
Buna göre;
a.
10 ar metrelik aralıklarla, 10 metreden 100 metreye
kadar olan derinlik-su basıncı tablosunu yapınız.
b.
f(x) in cebirsel ifadesini yazınız.
c.
0-100 metre derinlik aralığı için derinlik (m) – su basıncı (kg/cm2) grafiğini çiziniz.
32. 3 TL ile açılan bir taksimetre ilk 5 km de, her 100
m için 30 kr, 5 km den sonra her 100 m için 20 kr
ücret yazmaktadır. Gidilen yol km cinsinden x ile
gösterildiğinde, bu taksimetrenin ücret tarifesini
veren f(x) fonksiyonunu bulunuz.
33. Sıcaklık ölçü birimlerinden Fahrenhayt derece (°F)
ile Santigrat derece (°C) derece arasında
°F = 1,8 °C + 32
ilişkisi vardır. Buna göre;
a.
31.
Tabloyu doldurunuz.
°C
y
–10
0
10
24
37
100
°F
5
4
b.
3
2
Fahrenheit derece (°F) ile Celcius derece (°C) ilişkisini grafiksel olarak gösteriniz.
1
–4 –3 –2 –1
–1
0 1
2
3
4
5
6
7 x
Bir f fonksiyonunun grafiği şekildeki gibidir.
a.
f([–2, 5]) kümesi nedir?
b.
(0, 5) aralığının f altındaki görüntüsünü bulunuz.
c.
Araştırma Soruları
1.
Günlük hayattan fonksiyon olarak nitelendirilebilecek örnek durumlar bulunuz. Buna göre;
[0, 1] aralığının f altındaki görüntüsünü bulunuz.
a.
Bu fonksiyonların girdilerini ve çıktılarını bulunuz.
ç.
[1, 3] aralığının f altındaki ters görüntüsünü bulunuz.
b.
Bu fonksiyonların grafiklerini kabaca çiziniz.
d.
1’in f altındaki ters görüntüsünü bulunuz.
2.
Değişim oranı sabit olmayan bir fonksiyon doğrusal bir fonksiyon olabilir mi? Açıklayınız.
608
Ünite 3. Fonksiyonlar
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – I
1.
Aşağıda sözel olarak verilmiş x ve y arasındaki
ilişkileri cebirsel olarak ifade ediniz.
5.
a.
y çıktısı x girdisinin 2 katıdır.
a.
b.
x girdisi y çıktısının yarısından 1 eksiktir.
c.
y çıktısı x girdisinin karesinin 3 eksiğidir.
ç.
x girdisi y çıktısının karekökünün 1 fazlasıdır.
2.
Aşağıda cebirsel olarak verilmiş x ve y arasındaki
ilişkileri sözel olarak ifade ediniz.
a.
y=x
b. y = 2
c. y = 2x – 3
ç.
y = x2
d. y = x3
e. y = |x|
f: [1, 3] → [–2, 4], f(x) = 2x – 3 fonksiyonu veriliyor.
Buna göre;
a.
f fonksiyonunun tanım, değer ve görüntü kümelerini bulunuz.
c.
x+1
2
c.
h(x) =
ç. k(x) = 1 – 2x
6.
I.
y = 2x’tir.
II.
Ödeyeceğimiz para aldığımız kalemlerin sayısına bağlıdır.
III. Kalem sayısı değiştikçe ödenecek para da değişir.
3.
b.
Gerçek sayılarda tanımlı olan aşağıdaki fonksiyonların grafiklerini çiziniz.
1
f(x) = 5x – 2
b. g(x) = x - 2
2
Her birinin fiyatı 2 TL olan kalemlerden x tane aldığımızda ödeyeceğimiz paraya y diyelim. Buna göre
yukarıdaki ifadelerden hangileri doğrudur?
7.
f in grafiği üzerinde yer alan bazı noktaların koordinatlarını tablo ile gösterip grafiğini çiziniz.
3 5
Görüntü kümesindeki –1, 0, 1, , , 3 elemanları2 2
nın ters görüntülerini bulunuz.
Aşağıdakilerden hangileri bir fonksiyondur?
f: R → Z, f(x) = x2
1
II. f: R → R, f(x) =
x
III. f: Z → Z, f(x) = 3x2
I.
1
x-1
3x + 2
V. f: N → N, f(x) =
2
IV. f: R+ → R, f(x) =
4.
Aşağıdaki grafiklerden hangileri bir fonksiyona
aittir? Cevabınızı nedenleriyle açıklayınız.
I.
y
II.
y
III.
x
IV.
x
y
V.
x
8.
y
x
y
Aşağıdakilerden hangisi ya da hangileri bir fonksiyon grafiği belirtir?
I. Hareketsizken harekete başlayan ve düzgün
hızlanan otomobilin 0-10 saniye arasındaki konum-zaman grafiği
II. Hareketli iken düzgün hızlanan otomobilin hızlanma süresince konum-zaman grafiği
x
III. Hareketli iken düzgün hızlanan otomobilin hızlanma süresince hız-zaman grafiği
Ünite 3. Fonksiyonlar
609
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – I
9.
a.
2x - 1
fonksiyonu veriliyor. Buna
3
göre, aşağıdaki ifadelerin değerlerini bulunuz.
1
f(–1)
b. f(0)
c. f c m ç. f(2) d. f(2 5
2
f: R → R, f(x) =
x
+ 3 fonksiyonu veriliyor. Buna
2
göre aşağıdaki ifadelerin değerlerini bulunuz.
1
f(–6)
b. f(–2) c. f c m d. f(2) e. f ^2 5 h
4
10. f: R → R, f(x) =
a.
13.
x
f(x)
3
11
7
9
11
3
9
11
16
9
Yanda bir f fonksiyonunun
değerler tablosu verilmiştir.
Buna göre aşağıdaki
ifadelerin değerlerini
bulunuz.
a.
f(7)
b.
f(11)
c.
f(x) = 9 eşitliğini sağlayan x değerleri.
14. f: R → R, f(x) = 3x – 6 fonksiyonu veriliyor.
f(2a – 1) = 6 ise a değerini bulunuz.
11. f: R → R, f(x) = 2x – 3 fonksiyonu veriliyor. Buna
göre aşağıdaki ifadelerin eşiti bulunuz.
a.
f(x + 1)
ç.
f(3x – 1)
b. f(x – 1)
x
d. f a k
2
c. f(2x)
e. f(x2)
15. f: R → R, f(x) = 5x – n fonksiyonu veriliyor.
f(3) = 11 ise n değerini bulunuz.
x
16. f: R → R, f(x) = - c ve f(8) = 9 ise c değerini
2
bulunuz.
12. f: R → R, f(x) = (x + 2)2 fonksiyonu veriliyor. Buna
göre aşağıdaki ifadelerin değerlerini bulunuz.
a.
f(–1)
b.
f ^ 2 - 2h
c.
f fonksiyonunun görüntü kümesi
610
Ünite 3. Fonksiyonlar
17. f: R → R, f(x) = 2x + 3 ve g: R → R, g(x) = x – 2
olarak veriliyor. f(n) = g(3n) ise n kaçtır?
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – I
18. f: R → R, f(x) =
bulunuz.
x-t
ve f(2) = 4 ise t değerini
3
19. f: R → R, f(x) = 2x f(x – 1) + 1 ve f(4) = 10 ise f(1)
değerini bulunuz.
25. f: Z → N, f(x) = x2 fonksiyonunun bire bir olup
olmadığını yatay doğru testi ile gösteriniz.
26. f: Z → Z+, f(x) = x2 fonksiyonunun örten bir fonksiyon olup olmadığını inceleyiniz.
20. f: R → R, f(x) = f(x – 1) + 1 ve f(4) = 10 ise f(1) değerini bulunuz.
21. f: R → R, f(x) = 4x f(x + 1) ve f(3) = 32 ise f(5) değerini bulunuz.
27. Bir arabanın aldığı yolla harcadığı benzin arasında
doğrusal bir ilişki olduğunu varsayalım. Eğer bu
araba 10 km gittiğinde 1 L benzin, 20 km gittiğinde 2 L benzin harcıyorsa;
a.
Arabanın aldığı yolla, harcadığı benzin arasındaki
ilişkinin grafiğini çiziniz?
b.
Harcanan benzin miktarını, alınan yola bağlı olarak
ifade eden fonksiyonun kuralını bulunuz.
1
22. f: [–2, 2] – {0} → R, f(x) = fonksiyonun görüntü
x
kümesini bulunuz.
23. f: R → R, f(x) = 2x + 1 fonksiyonu veriliyor. Buna
göre;
a.
f fonksiyonunun grafiğini çiziniz.
b.
(2, 10) aralığının f altındaki görüntüsünü bulunuz.
24. Gerçek sayılarda tanımlı g(x) = x2 fonksiyonunun
tanım kümesinin bir alt kümesi olan [–1, 3] kümesinin bu fonksiyon altındaki görüntüsünü bulunuz.
28. Bir fabrikanın günlük gideri ile bu fabrikada üretilen ürün sayısı arasında doğrusal bir ilişki olduğu
bilinmektedir. Fabrikanın, günlük 3000 TL sabit
gideri varsa ve eğer bir günde 20 ürün üretilirse, o
günkü toplam gideri 15000 TL olmaktadır. Fabrikanın x ürün ürettiği bir güne ait toplam giderini f(x)
ile gösterelim. Buna göre;
a.
f(x) in cebirsel eşitini bulunuz.
b.
30 ürünün üretildiği bir gün için toplam gider nedir?
c.
Gider fonksiyonun 2 ≤ x ≤ 8 şartını sağlayan x değerleri için grafiğini çiziniz.
Ünite 3. Fonksiyonlar
611
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – I
29. Tuncay 2 saat boyunca ortalama 8 km/sa hızla
bisiklet sürüyor. Tuncay’ın t zamanda aldığı yolu
veren fonksiyon d(t) = 8t dir. Buna göre;
a.
b.
Tuncay’ın bu aktivitesinin ilk 15 dakikasında aldığı
yolla, bu aktivitesinin herhangi bir 15 dakikasında
aldığı yolu kıyaslayınız. Bulduğunuz sonucu nasıl
açıklarsınız?
32. Aşağıdaki fonksiyonları bire bir olma ve örten olma
durumlarına göre sınıflandırınız.
a.
f: R → R, f(x) = x2 + 1
b.
g: R → [1, + ∞), g(x) = x2 + 1
c.
h: [1, + ∞) → R, h(x) = x2 + 1
ç.
m: [1 + ∞) → [1, + ∞), m(x) = x2 + 1
d(m) = 6 km ise m kaç dakikadır?
30. f: A → R bir fonksiyon olsun. Eğer bir a ∈ A için
f(a) = a oluyorsa f in a da bir sabit noktası vardır
denir. Buna göre;
a.
g: [0, ∞) → R, g(x) = 2x – 3 fonksiyonunun varsa sabit noktasını bulunuz.
b.
Herhangi bir doğrusal fonksiyonun sabit noktası
var mıdır? Varsa kaç tanedir?
33. f: R → R, y = f(2x + 1) = 4x – 3 fonksiyonu veriliyor.
Buna göre, aşağıdaki ifadelerin değerlerini bulunuz.
a.
f(7)
b. f(8)
c.
f(3a)
ç. f(5x)
34. f: R → R, f d
a.
2
x3 + 1
x3 + 1
x3 + 1
n=d
n +4·
ise
3
3
3
b. f(3a) = ?
f(5) = ?
31. Aşağıdaki fonksiyonları bire bir olma ve örten olma
durumlarına göre sınıflandırınız.
i.
f: R → R, f(x) = x4
ii.
g: R → {2}, f(x) = 2
iii. h: {m, n} → {2, 4, 6}, h(m) = 2, h(n) = 4
iv. k: [0, ∞) → R, x → x5
v.
l: R → R, x → |x|
vi. m: [0, ∞) → R, x → –|x|
vii. n: R → [0, ∞), x → |x|
612
Ünite 3. Fonksiyonlar
35.
Grafiği verilen
doğrusal f
fonksiyonun
kuralını bulunuz.
y
4
3
2
1
y = f(x)
–4 –3 –2 –1 0 1 2 3 4
–1
x
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – I
36.
Grafiği
verilen
doğrusal f
fonksiyonun
kuralını
bulunuz.
y
4
3
2
1
–4 –3 –2 –1 0 1 2 3 4
–1
x
39.
y
y = f(x)
y = f(x)
7
6
5
4
3
2
1
y = g(x)
–6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8
–1
–2
37.
y
Grafiği verilen
doğrusal f
fonksiyou için
f(8) değerini
bulunuz.
y = f(x)
7
6
5
4
3
2
1
38.
f ve g fonksiyonlarının verilen grafiklerini kullanarak f(n) = g(n) eşitliğini sağlayan n değerleri
toplamını bulunuz.
40. Verilen f: R – {0} → R, f(x) =
–4 –3 –2 –1 0 1 2 3 4
–1
–2
x
x
1
fonksiyonu için
x
a.
A = {–1, 1} kümesinin f altındaki görüntüsü nedir?
b.
1
B = {–2, } kümesinin f altındaki ters görüntüsü ne2
dir?
c.
[–2, 0) aralığının f altındaki görüntüsü nedir?
ç.
(0, 2] aralığının f altındaki ters görüntüsü nedir?
y
7
6
5
4
3
2
1
y = g(x)
–4 –3 –2 –1 0 1 2 3 4 5 6
–1
–2
x
2x + 1,
41. f: R → R, fonksiyonu f(3x – 5) = *
5,
- x + 4,
x<1
x=1
x>1
biçiminde tanımlanmışsa f(–2) kaçtır?
g(m) = 0, g(t) = 7 ise m – t nin olabileceği değerler
nelerdir?
Ünite 3. Fonksiyonlar
613
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – I
2x - 1,
0,
42. f: R → R, fonksiyonu f(x) = *
x + 2,
biçiminde tanımlanıyor. Buna göre,
a.
f(–2) + f(1) + f(2)
b.
f(x4 + 1)
c.
f(–x2)
x<1
x=1
x>1
ifadelerinin değerlerini bulunuz?
46. Gerçek sayılarda tanımlı
x + 3,
x ≤, –2
ise
f (x) = * 3, - 2 < x <1 ise
- x 2,
1≤x
ise
fonksiyonu için;
a.
A = {–3, –2, 0, 1, 2} kümesinin f altındaki görüntüsünü
b.
B = {–1, 0, –4} kümesinin f altındaki ters görüntüsünü
c.
(–1, 0] aralığının f altındaki görüntüsünü
bulunuz.
43. Gerçek sayılarda tanımlı f fonksiyonu,
- 2x,
f (x) = * 4,
2x,
x d(- 3, - 2)
x d[- 2, 2]
x d (2, + 3)
ile veriliyor. f fonksiyonunun grafiğini çiziniz.
44. Bir kargo şirketi 0 ile 2 kg arasında olan gönderilere
m TL, 2 ile 5 kg arasında olan gönderilere 2m TL,
5 ile 15 kg arasında olan gönderilere 3m TL, 15 ile
30 kg arası gönderilere ise 4m TL ücret alıyor. Bu
şirketin fiyat tarifesini gösteren bir grafik çiziniz.
45. f: R → R, f(x) = |x – 2| + |x| fonksiyonu için
a.
A ={–3, 1, 4} kümesinin f altındaki görüntüsünü
b.
B = {2} kümesinin f altındaki ters görüntüsünü
c.
[2, 4) aralığının f altındaki ters görüntüsününü
ç.
[–2, 0] aralığının f altındaki görüntüsünü
bulunuz.
614
Ünite 3. Fonksiyonlar
- 2,
47. f: ^- 5, 5@ " R, f ^ x h = * x ,
x + 2,
- 5 < x < –2 ise
- 2 ≤ x < 2 ise
2 ≤ x ≤ 5 ise
fonksiyonu veriliyor. Buna göre;
a.
A = {–3, –2, 0, 1, 2} kümesinin f altındaki görüntüsünü
b.
B = { 0, 1, 2, 4} kümesinin f altındaki ters görüntüsünü
c.
(1, 3) aralığının f altındaki ters görüntüsünü
ç.
[–2, 1) aralığının f altındaki görüntüsünü
bulunuz.
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – II
1.
I.
3.
Aşağıda verilen ilişkilendirmelerden hangileri
fonksiyon belirtir?
A
II.
B
.1
.a
.b
IV.
A
A
.2
.a
.b
.3
.c
V.
B
III.
B
A
.a
.1
.b
.2
.a
.b
.c
.3
.c
.1
.2
.3
.4
.a
.b
.c
VI.
B
A
B)
y
y
x
B
.a
.b
.c
.d
.1
.2
.3
.4
A)
B
A
.1
.2
.3
.4
Aşağıdaki grafiklerden hangisi bir fonksiyon grafiği
değildir?
C)
.1
x
D)
y
y
x
x
A) I – III – V
B) II – IV – VI
D) II – III – V
C) I – III – IV – VI
E)
E) I – II – III – IV
y
x
2.
Fonksiyonlarla ilgili olarak aşağıdakilerden hangisi
doğrudur?
A) Bir fonksiyon bir tek kuralla verilmelidir.
B) Bir fonksiyonun bir grafiği vardır.
C) Her fonksiyon ya bire birdir ya da örtendir.
D) Bir kümenin her bir elemanını başka bir kümenin
yalnız bir elemanına eşleyen ilişkidir.
E) Cebirsel olarak ifade edilmeyen ilişkiler fonksiyon belirtmez.
4.
f: A → B bir fonksiyon A = {1, 3, 5, 7} ve
f(x) = 3x – 1 ise f’in görüntü kümesi aşağıdakilerden hangisidir?
A) {3, 11, 19, 27}
B) {1, 3, 5, 7}
D) {2, 10, 12, 18}
C) {2, 6, 10, 14}
E) {6, 10, 18, 30}
Ünite 3. Fonksiyonlar
615
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – II
5.
9.
B = {2, 5, 8, 11, 14} olmak üzere
f: A → B, f(x) = 3x – 1 ve f(A) = B ise A kümesi aşağıdakilerden hangisidir?
A) {0, 2, 4, 6, 8}
B) {1, 3, 5, 7, 9} C) {1, 2, 3, 4, 5}
D) {0, 3, 6, 9, 12}
f bir doğrusal fonksiyon ve f(x) = 4x – 6 olarak
veriliyor. Buna göre f(2 – x) + f(2x) ifadesinin eşiti
aşağıdakilerden hangisidir?
A) 4x – 4 B) 5x – 3 C) 6x – 2 D) 7x – 1 E) 8x
E) {4, 8, 12, 16, 20}
10. f: R → R ve f(x) = 2x – 9 fonksiyonu için
f(3) + f(4) = 3 · f(n + 2) + 3 ise a değeri kaçtır?
6.
f: R → R, f(x)3x + 5 olmak üzere f((2, 6]) kümesi
aşağıdakilerden hangisidir?
A) (11, 23)
B) (23, 11]
D) [11, 23)
A) 3
B) 4
C) 5
D) 6
E) 7
C) [23, 11)
E) (11, 23]
11. f: R → R, f(x) = 3x + 5 fonksiyonu veriliyor.
2f(1) + f(4) = 3f(n + 2) + 3 ise n değeri kaçtır?
A) 0
7.
B) 1
C) 2
D) 3
E) 4
Değer kümesi R olan bir f fonksiyonu için
Grafik(f ) = {(–2, 1), (–1, 2), (1, 3), (2, 3), (3, 4)} olarak
veriliyor.
Buna göre f fonksiyonunun tanım kümesi aşağıdakilerden hangisidir?
A) {1, 2, 3}
B) {-2, -1, 1, 2, 3}
D) {–2, –1, 3}
C) {–2, –1}
12. f: R → R, f(x – 4) = 5x – 9 fonksiyonu veriliyor. f(2) +
f(–1) + f(5) değeri kaçtır?
A) 1
B) 2
C) 3
D) 4
E) 5
E) {–1, 1, 2, 3, 4}
13. A = {–1, 0, 1} olmak üzere: f: A → Z, f(x) = 2x2 – 1,
fonksiyonu veriliyor.
8.
3x + 6
fonksiyonu veriliyor.
x-3
f(2) + f(4) – f(0) ifadesinin sonucu kaçtır?
f: N – {3} → R, f(x) =
A) 8
616
B) 7
C) 6
Ünite 3. Fonksiyonlar
D) 5
E) 4
f(A) kümesi aşağıdakilerden hangisidir?
A) {1}
B) {0, 1}
D) {–1, 1}
C) {–1, 0}
E) {–1, 0, 1}
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – III
1.
f: A → R, f(x) = 3x – 2 fonksiyonu veriliyor.
f(A) = {1, 4, 7} olduğuna göre A kümesi hangisidir?
A) {1, 2, 3}
B) {0, 1, 2}
D) {–2, –1, 0}
2.
C) 3
D) 5
I. İki otoparktan biri saat başına 2 TL sabit ücret,
diğeri ise her ay 50 TL sabit abonelik ücreti alıp
saat başına 50 kuruş ücret öneriyor. Birinci otoparkı tercih edince daha karlı çıkmak için bir
ayda en fazla kaç saat otopark kullanılmalıdır?
E) 8
II. En az karton kullanarak yapılabilecek 12 br3 hacimli bir silindirin yarıçapı ve yüksekliği nedir?
B) 4
C) 8
D) 9
III. Pınar’ın eviyle okulu arası 900 m dir. Pınar sabah
okula yürüyerek gitmeye karar veriyor. İlk 5 dakika 600 m yürüyor. Ama daha sonra yorulmaya
başlıyor ve hızını yarıya düşüyor. Pınar okuluna
evden çıktıktan kaç dakika sonra varır?
E) 12
A) I ve II
f: R → R, f(n + 1) = f(n) + n ve f(1) = m veriliyor.
f(4) = 16 ise m kaçtır?
A) 10
5.
E) {–3, –2, –1}
h: A → B olmak üzere, h fonksiyonu bire-bir ve örtendir. s(A) = 3a – 3 ve s(B) = 2a+ 1 ise bu fonksiyonun tanım kümesinin eleman sayısı, s(A) kaçtır?
A) 3
4.
B) –3
B) 9
C) 8
D) 7
B) 1210
C) 1220 D) 1230
B) II ve III
D) I, III
C) I, II ve III
E) Hiçbiri
E) 6
Tam sayılarda tanımlı bir f fonksiyonu için
f(x) – f(x + 2) = x eşitliği sağlanmaktadır. f(12) = 94
ise f(72) kaçtır?
A) 1200
Aşağıdaki problemlerden hangilerinin çözümünde
fonksiyonlardan yararlanılır?
C) {–1, 0, 1}
Gerçek sayılarda tanımlı f ve g fonksiyonları için
f(x) = 5x – 3, g(x) = 3x + 5 ve f(m) = g(2m) olduğuna göre m sayısını bulunuz.
A) –8
3.
6.
7.
Z 2
]] x + 2, x < 0 ise
f: R → R f^ x h = [ x,
0 ≤ x ≤ 5 ise
]
2
,
1
x
x ≥ 5 ise
\
olduğuna göre, f(–10) + f(3) + f(10) kaçtır?
E) 1240
A) 0
B) 3
C) 6
D) 9
E) 12
Ünite 3. Fonksiyonlar
617
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – III
8.
Grafiği verilen
fonksiyonun x ve y
değişkenleri
arasında ifade ettiği
ilişki aşağıdakilerden hangisidir?
y
2
x
2
A) y = x – 2
9.
A) 3
B) 4
C) 5
D) 6
E) 7
B) y = x + 2
D) y = x + 2
C) y = –x – 2
x
E) y = - 1
2
11. Bir top, 64 m yükseklikteki bir binanın tepesinden
aşağıya bırakılıyor. Topun bırakıldıktan t saniye
sonraki yüksekliği (metre) y(t) = –4t2 + 64 fonksiyonu ile veriliyor. Buna göre top kaç saniye sonra
yere düşer?
Kısmi zamanlı çalışan bir işçinin ilk 2 saate kadar
ücreti 40 TL dir. İki saatten sonraki her yarım saat
için 5 TL ücret ödenmektedir. bu durumda bir
günde 8 saate kadar çalışabilen bir işçiye ödenecek
ücretin zamana bağlı grafiği veriliyor. Bu grafiğe en
doğru şekilde karşılık gelen fonksiyon türü aşağıdakilerden hangisidir?
A) Mutlak değer fonksiyonu
12. Fonksiyonlarla ilgili aşağıdakilerden hangisi yanlıştır?
A) Sabit fonksiyon aynı zamanda bir örten fonksiyon da olabilir.
B) Her doğrusal fonksiyon bire bir fonksiyondur.
C) Birim fonksiyon bir doğrusal fonksiyondur.
D) Sabit fonksiyon bir birim fonksiyon türüdür.
E) Bir fonksiyon hem bire bir hem de örten fonksiyon olabilir.
B) Sabit fonksiyon
C) Doğrusal fonksiyon
D) Parçalı tanımlı fonksiyon
13. Grafiği verilen bir f fonksiyonunu için
E) Birim fonksiyon
y
3
10. A = {–1, 0, 1, 2, 3} kümesi ile A da tanımlı bir g fonksiyonu veriliyor.
Grafik(g) = {(0, 0), (1, 2), (2, 3), (–1, 1), (3, 0)} kümesine göre aşağıdakilerden hangisi yanlıştır?
–4
–3
–2
–1
1
B) g sabit bir fonksiyon değildir.
–3
E) g örten değildir.
Ünite 3. Fonksiyonlar
2
3
4
5
x
–1
–2
D) g nin değer kümesi A dır.
y = f(x)
1
A) g nin görüntü kümesi {0, 1, 2, 3} tür.
C) g bire birdir.
618
2
f(k) = 0 ise k nın alabileceği kaç değer vardır?
A) 0
B) 1
C) 2
D) 3
E) 4
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – IV
1.
4.
Grafiği verilen bir g fonksiyonu için
4
y = g(x)
3
Gerçek sayılarda tanımlı f fonksiyonunu bire bir
olduğu biliniyor. Bu fonksiyon için f(2a – 6) = b,
f(b) = 2, f(4) ve f(8) = 4 ise a kaçtır?
A) 5
2
B) 6
C) 7
D) 8
E) 9
1
–6 –5 –4
–3 –2 –1
1
–1
2
3
4
5
x
5.
y
8
y = f(x)
g(–2) + g(0) + g(5) + g(–6) işleminin sonucu kaçtır?
A) –3
B) 0
C) 3
D) 5
E) 6
a
2.
Grafiği verilen bir f fonksiyonu için
x
–1
Grafiği verilen doğrunun eğimi 2 ise a kaçtır?
y
3
A) 2
B) 4
C) 6
D) 8
E) 10
2
1
–4
–3 –2 –1
–1
1
2
3
4
5
6
y = f(x)
x
6.
y
8
f(2) + f(6) – f(–4) işleminin sonucu kaçtır?
A) 2
B) 3
C) 6
D) 9
E) 12
x
3.
f: R → R, f(x) = 3x – 4 fonksiyonu veriliyor.
f(2) = a, f(a) = b ve f(b) = c ise c kaçtır?
A) 0
B) 1
C) 2
D) 3
E) 4
Grafiği verilen doğrunun denklemi aşağıdakilerden hangisi olamaz?
A) y = 8 – x
C) y – x = 8
B) f(x) = –3x + 8
D) y + 4x = 8
y
x
E) + = 4
2 2
Ünite 3. Fonksiyonlar
619
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – IV
7.
f: R → R, f(x) = (a + 5)x3 + (b + 1)x2 + kx + t fonksiyonu bir birim fonksiyon ise a + b + k + t kaçtır?
A) –5
8.
B) –1
D) 1
E) 5
Gerçek sayılarda tanımlı f(x) = (4a – 8)x + b – 4
fonksiyonu bir birim fonksiyon olduğuna göre
a + 3b değeri kaçtır?
A) 14
9.
C) 0
B) 12
C) 2
D) 1
E) 0
Gerçek sayılarda tanımlı f(x) = 5ax + 2b – 29x + 12
fonksiyonunun bir birim fonksiyon olması için
a + b değeri kaç olmalıdır?
A) 4
B) 3
C) 2
D) 1
E) 0
10. f doğrusal bir fonksiyon, f(–1) = 3 ve f(1) = 5 ise f(x)
aşağıdakilerin hangisine eşittir?
A) –x + 3
B) 3x = 5
D) x + 4
C) –x + 4
E) x – 4
B) 7
C) 5
D) 3
A) 4
E) 1
B) 5
A) 5
B) 6
Ünite 3. Fonksiyonlar
D) 7
E) 8
C) 7
D) 8
E) 9
14. Bir A kümesinde tanımlı f fonksiyonu
8x - 12
f(x) =
ile verilyor. f bir sabit fonksiyon ise
4x + 2n
n + f(8) toplamı kaçtır?
A) –7
B) –6
C) 5
D) –4
E) –3
15. f: R → R ve f(x) = (a + 2b – 5)x3 + (2a – 3b + 4)x2 +
(a + 4)x + (–b) fonksiyonu doğrusal bir fonksiyon
ise f(4) değeri kaçtır?
B) 20
C) 22
D) 24
E) 26
16. f, doğrusal bir fonksiyondur. f(2) = 6 ve f(1) = –3 ise
f(x + 5) aşağıdakilerden hangisidir?
A) x + 7
B) 2x + 6
D) 4x + 5
620
C) 6
13. f: R → R ve f(x) = (a – 6)x2 + (2a – b) x + (3a – b)
fonksiyonu veriliyor. f bir sabit fonksiyon ise, f(41)
değeri kaçtır?
A) 18
11. f: R → R ve f(x) = (m + 5)x2 + (n – 8) x + n – k – 6
fonksiyonu bir birim fonksiyon olduğuna göre m +
n – k kaçtır?
A) 9
12. f: R → R ve f(x) = (a – 4)x + a + 3 fonksiyonu veriliyor. f bir sabit fonksiyon ise f(2014) değeri kaçtır?
C) 3x + 7
E) 5x + 4
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – V
1.
f, gerçek sayılar kümesinde tanımlı bir fonksiyondur. f(4x) – 3f(x) = 2x – 8 ise f(7) değeri kaçtır?
A) 12
2.
C) 16
D) 18
E) 20
f: R → R ve f(x) = (3a + 7)x + 7b + 1 fonksiyonu birim fonksiyon olduğuna göre, a . b çarpımı kaçtır?
A) 1
3.
B) 14
B) 2
C) 3
D) 4
6.
A) 6
7.
E) 5
3
6x + 6 - nx
f: R – c - m → R ve f(x) =
bir sabit
2
2x + 3
f: R → R ve f(x) = |x – 5| + |–2x + 3| olduğuna göre,
f(6) nın değeri aşağıdakilerden hangisidir?
C) 8
D) 9
E) 10
f: R → R ve f(3x + 4) = 8x + 9 olduğuna göre f(1)
kaçtır?
A) 1
8.
B) 7
B7 2
C) 3
D) 4
E) 5
f: R → R ve f(5x + 2) = –x + 7 olduğuna göre f(12)
nin değeri kaçtır?
fonksiyon olduğuna göre, f(n) değeri kaçtır?
A) 3
A) 1
4.
C) 3
D) 4
B) –4
C) 0
D) 4
E) 7
f: R → R ve f(x) = x2 – 6x + 8 olduğuna göre f(2) nin
değeri kaçtır?
A) –8
B) –4
C) 0
D) 4
B) 6
C) 7
D) 9
E) 11
E) 5
f: A → B fonksiyonu, f(x) = –x2 + 3 kuralıyla tanımlanıyor. A = {–1, 0, 1} olduğuna göre, f(A) kümesinin
elemanları toplamı kaçtır?
A) –7
5.
B) 2
E) 8
9.
f: R → R ve f(x2 + 3x) = –x2 – 6x + 4 olduğuna göre
3
f c m in değeri kaçtır?
2
A) –7
B) 5
C) 0
D) –5
E) –7
10. f: R → R ve f(3x) = 2nx ve f(81) = 64 olduğuna göre,
n kaçtır?
A) –2
B) 0
C) 2
D) 6
E) 8
Ünite 3. Fonksiyonlar
621
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – V
11. f: R – {6} → R – {7} ve f c
x+7
x+9
m=
olduğuna
x-1
6-x
göre, f(5) değeri kaçtır?
A) 1
B) 2
14. f: R → R ve f(x + 2) = f(x + 1) – 4x + 5 ve f(2) = 3
olduğuna göre f(0) kaçtır?
A) –11
C) 3
D) 4
B) –9
C) 0
D) 9
E) 11
E) 5
15. f(x) = (
x - 4, x < 1 ise
fonksiyonu için
x,
x ≥ 1 ise
A = {–2, 0, 1} kümesinin verilen fonksiyon altındaki
görüntüsü aşağıdaki kümelerden hangisidir?
12. f: R → R ve f(x) = x3 + 3x2 + 3x + 1 olduğuna göre
f(4x – 1) aşağıdakilerden hangisidir?
A) x3
B) 4x3
D) 32x3
C) 8x3
A) {–6, –4, –1}
B) {–6, –4, –3}
C) {–3, –2, 0}
E) 64x3
D) {–2, 0, 1}
E) {–4, –3, –2}
13. f: R → R ve f(a + b) = f(a) + f(b) eşitliğini gerçekleyen fonksiyonda f(2) = 3 olduğuna göre
f(0) + f(4) + f(8) toplamı kaçtır?
A) 17
B) 18
C) 19
D) 20
E) 21
16. f: R → R ve f(x) = (x– 3)(x + 3) fonksiyonu için A
= {0} kümesinin verilen fonksiyon altındaki ters
görüntüsü aşağıdaki kümelerden hangisidir?
A) {3}
B) {–1}
C) {–1, 3}
D) {–1, –3}
E) {0, –1, –3}
622
Ünite 3. Fonksiyonlar
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VI
1.
A = {–1, 0, 1, 2} ve B = {–2, 1, 4, 7} olmak üzere
f: A → B, f(x) = 3x + 1 fonksiyonunun grafiği aşağıdakilerden hangisidir?
A)
B)
8 y
7
6
5
4
3
2
1
–2
C)
D)
8 y
7
6
5
4
3
2
1
x
–3 –2 –1 0 1 2 3 4
–1
–2
–3
E)
x
–3 –2 –1 0 1 2 3 4
–1
–2
–3
–3 –2 –1 0 1 2 3 4
–1
8
7
6
5
4
3
2
1
y
–2 –1 0 1 2 3 4
–1
–2
–3
8 y
7
6
5
4
3
2
1
A = {0, 1, 2, 3, 4} kümesinin her bir elemanını
yarısının dört fazlasına eşleyen fonksiyonun grafiği
aşağıdakilerden hangisidir?
A)
8 y
7
6
5
4
3
2
1
x
2.
C)
6
B)
y
5
5
4
4
3
3
2
2
1
0
0
1
0
1
2
3
5x
4
y
6
D)
5
1
2
3
4
5 x
0
1
2
3
4
5
3
4
5x
0
y
6
5
4
x
y
6
4
3
3
2
2
1
0
1
0
0
1
2
3
E)
5x
4
x
y
6
5
4
3
2
1
0
0
1
2
–2 –1 0 1 2 3 4 x
–1
–2
–3
–4
Ünite 3. Fonksiyonlar
623
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VI
3.
y
2
1
Şekilde grafiği verilen f
fonksiyonu aşağıdakilerden hangisi olabilir?
5.
–1 0 1 2 3 x
–1
–2
–3
–4
–5
A = {–1, 0, 1, 3, 5} ve B = {–5, –3, –1, 0, 1, 3, 5, 7} kümeleri veriliyor. f: A → B, f(x) = –2x + 5 fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir?
A) {–5, –3, –1, 0, 1, 3, 5, 7}
B) {–5, –3, –1, 1, 3, 5, 7}
C) {–5, –1, 3, 5, 7}
D) {–5, –1, 0, 3, 5, 6}
–6
–7
E) {–5, –1, 1, 3, 5, 7}
–8
A) f: R → R, f(x) = 5x + 3
B) f: R → R, f(x) = 5x – 3
3
C) f: {–1, 0, ,1} → {–8, –3, 0, 2}, f(x) = 5x + 3
5
3
D) f: {–1, 0, ,1} → {–8, –3, 0, 2}, f(x) = 5x – 3
5
3
E) f: {–1, 0, ,1} → {–8, –3, 0, 2}, f(x) = –3x + 5
5
4.
y
4
3
y = f(x)
2
1
–2 –1
Şekilde grafiği verilen f
fonksiyonu aşağıdakilerden hangisidir?
6.
1
1
x – fonksiyonu için gö2
3
rüntü kümesi aşağıdakilerden hangisidir?
f: [–1, 2] → R, f(x) =
5 2
A) ;- , E
6 3
D) [–1, 2]
7.
4
3
B) f: (–∞, 2) → [0, ∞), f(x) = x – 2
624
y
–3 –2 –1 0 1 2 3 4 5 x
–1
–2
C) f: (–∞, 2] → [0, ∞), f(x) = 2 – x
Tanım Kümesi
5 2
C) c - , m
6 3
E) (–1, 2)
2
1
0 1 2 3 4 x
A) f: R → R, f(x) = 2 – x
5 2
B) ;- , m
6 3
Şekildeki grafiği
verilen fonksiyon
için tanım ve
görüntü kümesi
aşağıdakilerden
hangisidir?
Görüntü Kümesi
D) f: R → [2, ∞), f(x) = 2 – x
A)
[–3, 5] – {–1}
E) f: {–∞, 2] → R, f(x) = x – 2
B)
(–3, 5]
(–2, 3]
C)
(–3, 5] – {–1}
(–2, 3]
D)
(–2, 3]
(–3, 5] – {–1}
E)
(–2, 3] – {1}
(–3, 5] – {–1}
Ünite 3. Fonksiyonlar
(–2, 3) – {–1}
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VI
8.
4
3
y
Şekilde grafiği verilen
fonsiyon için tanım
ve görüntü kümesi
aşağıdakilerden
hangisidir?
2
1
0 1 2 3 4 x
–3 –2 –1
Tanım Kümesi
Görüntü Kümesi
A)
R
(2, ∞)
B)
(0, ∞)
R
C)
[0, ∞)
[2, ∞)
D)
[0, ∞)
{2} ∪ (3, ∞)
E)
[2, 2]
(2, ∞)
9.
4
3
y
2
1
–3 –2 –1 0 1 2 3 4 x
–1
10.
y
6
5
4
3
2
1
0
–4 –3 –2 –1
–1
–2
–3
–4
–5
y = f(x)
1 2 3 4 5 x
A) {–5, 0}
B) {–2, 1}
D) {–2, 2}
Şekilde grafiği verilen
fonksiyon için
sırasıyla tanım ve
görüntü kümesi
aşağıdakilerden
hangisidir?
C) {–5, 2}
E) {–5, 4}
y
11.
Şekildeki grafiği
verilen y = f(x)
fonksiyonu için
f(x) = 0 denkleminin çözüm kümesi
nedir?
4
3
A)
Tanım Kümesi
Görüntü Kümesi
2
(–3, 3)
[0, 2]
1
B) (–3, 3) – {–3, –2, –1, 0, 1, 2, 3}
C)
(–3, 3)
{0, 1, 2, 3}
{0, 1, 2}
D) (–3, 3) – {–3, –2, –1, 0, 1, 2, 3}
[0, 2]
E) (–3, 3) – {–3, –2, –1, 1, 2, 3}
{0, 1, 2}
–1
0
–1
Şekilde grafiği
verilen f fonksiyonu için f(2) = a
ve f(–2) = b ise
{a, b} aşağıdakilerden hangisidir?
1
A) {0}
2
3
4
x
B) {3, 0}
D) {–3}
C) {3}
E) { }
Ünite 3. Fonksiyonlar
625
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VI
12.
Şekilde grafiği
verilen
y = h(x)
fonksiyonu
için h(x) = 0
denkleminin
çözüm kümesi
aşağıdakilerden hangisidir?
y
4
3
2
1
–2 –1
0
1
–1
2
3
x
4
y = h(x)
–2
A) {–1, 0, 1}
E) {–1, 3}
4
3
2
1
y
B)
–2 –1 0 1 2 3 4
–1
C)
4
3
2
1
0
–2 –1
–1
x
1 2 3 4
x
4
3
2
1
0
–2 –1
–1
–2
4
3
2
1
0
–2 –1
–1
1 2 3 4
y
1 2 3 4
Ünite 3. Fonksiyonlar
x
y
1 2 3 4
x
y
B)
1 2 3 x
–3 –2 –1
–1
–2
4
3
2
1
0
x
4
3
2
1
0
y
–3 –2 –1
–1
–2
D)
y
1 2 3 x
E)
y
–2 –1
–1
D)
y
E)
626
4
3
2
1
0
4
3
2
1
0
–3 –2 –1
–1
–2
13. Aşağıda verilen grafiklerden hangisi bir fonksiyon
grafiği belirtmez?
A)
A)
C)
B) {–1, 0, 1, 2, 3} C) {–1, 1, 3}
D) {3, 1}
14. Aşağıda verilen grafiklerden hangisi bir fonksiyon
grafiğidir?
4
3
2
1
0
–3 –2 –1
–1
–2
4
3
2
1
0
–3 –2 –1
–1
–2
y
1 2 3 x
1 2 3x
y
1 2 3 x
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VII
1.
Şekilde f ve g
fonksiyonlarının grafiği
verilmiştir. f
fonksiyonun
eğiminin g
fonksiyonun
eğimine oranı
nedir?
y
3
y = g(x)
2
1
–2 –1
A) –1
2.
0 1
–1
B) -
2
3
y = f(x)
3
2
C)
4
2
3
x
D)
3
2
y
2
1
–2 –1 0 1 2
–1
3 x
4
3
2
1
B)
y
y
D)
3 x
4
3
2
1
y
–2 –1 0 1 2 3 4 5 x
–1
–2
–2 –1 0 1 2 3 4 5 x
–1
–2
4
3
2
1
y
–2 –1 0 1 2 3 4 5 x
–1
–2
–2 –1 0 1 2 3 4 5 x
–1
–2
4
3
2
1
4
3
2
1
y
–2 –1 0 1 2 3 4 5 x
–1
–2
–2
–2
C)
A)
E)
2
1
–2 –1 0 1 2
–1
x + 1, x > 2 ise
fonksiyonunun grafiği aşa1 - x, x ≤ 2 ise
ğıdakilerden hangisidir?
C)
y
B)
f(x) = (
E) 1
Aşağıda verilen grafiklerden eğimi en büyük olan
hangisidir?
A)
3.
y
2
1
y
D)
–2 –1 0 1 2
–1
3 x
2
1
–2 –1 0 1 2
–1
3 x
–2
–2
E)
y
2
1
–2 –1 0 1 2
–1
3 x
–2
Ünite 3. Fonksiyonlar
627
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VII
4.
Z - x + 1,
]]
1
f(x) = [
,
2
]]
x 2,
\
x > 1 ise
x = 1 ise fonksiyonunun grafiği
x < 1 ise
5.
2x - 1,
1,
f(x) = *
- x + 4,
x ≤ 1 ise
1 < x < 3 ise fonksiyonunun
x > 3 ise
aşağıdakilerden hangisidir?
grafiği aşağıdakilerden hangisidir?
A)
3
2
1
B)
y
–2 –1 0 1 2
–1
3
2
1
3
2
1
y
D)
3
2
1
–1
y
–2
–2
E)
3
2
1
–2
Ünite 3. Fonksiyonlar
0 1 2
3 4 5 x
C)
3 x
2
1
–1
y
–1
0 1 2
D)
3 4 5 x
y
0 1 2
2
1
3 4 5 x
–1
y
0 1 2
–2
–2
2
1
–1
3 x
2
1
–2
E)
y
–2 –1 0 1 2
–1
B)
y
–2
–2 –1 0 1 2
–1
3 x
2
1
3 x
–2
–2 –1 0 1 2
–1
628
A)
–2 –1 0 1 2
–1
3 x
–2
C)
y
–2
y
0 1 2
3 4 5 x
3 4 5 x
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VII
6.
Şekilde grafiği
verilen fonksiyon
aşağıdakilerden
hangisidir?
y
2
1
–2
0
–1
1
2
7.
f: R → R, f(x) = |5x| fonksiyonunun grafiği aşağıdakilerden hangisidir?
y
A)
B)
0
–1
1, x < - 1 ise
A) f: R → R, f(x) = * - x, - 1 ≤ x ≤ 1 ise
- 1,
x>1
ise
x < - 1 ise
- 1 ≤ x ≤ 1 ise
x<1
ise
1,
E) f: R → R, f(x) = * - x,
- 1,
x ≤- 1
ise
- 1 ≤ x < 1 ise
x>1
ise
–1
4
–2
3
–3
2
–4
1
–5
–1
0
1
x
y
–1
C)
1, x < 1 ise
C) f: R → R, f(x) = * - x, - 1≤ x ≤ 1 ise
- 1, x > - 1 ise
x,
D) f: R → R, f(x) = * 1,
- x,
5
x
x
- 1,
x < - 1 ise
B) f: R → R, f(x) = * - x, - 1 ≤ x ≤ 1 ise
- 1,
x>1
ise
y
–5 –4 –3 –2 –1
0
0 1
2
3
4
5
x
2
3
4
5
x
y
D)
–5 –4 –3 –2 –1
–1
0 1
–2
E)
y
5
4
3
2
1
–1
0 1
2
x
–2
–3
–4
–5
Ünite 3. Fonksiyonlar
629
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VII
8.
f: R → R, f(x) = |x – 1| – 2 fonksiyonun grafiği aşağıdakilerden hangisidir?
9.
Şekilde grafiği verilen
fonksiyon aşağıdakilerden hangisidir?
y
3
2
y
A)
1
0
2
1
–1
–2 –1 0 1
–1
2
3
4
x
–1
0 1
2
3
x
–2
B)
A) f: R → R, f(x) = |3x| – x
y
B) f: R → R, f(x) = |3x| + x
2
1
C) f: R → R, f(x) = |2x| + x
–2 –1 0 1
–1
2
3
4
x
D) f: R → R f(x) = 2x – |x|
–2
E) f: R → R, f(x) = |2x| – x
y
C)
10.
2
1
0
2
–2 –1
–1
1
2
3
4
–2
D)
0 1
y
1
0
1
x
1
B) f: R – {0} → R, f(x) =
x
1
C) f: R – {0} → R, f(x) =
x
1
D) f: R – {0} → R, f(x) =
x
A) f: R – {0} → R, f(x) =
1
2 x
–2
–3
–4
630
1
2
3
4
x
Şekilde grafiği verilen fonksiyon aşağıdakilerden
hangisidir?
–4
–1
0
2 x
–3
–2 –1
–1
–2
–2
E)
1
–1
y
–1
x
–2
1
–2 –1
y
Ünite 3. Fonksiyonlar
+1
–1
1
2
1
+
2
1 1
E) f: R – {0} → R, f(x) = 2 –
x 2
–
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VII
11. f: R → R, f(x) = x2 – 4 fonksiyonunun grafiği aşağıdakilerden hangisidir?
A)
B)
y
–2 –1
–1
2
x
–2 –1
–1
–2
–2
–3
–3
–4
–4
–2
0 1
y = g(x)
1
1
2
y
y = f(x)
y
1
0 1
12.
2 x
0
–1
1
2
x
Şekilde grafiği
verilen fonksiyonlar aşağıdakilerden hangisidir?
–1
y = h(x)
–2
A) f: R → R, f(x) = x – 1
C)
–2 –1
y
D)
y
4
4
3
3
2
2
1
1
–1
0 1
–2 –1
2 x
g: R → R, g(x) = x2 – 1
h: R → R, h(x) = –x2 + 1
B) f: R → R, f(x) = x + 1
g: R → R, g(x) = x2 – 1
0 1
2 x
h: R → R, h(x) = –x2 + 1
C) f: R → R, f(x) = x + 1
E)
y
g: R → R, g(x) = x2 + 1
1
–3 –2 –1
–1
–2
–3
–4
0 1
2
3 x
h: R → R, h(x) = –x2 + 1
D) f: R → R, f(x) = x – 1
g: R → R, g(x) = x2 + 1
h: R → R, h(x) = –x2 + 1
E) f: R → R, f(x) = x – 1
g: R → R, g(x) = –x2 – 1
h: R → R, h(x) = x2 + 1
Ünite 3. Fonksiyonlar
631
Ünite 3. Fonksiyonlar
ÜNİTE DEĞERLENDİRME – VII
13. Aşağıda grafikleri verilen fonksiyonlardan hangisi
bire birdir?
A)
3
2
1
f: R → R
1 2 3 4 x
–3 –2 –1
–1
–2
–3
C)
3
2
1
3
2
1
–3 –2 –1
–1
–2
–3
D)
y
f: R → R
–3 –2 –1
–1
–2
–3
E)
B)
y
1 2 3 4 x
3
2
1
f: R → R
1 2 3 4 x
E)
f: R → R
A)
B)
f: R → R
–3 –2 –1
–1
–2
–3
1 2 3 4 x
3
2
1
–3 –2 –1
–1
–2
–3
y
f: R → R
y
3
2 f: [0, 3] → [–2, 2]
1
–3 –2 –1
–1
–2
–3
632
1 2 3 4 x
Ünite 3. Fonksiyonlar
3
2
1
y
3
2
1
3
2
1
–3 –2 –1
–1
–2
B)
f: R → R
D)
y
1 2 3 x
f: R → R
y
1 2 3 4 x
f: R → R
3
2
1
y
–3 –2 –1
–1
–2
1 2 3 x
–3 –2 –1
–1
–2
1 2 3 4 x
E)
C)
1 2 3 4 x
f: R → R
–3 –2 –1
–1
–2
C)
3
2
1
y
3
2
1
15. Aşağıda grafikleri verilen fonksiyonlardan hangisi
birebir ve örtendir?
1 2 3 4 x
y
1 2 3 4 x
1 2 3 4 x
14. Aşağıda grafikleri verilen fonksiyonlardan hangisi
örten değildir?
A)
f: R → R
–3 –2 –1
–1
–2
–3
y
–3 –2 –1
–1
–2
–3
y
3
2
1
–3 –2 –1
–1
–2
–3
y
y
3
f: R → R
2
1
–3 –2 –1
–1
–2
–3
D)
3
2
1
1 2 3 x
f: R → R
y
–3 –2 –1
1 2 3 4 x
–1
–2 f: R–{1}→R–{–1}
Ünite
4
ÜÇGENLERDE
EŞLİK VE BENZERLİK
Bölüm 4.1. Eşlik
Bu Bölümde Neler
Öğreneceğiz?
•
Üçgenin iç ve dış açılarının ölçüleri
toplamını
•
İki üçgenin eşliğini
•
Üçgenin kenarları ile açıları arasındaki
ilişkiyi
•
Üçgenin kenarları arasındaki ilişkiyi
Neden Öğreneceğiz?
Birbiriyle tamamen aynı olan üçgenlere/
şekillere günlük hayatta birçok yapıda
rastlayabilirsiniz. Birçok yapının inşasında
destek amaçlı üçgensel şekiller kullanılır.
Örneğin evlerin çatıları ya da köprülerin
yapımında kullanılan eş üçgen şeklindeki
yapı elemanları, ağırlığı eşit dağıtarak
yapının daha dayanıklı olmasını sağlar.
Bölüm 4.1. Eşlik
HAZIR MIYIZ?
1.
a. Dar açı
b. Dik açı
c. Geniş açı
ç. Doğru açı
d. Doğru
e. Işın
f. Doğru parçası
g. Eşkenar üçgen
h. İkizkenar üçgen
ı. Dik üçgen
Aşağıda verilen şekillerin altındaki boşluklara, o şekli ifade eden doğru kavramın şıkkını yazınız.
A
A
C
B
B
A
C
B
B
A
C
2.
B
C
A
A
B
A
C
A
B
B
E
F
B
D
d2
d2 ∩ d3 = ......................
d1 ∩ d2 = ......................
d1 ...................... d2
d2 ...................... d3
C
%
m (EFD) = ......................
d3
A, E, B noktaları ....................................... noktalardır.
Aşağıda verilen denklem ve eşitsizliklerin çözüm kümelerini bulunuz.
a. 3x – 2 = 16
b. 4x + 5 < 17
ç. –2x + 1 > 19
d.
x
x
- 10 = + 2
2
3
4.
6 7
5 8
2 3
1 4
634
B
Aşağıdaki şekilde d2 ve d3 doğruları paraleldir. Buna göre boşluklara ⊥, //, ∅, doğrusal, {E} ve 90°
ifadelerini uygun olacak şekilde yerleştiriniz.
d1
3.
A
C
C
A
A
B
d1
d2
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
c. –3(x – 4) = 6 – x
e. –1 < 3x – 1 < 32
Yandaki şekilde d1 // d2 olduğuna göre numaralandırılmış
açılardan eş olanları belirleyiniz.
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında üçgenin iç açılarının ölçüleri toplamını inceleyeceğiz.
A
1
Araç ve Gereçler: Kareli kâğıt, kalem, cetvel
Adım 1
3
2
Kareli kâğıdınıza bir ABC üçgeni çiziniz.
B
C
A
1
Adım 2
D
AB ve AC kenarlarının orta noktalarını cetvel yardımıyla bulunuz. Bu noktaları
sırasıyla D ve E olarak isimlendiriniz.
E
3
2
B
C
A
Adım 3
D
E
ABC üçgenini A köşesinden [DE] boyunca katlayınız.
1
2
B
3
F
C
A
Adım 4
D
A noktasının katlama sonunda [BC] üzerindeki yeri F olsun.
[BF] nın orta noktasını G ve [FC] nın orta noktasını H olarak isimlendiriniz.
1
2
B
E
G
F
3
H
C
A
Adım 5
D
BDF üçgenini B köşesinden [DG] boyunca katlayınız. Benzer şekilde, FEC üçgenini C köşesinden [EH] boyunca katlayınız.
B
G
E
21 3
F
H
C
Sonuç: Yukarıdaki adımlar sonunda, ABC üçgeninin iç açılarının ölçüleri toplamı hakkında ne söyleyebilirsiniz?
Açıklayınız.
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
635
Bölüm
4.1
Eşlik
4.1.1. Üçgende Açılar
Neler Öğreneceğiz?
•
Bir üçgenin iç açılarının ölçülerinin toplamını
•
Bir üçgenin dış açılarının ölçülerinin toplamını
Başlarken
Bazı akarsu havzaları erozyona maruz kalmaktadır. Bu duruma bir çözüm olarak akarsu
yataklarına saptırıcılar (deflektörler) konur. Bu
saptırıcılar dik üçgen şeklindedir. İyi bir saptırıcının, akıntı tarafındaki bir iç açısının ölçüsünün 30° ile 45° arasında olması gerekir.
Hatırlayalım
Anahtar Terimler
•
Üçgen
•
Üçgenin köşeleri
•
Üçgenin kenarları
•
Açıortay
•
Kenarortay
•
Yükseklik
•
İç açı
•
Dış açı
A, B, C doğrusal olmayan üç nokta olsun.
Bu noktaların belirlediği doğru parçalarının birleştiril-
A
mesi ile oluşan geometrik şekle ABC üçgeni denir ve
D
ABC nde
D
A
� [AB] , [AC] , [BC] na üçgenin kenarları,
B
C F
•
•
[AB]
•
|AB|
Kenarortay
Açıortay
D
•
� A, B, C noktalarına üçgenin köşeleri,
% % %
� ABC , BCA ve CAB na üçgenin iç açıları veya açıları denir.
A, V
B ve W
C şeklinde
Üçgenin iç açıları genellikle W
gösterilir.
% %
%
� DAB , EBC ve ACF na üçgenin dış açıları denir.
Sembol ve Gösterimler
ABC
%
ABC
%
m (ABC)
ABC ile gösterilir.
B
E
•
D
C
Yükseklik
C
T
A
K
C
D
A
C
A
N
B
Üçgenin bir iç açısını iki eş parçaya bölen ışına, o açının iç açıortayı ve dış açısını iki eş parçaya
bölen ışına ise o açının dış açıortayı denir. Yukarıdaki şekilde
%
%
m (BAN) = m (NAC) ise [AN, A
açısına ait açıortaydır. Ayrıca
%
%
m^ TAK h = m^ KACh ise [AK, A
açısına ait dış açıortaydır.
636
H
B
Üçgenin bir köşesini
karşısındaki kenarın
orta noktasına
birleştiren doğru
parçasına, o kenara
ait kenarortay denir.
Yukarıdaki şekilde
D ∈ [BC] olmak üzere,
|BD| = |DC| ise [AD] ,
BC kenarına ait kenarortaydır.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
B
Üçgenin bir köşesinden
bu köşenin karşısındaki
kenara veya kenarın
uzantısına çizilen dik
doğru parçasına o kenara ait yükseklik denir.
Yukarıdaki şekilde
[AH] ⊥ [BC] ise [AH] ,
[BC] na ait yüksekliktir.
Üçgende Açılar
Daha önceki yıllarda ve bu bölümün başındaki atölye çalışmasında, üçgenin iç açılarının ölçüleri toplamının 180° olduğunu öğrenmiştiniz. Aşağıdaki teorem bu ilişkiyi
göstermekte ve bu teoremin ispatı ile de ilişkinin niçin doğru olduğu açıklanmaktadır.
Doğru ya da yanlış kesin
hüküm bildiren ifadelere
önerme denir. Doğruluğu
ispatlanan (ispat gerektiren)
önermelere teorem denir. Bir
teorem hipotez (verilenler)
ve hükümden (istenenler)
oluşur. Teoremin hipotezinden yola çıkıp hükmüne
ulaşmaya teoremi ispatlamak
denir. Bir teorem ispatlanırken daha önceki tanım ve
teoremler kullanılır.
Teorem
Üçgenin İç Açılarının Ölçüleri Toplamı
A
Anahtar Bilgi
Üçgenin iç açılarının ölçüleri toplamı
180° dir.
Yandaki ABC üçgeninde
B
C
m (W
A) + m ( V
B) + m ( W
C) = 180°
İspat:
D
A
Anahtar Bilgi
E
Verilenler: ABC bir üçgen
Matematikte ispat sadece
bir ifadenin doğru olup
olmadığını belirlemek için
değil, o ifadenin niçin doğru
olduğunu açıklamak için de
yapılır. Bir ifade ispatlanırken
ispatın yazımı aşamasında
farklı yazım biçimlerden
yararlanılabilir. Bu yazım
biçimlerinden biri de iki
kolonlu ispat biçimidir. İki
kolonlu ispatların yazımında
sütunlardan birine çıkarımlar, diğerine bu çıkarımların
gerekçeleri yazılır.
İstenen: m (W
A) + m ( V
B) + m ( W
C) = 180°
A noktasından [BC] na paralel DE doğrusunu çizelim.
B
İfade
Gerekçe
1
%
%
DAB ile ABC açıları eş açılardır.
İç ters açılar eştir.
2
%
%
EAC ile ACB açıları eş açılardır.
İç ters açılar eştir.
3
%
%
%
m (DAB) + m (BAC) + m (EAC) = 180°
Doğru açının ölçüsü 180° dir.
4
m (V
B) + m (W
A) + m ( W
C) = 180°
%
%
m (DAB) = m ( V
B) ve m (EAC) = m (W
C)
olduğundan
C
Anahtar Bilgi
Geometride bazen bir
teoremi ispatlayabilmek ya
da bir problemi çözebilmek
için ek çizimler yapılabilir. Bu
çizimlere yardımcı çizim adı
verilir.
Bu teorem rastgele seçilen herhangi üç açının her zaman bir üçgenin iç açıları olamayacağını, bu üç açının bir üçgenin iç açıları olabilmeleri için ölçüleri toplamının 180°
olması gerektiğini belirtmektedir. Bu durumda ölçüleri 30°, 45° ve 100° olan açılar bir
üçgenin iç açıları olamazken, ölçüleri 30°, 45° ve 105° olan açılar bir üçgenin iç açıları
olabilir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
637
Bölüm
4.1
Eşlik
1
Anahtar Bilgi
Yandaki ABC üçgeninde verilenlere göre x in değerini bulalım.
A
Üçgenler kenarlarına ve açılarına göre sınıflandırılabilir.
3x
Üçgenler kenarlarına göre;
eşkenar (kenar uzunlukları
eşit), ikizkenar (en az iki
kenar uzunluğu eşit) ve
çeşitkenar üçgen (kenar
uzunlukları farklı) olarak
sınıflandırılır.
80°
x
B
Üçgenler açılarına göre; dar
açılı (tüm iç açılarının ölçüleri
90° den küçük), dik açılı (bir
iç açısının ölçüsü 90°) ve geniş açılı (bir iç açısının ölçüsü
90° den büyük) üçgen olarak
sınıflandırılır.
C
ABC üçgeninin iç açılarının ölçüleri toplamı 180° olduğundan
m (W
A) + m ( V
B) + m ( W
C) = 180°
3x + x + 80° = 180° ise 4x + 80° = 180° eşitliğinden
x = 25° bulunur.
2
Yanda verilen ABC üçgeninde m (W
A) = a değerini
bulalım.
A
α
x + 20°
120° – x
B
C
ABC üçgeninin iç açılarının ölçüleri toplamı 180° olduğundan
m (W
A) + m ( V
B) + m ( W
C) = 180°
a + x + 20° + 120° – x = 180° eşitliğinden
a = 40° bulunur.
638
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Açılar
3
Anahtar Bilgi
Yandaki şekilde
F
A
[BG] ∩ [AD] = {C}
40°
80°
[BG] ∩ [FD] = {E}
α
40°
B
C
G
E
50°
Ölçüleri toplamı 180° olan iki
açıya bütünler, 90° olan iki
açıya ise tümler açılar denir.
Eğer bu açılar komşu açılar
ise, sırasıyla komşu bütünler
ve komşu tümler olarak
isimlendirilir.
olmak üzere verilen açı ölçülerine göre a nın
kaç derece olduğunu hesaplayalım.
D
G
A
ABC üçgeninin iç açılarının ölçüleri toplamından;
%
%
%
%
m (BAC) + m (ABC) + m (ACB) = 180° ise 80° + 40° + m (ACB) = 180° eşitliğinden
%
%
%
m (ACB) = 60° bulunur. m (ACB) = m (ECD) = 60° olup (ters açılar)
L
N
M
EFG üçgeninin iç açılarının ölçüleri toplamından
%
%
%
m (FEG) + m (EFG) + m (FGE) = 180° ise 70° + 40° + a = 180° eşitliğinden
Teorem
Üçgenin bir dış açısının ölçüsü, diğer iki iç
açısının ölçüleri toplamına eşittir.
Yandaki şekilde
%
m (W
A) + m ( V
B) = m (ACD)
C
D
İspat:
Verilenler: ABC bir üçgen
%
A) + m ( V
B) = m (ACD)
İstenen: m (W
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
K
Komşu Tümler Açılar
a = 70° olarak bulunur.
B
E
Komşu Bütünler Açılar
CDE üçgeninin iç açılarının ölçüleri toplamından
%
%
%
%
m (ECD) + m (CDE) + m (DEC) = 180° ise 60° + 50° + m (DEC) = 180° eşitliğinden
%
%
%
m (DEC) = 70° bulunur. m (DEC) = m (FEG) = 70° olup (ters açılar)
A
C
639
Bölüm
4.1
Eşlik
m (W
A) + m ( V
B) + m ( W
C) = 180°
%
m (W
C) + m (ACD) = 180°
ABC nin iç açılarının ölçüleri toplamı
Komşu bütünler açıların ölçüleri toplamı
Anahtar Bilgi
Teoremleri ispatlarken kullanmış olduğumuz ispat yazma biçimlerinden biri de akış
diyagramı ile ispat biçimidir.
Akış diyagramında ifadeler
mantıksal bir sıra içerisinde,
bu ifadelerin gerekçeleri ise
hemen altlarındaki kutulara
yazılır. Oklar ifadeler arasındaki ilişkileri göstermektedir.
D
%
m (W
A) + m ( V
B) + m ( W
C) = m ( W
C) + m (ACD)
Aynı ifadeye eşit olan iki ifade birbirine eşittir.
%
m (W
A) + m ( V
B) = m (ACD)
Sadeleştirme
4
D
Yanda verilen ABC nde
A
%
m (BAC) = a
%
m (ABD) = 160° - 2a ve
%
m (ACD) = 120°
α
120°
160° – 2α
C
B
D
olduğuna göre a nın kaç derece olduğunu
bulalım.
Üçgenin bir dış açısının ölçüsü, diğer iki iç açısının ölçüleri toplamına eşit olduğundan
160° – 2a + a = 120°
160° – a = 120°
a = 40° bulunur.
640
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Açılar
Matematik Tarihi
5
EUKLEİDES (Öklid)
C
100°
D
20°
A
20
°
B
120°
20°
A
Öklid (MÖ yaklaşık 300),
Antik Yunan’da en ünlü
matematik ve geometri
bilginlerinden biridir.
Yaşamına ilişkin bilinenler
onun yalnızca Mısır’da
yaşamış olduğu ve dünyanın en önemli öğrenim
merkezi olan İskenderiye
kentinde bir okul kurduğudur. Öklid, matematikle
ilgilenen hemen herkesin
çağlar boyunca gözdesi
olmuştur. Öklid’e gelene
kadar geometri bilgisi
oldukça ilerlemişti ama bu
bilgi büyük ölçüde birbiriyle bağıntısız kurallardan
oluşuyordu. Öklid kendinden önceki geometricilerin çalışmalarını bir
araya toplayarak bunların
aralarındaki bağlantıları
kurdu. Bu yolla geometriyi
sistematik bir hale getirdi.
Bütün bu çalışmalarını 13
ciltten oluşan “Elementler”
adlı yapıtında topladı. Bu
yapıt daha sonra başka
dillere de çevrildi ve 2000
yılı aşkın bir süre geometri
öğretiminde kullanıldı.
[BD] nı uzatarak BCE üçgenini oluşturalım.
%
%
%
m (BEA) = m (BCE) + m (CBE) eşitliğinden,
C
E
Yanda verilen uçurtma resminde
%
m (CAD) = 20°
%
m (CBD) = 20° ve
%
m (ACB) = 100°
%
olduğuna göre m (ADB) kaç derece olduğunu bulalım.
100°
%
%
m (BEA) = 100° + 20° ise m (BEA) = 120°
D
140°
°
20
%
%
%
m (ADB) = m (EAD) + m (BEA) eşitliğinden,
B
%
%
m (ADB) = 20° + 120° ise m (ADB) = 140°
olarak bulunur.
6
Yandaki şekilde
%
m (EBD) = θ
%
m (CAB) = β
A
β
E
115°
D
%
m (ABE) = 30° ve
30°
θ
C
B
%
m (ACD) = 115°
olduğuna göre β + θ değerini bulalım.
D
%
%
A) + m (ABD) = m (ACD) olduğundan
ABC nde m (W
β + 30° + θ = 115°
β + θ = 115° – 30°
Göker, L., (1997). Matematik
Tarihi ve Türk İslam Matematikçilerinin Yeri, M. E. B.
β + θ = 85° olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
641
Bölüm
4.1
Eşlik
Üçgenin Dış Açılarının Ölçüleri Toplamı
Dikkat
Herhangi bir ABC üçgeninin
dış açıları genellikle X
A' , X
B'
Teorem
D
Bir üçgenin dış açılarının ölçüleri toplamı
360° dir.
A
ve X
C' ile gösterilir.
Yandaki şekilde
%
%
%
m (CAD) + m (BCF) + m (ABE) = 360°
E
B
C
F
İspat
% %
%
A' , X
B' ve X
C' ile gösterelim.
CAD , ABE ve BCF nı sırasıyla X
Anahtar Bilgi
Verilenler: ABC bir üçgen; A’, B’, C’ üçgenin dış açıları
Geometride teoremlerin ispatlanmasında kullanılan yazım biçimlerden biri paragraf
ispat biçimidir. Paragraf ispat
biçiminde ispat paragraf şeklinde detaylı açıklamalarıyla
birlikte verilir.
A') + m ( X
B') + m (X
C') = 360°
İstenen: m (X
D
%
% %
%
%
%
ABC nde ikişer ikişer CAD ile BAC , ABC ile ABE ve ACB ile BCF komşu bütünler açılar olduklarından ölçüleri toplamı 180° dir.
Bu durumda,
_
m (W
A) + m ( X
A') = 180° b
b
m (V
B) + m ( X
B') = 180° ` eşitlikleri yazılabilir.
bb
m (W
C) + m ( X
C') = 180° a
Bu eşitlikler taraf tarafa toplanırsa;
m (W
A) + m ( X
A') + m ( V
B) + m ( X
B') + m (W
C) + m ( X
C') = 180° + 180° + 180° eşitliğinden
m (W
A) + m ( V
B) + m ( W
C) + m (X
A') + m ( X
B') + m (X
C') = 540° elde edilir.
Üçgenin iç açıları ölçüleri toplamı 180° olduğundan
m (W
A) + m ( V
B) + m ( W
C) ifadesi yerine 180° yazılırsa
180° + m (X
A') + m ( X
B') + m (X
C') = 540° eşitliği elde edilir.
Bu eşitlikten ABC üçgeninin dış açıları ölçüleri toplamının
m (X
A') + m ( X
B') + m (X
C') = 360° olduğu sonucuna varılır.
642
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Açılar
7
α
Şekildeki ABC üçgeninde verilen açı ölçülerine göre a
nın değerini hesaplayalım.
A
130°
B
C
140°
ABC üçgeninin dış açılarının ölçüleri toplamı 360° olduğundan
m (X
A') + m ( X
B') + m (X
C') = 360°
a + 140° + 130° = 360° eşitliğinden
a = 90° olarak bulunur.
8
A
2x + 20°
B
Şekildeki ABC üçgeninde verilen açı
%
ölçülerine göre m (BAC) değerini hesapla-
x + 10°
yalım.
60°
C
m (W
C) + m ( X
C') = 180° olduğundan m (X
C') = 120° dir.
Üçgenin dış açılarının ölçüleri toplamı 360° olduğundan
2x + 20° + x + 10° + 120° = 360°
3x + 150° = 360° eşitliğinden
%
x = 70° bulunur. m^BACh = 180° – ^x + 10°h = 180° – ^70° + 10°h = 100° olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
643
Üçgende Açılar
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
açıortay
kenar
doğru parçası
yükseklik
köşe
kenarortay
Yukarıda verilen kavramları aşağıdaki boşluklara
uygun şekilde yerleştiriniz.
a.
Bir açıyı iki eşit parçaya bölen ışına o açının
. . . . . . . . . . . . . . . . . . . . . . . . . . . . denir.
b.
Üçgende, bir köşeyi karşısındaki kenarın orta noktasıyla birleştiren doğru parçasına . . . . . . . . . . . . . . . . . . . . . . . . . . . .
denir.
c.
d.
( . . . . . ) [BF], ABC üçgeninin [AC] kenarına ait yüksekliktir.
e.
%
%
( . . . . . ) m (AGB) = m (ABD) dir.
f.
%
%
%
( . . . . . ) m (AGB) = m (AEB) + m (EBD) dir.
g.
( . . . . . ) BEC açısı geniş açıdır.
h.
( . . . . . ) BFE açısı dar açıdır.
3.
A
Üçgenin bir köşesinden karşısındaki kenarı taşıyan
doğruya indirilen dik doğru parçasına o kenarın
. . . . . . . . . . . . . . . . . . . . . . . . . . . . denir.
B1C 2 D 3 E 3 F
2.
A
E
F
G
70°
D
C
B
ABC üçgeninde
%
m (ABG) = 10°
%
m (GBF) = 10°
%
m ( FBE ) = 15°
%
m (EBD) = 25°
%
m (DBC) = 10° ve
%
m (CAB) = 70° dir.
Bu verilere göre aşağıdaki ifadelerin doğruluğunu
belirleyerek yanlarındaki boşluğa doğru olanlar
için “D”, yanlış olanlar için “Y” yazınız.
a.
( . . . . . ) [BG], ABF üçgeninde B açısının açıortayıdır.
b.
( . . . . . ) [BE], ABC üçgeninde B açısının açıortaydır.
c.
( . . . . . ) [BE], ABD üçgeninde B açısının açıortaydır.
ç.
( . . . . . ) [BE], GBD üçgeninde B açısının açıortaydır.
644
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
6
G
Yukarıda BG doğru parçası, uzunlukları sırasıyla
1, 2, 3, 3 ve 6 birim şeklinde beş parçaya bölünmüştür. Buna göre aşağıdaki ifadelerin doğruluğunu belirleyerek yanlarındaki boşluğa doğru olanlar
için “D”, yanlış olanlar için “Y” yazınız.
a.
( . . . . . ) [AD], ABE üçgeninde kenarortaydır.
b.
( . . . . . ) [AE], ADF üçgeninde kenarortaydır.
c.
( . . . . . ) [AC], ABD üçgeninde kenarortaydır.
ç.
( . . . . . ) [AF], ADG üçgeninde kenarortaydır.
d.
( . . . . . ) [AE], ABG üçgeninde kenarortaydır.
Üçgende Açılar
KENDİMİZİ SINAYALIM
4.
Aşağıda verilen şekillere göre istenenleri yanlarına.
daki boşluklaraByazınız.C
b.
D
a.
β
α
C
a αx+ β = ............
y
A
A
• ( .....) a + θ = z
A
x
B
• ( . . . . . ) a + β + θ = 180°
α
E
θ
B
D
• ( . . . . . ) x + y + z = 180°
C
y
b. B
c.
C
x
D
•
Aşağıda verilen şekillerde a, x, y, z, a, β, θ sıfırdan
büyük açı değerleri olmak üzere; eşitliklerde verilen ifadelerin doğruluğunu belirleyiniz ve yanlarındaki boşluğa doğru olanlar için “D”, yanlış olanlar
için “Y” yazınız.
B
D
a x
F
x
θ
D
θ
α
B
C
D
( .....) a > x
•
( .....) y + z = x + θ
•
( .....) x > y
•
( .....) y + z + θ = a
y
x
6.
E
A
α
( . . . . . ) a + x = 90°
•
( .....) a = y
•
( . . . . . ) a + x + y = 180°
Yandaki şekilde
verilen x, y, z açı
ölçülerini
büyükten
küçüğe doğru
sıralayınız.
A
A
•
x
α
b.
C
z
θ
B
C
y
E
z
β
D
y
x
B
G
β
E
y
B
a.
A
y
x + y = ............
z
5.
ç.
A
[AB] ⊥ [AD]
A
z
β
C
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
645
y
E
z
Üçgende Açılar
KENDİMİZİ SINAYALIM
7.
Yandaki şekilde
verilenlere göre
x+y+z=a
olduğu aşağıda
ispatlanmaktadır.
A
x
C
α
y
z
B
2.
Yandaki şekli
dikkate alarak
ispat aşamasındaki gerekçeler
kısmını doldurunuz.
x
E
C
α
y
z
B
c
[BD] ⊥ [CD] dir.
a
C
B
3.
e
Gerekçeler
1
%
m (BED) = m (W
A) + m ( V
B)
.............................
2
%
%
%
m (BCD) = m (BED) + m (EDC)
3
a=x+y+z
B
C
4.
Yandaki şekilde
A
[AE] ⊥ [BC] dir.
30°
y
.............................
B
e
D
b
D
Verilenlere göre
x, y değerlerini
bulunuz.
x
20°
E
C
Yandaki şekilde
[AB] ⊥ [BC]
A
c
48°
D
.............................
Alıştırmalar
E
d
Verilenlere göre
a, b, c değerlerini bulunuz.
Yandaki şekilde
%
[AD], BAC nın
açıortayıdır.
Verilenlere göre
e, d değerlerini
bulunuz.
A
D
İfadeler
[BD] ⊥ [CD] dir.
a
5.
20
°
40°
C
y
50°
E
a, b, c, d, e değerlerini bulunuz.
B
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Yandaki şekilde
d
A
x
Verilenlere göre
d
646
[AB] ⊥ [AC]
°
28
32°
56°
B
E
b
D
A
1.
Yandaki şekilde
D
A
d // [BC] dir.
C
y + 40°
D
Verilenlere göre x,
y değerlerini bulunuz.
Üçgende Açılar
KENDİMİZİ SINAYALIM
6.
O
A
78°
D
y
x
118°
40°
B
E
C
F
C
7.
Yandaki ABC nde
B, E, C, F doğrusal
noktalardır.
Verilenlere göre
x, y değerlerini
bulunuz.
dir. Verilenlere
göre m değerini
bulunuz.
E
m + 52°
D
F
A
B
D
11.
E
C
D
α
B
E
d
c
C D
12.
9.
0°
–5
2α
°
30
α+
E
C
A
d2
A
Şekildeki ABC ve
F
A
B
d1
Yukarıda verilen şekilde d1 // d2, [AD] ⊥ d1
%
%
%
m (ECB) = m (BCA) , m (CAD) = 40°
olduğuna göre a kaç derecedir?
Yandaki şekilde
%
m^CAEh = 100°
%
m^ABFh = 140° olduğuna göre a, b, c, d
değerlerini bulunuz.
A 100°
a
140° b
F B
C
40°
B
8.
E
%
Yukarıda verilen şekilde [AE] , DAC nın,
%
%
[AB] , DAF nın açıortayı olduğuna göre m (BAE)
kaç derecedir?
Yandaki şekilde
%
%
m^ABCh = m^ADCh
5m
A
10.
D
FED üçgenlerinde
%
%
m^ABCh = m^FDEh
%
%
m^ACBh = m^FEDh
dir.
40°
B
α
30°
D
C
%
Yukarıdaki şekilde [AD], BAC nın açıortayıdır. Veri%
lenlere göre m^ADBh = a kaç derecedir?
Verilen açı ölçülerine göre a kaç derecedir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
647
Üçgende Açılar
KENDİMİZİ SINAYALIM
13.
a e b
B
40° E
70°
c
80°
F
14.
[BC] // [FG] dir.
D
70°
Uygulama ve Problem Çözme
Yandaki şekilde
A
50°
30°
C
d
1.
Verilen açı ölçülerine göre a, b,
c, d, e ölçülerini
bulunuz.
[AD] ⊥ [BC]
%
%
m (BAD) = m (ACB)
G
A
B
[AB] // [DG]
2.
C
E
A
D
%
Buna göre m (BDC) kaç derecedir?
Şekilde ABC
üçgeninin iç ve
dış açıları
gösterilmektedir.
2x + 20°
a
B
x–5
Yandaki şekilde
[AB] ⊥ [AC] B ve C
köşelerinden
geçen açıortaylar
D noktasında
kesişmektedir.
B
F
c
C
[AF] // [DE] dir.
Verilenlere göre
a + β + θ kaç derecedir?
β
15.
C
A
[BE] // [GF]
θ
G
D
olduğuna göre
%
BAC nın ölçüsü kaç
derecedir?
Yandaki şekilde
D
α
B
Yandaki şekilde
A
45°
b
C
Verilenlere göre
a, b, c açı ölçülerini bulunuz.
3.
Yandaki ABC
üçgeninde
A
[BE] A V
BC nın
açıortayı ve
20°
E
α
[AD] ⊥ [BC] dir.
40°
B
D
C
%
Verilenlere göre m (BEC) = a kaç derecedir?
648
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Açılar
KENDİMİZİ SINAYALIM
4.
Yandaki şekilde
A
7.
Yandaki şekilde
A
[AB] ⊥ [BC]
α
B
D
[AD] ⊥ [DE]
%
[AD], BAC nın
açıortayıdır.
E
β
ABC ve ACD dik
üçgenlerinde
50°
θ
[AB] ⊥ [CB]
[AC] ⊥ [CD]
θ
C
E
C
Verilenlere göre a, θ, β değerlerini bulunuz.
B
[AD] , A açısının
açıortayı ve
β
θ + β = 100° olduğuna göre
D
%
m (CAD) kaçtır?
5.
B
A
Yandaki ABD
üçgeninde
α
[AE] ve [AC]
W
sırasıyla BAD
açısının iç ve dış
açıortaylarıdır.
E
40°
D
8.
D
A
105°
75°
E
C
%
Verilenlere göre m (AEC) = a kaç derecedir?
B
6.
C
Yukarıdaki şekilde [AC] ∩ [BD] = {E} , [BD] ve [CA]
sırasıyla B ve C açılarının açıortayları olduğuna
göre BEC açısının ölçüsü kaç derecedir?
A
a
F
E
b
L
e
G
c
B
D
9.
K
H
C
d
Şekildeki ABC
üçgeninde A açısı üç eş parçaya
bölünmüştür.
125°
D
C
Yukarıdaki şekle göre a + b + c + d + e değerini
bulunuz.
α
β
E
A
130°
B
Verilen açı ölçülerine göre a
ve β değerlerini
bulunuz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
649
Üçgende Açılar
KENDİMİZİ SINAYALIM
10.
A
Şekilde
13.
Nehir yatağı
[AB] ⊥ [BC]
[CE] ⊥ [ED]
E
C
Saptırıcı
(Deflektör)
[AC] ⊥ [CD] dir.
B
Verilenlere göre
%
m (CAB) kaç
40°
Bazı akarsu havzaları erozyona maruz kalmaktadır.
Bu duruma bir çözüm olarak akarsu yataklarına
saptırıcılar (deflektörler) konur. Bu saptırıcılar dik
üçgen şeklindedir. Bu dik üçgenin dik olmayan
açılarından birinin ölçüsü 30° ile 45° arasında
olmalıdır.
derecedir?
D
11.
Şekildeki ABC
üçgeninde
%
%
m^ADEh = m^DBCh
dir. Verilenlere
göre a ve b değerlerini bulunuz.
A
E
b
a
10°
D
80°
B
Buna göre dik üçgenin diğer iç açısının ölçüsü
hangi dereceler arasında olur?
14.
Şekildeki ABC
üçgeninde
A
C
D
α
A nın ve
[AD] W
W
[CD] C nın açıortayıdır.
E
40°
B
12.
α
α
B
[AD] ve [BE]
sırasıyla A ve B
açılarının açıortaylarıdır.
E
40°
D
%
Verilenlere göre m (CDE) = a kaç derecedir?
Şekildeki ABC
üçgeninde
A
C
A
15.
100°
D
C
α
Verilenlere göre a kaç derecedir?
Şekildeki ABC
üçgeninde
%
%
m (DBA) = m (DCB)
%
%
m (DBC) = m (DCA)
C dır.
%
Verilenlere göre m (BDC) = a kaç derecedir?
B
650
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Açılar
KENDİMİZİ SINAYALIM
16.
Şekildeki ABC
üçgeninde
A
19.
Şekilde görüldüğü gibi ABC
üçgeninin bir
kısmı [DE]
boyunca katlanmıştır.
A
%
%
m (ACB) = m (BAE)
β
α
B
E
D
ve [AD] , EAC açısının açıortaydır.
D
C
Buna göre a ile β arasındaki ilişki nedir?
50°
E
x
y
B
45°
C
A’
Buna göre x + y kaç derece olur?
17.
Şekildeki ABC
üçgeninde
A
D
50°
E
[CD] ⊥ [AB]
[BE] ⊥ [AC] dir.
α
20°
B
C
%
Verilenlere göre m (DCB) = a kaç derecedir?
18.
Şekildeki ABC
üçgeninde A
açısı üç eş
parçaya ayrılmıştır.
A
F
x
y
80°
50°
B
D
E
C
[CF] , C açısının
açıortayıdır.
Verilenlere göre x + y kaç derecedir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
651
Bölüm
4.1
Eşlik
4.1.2. Üçgenlerin Eşliği
Neler Öğreneceğiz?
•
İki üçgenin eşliğini
•
Üçgenlerin eş olması için gerekli
olan asgari koşulları
Başlarken
Mühendisler ve mimarlar, yapıların tasarımında ağırlıktan kaynaklanan basıncın dağıtılması için destek elemanlarını eş üçgenler
oluşturacak şekilde yerleştirmektedirler.
Böylece daha güvenli ve estetik yapılar inşa
edilebilmektedir.
Anahtar Terimler
•
Kenar – Açı – Kenar (K. A. K.)
•
Açı – Kenar – Açı (A. K. A.)
•
Kenar – Kenar – Kenar (K. K. K.)
Eş Üçgenler
Ölçüleri eşit olan açılara eş açı, uzunlukları eşit olan doğru parçalarına da eş doğru
parçaları denir.
D
B
C
F
Sembol ve Gösterimler
•
% %
ABC , DEF
•
6AB@ , 6CD@
•
ABC , DEF
D
A
C
E
D
A
B
Eş doğru parçaları
D
Eş açılar
% %
CAB , FDE
6AB@ , 6CD@
İki üçgenin köşeleri arasında kurulan bire bir eşlemede, karşılıklı açılar ve kenarlar
D
D
eş ise bu iki üçgene, eş üçgenler adı verilir. Eğer ABC ve DEF eş ise, bu durum
D
D
ABC , DEF şeklinde gösterilir.
D
D
ABC b DEF
Karşılıklı Eş
Açılar
Karşılıklı Eş
Kenarlar
W
A,W
D
6AB@ , 6DE@
E
A
D
B
W
C,V
F
C
F
652
V
B,V
E
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
6AC@ , 6DF@
6BC@ , 6EF@
Üçgenlerin Eşliği
1
Anahtar Bilgi
Yandaki şekilde KLM ve PRS üçgenlerinin eş açı ve kenarları gösterilmiştir.
K
R
Eş üçgenler yansıma, öteleme ve dönme dönüşümleri
yardımıyla üst üste getirilebilir.
Buna göre, bu üçgenler arasındaki
eşlik ifadesini yazalım.
M
Yansıma
d
P
S
L
Şekilde de görüldüğü gibi KLM ve PRS üçgenlerinde
Öteleme
M,V
R
Eş açılar: V
K,V
P, U
L,V
S, X
Eş kenarlar: 6KL@ , 6PS@ , 6LM@ , 6SR@ , 6MK@ , 6RP@ olduğundan iki üçgenin eşlik ifaD
D
desinde eş olan elemanlar aynı sırada yazılırsa KLM , PSR olur.
2
Dönme
A
B
C
D
D
D
D
D
ABC , DEF ise bu üçgenlerin eş açı ve kenarlarını belirleyerek
şekil üzerinde gösterelim.
F
E
A
D
ABC , DEF eşlik ifadesinde karşılıklı açılar ve kenarlar birbirine eş olacağından
Dikkat
W
B,V
E ve W
C,V
F ve
A,W
D, V
B
C
Eş iki üçgen arasındaki eşlik
ifadesi yazılırken üçgenlerin köşelerinin yazım sırası
önemlidir.
6AB@ , 6DE@ , 6BC@ , 6EF@ , 6AC@ , 6DF@ olur.
F
E
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
653
Bölüm
4.1
Eşlik
3
2y + 20°
A
P
3x – 40°
ABC ve PRS üçgenleri için
D
S
B
2x – 10°
C
R
3y – 20°
D
PSR , ABC
%
m (RPS) = 3x - 40°
%
m (ACB) = 2x - 10°
%
m (SRP) = 3y - 20° ve
%
m (BAC) = 2y + 20°
%
olduğuna göre ABC nın kaç derece olduğunu bulalım.
D
D
%
%
ABC , PSR eşlik ifadesinden, m (RPS) = m (CAB) olduğundan 3x – 40° = 2y + 20° ve
İnceleyelim
%
%
m (SRP) = m (BCA) olduğundan 3y – 20° = 2x – 10° olur.
İki üçgenin eş olup olmadığına karar vermede üçgenlerin
karşılıklı 6 elemanının (karşılıklı üçer açı ve kenar) eş
olması gerektiğini öğrendik.
Üçgenlerin daha az sayıda
elemanı kullanılarak iki
üçgenin eş olduğu gösterilebilir mi? Bu asgari elemanlar
hangileri olmalıdır? Örneğin
iki üçgen arasında kurulan
bire bir eşlemede, karşılıklı
ikişer kenar ve bu kenarların oluşturduğu açıların
eş olması bu iki üçgenin eş
olması için yeterli midir? Ya
da karşılıklı açıları eş olan iki
üçgen eş midir?
3x – 40° = 2y + 20 ise 3x – 2y = 60°
3y – 20° = 2x –10 ise 3y – 2x = 10°
123
Bu denklemler alt alta yazılıp düzenlenirse
denklem sistemi çözülürse
2/ 3x - 2y = 60° 6x - 4y = 120°
3
3/ 3y - 2x = 10° 9y - 6x = 30°
+
5y = 150° ise y = 30°
ve y değeri denklemlerin birinde yerine yazılırsa x = 40° bulunur. Bu durumda,
%
%
m (ACB) = 2x - 10° = 2 · 40° - 10° = 70° , m (BAC) = 2y + 20° = 2 · 30° + 20° = 80° ve
ABC üçgeninin iç açıları toplamı 180° olduğundan
%
%
m (ABC) + 70° + 80° = 180° ise m (ABC) = 30° bulunur.
4
Köşeleri A, B, C ve D, E, F olan iki eş üçgenin karşılıklı eşlenen köşeleri aşağıda verilmiştir:
A köşesi ile D, B köşesi ile E, C köşesi ile F
Buna göre aşağıdaki üçgenlerin eşlerini yazalım.
D
BAC , .....
D
D
D
DEF , .....
D
D
D
ACB , .....
D
D
D
FED , .....
D
D
D
D
CAB , .....
EFD , .....
D
D
D
D
BAC , EDF ; DEF , ABC ; ACB , DFE ; FED , CBA ; CAB , FDE ; EFD , BCA dir.
654
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında karşılıklı ikişer kenarı ve bu kenarların oluşturduğu açıları eş olan iki üçgenin eş olup olmadığını inceleyeceğiz.
Araç ve Gereçler: Kareli kâğıt, kalem, cetvel, açıölçer
Adım 1
Kareli kâğıt üzerinde bir ABC üçgeni çiziniz.
Adım 6
Cetvel yardımıyla ABC ve KTS üçgenlerinin her bir kenar
uzunluğunu ve bu üçgenlerin tüm iç açılarını açıölçer
yardımıyla ölçerek aşağıya not ediniz.
D
Adım 2
Çizdiğiniz ABC üçgeninin [AB] ve [BC] nın uzunluklarını
%
ve ABC nın ölçüsünü cetvel ve açıölçer yardımıyla ölçerek aşağıya not ediniz.
|AB| = . . . . . . . . . . . .
|BC| = . . . . . . . . . . . .
%
m (ABC) = . . . . . . . . . . . .
D
ABC
KTS
|AB| = . . . . . . . . . . . . . . . . .
|KT| = . . . . . . . . . . . . . . . . .
|BC| = . . . . . . . . . . . . . . . . .
|TS| = . . . . . . . . . . . . . . . . .
|AC| = . . . . . . . . . . . . . . . . .
|KS| = . . . . . . . . . . . . . . . . .
m (V
B) = . . . . . . . . . . . . . . . . .
m (V
T) = . . . . . . . . . . . . . . . .
m (W
A) = . . . . . . . . . . . . . . . . .
m (W
C) = . . . . . . . . . . . . . . . . .
m (V
K) = . . . . . . . . . . . . . . . .
m (V
S) = . . . . . . . . . . . . . . . .
Adım 3
Kareli kâğıtta bir T noktası belirleyerek bu noktadan [BC]
na eşit uzunlukta [TS] nı oluşturunuz.
Adım 4
%
Açıölçer yardımıyla köşesi T noktası olan ABC na eş ola%
cak şekilde TR ışınını çizerek RTS nı oluşturunuz.
Adım 5
TR ışını üzerinde |AB| = |TK| olacak şekilde K noktasını belirleyerek KTS üçgenini oluşturunuz.
Adım 7
ABC ve KTS üçgenlerinin açı ve kenarları arasında nasıl
bir ilişki vardır?
Bu ilişkiye göre ABC ve KTS üçgenlerin eşliği hakkında
ne söyleyebilirsiniz?
...................................................................................
...................................................................................
Sonuç: Yapmış olduğunuz çalışma sonucunda karşılıklı
olarak ikişer kenarları ve bu kenarlar arasındaki açıları eş
olan üçgenlerin eşliği hakkında ne söyleyebilirsiniz?
Açıklayınız.
...................................................................................
...................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
655
Bölüm
4.1
Eşlik
Kenar – Açı – Kenar (K. A. K.) Eşlik Kuralı
Dikkat
Üçgenlerin eşliği ile ilgili tanım incelendiğinde, iki üçgenin eş olabilmesi için karşılıklı
olarak üçer açı ve kenarlarının eş olması gerektiği görülmektedir. Ancak üçgenin tüm
kenarlarını ve açılarını incelemeden bazı kenar ve açılarının incelenmesi ile de iki üçgenin eş olup olmadığına karar verilebilir. İki üçgenin eş olması için asgari durumlar
olarak adlandırabileceğimiz bu durumlar, dikkate alınmayan kenar ya da açıların da
eş olmasını garanti altına almaktadır. Bu kısımda, bu asgari durumlardan biri olan Kenar-Açı-Kenar durumu incelenmiştir.
K. A. K. yazımında sıralama
önemlidir.
Kenar – Açı – Kenar Eşlik Kuralı
İki üçgen arasında kurulan birebir eşlemede, karşılıklı ikişer kenar ve bu kenarların oluşturduğu açılar eş ise bu iki üçgen eştir. Bu eşliğe, Kenar-Açı-Kenar (K. A. K.)
eşlik kuralı denir.
P
Yandaki şekilde
6AB@ , 6PR@
% %
ABC , PRS
6BC@ , 6RS@
A
R
S
D
_b
bb
b
`b ise
bb
b
a
D
ABC , PRS dir.
B
C
1
M
R
Yandaki üçgenlerde verilenlere göre üçgenlerin eş olup olmadığını belirleyip, eş iseler
aralarındaki eşlik ifadesini yazalım.
Y
N
T
Z
İki üçgenin Kenar-Açı-Kenar eşlik kuralına göre eş olabilmesi için karşılıklı ikişer kenarı
ve bu kenarların oluşturduğu açıların eş olması gerekmektedir.
%
%
Verilen üçgenlerde NT = YZ , m (NTM) = m (YZR) ve MT = RZ olduğundan bu iki
üçgen K. A. K. eşlik kuralına göre eştir. İki üçgen arasındaki eşlik ifadesi yazılırken karşıD
D
lıklı kenar ve açılar eş olacağından bu eşlik ifadesi NTM , YZR şeklinde yazılır.
656
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Eşliği
2
Yandaki şekilde bir köprünün bazı destek elemanları
gösterilmiştir. P noktası hem [MN] hem de [KL] nin orta
noktası ise 6KN@ , 6ML@ olduğunu gösterelim.
K
N
M
P
L
P noktası [MN] ve [KL] nın orta noktası olduğu için |KP| = |PL| ve |NP| = |PM| dir.
% %
%
%
KPN ve LPM açıları ters açılar olduğundan KPN , LPM dir.
6KP@ , 6PL@ _bb
b
D
D
% % b
KPN , LPM `bb şartları sağlandığından K. A. K. eşlik kuralına göre KPN , LPM dir.
b
6NP@ , 6PM@ b
a
Eş üçgenlerin karşılıklı elemanları eş olduğundan 6KN@ , 6ML@ dir.
3
x
B
2
7
C
E
Yanda verilen şekilde |AE| = |AC| = 8 cm
|DE| = 7 cm
8
8
|AD| = 10 cm
|BE| = 2 cm ve
D
10
A
%
%
m (BAC) = m (EAD)
olduğuna göre |BC| = x in kaç cm olduğunu bulalım.
_b
AE = AC
bb
D
D
%
% b`
m (DAE) = m (BAC) b olduğundan K. A. K. eşlik kuralına göre DAE , BAC dir.
bb
bb
AD = AB
a
Eş üçgenlerde karşılıklı açı ve kenarlar birbirine eş olduklarından 6DE@ , 6BC@ olup
x = 7 cm olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
657
Bölüm
4.1
Eşlik
4
x+y
C
D
Yanda yer alan şekilde
[AB] // [CD]
x
|AB| = |CE| = x
E
θ
A
x
70°
|BE| = y
y
B
|CD| = x + y ve
%
m (BED) = 70° olduğuna göre
%
BAC nın kaç derece olduğunu bulalım.
%
%
%
%
[AB] // [CD] olduğundan DCB ve ABC iç ters açılar olup m (DCB) = m (ABC) dir.
%
%
|AB| = |CE| , m (DCB) = m (ABC) ve |BC| = |CD| olduğundan
D
D
%
K. A. K. eşlik kuralına göre ABC , ECD dir. m (CED) + 70° = 180° olduğundan
%
%
%
%
m (CED) = 110° ve m (BAC) = m (CED) = 110° den m (BAC) = 110° elde edilir.
Matematik Tarihi
5
Thales (Tales)
Bir üçgenin iki kenarı eş ise bu kenarların karşısındaki
açıların da eş olduğunu gösterelim.
A
C
B
Tales (M.Ö. 625-547),
Sokrates öncesi dönemde
Anadolu’da yaşamış bir
filozoftur. Geometride
ikizkenar üçgenin taban
açılarının eş olduğunu
göstermiştir.
A
C
Verma, S. (2008). The Little
Book Of Maths Theorems 8
Things. New Holland Publishers.
D
B
A nın açıortayını çizelim. Açıortayın [BC]
ABC üçgeninde W
nı kestiği noktayı D olarak isimlendirelim.
% %
[AD], açıortay olduğu için BAD , DAC dır.
%
%
|AD| = |AD| , m (BAD) = m (DAC) ve |AB| = |AC| olduğunD
B,W
C olur.
Bu durumda V
658
D
dan K. A. K. eşlik kuralına göre BAD , CAD dir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında karşılıklı ikişer açısı ve bu açılar arasındaki kenarları eş olan üçgenlerin kendilerinin de eş
olup olmadığını inceleyeceğiz.
Araç ve Gereçler: Kareli kâğıt, kalem, cetvel, açıölçer, makas
Adım 1
A
O
Kareli kâğıt üzerinde bir ABC çizerek [BC] nın uzunluğunu ve B ile C açılarının ölçülerini
cetvel ve açıölçer yardımıyla ölçerek aşağıya not ediniz.
|BC| = . . . . . . . . . . .
m (V
B) = . . . . . . . . . . .
m (W
C) = . . . . . . . . . . .
B
C
Adım 2
L
Kâğıt üzerinde [BC] na eş olacak şekilde [LM] çiziniz.
Adım 3
M
S
%
Açıölçer yardımıyla köşesi L olan ve ölçüsü B açısının ölçüsüne eşit olan MLS açısını oluşturarak LS ışınını çiziniz.
L
Adım 4
M
S
R
%
Açıölçer yardımıyla köşesi M olan ve ölçüsü C açısının ölçüsüne eşit olan LMR açısını oluşturarak MR ışınını çiziniz.
L
M
Adım 5
LS ve MR ışınlarını uzatarak kesiştikleri noktayı K olarak adlandırıp ABC ve KLM üçgenlerini keserek üst üste yerleştiriniz. Bu iki üçgen arasında nasıl bir ilişki bulunmaktadır?
.....................................................................................................................................................................................................
Sonuç
Yukarıda ulaşmış olduğunuz sonuçları göz önüne aldığınızda karşılıklı ikişer açıları ve bu açılar arasındaki kenarları eş
olan üçgenlerin eşliği hakkında ne söyleyebilirsiniz? Açıklayınız.
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
659
Bölüm
4.1
Eşlik
Açı – Kenar – Açı (A. K. A) Eşlik Kuralı
İki üçgenin köşeleri arasında kurulan bire bir eşlemede, karşılıklı ikişer açı ve bu
açıların arasında kalan kenarlar eş ise bu iki üçgen eştir.
Bu eşliğe, Açı – Kenar – Açı (A. K. A) eşlik kuralı denir.
A
D
B
C
E
F
Yandaki şekilde
6BC@ , 6EF@ _bb
b
% % b
ABC , DEF `b
% % bb
BCA , EFD b
a
ise
O
O
ABC b DEF dir.
1
Aşağıda verilen üçgenlerden hangilerinin eş olduğunu belirleyip eşlik ifadesini yazalım.
A
35°
B
Z
P
60°
5 cm
C
35°
60°
R
50°
5 cm
5 cm
V
35°
Y
S
D
D
V
B,V
Y , 6BC@ , 6YZ@ ve W
C,V
Z olduğundan ABC , VYZ olur.
2
Yandaki şekilde
A
|BD| = |CF|
8
C
B
F
%
%
m (ABC) = m (EFD)
|AB| = 8 cm ve
D
[AC] // [DE] dir.
E
660
Buna göre |EF| nun kaç cm olduğunu hesaplayalım.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Eşliği
%
%
[AC] // [DE] olduğundan m (ACB) = m (EDF) (iç ters açılar) dir.
|BC| = |BD| + |DC|
|DF| = |DC| + |CF| ve
|BD| = |CF| olduğundan |BC| = |DF| olur.
%
%
m (ABC) = m (EFD)
%
%
|BC| = |DF| ve m (ACD) = m (EDF) olduğundan A. K. A eşlik kuralı gereği
D
D
D
D
ABC , EFD dir. ABC ile EFD nin eşliğinden
|EF| = |AB| olup |EF| = 8 cm elde edilir.
3
Yandaki şekilde
A
m (V
B) = m ( W
D) = 90°
|BC| = |CD|
B
olduğuna göre verilen üçgenler için eşlik ifadesini yazalım.
C
D
E
%
%
ACB ve ECD ters açılar olduğundan ölçüleri eşittir.
m (V
B) = m ( W
D) ve |BC| = |CD| olduğundan
D
D
A. K. A. eşlik kuralı gereği ABC , EDC dir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
661
Bölüm
4.1
Eşlik
4
B
A
D
E
C
Thales, gemilerin kıyıya olan uzaklığının aşağıdaki yöntemle hesaplanabileceğini
iddia etmiştir:
•
Şekildeki gibi, geminin yeri A noktası ve bizim kıyıdaki yerimiz ise B noktası olsun.
•
B noktasından sahil boyunca belli bir mesafe yürüyerek C noktasına gidilir. B ile C
uç noktalarının orta noktası D olarak işaretlenir.
•
C noktasından kıyıya ([BC] na) dik olacak şekilde yürüyen kişinin konumu D ve A
noktalarıyla aynı hizada oluncaya kadar yürünür. Doğrusallık sağlanınca bulunan
yer E olarak işaretlenir. Böylece [AB] ⊥ [BC] ve [EC] ⊥ [BC] olur.
•
|EC| ölçülür. Geminin kıyıya olan uzaklığı |EC| kadardır.
•
Thales’in yönteminin gerçekten geminin kıyıya olan uzaklığını hesaplamada geçerli olup olmadığını inceleyelim.
İfadeler
1
6BD@ , 6CD@
Gerekçeler
Verilen
2
% %
EDC , ADB
Ters açılar
3
V
B,W
C
Verilen
4
ABD , ECD
D
D
Yanda verilen ispata göre
D
D
ABD , ECD (A. K. A. eşlik kuralı) olur.
A. K. A. eşlik kuralı
Geminin kıyıya olan uzaklığı |AB| olduğundan bu uzaklığı bulmak için |EC| nu bilmek
yeterlidir.
662
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında karşılıklı kenarları eş olan üçgenlerin kendilerinin de eş olup olmadığını inceleyeceğiz.
Aşağıda kenarları bir ABC üçgeninin kenarlarına eş olan DEF üçgeninin nasıl oluşturulabildiği açıklanmıştır.
Araç ve Gereçler: Kareli kâğıt, kalem, cetvel, pergel, makas
P
Adım 4
M
Adım 1
K
A
R
E
D
%
D
ABC de pergeli [CA] kadar açarak merkezi E olan KM nı
çiziniz.
C
B
D
Kareli kâğıt üzerinde bir ABC çiziniz.
P
Adım 5
M
F
K
R
Adım 2
E
D
E
D
Pergelinizin sivri ucunu B noktasına yerleştirerek pergeli
[BC] kadar açıp kareli kâğıt üzerinde [BC] na eş bir [DE]
oluşturunuz.
$ %
D
PR ve KM nın kesim noktasını F olarak adlandırıp DEF
ni oluşturunuz.
P
Adım 6
M
F
K
R
Adım 3
P
D
D
E
D
ABC ile FDE ni makas ile keserek üst üste yerleştiriniz. Bu
iki üçgen arasında nasıl bir ilişki bulunmaktadır?
R
...............................................................................................
D
E
$
D
ABC de pergeli [BA] kadar açarak merkezi D olan PR nı
çiziniz.
Sonuç
Yukarıda ulaşmış olduğunuz sonuçları göz önüne aldığınızda, karşılıklı kenarları eş olan üçgenlerin eşliği hakkında ne söyleyebilirsiniz?
...............................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
663
Bölüm
4.1
Eşlik
Kenar – Kenar – Kenar (K. K. K.) Eşlik Teoremi
İnceleyelim
İki üçgenin eş olabilmesi için asgari koşullardan ikisinin K. A. K. ve A. K. A. olduğunu
öğrenmiştik. Bu kısımda, bu asgari koşullardan bir diğeri olan Kenar – Kenar – Kenar
durumu incelenmiştir.
Teorem
Kenar – Kenar – Kenar Eşlik Teoremi
İki üçgenin köşeleri arasında kurulan birebir eşlemede, karşılıklı kenarlar eş ise
bu iki üçgen eştir.
Bu eşliğe, Kenar – Kenar – Kenar (K. K. K.) eşlik teoremi denir.
A
Parkta gezintiye çıkan iki
arkadaş bir süre sonra
susuzluklarını gidermek
için limonata içmeye karar
verirler. Fakat limonata
almaya gittiklerinde yalnızca
bir bardak alacak kadar
paralarının olduğunu fark
ederler. Bunun üzerine iki
arkadaş bir bardak limonata
alıp yarı yarıya bölüşmeye
karar verirler. İçlerinden biri
limonatayı içerken diğeri
“tamam, yarısını bitirdin,
sıra bende” der. Sizce bu kişi
limonatanın yarılandığını
nasıl belirlemiştir?
Yandaki şekilde
D
B
C
E
6AB@ , 6DE@ _bb
bb
6BC@ , 6EF@ `b ise
bb
6AC@ , 6DF@ b
a
F
D
D
ABC , DEF dir.
Bu teoremin ispatı için 669. sayfadaki 4. soruyu çözünüz.
1
Aşağıda verilen üçgenlerden hangilerinin eş olduğunu belirleyip eşlik ifadesini yazalım.
4
4
6
Y
R
A
7
E
7
7
B
C
8
6
V
S
4
Z
|AB| = |ES| , |AC| = |ER| ve |BC| = |SR| olduğundan K. K. K. eşlik teoremine göre
D
D
ABC , ESR olur.
664
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Eşliği
2
Yanda verilen şekilde
A
|AC| = |ED|
7
|AB| = 7 cm
7
|EA| = 7 cm
D
5
120° 2
B
E
C
3
|ED| = 5 cm
|BC| = 3 cm
|CD| = 2 cm dir.
%
%
Buna göre m (ACB) = 120° ise ADE nın ölçüsünü bulunuz.
Anahtar Bilgi
|AC| = |ED| olduğundan
A
|AD| = |AC| – |CD| = 5 – 2 = 3 cm olur.
7
3
7
D
B
3
Buna göre |AB| = |EA| , |BC| = |AD| ve
|AC| = |ED| olduğundan
5
120° 2
Üçgenlerin eş olduğu bilinirse herhangi biri üzerinde
ulaşılan sonucun diğerleri
için de geçerli olduğu tespit
edilmiş olur.
E
C
D
D
K. K. K. eşlik teoremine göre ABC , EAD dır.
%
%
%
Buna göre m (ACB) = m (ADE) olup m (ADE) = 120° elde edilir.
3
A
B, C, E noktaları doğrusal
D
%
m (BAC) = 80°
80°
α
B
C
%
m (DEC) = 40°
40°
E
%
m (ACD) = a
olmak üzere, yanda verilen ABC ve CDE üçgenlerinin karşılıklı eş kenarları işaretlenmiştir.
%
Buna göre m (ACD) = a nın kaç derece olduğunu bulalım.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
665
Bölüm
4.1
Eşlik
A
D
80°
60°
40°
60°
B
α
|AB| = |CE| , |BC| = |DE| , |AC| = |CD| olduğundan
D
Eş üçgenlerde karşılıklı elemanlar eş olacağından,
%
%
m (DEC) = m (ABC) = 40°
%
%
ve m (BAC) = m (DCE) = 80° olur.
40°
80°
C
D
K. K. K. eşlik teoremi gereği ABC , CED dir.
E
D
ABC nde iç açı ölçüleri toplamı yazılırsa
%
%
80° + 40° + m (ACB) = 180° ise m (ACB) = 60° olur.
%
BCE doğru açı olduğundan
60° + a + 80° = 180° ve buradan a = 40° bulunur.
Eş Üçgenlerin Yardımcı Elemanları Arasındaki İlişki
A
D
B
F
K
C
E
G
Eş üçgenler farklı dönüşümler kullanılarak (yansıma, öteleme ve dönme) üst üste
çakıştırılabilirler. Bu nedenle eş üçgenlerin karşılıklı yardımcı elemanları da (açıortay,
kenarortay ve yükseklik) eş olmak zorundadır. Aşağıda ABC ve DFE eş üçgenlerinin
D
D
(ABC , DFE ) eş açılarının açıortaylarının niçin eş olduğu gösterilmiştir.
D
D
% %
ABC , DFE olduğundan BAC , EDF dir.
% %
[AK] ile [DG] açıortay olduğundan BAK , FDG olur.
D
D
% %
ABC ile DFE eş üçgenler olduğundan 6AB@ , 6DF@ ve DFE , ABC dir.
D
D
% % % %
ABK ve DFG üçgenlerinde 6AB@ , 6DF@ , ABK , DFG ve BAK , FDG olduğundan
A. K. A. eşlik kuralı gereği ABK , DFG olur. Buradan 6AK@ , 6DG@ elde edilir.
D
D
Benzer şekilde eş üçgenlerin karşılıklı kenarortaylarının ve yüksekliklerinin de eş olduğu gösterilebilir.
İspat için 670. sayfadaki 5. soruyu çözünüz.
666
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında karşılıklı ikişer kenarları ve bu kenarlar arasında olmayan açıları eş olan iki üçgenin eş olup
olmadığını inceleyeceğiz.
Araç ve Gereçler: Kareli kâğıt, cetvel, açıölçer, pergel
Aşağıda bazı ölçümleri verilen ABC üçgenini oluşturalım.
|AB| = 4 cm
|BC| = 11 cm
%
m (BCA) = 20°
Adım 1
C
Cetvelinizi kullanarak 11 cm uzunluğunda olacak şekilde [BC] nı oluşturunuz.
11
B
Adım 2
İletkinizi kullanarak C köşesinde 20° lik bir açı oluşturunuz.
20°
C
20°
C
20°
C
11
B
A
Adım 3
A’
Pergelinizi 4 cm açıp merkezi B olan ve C açısının bir kolunu, yandaki şekilde olduğu gibi A ve A’ noktalarında kesen bir yay çiziniz.
11
B
Adım 4
A
A’
B noktası ile A ve A’ noktalarını birleştiriniz.
4
Adım 5
4
B
11
ABC ve A’BC üçgenlerinin eş olup olmadığı hakkında ne söylenebilir?
.....................................................................................................................................................................................................
Sonuç
Yukarıda ulaşmış olduğunuz sonuçları göz önüne aldığınızda, karşılıklı ikişer kenarı ve bu kenarlar arasında olmayan
bir açısı eş olan üçgenlerin eşliği hakkında ne söyleyebilirsiniz?
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
667
Üçgenlerin Eşliği
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
Aşağıdaki üçgenlerde karşılıklı eş elemanları belirterek iki üçgen arasındaki eşliği şekillerin altındaki
boşluğa yazınız.
a.
D
A
B
C
........
E
F
2.
Aşağıdaki ifadelerin yanlarına doğru olanlar için
“D”, yanlış olanlar için “Y” yazınız.
a.
(. . . . . . ) İki üçgen eş ise karşılıklı açı ölçüleri ve kenar
uzunlukları eşittir.
b.
(. . . . . . ) İki üçgen eş ise eş kenarlara ait yükseklikler de
eştir.
c.
(. . . . . . ) İki üçgenin eşliği yazılırken kenar ve açı sırasının önemi yoktur.
ç.
(. . . . . . ) İki üçgenin karşılıklı açıları eş ise bu iki üçgen
daima eştir.
3.
Aşağıda verilen üçgenlerde eş olan açı ve kenarlar
gösterilmiştir.
, .......
Buna göre, bu üçgenler arasındaki eşlik kuralını
gerekçesiyle birlikte altlarındaki boşluğa yazınız.
P
b.
R
X
a.
b.
A
a
b
D
E
a+b
b
Y
Z
B
S
........
C
........
, .......
B
, ........
C
........
Gerekçesi: . . . . . . . . . . . . . . . . . . . . .
c.
D
A
, ........
Gerekçesi: . . . . . . . . . . . . . . . . . . . . .
L
H
c.
ç.
A
P
B
C
A
C
B
J
K
........
R
D
, .......
D
........
, ........
Gerekçesi:
668
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
.....................
........
, ........
Gerekçesi:
.....................
Üçgenlerin Eşliği
KENDİMİZİ SINAYALIM
d. A
e.
A
B
D
|DE| = |BH| olacak şekilde bir H noktası alıp bu H
noktasını A ve C noktaları ile birleştirelim.
C
B
, ........
Gerekçesi:
4.
D
([AB] // [CD] ve
[AC] // [BD])
C
........
Bunun için V
E na eş ABC üçgeninin BC kenarına
%
şekildeki gibi bir GBC çizelim. BG kenarı üzerinde
........
, ........
Gerekçesi:
.....................
.....................
Aşağıda K. K. K. eşlik teoreminin ispatı iki kolonlu
ispat biçiminde verilmektedir. Buna göre gerekçeler kısmında boş bırakılan yerleri uygun şekilde
doldurunuz.
A
İfadeler
Gerekçeler
1.
|BC| = |EF|
Verilen
2.
%
%
m (CBH) = m (FED)
........................
3.
|BH| = |DE|
Çizimden
4.
HBC , DEF
........................
5.
|AB| = |BH|
Verilen ve 4. adımdan
6.
%
%
m (BAH) = m (BHA)
5. adımdan
7.
|AC| = |CH|
........................
8.
%
%
m (CAH) = m (CHA)
7. adımdan
9.
%
%
m (BAC) = m (CHB)
6. ve 8. adımdan
10.
ABC , HBC
11.
ABC , DEF
D
E
B
C
F
D
D
D
D
D
D
........................
4. ve 10. adımın
sonucu olarak
H
G
Yukarıdaki ABC ve DEF üçgenlerinde
6AB@ , 6DE@ _bb
bb
D
D
6BC@ , 6EF@ `b ise ABC , DEF
bb
6AC@ , 6DF@ b
a
olduğunu göstereceğiz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
669
Üçgenlerin Eşliği
KENDİMİZİ SINAYALIM
5.
Eş üçgenlerin eş kenarlarına ait kenarortaylarının ve yüksekliklerinin de eş olduğunun ispatı aşağıda akış diyagramı biçiminde verilmiştir. Buna göre diyagramlardaki boşlukları uygun şekilde doldurunuz.
a.
ABC , DEF olsun.
D
D
A
B
D
K
C
E
P
F
|AB| = |DE|
m (V
B) = m ( V
E)
|BC| = |EF|
.......................
Üçgenlerin eşliğinden
.......................
D
|BK| = |EP|
D
ABK , DEP
K. A. K. eşlik teoreminden
.......................
6AK@ , 6DP@
.......................
b.
D
D
ABC , DEF olsun.
A
B
R
D
C
E
H
m (W
C) = m ( V
F)
%
%
m (ARC) = m (DHF)
|AC| = |DF|
Üçgenlerin eşliğinden
.......................
Üçgenlerin eşliğinden
%
%
m (RAC) = m (HDF)
.......................
D
D
ARC , DHF
A. K. A. eşlik teoreminden
6AR@ , 6DH@
.......................
670
F
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Eşliği
KENDİMİZİ SINAYALIM
Alıştırmalar
1.
5.
D
|AB| = |BF|
4
x+
2x – 3
|BE| = |ED| E
C
E
F
B
X
C
Y
|EB| = |BC|
5–x
x
C
|AE| = 8 birim ise
B
x kaç br dir?
D
Şekilde
A
[AB] ⊥ [BD] dir.
5
%
%
m (BAC) = m (EDB)
E
olduğuna göre
3
3
Yandaki şekilde A, X, Y
doğrusal ve verilenler
D
D
göre BXY , CXY olduğunu gösteriniz.
A
Şekilde
%
%
m^AEDh = m^ACDh
8
C
6.
olduğuna göre x
kaçtır?
A
B
D
B, E, CFdoğrusal
5–x
%
_%i
D m^xABC hC= m EDC B
D
4.
D
Buna göre ABC , DEF olduğunu gösteriniz.
x kaçtır?
8
B
D
F
A
Şekildeki
E
E
C
[AB] // [DE] , [AC] // [DF] , |BE| = |CF| dir.
|BC| = 2x – 3 ise
A
3.
E
Yukarıdaki şekilde B, E, C, F doğrusal
|BD| = x + 4
C
x+3
A
B
|AD| = |CF|
F
2.
D
Yandaki şekilde A, D,
C, F doğrusal
A
B
A
C
x
D
x kaç br dir?
7.
A
E
b
a
B
C
D
x
Yukarıdaki şekilde B, C, D doğrusal, |AB| = b, |ED| = a
olduğuna göre
|BD| = x in a ve b türünden değerini bulunuz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
671
Üçgenlerin Eşliği
KENDİMİZİ SINAYALIM
Uygulama ve Problem Çözme
1.
4.
A
ABC ikizkenar üçgen
A
|BE| = |DC|
E
|AB| = |AC|
D
B
E
B
C
D
F
Şekilde origami ile kâğıttan bir kuşun yapım aşaması görülmektedir. Verilenlere göre
%
%
[AD] ⊥ [BC] , [AB] , [AC] , m (DBE) = m (DCF)
C
olduğuna göre |BD| = |EC| olduğunu gösteriniz.
%
%
m^EDBh = m^CDFh olduğuna göre
2.
E
A
D
Yandaki şekilde
a.
%
%
m (ACD) = m (ABD) olduğunu gösteriniz.
[AB] // [FE]
b.
[BE] , [CF] olduğunu gösteriniz.
[AC] ⊥ [BE]
C
[FD] ⊥ [BE]
F
B
5.
|BC| = |DE|
olduğuna göre aşağıdaki eşitlikleri gösteriniz.
a.
|AC| = |DF|
c.
%
%
m (ADB) = m (ECF)
b.
A
|AD| = |CF|
B
D
C
E
Bir derenin
genişliğini
hesaplamak için
Thales’in
gemilerin kıyıya
olan uzaklığını
hesaplamada
kullandığı
yöntemi kullanalım. Şekle göre
3.
D
C
ABCD
dörtgeninde
|BD| = |DC|, [AB] ⊥ [BC] ve [EC] ⊥ [BC] ise
[AB] // [CD] ve
[AD] // [BC]
A
672
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
D
ABD ile ECD üçgenleri eş midir? Eğer eş ise eş
olduklarını gösterirken hangi eşlik kuralı kullanılmaktadır?
b.
Derenin genişliğini bulmak için hangi doğru parçasının uzunluğunu bulmalıyız? Açıklayınız.
B
olduğuna göre |AB| = |CD| ve |BC| = |AD| olduğunu
gösteriniz.
D
a.
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında ikizkenar üçgenin sahip olduğu bazı özellikleri inceleyeceğiz.
Araç ve Gereçler: Dinamik geometri yazılımı
Adım 3
A
Adım 1
C
D
B
A
Yazılımın “Açıortay”
özelliğini kullanarak ABC
üçgeninin A açısına ait
açıortayını çiziniz.
Adım 4
%
Çizdiğiniz şekildeki V
B, W
C ve ADC nın ölçülerini; |BD|,
|DC| nu hesaplayınız. Bu değerleri not ediniz.
Dinamik geometri yazılımı yardımıyla merkezi A olan bir
çember çiziniz.
Adım 5
Etkinlikteki ilk dört adımı farklı ikizkenar üçgenler için
uygulayıp oluşturduğunuz yapılar üzerinde ilgili ölçümler yaparak aşağıdaki tabloyu doldurunuz.
m (V
B)
Adım 2
A
m (W
C)
%
m (ADC)
|BD|
|DC|
C
Adım 6
B
Bir köşesi A olan, diğer iki köşesi çemberin üzerinde olan
ABC üçgenini oluşturunuz ve ardından çemberi gizleyiniz.
Oluşturmuş olduğunuz ABC üçgeninin ikizkenar üçgen
olup olmadığını gerekçeleri ile birlikte açıklayınız.
..............................................................................................
%
B) , m ( W
C) , m (ADC) , BD , DC arasınTabloya göre m ( V
da belirlemiş olduğunuz ilişkileri aşağıya yazınız.
..............................................................................................
Sonuç
Yaptığınız bu çalışma sonucunda ikizkenar üçgen için
belirlemiş olduğunuz özellikleri aşağıya yazınız.
..............................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
673
Bölüm
4.1
Eşlik
4.1.3. İkizkenar ve Eşkenar Üçgen
Neler Öğreneceğiz?
•
İkizkenar üçgen ve özelliklerini
•
Eşkenar üçgen ve özelliklerini
Başlarken
Yandaki şekilde de görüldüğü gibi
özellikle piramit şeklindeki büyük
yapılar tasarlanırken yapının dengeli
olabilmesi için ikizkenar ve eşkenar
üçgenlerden sıklıkla yararlanılır.
Anahtar Terimler
•
İkizkenar üçgen
•
Eşkenar üçgen
Daha önceki yıllarda ikizkenar ve eşkenar üçgeni tanımış ve bu üçgenlerin sahip olduğu bazı özellikleri incelemiştik. Bu bölümde önce eşkenar ve ikizkenar üçgenle ilgili
bilgilerimizi gözden geçirip ardından özelliklerini gerekçeleri ile birlikte inceleyeceğiz.
İkizkenar Üçgen
İnceleyelim
A
Yüzey Şakülü
Tepe açısı
Taban açısı
B
Özellikle Eski Mısır’da yüzeylerin düz olup olmadığını
belirlemek için yukarıdaki
resimde görülen yüzey şakülleri kullanılırdı. Bu yüzey
şaküllerinde aslında ikizkenar
üçgenin özellikleri kullanılmaktadır. Bu aracın yüzeyin
eğimli olup olmadığını
belirlemede nasıl yardımcı
olabileceğini düşününüz.
C
Taban açısı
İki kenarı eş olan üçgene ikizkenar üçgen
denir. İkizkenar üçgende eş kenarların
oluşturduğu açı tepe açısı, diğer açılar
taban açıları ve eş olmayan kenar da
taban olarak isimlendirilir.
İkizkenar üçgen bir çok özelliğe de
sahiptir. Aşağıda bu özelliklerden bazıları
incelenmiştir.
Özellik – I
A
C
İkizkenar üçgenin taban açılarının ölçüleri
birbirine eşittir.
B
Bu özellik K. A. K. eşlik kuralının bir uygulaması olarak ispatlanmıştır. Şimdi bu kuralı
kullanarak aşağıdaki örneği yapalım.
674
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
İkizkenar ve Eşkenar Üçgen
1
Anahtar Bilgi
A
Yandaki ABC üçgeninde
50°
|AB| = |AC| ve
İki kenarı eş olan üçgenlerin
eş kenarlarının karşısındaki
açılar da eş olduğu gibi iki
açısı eş olan üçgenlerin de
karşılarındaki kenarlar eştir.
m (W
A) = 50° dir.
Buna göre m ( V
B) nün değerini bulalım.
C
B
|AB| = |AC| olduğundan ABC bir ikizkenar üçgendir. İkizkenar üçgenin taban açılarının ölçüB) = m ( W
C) dir. Üçgenin iç açılarının ölçüleri toplamı 180°
leri birbirine eşit oludğundan m ( V
W
W
V
olduğundan m ( A) + m ( B) + m ( C) = 180° ise 2m ( V
B) = 130° olduğundan m ( V
B) = 65° dir.
Özellik – II
A
C
İkizkenar üçgende tepe açısına ait açıortay
hem kenarortay hem de yüksekliktir.
D
B
Yandaki şekilden de görüldüğü gibi A. K. A. eşlik
A
D
C
D
B
D
kuralına göre BAD , CAD olduğundan
% %
|BD| = |CD| ve BDA , CDA dır.
%
%
m (BDA) + m (CDA) = 180° olduğundan
%
%
m (BDA) = m (CDA) = 90° olur.
Yukarıda incelenen özelliklerin karşıtları da doğrudur.
Özellik – III
•
Bir üçgenin iki açısı eş ise bu açıların karşısındaki kenarlar da eştir. (İki açısı
eş olan üçgen ikizkenar üçgendir.)
•
İkizkenar üçgende tabana çizilen yükseklik hem kenarortay hem de açıortaydır.
•
İkizkenar üçgende tabana çizilen kenarortay hem yükseklik hem de açıortaydır.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
675
Bölüm
4.1
Eşlik
2
ABC ikizkenar bir üçgen
A
|AB| = |AC| ve
%
m (ACD) = 110°
110°
B
C
D
%
olduğuna göre BAC nın ölçüsünün kaç derece
olduğunu bulalım.
%
%
ACB ve ACD komşu bütünler açılar olduğundan
%
%
%
%
m (ACB) + m (ACD) = 180° ise m (ACB) + 110° = 180° eşitliğinden m (ACB) = 70° olur.
İkizkenar üçgende taban açılarının ölçüleri eşit olduğundan
D
%
%
m (ABC) = m (ACB) = 70° olup ABC de iç açılar toplamından
%
%
70° + 70° + m (BAC) = 180° ise m (BAC) = 40° elde edilir.
3
Yandaki şekilde köşeleri A, D ve G olan ikizkenar üçgen şeklinde bir kitaplık görülmektedir.
%
Bu kitaplıkta |AD| = |DG|, |AR| = |GR| ve m (GDR) = 36°
%
ise DAR açısının ölçüsünün kaç derece olduğunu
D
bulalım.
A
R
G
DAG üçgeni ikizkenar üçgen ve |AR| = |GR| olduğundan [DR] kenarortayı aynı zamanda
açıortay ve yüksekliktir.
%
Buna göre [DR] ⊥ [AG], yani m (DRA) = 90° ve [DR] açıortay olduğundan
%
%
m (GDR) = m (ADR) = 36° olur.
DAR üçgeninin iç açılarının ölçüleri toplamı 180° olduğundan
%
%
%
m (DAR) + m (ADR) + 90° = 180° dir. m (ADR) = 36° olduğundan
%
m (DAR) = 180° - 90° - 36° = 54° olarak bulunur.
676
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
İkizkenar ve Eşkenar Üçgen
4
Bunu biliyor muydunuz
ABC üçgeninde [BE], B açısının açıortayı
A
[BE] ⊥ [AC]
%
m (BAC) = 70° ve
70°
E
B
C
D
A
70°
E
70°
B
C
D
|AE| = |CD| olduğuna göre
%
EDC nın ölçüsünün kaç derece olduğunu bulalım.
ABC üçgeninde [BE] hem yükseklik hem de açıortay
olduğundan ABC üçgeni ikizkenar üçgen olup [BE]
aynı zamanda kenarortaydır.
%
%
Yani |AE| = |EC| ve m (BAC) = m (ACB) = 70° dir.
%
%
|EC| = |CD| olduğundan m (DEC) = m (EDC) dir.
Dayanıklı ve estetik yapıların
tasarımında eşkenar üçgenlerden sıklıkla yararlanılmaktadır.
%
%
%
%
m (DEC) + m (EDC) = 70° ise 2m (EDC) = 70° eşitliğinden m (EDC) = 35° elde edilir.
5
Yanda verilen şekilde
A
|AD| = |DF| = |EB|
D
|EF| = |BC| ve
%
m (ABC) = 108°
F
%
olduğuna göre DEC nın ölçüsünün kaç derece olduğunu
hesaplayalım.
108°
E
B
C
|AD| = |DF| ve |DE| = |EC| olduğundan
A
x
D
x 2x
F
108°
E
B
2x
C
ADF ve DEC üçgenleri ikizkenar üçgenlerdir.
%
%
m (DAF) = m (AFD) = x olsun.
%
%
%
m (EDC) = m (DAF) + m (AFD) olduğundan
%
m (EDC) = 2x ve DEC üçgeni ikizkenar olduğundan
%
m (DCE) = 2x olur. ABC üçgenin iç açılarının ölçüleri toplamından; x + 2x + 108° = 180° ise 3x = 72° eşitliğinden
x = 24° olur. EDC üçgeninin iç açıları toplamından
%
%
2x + m^DECh + 2x = 180° ise m^DECh = 180° – 4x = 180° – 4 · 24° = 84° elde edilir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
677
Bölüm
4.1
Eşlik
Eşkenar Üçgen
A
Üç kenarının uzunlukları birbirine eşit olan üçgene eşkenar üçgen denir.
Yandaki ABC eşkenar üçgeninde
C
|AB| = |BC| = |CA| dır.
B
İkizkenar üçgende olduğu gibi eşkenar üçgenin de sahip olduğu bazı temel özellikler
vardır. Aşağıda bu özellikler sunulmuştur.
Özellik – I
A
Eşkenar üçgenin iç açılarının ölçüleri birbirine
eşit ve her biri 60° dir.
C
B
İlköğretim yıllarından beri bildiğimiz bu özelliğin niçin doğru olduğunu inceleyelim.
D
D
ABC ve ACB üçgenlerini düşünüldüğünde
6AB@ , 6AC@ _bb
b
D
D
6BC@ , 6CB@ `b olduğundan K. K. K. eşlik kuralına göre ABC , ACB olur.
bb
6CA@ , 6BA@ b
a
A,V
B,W
C dir.
Eş üçgenlerin karşılıklı açıları eş olduğundan W
Bu özellik ikizkenar üçgenin özellikleri kullanılarak da rahatça gösterilebilirdi. Her eşkenar üçgen aynı zamanda bir ikizkenar üçgen olduğundan ikizkenar üçgenin sahip olduğu özelliklere eşkenar üçgenler de sahiptir.
B,W
C olur.
Yukarıdaki ABC üçgeninde [AB] , [AC] olduğundan V
A,V
B ve böylece W
A,V
B,W
C olur.
Ayrıca [BC] , [AC] olduğundan W
Üçgenin iç açıları 180° ve açılar eş olduğundan eşkenar üçgenin her bir iç açısı 60° olur.
678
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
İkizkenar ve Eşkenar Üçgen
Özellik – II
Anahtar Bilgi
Her eşkenar üçgen bir ikizkenar üçgendir.
A
°
30
°
30
Bir eşkenar üçgende bir açının açıortayı, karşı
kenara ait hem kenarortay hem de yüksekliktir.
C
D
B
Eşkenar üçgen de bir ikizkenar üçgen olduğu için ikizkenar üçgen için geçerli olan bu
özelliğin, eşkenar üçgen için de geçerli olduğu rahatlıkla görülebilir.
6
ABC eşkenar üçgeninde
B
|AE| = |CE| ve
%
m (DCB) = 23°
%
olduğuna göre CDE nın ölçüsünü bulalım.
D
23°
C
E
A
ABC eşkenar üçgeninde |AE| = |CE| olduğundan [BE] kenarortaydır ve aynı zamanda
açıortaydır.
%
%
Bu durumda m (ABE) = m (EBC) = 30° olur.
Bir üçgende iki iç açının ölçüsünün toplamı bu açılara komşu olmayan üçüncü açının
dış açısının ölçüsüne eşit olduğundan BDC üçgeninde
%
%
%
m (CDE) = m (DBC) + m (DCB) = 30° + 23° = 53° olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
679
Bölüm
4.1
Eşlik
7
C
E
D
x
20°
A
ABC ve BED eşkenar üçgenler
%
m (EAB) = 20°
%
olduğuna göre AEB nın ölçüsünün kaç derece olduğunu hesaplayalım.
B
C
E
D
x
ABC ve BED üçgenleri eşkenar üçgenler olduğun%
%
dan m (ABC) = m (EBD) = 60° olup ABE üçgeninde
iç açılar toplamından
20° + 120° + x = 180°
20°
A
140° + x = 180°
B
x = 40° olur.
8
Yandaki ABC eşkenar üçgeninde
%
|BE| = |CD| ise AFE ölçüsünü bulalım.
A
E
F
B
D
C
Eşkenar üçgenin tüm iç açılarının ölçüleri 60° ve tüm kenar uzunlukları eşit olduğundan
%
%
|CB| = |AC| , m (EBC) = m (DCA) = 60° ve |EB| = |DC|
A
β
olduğundan K. A. K. eşlik kuralına göre
E
60°
B
F
D
D
D
%
%
EBC , DCA dır. Buna göre m (BCE) = m (CAD) olur.
θ
β
C
%
%
%
m (BCE) = m (CAD) = β ve m (ECA) = θ olsun.
%
Buna göre β + θ = 60° olur. AFE , AFC üçgeninin dış açısı olduğundan
%
%
m (AFE) = β + θ dır. Dolayısıyla, m (AFE) = 60° elde edilir.
680
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
İkizkenar ve Eşkenar Üçgen
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
Alıştırmalar
1.
Aşağıdaki ifadelerin yanlarına doğru olanlar için
“D”, yanlış olanlar için “Y” yazınız.
1.
a.
(. . . .) İkizkenar üçgende taban açı ölçüleri eştir.
a.
b.
(. . . .) Eşkenar üçgenin tüm iç açı ölçüleri eşit ve 60°
dir.
c.
(. . . .) İkizkenar üçgenin taban açıları dar açı olmak
zorundadır.
d.
(. . . .) İkizkenar üçgenin tabanına ait yükseklik aynı
zamanda kenarortay ve açıortaydır.
f.
b.
A
A
x
E
80°
(. . . .) Her ikizkenar üçgen aynı zamanda eşkenar
üçgendir.
ç.
e.
Aşağıdaki şekillerde verilen açı ölçüleri ve eş kenarlara göre x değerlerini bulunuz.
165°
x
4x
B
C
c.
B
50°
100°
C
B
E
D
H
E
d.
β
θ
B
θ
B
K
C
F
10°
D
B
i. a > β
D
α
D
x
A
Yandaki şekilde
verilenlerle ilgili
aşağıdaki ifadelerin
doğruluğunu gösterin.
A
F
A
x
(. . . .) Bir ikizkenar üçgen geniş açılı üçgen ise geniş
açı tepe açısı olmak zorundadır.
2.
C
ç.
A
(. . . .) İkizkenar üçgenin tüm kenarlarına ait yükseklikler her zaman eştir.
D
x
C
ii θ < 45°
θ
θ
C
iii. |AB| = |AC|
2.
Yandaki şekilde
A
A nın açıortayı
[AD], W
iv. a > 90°
|EC| = |DC| dir.
E
β
α
B
D
C
Verilenlere göre a ile β arasındaki bağıntıyı bulunuz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
681
İkizkenar ve Eşkenar Üçgen
KENDİMİZİ SINAYALIM
3.
Uygulamalar ve Problem Çözme
Yandaki şekilde
A
[BD] , B açısının
açıortayı
D
1.
αα
[BA] ⊥ [EA
B
α
C
E
E
[BD] ⊥ [DC]
[AD] ⊥ [BC]
α
B
b.
A
D
C
%
%
%
m^ABEh = m^BADh = m^DAC h
Aşağıdaki üçgenlerde verilenlere göre a değerlerini bulunuz.
a.
ABC dar açılı bir üçgendir.
[AE] ⊥ [BE]
%
olmak üzere m (DEC) = a kaç derecedir?
4.
Yandaki şekilde
A
Verilenlere göre
AE
oranı kaça eşittir?
BC
A
α
2.
30°
Yandaki şekilde
A
ABC eşkenar üçgen
40°
B
H
α
C
B
H
|AE| = |BD| = |FC|
E
C
F
c.
ç.
A
α
A
B
30°30°
D
C
%
olduğuna göre m (FDE) = a kaç derecedir?
α
B
H
d.
A
α
30°
C B
H
C
3.
ABC ikizkenar
üçgen
D
48°
α
B
H
Yandaki şekilde
A
y
x
z
C
B
E
|AC| = |BC|
F
|AD| = |BE|
|AF| = |DB|
70°
C
%
m (FCE) = 70° dir.
Verilenlere göre x, y, z değerlerini bulunuz.
682
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
İkizkenar ve Eşkenar Üçgen
KENDİMİZİ SINAYALIM
4.
7.
A
Yandaki ABC
üçgeninde
A
E
120°
x
E
|DE| = |DC| = |EB|
α
B
b
a
|AD| = |AE|
D
D
B
%
ve m (BEC) = 120°
C
%
ise m (ECB) = a kaç derecedir?
C
Yukarıdaki şekilde ABC eşkenar üçgen
%
%
%
m (CBE) = m (BAD) = m (ACD) , |BE| = a, |ED| = b ise
|AD| = x uzunluğunun a ve b cinsinden ifadesini
bulunuz.
8.
Yandaki şekilde
A
�
D
5.
α
ABC eşkenar üçgendir.
E
α
ABC ve DCE eşkenar üçgenler
F
Yandaki şekilde
A
B
D
C
E
B, C, E doğrusal
noktalardır.
%
Buna göre m ( EFB ) = a kaç derecedir?
110°
B
C
%
Şekilde verilenlere göre m (AED) = a kaç derecedir?
6.
Yandaki ABC
üçgeninde
%
m^DBCh = a
A
B
2α
α
D
x
C
[AD] ⊥ [BD]
%
%
m^BADh = m^DAC h
%
%
m^ABDh = 2 · m^DBC h
olmak üzere verilenlere göre x ile a arasındaki
ilişkiyi bulunuz.
9.
Yandaki şekilde
A
�
ABC ve AFE eşkenar üçgenler ve
E
D
θ
B, F, D, E doğrusal
noktalardır.
F
B
C
%
Buna göre m (BEC) = θ kaç derecedir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
683
İkizkenar ve Eşkenar Üçgen
KENDİMİZİ SINAYALIM
10. �
Yandaki
A
ABC üçgeninde
[AD] , A açısının
açıortayı ve
E
60°
B
10°
D
x
C
[AD] ⊥ [DE] dır.
13. � ABC eşkenar üçgen ve içinde bir nokta D olsun.
%
%
DBC üçgeni için m (DBC) = θ ve m (DCB) = a dır.
ABC üçgeninin dışında [AC] üzerine kurulan AEC
%
%
üçgeni için de m (CAE) = θ ve m (ACE) = a oldu%
ğuna göre m (DEC) = x kaç derecedir?
%
Yukarıdaki verilenlere göre m (ECB) = x kaç derecedir?
14. �
11. �
Yanda verilen
şekilde
A
Yandaki şekilde
A
|AB| = |AC|
E
|BD| = |CE|
α
E
D
y
%
m (ACB) = 80°
x
B
%
%
m (ABD) = m (ACE)
D
C
ABC ve ADE eşkenar üçgenler
ise
x = y olduğunu
gösteriniz.
%
m (AED) = a
80°
C
B
%
Yukarıda verilenlere göre m (AED) = a kaç derecedir?
15. �
12. �
x
H
B
|AB| = |AC|
α
olduğuna göre
%
m (AED) = a kaç derecedir?
E
C
y
E
Buna göre x = y olduğunu gösteriniz.
684
20°
Yanda verilen
şekilde ABC ve BHE
birer eşkenar üçgendir.
A
Yanda verilen ABC
üçgeninde
A
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
30°
D
B
20°
C
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında üçgenin kenar uzunlukları ile açı ölçüleri arasında bir ilişki olup olmadığını inceleyeceğiz.
Araç ve Gereçler: Kâğıt, kalem, cetvel, açıölçer
Adım 1
Kâğıt üzerine bir ABC üçgeni çiziniz.
A
B
C
Adım 2
Açıölçer ve cetvel yardımıyla çizdiğimiz üçgenin açı ve kenar ölçülerini
belirleyerek aşağıdaki tabloyu doldurunuz.
A
B
C
Açı Ölçüleri
Kenar Uzunlukları
%
m (ABC) = . . . . . . . . . . . .
|AC| = . . . . . . . . . . . .
%
m (BCA) = . . . . . . . . . . . .
|AB| = . . . . . . . . . . . .
%
m (CAB) = . . . . . . . . . . . .
|BC| = . . . . . . . . . . . .
Sonuç
Elde ettiğiniz verilere göre üçgenin kenar uzunlukları ile açılarının ölçüleri arasında büyüklük küçüklük bakımından
nasıl bir ilişki vardır? Ulaştığınız bu sonucu aşağıya yazınız ve farklı üçgenler için test ediniz.
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
685
Bölüm
4.1
Eşlik
4.1.4. Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
Neler Öğreneceğiz?
•
Başlarken
Üçgen kenarları ile üçgenin
açıları arasındaki ilişkileri
Kara ve deniz ulaşımının aynı anda gerçekleştirilebilmesi için bazı köprüler ayrılabilir şekilde
inşa edilmiştir. Böylece yüksek deniz taşıtlarının
bir köprünün altından geçebilmesi mümkün
olmaktadır. Yandaki resimde bu amaçla tasarlanan
İstanbul’daki Galata Köprüsü görülmektedir. Sizce
köprünün havada olan kanatlarının uzunlukları
toplamı, kanatlar indirildiğinde bir köprü oluşturabilmesi için ne kadar olmalıdır?
Anahtar Terimler
•
Üçgen eşitsizliği
Aşağıda verilen üçgenlerin iç açılarının ölçülerini büyükten küçüğe doğru sıralayalım.
Sembol ve Gösterimler
•
a>b
•
x<y
D
A
9
71°
12
E
63°
56°
B
14
C
F
D
Yukarıdaki şekildeki ABC nde tüm açı ölçüleri verildiğinden bu üçgenin açı ölçülerinin
A) > m ( V
B) > m ( W
C) şeklinde belirleyebiliriz. Bununla birlikte
büyüklük sıralamasını m (W
D
DEF nde ise sadece kenar uzunlukları belirtilmiştir. Acaba bir üçgenin sadece kenar
uzunlukları verilirse hangi açının ölçüsünün daha büyük olduğuna, kenar uzunluklarına bakarak karar verebilir miyiz?
Aşağıdaki teorem, bir üçgenin kenar uzunlukları ile açılarının ölçüleri arasındaki ilişkiyi
belirlememize yardımcı olmaktadır.
Teorem
A
b
c
B
686
a
C
Bir üçgende iki kenar eş değilse bu kenarlardan uzun olanın karşısındaki açının ölçüsü,
kısa olanın karşısındaki açının ölçüsünden
büyüktür.
B) > m ( W
C) dir.
Yandaki şekilde b > c ise m ( V
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
İspat
D
Verilenler: ABC , b > c
B) > m ( W
C)
İstenen: m ( V

A
c


c
D
ABC nde |AC| > |AB| olduğundan [AC] kenarı
üzerinde |AB| = |AD| olacak şekilde bir D noktası
alınabilir.
b



D
Alınan bu noktayı B köşesi ile birleştirelim.

B
C
D
Bu durumda ABD ikizkenar üçgen olacağından
%
%
m (ABD) = m (ADB) dır.
Bir üçgende, bir dış açının ölçüsü kendisine komşu olmayan iki iç açının ölçüleri
D
%
%
%
%
toplamına eşit olduğundan BCD de m (ADB) > m (DCB) ve m (ABD) = m (ADB) den
%
%
m (ABD) > m (DCB) dir.
D
D
%
%
%
ABD ikizkenar üçgen ve ABC de m (ABC) = m (ABD) + m (DBC) olduğundan
%
%
m (ABC) > m (DCB) dir.
D
Bu teoreme göre yukarıda kenar uzunlukları 9, 12 ve 14 birim olarak verilen DEF nin açı
ölçülerinin büyüklük sıralaması
m (W
D) > m ( V
E) > m ( V
F) şeklindedir.
1
D
A
ABC de
a = 12 cm
c
b
b = 9 cm ve
c = 11 cm
a
B
C
A) , m ( W
C) ve m ( V
B) değerlerini
olduğuna göre m (W
sıralayalım.
D
ABC de a > c > b dir. Bir üçgende büyük kenar karşısında ölçüsü büyük açı olduğundan
A) > m ( W
C) > m ( V
B) şeklinde olur.
ve W
A, V
B ve W
C nın ölçülerinin sıralaması m (W
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
687
Bölüm
4.1
Eşlik
2
Bunu biliyor muydunuz
C
Yandaki şekilde
B
A, E, B ve C, E, D noktaları doğrusaldır.
E
|AC| > |AE| > |CE| ve
|DE| > |BD| > |BE|
A
Galata Köprüsü 490 metre
uzunluğunda ve 80 metrelik
kısmı açılabilen bir köprüdür.
Üzerinden iki şerit tramvay
yolu geçen Galata Köprüsü
İngiltere ve ABD’deki birkaç
köprünün yanı sıra, dünyada
üzerinden tramvay geçen
ender köprülerden biridir.
D
sıralamaları olduğuna göre en büyük ölçülü açıyı
bulalım.
D
ACE nin kenar uzunlukları arasındaki sıralama |AC| > |AE| > |CE| şeklindedir.
En uzun kenar karşısında, ölçüsü en büyük açı olduğundan
D
E) > m ( W
C) > m (W
A) biçimindedir.
ACE nin iç açı ölçüleri arasındaki sıralama m ( V
D
Diğer taraftan BED nin kenar uzunlukları arasındaki sıralama
D
|DE| > |BD| > |BE| şeklinde olduğundan BED nin iç açı ölçüleri arasındaki sıralama
m (V
B) > m ( V
E) > m ( W
D) biçimindedir.
D
D
ACE ile BED nin iç açı ölçüleri arasındaki sıralamalar birlikte düşünülürse ölçüsü en büyük açı V
B olur.
Sonuç
Bir üçgende uzun kenar karşısında ölçüsü büyük açı olduğu gibi bu ifadenin karşıtı da doğrudur.
A
b
a
B
C
Bir üçgende iki açı eş değilse ölçüsü daha
büyük olan açının karşısında daha uzun
kenar bulunur.
D
A) > m ( V
B) şeklinde ise a > b dir.
ABC nde m (W
688
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
3
D
Yanda ABC de verilen açı ölçülerine göre a, b ve c kenar
uzunluklarını sıralayalım.
A
84°
b
c
42°
a
B
C
D
A) + m ( V
B) + m ( W
C) = 180° olduğundan
ABC nde m (W
84° + m ( V
B) + 42° = 180° ve m ( V
B) = 54° olarak bulunur.
D
ABC de m (W
A) > m ( V
B) > m ( W
C) olduğundan a > b > c dir.
4
B
b
a
100° 40°
D
e
60°
30°
c
A
Şekilde verilen açı ölçülerine göre en kısa
kenarı bulalım.
d
C
Dikkat
D
B
b
30°
A
a
100° 40°
e
c
50°
80°
60°
C
d
D
Farklı üçgenlerin kenar
uzunlukları arasındaki ilişki
incelenirken bu kenarların
karşılarındaki açıların ölçülerinden yararlanmak, doğru
olmayan sonuçlara ulaşmamıza neden olabilir. Örneğin
yandaki örnekte ölçüsü en
küçük açı A açısı olmasına
rağmen, şekildeki en kısa
kenar bu açının karşısındaki
kenar değildir.
ABC ve BCD nin iç açıları ölçüleri toplamından
%
%
D m (ACB) = 50° ve m (CDB) = 80° bulunur.
D
ABC nin açı ölçülerine göre kenar uzunluklarıD
nın sıralaması c > b > e ve BCD nin kenar uzunluklarının sıralaması ise e > a > d şeklinde olur.
O hâlde tüm şekilde kenar uzunluklarının sıralaması c > b > e > a > d şeklinde olacağından en kısa kenar CD kenarıdır.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
689
Bölüm
4.1
Eşlik
5
Dikkat
•
Bir doğruya dışındaki bir noktadan inilen
dikmenin, o noktayı doğru üzerindeki noktalarla birleştiren en kısa doğru parçası olduğunu
gösterelim.
A
Düzlemde iki nokta arasındaki en kısa mesafe bu
noktaları birleştiren doğru
parçasının uzunluğudur.
B
en kısa mesafe
•
A
d
H
B
Yukarıdaki şekilde [AH] ⊥ d ve doğru üzerinde H noktasından farklı herhangi bir B noktası olsun. Buna göre |AH| < |AB| olduğunu göstermeliyiz.
%
[AH] ⊥ d ise ABH üçgeninde en büyük iç açı AHB olduğundan |AH| < |AB| dır.
Bir noktanın bir doğruya
en yakın mesafesi noktadan doğruya indirilen dik
doğru parçasının uzunluğudur.
Dolayısıyla [AH] dikmesinin uzunluğu, [AB] nın uzunluğundan daha kısa olanıdır.
A
x
y
z
6
d
x<y<z
A
1
4
B
3
D
2
5
C
Yandaki şekilde [AD] ile [AC] ve [AB]
ile [BC] yolları dik kesişmektedir. A
noktasından sabit hızla yola çıkan
bir araç sırasıyla 1, 2, 3, 4, 5 numaralı yollardan ilerleyip C noktasına
varıyor.
Bu aracın hangi yolu en uzun sürede geçtiğini bulalım.
D
D
%
ABC nde m (ABC) = 90° olup bu, ABC nin en büyük ölçülü açısı olduğundan bu açının
karşısında yer alan 3 numaralı yol, 1 ve 2 numaralı yollardan daha uzun olacaktır.
D
%
ADC nde m (DAC) = 90° olduğundan bu açının karşısında yer alan 5 numaralı yol, 3 ve
4 numaralı yollardan daha uzun olacaktır.
Sonuç olarak, 5 numaralı yol diğer tüm yollardan uzun olduğundan araç en uzun süreyi
bu yolda harcayacaktır.
690
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında üç doğru parçasının üçgen oluşturabilmesi için uzunlukları arasında nasıl bir ilişki olması
gerektiğini inceleyeceğiz.
2. Durum
Araç ve Gereçler: Kâğıt, kalem, cetvel, makas
8 cm
A
B
m
5c
Adım 1
Cetvel yardımıyla uzunlukları sırasıyla 8 cm ve 5 cm
olan dikdörtgen biçiminde
iki kâğıt şeridi oluşturunuz.
8 cm
5 cm
C
3. Durum
B
8 cm
m
A
5c
Adım 2
8 cm
m
çizim
cetvel
B
C
5c
A
Kâğıt şeridini şekilde
görüldüğü gibi B noktasında uç uca getirerek bu
durumda oluşacak ABC
üçgeninin [AC] nın
uzunluğunu cetvelle
belirleyiniz.
C
4. Durum
8 cm
A
C
B
5 cm
|AB|
|BC|
|AB| + |BC|
|AB| – |BC|
|AC|
1. Durum
2. Durum
Adım 3
İkinci adımda yaptığımız ölçme işlemini, aşağıda verilen
%
durumlarda görüldüğü gibi ABC nın farklı durumları için
tekrarlayarak tabloyu doldurunuz.
4. Durum
Adım 4
Yukarıda yaptığınız ölçümler neticesinde aşağıda verilen
ifadelerde boş bırakılan yerleri doldurunuz.
1. Durum
•
8 cm
A
3. Durum
B
5 cm
•
C
Bir üçgenin iki kenarının uzunlukları toplamı, üçüncü kenarının uzunluğundan . . . . . . . . . . . . . . . . . . . . . . . . . . .
Üçgende herhangi bir kenarın uzunluğu, diğer iki kenar uzunlukları farkının mutlak değerinden . . . . . . . . . . . . . . .
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
691
Bölüm
4.1
Eşlik
Üçgen Eşitsizliği
Aşağıda verilen iki durumda doğru parçalarından üçgenler oluşturmaya çalışalım.
1. Durum
a=2
2. Durum
b=4
c=3
2 ve 3 cm lik doğru parçalarını 4 cm lik
doğru parçasının uç noktalarıyla birleştirip, yaylar oluşturduğumuzda bu yaylar
aşağıdaki şekildeki gibi kesişir.
a=2
b=4
c=1
2 ve 1 cm lik doğru parçalarını 4 cm
lik doğru parçasının uç noktalarıyla
birleştirip, yaylar oluşturduğumuzda bu yaylar aşağıdaki şekilde
görüldüğü gibi kesişmemektedir.
3
2
2
4
1
4
Yukarıda birinci durumda verilen doğru parçaları bir üçgen oluştururken, ikinci durumda verilen doğru parçaları üçgen oluşturmamaktadır. Verilen üç doğru parçası acaba
hangi durumlarda bir üçgen belirtir?
Teorem
A
Bir üçgende herhangi bir kenarın uzunluğu, diğer
iki kenarın uzunlukları toplamından küçüktür.
b
c
a
B
C
Yandaki şekilde a < b + c dir.
D
İspat
α
b
D
Verilenler: ABC nde kenar uzunlukları: a, b ve c
A
İstenen: a < b + c
β
B
692
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
b
c
[BA üzerinde |AD| = |AC| olacak şekilde bir D noktası alalım.
a
α
C
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
İfade
Gerekçe
1.
|BD| = |BA| + |AD|
B, A, D doğrusal
2.
%
m (W
D) = m (DCA)
CAD ikizkenar üçgen
3.
%
%
m (BDC) < m (DCB)
β>0
4.
a<b+c
Büyük açı karşısında büyük kenar bulunur.
D
Yukarıdaki ispata benzer şekilde, diğer kenarlar için de b < a + c ve c < a + b olduğu
gösterilebilir.
b < a+c
c < a+b
2 ifadelerinden
b-c < a
c-b < a
2 elde edilir.
Son eşitsizlik ifadelerinde b – c < a ve c – b < a olduğundan |b – c| < a dır.
Sonuç
Bir ABC üçgeninde a, b, c kenar uzunlukları olmak üzere,
|b – c| < a < b + c
|a – c| < b < a + c
|a – b| < c < a + b
eşitsizliklerinin her üçü de sağlanır.
1
A
D
ABC nde
|AB| = 14 cm ve
10
14
|AC| = 10 cm ise
|BC| = x in alabileceği değerlerin kümesini bulalım.
x
B
C
D
ABC nde üçgen eşitsizliğinden
|14 – 10| < x < |14 + 10| ve buradan 4 < x < 24 bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
693
Eşlik
2
A) > m ( V
B) dir.
ABC çeşitkenar üçgeninde m (W
A
x in alacağı tam sayı değerlerinin kaç tane olduğunu
bulalım.
x
7
B
10
C
Üçgen eşitsizliğinden 3 < x < 17 dir. ... (*)
m (W
A) > m ( V
B) olduğundan 10 > x dir. ... (**)
(*) ve (**) dan 3 < x < 10 olur.
Çeşitkenar üçgende tüm kenar uzunlukları birbirinden farklı olduğundan x ≠ 7 ve x ≠ 10
olmalıdır. Bu durumda, x in tam sayı değerleri 4, 5, 6, 8, 9 olup 5 tanedir.
3
A
C
m
80 c
100 cm
Şekildeki bilardo masasında B ve C toplarının A köşesindeki deliğe uzaklıkları sırasıyla
80 cm ve 100 cm’dir.
Masaya konulacak bir D topunun C topuna
uzaklığı 70 cm, B topuna uzaklığı 60 cm
olacağına göre A köşesindeki deliğe uzaklığının en büyük tam sayı değeri kaç cm’dir?
B
Verilenlere uygun olacak biçimde bir D
topu alalım.
A
C
x
B 6
0 cm
m
m
80 c
100 cm
70 c
Bölüm
4.1
D
D
ACD nde üçgen eşitsizliğinden 30 < x < 170
D
ve ABD nde üçgen eşitsizliğinden
20 < x < 140 olur.
İki eşitsizlik birlikte düşünülürse
30 < x < 140 olduğu görülür.
Bu durumda x in en büyük tam sayı değeri 139 cm’dir.
694
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
4
A
D
ABC nde
|AB| = 10 cm
|AC| = 3x ve
3x
10
D
|BC| = 2x olduğuna göre ABC nin çevresinin en büyük ve
en küçük tam sayı değerini bulalım.
C
2x
B
Dikkat
x’in tam sayı olduğu vurgulanmadığı sürece x’i tam sayı
seçemeyiz.
Yandaki soruda x’in aralığı
2 < x < 10 olarak bulunduğundan çevrenin en küçük
değeri x’in aralığı genişletilerek hesaplanır.
Üçgen eşitsizliğinden 3x – 2x < 10 < 3x + 2x ve x < 10 < 5x’tir.
Bu eşitsizlikten x in çözüm aralığı 2 < x < 10 olarak bulunur.
D
ABC nin çevresi 5x + 10 olduğundan x in aralığından yararlanarak çevrenin aralığını
bulalım:
2 < x < 10 ise 10 < 5x < 50
20 < 5x + 10 < 60’tır. Buradan çevrenin en küçük tam sayı değeri 21 cm ve en büyük
123
tam sayı değeri 59 cm olur.
D
Ç (ABC)
5
A, B, C birer baz istasyonunu temsil etmektedir. ABC üçgeninin çevre uzunluğu 48 km’dir.
Bu üçgenin içindeki bir noktaya baz istasyonlarının kontrol merkezi yapılacaktır.
A
D noktası kontrol merkezini göstermek üzere,
kontrol merkezinin baz istasyonlarına olan
uzaklıkları toplamının en küçük tam sayı
değeri nedir?
D
B
C
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
695
Bölüm
4.1
Eşlik
Bunu biliyor muydunuz
Şekilde ADC, ADB ve DCB üçgenlerinde üçgen
eşitsizlikleri yazılırsa
a<y+z
b<x+z
A
c < x + y olur.
x
c
b
D
y
z
a
B
C
Eşitsizlikler taraf tarafa toplanırsa
Bir üçgenin köşelere olan
uzaklıklarının toplamının
en küçük olduğu noktaya
Fermat-Toricelli noktası adı
verilir.
a + b + c < 2(x + y + z) olur.
D
Ç (ABC) = 48 br olduğundan
48 < 2 (x + y + z) ve 24 < (x + y + z) elde edilir.
Sonuç olarak, kontrol merkezinin baz istasyonlarına olan uzaklıkları toplamının en küçük tam sayı değeri 25 km’dir.
A
120° P 120°
B
120°
Sonuç
C
Bir üçgenin içinde alınan herhangi bir
noktanın köşelere olan uzaklıkları toplamı
üçgenin çevresinden küçük, çevrenin
yarısından büyüktür.
A
Bu noktayı üçgenin köşelerine birleştiren doğru parçaları
arasında oluşan açıların ölçüleri 120° dir.
x
c
Yağcı, M. (2004) Fermat-Toricelli
Noktası. Matematik Dünyası.
b
D
y
B
696
a
z
C
a+b+c
< x+y+z
2
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
A
B
79°
82°
52°
40°
D
C
Yandaki şekilde
verilen açı
ölçülerine göre
boşlukları <, >, =
sembollerinden
uygun olanıyla
doldurunuz.
|AB| . . . . . |BD|
•
|AD| . . . . . |AB|
•
3.
Yandaki üçgende
verilenlere göre
aşağıdakilerden
hangileri her
zaman doğrudur?
A
E
B
20°
D
C
a.
|BE| = |BD|
b.
|DC| < |AC|
c.
|BE| > |ED|
4.
Aşağıdaki ifadelerin yanlarına doğru olanlar için
“D”, yanlış olanlar için “Y” yazınız.
a.
(. . . . . ) Bir dik üçgende dik açının karşısındaki kenar
en uzundur.
b.
(. . . . . ) Bir üçgende eşit uzunlukta iki kenar varsa bu
kenarların karşısındaki açı ölçüleri eşittir.
c.
(. . . . . ) Uzunlukları 3, 4, 7 cm olan doğru parçaları ile
bir üçgen oluşturulabilir.
ç.
(. . . . . ) Bir üçgenin çevresi 20 cm ise kenarlarından
biri 10 cm olabilir.
d.
(. . . . . ) Bir üçgende en kısa kenarı gören açı ölçüsü
61° olamaz.
e.
(. . . . . ) Bir üçgende bir köşeden karşı kenara indirilen
dikme diğer iki kenardan da uzundur.
f.
(. . . . . ) Bir üçgende yükseklikler toplamı çevreden
büyüktür.
|DC| . . . . . |BC|
•
2.
B
4
A
3
C
•
7
5
10
D
7
5 3
E
%
%
m (BCE) . . . . . m (CBE)
•
%
%
m (BAE) . . . . . m (BEA)
•
%
%
m (DBE) . . . . . m (BDE)
•
%
%
m (ECD) . . . . . m (EDC)
Yandaki şekilde B, C, D
noktaları doğrusal
olmak üzere boşlukları
<, >, = sembollerinden
uygun olanıyla
doldurunuz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
697
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
5.
Yandaki üçgende
verilenlere göre
aşağıdakilerden
hangileri doğrudur?
A
72° 36°
B
D
36°
|BC| > |AB|
c.
|BD| < |AD|
ç.
Şekildeki bütün üçgenler ikizkenardır.
A
20
40° °
D
|AD| = |AB|
b.
|AC| > |BC|
c.
|AB| < |AC|
ç.
|DC| > |AB|
d.
|BD| < |AB|
698
a
C
Buna göre aşağıdaki ifadeleri doğru veya yanlış
olarak sınıflandırınız.
b.
a.
b
B
|BD| > |DC|
B
Yandaki ABC
üçgeninde
m (V
B) > m ( W
C) dir.
A
c
C
a.
6.
7.
50°
C
Yandaki ABC
üçgeninde
verilen açı
ölçülerine göre
aşağıdakilerden
hangileri doğrudur?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
a.
b>c
b.
a>b+c
c.
b<a+c
ç.
|a – b| > c
8.
A
B
D
C
Yandaki ABC
A
üçgeninde [AD], W
nın açıortayı
olduğuna göre
aşağıdaki önermelerin doğruluğunu
gösteriniz.
a.
|AC| > |DC|
b.
%
m (ADC) > 90° ise |AC| > |AB| dir.
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
Alıştırmalar
Aşağıdaki şekillerde verilen açı ölçülerine göre
harflendirilen kenar uzunluklarını sıralayınız.
a.
b.
A
b
c
B
c.
K
ç.
ç.
d
H
P
L
a
44°
a
b
72°
K
68°
b
L
e g
N
h
M
................................
M
59°
R
f
G
H
c
3.
b
T
e.
................................
a.
Y
E
d
d
C
e d
60°
E
F
B
Z
................................
60°
M f R
f.
g. T
α>β
a
N
α
P
d
e
B
c
72°
L
β
................................
R
S
G
M
36°
................................
d
80°
d
a
70°
a
R
S
b
c
b
d
40°
H
ç.
40°
L
36°
e
f
e
b
...............................
K
................................
A
F
N
c.
................................
e
D
d
c
D
20
b
e
c
50°
a H
°
°
c
°
°
80°
10°
30
20
A
b.
B
a
b
S
Aşağıdaki şekillerde verilen açı ölçülerine göre en
kısa kenarı belirleyiniz.
A
a
91° h
S
................................
d.
V
e
61°
N
................................
f
d
a
38°
50°
P
R 100°
f
e
c
84°
c
................................
c.
................................
b
40°
50°
G
e
F
H
100°
c
60°
C
................................
E
C
................................
c
a
d
d
b
F
E
D
c
B
20°
50°
b.
e
a
b
a
60°
a. A
a
100°
70°
Aşağıdaki şekillerde verilen açı ölçülerine göre en
uzun kenarı belirleyiniz.
D
18
1.
2.
50°
30°
c
72°
75°
e
f
b
70°
40°
V
65°
g
N
T
R
................................
................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
699
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
4.
ABC eşkenar üçgen
A
D ∈ [BC] olmak
üzere,
x
6.
Aşağıda verilen üçgenlerde x’in alabileceği değerler kümesini bulunuz.
A
a.
|AB| = x
y
|AD| = y
z
B
D
x
B
c.
C
x
K
2
T
ç.
L
F
8
x
4
4
x
S
7
7
8
M
10
x
R
9
V
N
4
b.
10
E
Aşağıda hangi şıklarda verilen uzunluklar ile bir
üçgen oluşturulabilir?
a.
10
C
olduğuna göre x, y, z değerlerini sıralayınız.
5.
5
2
|BD| = z
D
b.
6
10
c.
7.
3
A
D
3
B
50°
6
ç.
E
4
1
C
4
d.
5
12
8
700
48°
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
[BC] nın tam ortasındaki E noktasında bulunan Ali,
A noktasına gidecektir. B noktasına uğrayarak giderse a metre, yalnız C noktasına uğrayarak giderse b metre, C ve D noktalarına uğrayarak giderse c
metre yol yürüyecektir.
Buna göre a, b, c arasındaki sıralamayı bulunuz.
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
8.
D
Yandaki ABC nde
A
4.
m (V
B) > m ( W
C) dir.
40°
|AB| = 14 br
x
14
18
[AB] ⊥ [BC]
y
|BC| = 18 br olduğuna göre
B
Yandaki ABC ve
ADB birer dik
üçgen
A
z
C
t
|AC| = x in alabileceği kaç tane tam sayı değeri vardır?
p
B
c
a > c > b sıralaması
olduğuna göre
b
α
%
m (ABC) = a nın
5.
E
C
A
en büyük tam sayı
a
C
değeri kaçtır?
C
y
x
Yandaki şekilde
A
14
10
B
2.
olmak üzere,
Yandaki şekilde
A
B
k
|AB| = x , |AD| = y , |BD| = t , |AC| = z , |BE| = p ,
|DE | = k uzunluklarını sıralayınız.
Uygulama ve Problem Çözme
1.
D
[AD] ⊥ [BD]
%
m (BAD) = 40°
x
3
z
4
Yandaki şekilde
verilen uzunluklara göre BCD
üçgeninin açı
ölçüleri olan x, y
ve z yi sıralayınız.
D
|AB| = |AC|
m (W
A) < 80° ise
m (V
B) nün alabileceği
kaç farklı tam sayı
değeri vardır?
B
ABC üçgeninde
verilen açı ölçülerine göre
59°
b
a
|b – a| + |c – a| – |c – b|
61°
C
B
|AB| = x br
3x
x
A
c
Yandaki şekilde
A
C
3.
B
6.
|AC| = 3x br
14
C
|BC| = 14 br dir.
Kenar uzunlukları tam sayı olan ABC üçgeninin
çevresinin en küçük değerini hesaplayınız.
işleminin sonucunu bulunuz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
701
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
7.
e
E
D
50°
58°
d
A
h
f
62°
20°
Yandaki şekilde
verilen açı ölçülerine göre en uzun
kenarı bulunuz.
10.
c
60°
c
40°
a
Yandaki ABC
üçgeninde kenar
uzunlukları
arasında a > b > c
A
b
58°
C
a
B
C
tam sayı değeri ne
olur?
b
B
11.
A
H
F
8.
Yandaki ABC
üçgeninde
A
3
D
x
C nın açıortayı
[CD], W
B
B
|AD| = 3 cm
|AF| = |FB| , |AH| = |HC| , [DF] ⊥ [AB] , [AC] ⊥ [EH]
ve |DE| = 3 cm olduğuna göre |BC| nin alabileceği
en küçük tam sayı değeri kaç cm dir?
C
olduğuna göre x in alabileceği en küçük tam sayı
değeri kaçtır?
D 3 E
C
Yukarıdaki ABC üçgeninde
|AC| = x cm
12. A
x
D
3
9.
40°
x
x
B
Yandaki ABC üçgeninde
A
2
|AB| > |AC| dir.
B
C
C
%
Buna göre m (ABC) nin en büyük tam sayı değerini
bulunuz.
702
sıralaması varsa
m (W
A) nın en küçük
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
•
x>1
•
x>
3
2
•
3
<x<5
2
•
x<5
Yandaki şekilde
verilen x uzunluğu
için aşağıdakilerden hangisi her
zaman söylenebilir?
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
13.
Yandaki şekilde
verilenlere göre
A
5
7
B
C
4
x
17.
|BD| nun alabileceği en küçük tam
sayı değeri nedir?
Yandaki ABC
üçgeninde
E
|AE| = a cm
a+3
|EC| = a + 3 cm
B
D
C
Yandaki ABC
üçgeninde verilen
uzunluklara göre
2x
18.
A
Yandaki ABC
üçgeninde göre
D
D
Ç (ABC) nin alabileB
|BD| = |DC|
olduğuna göre |AB| = x in alabileceği en küçük tam
sayı değeri kaçtır?
A
9
a
x
D
14.
A
x
C
3
ceği en büyük tam
sayı değeri kaçtır?
4
E
10
B
|AE| = |EC|
C
[CD] ⊥ [DE]
|AB| = 3 br
15.
|BC| = 10 br
Yandaki ABC üçgeninin kenar uzunlukları
tam sayı ve |AB| =
A
|CD| = 4 br
olduğuna göre |AC| nin alabileceği kaç farklı tam
sayı değeri vardır?
|AC| olduğuna göre
D
Ç (ABC) nin alabileceği en küçük değer
kaçtır?
B
8
19.
C
Yandaki ABC
üçgeninde
A
x
16.
Yandaki ABC
üçgeninin çevresinin alabileceği en
küçük tam sayı
değeri kaçtır?
A
B
14
C
|AC| = 6 br
6
|BC| = 10 br
B
10
C
|AB| = x br ve
m (W
A) > m ( W
C)
olduğuna göre ABC üçgeninin çevresinin alabileceği en büyük ve en küçük tam sayı değerlerini
bulunuz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
703
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
20.
Yandaki ABC
üçgeninde
A
2x + 1
x
23.
[AC] ⊥ [BC]
|AB| = x br
10
10
C
|AD| = 6 br ve
|BC| = 10 br
olduğuna göre ABC üçgeninin çevresinin en büyük
tam sayı değeri kaç br dir?
21.
|AB| = 10 br
6
|AC| = 2x+1 br
B
ABC üçgen
A
B
E
D
E ∈ [BD]
C
olduğuna göre |AE| = x in alabileceği tam sayı
değerleri kaç tanedir?
A
6m
18m
B
10m
24. �
Yandaki şeklide
ABC ikizkenar dik
üçgen
A
C
Şekilde görülen evden sırasıyla 6, 18, 10 m uzaklıklarda bulunan A, B, C kulübeleri inşa edilecektir.
B kulübesi A ve C kulübelerine eşit uzaklıkta olacağına göre B kulübesinin A ve C kulübelerine olan
uzaklıkları toplamının alabileceği en büyük tam
sayı değeri kaçtır?
22.
y
α
|AB| = |AC| ve
D
x
θ
z
B
C
olduğuna göre x, y, z uzunluklarını sıralayınız.
A
25. �
D
A
3
C
D
B
C
Yukarıdaki şekilde D, ABC üçgeni içerisinde bir
D
nokta ve Ç (ABC) = 18 br dir.
|DA| + |DB| + |DC| nin alabileceği en küçük tam sayı
değeri kaçtır?
704
a>β
β
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
2
B
8
6
E
Yandaki şekilde
verilen uzunluklara göre
D
Ç (ABC) nin
alabileceği en
büyük tam sayı
değeri kaçtır?
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
26. �
28. �
40 cm
50 cm
4 cm
A
Bir mobilyacı uzunlukları tam sayı olan farklı ahşap
çubuklardan üçgen çerçeveler üretmektedir. Bu
parçalardan ikisi 40 cm ve 50 cm uzunluğunda
olup bu iki parçanın yanına seçtiği her parça ile bir
üçgen çerçeve oluşturabilmektedir.
Buna göre mobilyacının elinde uzunlukları farklı,
birer tam sayı olan en fazla kaç tane farklı ahşap
çubuk olabilir?
27. � Bir öğrenci, uzunluğu a br olan bir telin uç
kısımlarından b br ve c br uzunluğundaki kısımları
işaretleyip b br ve c br yarıçaplı çember yaylarını
çiziyor.
12 cm
B
Bir öğrenci, 12 cm’lik çubuğun A noktasına pergelini koyarak 4 cm yarıçaplı bir çember çiziyor.
C noktası çember yayı üzerindeki bir nokta ise |CB|
nun alabileceği değerler kümesini bulunuz.
29. �
A
P
b
c
Şekil I
B
C
D E
F
d
d doğrusu üzerinde alınan X noktası için
AX - PX farkı B, C, D, E, F noktalarından hangisi
b
c
Şekil II
için en büyüktür?
c
b
Şekil III
Buna göre hangi durumlarda kenar uzunlukları b, c,
a – (b + c) olan bir üçgenin çizilebileceğini göstermiş olur?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
705
Üçgenin Kenarları ile Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
30.
ABC ve CED birer
üçgen
A
10
B
F
A, C, E doğrusal
H
C
D
9
E
B, C, D doğrusal
F ∈ [BC]
H ∈ [CD] ve
|AF| = 10 br
|HE| = 9 br
olduğuna göre ABC ve DEC üçgenlerinin çevreleri
toplamının en küçük tam sayı değeri kaçtır?
31.
A
B
C
Bir köyde, A ve B su depolarıyla aynı doğrultuda
olmayacak şekilde inşa edilecek C çeşmesine su alınacaktır. Çeşmenin B deposuna daha yakın olacağı
bilinmektedir.
Bu iş için 58 m boruya ihtiyaç olduğuna göre,
i.
Depolar arasındaki mesafenin en büyük tam sayı
değeri nedir?
ii.
Çeşmenin B deposuna uzaklığının en büyük tam
sayı değeri kaçtır?
706
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Eşlik
BÖLÜM ÖZETİ
Üçgende Açılar
•
Bir üçgenin iç açılarının ölçüleri toplamı 180° dir.
A
m (W
A) + m ( V
B) + m ( W
C) = 180°
B
•
C
Bir üçgende, bir dış açının ölçüsü kendisine komşu olmayan iki iç açının ölçüleri
toplamına eşittir.
A
m (W
A) + m ( V
B) = m ( X
C')
•
B
C
D
Bir üçgenin dış açılarının ölçüleri toplamı 360° dir.
m (X
A') + m ( X
B') + m (X
C') = 360°
•
•
Üçgenlerin Eşliği
Karşılıklı açı ve kenarları eş olan üçgenler eş üçgenlerdir.
_
m (W
A) = m ( W
D) bbb
E
bb
A
b
V
V
m ( B) = m ( E) bb
bb
m (W
C) = m ( V
F) bbb
D
D
`b ABC , DEF
ve
bb
D
bb
AB = DE
bb
B
bb
C
BC = EF
bb
bb
F
b
AC = DF
a
K. A. K. Eşlik Kuralı: İki kenarı ve bu kenarların oluşturduğu açıları eş olan üçgenler eş üçgenlerdir.
_b
AB = DE
bb
b D
D
V
V
m ( B) = m ( E) `b ABC , DEF
bb
bb
BC = EF
a
A
B
D
C
E
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
F
707
Bölüm
4.1
•
Eşlik
A. K. A. Eşlik Kuralı: Karşılıklı ikişer açısı ve bu açıların arasında kalan kenarlar eş olan üçgenler eş üçgenlerdir.
_
m (V
B) = m ( V
E) bbb
b
D
D
`b ise ABC , DEF
BC = EF
bb
m (W
C) = m ( V
F) bb
a
•
A
D
B
C
E
F
K. K. K. Eşlik Kuralı: Karşılıklı üç kenar uzunluğu eşit olan üçgenler eş üçgenlerdir.
_
AB = DE bb
b
D
D
BC = EF `b ise ABC , DEF
b
AC = DF bb
a
A
B
•
D
C
E
F
Eş iki üçgenin karşılıklı açıortay, kenarortay ve yükseklikleri de eştir.
İkizkenar ve Eşkenar Üçgen
•
İkizkenar üçgenin taban açılarının ölçüleri eşittir.
İkizkenar üçgende tepe açısına ait açıortay hem kenarortay hem de yüksekliktir.
Eşkenar üçgenin iç açılarının ölçüleri birbirine eşit ve 60° derecedir.
Bir eşkenar üçgende bir açının açıortayı, karşı kenara ait hem kenar ortay hem de yüksekliktir.
•
•
•
Üçgenlerin Kenarları İle Açıları Arasındaki İlişkiler
•
Bir üçgende uzun kenar karşısında ölçüsü büyük açı, kısa kenar karşısında ölçüsü küçük açı bulunur.
A
m (V
B) > m ( W
C) ise b > c
b
c
•
B
C
Bir üçgende herhangi bir kenar uzunluğu, diğer iki kenarın uzunlukları toplamından küçük, farkının mutlak değerinden büyüktür.
A
b + c > a > |b – c|
a + c > b > |a – c|
b
c
a + b > c > |a – b|
B
708
a
C
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Bölüm 4. 1. Eşlik
BÖLÜM DEĞERLENDİRME
1.
A
Yandaki ABC
üçgeninde
140°
D
α
150°
β
B
E
C
4.
D
[AE] A açısının, [CD]
C açısının
açıortaylarıdır.
α
B
ABC üçgeninde
%
%
m (ABC) = m (ADE)
%
%
m (BAD) = m (DAC)
%
C m (DEC) = 100°
A
E
100°
α
B
D
E
%
%
m (BAE) = 120° olduğuna göre m (ACD) = a kaç
derecedir?
5.
ABC üçgeninde
A
E
|AB| = |EC| ve
|BD| = |DC|
75°
B
%
olduğuna göre m (ADB) = a kaç derecedir?
3.
C
ABE üçgeninde |AB| = |AC| = |CD| = |DE| ve
Verilenlere göre a + β kaç derecedir?
2.
A
D
α
C
%
m (ABC) = 75° ve
[ED| ⊥ [BC]
%
olduğuna göre m (ACB) = a kaç derecedir?
A
F
D
E
6.
ABC üçgeninde
A
α
|AC| = |BC|
D
B
|BE| = |AD|
C
ABC ve BEC birer üçgen ve B, D, F, E doğrusal noktalardır.
%
%
m (BAC) = m (BEC) = 90°
%
%
m (ABE) = m (EBC) ve
%
%
%
m (BCD) = m (DCF) = m (FCE)
|AD| + 2 = |DC| ve
E
|AB| = 10 cm
C
B
olduğuna göre DEC üçgeninin çevre uzunluğunu
bulunuz.
%
olduğuna göre m (DFC) = a kaç derecedir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
709
Bölüm 4. 1. Eşlik
BÖLÜM DEĞERLENDİRME
7.
A
E
α
B
D
C
Yandaki şekilde
ABC ve ADE
eşkenar üçgenlerdir.
%
m (ACE) = a kaç
derecedir?
10.
A
4
Yandaki şekilde
B
|AB| = |DC| = 4 br
x
|EC| = 10 br ve
%
%
m (ABC) = m (EDC)
dir.
D
4
E
10
C
[AB] // [EC] olduğuna göre |AD| = x değerini bulunuz.
8.
Yandaki ABC
üçgeninde
A
α
11.
|BD| = |AC|
20°
D
A
C
x–2
B
%
m (ACB) = 40°
B
|BC| = |CD|
3x – 8
E
A, C, E ve B, C, D doğrusal noktalar olduğuna göre
x in değerini bulunuz.
710
%
m (BAC) = 60°
30°
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
%
m (BCD) = 30°
C
olduğuna göre aşağıdakilerden hangisi yanlıştır?
A) |AC| < |AB|
B) |BC| > |DC|
C) |AD| > |DC|
D) |BD| < |BC|
E) |AB| > |BC|
12.
A
d
|AB| = x – 2 br ve
|DE| = 3x – 8 br dir.
D
%
m (ABC) = 50°
50°
Yandaki şekilde
|AC| = |CE|
C
60°
D
%
olduğuna göre m (BAD) = a kaç derecedir?
9.
Yandaki şekilde
%
m (ABC) = 20° ve
40°
B
A
B
20°
a
110°
75°
c
e
D
60°
b
C
Yukarıdaki şekilde verilen açı ölçülerine göre a, b, c,
d, e kenarlarından en kısa olanı bulunuz.
Bölüm 4. 1. Eşlik
BÖLÜM DEĞERLENDİRME
13.
Yandaki ABC
üçgeninde
A
35
15
25°
°
°
x
16.
Yandaki ABC
üçgeninde
A
3x
x
|AB| = |AC| dir.
y
B
B
z
D
E
A) x > y > z
18
C
C
B) y > z > x
D) z > x > y
C) x > z >y
17.
A
a
10
7
B
D
d
A
60°
e
a
b
B
c
C
A) a > b
B) e > a
C) e > d
Yandaki şekilde
verilen açı
ölçülerine göre
aşağıdakilerden
hangisinin
doğruluğu kesin
değildir?
D) d > c
6
B) 2
C) 5
D) 14
C
5
Verilen uzunluklara göre |AD| = a nın alabileceği en
büyük tam sayı değerini bulunuz.
18.
A noktasındaki
radar 5 km çaplı
bir alanı, B deki
radar ise 6 km
çaplı bir alanı
tarayabilmektedir.
C
A
A) 1
E
E) e > b
15. Çevresi 30 cm olan bir üçgenin bir kenar uzunluğu
aşağıdakilerden hangisi olamaz?
E) 15
|BC| = 18 br
Yanda verilen
şekilde ABE ve
DEC birer üçgendir.
D
E) z > y > x
14.
|AC| = 3x br
olduğuna göre ABC üçgeninin çevresinin alabileceği en büyük tam sayı değerini bulunuz.
Verilen açı ölçülerine göre ADE üçgeninin kenar
uzunlukları olan x, y, z arasındaki sıralama aşağıdakilerden hangisinde doğru olarak verilmiştir?
70°
|AB| = x br
B
A, B, C doğrusal olmamak üzere A dan C ye şekildeki gibi B üzerinden giden uçak, A veya B radarlarında daima göründüğüne göre A ile C arasındaki
mesafenin km cinsinden en büyük tam sayı değeri
kaçtır?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
711
Bölüm 4. 1. Eşlik
BÖLÜM DEĞERLENDİRME
19.
ABC üçgeninde
[AD], A açısının
açıortayıdır.
A
B
D
C
Buna göre aşağıdakilerden hangisi kesinlikle doğrudur?
A) |AB| = |AC|
B) |AC| > |DC|
D) |BD| < |DC|
20.
C) |AB| < |AC|
E) |AB| > |AD|
A
20
°
D
100°
C
30°
B
Yukarıdaki şekilde verilen açı ölçülerine göre;
I. [AB] en uzun kenardır.
II. [DC] en kısa kenardır.
III. |AC| + |CB| > |AB| dir.
yargılarından hangileri doğrudur?
A) Yalnız I
D) I ve III
712
B) Yalnız II
C) I ve II
D) I, II ve III
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Ünite
4
ÜÇGENLERDE
EŞLİK VE BENZERLİK
Bölüm 4.2. Benzerlik
Bu Bölümde Neler
Öğreneceğiz?
•
Bir üçgenin kenarlarından birine paralel
olacak şekilde çizilen doğrunun, kestiği
kenarlar üzerinde ayırdığı parçaların
uzunlukları arasındaki ilişkiyi
•
İki üçgenin benzerliğini
•
Üçgenlerin benzerliğini modelleme ve
problem çözmede kullanmayı
Neden Öğreneceğiz?
Farklı nedenlerden dolayı (nesneye yaklaşmanın tehlike oluşturması, zaman alması
vb.) bazı nesnelerin uzunluklarını doğrudan
ölçemeyebiliriz. Örneğin bir geminin karaya
olan uzaklığını doğrudan ölçme ile belirlemek çok zor olabilir. Böyle durumlarda benzer üçgenler ölçmek istediğimiz uzunlukları
belirlemede bize yardımcı olabilir.
Ölçekli modeller şehir planlamacılığı, haritacılık ve sinema sektörü gibi birçok farklı
alanda gerçeğine benzer yapıların oluşturulması amacıyla sıklıkla kullanılmaktadır.
Bu modelleri oluşturmak için gerçek şekillerin ölçülerini bilmek gerekir. Bu ölçüler belli
oranlarda küçültülerek gerçek şekillerin
modelleri oluşturulabilir. Resimde, ünlü
birçok tarihi eserin belli oran kullanılarak
oluşturulmuş modellerinin sergilendiği
ülkemizin ilk minyatür parkı olan Miniatürk’teki Anıtkabir ve Selimiye Camii’nin
modelleri görülmektedir.
Bölüm 4.2. Üçgenlerin Benzerliği
HAZIR MIYIZ?
1.
Oran ve orantı kavramlarını açıklayarak bu iki kavram arasındaki farkı belirtiniz.
2.
Şekildeki kare, 36 eş kareye bölünmüş ve beş farklı renge boyanmıştır. Buna göre aşağıdaki soruları cevaplayınız.
a.
Mavi karelerin sayısının yeşil karelerin sayısına oranını bulunuz.
b. Siyah karelerin sayısının beyaz karelerin sayısına oranını bulunuz.
c.
Pembe karelerin sayısının beyaz karelerin sayısına oranını bulunuz.
ç.
Siyah karelerin sayısının yeşil karelerin sayısına oranını bulunuz.
d. Yukarıda elde ettiğiniz oranlardan hangileri birbirine eşittir?
Yazınız.
714
3.
Aşağıda verilen ikililerden doğru orantı oluşturanların yanındaki boşluğa (X) işareti koyunuz.
a.
2 6
(. . . )
,
3 9
b.
2 6
,
(. . . )
4 3
c.
9 2
,
(. . . )
12 1
ç.
8 3
,
(. . . )
12 4
d.
8 6
,
(. . . )
3 16
e.
4 12
,
(. . . )
5 15
4.
Aşağıdaki orantılarda verilmeyen a, r, k, b ve y bilinmeyenlerinin alabilecekleri değerleri bulunuz.
a.
2
a
=
5
10
b.
ç.
5
25
=
7
b
d.
3
r
=
7
2
y
4
=
y
9
c.
2
13
=
k
5
5.
Aydın Bey, eni 10 cm ve boyu 15 cm olan fotoğrafın en-boy oranını değiştirmeden, eni 12 cm olacak
şekilde fotoğrafın boyutlarını değiştirmek istiyor. Buna göre yeni fotoğrafın boyu kaç cm olmalıdır?
6.
Aşağıdaki tabloda verilen x ve y sayıları arasında belli bir oran bulunduğuna göre verilen boşlukları
uygun şekilde doldurunuz.
x
3
y
5
9
10
12
21
25
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
30
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında, bir üçgenin kenarlarından birine paralel ve diğer iki kenarı kesecek şekilde çizilen doğrunun, bu kenarlar üzerinde ayırdığı doğru parçalarının uzunlukları arasındaki ilişkiyi inceleyeceğiz.
Araç ve Gereçler: Dinamik geometri yazılımı
A
Adım 1
C
Bir dinamik geometri yazılımını kullanarak ABC üçgeni çiziniz.
B
A
Adım 2
E
AB kenarı üzerinde herhangi bir D noktası belirleyerek D noktasından BC kenarına
paralel bir doğru çizip doğrunun AC kenarını kestiği noktayı E olarak isimlendiriniz.
D
C
B
Adım 3
|AD|
|DB|
AD
DB
|AE|
|EC|
AE
EC
Dinamik geometri yazılımının uzunluk ölçme ve hesap
makinesi özellikleri yardımıyla [AD], [DB], [AE] ve [EC] nın
uzunluklarını belirleyerek yandaki tablonun birinci
satırını tamamlayınız. D noktasının [AB] üzerindeki yerini
değiştirerek farklı durumlar için tabloyu doldurunuz.
Adım 4
Yukarıdaki tabloya göre
AD
AE
ve
oranları arasında nasıl bir ilişki olduğunu açıklayınız.
EC
DB
.....................................................................................................................................................................................................
Sonuç
Bir üçgenin kenarlarından birine paralel ve diğer iki kenarı kesecek şekilde çizilen doğrunun, bu kenarlar üzerinde
ayırdığı doğru parçalarının uzunlukları hakkında ne söylenebilirsiniz? Açıklayınız.
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
715
Bölüm
4.2
Benzerlik
4.2.1. Üçgende Orantılı Doğru Parçaları
Neler Öğreneceğiz?
•
Başlarken
Bir üçgenin kenarlarından birine
paralel olan ve diğer iki kenarı
kesen doğrunun, bu kenarlar
üzerinde ayırdığı doğru parçalarının uzunlukları arasındaki
ilişkiyi
•
Ressamlar, eserlerini yaparken derinlik hissi
uyandırmak için orantılı doğru parçalarından
yararlanırlar. İlgili oranları dikkate almamak
görüntünün gerçek dışı görülmesine sebep
olabilir.
Birbirine paralel en az üç doğrunun farklı iki kesen üzerinde
ayırdığı karşılıklı doğru parçalarının uzunlukları arasındaki ilişkiyi
Bu bölümde ele alacağımız yeni kavram ve ilişkileri daha iyi anlayabilmek için önceki yıllarda
öğrendiğimiz bazı kavramlara ihtiyaç duymaktayız. Bunların başında üçgenin alan bağıntısı
gelmektedir. Üçgenin alan bağıntısına yönelik bazı hatırlatmalar aşağıda yer almaktadır.
Hatırlayalım
Üçgenin Alanı
Anahtar Terimler
•
Temel Orantı Teoremi ve
karşıtı
•
Thales Teoremi
Daha önceki yıllarda bir üçgenin alanının, bir kenarının uzunluğu ile o kenara ait yüksekliğin uzunluğunun çarpımının yarısı olduğunu öğrenmiştik.
A
ha
D
A (ABC) =
B
D
C
a
Aşağıda birer kenarları eş olan üçgenlerin alanları oranının, o kenarlara ait yüksekliklerin uzunlukları oranına, yükseklikleri eş olan üçgenlerin alanlarının oranının ise eş yüksekliklerin çizildiği kenarların uzunlukları oranına eşit olduğu
gösterilmiştir.
Sembol ve Gösterimler
• //
•
a · ha
2
//
Birer Yükseklikleri Eş Üçgenler
A
Birer Kenarları Eş Üçgenler
D
A
D
h
h
hd
B
H
C E
G
F
a
d
B
H
C E 
G
F
a
a
|AH| = |DG| = h olmak üzere,
|BC| = |EF| = a olmak üzere,
D
A (ABC)
a
=
D
d
A ( DEF)
716
ha
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
D
A (ABC)
D
A ( DEF)
=
ha
hd
Üçgende Orantılı Doğru Parçaları
Aşağıdaki teorem, bir üçgenin kenarlarından birine paralel olacak şekilde çizilen doğrunun diğer kenarları kesmesi durumunda, kestiği kenarlar üzerinde ayırmış olduğu
parçaların uzunlukları arasındaki ilişkiyi açıklamaktadır.
Teorem
Temel Orantı Teoremi
A
E
D
Bir üçgenin, bir kenarına paralel olan ve
üçgenin diğer kenarlarını farklı noktalarda kesen bir doğru, kestiği kenarları
orantılı olarak böler. Yandaki şekilde
d2
B
d1
C
d1 // d2 ise
AE
AD
=
dir.
EB
DC
İspat
D
Verilenler: ABC , d1 // d2
İstenen:
AE
AD
=
olduğunun gösterilmesi
EB
DC
A
B ile D , C ile E noktalarını birleştirelim.
E
D
B
C
İfade
A (AED)
D
A ( EBD)
=
AE
EB
AED ve EBD nin D köşesinden çizilen yükseklikleri eş
=
AD
DC
AED ve EDC nin E köşesinden çizilen yükseklikleri eş
D
2
A (AED)
D
A ( EDC)
D
3
4
d1
Gerekçe
D
1
d2
D
A ( EBD) = A ( ECD)
AE
AD
=
DC
EB
D
D
D
D
D
D
EBD ve ECD nin birer kenar ve bu kenarlara ait yükseklikleri eş
1., 2. ve 3. adımlardan
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
717
Bölüm
4.2
Benzerlik
İnceleyelim
1
Yandaki şekilde
A
[ED] // [BC]
4
x
|AD| = 4 cm
|DC| = 2 cm ve
D
E
3
Bir dinamik geometri yazılımı
kullanarak bir ABC üçgeni
oluşturunuz. Bu üçgenin
kenarlarının orta noktalarını
birleştirip yeni bir üçgen
oluşturunuz. Bu üçgen ile
ABC üçgeni arasındaki ilişkileri inceleyiniz.
olduğuna göre |AE| = x değerini bulalım.
C
B
D
ABC nde [ED] // [BC] olduğundan Temel Orantı Teoremine göre
A
E
|EB| = 3 cm
2
Buradan
x
4
= eşitliğinden x = 6 cm bulunur.
3
2
D
2
Resimde bir evin çatısı görülmektedir.
A
B
F
AE
AD
=
olmalıdır.
EB
DC
x
2,4
C
|AB| = 2,4 m
D
B
3,6
x+
C
E
7
5
|BC| = 3,6 m
|AD| = x
7
ve
5
[BD] // [CE] olduğuna göre |AD| = x in kaç
metre olduğunu bulalım.
DE = x +
Verilen resimde [BD] // [CE] olduğundan Temel Orantı Teoremine göre
Dolayısıyla
2, 4
=
3, 6
x
x+
7
5
AB
AD
=
dir.
BC
DE
eşitliğinden
2
x
2
5x
ve buradan da =
eşitliği elde edilir. Bu denklemden
=
3
3
5x + 7
5x + 7
5
10x + 14 = 15x olur. Son eşitlikten 14 = 5x ve x = 2,8 m bulunur.
718
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Orantılı Doğru Parçaları
3
A
12
9
[EF] // [BC]
G
x
E
Dikkat
Yandaki şekilde
F
A
[FG] // [CD]
D
D
|AE| = 12 cm
16
B
E
|EB| = 16 cm
C
B
|AG| = 9 cm
olduğuna göre |GD| = x değerini bulalım.
C
[DE] // [BC] olmak üzere
AE
AF
=
[EF] // [BC] olduğundan Temel Orantı Teoreminden
... (*) dir.
EB
FC
[FG] // [CD] olduğundan Temel Orantı Teoremine göre
(*) ve (**) dan
AD
AE
DE
=
≠
DB
EC
BC
AF
AG
... (**) dir.
=
FC
GD
olduğuna dikkat ediniz.
AE
AG
12
9
=
olur. O hâlde
= dir. Buradan x = 12 cm olarak bulunur.
EB
GD
16
x
4
Yandaki şekilde
A
8
[DE] // [FC]
D
F
4
[FE] // [BC]
E
|AD| = 8 cm
x
B
|DF| = 4 cm
C
olduğuna göre |FB| = x in kaç cm olduğunu bulalım.
[DE] // [FC] olduğundan Temel Orantı Teoremine göre
AD
AE
=
... (*) dir.
DF
EC
[FE] // [BC] olduğundan Temel Orantı Teoremine göre
AF
AE
=
... (**) dir.
FB
EC
(*) ve (**) birlikte düşünüldüğünde
AD
AF
=
olur.
DF
FB
Uzunluklar orantıda yerine yazılırsa
8
12
buradan x = 6 cm olarak elde edilir.
=
4
x
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
719
Bölüm
4.2
Benzerlik
Anahtar Bilgi
Sonuç
A
A
D
E
E
B
B
D
d2
C
Bir üçgenin iki kenarının
orta noktalarını birleştiren
doğru parçası, üçgenin diğer
kenarına paraleldir. Bu doğru
parçasına üçgenin orta
tabanı denir.
C
Temel orantı teoreminin karşıtı da doğrudur.
Bir doğru, bir üçgenin iki kenarını kestiğinde,
kestiği kenarlar üzerinde oluşan karşılıklı
doğru parçalarının uzunlukları orantılı ise bu
doğru, üçgenin üçüncü kenarına paraleldir.
Yandaki şekilde
AE
AD
ise d2 // d1 dir.
=
EB
DC
d1
Yandaki ABC üçgeninin [AB] ve [AC] nın orta noktalarını
birleştiren [DE] nın, [BC] na paralel olduğu yukarıdaki sonuçtan kolayca görülebilir.
A
|AD| = |DB| ve |AE| = |EC| ise
E
D
[DE] // [BC] dir.
Çünkü
C
B
AD
AE
=
= 1 dir.
DB
EC
5
Yandaki şekilde
A
15
D
10
|AD| = 15 cm
17
|AE| = 17 cm
E
1 F
1
G
|DB| = 10 cm
11
|GC| = 11 cm olup
B
C
|EF| = |FG| = 1 cm dir.
Buna göre D noktasından geçen ve AC kenarını kesen doğrulardan hangisinin BC kenarına paralel olduğunu bulalım.
D noktasından geçen ve BC kenarına paralel olan doğrunun AC kenarını kestiği nokta X ol3
AX
AD
AX
15
=
sun. Temel Orantı Teoremine göre
=
olmalıdır. Buradan
elde edilir.
DB
XC
10
XC
3
2
AG
AE
17 AF
18
19
ve
=
,
=
=
olduğundan F noktasının paralelliği sağlayan
13 FC
12
GC
11
EC
2
nokta olduğu görülür. Yani [DF] // [BC] dir.
720
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Orantılı Doğru Parçaları
İnceleyelim
6
Herhangi bir dörtgenin kenarlarının orta noktalarının birleştirilmesi ile oluşan dörtgenin karşılıklı kenarlarının paralel olduğunu gösterelim.
A
Yandaki ABCD dörtgeninin kenarlarının orta noktaları
E, J, G ve F olsun.
F
D
Buna göre EJGF dörtgeninin karşılıklı kenarlarının
paralel olduğunu, yani EJGF dörtgeninin paralelkenar
olduğunu göstermeliyiz.
E
G
B
J
Bir dinamik geometri yazılımı
kullanarak çizdiğiniz herhangi bir dörtgenin kenarlarının
orta noktaları birleştirip yeni
bir dörtgen oluşturunuz. Bu
dörtgenin yandaki örnekte
ulaşılan sonuçtan farklı özelliklere sahip olup olmadığını
inceleyiniz.
ABCD dörtgeninin köşegenleri olan [AC] ve [BD] nı
çizelim.
C
Buna göre E ve J, sırasıyla [AB] ve [BC] nın orta noktaları olduğundan BAC üçgeninde
BE
BJ
=
= 1 dir.
EA
JC
Temel Orantı Teoreminin karşıtına göre [EJ] // [AC] ... (*) olur.
Benzer şekilde G ve F, sırasıyla [CD] ve [DA] nın orta noktaları olduğundan
DAC üçgeninde
DF
DG
=
= 1 dir.
FA
GC
Temel Orantı Teoreminin karşıtına göre [FG] // [AC] ... (**) olur.
(*) ve (**) dan [EJ] // [FG] olur.
Benzer şekilde [EF] // [JG] olduğu da gösterilebilir. Böylece EJGF dörtgeninin paralelkenar olduğu belirlenmiş olur.
Teorem
Thales Teoremi
d1
A
B
C
d3
Birbirine paralel en az üç doğru, verilen
iki doğruyu kestiğinde bu iki doğru üzerinde orantılı doğru parçaları oluşturur.
d4
Yandaki şekilde d3 // d4 // d5 ise
d2
D
E
F
d5
AB
DE
=
dir.
BC
EF
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
721
Bölüm
4.2
Benzerlik
İspat
Matematik Tarihi
Verilenler: d3 // d4 // d5
AB
DE
=
BC
EF
İstenen:
d1
A
D
D
B
Thales (Mö 624-Mö 547)
Mısır’a yaptığı yolculuğunda orada yaşayan insanlar
için ölçülemez olarak gözüken Keops Piramidi’nin
yüksekliğini kendine has
yöntemiyle hesaplamıştır.
A ve F noktalarını birleştirerek ACF üçgenini
d2
G
d3
E
d4
F
C
d5
oluşturalım. [AF] ∩ BE = {G} olsun. ACF nde d4
doğrusu CF kenarına paralel olduğu için bu
doğru Temel Orantı Teoremi gereğince [AC] ve
[AF] nı orantılı doğru parçalarına ayırır.
Dolayısıyla
AB
AG
=
... (*) olur.
BC
GF
D
Benzer şekilde AFD nde d4 // [AD] olduğundan Temel Orantı Teoremine göre
AG
DE
... (**) olur.
=
GF
EF
Karadağ, N. (2004). Gölgelerin Gücü ve Thales. Bilim ve
Teknik, 441,58-59.
(*) ve (**) birlikte düşünüldüğünde
AB
DE
=
elde edilir.
BC
EF
7
F
x
30 m
E
D
Yandaki şekilde birbirine paralel duran
ağaçlar görülmektedir. D noktasından E
ye uğrayarak F ye bir doğru boyunca
uçan kuşun izlediği yol verilmiştir.
|AB| = 20 m
|BC| = 24 m
A
20 m
B
24 m
C
|DE| = 30 m ve D, E, F noktaları doğrusal
olduğuna göre |EF| = x değerini bulalım.
[AD] // [BE] // [CF] olduğundan Thales Teoremi’nden
AB
DE
20
30
=
olup verilen uzunlukları orantıda yerine yazılırsa
eşitliği elde edilir.
=
BC
EF
24
x
Buradan x = 36 m bulunur.
722
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Orantılı Doğru Parçaları
8
Yandaki şekilde
A
D
6
B
2x – 1
8
|AB| = 6 cm
|BC| = 8 cm
E
|DE| = 2x – 1 cm
x+2
C
F
|EF| = x + 2 cm ve AD // BE // CF dir.
Buna göre x değerini bulalım.
AD // BE // CF olduğundan Thales Teoremi’ne göre bu üç paralel doğrunun diğer iki
doğru üzerinde ayırdığı doğru parçaları orantılıdır.
3
AB
DE
6
2x - 1
Dolayısıyla
=
orantısından
=
elde edilir.
BC
8
x+2
EF
4
Orantı özelliğinden 3(x + 2) = 4(2x – 1) ve bu son eşitlikten
5x = 10 ve x = 2 cm olarak bulunur.
9
Yandaki şekilde
A
B
E
5
3
|AB| = 5 cm , |BC| = 4 cm
F
C 4
y G
x
6
D
|CD| = x cm , |EF| = 3 cm
|FG| = y cm
H
|GH| = 6 cm olup [AE] // [BF] // [CG] // [DH] dir.
Buna göre x ve y değerlerini bulalım.
[AE] // [BF] // [CG] olduğundan Thales Teoremi gereği,
AB
EF
5
3
12
bulunur.
=
ise
=
ve buradan y =
BC
FG
4
y
5
Benzer şekilde [BF] // [CG] // [DH] olduğundan Thales Teoremi gereği,
12
y
BC
FG
4
4
=
=
= 5 olduğundan
ise
ve
CD
GH
x
6
x
6
2
4
12
=
& 2x = 20 eşitliğinden x = 10 cm bulunur.
x
30
5
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
723
Üçgende Orantılı Doğru Parçaları
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
Aşağıdaki ifadelerden doğru olanların başına “D”
yanlış olanların başına “Y” yazınız.
a.
(. . . . . ) Bir üçgenin bir kenarına paralel olacak şekilde
çizilen doğru kestiği kenarlar üzerinde orantılı doğru parçaları oluşturur.
b.
c.
4.
Aşağıdaki şekillerde verilen uzunluk ölçülerine
göre d1 ve d2 doğruların paralel olup olmadıklarını
inceleyiniz.
a.
A
4
E
(. . . . . ) Bir üçgenin bir kenarının orta noktasından diğer kenarlardan birine çizilen paralel doğru üçüncü
kenarı ortalar.
D
A
B
B
d1 .... d2
A
C
9
6
E
E
D
2
F
G
c.
AB
..........
=
BD
CE
B
BD
=
..........
3.
AD
AE
=
DF
..........
b.
CE
EG
AB
AD
=
AC
..........
ç.
Şekildeki ABC üçgeninde
A
AD
3
=
DB
2
E
F
D
|AE| = 3 br
G
C
K
B
|FG| = |GH| = |HK| = 1 br
C
olduğuna göre D noktasından [BC] na çizilen paralel doğru [AC] üzerinde işaretlenmiş noktalardan
hangisinden geçer?
724
d1 .... d2
c.
d1
d2
3
A
D
2
3
E
2
B
|EF| = |KC| = 2 br ve
H
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
d1
4
Yukarıdaki şekilde [BC] // [DE] // [FG] olduğuna
göre boşlukları uygun biçimde doldurunuz.
a.
d2
C
b.
D
d1
3
2
2
(. . . . . ) Bir üçgenin iki kenarını orantılı şekilde bölen
doğru üçüncü kenara paralel olmayabilir.
2.
3
d1 .... d2
C
d2
Üçgende Orantılı Doğru Parçaları
KENDİMİZİ SINAYALIM
Alıştırmalar
1.
5.
A
3
Yandaki ABC üçgeninde
[DE] // [BC] dir.
4
D
Verilenlere göre |EC| = x
kaçtır?
E
x
6
d4
x
2
x
Verilen uzunluklara
göre |FB| = x ve |EG| = y
kaçtır?
E
y
G
2
B
d1
c.
y
6
E
F
x
B
4.
[FG] // [AD] dir.
4
Verilen uzunluklara göre
x · y kaçtır?
Yandaki ABC üçgeninde
A
x
2
D
3
F
z
B
d5
x–1
d4
G
C
d4
d3
x
4
Yandaki ABC ve ACD üçgenlerinde [EF] // [BC]
D
x+1
d2
8
A
7
d5
C
3.
x
Yandaki ABC üçgeninde
[DE] // [FG] // [BC] dir.
4
D
d2
d3
3
5
2
A
8
d1
b.
d3
C
2.
d2
d1
a.
4
B
F
Aşağıdaki şekillerde d3 // d4 // d5 ve verilen uzunluk
ölçülerine göre x değerini bulunuz.
E
d5
6.
[DE] // [FG] // [BC] dir.
y
6
Verilen uzunluklara
göre
G
4
T
x
a. x · y
C
b. y · z
Yandaki şekilde
A
B
y
L
2
M
d // [BC] ve verilen
uzunluk ölçülerine
göre
4
S
d
z
y · (x + z) işleminin
sonucu kaçtır?
C
değerleri kaçtır?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
725
Üçgende Orantılı Doğru Parçaları
KENDİMİZİ SINAYALIM
7.
3.
A
28
D
x
20
Yandaki şekilde
A
F
63
[ED] // [BC] ve
6
E
72
y
[EF] // [BD] olup
F
B
H
D
C
B
C
olduğuna göre |DC| = x kaç br dir?
4.
D
Yandaki şekilde
4
D
|DE| = 4 cm
olduğuna göre |AC| nu bulunuz.
5.
a
olduğuna göre |AE| = x kaçtır?
D
c
F
e
6
2.
B
Yandaki şekilde
4
E
9
F
x
D
[FA] ile [DF] sırasıyla
%
%
EFB ve ADC nın açıortaylarıdır.
C
Verilen uzunluklara göre |FC| = x kaçtır?
726
B
[AB] // [EF] // [DC] dır.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Aşağıdaki eşitliklerin doğruluğunu
gösteriniz.
A
|EC| = 3 cm
C
A
|AB| = 12 cm
C
|AD| = 8 cm
3
B
DF
3
= ve
2
EG
G
B
[BE], B açısının açıortayıdır.
E
[DE] // [FG] // [BC]
E
F
[DE] // [BC] ve
x
8
Yandaki şekilde
A
Uygulama ve Problem Çözme
A
|FD| = 3 br
x
Şekilde verilen üçgen şeklindeki uçurtma resminde [DE] // [BC] olduğuna göre x ve y uzunluklarını
bulunuz.
1.
|AF| = 6 br
3
E
a.
a
b
=
e
f
b.
a+e
b+f
=
c
d
c.
a+c
b+d
=
c+e
d+f
b
E
d
G
f
C
Üçgende Orantılı Doğru Parçaları
KENDİMİZİ SINAYALIM
6.
8.
H
G
F
72 m K
A 20 m B 40 m C
60 m
D
A
80 m
Yandaki şekilde
E
L
F
E
2
D
[AE] // [FD] // [BG],
x
[AD] // [FG] // [BC]
G
|ED| = 2 cm
8
Yukarıda bir uçağın iniş aşamaları görülmektedir.
B
Verilen uzunluklara göre |FG|, |GH|, |KL| nu bulunuz.
7.
|GC| = 8 cm
C
olduğuna göre |DG| = x kaç cm dir?
B
F
9.
G
dde
dde
D
|AD| = 3 cm
3
D
2. Ca
1. Ca
A
Yandaki şekilde
A
�
E
F
|EC| = 4 cm ve
E
[AH] ⊥ [BC] dir.
4
H
B
Birbirine paralel olan 1. ve 2. cadde şekilde görülmektedir. A noktasındaki evin; 1. caddenin köşesi
olan D noktasına uzaklığı 60 m, 2. caddenin köşesi
olan E noktasına uzaklığı 108 m; B noktasındaki
evin 1. caddenin köşesi olan F noktasına uzaklığı
45 metredir.
H
C
[DE] // [BC]
olduğuna göre aşağıdaki yargılardan hangileri
kesinlikle yanlıştır?
I. |DB| · |AE| = 12
II. |AE| = 2 cm
III. |FH| = 5 cm
G ile H noktaları arasındaki uzaklık 54 m olduğuna
göre;
a.
F ile G noktaları arasındaki uzaklık,
b.
E ile H noktaları arasındaki uzaklık kaç metredir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
727
Bölüm
4.2
Benzerlik
4.2.2. Üçgenlerin Benzerliği
Neler Öğreneceğiz?
•
İki üçgenin benzerliğini
•
İki üçgenin benzer olması için
gerekli olan asgari koşulları
Başlarken
Fotokopi makineleri kullanılmaya başlamadan
önce insanlar, bir şekli büyütmek ya da küçültmek
için pantagraf adı verilen araçları kullanırlardı. Bu
araçta resim, birbirine paralel üç küçük çivi ve bir
iğne kullanılarak iğnenin orijinal resim üzerindeki
hareketine göre çizilir. Pantagrafta |AB| nun |AD|
na ve |AC| nun |AE| na oranı eşittir. Ayrıca bağlantı
noktası (A), iğne (B) ve kalem (D) doğrusaldır.
Anahtar Terimler
•
Benzerlik
•
Benzerlik Oranı
•
Açı-Açı (A. A.)
•
Kenar-Açı-Kenar (K. A. K.)
•
Kenar-Kenar-Kenar (K. K. K.)
B
A
C
E
Yan tarafta pantagraf ile bir fotoğrafın benzeri
D
D
çizilmektedir. Buna göre oluşan ABC ile ADE nin
benzer olduğunu nasıl gösterebiliriz?
Gerçeğine benzer maketler şehir planlamacıları, inşaat sektörü ve sinema dünyası gibi
farklı birçok alanda gerçek yapıyı daha iyi anlayabilmek ve incelemek amacıyla sıklıkla
kullanılmaktadır. Bu tür maketlerin en önemli özelliği gerçek yapıların belli bir oranda
küçültülmüş hâlleri olmalarıdır. Biri diğerinin büyütülmüş ya da küçültülmüş hâli olan
şekillere benzer şekiller adı verilir.
Sembol ve Gösterimler
•
H
D
D
D
ABC + DEF
Daha önceki bölümde iki üçgenin karşılıklı açıları ve kenarları eş ise bu iki üçgenin eş
olduğunu öğrenmiştik. Şimdi ise benzer iki üçgenin karşılıklı açıları ile kenar uzunlukları arasındaki ilişkiyi inceleyelim.
Bunu biliyor muydunuz
İki üçgenin köşeleri arasında kurulan bire bir eşlemede, karşılıklı açılar eş ve karşılıklı kenar uzunlukları orantılı ise bu üçgenlere benzer üçgenler adı verilir. Eğer
Matruşka aynı görünüşe
fakat farklı boyutlara sahip
tahtadan yapılmış bir oyuncaktır. Aşağıdaki matruşkaların benzer olduğunu görüyor
musunuz?
D
D
D
D
ABC ve DEF benzer üçgenler ise bu durum ABC + DEF şeklinde gösterilir.
W
A,W
D
BC
AC
AB
V
V
B , E ve
=
=
= k , k ! R+
EF
DF
DE
W
C,V
F
A
D
D
B
C
E
F
D
ise ABC + DEF olur.
k pozitif gerçek sayısına benzerlik oranı adı verilir. Miniatürk’te yer alan maket yapılar genellikle 1/25 ölçeği ile yapılmıştır. 1/25 ölçeği, eserin maketinin parçalarının
uzunluğunun gerçek eserin ilgili parçalarının uzunluğuna oranını ifade etmektedir.
728
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
1
Anahtar Bilgi
Yanda verilen ABC ve DEF üçgenlerinde
D
26
39
38
B
m (V
B) = m ( V
E)
C
•
Her üçgen kendine benzerdir.
m (W
C) = m ( V
F) ve
57
E
20
Üçgenler arasında kurulan
benzerlik ifadesi aşağıdaki
özelliklere sahiptir.
m (W
A) = m ( W
D)
A
30
F
D
•
ABC üçgeni DEF üçgenine
benzer ise DEF üçgeni de
ABC üçgenine benzerdir.
ABC ve DEF üçgenlerinin benzer üçgenler olup
olmadıklarını araştıralım.
D
_
m (W
A) = m ( W
D) bbb
b
AB
AC
26
2 BC
20
2
38
2
=
=
m (V
B) = m ( V
E) `b ve
ve
=
= ,
=
=
bb
DE
39
3 EF
30
3
DF
57
3
m (W
C) = m ( V
F) b
a
olduğundan iki üçgenin benzer olması için gerekli olan karşılıklı açıların eşliği ve karşı-
E
12
15
F
D
Yandaki şekilde ABC ve DEF üçgenlerinin bazı keD
D
nar uzunlukları verilmiştir. ABC + DFE ise benzerlik oranını ve |ED| = x değerini bulalım.
x
6
B
D
D
D
ABC + DFE olduğundan
AB
AC
3
12
15
3 BC
6
=
= ,
= =
=
ve
değerlerinin
DF
20
4 FE
8
4
DE
x
her biri benzerlik oranı olup birbirine eşittir.
Bu oranları birbirine eşitlersek
12
3
= ve buradan x = 16 br olarak bulunur.
x
4
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
D
D
D
ise ABC + GKL dir.
D
20
C
D
ABC üçgeni DEF üçgenine
benzer, DEF üçgeni de
GKL üçgenine benzer ise
ABC üçgeni GKL üçgenine
benzerdir.
D
2
8
D
D
ABC + DEF ve DEF + GKL
lıklı kenarların orantılı olması şartları sağlandığından ABC + DEF olur.
A
D
ABC + DEF ise DEF + ABC
dir.
•
D
D
ABC + ABC
üçgenlerin kenar uzunlukları şekil üzerinde gösterilmiştir.
729
Bölüm
4.2
Benzerlik
3
Dikkat
D
A
α
İki üçgenin benzerliğini
gösteren matematiksel ifade
yazılırken iki üçgenin eşliğinde olduğu gibi sıralamaya
dikkat edilmelidir.
D
E
70°
B
D
Yandaki şekilde ABC + DEF ve verilen açı ölçülerine
göre a nın kaç derece olduğunu bulalım.
50°
F
C
D
D
B) = m ( V
E) = 70° dir.
ABC + DEF olduğundan m ( V
D
ABC de iç açı ölçüleri toplamı 180° olduğundan
a + 70° + 50° = 180°
a = 60° bulunur.
Eş iki üçgenin karşılıklı açılarının ve kenarlarının eş olduğunu öğrenmiştik. Bir diğer
D
D
ifade ile ABC , DEF ise
W
A,W
D, V
B,V
E, W
C,V
F ve |AB| = |DE| , |BC| = |EF| , |AC| = |DF| dir.
Bu eşitlikten
D
D
AB
BC
AC
=
=
= 1 elde edilir. Bu ise ABC + DEF olduğunu gösterDE
EF
DF
mektedir.
Bir diğer ifade ile eşlik, benzerliğin benzerlik oranı 1 olan özel bir hâlidir.
Anahtar Bilgi
Bu sonuç, eş üçgenlerin aynı zamanda benzer üçgenler olduğunu ifade etmektedir.
Ancak bunun karşıtı doğru değildir. Benzer olan üçgenler her zaman eş olmak zorunda
değildirler.
İki üçgen eş ise bu üçgenler
aynı zamanda benzerdir. Bu
üçgenlerin karşılıklı açıları
ve kenarları eş olduğundan
benzerlik oranı 1 (bir) dir.
Hatırlayacağınız gibi iki üçgenin eş olması için asgari koşullar olarak K. A. K., A. K. A. ve K.
K. K. eşlik kurallarını öğrenmiştik. Şimdi de iki üçgenin benzer olması için gerekli olan
asgari koşulları inceleyelim.
730
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında eş açılara sahip üçgenlerin kenar uzunlukları arasındaki ilişki incelenecektir. Çalışmayı bir
arkadaşınızla birlikte grup etkinliği olarak yapmanız ve her ikinizden de aşağıdaki yönergeleri takip ederek iç açı
ölçüleri 50°, 60° ve 70° olan üçgenler çizmeniz beklenmektedir.
Araç ve Gereçler: Cetvel, açıölçer, kareli kâğıt, hesap makinesi
Adım 1
AB
= 2 olacak şekilde grup üyelerinden biri [AB] nı çizerTS
ken, diğeri [TS] nı oluştursun.
Kareli kâğıt üzerinde
A
B
C
Adım 2
[AB] nı oluşturan grup üyesi açıölçer yardımıyla m (W
A) = 50° ve m ( V
B) = 70° olacak şekilde ışınlar çizsin. Bu ışınların kesiştiği noktayı C olarak isimlendirsin.
Diğer grup üyesi, işlemleri T ve S noktası için yaparak ışınların kesiştiği noktayı
P olarak isimlendirsin.
50°
Adım 3
D
70°
A
B
D
ABC ve TSP nde ilgili ölçümleri ve hesaplamaları yaparak aşağıdaki tabloyu grup arkadaşınızla birlikte doldurunuz.
D
D
ABC
|AB|
|BC|
AB
=
TS
TSP
|AC|
|TS|
BC
=
SP
|SP|
|TP|
AC
=
TP
Adım 4
D
D
Yukarıdaki tabloya göre ABC ve TSP üçgenlerinin kenarlarının uzunlukları arasındaki ilişkiyi yazınız.
.....................................................................................................................................................................................................
Sonuç
Yukarıda yaptıklarınızı göz önüne aldığınızda açıları eş olan üçgenlerin benzerliği hakkında ne söyleyebilirsiniz?
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
731
Bölüm
4.2
Benzerlik
Açı – Açı (A. A.) Benzerlik Kuralı
Üçgenlerin benzerliği ile ilgili tanım incelendiğinde iki üçgenin benzer olabilmesi için
karşılıklı açılarının eş ve kenarlarının uzunluklarının orantılı olması gerektiği görülmektedir. Ancak üçgenin tüm kenarlarını ve açılarını incelemeden, bazı kenar ve açılarının
incelenmesiyle de iki üçgenin benzer olup olmadığına karar verilebilir. İki üçgenin benzer olabilmesi için asgari durumlar olarak adlandırabileceğimiz bu durumlar dikkate
alınmayan açıların eş ve kenarların orantılı olmasını garanti altına almaktadır. Bu kısımda, asgari durumlardan biri olan Açı-Açı (A. A.) durumu incelenmiştir.
Açı – Açı Benzerlik Kuralı
İki üçgen arasında kurulan bire bir eşlemede, karşılıklı ikişer açısının ölçüleri eşit
ise bu iki üçgen benzerdir. Bu benzerliğe, Açı-Açı (A. A) benzerlik kuralı denir.
A
F
B
Yandaki şekilde
D
D
m (V
B) = m ( W
D)
4 ise, ABC + FDE dır.
W
V
m ( C) = m ( E)
D
Dikkat
C
Bir üçgenin iki açısı verildiğinde, üçüncü açısı belli
olduğundan A. A. Benzerlik
Kuralı, bazen A. A. A. Benzerlik Kuralı olarak da ifade
edilmektedir.
E
Yukarıdaki kural karşılıklı iki açısı eş olan iki üçgenin benzer olduğunu belirtmektedir.
Aşağıdaki örneklerle bu kuralın uygulamalarını inceleyelim.
1
Yandaki ABC üçgeninde
A
10
5
a
D
C
18
|BC| = 18 cm dir.
[DE] // [BC]
B
A
|BD| = 5 cm ve
x
D
Anahtar Bilgi
|AD| = 10 cm
E
olduğuna göre |DE| =x değerini bulalım.
c
e
E
%
%
%
%
[DE] // [BC] olduğundan m (ADE) = m (ABC) ve m (AED) = m (ACB) (yöndeş açılar) dır.
d
b
ADE ve ABC üçgenlerinin ikişer açılarının ölçüleri eşit olduğundan A. A. benzerlik kuraB
f
C
D
D
lına göre ADE + ABC olur. Benzer üçgenlerin karşılıklı kenar uzunlukları orantılı oldu-
[DE] // [BC] ise
a
c
e
dir.
=
=
a+b
c+d
f
ğundan
732
AD
DE
10
x
=
ve buradan
olup x = 12 cm olarak bulunur.
=
15
18
AB
BC
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
2
Dikkat
Yandaki şekilde ABC bir üçgen
A
İki üçgenin benzerlik oranı
yazılırken eş olan açıların karşılarındaki kenar uzunlukları
oranlanır.
[BF] ve [CF] sırasıyla B ve C açılarının açıortaylarıdır.
6
F
D
3
[DE] // [BC]
E
4
x
B
|AD| = 6 cm
C
|DB| = 3 cm
|EC| = 4 cm
olduğuna göre |BC| = x değerini bulalım.
Anahtar Bilgi
%
%
%
%
İç ters açıların ölçüleri eşit olduğundan m (DFB) = m (FBC) ve m (EFC) = m (FCB) dir.
D
b
D
[DE] // [BC] olduğundan A. A. benzerlik kuralına göre ADE + ABC olur.
İlgili oranlar eşitlenerek
AD
DE
=
elde edilir.
AB
BC
C
B
a
c
f
D
a
b
e
= =
d
c
f
dir. Bu durum genellikle
[AB] // [CD] ise
ikinci Thales Teoremi olarak
adlandırılır.
3
Yandaki şekilde
B
A
E
d
6
7
Orantıda değerler yerine yazılırsa = ve bu orantıdan x = 10,5 cm olarak bulunur.
9
x
8
e
A
D
D
Bu durumda BDF ve FEC ikizkenar üçgenler olup, |DF| = 3 cm ve |FE| = 4 cm olduğundan |DE| = 7 cm dir.
A, E, D ve B, E, C noktaları doğrusaldır.
6
[AB] // [CD]
E
D
12
|AB| = 8 cm
|CE| = 12 cm
x
|EB| = 6 cm
olduğuna göre |CD| = x değerini bulalım.
C
%
%
%
%
[AB] // [CD] olduğundan m (BAE) = m (EDC) ve m (EBA) = m (ECD) (iç ters açılar) dır.
D
D
Bu durumda ABE + DCE (A. A. benzerlik kuralı) dır. Benzer üçgenlerin karşılıklı kenar
AB
BE
8
6
=
uzunlukları orantılı olduğundan
ve buradan =
elde edilir.
DC
CE
x
12
Denklem çözülürse x = 16 cm olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
733
Bölüm
4.2
Benzerlik
4
Bunu biliyor muydunuz
Orantılı bölen
Yandaki ABC üçgeninde
D
[DE] ∩ [CA] = {F}
|DF| = |FE|
A
“Orantılı Bölen”, verilen bir
uzunluğu belli bir oranda
büyütmek veya küçültmek için bir uzunluğu eşit
aralıklara bölmede kullanılan
bir araçtır. Aslında bu araç
üçgenlerin benzerliği fikri
üzerine inşa edilmiştir.
|AB| = 8 br
F
|CE| = 5 br
8
|EB| = 3 br
C
5
E
3
B
ise |DA| = x değerini bulalım.
F noktasından [EB] na paralel bir [FK] çizelim.
D
[FK] // [EB] olduğundan A . A. benzerlik kuralına göre
O
F
O
DFK + DEB dir. Buna göre
A
3/2
| DF |
| FK |
| DF |
| FK |
3
&
& | FK | = br bulunur.
=
=
2 | DF |
3
2
| EB |
| DE |
K
ABC üçgeninde [FK] // [CB] oludğundan yine A. A.
O
O
benzerlik kuralına göre A FK + ACB dir. Buna göre
C
5
E
3
B
| AK |
| FK |
| AK |
3/2
3
&
& | AK | = br bulunur.
=
=
| AB |
8
8
2
| CB |
[FK] // [EB] ve |DF| = |FE| olduğundan |DK| = |KB| olmalıdır. Buna göre
|DA| + |AK| = |KB| ise |DA| + |AK| = |AB| – |AK| eşitliğinden
|DA| = |AB| – 2|AK| = 8 – 2·
3
= 5 br bulunur.
2
5
A
D
Yandaki şekilde
F, G, B ve D, E, F doğrusaldır.
4
[DF] // [BC]
E
2
F
G
B
|EG| = 2 cm
x
C
734
|AE| = 4 cm
|DE| = |EF|
olduğuna göre |GC| = x değerini bulalım.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
A
|DE| = |EF| = a ve |BC| = b olsun.
D
D
EFG + CBG (A. A. benzerlik kuralı) olduğundan
4
D
a
E
a
2
F
D
G
D
Diğer taraftan ADE + ABC (A. A. benzerlik kuralı) olduğundan
x
B
EF
EG
a
2
ve buradan =
... (*) olur.
=
CB
CG
b
x
AE
DE
4
a
= ... (**) olur.
ve buradan
=
AC
BC
6+x
b
b
C
(*) ve (**) dan
4
2
= ve buradan
6+x
x
4x = 12 + 2x elde edilir. O halde x = 6 cm olarak bulunur.
6
Yandaki şekilde ABC ve CDE birer dik üçgen
A
E
24
B, C, D noktaları doğrusaldır.
x
18
B
C
[AB] ⊥ [BD], [ED] ⊥ [BD]
12
D
[AC] ⊥ [CE]
|BC| = 18 cm
|AC| = 24 cm
|DE| = 12 cm
olduğuna göre |CE| = x değerini bulalım.
A
a
E
24
x
18
12
C
a + b + 90° = 180° olduğundan
%
%
m (DCE) = a ve m (CED) = b olur.
D
a
b
B
b
D
%
%
ABC nde m (BAC) = a ve m (ACB) = b olsun.
D
D
ABC ve CDE nin iç açı ölçüleri eşit olduğundan bu
D
D
üçgenler benzerdir. Yani ABC + CDE dir.
3
AC
BC
24
18
orantısından
=
ve x = 16 cm bulunur.
Buradan
=
x
12
CE
DE
2
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
735
Bölüm
4.2
Benzerlik
7
A
Yandaki şekilde
%
%
m (ABC) = m (DAC)
x
|BD| = 4 cm
B
4
D
2
|DC| = 2 cm
C
olduğuna göre |AC| = x değerini bulalım.
A
D
α
%
%
m (ABC) = m (DAC) olduğundan ABC ve DAC üçgenlerinin üçüncü açılarının da eşit olduğu görülür.
x
β
α
B
4
Buradan
D
C açısı, ABC ve ADC nde ortak açı ve bu üçgenlerde
D
2
C
D
D
Bu durumda, A. A. benzerlik kuralına göre ABC + DAC
dir.
BC
AC
6
x
=
ve
= orantısından x = 2 3 cm olarak bulunur.
AC
x
2
DC
8
Yandaki şekilde
A
D
E
4
[AB] // [EF] // [DC]
3
|AB| = 4 br
x
B
F
C
|DC| = 3 br
ise |EF| = x değerini bulalım.
Anahtar Bilgi
D
D
D
D
CAB üçgeninde, [AB] // [EF] olduğundan A. A. benzerlik kuralına göre CEF + CAB dir.
A
D
E
a
Buna göre
b
BDC üçgeninde [EF] // [DC] olduğundan A. A. benzerlik kuralına göre BEF + BDC dir.
C
Buna göre
x
B
F
CF
EF
CF
x
= ... (*) dir.
dir. O hâlde
=
CB
4
AB
CB
[AB] // [EF] // [DC] ise
EF
BF
BF
x
=
dir. O hâlde
... (**) dir.
=
BC
3
BC
DC
(*) ve (**) eşitlikleri taraf tarafa toplanırsa,
1
1 1
dir.
= +
x
a b
CF + BF
CB
CF
BF
x x
7x
7x
7x
12
+
= +
ise
=
den
=
ve 1 = 12 den x = 7
4 3
CB
12
CB
12
CB
CB
olarak bulunur.
736
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında ikişer kenar uzunlukları orantılı ve bu kenarların oluşturduğu açıları eş olan üçgenlerin benzerliğini inceleyeceğiz. Bunun için kenar uzunluklarından ikisi 4 cm, 6 cm ve bu kenarların oluşturduğu açısının ölçüsü 60°
D
D
olan ABC ile kenar uzunluklarından ikisi 6 cm, 9 cm ve bu kenarların oluşturduğu, açısının ölçüsü 60° olan PRS ni çizelim.
Adım 1
Adım 3
B
C
P
Kareli kâğıt üzerinde uzunluğu 6 cm olan bir [BC] oluşturunuz.
6 cm
60°
R
9 cm
S
Benzer işlemleri diğer üçgenin verilen elemanları için yaD
parak PRS ni çiziniz.
Adım 2
Adım 4
D
D
Yukarıdaki adımlardan sonra oluşturduğunuz ABC ve PRS
nde ilgili ölçümleri yaparak aşağıdaki tabloyu doldurunuz.
A
m (W
A)
4 cm
60°
B
6 cm
m (V
P)
m (W
C)
m (V
S)
Adım 5
C
D
Açıölçer yardımıyla köşesi B olan 60° lik ışını çizerek cetvel
yardımıyla bu ışın üzerinde, B noktasından 4 cm uzaklıkta
D
olan A noktasını belirleyiniz. Bu işlemlerden sonra ABC ni
çiziniz.
D
Yukarıdaki tabloya göre ABC ile PRS açıları arasında nasıl bir ilişki vardır?
..............................................................................................
Sonuç
Yaptığınız çalışmalar sonucunda ikişer kenar uzunlukları
orantılı ve bu kenarların oluşturduğu açıları eş olan üçgenlerin benzerliği hakkında ne söyleyebilirsiniz? Açıklayınız.
..............................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
737
Bölüm
4.2
Benzerlik
Kenar – Açı – Kenar (K. A. K.) Benzerlik Kuralı
İki üçgenin benzer olabilmesi için asgari koşullardan birinin, bu iki üçgenin karşılıklı
açılarının eş olması gerektiğini öğrenmiştik. Bu asgari koşul iki üçgenin benzerliğini
sağlayan tek asgari koşul değildir. Bu kısımda, bu asgari durumlardan bir diğeri olan
Kenar - Açı - Kenar (K. A. K.) durumu incelenmiştir.
Kenar – Açı – Kenar Benzerlik Kuralı
İki üçgenin köşeleri arasında kurulan bire bir eşlemede, karşılıklı iki kenar uzunlukları orantılı ve bu kenarların oluşturduğu açılar eş ise bu üçgenler benzerdir.
Bu benzerliğe Kenar-Açı-Kenar (K. A. K) benzerlik kuralı denir.
A
D
Yandaki şekilde
D
c
k·c
a
B
D
ABC ve DEF için
DE
EF
% %
=
= k ve ABC , DEF
AB
BC
C
D
k·a
E
F
D
ise ABC + DEF dir.
Yukarıdaki kural, karşılıklı ikişer kenar uzunlukları orantılı ve bu kenarların oluşturduğu
açıları eş olan iki üçgenin benzer olduğunu belirtmektedir. Aşağıdaki örnek bu kuralın
uygulamasını içermektedir.
Aşağıda verilen üçgenleri inceleyerek bu üçgenlerin benzer olup olmadıklarını
belirleyelim.
D
A
6
60° 3
C
4
K
60° 2
60° 2
50°
F
E
T
6
12
S
B
4
Y
M
L
D
•
D
ABC ile DEF nin kenar uzunlukları arasında
AB
AC
3
=
= olup, her iki üçgenDE
DF
2
de uzunlukları oranlanan kenarların oluşturduğu açı 60° olduğundan K. A. K. benD
D
zerlik kuralına göre ABC + DEF dir.
•
738
AB
AC
1
=
=
oranı
KL
KM
2
bulunmaktadır. Bununla birlikte ABC ndeki [AB] ve [AC] nın oluşturduğu açının
D
D
ABC ile KLM nin kenarlarının uzunlukları arasında
D
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
D
ölçüsü 60° iken, KLM ndeki [KL] ve [KM] arasındaki açının ölçüsü 50° olduğundan
bu üçgenlerin benzer olduğunu söyleyemeyiz. K. A. K. benzerlik kuralı, ikişer kenar
uzunlukları orantılı ve bu kenarlar arasındaki açıları eş olan üçgenler için geçerlidir.
•
D
3
oranı bulunmaktadır. Bununla birlikte ABC
2
m (W
A) = 60° iken, m (V
Y) değeri üçgende belirtilmemiştir. Bir önceki maddede olduğu gibi üçgenlerin sadece kenar uzunluklarının orantılı olması bu üçgenlerin
benzer olması için yeterli değildir.
D
D
ABC ile TSY nin kenarları arasında
1
E
Yandaki şekilde verilenlere göre x değerini bulalım.
A
3
B
4
9
x
6
F
C
12
D
AB
3
1 BC
4
1
=
=
= = ,
EF
9
3 FD
12
3
[AB] ile [BC] nın ve [EF] ile [FD] nın oluşturdukları açıların ölçüleri eşit olduğundan
D
D
K. A. K. benzerlik kuralına göre ABC + EFD dir.
Bu durumda
AB
AC
3
6
=
=
ve
orantısından x = 18 bulunur.
9
x
EF
ED
2
Yandaki şekilde B, C, K ve A, C, L noktaları doğrusal
A
8
B
|AC| = 5 br
5
10
C
6
3
L
K
|BC| = 10 br
|CK| = 6 br
|CL| = 3 br
|AB| = 8 br
ise |LK| nu bulalım.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
739
Bölüm
4.2
Benzerlik
Verilen şekilde
AC
BC
AC
BC
5
10
5
=
=
=
ve
=
ise
CL
3
CK
6
3
CL
CK
D
D
%
%
ve m (ACB) = m (LCK) olduğundan K. A. K. benzerlik kuralına göre ABC + LKC dir.
| AB |
| AC |
5
=
= olmalıdır.
| CL |
3
| LK |
Buna göre
Dolayısıyla
8
5
24
br olarak bulunur.
= ise LK =
3
5
LK
3
Yandaki şekilde
A
|AB| = 6 cm
6
|BE| = 3 cm
E
3
B
9
2
6
C
5
|EC| = 6 cm
BD =
D
9
cm
2
|DE| = 5 cm olarak verilmiştir.
% %
ABC , EBD olduğuna göre |AC| değerini bulalım.
AB
BC
% %
=
= 2 ve ABC , EBD olduğundan
BE
BD
A
6
D
E
3
B
9
2
D
K. A. K. benzerlik kuralı gereği ABC + EBD dir.
5
D
6
C
Benzer üçgenlerin karşılıklı kenar uzunlukları
orantılı olduğundan
AB
BC
AC
=
=
= 2 olur.
EB
BD
ED
AC
= 2 olduğundan |AC| = 10 cm olarak bulunur.
5
740
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
4
Yandaki şekilde verilen uzunluklara göre
A
4
|DE| = x değerini bulalım.
6
D
x
8
E
C
10
B
2
D
D
A açısı ADE ve ABC nde ortak açı,
AD
AE
4
1
6
1
=
= olup bu oranlar
= =
ve
AC
8
2
AB
12
2
D
D
birbirine eşittir. Bu nedenle K. A. K. benzerlik kuralına göre ADE + ACB olur.
Bu durumda
AD
DE
4
x
=
ve
=
orantısından x = 5 bulunur.
8
10
CB
AC
5
Şekildeki üçgende
A
|AD| = |DB| ve
D
|AE| = |EC| olarak veriliyor.
E
D
D
Buna göre ADE + ABC olduğunu gösterelim.
B
C
Anahtar Bilgi
Üçgende orta taban uzunluğu paralel olduğu kenarın
uzunluğunun yarısına eşittir.
Şekilde |AB| = |AD| + |DB| ve |AC| = |AE| + |EC| dir. |AD| = |DB| ve |AE| = |EC| olduğundan
|AB| = 2|AD| ve |AC| = 2|AE| olur. Buradan
AD
AE
AD
AE
1
=
dir. Yani
dir.
= =
AB
AB
2
AC
AC
D
D
Ayrıca W
A , hem DAE hem de BAC üçgeneleri için ortak olduğundan K. A. K. benzerlik
D
E
A
D
kuralına göre ADE + ABC dir.
x
2
Yukarıdaki örnek, ABC üçgenin iki kenarının orta noktalarının birleştirilmesi sonucu
oluşan ADE üçgenin ABC üçgenine benzer olduğunu göstermektedir. Benzer üçgen% % % %
lerin karşılıklı açılarının ölçüleri eşit olduğundan ABC , ADE ve ACB , AED dir. Bu du-
x
D
rum [DE] nın [BC] na paralel olduğunu gösterir. Ayrıca iki üçgen arasındaki benzerlik
1
oranı olduğundan |BC| = 2|DE| dir.
2
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
C
B
741
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında kenar uzunlukları orantılı üçgenlerin açı ölçüleri arasındaki ilişkiyi inceleyeceğiz. Bunun
D
için aşağıdaki yönergeleri takip ederek kenar uzunlukları 8 cm, 10 cm ve 12 cm olan ABC ile kenar uzunlukları
D
4 cm, 5 cm ve 6 cm olan KLM ni oluşturmalısınız.
Araç ve Gereçler: Dinamik geometri yazılımı
Adım 3
M
Adım 1
5 cm
4 cm
12 cm
A
B
K
Bir dinamik geometri yazılımında 12 cm uzunluğunda
[AB] oluşturunuz.
6 cm
L
Yukarıdaki adımları, kenar uzunlukları 4 cm, 5 cm ve 6
D
cm olan KLM ni oluşturmak için tekrarlayınız.
Adım 4
Adım 2
D
D
ABC ve KLM nin iç açı ölçülerini, yazılımın açı ölçme
özelliğini kullanarak ölçünüz ve aşağıdaki boşlukları doldurunuz.
C
8 cm
m (W
A) = . . . . .
10 cm
m (V
K) = . . . . .
12 cm
A
m (V
B) = . . . . .
m (U
L) = . . . . .
m (W
C) = . . . . .
m (X
M) = . . . . .
B
Adım 5
D
[AB] nın A köşesinden 8 cm, B köşesinden 10 cm yarıçaplı çemberler çizerek kesim noktasını C olarak isimlendiriD
niz ve ABC ni oluşturunuz.
D
Yaptığınız ölçümler sonucunda ABC ile KLM nin açı ölçüleri arasındaki ilişkiyi belirleyerek yazınız.
..............................................................................................
Sonuç
Yaptığınız çalışmalar sonucunda kenar uzunlukları orantılı üçgenlerin benzerliği hakkında ne söyleyebilirsiniz?
Açıklayınız.
..............................................................................................
..............................................................................................
742
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
Kenar – Kenar – Kenar (K. K. K.) Benzerlik Kuralı
Şu ana kadar iki üçgenin benzer olabilmesi için asgari koşullar olarak
•
karşılıklı açılarının eş (A. A. eşlik kuralı)
•
karşılıklı iki kenar uzunluklarının orantılı ve orantılı kenarların oluşturduğu açıların eş
(K. A. K. eşlik kuralı)
olması gerektiğini öğrenmiştik.
Bu kısımda iki üçgenin benzer olması için kenarlarının orantılı olmasının yeterli olup
olmadığı incelenmiştir.
Kenar – Kenar – Kenar Benzerlik Kuralı
İki üçgenin köşeleri arasında kurulan bire bir eşlemede karşılıklı kenar uzunlukları orantılı ise bu üçgenler benzerdir. Bu benzerliğe Kenar-Kenar-Kenar (K. K. K.)
benzerlik kuralı denir.
A
c
b
a
B
D
D
k·c
D
Yandaki ABC ve DEF için
DE
DF
EF
=
=
= k ise
AB
AC
BC
k·b
C
D
D
ABC + DEF dir.
k·a
E
F
Yukarıdaki kural, karşılıklı kenar uzunlukları orantılı üçgenlerin benzer olduğunu belirtmektedir. Aşağıdaki örnekte, bu kuralı kullanarak verilen üçgenlerin benzer olup
olmadığını inceleyelim.
A
6
D
9
B
P
K
2
3
12
C
E
4
F
8
M
4
4
6
6
L
R
9
S
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
743
Bölüm
4.2
Benzerlik
D
•
D
ABC ile DFE nin kenar uzunlukları arasında
D
AB
AC
BC
=
=
= 3 olduğundan
DF
DE
FE
D
K. K. K. benzerlik kuralına göre ABC + DFE dir.
D
•
D
ABC ile KLM nin kenar uzunlukları arasında
AB
AC
BC
3
=
=
= oranı olduKL
KM
LM
2
D
D
ğundan K.K.K. benzerlik kuralına göre ABC ile KLM benzerdir. Bu üçgenlerin benD
D
D
D
D
D
zerlik ifadesi ABC + KLM şeklindedir. Ayrıca ABC + DFE ve ABC + KLM olduğunD
D
dan DFE + KLM dir.
•
AB
AC
3
=
= oranı olmasına rağPR
PS
2
men, bu oran üçüncü kenar uzunlukları arasında bulunmamaktadır. Bu yüzden
D
D
ABC ile PRS nin kenar uzunlukları arasında
D
D
ABC ve PRS benzer değildir.
1
Yandaki şekilde
A
8
D
|DB| = 3 br
E
|BC| = 16 br
9
3
B
|AD| = 7 br
5
7
16
|AE| = 5 br
C
|EC| = 9 br
|DE| = 8 br
%
%
m (ABC) = 60° ise m (AED) nün kaç derece olduğunu bulalım.
Verilenlere göre
|AB| = 3 + 7 = 10 br ve |AC| = 5 + 9 = 14 br olur.
AD
ED
7
1 AE
5
1
8
1
=
= olduğundan
=
= ,
=
=
ve
AC
14
2 AB
10
2
BC
16
2
D
D
AD
AE
ED
1
=
=
= dir. Buradan K. K. K. benzerlik kuralına göre ABC + AED dir.
AC
AB
BC
2
%
%
Benzer üçgenlerin karşılıklı açıları eş olduğundan m (AED) = m (ABC) = 60° elde edilir.
744
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
2
11
E
D
10
8
4
F
12
B
Yandaki şekilde
A
x
|BE| = 10 cm
6
G 5
|EF| = 8 cm
C
|BF| = 12 cm
|AD| = 11 cm
|CD| = 6 cm
|GC| = 5 cm ve
|DG| = 4 cm olarak veriliyor.
Buna göre |AE| = x değerini bulalım.
A
x
10
B
D
8
12
BE
EF
BF
=
=
= 2 olduğundan
CG
DG
CD
11
E
4
F
D
6
G 5
C
D
K. K. K. benzerlik kuralına göre EBF + GCD ve
% %
buradan EBF , GCD dir.
D
Bu benzerlikte BV , CW olduğundan ABC ikizkenar üçgen olur. İkizkenar üçgende eş
açılar karşısında eş kenarlar bulunduğundan |AB| = |AC| elde edilir.
10 + x = 17 ve buradan da x = 7 cm olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
745
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında, benzer üçgenlerin yüksekliklerinin uzunlukları arasındaki ilişkiyi inceleyeceğiz. Bunun
için aşağıdaki yönergeleri takip ederek benzer iki üçgen oluşturmalısınız.
Araç ve Gereçler: Dinamik geometri yazılımı
Adım 3
P
Adım 1
A
b
A
c hb
b
c
r
C
s
a
C
B
a
S
hr
p
B
R
D
Bir dinamik geometri yazılımından bir ABC oluşturunuz.
D
D
ABC de AC kenarına ait yüksekliği ve PRS de PS kenarına ait yükseklikleri oluşturarak yüksekliklerin uzunluklarını ölçünüz.
Adım 2
P
A
b
Adım 4
r
c
C
Yazılımın ilgili özelliğini kullanarak
s
S
a
B
p
D
hr
değerini bulunuz.
hb
D
Bulduğunuz bu değer ile ABC ve PRS arasındaki benzerlik oranı arasında nasıl bir ilişki olduğunu açıklayınız.
..............................................................................................
R
Yazılımın şekilleri genişletme özelliğini kullanarak kenar
D
uzunlukları ABC nin kenar uzunluklarının 2 katı olan
D
PRS ni oluşturunuz.
Sonuç
Yaptığınız işlemler sonucunda benzer üçgenlerin orantılı kenarlarına ait yükseklikleri arasındaki ilişkiyi ifade
ediniz.
..............................................................................................
..............................................................................................
746
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
Benzer Üçgenlerin Karşılıklı Yardımcı Elemanlarının Karşılaştırılması
Eşlik bölümünde, eş üçgenlerin karşılıklı yardımcı elemanlarının da eş olduğunu öğrenmiştik. Bu bölümde, benzer üçgenlerin karşılıklı yardımcı elemanlarının uzunlukları
arasındaki ilişkiyi inceleyeceğiz. Bunun için benzer iki üçgen çizelim ve bu üçgenlerin
karşılıklı kenarlarına ait yüksekliklerinin uzunluklarını karşılaştıralım.
D
D
Yandaki şekilde DEF + ABC olmak üzere
D
|EH| ile |BG| nu karşılaştırmayı amaçlıyoruz.
A
D
D
DEF + ABC olduğundan bu üçgenlerin karşılıklı
kenarları orantılı ve karşılıklı açıları eştir.
Bir diğer ifade ile
E
H
B
F
G
DE
EF
DF
=
=
= k ve
BC
AC
AB
W
A,W
D, W
C,V
F ve V
B,V
E dir.
C
Bu durumda,
D
%
%
W
A,W
D ve m (EHD) = m (BGA) = 90° olduğundan
A
D
D
A. A. benzerlik kuralı gereğince DEH + ABG dir.
Benzer üçgenlerin karşılıklı kenar uzunlukları
E
H
F
orantılı olduğundan
B
G
C
DH
EH
DE
dir.
=
=
AG
BG
AB
DE
EH
= k olduğundan
= k olur.
BG
AB
Bir diğer ifade ile benzerlik oranı k olan benzer iki üçgenin karşılıklı kenarlarına ait yüksekliklerin uzunlukları arasında da aynı oran vardır. Benzer şekilde, aynı oranın bu üçgenlerin karşılıklı açıortay ve kenarortay uzunlukları arasında da olduğu gösterilebilir.
O hâlde benzer üçgenlerin karşılıklı yardımcı elemanlarının uzunlukları için aşağıdaki
sonuçlar çıkarılabilir:
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
747
Benzerlik
Sonuç
•
Benzer iki üçgenin orantılı kenarlarına ait yüksekliklerin uzunlukları oranı
•
Benzer iki üçgenin orantılı kenarlarına ait kenarortayların uzunlukları oranı
•
Benzer iki üçgenin eş açılarına ait açıortayların uzunlukları oranı benzerlik
oranına eşittir.
1


A, E, D ve B, E, C noktaları doğrusaldır.

4
D





E
x
CD = 9 cm



A
AB = 6 cm


F

6
Yandaki şekilde
B

EF = 4 cm
9

G



|AF| = |FB|

|CG| = |GD| ve

Bölüm
4.2
C
[AB] // [CD]
olduğuna göre |EG| = x değerini bulalım.
D
D
[AB] // [CD] olduğundan A. A. benzerlik kuralı gereği ABE + DCE olur.
Benzer üçgenlerin karşılıklı yardımcı elemanlarının uzunlukları oranı benzerlik oranına
D
D
eşit ve [EF] ile [EG] sırasıyla ABE ve DCE üçgenlerinin kenarortayları olduğundan
EF
AB
olur.
=
EG
DC
Buradan
748
4
6
= ve x = 6 cm bulunur.
x
9
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
2
Şekilde, zemine dik duran bir kamera ile bir
kız çocuğunun kamerada görüntüsünün
nasıl oluştuğu gösterilmektedir. Kameranın
arka duvarında oluşan ters görüntünün
uzunluğu 35 mm, bu görüntünün kameranın
objektifine olan uzaklığı 42 mm ve kameranın kız çocuğuna olan uzaklığı 1,8 m ise
resmi çekilen kızın boyunun kaç cm olduğunu hesaplayalım.
A
Kamera ve kız çocuğu zemine dik olduklarından [AB] // [CD] dir. Bu durumda A. A.
H
B
D
1,8
D
benzerlik kuralına göre ABN + DCN dir.
m
N
42
mm C
35 mm
K
D
Benzer üçgenlerin karşılıklı kenar uzunlukları orantılı ve karşılıklı yüksekliklerinin uzunlukları da benzerlik oranına eşit
NH
AB
AB
1800
=
=
ve
olduğundan
42
35
NK
DC
yazılır.
Buradan |AB| = 1500 mm = 150 cm olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
749
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
4.
Yandaki şekilde
A
D ∈ [AB] ve
1.
a.
b.
D
D
ABC + DEF ise aşağıdaki boşlukları doldurunuz.
E ∈ [AC]
AB
BC
...
=
=
DE
DF
...
D
m (V
B) = ...... ,
m (W
A) = ...... ,
m (W
C) = ......
B
2.
Yandaki şekilde
[DE] // [BC]
olduğuna göre
aşağıdaki boşlukları doldurunuz.
A
D
E
B
a.
C
a.
AD
AE
ise [DE] // [BC] dir.
=
DB
EC
b.
DE =
c.
|AD| = |DB| ve [DE] // [BC] ise |AE| = |EC| dir.
AD
AE
=
...
AC
DE
AE
=
BC
...
b.
DB
EC
=
AB
...
3.
ç.
D
Yandaki şekilde
A
F
|AD| · ... = |AE| · |DB|
K
E
[EF] // [CK]
olduğuna göre
aşağıdakilerden
hangileri kesinlikle
doğrudur?
e
B
c
C
E
b
f
a.
d
B
C
Buna göre aşağıdaki ifadelerin yanlarına doğru
olanlar için “D”, yanlış olanlar için “Y” yazınız.
a.
.....
a
e
=
b
f
b.
.....
a
e
=
a+b
e+f
c.
.....
a
c
=
b
d
ç.
.....
c
e
=
d
e+f
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
DF =
|AD| = |DB|
[DE] // [BC]
D
Yandaki şekilde
[DE] // [BC] dir.
A
a
750
BC
ise [DE] // [BC] dir.
2
C
5.
c.
olduğuna göre
aşağıdaki yargılardan
hangileri kesinlikle
doğrudur?
E
BK
2
b.
E ! 6BK@
c.
|AF| = |FK|
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
6.
Aşağıdaki ifadelerden doğru olanların yanındaki
boşluğa “D”, yanlış olanlarınkine “Y” yazınız.
a.
..... Benzer üçgenlerin karşılıklı açıları eştir.
b.
..... İki üçgenin ikişer kenar uzunluğu orantılı ise bu
üçgenler kesin olarak benzerdir.
K
A
4
..... Tüm eşkenar üçgenler benzerdir.
ç.
..... Eş üçgenler aynı zamanda benzer üçgenlerdir.
d.
..... Tüm ikizkenar üçgenler benzerdir.
e.
..... Tüm dik üçgenler benzerdir.
8
D
ç.
K
A
Aşağıda her bir seçenekte verilen üçgenler benzer
olduğuna göre benzerlik ifadesini ve gerekçesini
yazınız.
75°
E
55°
55°
0,9
3,4
L
1,8
2,4
1,7
B
D
A
B
M
8
L
ABC + ...
Alıştırmalar
a.
16
C
B
c.
1.
c.
C
4,8
50°
M
D
ABC + ...
F
C
D
ABC + ...
d.
K
4
b.
A
C
8
D
D
ABC + ...
P
16
E
B
4
N
L
8
6
M
D
KLM + ...
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
751
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
2.
Aşağıda şekillerde verilmeyen x ve y değerlerini
bulunuz?
a.
ç.
[DE] // [BC]
A
[GE] // [HD] // [BC]
A
G
6
F
4
8
y
H
6
D
E
D
E
x
B
x
C
12
B
b.
C
5
A
[DE] // [AB]
B
d.
12
A
8
x+1
D
E
x
E
2
[AB] // [CD]
B
x
C
D
10
C
c.
[FG] // [BC]
A
e.
[GD] // [AE]
5
E
F
x
F
10
G
[FE] // [BC]
A
6
G
B
752
24
C
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
E
2
H
D
6
4
3
B
x
D
y
C
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
Uygulama ve Problem Çözme
1.



9
3



6
B
C
Yandaki şekilde
%
%
m (EDC) = m (ABC) = 90°
x
C
k
5
a.
x
y
5.
A
6
6
olduğuna göre |AD| = x
kaçtır?
C
E
B
a.
4
F
b.
|EF|
3
F
E y
G
olduğuna göre
aşağıdaki oranları
bulunuz.
z
x
y
6
y
z
|FC|
E
K
L
D M
B
20
C
Yukarıdaki ABC üçgeninde A, G, F, E, D, B ve B, M, L,
K, H noktaları doğrusal
C
b.
F
[DF] // [BC]
x
C
Yandaki şekilde
[AB] // [EF] // [DC]
[BD] ∩ [AC] = {E}
ve B, F, C doğrusal
olduğuna göre
aşağıdaki uzunlukları bulunuz.
H
G
a.
3
l
k
A
Yandaki şekilde
2
D
c.
D
|DC| = 5 br
A
B
l
a
b
b.
6.
D
E
|BC| = 6 br
F
3.
4
Yukarıdaki şekilde [AB] // [CD] olduğuna göre aşağıdaki oranları bulunuz.
|EB| = 4 br
D
B
F
|BD| = 6 br
A
4
3
y
olduğuna göre |AB| = x kaçtır?
E
x
H
b
|AC| = 9 br
2.
a
3
|ED| = 3 br
D
B
BED üçgenlerinde
%
%
m (BAC) = m (BDE)

E
A
A Şekildeki ABC ve

x
4.
c.
x
z
|AG| = |GF| = |FE| = |ED| = |DB|
[BC] // [GH] // [FK] // [EL] // [DM] , |BC| = 20 cm
olduğuna göre |DM| = x kaç cm dir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
753
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
7.
Yandaki şekilde
A
10.
A
D
B, G, D noktaları doğrusal
D
H
[FE] // [BC]
F
1
|AD| = |DE| = |EC|
E
G
K
B
|FG| = 1 br
x
B
D
6
D
D
E
D
Ç (ABC) = 32 br ise Ç ( EFD) kaç br dir?
11.
E
[DE] // [BC]
%
[EF], ^DECh nın açıortayı
9
D
|BH| = 8 br , |KF| = 6 br ve ABC + EFD dir.
Yandaki ABC üçgeninde
A
E
Yukarıdaki şekilde
C
olduğuna göre |BC| = x kaç br dir?
8.
C
|AE| = 9 br
Yandaki şekilde
A
[EF] // [AB]
45
F
[ED] // [AC]
30 B
|EF| = 45 cm
D 20 C
60
|FB| = 30 cm
|DE| = 6 br
B
x
F
3
F
|BD| = 60 cm
C |FC| = 3 br
|DC| = 20 cm olduğuna göre |AB| kaç cm dir?
olduğuna göre |BF| = x kaç br dir?
12. A
9.
D
A
8
D
B
N
C
10
x

E
T
x
4
|AN| = 8 cm , |BC| = 10 cm , |EF| = 4 cm ve
D
ABC + DFE olduğuna göre |DT| = x kaç cm dir?
754
H
B
5
F
3
C
4
E
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
[AB] ⊥ [BE]
[DE] ⊥ [BE]
[AC] ⊥ [DF]
F
Yukarıdaki şekilde
D
4
Yandaki şekilde
ABC ve DEF dik
üçgeninde
|BF| = 5 br , |FC| = 3 br , |CE| = 4 br , |DE| = 4 br
olduğuna göre |AB| = x kaç br dir?
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
13. A
C 2
10
D
x
13
E
B
Yandaki şekilde
ABD ve DEC dik
üçgen
16.
4
12
[AB] ⊥ [BD]
5
B
[AD] ⊥ [DE]
Yandaki şekilde
ABC ve DEC dik
üçgen
D
10
x
B
E
6
Verilen uzunluklara göre |DE| = x kaç br dir?
17.
E
6
|DC| = 10 br
2
12
C
Yandaki şekilde
D
|AD| = 2 br
y
10
18.
2
C
[DF] // [BC]
3
D
|BE| = 10 br
E
Yandaki şekilde
A
|DC| = 4 br
4
x
B
F
|AB| = |AC| dir.
4
Verilen uzunluklara göre |GF| = x kaç br dir?
olduğuna göre |BE| = x kaç br dir?
A
G
x
5
B 2 D
|EC| = 6 br
15.
Yandaki şekilde
ABC ikizkenar
üçgen ve
A
|AD| = 5 br
C
C
E
olduğuna göre |CE| = x kaç br dir?
5
5
6
|AB| = 10 br , |BC| = 13 br , |CD| = 2 br
A
D
x
[CE] ⊥ [BD]
14.
Yandaki şekilde
ABC ve DEC üçgen
%
%
m (ECD) = m (ACB)
dir.
A
4
E
x
6
|EC| = 2 br
F
H
|AD| = 3 cm
y
|DB| = 6 cm
|DE| = x
|AB| = y
olduğuna göre
x
oranı kaçtır?
y
[BF] , B açısının açıortayı
B
olduğuna göre
C
|DE| = 4 cm
EH
x
= değeri kaçtır?
HC
y
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
755
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
19.
Yandaki şekilde
A
D
F
E
[BE] , B açısının açıortayı
H
6
10
C
olduğuna göre
|BD| = |DC|
|DB| = 6 cm
B
|BC| = 10 cm
ise |DE| = x kaç br dir?
AF
x
= değeri kaçtır?
HC
y
|AB| = 10 br
E
x
|DF| = 2 cm
y
B
Yandaki şekilde
%
%
m (BAC) = m (AED)
A
[DE] // [BC]
x
2
22.
D
23.
C
Yandaki şekilde
A
|AD| = |DB|
N
D
20.
Yandaki şekilde
A
H
F
E 3
4
x
H
B
|AC| = 15 cm
D
|NH| = |HB|
K
4
[FH] // [BC]
|AE| = |EC|
E
|NK| = |KC| ve
|HK| = 4 br
C
ise |DE| = x kaç br dir?
|FE| = 4 cm
|EH| = 3 cm
B
12
C
|BC| = 12 cm
24.
A
olduğuna göre |ED| = x kaç cm dir?
12
A
2
x
D
4
8
|DC| = 15 cm
D
15
C
|AD| = 10 cm
olduğuna göre |AC| = x kaç cm dir?
Yandaki şekilde
B
|AB| = 12 cm
x
10
B
21.
Yandaki şekilde
%
%
m (CAE) = m (ADB)
E
|AB| = 2 br
3
|BC| = 3 br
C
25.
A
10
Yandaki şekilde
B
AB // EF // CD
|AC| = 4 br
|DC| = 8 br ve
E
16
|AB| = 10 br
F
|EF| = 16 br
[AB] // [DC] ise |AD| = x kaç cm dir?
C
x
D
3 · |EC| = 2 · |EA|
olduğuna göre |CD| = x kaç br dir?
756
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
26.
Bir şeklin ardışık olarak aynı oranda küçültülmesi veya büyültülmesiyle inşa edilen
geometrik şekillere fraktal denir. Fraktalların en temel özelliği öz-benzerliktir.
Öz-benzerlik, daha küçük parçalarının şeklin orijinal formu ile aynı geometrik
özelliklere sahip olması olarak tanımlanır. Bu nedenle fraktal bir şekilde, şeklin
farklı oranlardaki tüm parçaları hep aynı ve şeklin bütününe benzer olarak
görünür.
En bilinen fraktal yapılardan biri Sierpinski üçgenidir. Aşağıda Sierpinski üçgeninin oluşturulma adımları verilmiştir.
0. Adım
1. Adım
2. Adım
Bir ABC eşkenar üçgeni çizilir.
ABC üçgeninin kenarlarının orta noktaları
bulunur. Oluşan DEF üçgeni kesilerek
çıkarılır.
Kalan eşkenar üçgenler için bu işlem
devam ettirilir.
A
A
A
A
D
B
B
BC B
A
D E
C BF
A
A
D ED
C BFC B
A
A
ED E
FC BF
D E
C BFC
E
FC
C
Sierpinski üçgeninin oluşturulması için yukarıdaki işlemin sürekli olarak devam ettirilmesi gerekir. Buna göre
a.
Dördüncü adımda çıkarılan eşkenar üçgenlerden biri ile ABC üçgeni arasındaki benzerlik oranını bulunuz.
b.
5. adıma kadar toplam kaç eşkenar üçgen çıkarılmıştır?
c.
ABC üçgeninin bir kenar uzunluğu 16 cm olduğuna göre 4. adımda çıkarılan üçgenlerin çevrelerinin toplamı kaç
cm dir?
A
27. Koch kartanesi olarak bilinen fraktal, bir eşkenar üçgenin kenarlarını üç eşit
parçaya bölüp ortada oluşan parça üzerine her seferinde bir eşkenar üçgen
yerleştirmekle oluşmaktadır. Yandaki şekilde Koch kartanesinin 4. adımdaki
şekli görülmektedir. Şekildeki SRT üçgeninin bir kenar uzunluğu 1 cm olduğuna göre KLM üçgeninin LM kenar uzunluğunu bulalım.
K
M
S
T
R
L
B
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
C
757
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
28. �
Yandaki şekilde
ABC ve ADE
eşkenar üçgen
A
x
31. �
A
D
|AD| = 6 br
F
B
|AF| = 5 br
E
D
4
x
8
2
F
C
E
C
olduğuna göre |AB| = x kaç br dir?
B
Yukarıdaki şekilde ABC ve DEF üçgenlerinde
%
%
%
m (BAE) = m (ACD) = m (CBF)
|DE| = 4 cm , |DF| =2 cm , |AC| = 8 cm
29. �
Şekildeki ABC
üçgeninde
A
6
4
2α
B
|AB| = 4 cm
α
x
C
olduğuna göre |AB| = x kaç cm dir?
32. �
Yandaki şekilde
[BD] , B açısının
açıortayı
A
36°
|AC| = 6 cm
%
%
m (ABC) = 2 · m (ACB)
%
m (BAC) = 36°
D
olduğuna göre |BC| = x kaç cm dir?
%
m (ACB) = 72°
x
72°
B
1
|BC| = 1 cm
C
|DC| = x
olduğuna göre x2 + x işleminin sonucu kaçtır?
33. �
A
A

30. �



D
15
x

B 2 D
x
E
8
C
B
3
6
E
C
Yukarıdaki şekilde ADE eşkenar üçgen
%
|BD| = 2 cm , |EC| = 8 cm , m (BAC) = 120°
Şekildeki ABC üçgeninde
%
%
m (ACB) + m (ADE) = 180°
olduğuna göre |DE| = x kaç cm dir?
|BE| = 3 cm , |DE| = 6 cm , |AC| = 15 cm
olduğuna göre |AB| = x kaç cm dir?
758
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
34. �
Şekildeki ABC ve
DEF üçgenlerinde
A
D
D Yandaki şekilde
A
%
%
m (ACB) = m (DCA)
|AB| = 2 · |DF|
x
B
37. �
E
F
C, E, A doğrusal
E
|BC| = 2 · |DE|
|CA| = |CD|
|AC| = 2 · |EF|
C
|CE| = |CB|
B
%
%
m (DEF) + m (BAC) = 110° olduğuna göre
|ED| = 4 br
%
m (EDF) = x kaç derecedir?
C
35. �
[BF] // [AG]
A
[BD] // [FG]
B
C
38. �
A
5
[BG] ∩ [FA] = {E}
D
[BD] ∩ [AF] = {C}
G
E
4
C
A, D, G, doğrusal
E
F
ise |AB| kaç birimdir?
F
G
2
4
8
D
B
ise |FE|2 = |EC| · |EA| olduğunu gösteriniz.
Yandaki ABC
üçgeninde E, D,
G noktaları
sırasıyla [AC],
[BC] ve [AB]
kenarlarının
üzerindedir.
[AD] ∩ [BE] ∩ [CG] = {F}
|CD| = 8 br , |DB| = 4 br , |BG| = 2 br , |AE| = 5 br
|EC| = 4 br ise |AG| kaç birimdir?
36. �
Yandaki
şekilde
A
|BD| = 2 br
x
B 2 D
8
|DE| = 8 br
E
4
C
|EC| = 4 br
%
%
m (BAD) = m (EAC)
AD = 3 15 br
ise |AE| = x kaç birimdir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
759
Bölüm
4.2
Benzerlik
4.2.3. Üçgenlerin Benzerliğini Problem Çözme
ve Modellemede Kullanma
Neler Öğreneceğiz?
•
Problem çözme ve modellemede üçgenlerin benzerliğini
kullanmayı
Başlarken
Üçgenlerin benzerliği, gerçek
yaşamda uzunluklarını farklı
nedenlerden dolayı (çok yüksek
olması, ölçülecek nesneye
ulaşılamaması vb.) doğrudan
ölçemediğimiz nesnelerin
uzunluklarını ölçmede sıklıkla
kullanılır.
Anahtar Terimler
•
Modelleme
Sembol ve Gösterimler
•
D
D
ABC + DEF
1
İnceleyelim
186 cm boyundaki Ahmet, yandaki gibi
bir bayrak direğinin boyunu bulmak
istiyor. Bunun için bayrak direği ile
bulunduğu yer arasına, kendinden 50 cm
uzağa, direğin tepe noktasını görecek
şekilde yere bir ayna koyuyor. Ahmet
direkten 200 cm uzakta olduğuna göre
direğin boyunu bulalım.
Siz de yanda verilen örnekteki gibi bir ayna kullanarak
okulunuzun yüksekliğini
hesaplayınız.
Anahtar Bilgi
Aşağıdaki şekilde düzlem
aynada bir ışının yansıması
resmedilmiştir. Bu şekildeki
bir yansıma olayında ışığın
gelme açısı yansıma açısına
eşittir.
Gelen
ışın
Normal
D
Yansıyan
ışın
A
θ
α α
θ
(Yüzeyin normali yüzeyle 90°
lik açı yapan dik doğrudur.)
B
760
C
E
Problemde verilenleri yandaki gibi
modelleyelim. Bayrak direğinin boyunun
yani [DE] nın uzunluğunu bulmamız
istenmektedir.
Yansıma prensibine göre, gelen ışık düz
aynadan aynı açıyla yansıdığına göre
%
%
m (ACB) = m (ECD) dir. Ayrıca Ahmet ve
bayrak direği zemine dik durumlu olduk%
%
larından m (ABC) = m (DEC) = 90° dir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliğini Problem Çözme ve Modellemede Kullanma
D
D
Dolayısıyla A. A. benzerliğine göre ABC + DEC olur.
Buna göre iki üçgenin benzerliğinden yararlanarak [DE] nın uzunluğunu bulabiliriz.
Ahmet’in boyu |AB| = 186 cm, Ahmet’in bulunduğu yerden aynanın uzaklığı |BC| = 50 cm dir.
Ahmet bayrak direğinden 200 cm uzakta olduğundan aynanın direkten uzaklığı
|EC| = 200 – 50 = 150 cm dir. Direğin boyuna |DE| = x cm dersek
D
D
ABC + DEC benzerliğinden
AB
BC
186
50
=
=
’dir.
ve
DE
EC
x
150
Buradan bayrak direğinin boyu |DE| = 558 cm bulunur.
2
Merve, çizimde gösterildiği gibi arkasındaki ağacın boyunu
hesaplamak istiyor. Bunun için kendi gölgesinin uç noktası ile
ağacın gölgesinin uç noktası çakışacak şekilde, ağaçtan 480 cm
uzakta duruyor.
Merve’nin boyu 175 cm ve gölgesinin uzunluğu 240 cm olduğuna göre ağacın boyunun uzunluğunu bulalım.
Problemde anlatılanları yandaki gibi
modelleyebiliriz. Ağacın boyunu yani
[BC] nın uzunluğunu bulmamız
istenmektedir.
B
Merve ve ağaç zemine dik olduklarından [DE] // [BC] dır.
%
%
Buna göre m (EAD) = m (CAB) ve
%
%
m (DEA) = m (BCA) = 90° olup
D
175 cm
E
A
240 cm
C
480 cm
D
D
A. A. benzerlik kuralına göre ADE + ABC dir.
Merve’nin boyu |DE| = 175 cm, gölgesinin boyu |AE| = 240 cm ve ağacın gölgesinin
boyu |AC| = 480 + 240 = 720 cm dir.
Ağacın boyunun uzunluğuna |BC| = x dersek
AE
DE
175 · 720
240
175
=
=
eşitliğinden x =
= 525 cm olarak bulunur.
ve
240
AC
BC
720
x
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
761
Bölüm
4.2
Benzerlik
3
tavan
Ayşe, doğrudan ölçmek yerine farklı bir
yöntemle sınıfın tavan yüksekliğini ölçmek
istiyor. Bunun için duvarla tabanın kesiştiği
köşeye 500 cm uzunluğunda bir ip bağlıyor.
İpin diğer ucunu sağ eliyle gergin olacak
duvar
şekilde gözüne doğru yaklaştırıyor. Sol eliyle de
10 cm lik bir cetveli ipin üstüne, gözünün
önüne duvarın üst kenarını göremeyecek ve
duvara paralel olacak şekilde tutuyor. Cetvelin
ipe değdiği nokta ile Ayşe’nin ipi tuttuğu nokta
arası 20 cm ise sınıfın yüksekliğini bulalım.
B
Problemde verilenleri yandaki gibi modelleyelim. Bizden
tavan yüksekliğini yani [BC] nın uzunluğunu bulmamız
istenmektedir.
cetvel
ip
taban
D
A
10
20 E
480
C
Cetvelin uzunluğu |DE| = 10 cm, cetvelin ipe değdiği
nokta ile Ayşe’nin ipi tuttuğu nokta arası |AE| = 20 cm,
ipin uzunluğu |AC| = 500 cm dir. Cetvel duvara paralel
%
%
yani [DE] // [BC] olduğundan m (AED) = m (ACB) dir.
D
D
%
%
m (EAD) = m (CAB) olduğundan A. A. benzerlik kuralına göre AED + ACB dir.
Buradan
AE
DE
20
10
=
olup
den |BC| = 250 cm bulunur.
=
500
BC
BC
AC
4
Erzurum Palandöken Dağı’ndaki kayak
pistine dik üçgen şeklinde yeni yapılacak
atlama rampasının düşey desteğinin
yüksekliği 1,2 m ve rampanın tabanı
3 metre olarak tasarlanmıştır. Rampanın
dayanıklılığını artırmak için en yüksek
yerinden 1,8 m uzaklığa, diğer desteğe
paralel başka bir destek konmak isteniyor.
Bu desteğin yüksekliği kaç metre olmalıdır?
762
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenlerin Benzerliğini Problem Çözme ve Modellemede Kullanma
E
G
1,2 m
destek
C
F
1,8 m
D
3m
Problemde verilenleri yandaki gibi
modelleyebiliriz. Bizden pistin altına
konulacak kısa desteğin boyunu yani
[GF] nın uzunluğunu bulmamız istenmektedir. Rampaya konulacak destek
rampanın tabanına dik olması gerektiğinden [GF] // [ED] olmalıdır.
|CD| = 3 m , |FD| = 1,8 m , |ED| = 1,2 m ve |CF| = 3 – 1,8 = 1,2 m dir. |GF| = x olsun.
D
D
[GF] // [ED] olduğundan A. A. benzerlik kuralına göre CFG + CDE dir.
CF
GF
1, 2
x
=
olup
den x = 0,48 m olarak bulunur.
=
CD
ED
3
1, 2
Buna göre
5
Kanser tedavisinde kullanılan kemoterapi sırasında
hastaya doğru miktarda radyasyon vermek hayati
öneme sahiptir. Eğer radyasyon gereğinden fazla
verilirse bu durum hastanın durumunu daha da
kötüleştirebilir, hayatını tehlikeye sokabilir.
Yandaki şekilde iki radyasyon kaynağından hastaya verilen radyasyonların vücuda ve kanserli olan
bölgeye değdikleri yerler gösterilmektedir. Doktorların dikkat etmeleri gereken nokta iki ışının kanserli
bölgede üst üste gelmemesidir. Bu durumda, o bölge
aşırı miktarda radyasyona maruz kalacaktır.
Şekilde, radyasyon kaynağı deriden 100 cm yukarıda radyasyon ışınını vücuda göndermekte ve vücutta kanserli bölge deriden 5 cm aşağıdadır. Eğer radyasyon ışını, deride
15 cm lik bir bölgeye verilirse kaç cm lik kanserli bölgeye etki eder?
Radyasyonun deriye değdiği bölgede oluşan üçgen
ile kanserli bölgeye değdiği bölgede oluşan üçgenler
A. A. benzerlik kuralına göre benzerdir (Neden?).
100
15
105 · 15
Buna göre
ise x =
=
= 15, 75 cm dir.
105
x
100
100 cm
15 cm
5 cm
Bunu biliyor muydunuz
Benzer üçgenler ağaçların,
binaların ya da köprülerin
uzunluklarının belirlenmesinin yanında tıpta da
kullanılmaktadır.
O hâlde doktorlar, 15 cm lik bir alana radyasyon
verdiklerinde derinin 5 cm aşağısında 15,75 cm lik bir
alanı taradıklarını bilmelidirler.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
763
Üçgenlerin Benzerliğini Problem Çözme ve Modellemede Kullanma
KENDİMİZİ SINAYALIM
Problemler
3.
1.
B
A
C
150 m
100 m
D
A
E
Kıyı
A ve B noktalarında bulunan iki kayığın kıyıya
uzaklıkları sırasıyla 100 m ve 150 m dir. A noktasındaki kayık E noktasına doğru ve B noktasındaki
kayık D noktasına doğru ok yönünde şekilde gösterildiği gibi ilerlemektedir.
B
240 cm
12 m
Şekildeki ağacın gölgesinin boyu 12 m, 160 cm
boyundaki Can’ın gölgesi ise 240 cm dir.
Kayıklar belirli bir süre sonra C noktasında çarpıştıklarına göre C noktasının kıyıya olan uzaklığını
bulunuz.
Ağacın ve Can’ın gölgesinin uç noktası A noktası
olduğuna göre ağacın boyunu bulunuz.
4.
2.
B
A
E
B
A
X
C
Y
Dikdörtgen biçimindeki bir bilardo masasında A
noktasından topa vurulduğunda topun izlediği yol
şekildeki gibidir.
%
%
m (ACX) = m (BCY)
|AX| = 20 cm , |XC| = 40 cm , |CY| = 120 cm
olduğuna göre |BY| kaçtır?
764
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
D
Şekildeki kuyunun derinliğini hesaplamak isteyen
Hasan, ayağının altındaki tahtanın E ucu ve D
noktasını aynı hizada görecek şekilde tahtayı iterek
konumlandırıyor.
|AE| = 40 cm , |AB| = 240 cm ve Hasan’ın boyu 180 cm
olduğuna göre kuyunun derinliğini hesaplayınız.
Üçgenlerin Benzerliğini Problem Çözme ve Modellemede Kullanma
KENDİMİZİ SINAYALIM
5.
7.
10 m
4m
15 m
10 m
12 m
Duvardan 10 m gerideki Ali, yerden 2 m yükseklikte tuttuğu feneri 10 m yüksekliğindeki duvara
doğru tutuyor.
36 m
Oturdukları evin yerden yüksekliğini hesaplamak
isteyen Mehmet, evden 36 m uzaklaşıp evine doğru baktığında 12 m ileride bulunan 4 m boyundaki
ağacın en üst noktasıyla evin en üst kısmını şekilde
gösterildiği gibi aynı hizada görüyor.
Duvardan 15 m arkada bulunan ağacın en üstten
itibaren 5 m lik kısmı aydınlandığına göre ağacın
boyu kaç metredir?
Mehmet’in boyu 2 m olduğuna göre evin yüksekliğini bulunuz.
6.
8.
x
x
1,8 m
C
1m
A
2m
B
B
2,4 m
9,6 m
B noktasındaki direğin boyunu ölçmek isteyen
Doruk, C noktasına ayna koyuyor ve aynadan 2,4 m
uzaklıktaki A noktasına gelip, aynaya baktığında
direğin uç noktasını görebiliyor.
Doruk’un boyu 1,8 m ve Doruk’un direğe uzaklığı
9,6 m olduğuna göre direğin boyu kaç metredir?
A
8m
C
12 m
A noktasındaki ışık geçirmeyen 2 m yüksekliğindeki engele doğru B noktasından, yerden 1 m
yükseklikten fener tutan Mert, arkada bulunan
perdenin yerden x br yüksekliğine kadar olan
kısmını göremiyor. Engeli ok yönünde 4 m kaydırdıktan sonra yine B noktasından ilk durumdaki
gibi perdeye doğru fener tuttuğunda ise perdede
göremediği bölgenin yüksekliği y br oluyor.
x
Buna göre oranı kaçtır?
y
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
765
Üçgenlerin Benzerliğini Problem Çözme ve Modellemede Kullanma
KENDİMİZİ SINAYALIM
9.
x
1,7 m
3,6 m
0,72 m
Güneşli bir günün belli bir anında 1,7 m boyundaki
bir kişinin gölgesi 0,72 m olmaktadır.
Buna göre aynı anda gölgesi 3,6 m uzunluğunda
olan bayrak direğinin yüksekliği kaç metredir?
10.
F
Deniz
x
A
B
Kara
C
Deniz kenarında gezerken açıktaki sabit bir kayığın
kıyıya olan uzaklığını yaklaşık olarak ölçmek isteyen Ahmet Yiğit, bir A noktasından kıyı boyunca ok
yönünde 20 m ilerleyip bir B noktasına geliyor ve
buraya bir çubuk dikiyor. Sonra aynı yönde 45 m
daha yürüyüp C noktasına geliyor. Bundan sonra,
kıyıya dik bir şekilde ilerlerken bir yandan kayığa
bakıyor ve kayıkla B noktasına diktiği çubuk aynı
hizaya geldiğinde duruyor.
Ahmet Yiğit, kıyıdan içeriye doğru 81 m yürüdüğüne göre kayığın kıyıdan uzaklığını bulunuz.
766
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Benzerlik
BÖLÜM ÖZETİ
Temel Orantı Teoremi
Bir üçgenin kenarlarından birine paralel olan ve diğer iki kenarını kesen doğru, kestiği kenarlar üzerinde orantılı doğru parçaları oluşturur.
A
D
ABC nde [DE] // [BC] ise
AD
AE
=
dir.
EC
DB
D
E
B
C
Temel Orantı Teoreminin Karşıtı
Bir üçgenin iki kenarını farklı noktalarda kesen bir doğru bu kenarlar üzerinde orantılı doğru parçaları ayırıyorsa bu doğru üçgenin üçüncü kenarına paraleldir.
A
D
ABC nde
D
AD
AE
ise
=
DB
EC
E
B
[DE] // [BC] dir.
C
Thales Teoremi
Birbirine paralel en az üç doğru, kendilerini kesen doğrular üzerinde uzunlukları
orantılı doğru parçaları oluşturur.
F
E
[AD] // [BE] // [CF] ise
D
A
B
AB
DE
AC
DF
AB
DE
,
=
,
=
dir.
=
AC
DF
BC
EF
BC
EF
C
Üçgenlerin Benzerliği
İki üçgenin köşeleri arasında kurulan bire bir eşlemede, karşılıklı açılar eş ve karşılıklı kenar uzunlukları orantılı ise bu
üçgenlere benzer üçgenler adı verilir.
D
Karşılıklı Eş Açılar
D
ABC + DEF
A
W
A,W
D
D
B
C E
V
B,V
E
F
W
C,V
F
Karşılıklı Oranlı Kenarlar
BC
AC
AB
=
=
=k
EF
DF
DE
k ∈ R+
Benzer üçgenlerin karşılıklı kenar uzunluklarının oranı pozitif bir k gerçek sayısına eşittir. Bu k değerine benzerlik oranı
adı verilir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
767
Bölüm
4.2
Benzerlik
Benzerlik Kuralları
a.
Açı – Açı (A. A.) Benzerlik Kuralı
İki üçgen arasında kurulan bire bir eşlemede, karşılıklı iki açısının ölçüleri eşit ise bu üçgenler benzerdir.
A
B
C
D
D
b.
m (V
B) = m ( W
D)
4 ise
W
V
m ( C) = m ( E)
F
E
D
ABC + FDE dir.
Kenar – Açı – Kenar (K. A. K.) Benzerlik Kuralı
İki üçgen arasında kurulan bire bir eşlemede, karşılıklı iki kenar uzunlukları orantılı ve bu kenarların oluşturduğu açılar
eş ise bu üçgenler benzerdir.
C
B
E
D
c.
AB
BC _bb
=
b
FD
DE ` ise
bb
b
m (V
B) = m ( W
D) b
a
F
A
D
D
ABC + FDE dir.
Kenar – Kenar – Kenar (K. K. K.) Benzerlik Kuralı
İki üçgen arasında kurulan bire bir eşlemede, karşılıklı kenarların uzunlukları orantılı ise bu iki üçgen Kenar-Kenar-Kenar (K. K. K) benzerlik kuralına göre benzerdir.
F
AB
AC
BC
ise
=
=
FD
FE
DE
A
D
B
C
D
E
D
ABC + FDE dir.
Benzer Üçgenlerin Yardımcı Elemanları
Benzer iki üçgende;
•
Karşılıklı yüksekliklerinin uzunluklarının oranı,
•
Karşılıklı kenarortaylarının uzunluklarının oranı,
•
Karşılıklı açıortaylarının uzunluklarının oranı benzerlik oranına eşittir.
768
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Bölüm 4. 2. Üçgenlerin Benzerliği
BÖLÜM DEĞERLENDİRME
1.
D
Yandaki şekilde
4.
M
[AB] // [CD]
B
A
d2
|AE| = 8 br
E
8
d1
|BE| = 5 br
5
4 R
S
12
O
T
2
P
|EC| = 10 br
10
N
d3
1
C
Yukarıdaki şekilde d1 // d2 // d3 ve bu doğruları
kesen l1 ve l2 doğruları verilmektedir.
ise |ED| kaç birimdir?
|OP| = 3 · |NO| , |MR| = 4 br , |ST| = 12 br
2.
C
B
6
3
4
|MP| = 15 br ise |MN| + |RS| toplamı kaç birimdir?
Yandaki şekilde
D
[BD] ∩ [CE] = {F}
F
7
8
|CF| = 3 br
|BF| = 4 br
E
5.
D
|FD| = 6 br
4x
|FE| = 8 br
E
C
4
6
F
D
ise |AG| kaç birimdir?
C 3
E
Yandaki şekilde
B
[FE] // [DC] ve
A
9
[DE] ⊥ [EB]
|DE| = 3x , |AB| = 4x , |BC| = 9 br , |CE| = 3 br
%
B, C, E doğrusal ve m (DCA) = 90° ise |DE| kaç
birimdir?
ise |BC| kaç birimdir?
G 3
[AB] ⊥ [BE]
3x
B
|ED| = 7 br
3.
Yandaki şekilde
A
6.
A
E
[EG] // [CB] dir.
|EF| = 4 br
|DC| = 6 br
|GB| = 3 br
B
3
D
F
Yandaki ABC
üçgeninde E, D
noktaları
sırasıyla [AB] ve
C [AC] kenarları
üzerindedir.
[ED] // [BC] , [BD] ∩ [CE] = {F} dir.
3|AE| = |EB| , |EF| = 3 br ise |FC| kaç birimdir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
769
Bölüm 4. 2. Üçgenlerin Benzerliği
BÖLÜM DEĞERLENDİRME
7.
Yandaki ABC
üçgeninde
A
7
8
6
A
|DB| = 5 br
D
[EF] ⊥ [GF] ve
ABCD bir karedir.
E
9
B
C 3 G
|BE| = 6 br
x
B
Yandaki şekilde
F
|AD| = 7 br
D
5
10.
E
4
C
|EB| = 9 br
|CG| = 3 br
|EC| = 4 br
ise karenin bir kenar uzunluğu kaç birimdir?
|AC| = 8 br
ise |DE| = x kaç birimdir?
11. A
8.
Yandaki şekilde
CFE ve CBA
üçgenleri dik
üçgenler
F
A
x
15
C
9
12
B
E
x
A
|AB| = 6 cm
3|AF| = |AC|
%
m (CFE) = 90°
Yandaki şekilde
F
E
4
3
4
4
B
C
EF =
4
br
3
ise |AB| = x kaç birimdir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
|BC| = 4 cm
C
|DE| = 4 cm
ise |AE| kaç cm dir?
12.
A
5
E
Yandaki şekilde
D
G
[BC] ∩ [AD] = {E}
|CD| = 4 br
770
[AB] ⊥ [BC]
[AB] // [FE] // [CD]
B
[DE] ⊥ [AC]
E
6
|AC| = 15 br, |AB| = 9 br , |CB| = 12 br ise |EF| = x
değeri kaç birimdir?
D
[AD] // [BC]
4
%
m (ABC) = 90°
9.
Yandaki şekilde
D
F
x
[AD] // [BC] ve
4
B
[AB] // [CD] dir.
C
D, G, F, E noktaları
ile E, B, C noktaları
doğrusaldır.
|EF| = 5 br , |FG| = 4 br ise |GD| kaç birimdir?
Bölüm 4. 2. Üçgenlerin Benzerliği
BÖLÜM DEĞERLENDİRME
13.
Yandaki şekilde
A
16.
4
[DE] // [FG]
E
G
B
F
|AE| = |ED|
E
3|FC| = 2|BF|
4
G
|AD| = |DB|
D
Yandaki ABC
üçgeninde
A
B
D
F
C
|FG| = 4 cm
2|DC| = |FD|
|AG| = 4 br
ise kaç |GC| birimdir?
C
ise |DE| = x kaç cm dir?
14.
A
D
B
2
G
F
6
E
3
C
Yandaki ABC
üçgeninde D ve E
noktaları sırasıyla
[AB] ve [AC]
kenarlarının orta
noktalarıdır.
17.
8
D
5
B
[CD] ∩ [EF] = {G}
Yandaki ABC
üçgeninde
A
18.
D
Yandaki şekilde
%
%
m (ECB) = m (ADE)
A
x
3
E
%
m (BCA) = 64°
7
12
[AB] ∩ [CD] = {E}
|ED| = 3 br
2x
|EB| = 12 br
|BD| = 7 br
|BC| = 8 br
B
C
%
m (CDA) = 116°
D 116°
%
%
m (DBA) = m (ACB)
|AD| = 8 br , |DC| = 5 br ise |AB| kaç birimdir?
|BF| = 2 cm , |FC| = 6 cm , |CG| = 3 cm ise |GD| kaç
cm dir?
15.
Yandaki ABC
üçgeninde D
noktası, [AC]
kenarının üzerindedir.
A
8
ise |AD| kaç birimdir?
C
B
C
|AE| = x
|EC| = 2x
ise |EC| kaç birimdir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
771
Bölüm 4. 2. Üçgenlerin Benzerliği
BÖLÜM DEĞERLENDİRME
19.
A
E
D
G
B
6
C
F
Yandaki ABC
üçgeninde D ve E
noktaları, sırasıyla
[AB] ve [AC]
kenarlarının orta
noktalarıdır.
22.
Yandaki ABC üçgeninde
A
[AF] ∩ [CD] = {E}
D
|AD| = |DB|
E
|BF| = 6 br , 3|BG| = 2|GE| ise |FC| kaç birimdir?
F
12
B
C
|CE| = |ED|
|BF| = 12 br
ise |FC| kaç birimdir?
20.
C
18
D
|AB| = 9 br
B
|BL| = 5 br
21.
3
F
2
Yanda verilen
şekilde
B
B, E, C ; A, E, D ve
F, E, G noktaları
doğrusaldır.
E
[AB] // [CD]
x
C
G
8
D
|AF| = 2 br
|FB| = 3 br
|GD| = 8 br
olduğuna göre |CG| = x değerini bulunuz.
772
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
6
Yandaki şekilde, B,
C ve D doğrusal
noktalardır.
%
%
m (DCE) = m (ECA)
F
|CD| = 18 br
L
E
G
C
D
|AF| = |FB|
|AC| = 8 br
|BC| = 6 br
%
m (AEC) = 90° ise |EF| kaç birimdir?
ise |LD| kaç birimdir?
A
A
[BC] ∩ [AD] = {K}
K
9
5
23.
[AB] // [KL] // [CD]
A
B
Yandaki şekilde
24.
Sultanahmet’i gezen bir
turist Dikilitaş’ın yüksekliğinin kaç metre olduğunu
merak ediyor. Bunu
belirlemek için Dikilitaş’tan 7 m uzağa bir düz
ayna koyuyor. Kendisi de
aynadan Dikilitaş’ın en uç
noktasını görene kadar
0,5 m kadar uzaklaşıyor.
Turistin boyu 1,82 m olduğuna göre Dikilitaş’ın
yüksekliğini bulunuz.
Ünite
4
ÜÇGENLERDE
EŞLİK VE BENZERLİK
Bölüm 4.3.
Bu Bölümde Neler
Öğreneceğiz?
•
Açıortay ve üçgenin açıortaylarının özelliklerini
•
Üçgenin kenarortaylarının özelliklerini
•
Orta dikme ve üçgenin kenar orta dikmelerinin özelliklerini
•
Üçgenin yüksekliklerinin özelliklerini
Neden Öğreneceğiz?
Üçgenin yardımcı elemanları hem üçgenleri
daha iyi tanımada hem de daha karmaşık
geometrik şekilleri analiz etmede önemli
bilgiler sunar. Örneğin üçgenin ağırlık merkezi
kullanılarak daha karmaşık şekillerin ağırlık
merkezleri bulunabilir.
Üçgenin Yardımcı Elemanları
Bölüm 4.3. Üçgenin Yardımcı Elemanları
HAZIR MIYIZ?
1.
%
Şekilde [AD, BAC
nın açıortayı
olduğuna göre x
kaçtır?
B
D
4°
+1
3x
5x – 6°
A
5.
Aşağıda kesişen d, k, l, n ve m doğruları ile
ilgili verilen ifadelerdeki boşlukları uygun
şekilde doldurunuz.
d
k
T
J
C
C
L H
K
l
G
D
F
E
2.
Bir doğrunun bir çembere teğet olmasının
ne anlama geldiğini açıklayınız.
3.
C
l
4.
F
G
E
H
K
Yandaki
şekilde C
noktasının l
doğrusuna
olan uzaklığını
gösteren
doğru parçası
hangisidir?
(. . . . ) İki doğru paralel değilse kesişirler.
b.
(. . . . ) Çakışık olmayan iki doğru birden fazla
noktada kesişebilirler.
c.
a.
noktaları d doğrusu üzerindeki
doğrusal noktalardır.
b.
noktaları k doğrusu üzerindeki
doğrusal noktalardır.
c.
k ve l doğruları
mektedir.
ç.
m ve d doğruları
mektedir.
6.
Aşağıda verilen üçgenleri açılarına göre
sınıflandırınız.
........................
........................
Aşağıdaki ifadelerin yanlarındaki boşluğa
doğru olanlar için “D” yanlış olanlar için “Y”
yazınız.
a.
C
...............
A ve B noktaları arasında ve |AP| = |PB| ise
1
1
AP = AB ve PB = AB dir.
2
2
774
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
noktasında kesiş-
G
D
G
60°
E
F
70°
60°
60°
H
K
(. . . . ) K noktası [AB] nın orta noktası ise
|AK| = |KB| dir.
(. . . . ) A, P ve B noktaları doğrusal P noktası
noktasında kesiş-
...............
I
ç.
m
n
30°
110°
J
M
O
P
L
30°
N
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında bir açının açıortayı üzerinde alınan bir noktanın açının kollarına olan uzaklıkları arasındaki
ilişkiyi inceleyeceğiz.
Araç ve Gereçler: Dinamik geometri yazılımı
A
Adım 1
%
Dinamik geometri yazılımında bir ABC çiziniz.
B
Adım 2
C
%
Yazılımın “Açıortay” özelliğini kullanarak ABC nın açıortayını çiziniz.
A
Adım 3
D
B
Açıortay üzerinde herhangi bir D noktası alınız.
C
A
Adım 4
G
D noktasından AB ve BC kenarlarına dik doğrular çiziniz. Çizdiğiniz dik doğruların
AB ve BC kenarlarıyla kesim noktalarını sırasıyla G ve H olarak isimlendiriniz.
H
Adım 5
|DG|
D
B
|DH|
|BG|
|BH|
C
Yazılımın uzunluk ölçme özelliğini kullanarak |DG| ,
|DH| , |BG| ve |BH| değerlerini ölçünüz ve yandaki
tablonun birinci satırını doldurunuz. Ardından D
noktasını açıortay üzerinde sürükleyerek D noktasının farklı konumları için tablodaki uzunlukların
aldığı değerleri gözlemleyerek tablonun diğer
satırlarını da doldurunuz.
Sonuç
Yukarıdaki tabloyu inceleyerek bir açının açıortayı üzerinde alınan bir noktadan açının kollarına çizilen dikmelerin
uzunlukları ve bu dikmelerin açının kolları üzerinde ayırdığı doğru parçalarının uzunlukları arasındaki ilişkiyi belirleyiniz. Belirlediğiniz ilişkilerin gerekçelerini açıklayınız.
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
775
Bölüm
4.3
Üçgenin Yardımcı Elemanları
4.3.1. Açıortay
Neler Öğreneceğiz?
•
Bir açının açıortayını çizmeyi
•
Üçgenin iç ve dış açıortaylarının
özelliklerini
Başlarken
Oda duvarlarının zeminle birleştiği yerlerde kenar pervazları (süpürgelik) bulunur. Marangozlar, kenar pervazlarını
duvarların köşelerine yerleştirirken öncelikle duvarın köşe
açısını belirlemek zorundadır. Bunun nedeni köşelerde süpürgeliklerin tam olarak birleşmesidir. Açı belirlendikten
sonra her bir pervaz uçlarından belirlenen açının yarısı
ölçüsünde kesilir. Böylece pervazlar duvarın köşelerinde
tam olarak birleşir. Marangozlar aslında duvarın köşesinde oluşan açının açıortayını oluşturmaktadırlar.
Anahtar Terimler
•
Açıortay
•
İç Açıortay Teoremi
•
İç teğet çember
•
Dış teğet çember
•
Dış Açıortay Teoremi
Daha önceki yıllarda bir açıyı eş iki parçaya ayıran ışına açıortay denildiğini öğrenmiştik. Aşağıdaki çizim çalışmasında pergel-cetvel kullanılarak verilen bir açının açıortayının nasıl çizilebileceği açıklanmıştır.
Bir Açının Açıortayını Çizme
1. Adım
2. Adım
Sembol ve Gösterimler
•
Geometrik Çizim
T
T
nA , n’A
A
S
A
S
Pergelin sivri ucu A noktasına konularak açının kollarını T ve S noktalarında
kesen bir yay çiziniz.
Pergeli |TS| nun yarısından fazla olacak
şekilde açınız ve merkezi S olan bir yay
çiziniz.
3. Adım
4. Adım
N
T
T
A
N
S
Pergelin açıklığını bozmadan merkezi
T olan ve bir önceki yayı kesen farklı bir
yay çiziniz. Yayların kesim noktasını N
olarak isimlendiriniz.
776
A
S
A ile N noktalarını cetvelle birleştiriniz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
A nın
Yukarıdaki geometrik çizim çalışması sonucunda pergel ve cetvel kullanarak W
W
açıortayını çizdiniz. Şimdi de çizmiş olduğunuz [AN nın niçin A nın açıortayı olduğunu
inceleyelim:
T
A
N
S
İlk çizilen yayın merkezi A noktası ve bu yay açının
kollarını T ve S noktalarında kestiğinden
6AS@ b 6AT@ ( 6AS@ ve 6AT@ , A merkezli çemberin
yarıçapları)dir. Benzer sebepten dolayı 6SN@ , 6TN@
dir. Ayrıca 6AN@ , 6AN@ olduğundan K. K. K. eşlik
D
D
kuralına göre ATN b ASN dir. Eş üçgenlerin
% %
karşılıklı açıları eş olduğundan TAN , SAN olur.
A nı iki eş parçaya ayırır.
Böylece [AN, W
Anahtar Bilgi
Aşağıdaki şekilde açının oluşturduğu iç ve dış bölgeler
gösterilmiştir.
Konu başında yapılan etkinlikte bir açının açıortayı üzerinde alınan bir noktanın açının kollarına olan uzaklıkları arasındaki ilişkiyi incelemiştik. Aşağıdaki teorem bu ilişkiyi göstermektedir.
İç bölge
Teorem
Dış bölge
B
F
D
A
E
N
Bir açının açıortayı üzerinde alınan herhangi
bir noktadan açının kollarına çizilen dikmelerin uzunlukları eşittir.
C
İspat:
%
Verilenler: [AN , BAC nın açıortayı; D ∈ [AN , [DF] ⊥ [AB ve [DE] ⊥ [AC
İstenen: |DF| = |DE|
%
%
%
%
[AN açıortay ise m (BAN) = m (NAC) dir. m (AFD) = m (AED) = 90° olduğundan FAD
üçgeni ile EAD üçgenlerinin üçüncü açılarının ölçüleri de eşit olur.
% % _
FAD , EAD bbb
b
D
D
O halde, 6AD@ , 6AD@ b` ise A. K. A. eşlik kuralına göre FAD , EAD elde edilir.
bb
% % b
FDA , EDA b
a
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
777
Üçgenin Yardımcı Elemanları
Eş üçgenlerin karşılıklı kenarları eş olacağından |DF| = |DE| olur.
Bu teorem, [AN açıortayı üzerinde alınan her noktanın, açının kollarına eşit uzaklıkta
olduğunu göstermektedir.
D
D
FAD , EAD eşliği aynı zamanda |AF| = |AE| olduğunu da göstermektedir.
Sonuç
Yukarıdaki teorem bir üçgenin açıortayı üzerinde alınan herhangi bir noktanın
açının kollarına eşit uzaklıkta olduğunu belirtmektedir. Bu teoremin karşıtı da
doğrudur. Bir açının iç bölgesinde alınan bir nokta açının kollarına eşit uzaklıkta
ise bu nokta açının açıortayı üzerindedir.
1
%
Yandaki şekilde BAC na ait açıortay [AN olmak üzere [AN
açıortayı üzerinde alınan D noktasının [AB] na olan
uzaklığı 7 cm ise bu noktanın [AC] na olan uzaklığını
bulalım.
B
F
7 cm
D
A
N
x
G
C
Açıortay üzerinde alınan bir noktanın açının kollarına olan uzaklığı eşit olduğundan
|DF| = |DG| = 7 cm olur.
2
%
Yandaki şekilde verilen D noktası BAC nin iç
%
bölgesindedir. D noktasının BAC nın kollarına olan
uzaklıkları 5 er cm dir.
D
5 cm
0°
+2
°
–2
F
5x
B
5 cm
E
C
%
%
m (DAB) = 5x - 2° ve m (DAC) = 3x + 20° olduğu%
na göre m (DAB) nın kaç derece olduğunu bulalım.
3x
Bölüm
4.3
A
778
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
%
A nın açıortayı üzerinD noktası BAC nın kollarına eşit uzaklıkta olduğundan bu nokta W
%
%
dedir. Açıortay bir açıyı iki eş parçaya ayırdığından m (DAB) = m (DAC) olur.
Verilenler yerine yazılırsa 3x + 20 = 5x – 2 ve buradan x = 11° olarak bulunur.
%
m (DAB) = 5 · 11 - 2 = 53° dir.
3
Bir faul atışında, kalecinin kaleye gelen topu
kurtarabilmesi için, topun izleyebileceği
yollara eşit uzaklıkta olması gerekir. Aksi
takdirde kalenin bir tarafını daha çok açık
bırakmış olur ki bu onun o tarafa uzanabilme potansiyelini düşürür.
Buna göre kalecinin topun kaleye geldiği
anda nasıl bir pozisyon alması gerektiğini
bulalım.
B
C
A
Kalecinin iyi pozisyon alması ve kalenin bir
tarafını açık bırakmaması için, topun izleyebileceği en uç yollara (gol olmasını sağlayacak
yollar) eşit uzaklıkta olması gerekir. Dolayısıyla kale direklerinin zemine değdiği noktaları
B ve C, topun bulunduğu konumu A noktası
olarak isimlendirirsek, bir açının açıortayı
üzerinde bulunan her nokta açının kollarına
%
eşit uzaklıkta olduğundan kalecinin BAC nın
açıortayı üzerinde olması gerektiği sonucuna
ulaşılır.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
779
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında bir üçgenin bir iç açıortayının bu açının karşısındaki kenar üzerinde oluşturduğu doğru
parçalarının uzunlukları ile üçgenin o açıyı oluşturan kenarlarının uzunlukları arasındaki ilişkiyi inceleyeceğiz.
Araç ve Gereçler: Dinamik geometri yazılımı
Adım 1
A
Dinamik geometri yazılımı
yardımıyla bir ABC üçgeni
çiziniz.
Adım 5
ABC üçgenini köşe noktalarından hareket ettirerek farklı
AB
üçgenler oluşturunuz. Oluşan her yeni üçgen için
AC
BN
ile
oranlarındaki ilişkiyi inceleyiniz. Dördüncü
NC
adımda elde etiğiniz ilişki değişiyor mu?
..............................................................................................
C
B
Adım 6
Adım 2
ABC üçgeninin A açısına ait
açıortayını çiziniz. Bu
açıortayın BC kenarını
kestiği noktayı N olarak
isimlendiriniz.
A
N
B
C
Adım 3
Yazılımın uzunluk ölçme özelliğini kullanarak ABC üçgeninin AB ve AC kenar uzunlukları ile [BN] ve [NC] nın
uzunluklarını bulup aşağıya yazınız.
|AB| = . . . . . . .
|AC| = . . . . . . .
|BN| = . . . . . . .
|NC| = . . . . . . .
..............................................................................................
Adım 7
ABC üçgenini köşe noktalarından hareket ettirdiğinizde
a. Oluşan dar açılı üçgenler için iç açıortaylar tek bir
noktada mı kesişmektedir?
b. Oluşan dik üçgenler için iç açıortaylar tek bir noktada mı kesişmektedir?
c. Oluşan geniş açılı üçgenler için iç açıortaylar tek bir
noktada mı kesişmektedir?
ç. ABC üçgeninin iç açıortaylarının kesim noktası her
zaman üçgenin iç bölgesinde midir?
Sonuç
Adım 4
Yazılımın ilgili özelliğini kullanarak uzunlukları aşağıdaki
gibi oranlayınız. Elde ettiğiniz oranlar arasındaki ilişkiyi
yazınız.
AB
= .......
AC
BN
= .......
NC
..............................................................................................
780
ABC üçgeninin B ve C açılarına ait iç açıortaylarını çiziniz.
ABC üçgeninin iç açıortaylarının tümü aynı noktada mı
kesişmektedir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Yukarıda yapmış olduğunuz çalışmalar sonucunda
• bir üçgenin bir iç açıortayının karşı kenarda ayırdığı
parçalarla üçgenin diğer kenarlarının uzunlukları
arasındaki ilişkiyi ve
• üçgenin iç açıortaylarının kesim noktası için elde
ettiğiniz ilişkiyi yazınız.
............................................................................................
Açıortay
Üçgenin İç Açıortayları
A
K
nC
N
B
nA
C
Bir üçgenin herhangi bir iç açısını eş iki parçaya bölen ışının, köşe ile karşı kenar arasında kalan parçasına, üçgenin o köşesine ait iç açıortayı denildiğini
A nı eş
öğrenmiştik. Yandaki ABC üçgeninde [AN], W
iki açıya böldüğünden, açıortaydır. Bir ABC üçgeninin “A” açısına ait açıortayın uzunluğu genellikle “nA”
ile gösterilir.
Bir ABC üçgeninin A açısına ait iç açıortayın karşı kenarı kestiği N noktasının karşı kenar
üzerinde oluşturduğu [BN] ve [NC] nın uzunlukları ile üçgenin AB ve AC kenarlarının
uzunlukları arasında bir ilişki bulunmaktadır. Aşağıdaki teorem bu ilişkiyi ifade etmektedir.
Teorem
İç Açıortay Teoremi
Bir üçgende, herhangi bir iç açıortayın karşı kenar
üzerinde ayırdığı parçaların uzunlukları oranı,
diğer iki kenarın uzunlukları oranına eşittir.
A
Yandaki şekilde [AN], A açısının açıortayı olmak
üzere
B
N
C
NB
AB
dir.
=
NC
AC
İspat:
Verilenler: [AN] , W
A nın açıortayı
İstenen:
NB
AB
=
NC
AC
A
B
C noktasından geçen ve [AN] na paralel olan bir doğru
çizelim. Bu doğru AB kenarının uzantısını E noktasında
kessin. Buna göre,
%
%
m (BAN) = m (NAC) (verilen)
%
%
m (BAN) = m (BEC) (yöndeş açılar)
olduğundan
%
%
m (NAC) = m (ACE) (iç ters açılar)
%
%
m (BEC) = m (ACE) bulunur. Bu durumda, ACE üçgeni, ikizkenar üçgen olduğundan |AC| = |AE| olur. BCE üçgeninde,
14243
E
N
C
[AN] // [CE] olduğundan temel orantı teoremine göre,
NB
AB
=
olur. |AC| = |AE| olduğundan bu eşitlikte |AE|
NC
AE
NB
AB
=
yerine |AC| yazılırsa
elde edilir.
NC
AC
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
781
Bölüm
4.3
Üçgenin Yardımcı Elemanları
1
Yandaki ABC üçgeninde [AD], A açısına ait açıortaydır.
C
6
A
|AB| = 4 cm
|AC| = 6 cm
D
4
2
|BD| = 2 cm
B
olduğuna göre |DC| nu bulalım.
ABC üçgeninde [AD] A açısına ait açıortay olduğundan, İç Açıortay Teoremine göre
AB
BD
=
dir.
AC
DC
Buna göre,
4
2
den, |DC| = 3 cm olarak bulunur.
=
6
DC
2
Yandaki şekilde [AE] ve [DE] sırasıyla A ve D açılarının açıortaylarıdır.
A
6
B
C
E
8
12
|AB| = 6 br , |DB| = 8 br ve |DC| = 12 br
ise |AC| nun kaç br olduğunu bulalım.
D
Anahtar Bilgi
%
[DE], BDC nın açıortayı olduğundan BDC üçgeninde İç Açıortay Teoremi uygulanırsa,
ABC ve DBC üçgenlerinde
[AE] ve [CE] sırasıyla A ve C
açılarının açıortaylarıdır.
DB
BE
=
... (*) dir.
DC
EC
A
d
%
[AE], BAC nın açıortayı olduğundan ABC üçgeninde İç Açıortay Teoremine göre,
c
B
D
E
a
AB
DB
AB
BE
... (**) dir. (*) ve (**) dan
=
orantısı elde edilir.
=
AC
DC
AC
EC
b
C
Buna göre,
Buna göre a · c =b · d dir.
782
6
8
den |AC| = 9 br olarak bulunur.
=
AC
12
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
3
A
42
|AD| = 42 br
D
56
F
70
|DB| = 70 br
|AC| = 56 br
C
E
B
%
%
Yandaki şekilde [AE] ve [DE] sırasıyla BAC ve BDC nın
açıortaylarıdır. [AE] ∩ [DC] = {F}
ise |DF| nu bulalım.
%
[AE], BAC nın açıortayı olduğundan ABC üçgeninde İç Açıortay Teoremi uygulanırsa,
AB
EB
=
... (*) dir.
EC
AC
%
[DE], BDC nın açıortayı olduğundan DBC üçgeninde İç Açıortay Teoremi’ne göre,
DB
EB
AB
DB
=
... (**) dir. (*) ve (**) dan
=
orantısı elde edilir.
DC
EC
AC
DC
Buna göre,
112
70
den |DC| = 35 br elde edilir.
=
56
DC
|DF| = x br olsun. Buna göre, |FC| = 35 – x br olur.
[AF] , ADC üçgeninde A açısına ait açıortay olduğundan, İç Açıortay Teoremi’ne göre,
AD
DF
42
x
3
x
=
orantısından,
den
=
&
=
AC
FC
56
35 - x
4
35 - x
105 – 3x = 4x ise 7x = 105 olur. Buradan x = 15 br olarak bulunur.
4
%
Yandaki şekilde [BE] , ABC nın açıortayıdır.
A
6
F
B
E
D, [BC] nın orta noktası
8
4
|AE| = 6 br
C
D
|EC| = 8 br
|FD| = 4 br
ise |AF| nu bulalım.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
783
Bölüm
4.3
Üçgenin Yardımcı Elemanları
%
[BE], ABC nın açıortayı olduğundan ABC üçgeninde İç Açıortay Teoremine göre,
BA
AE
BA
6
=
orantısından,
= elde edilir. Buna göre, |BA| = 6k, |BC| = 8k olarak alıBC
BC
EC
8
nabilir.
D, [BC] nın orta noktası olduğundan |BD| = |DC| = 4k olur.
[BF], ABD üçgeninde V
B nın açıortayı olduğundan, İç Açıortay Teoremine göre,
AF
AB
AF
6k
=
orantısından,
eşitliğinden |AF| = 6 br elde edilir.
=
4k
4
BD
FD
Üçgenin iç açıortaylarını gözlemlediğiniz atölye çalışmasında üçgenin iç açıortaylarının bir noktada kesiştiğini belirlemiştiniz. Şimdi ulaşmış olduğunuz bu sonucu teorem
olarak ifade edelim ve üçgenin iç açıortaylarının neden bir noktada kesiştiğini ispatlayalım.
Teorem
A
R
K
Üçgenin iç açıortayları bir noktada kesişir.
I
B
N
C
İspat
Verilenler: ABC bir üçgen; [AN], [BR], [CK] sırasıyla A, B ve C açılarının iç açıortayları
İstenen: [AN] ∩ [BR] ∩ [CK] = {I}
A
R
K
I
ABC ve ACB açılarının açıortaylarını çizelim. Bu
açıortaylar I noktasında kesişsin.
C
B
784
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
I noktasından üçgenin kenarlarına dik doğrular
çizelim. Açıortay üzerinde alınan bir noktadan
açının kollarına çizilen dikmelerin uzunlukları eşit
olduğundan
A
D
E
K
R
I
C
|IE| = |IF| ve |ID| = |IF| olur.
F
B
Buradan |IE| = |ID| elde edilir.
I noktası ile A noktasını birleştirelim. Bir açının
kollarından eşit uzaklıkta bulunan her nokta bu
açının açıortayı üzerinde olduğundan [AI] açıortay
olur. Bir diğer ifadeyle üçgenin iç açıortayları bir
noktada kesişir.
A
D
E
K
R
I
C
F
B
Anahtar Bilgi
Yukarıdaki teoremde, iç açıortayların kesişimi olan I noktasının üçgenin kenarlarına
olan uzaklıklarının birbirine eşit olduğu görülmektedir. Bu nedenle aşağıdaki sonucu
yazabiliriz.
Üçgenin iç açıortayları daima
üçgenin iç bölgesinde kesişir.
Bu nokta üçgenin iç teğet
çemberinin merkezidir.
Sonuç
Üçgenin iç açıortaylarının kesim noktası üçgenin kenarlarından eşit uzaklıktadır.
İç açıortayların kesim noktası olan I, üçgenin kenarlarından eşit uzaklıkta olduğundan, I noktasını merkez, bu noktanın kenara olan uzaklığını da yarıçap kabul
eden bir çember çizilebilir. Bu çembere üçgenin iç teğet çemberi denir.
Anahtar Bilgi
d
Aşağıdaki şekillerde bazı üçgenlerin iç teğet çemberleri gösterilmiştir.
A
A
A
R
R
K
N
Dar Açılı Üçgen
C
B
O
K
K
B
A
R
N
C
Dik Üçgen
B
N
C
d doğrusu ile O merkezli
çember tek noktada kesişirse
d doğrusu çembere teğettir
denir.
Geniş Açılı Üçgen
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
785
Bölüm
4.3
Üçgenin Yardımcı Elemanları
Aşağıdaki çizim çalışmasında verilen bir üçgenin iç teğet çemberinin dinamik geometri yazılımı kullanılarak nasıl çizilebileceği adım adım gösterilmiştir.
Üçgenin İç Teğet Çemberini Çizme
Geometrik Çizim
2. Adım
1. Adım
A
A
R
K
K
I
C
B
B
I
C
N
Bir dinamik geometri yazılımı kullanarak bir ABC üçgeni çiziniz. Yazılımın
“Açıortay” özelliğini kullanarak ABC
üçgeninin iç açılarının açıortaylarını
çiziniz. Açıortayların kesim noktasını “I”
olarak isimlendiriniz.
Yazılımın “Dik Doğru” özelliğini kullanarak “I” noktasından kenarlardan
herhangi birine dik doğru çiziniz. Bu
dik doğrunun kenarı kestiği noktayı “D”
olarak isimlendiriniz.
3. Adım
4. Adım
Üçgeninizi köşelerinden tutarak hareket
ettiriniz. Üçgenin farklı durumları için
içteğet çemberi inceleyiniz.
A
R
D
K
C
N
B
Yazılımın “Çember” özelliğini kullanarak
merkezi I olan ve D noktasından geçen
bir çember çiziniz.
786
R
D
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
5
A
Yandaki şekilde, ABC bir üçgen ve I noktası da bu üçgenin iç teğet çemberinin merkezidir.
|AC| = 8 br
8
I
x
B
4
4
D
ise |BD| nu bulalım.
C
A
αα
2k
8
I
4
k
β
B
x
D
4
|CI| = |CD| = 4 br
β
β
I noktası ABC üçgeninin iç teğet çemberinin merkezi
olduğundan bu nokta iç açıortayların kesim noktasıdır. [CI] açıortay olduğundan, ACD üçgeninde İç
Açıortay Teoremine göre,
AI
CA
AI
8
= = 2 olur.
eşitliğinden
=
ID
4
CD
ID
C
Buna göre, |ID| = k ise |AI| = 2k olur.
%
%
m^DACh = a ve m^ACIh = b olsun
%
%
|CI| = |CD| = 4 br olduğundan CID üçgeni ikizkenar üçgen ve m ( CID ) = m ( IDC ) olur.
Bir üçgende bir dış açının ölçüsü kendisine komşu olmayan iki iç açının ölçüleri topla%
%
mına eşit olduğundan AIC üçgeninde, m ( CID ) = α + β ve m ( IDC ) = α + β olur.
%
%
%
%
%
m (ADC) = m (DAB) + m (ABD) eşitliğinden α + β = α + m (ABD) olup m (ABD) = β olur.
%
%
%
%
m (ABD) = m ( ACI ) = β ve m (DAB) = m ( IAC ) = a olduğundan A. A. benzerlik kuralına
D
D
göre, ABD + ACI dır.
|BD| = x olsun.
Buna göre,
AD
BD
3k
x
=
eşitliğinden
= ise x = 6 br bulunur.
CI
2k
4
AI
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
787
Bölüm
4.3
Üçgenin Yardımcı Elemanları
6
Yandaki ABC üçgeninde I noktası iç teğet çemberin
merkezi
A
3
5
D
|AC| = 5 br
I
6
C
E
x
|AD| = 3 br
|DB| = 6 br
B
ise |BE| = x kaç birimdir?
A
3
D
3t I
6
x = 9k
E
5
5t
5k
C
B
Bir üçgenin iç teğet çemberinin merkezi iç açıortayların kesim noktası olduğundan, [CD] ve [AE], sırasıyla C
ve A açılarının açıortayıdır. İç açıortaylar tek noktada
kesiştiğinden [BI], B açısının açıortayı olur.
[AE], A açısının açıortayı olduğundan ABC üçgeninde
İç Açıortay Teoremine göre,
BE
AB
BE
9
eşitliğinden =
den |BE| = 9k olarak alınırsa, |EC| = 5k olur.
=
5
EC
AC
EC
AD
DI
DI
3
ADC üçgeninde [AI] açıortay olduğundan,
=
eşitliğinden =
eşitliğinden
AC
IC
5
IC
|DI| = 3t ise, |IC| = 5t olur. DBC üçgeninde [BI] açıortay olduğundan,
BD
DI
5
6
3t
=
eşitliğinden,
den k = br bulunur.
=
BC
IC
7
14k
5t
5
45
br bulunur.
|BE| = x = 9k = 9 · =
7
7
Üçgenin Dış Açıortayları
Bir üçgenin herhangi bir iç açıortayının karşı kenar üzerinde ayırdığı doğru parçalarının
uzunluklarının üçgenin diğer kenar uzunlukları ile orantılı olduğunu öğrendik. Aşağıdaki
teorem benzer bir ilişkinin dış açıortaylar için de geçerli olduğunu ifade etmektedir.
Teorem
Dış Açıortay Teoremi
Bir ABC üçgeninde, A açısının dış açıortayı BC
kenarının uzantısını E noktasında kesiyorsa,
A
B
788
C
EB
AB
dir.
=
EC
AC
E
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
İspat
Verilenler: ABC bir üçgen, [AE] , W
A nın dış açıortayı
İstenen:
EB
AB
=
EC
AC
G
C noktasından AE doğrusuna paralel olan bir doğru
çizelim. Bu doğru AB kenarını F noktasında kessin.
%
%
m (CAE) = m (ACF) (iç ters açılar)
olduğundan
%
%
m (AFC) = m (GAE) (yöndeş açılar)
%
%
m (AFC) = m (ACF) olur.
123
A
F
B
C
E
Bu durumda AFC üçgeni bir ikizkenar üçgendir.
Yani, |AF| = |AC| dir.
ABE üçgeninde, [CF] // [AE] olduğundan, Temel Orantı Teoremi’nden,
Bu eşitlikte |AF| yerine |AC| yazılırsa
EB
AB
olur.
=
EC
AF
EB
AB
olur.
=
EC
AC
7
B
Yandaki şekilde
D
[BE] , ABC üçgeninin B açısının dış açıortayı
|AC| = 5 br , AB =
A
C
5
· BC
2
olduğuna göre |EC| nu bulalım.
E
Dış Açıortay Teoremi’ne göre
EC
BC
EC
2
=
olduğundan
= dir.
EA
BA
EC + 5
5
Buradan 5 · EC = 2 · EC + 10 ve buradan EC =
10
br olarak bulunur.
3
8
Yandaki şekilde
A
%
%
m (ACD) = 2m (CAD)
C
B
4
D
AB = BC =
3
AC
2
|CD| = 4 br
olduğuna göre |BD| nu bulalım.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
789
Üçgenin Yardımcı Elemanları
%
%
%
m (CAD) = a olarak alalım. m (ACD) = 2m (CAD)
%
olduğundan m (ACD) = 2a olur.
3k
°–
2α
E
A α
α
2k
180
Bölüm
4.3
180° – 2α
3k
2α
C
D
4
%
Buradan m (ACB) = 180° - 2a dır. |AB| = |BC| oldu%
ğundan m (BAC) = 180° - 2a elde edilir.
D
ABD nin AB kenarını BA doğrultusunda uzatalım ve B,
A, E noktaları doğrusal olacak şekilde bir E noktası ala%
lım. Bu durumda m (EAD) = a olmalıdır. Buradan [AD], BAC açısının dış açıortayı olur.
3
|AB| = |BC| = |AC| olduğundan |AC| = 2k dersek |AB| = |BC| = 3k olur.
2
DC
AC
4
2
ve buradan
= denklemi elde edilir.
Dış Açıortay Teoremine göre,
=
DB
AB
4 + 3k
3
B
2
2
Bu denklem çözülürse 8 + 6k = 12 ise k = olur. BD = 3k + 4 = 3 · + 4 = 6 br elde
3
3
edilir.
9
B
4
E 2
C
Yandaki ABC üçgeninde [AE], A açısına ait iç açıortay ve
[AN], A açısına ait dış açıortaydır.
D
A
|BE| = 4 br , |EC| = 2 br , |CN| = x
x
N
ise x değerini bulalım.
[AE], ABC üçgeninde A açısına ait iç açıortay olduğundan İç Açıortay Teoremine göre,
AB
EB
=
... (*) dir. [AN], aynı üçgende A açısına ait dış açıortay olduğundan, Dış
AC
EC
AB
EB
NB
NB
Açıortay Teoremine göre,
... (**) dir. (*) ve (**) dan
=
elde edilir.
=
EC
NC
AC
NC
Dolayısıyla,
4
6+x
orantısından, 4x = 12 + 2x den x = 6 br elde edilir.
=
2
x
Sonuç
D
A
ABC üçgeninde, B açısının iç açıortayı
[BE] ve dış açıortayı [BD] ise,
E
C
B
790
DA
AE
dir.
=
DC
EC
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Önceki çalışmalarımızda üçgenin iç açıortaylarının bir noktada kesiştiğini öğrenmiştik. Bu atölye çalışmasında bir
üçgenin iki dış açıortayının kesim noktasının sahip olduğu özelliği inceleyeceğiz.
Araç ve Gereçler: Dinamik geometri yazılımı
A
Adım 1
C
Dinamik geometri yazılımını kullanarak bir ABC üçgeni çiziniz.
B
Adım 2
A
B ve C açılarının dış açıortaylarını çiziniz. Bu açıortayların kesim noktasını F olarak isimlendiriniz.
C
B
Adım 3
F noktası ile ABC üçgeninin A köşesini doğru parçası ile birleştiriniz.
F
A
Adım 4
%
%
Oluşan FAB ile FAC nın ölçülerini yazılımın ilgili özelliğini kullanarak bulunuz ve aşağıdaki tablonun ilk satırına yazınız. Ardından ABC üçgenini köşe noktalarından sürükleyiniz.
%
%
m^FABh ve m ^FACh nün farklı değerleri için tablonun diğer satırlarını doldurunuz.
%
m (FAB)
%
m (FAC)
C
B
F
Sonuç
Elde ettiğiniz sonuçlara göre bir üçgenin iki dış açıortayının kesim noktası hakkında ulaştığınız sonucu açıklayınız.
.................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
791
Bölüm
4.3
Üçgenin Yardımcı Elemanları
Üçgenin dış açıortaylarının kesişimi ile ilgili yaptığınız atölye çalışmasında üçgenin iki
köşesine ait dış açıortayların ve diğer köşeye ait iç açıortayın bir noktada kesiştiğini
belirlemiştiniz. Ulaşmış olduğunuz bu sonucun tüm üçgenlerde niçin geçerli olduğu
aşağıda açıklanmıştır.
Anahtar Bilgi
Bir üçgende iki dış açıortay
ile bu dış açılara komşu
olmayan iç açının açıortayı
tek noktada kesişir.
A
C
B
ABC üçgeninde B ve C açılarının dış açıortayını çizelim. Bu açıortaylar F noktasında kesişsin.
F
A
K
B
L
C
F noktasından üçgenin kenarlarına dik doğrular çizelim. Açıortay üzerinde alınan bir noktadan açının
kollarına çizilen dikmelerin uzunlukları eşit olduğundan |KF| = |LF| ve |FM| = |LF| olur.
Buradan |MF| = |KF| elde edilir.
F
M
A
K
B
L
C
F noktası ile A noktasını birleştirelim. |MF| = |KF| ve
bir açının kollarından eşit uzaklıkta bulunan her
nokta bu açının açıortayı üzerinde olduğundan [AF]
A açısının açıortayı olur.
Bir üçgenin iki dış ve bunlara komşu olmayan iç açısının iç açıortayının bir noktada kesiştiğini gösteren
F
yukarıdaki açıklamadan, F noktasının üçgenin keM
narlarına veya kenarlarının uzantılarına olan uzaklıkları arasında, |FK| = |FL| = |FM| ilişkisinin olduğu görülebilir. Dolayısıyla F noktasını
merkez, bu noktanın kenarlara olan uzaklığını yarıçap kabul eden bir çember çizilebilir.
Bu çembere üçgenin dış teğet çemberi denir. Bir üçgenin üç tane dış teğet çemberi
vardır. Dış teğet çemberlerin merkezleri genellikle Ia, Ib ve Ic ile gösterilir. Aşağıdaki şekilde üçgenin dış teğet çemberleri gösterilmiştir.
792
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
Ib
A
Aşağıdaki çizim çalışmasında verilen bir üçgenin dış
teğet çemberlerinden birinin dinamik geometri yazılımı kullanılarak nasıl çizilebileceği gösterilmiştir.
Ic
C
B
Ia
Üçgenin dış teğet çemberini çizme
Geometrik Çizim
1. Adım
2. Adım
A
A
C
B
D
F
F
Bir dinamik geometri yazılımı kullanarak
bir ABC üçgeni çiziniz. Yazılımın “Açıortay”
özelliğini kullanarak B ve C açılarının dış
açıortaylarını çiziniz. Açıortayların kesim
noktasını “F” olarak isimlendiriniz.
A
B
Yazılımın “Dik Doğru” özelliğini kullanarak “F” noktasından kenarlardan
herhangi birine dik doğru çiziniz. Bu
dik doğrunun kenarı kestiği noktayı “D”
olarak isimlendiriniz.
4. Adım
3. Adım
D
C
B
C
Benzer şekilde üçgenin diğer dış teğet
çemberlerini de çiziniz. Üçgeninizi
köşelerinden tutarak hareket ettiriniz.
Üçgenin farklı durumları için dış teğet
çemberleri inceleyiniz.
F
Yazılımın “Çember” özelliğini kullanarak
merkezi F olan ve D noktasından geçen
bir çember çiziniz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
793
Bölüm
4.3
Üçgenin Yardımcı Elemanları
Üçgenin Açıortaylarının Oluşturduğu Açıların Ölçüsü
Bu bölümde üçgenin açıortaylarının kesişimleri ile oluşan açılar incelenecektir. Bunun
için aşağıdaki örnek durumu inceleyelim.
B
D
A
C
Müzikte bir çalgı aleti olarak kullanılan
üçgen çalgının iç kısmına şekildeki gibi
metalden yeni bir bölme yapılmak isteniyor. Bu yeni bölmenin köşe noktası olan D
nin, köşeleri A, B ve C ile gösterilen üçgen
çalgının kenarlarına eşit uzaklıkta olması
isteniyor. Oluşan D açısının ölçüsü ile A
açısının ölçüsü arasındaki ilişkiyi bulalım.
Üçgen çalgı köşeleri olan A, B, C noktaları ile
bir ABC üçgeni oluşturalım.
D noktası ABC üçgeninin kenarlarına eşit uzaklıkta olduğundan iç teğet çemberinin
merkezi ve dolayısıyla D noktası aynı zamanda ABC üçgeninin iç açıortaylarının kesim
noktasıdır.
%
%
m (W
C)
m (V
B)
dir.
ve m (DCB) =
Buna göre m (DBC) =
2
2
DBC üçgeninde iç açıların ölçüleri toplamı 180° ve
%
m (V
B) m ( W
C)
m (BDC) +
+
= 180° olduğundan
2
2
%
m (V
B) + m ( W
C)
m (BDC) = 180° ... (*) olur.
2
ABC üçgeninde m (W
A) + m ( V
B) + m ( W
C) = 180° olduğundan
m (V
B) + m ( W
C) = 180° - m (W
A) ... (**) dir.
A) değeri (*) de yerine yazarsak
(**) eşitliğindeki 180° – m (W
%
m (V
B) + m ( W
C)
180° - m (W
A)
m (BDC) = 180° = 180° olduğundan
2
2
%
m (W
A)
m (BDC) = 90° +
elde edilir. D açısının ölçüsü A açısının ölçüsünün yarısına 90°
2
eklenerek bulunur. Benzer şekilde üçgenin diğer açıortaylarının oluşturduğu açılar da
bulunabilir.
794
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
Aşağıdaki tabloda bu ilişkiler sunulmuştur.
ABC üçgeninde [BD] ve [CD] iç açıortaylar olmak üzere
B
%
m (W
A)
dir.
m (BDC) = 90° +
2
D
A
C
ABC üçgeninde [BT] ve [CT] dış açıortaylar olmak üzere
T
%
m (W
A)
dir.
m (BTC) = 90° 2
B
C
A
ABC üçgeninde [BS], B açısına ait dış
açıortay ve [CS], C açısına ait iç açıortay
olmak üzere
%
m (W
A)
dir.
m (BSC) =
2
A
S
D
B
C
1
Yandaki ABC üçgeninde [AI] ve [CI] sırasıyla A ve C açılarına ait
iç açıortaylardır.
%
%
m (CBA) = 70° ise m ( CIA ) değerini bulalım.
A
B 70°
I
C
%
%
m (CBA)
[AI] ve [CI] iç açıortaylar ve m ( CIA ) = 90° +
olduğundan
2
%
70°
m ( CIA ) = 90° +
= 90° + 35° = 125° elde edilir.
2
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
795
Bölüm
4.3
Üçgenin Yardımcı Elemanları
2
A
75°
C
30°
%
m ( IAB ) = 75°
%
m (BAC) = 30°
70°
55° B
%
m (CBA) = 70° ve
%
m ( ABI ) = 55° ise
%
m ( ICB ) kaç derece olduğunu bulalım.
I
E
75°
A
75°
C
30°
70°
55° B
55°
D
I
Yandaki şekilde
Yandaki gibi E ∈ [CA ve D ∈ [CB olacak şekilde E ve D
noktaları belirleyelim.
%
%
%
m ( EAI ) + m ( IAB ) + m (BAC) = 180° olduğundan
%
%
%
%
m ( EAI ) = 75° ve m ( DBI ) + m ( IBA ) + m (ABC) = 180°
%
eşitliğinden m ( DBI ) = 55° bulunur.
Dolayısıyla [AI] ve [BI], ABC üçgeninde sırasıyla A ve
B açılarının dış açıortayları olur.
Bir üçgende iki dış açıortay ve diğer köşeye ait bir iç
açıortay bir noktada kesiştiklerinden [CI], ABC üçgeninde C açısına ait iç açıortay olur.
Bir üçgenin iç açılarının ölçüleri toplamı 180° olduğundan,
%
%
%
%
m (ACB) + m (CBA) + m (BAC) = 180° eşitliğinden m (ACB) = 80° olur.
%
%
80°
m (ACB)
=
= 40° bulunur.
[CI] açıortay olduğundan m ( ICB ) =
2
2
796
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Açıortay
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
3.
Yandaki şekilde
F noktası ABC
üçgeninin iç
teğet çemberinin merkezi ve E
noktası ise dış
teğet çemberlerden birinin
merkezidir.
P
Aşağıdaki şekillerden hangilerinde D noktasının
A açısının açıortayı üzerinde olduğu kesinlikle
söylenebilir?
a.
b.
E
3
R
5
D
2
A
E
F
D
E
5
A
A
F
c.
E
F
T
B
Buna göre aşağıda soru işareti
ile gösterilen
ifadeleri bulunuz.
K
H
C
G
6
D
A
6
a.
AK
AB
=
KC
?
PA
?
=
PB
BC
b.
E
2.
Aşağıdaki ifadelerin önlerindeki boşluğa doğru
olanlar için “D”, yanlış olanlar için “Y” yazınız.
a.
(. . . . ) Dar açılı bir üçgende iç teğet çemberin merkezi
üçgenin içindedir.
b.
4.
B
6
(. . . . ) Dik üçgende üçgenin iç teğet çemberinin merkezi üçgenin hipotenüsü üzerindedir.
c.
(. . . . ) Geniş açılı üçgende üçgenin iç açıortayları aynı
noktada kesişmezler.
ç.
(. . . . ) Üçgenin iç teğet çemberinin merkezi daima üçgenin iç bölgesindedir.
d.
(. . . . ) Bir üçgenin üç tane dış teğet çemberi vardır.
A
O
C
D
E
13
F
Yandaki şekilde
%
[OC, AOF nın
açıortayı olmak
üzere bu açıortay
üzerindeki D ve C
noktalarından
%
AOF nın kollarına
dikmeler çiziliyor.
|OB| = 6 cm, |OF| = 13 cm veriliyor.
Buna göre aşağıdaki ifadelerden doğru olanların
yanına “D”, yanlış olanların yanına “Y” yazınız.
a.
(. . . . ) |OE| = 6 cm
b.
(. . . . ) |OA| =13 cm
c.
(. . . . ) |EF| = 7 cm
ç.
(. . . . ) |AB| = 5 cm
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
797
Açıortay
KENDİMİZİ SINAYALIM
Alıştırmalar
1.
5.
Yandaki ABC
üçgeninde
A
8
D
|AB| = 16 br
6
C
16
12
α
B
9
6
|CH| = 8 br , |CE| = 3 br
|DC| = 6 br
%
m (ABD) = a
olduğuna göre |BE| değeri kaçtır?
6.
4
D
3.
D
Şekildeki ABC nde
A
Yandaki ABD
üçgeninde
D
5
7.
70°
I
C
4.
|BC| = 5 cm
%
olduğuna göre m^BICh kaçtır?
8.
F
C
B
olduğuna göre
|AB| · |DC| değeri kaçtır?
A
80°
A
C
3
B
D
4
C
Yukarıdaki ABC üçgeninde [AC] , FAD açısının açıortayı , |AB| = 6 cm , |AD| = 3 cm , |DC| = 4 cm
ise |BD| kaçtır?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
[AN] , A açısının iç açıortayı
[AC] , A açısının dış açıortayı
Şekildeki ABC
üçgeninde
A
|AD| = 4 cm
D
798
C
%
%
m (ACB) = 40° ise m (ANC) kaçtır?
B nın açıortayı
[BD] , V
4
B
F
C
olduğuna göre |DC| kaçtır?
6
N
B
|AB| = 6 cm , |AC| = 9 cm , |BD| = 4 cm
B
A
40°
açıortayı
B
[AE] , BAC açısının iç açıortayı
ve [AH] ise dış
açıortayıdır.
H
|AD| = 8 br
Şekildeki
D
üçgeninde ABC
A nın
nde [AD] , W
A
8
C
E 3
B
|BC| = 12 br
%
olduğuna göre m (ABC) nin a cinsinden değeri nedir?
2.
Yandaki ABC
üçgeninde
A
I
I, B ve C açılarının iç açıortayların kesim noktası
%
ve m (BAC) = 70°
Yandaki şekilde I,
ABC üçgeninin, B
ve C açılarının dış
açıortaylarının
kesim noktası ve
%
m (BAC) = 80°
olduğuna göre
%
m ( BIC ) kaçtır?
Açıortay
KENDİMİZİ SINAYALIM
9.
3.
A
C
N
40°
A
B
I
K
110°
C
B
Şekildeki ABC üçgeninde N noktası ABC üçge-
Yukarıdaki şekilde I ve K noktaları sırasıyla ABC
üçgeninin iç teğet ve dış teğet çemberlerinin mer%
%
kezileri ve m ( CIB ) = 110° olduğuna göre m (CKB)
nin dış teğet çemberinden birinin merkezi ve
%
%
m (BNC) = 40° olduğuna göre m^BACh kaçtır?
Uygulama ve Problem Çözme
1.
A
12
D
9
C
F
4.
Yandaki
şekilde F
noktası ABC
üçgeninin iç
teğet çemberinin merkezi
A
B
6
|AB| = 9 br
Şekildeki üçgen biçimindeki düzenekte sarı ışık BC
kenarından mavi ışık ise AB kenarından içeriye dik
olarak girmekte ve eşit hızda ilerlemektedir. Işıklar
ilk kez kesiştiklerinde yeşil nokta oluşmaktadır.
|BC| = 6 br
AF
oranı kaçtır?
olduğuna göre
FE
2.
B
D
8
E
6
F
A
C
Şekildeki ABC
üçgeninde E
noktası iç teğet
çemberin
merkezi ve A,E
ve D noktaları
doğrusaldır.
|AB| = 8 br , |DF| = 6 br ve m ( V
B) = 90°
ise
AE
oranı kaçtır?
ED
C
|AC| = 12 br
E
B
kaçtır?
Düzenekte |AB| =15 cm, |BC| = 9 cm, |AC| = 12 cm
olduğuna göre [AC] kenarı üzerinde oluşan yeşil
ışık A ve C köşelerine kaç cm uzaklıktadır?
5.
A
I
B
N
C
9
Şekilde I, ABC
üçgeninin iç teğet
çemberinin
merkezi ve A, I, N
doğrusal olmak
üzere
|AB| + |AC| = 15 cm
|BC| = 9 cm
AI
oranı kaçtır?
olduğuna göre
IN
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
799
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında bir üçgenin ağırlık merkezini (üçgenin sınırladığı bölgenin ağırlık merkezi) nasıl belirleyeceğimizi ve ağırlık merkezinin üçgenin kenarortaylarıyla olan ilişkisini inceleyeceğiz.
Araç ve Gereçler: Karton kâğıt, makas, kalem, cetvel.
Adım 1
Bir kartona üçgen çiziniz ve makasla kesip çıkarınız.
Adım 2
Kaleminizin arka düz kısmı ile üçgeni zemine paralel olacak şekilde dengeye getiriniz.
Adım 3
Üçgen dengede iken kalemin üçgene değdiği noktayı G olarak işaretleyiniz.
A
Adım 4
Üçgenin köşelerini A, B, C olarak isimlendiriniz. Cetvelinizi kullanarak üçgenin köşeleri ile G noktasından geçen doğrular çiziniz. Bu doğruların üçgenin
kenarlarını kestiği noktaları D, E, F ile gösteriniz.
G
B
800
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
F
D
E
C
MATEMATİK ATÖLYESİ
Adım 5
Cetvelinizi kullanarak üçgenin AB, BC ve AC kenarlarında oluşan doğru parçalarının uzunluklarını belirleyiniz ve aşağıdaki tabloda uygun boşluklara yazınız.
[AB] kenarı
|AD| = . . . . . . .
|DB| = . . . . . . .
[BC] kenarı
|BE| = . . . . . . .
[AC] kenarı
|EC| = . . . . . . .
|CF| = . . . . . . .
|FA| = . . . . . . .
Adım 6
Tabloya göre üçgenin AB, BC ve AC kenarlarında oluşan doğru parçalarının uzunlukları arasındaki ilişkiyi açıklayınız.
Adım 7
Cetvelinizi kullanarak G noktasının, üçgenin A, B ve C köşeleri ile D,E,F noktalarına olan uzaklıklarını ölçünüz. Elde
ettiğiniz sonuçları aşağıdaki tabloya yazınız.
G noktasının köşe noktalarına uzaklığı
G noktasının D, E, F noktalarına olan uzaklığı
Oranlar
|AG| = . . . . . . .
|GE| = . . . . . . .
AG
= .......
GE
|BG| = . . . . . . .
|GF| = . . . . . . .
BG
= .......
GF
|CG| = . . . . . . .
|GD| = . . . . . . .
CG
= .......
GD
Tabloya göre G noktasının üçgenin köşelerine olan uzaklıkları ile kenarlarına olan uzaklıklarının oranı arasındaki ilişkiyi
açıklayınız.
....................................................................................................................................................................................................
....................................................................................................................................................................................................
Sonuç
Yaptığınız işlemler sonunda üçgenin ağırlık merkezine ilişkin olarak belirlemiş olduğunuz özellikleri açıklayınız.
....................................................................................................................................................................................................
....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
801
Bölüm
4.3
Üçgenin Yardımcı Elemanları
Neler Öğreneceğiz?
•
4. 3. 2. Üçgende Kenarortay
Üçgenin kenarortaylarının kesim
noktası ve kenarortayla ilgili
özellikleri
Başlarken
Anadolu’nun en eski camilerinden biri olan Sivas
Ulu Camii, minaresinin eğikliği ile dikkat çekmektedir. Caminin minaresi kendi eksenine göre 25°
eğik durumdadır. Her yıl eğilmeye devam eden
minarenin yıkılmaması için yenileme çalışmaları
yapılmaktadır. Minarenin eğilmesine karşın henüz
yıkılmamasının nedeni ağırlık merkezidir. Binalarda ağırlık merkezinin en uygun noktada oluşturulması binanın her türlü yük altında daha dayanıklı
olmasını sağlamaktadır.
Anahtar Terimler
•
Kenarortay
•
Ağırlık merkezi
Önceki konularımızda bir üçgenin açıortaylarını ve bu açıortayların sahip olduğu temel
özellikleri öğrendik. Bu konumuzda üçgenin diğer bir yardımcı elemanı olan kenarortayı ve temel özelliklerini öğreneceğiz.
Sembol ve Gösterimler
•
Va
•
G
Bir üçgende, bir köşeyi karşısındaki kenarın orta
noktasına birleştiren doğru parçasına, üçgenin o
kenarına ait kenarortayı denildiğini öğrenmiştik.
Yandaki şekilde ABC üçgeninin BC kenarına ait
AD kenarortayı çizilmiştir.
A
B
Bunu biliyor muydunuz
D
C
ABC üçgeninin a, b, c kenarlarına ait kenarortayların uzunlukları genellikle Va, Vb ve Vc
ile gösterilir.
Yapmış olduğunuz atölye çalışmasında bir üçgenin ağırlık merkezi ile ağırlık merkezinin üçgenin kenarortaylarıyla olan ilişkilerini belirlediniz. Aşağıdaki teorem bir üçgenin
kenarortaylarının bir noktada kesiştiğini göstermektedir.
Teorem
A
D
Kule yapan çocukların yaptıkları kulenin yıkılmaması
için ağırlık merkezini doğru
ayarlamaları gerekir.
Bir üçgenin kenarortayları bir noktada
kesişir.
F
G
B
802
E
C
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Kenarortay
İspat
Bunu biliyor muydunuz
Verilenler: ABC bir üçgen; [AE], [BF], [CD] sırasıyla BC, AC ve AB kenarlarına ait kenarortaylar
İstenenler: [AE] ∩ [BF] ∩ [CD] = {G}
BC ve AC kenarlarına ait AE ve BF kenarortaylarını çizelim.
A
Bu kenarortaylar G noktasında kesişsin.
F
G
B
E
C
E ve F noktalarını birleştirelim. [EF] orta taban olAB
duğundan [EF] // [AB] ve EF =
dir.
2
Bu durumda A. A. benzerlik kuralına göre
A
F
G
B
D
E
Sivas Ulu Cami’nin minaresi
25° lik bir eğriliğe sahip olmasına karşın yıkılmamaktadır. Bunun nedeni minarenin
ağırlık merkezinin düşey
izdüşümünün, minarenin
yer ile temas alanının içinde
kalmasıdır. Eğer önlem
alınmaz ve minare eğrilmeye
devam ederse, rüzgâr vb. dış
kuvvetlerin etkisiyle minarenin ağırlık merkezi minarenin
yer ile teması alanlarının
dışına taşacak ve minare bu
nedenle yıkılabilecektir.
C
D
AGB + EGF ve
AG
AB
=
= 2 dir.
GE
EF
A
Şimdi de ABC üçgeninde BC ve AB kenarlarına
ait AE ve CD kenarortaylarını çizelim. Bu kenarortaylar G’ noktasında kesişsin.
D
G’
B
E
C
Bunu biliyor muydunuz
D ve E noktalarını birleştirelim. [DE] orta taban
A
AC
dir.
2
Bu durumda A. A. benzerlik kuralına göre
olduğundan [DE] // [AC] ve DE =
D
G’
B
D
E
C
D
AG'C + EG'D ve
AG'
AC
=
= 2 dir.
G'E
ED
Planörün düzgün uçabilmesi için ağırlığın planörün
kanatlarına eşit dağılabilmesi
gerekir. Bu yüzden planöre
binecek olan pilot, planörün
ağırlık merkezinde bulunmalıdır.
AC ve AB kenarlarına ait kenarortaylar, BC kenarına ait kenarortayı aynı oranda böldüğü
için G ve G’ noktaları çakışıktır. Bu nedenle üçgenin kenarortayları bir noktada kesişir.
Yukarıdaki teorem üçgenin kenarortaylarının bir noktada kesiştiğini göstermektedir.
İspattan da görülebileceği gibi bu nokta üçgenin kenarortaylarını belli bir oranda bölmektedir. Aşağıdaki sonuç bu durumu açıklamaktadır.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
803
Bölüm
4.3
Üçgenin Yardımcı Elemanları
Sonuç
Anahtar Bilgi
Kenarortayların kesim
noktası niçin üçgenin ağırlık
merkezidir?
Bir üçgenin kenarortaylarının kesim
noktasına üçgenin ağırlık merkezi
denir. Ağırlık merkezi üçgenin kenarortaylarını 2’ye 1 oranında böler.
A
Bildiğiniz gibi bir doğru
parçasının orta noktası bu
doğru parçasının denge
noktasıdır.
D
n
2m
B
A
2k
G
m
k
F
2n
E
C
BG
CG
AG
=2,
= 2 dir.
=2,
GF
GD
GE
1
Yandaki şekilde
C
B
D
C
G noktası ABC üçgeninin ağırlık merkezi
|AG| = (4x – 2) br
Bir ABC üçgeninin sınırladığı
bölge şekilde de görüldüğü
gibi [BC] ye paralel doğru
parçalarıyla doldurulabilir.
Bu doğru parçalarının denge
noktaları ABC üçgeninin [BC]
kenarına ait kenarortayını
oluşturur. Bu nedenle ABC
üçgeninin ağırlık merkezi
bu kenarortay üzerinde olur.
Benzer durum diğer kenarortaylar için de geçerlidir.
O halde üçgenin ağırlık
merkezi bu kenarortayların
kesim noktasıdır.
D
|GD| = (x + 3) br
G
olduğuna göre |AD| nu bulalım.
A
B
G noktası, ABC üçgeninin ağırlık merkezi olduğundan
AG
= 2 dir.
GD
4x - 2
= 2 orantısından x = 4 br olarak bulunur. |AD| = |AG| + |GD| olduğunx+3
dan |AD| = 4x – 2 + x + 3 = 5x + 1 ve buradan |AD| = 5 · 4 + 1 = 21 br olur.
Buradan
2
Yandaki ABC üçgeninde
C
[AD] ∩ [BF] = {G}
|AF| = |FC|
F
3
G
2
D
|CD| = |DB|
|GD| = 2 cm
A
B
|GF| = 3 cm
olduğuna göre AGB üçgeninin çevresinin tam sayı olarak en az ve en
çok kaç cm olacağını bulalım.
804
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Kenarortay
|AF| = |FC| , |CD| = |BD| ve [AD] ∩ [BF] = {G} olduğundan G noktası ABC nin ağırlık merkezidir.
G noktası ABC üçgeninin ağırlık merkezi olduğundan
|GD| = 2 cm ise |AG| = 2 · |GD| = 4 cm ve |GF| = 3 cm ise |BG| = 2 · |GF| = 6 cm olur.
AGB üçgeninde üçgen eşitsizliğine göre, 6 – 4 < |AB| < 6 + 4 ve 2 < |AB| < 10 yazılır.
AGB üçgeninin çevresi kenar uzunluklarının toplamı olduğundan,
D
2 + 4 + 6 < AB + 4 + 6 < 10 + 4 + 6 ve 12 < Ç (ABC) < 20 bulunur.
144444Çevre
2444443
O halde AGB üçgeninin çevresi tam sayı olarak en az 13 cm ve en fazla ise 19 cm olarak
bulunur.
3
Yandaki şekilde G noktası ABC üçgeninin ağırlık
merkezidir.
A
G ∈ [AD] ve [BG] , B açısının açıortayıdır.
6
G
B
D
x
C
|AB| = 6 br
olduğuna göre |DC| = x değerini bulalım.
G noktası ABC üçgeninin ağırlık merkezi ve G ∈ [AD] olduğundan [AD], BC kenarına ait
kenarortay olup
GA
= 2 dir.
GD
[BG], B açısının açıortayı olduğundan ABD üçgeninde İç Açıortay Teoremine göre,
BA
GA
eşitliği yazılabilir.
=
BD
GD
Buradan
6
= 2 eşitliğinden |BD| = 3 br bulunur.
BD
[AD] kenarortay olduğundan |BD| = |DC| dir.
Dolayısıyla |DC| = x = 3 br elde edilir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
805
Bölüm
4.3
Üçgenin Yardımcı Elemanları
4
Yandaki şekilde
A
G noktası ABC üçgeninin ağırlık merkezidir.
T
2
K
[KL] ∩ [AD] = {T}
L
|TG| = 2 cm
G
B
D
C
olduğuna göre |AD| nu bulalım.
Anahtar Bilgi
|AT| = x cm olsun.
A
A
D
3k
K
k
2k
B
L
T
2
K
M
x
Benzer üçgenlerin karşılıklı kenar uzunlukları oranAL
AT
tılı olduğundan
=
olur.
AD
AC
L
G
G
N
C
B
Üçgenin ağırlık merkezi ile
orta tabanın kenarortay
üzerinde ayırdığı uzunluklar
köşeden başlamak üzere 3,1
ve 2 sayılarıyla orantılıdır.
D
C
1
x
=
ve |AD| = 2x elde edilir.
AD
2
5
|LG| = k
Yandaki şekilde
A
|GN| = 2k
G noktası ABC üçgenin ağırlık merkezi
4x
H ∈ [AC] ve [GH] // [BC] dir.
|AH| = 4x
H
G
x+6
B
C
Anahtar Bilgi
A
k
B
Bu orantıdan
|AD| = |AT| + 2 + |GD| eşitliğinden |GD| = x – 2 olarak bulunur. ABC üçgeninde G noktası
ağırlık merkezi olduğundan |AG| = 2|GD| ve x + 2 = 2 · (x – 2) eşitliğinden x = 6 cm elde
edilir. |AD| = 2x = 2 · 6 = 12 cm olarak bulunur.
|AL| = 3k
2k
D
[KL] // [BC] olduğundan ATL + ADC dir.
A
M
4x
G
G
C
B
Üçgenin herhangi bir kenarortayı üzerinde alınan bir
nokta, kenarortay uzunluğunu 2’ ye 1 oranında bölüyorsa
bu nokta ağırlık merkezidir.
H
x+6
D
C
|HC| = x + 6
olduğuna göre |AC| nu bulalım.
BC kenarına ait AD kenarortayını çizelim.
AG
G noktası ağırlık merkezi olduğu için,
= 2 dir.
GD
[GH] // [BC] olduğundan Temel Orantı Teoremine
AG
AH
=
eşitliği yazılabilir.
göre,
GD
HC
4x
Bu eşitlikten,
= 2 ve x = 6 cm elde edilir.
x+6
|AC| = |AH| + |HC| = 5x + 6 = 5 · 6 + 6 = 36 cm olarak
bulunur.
806
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgende Kenarortay
İnceleyelim
6
Üçgenin ağırlık merkezinden
yararlanarak dörtgenlerin
ağırlık merkezlerini belirleyebiliriz. Bunun için aşağıdaki
etkinliği yapabilirsiniz.
Yandaki ABC üçgeninde
A
[CF] , AB kenarına ait kenarortay
F
E
5
3
6
K
|CK| = 6 br
C
Bir kartona ABCD dörtgeni
çizip makasla kesiniz.
|KF| = 3 br
D
|KE| = 5 br
B
ise |BK| nu bulalım.
CK
6
= = 2 olduğundan K noktası ABC üçgeninin ağırlık merkezi
[CF] kenarortay ve
KF
3
C
A
olur. K noktası ağırlık merkezi olduğundan [BE] , AC kenarına ait kenarortay ve
B
BK
BK
= 2 ve |BK| = 10 br olarak bulunur.
= 2 dir. Buradan
5
KE
Cetvelinizi kullanarak ABCD
dörtgeninin [AC] nı çizerek
dörtgeni iki üçgene ayırınız.
Bu üçgenlerin ağırlık merkezlerini bularak G1 ve G2 ile
gösteriniz.
7
A
Yandaki şekilde
D
G noktası ABC üçgeninin ağırlık merkezi
%
m (BGC) = 130°
G
G1
|BG| = |AC|
130°
C
B
A
%
ise m (AGB) değerini bulalım.
C
G2
B
[BG] nı uzatarak AC kenarını kestiği noktayı D ile
isimlendirelim. [BD] kenarortay ve G ağırlık
BG
merkezi olduğundan, GD =
dir.
D
2
G
D, [AC] nin orta noktası olduğundan
130°
AC
ve |BG| = |AC| olduğundan,
AD = DC =
C
2
B
|GD| = |AD| = |DC| elde edilir.
%
%
%
m (BGC) + m (CGD) = 180° olduğundan m (CGD) = 50° dir. GDC üçgeni ikizkenar üç%
gen ve üçgenin iç açı ölçüleri toplamı 180° olduğundan m (CDG) = 80° bulunur.
%
%
%
ADG ikizkenar üçgeninde m (DGA) + m (GAD) = m (CDG) = 80° olduğundan
%
%
%
%
%
m (DGA) = 40° dir. m (BGC) + m (CGD) + m (DGA) + m (AGB) = 360° olduğundan
%
%
130° + 40° + 50° + m (AGB) = 360° dir. Bu eşitlikten m (AGB) = 140° olarak bulunur.
Benzer şekilde [BD] nı çiziniz
ve aynı işlemleri yapınız.
Oluşan bu iki üçgenin ağırlık
merkezini G3 ve G4 ile gösteriniz.
A
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
D
A
G4
G3
C
B
[G1G2] ve [G3G4] doğru
parçalarının kesim noktasını
belirleyiniz. Elde ettiğiniz
nokta dörtgenin ağırlık
merkezidir.
807
Üçgende Kenarortay
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
3.
1.
Aşağıda verilen boşlukları uygun ifadelerle tamamlayınız.
a.
Üçgenin ağırlık merkezi üçgenin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
kesim noktasıdır.
b.
Yandaki şekilde G
noktası ABC
üçgeninin ağırlık
merkezidir.
A
E
K
F
|AD| = 12 cm
G
Bir üçgende ağırlık merkezi kenarortayları . . . . . . . . . . . . . . . . .
oranında böler.
B
D
C
olduğuna göre |KG| kaçtır?
4.
Alıştırmalar
1.
D
Yandaki şekilde
G noktası ABC
üçgeninin
ağırlık merkezi
A
D
3x
5x +
G
A
2
B
C
B
Yukarıdaki ABC üçgeninde
|DG| = 3x
|BE| = |EC| , |AF| = 4 br , |FE| = 2 br , |FD| = 3 br
ise |CF| kaçtır?
G
B
E
K
D
C
808
|AD| = 18 cm ise
|KD| kaçtır?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
[AD] , ABC üçgeninde
BC kenarının kenarortayı
A
E
G noktası ABC
üçgeninin, K
noktası BGC
üçgeninin ağırlık
merkezleridir.
F
2
C
5.
A
4
E
|CG| = 5x + 2 olduğuna göre |CD| kaçtır?
2.
F
3
6
C
15
D
[AB] // [DE]
|AB| = 15 cm
|EC| = 6 cm
B
ise |AE| + |ED| kaçtır?
Üçgende Kenarortay
KENDİMİZİ SINAYALIM
Uygulama ve Problem Çözme
1.
Yandaki şekilde G
noktası ABK
üçgeninin, M
K noktası CDK
üçgeninin ağırlık
merkezidir.
A
C
12
E
M
G
F
D
3.
K
F
E
G
C
D
B
[AD] ve [BE],
ABC üçgeninin
sırasıyla BC ve
AC kenarlarına
ait kenarortaylarıdır.
[FE] // [BC]
|AD| = 18 cm
[AB] // [CD] // [EF]
ve |AB| = 12 br
B
A
ise |KG| kaçtır?
olduğuna göre;
a.
|CG| ve |CD| kaçtır?
b.
|EF| kaçtır?
2.
Yandaki şekilde G
noktası ABC üçgeninin
ağırlık merkezi ve ABC
üçgeninin kenarortaylarının uzunlukları
toplamı 45 cm olduğuna göre,
A
G
B
4.
E
[EG] // [AC]
2
|EG| = 2 cm
G
B
C
C
|AG| + |BG| + |CG| kaçtır?
G noktası ABC üçgeninin
ağırlık merkezi
A
ise |AC| kaçtır?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
809
Üçgende Kenarortay
KENDİMİZİ SINAYALIM
5.
Yanda verilen şekilde
D, E ve F noktaları ABC
üçgeninin kenarlarının
orta noktalarıdır.
A
D
F
7.
Yandaki şekilde G
noktası ABC üçgenin, F
noktası BGC üçgeninin
ağırlık merkezleri, A, G,
F, D ve B, F, E noktaları
doğrusal
A
B
G
E
8
C
B
D
Çevre (ABC)
Buna göre
D
Çevre ( DEF)
oranı kaçtır?
2
D
olduğuna göre |AG| + |FE| kaçtır?
E
4
B
K
F
D
G
C
|FG| = |GD|
A, K, F noktaları doğrusal ve |FK| = 4 cm ise
|AK| kaçtır?
810
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Yandaki ABC
üçgeninde [BD] ve
[CE] ABC üçgeninde
kenarortaydır.
A
[BD] ve [CE] , ABC
üçgeninin sırasıyla
AC ve AB kenarlarına ait kenarortaylardır.
A
|BF| = 8 cm
C
8.
6.
|FD| = 2 cm
E
F
E
3x x+2 K
6 D
|BK| = x + 2
G
|GD| = 3x – 6
B
F
C
olduğuna göre |KG| kaçtır?
Üçgende Kenarortay
KENDİMİZİ SINAYALIM
9.
[BE] ve [CD] ABC
üçgeninde sırasıyla
AC ve AB kenarlarına ait kenarortaylar
A
D
6
4 G
L
E
F
H
F
|AF| = |FE|
D
G
[DF] // [AC]
C
Yandaki şekilde G
noktası ABC üçgeninin ağırlık
merkezi
A
[EF] // [AB]
K
B
12.
B
|GL| = 4 cm
E
|DG| = 6 cm
C
olduğuna göre |BL| + |GK| kaçtır?
10.
ise HD =
ABC üçgeninde
A
D iç teğet çemberin merkezi
12
AC
olduğunu gösteriniz.
6
2
3
16
A
E ağırlık merkezi
[DE] // [BC]
D E
B
13.
C
|DE| =
D
2
cm
3
|AB| = 12 cm
|AC| = 16 cm
ise |BC| kaçtır?
4
E
H
G
F
B
2
L
d
C
Yukarıdaki şekilde G noktası ABC üçgeninin ağırlık
merkezidir. G noktasından geçen bir d doğrusu
üçgenin AB ve AC kenarlarını sırasıyla E ve F noktalarında kesiyor.
[AH] ⊥ d , [BD] ⊥ d , [CL] ⊥ d
11. ABC üçgeninin kenarlarının orta noktaları D, E, F
olsun.
ABC üçgeninin kenarortaylarının uzunlukları
toplamı 60 cm ise D, E, F noktalarını köşe kabul
eden DEF üçgeninin kenarortaylarının uzunlukları
toplamı kaç cm’dir?
|BD| = 4 br , |CL| = 2 br
olduğuna göre |AH| kaçtır?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
811
MATEMATİK ATÖLYESİ
Bu atölye çalışmasında bir üçgenin kenar orta dikmelerinin ve yüksekliklerinin kesim noktalarını inceleyeceğiz.
Araç ve Gereçler: Dinamik geometri yazılımı
A
E
Adım 1
Bir ABC üçgeni çiziniz. ABC üçgeninin kenarlarının orta noktalarını bulunuz. Bu
noktalardan ABC üçgeninin kenarlarına dikmeler çiziniz. (Aynı işlemi yazılımın
“orta dikme” özelliğini kullanarak da yapabilirsiniz.)
B
H
D
F
C
Adım 2
Çizdiğiniz kenar orta dikmelerinin kesim noktasını gözlemleyiniz. Tüm kenarların orta dikmeleri aynı noktada mı kesişmektedir?
.....................................................................................................................................................................................................
Adım 3
ABC üçgenini köşe noktalarından tutarak sürükleyiniz. Üçgenin kenar orta dikmelerinin kesişimlerini gözlemleyerek
aşağıdaki soruları cevaplandırınız.
a.
Oluşan dar açılı üçgenler için kenar orta dikmeler tek noktada mı kesişmektedir?
b.
Oluşan dik üçgenler için kenar orta dikmeler tek noktada mı kesişmektedir?
c.
Oluşan geniş açılı üçgenler için kenar orta dikmeler tek noktada mı kesişmektedir?
ABC üçgeninin kenar orta dikmelerinin kesim noktası her zaman üçgenin iç bölgesinde midir? Açıklayınız.
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
Sonuç
Yukarıda yapmış olduğunuz çalışmalar sonucunda üçgenin kenar orta dikmelerinin kesim noktası için elde ettiğiniz
ilişkileri yazınız.
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
812
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
MATEMATİK ATÖLYESİ
Adım 4
A
Yazılımın ilgili özelliğini kullanarak çizdiğiniz kenar orta dikmeleri gizleyiniz. Şimdi de ABC üçgeninin her bir kenarına ait yükseklikleri çiziniz.
F
B
F
C
Adım 5
Çizdiğiniz yüksekliklerin kesim noktasını gözlemleyiniz. Bütün kenarlara ait yükseklikler aynı noktada mı kesişmektedir?
.....................................................................................................................................................................................................
Adım 6
ABC üçgenini köşe noktalarından tutarak sürükleyiniz. Üçgenin yüksekliklerinin kesişimlerini gözlemleyerek aşağıdaki
soruları cevaplandırınız.
a.
Oluşan dar açılı üçgenler için yükseklikler tek noktada mı kesişmektedir?
b.
Oluşan dik üçgenler için yükseklikler tek noktada mı kesişmektedir?
c.
Oluşan geniş açılı üçgenler için yükseklikler tek noktada mı kesişmektedir?
ABC üçgeninin yüksekliklerinin kesim noktası her zaman üçgenin iç bölgesinde midir? Açıklayınız
Sonuç
Yukarıda yapmış olduğunuz çalışmalar sonucunda üçgenin yüksekliklerinin kesim noktası için elde ettiğiniz ilişkileri
yazınız.
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
.....................................................................................................................................................................................................
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
813
Bölüm
4.3
Üçgenin Yardımcı Elemanları
4. 3. 3. Üçgenin Kenar Orta Dikme ve Yükseklikleri
Neler Öğreneceğiz?
•
Üçgenin kenar orta dikmelerinin
kesim noktasını
•
Üçgenin çevrel çemberini
•
Üçgenin yüksekliklerinin kesim
noktasını
Başlarken
Çekül, bir ipin ucuna küçük bir ağırlık bağlayarak
düz, dikey bir çizginin elde edilmesi amacıyla
oluşturulmuş bir araçtır. Marangozlar ve inşaat
ustaları çekül kullanarak yaptıkları mobilya ya da
duvarların zemine dik ve düz bir yüzey oluşturup
oluşturmadığını belirler.
Anahtar Terimler
•
Orta dikme
•
Çevrel çember
•
Yükseklik
•
Diklik merkezi
Bir doğru parçasına orta noktasından dik olan doğruya, orta dikme denir. Yandaki şekilde CP doğrusu
[AB] nın orta dikmesidir.
C
B
Aşağıdaki çizim çalışmasında pergel-cetvel kullanılarak verilen bir doğru parçasının orta dikme doğrusunun nasıl çizilebileceği açıklanmıştır.
P
A
Doğru Parçasının Orta Dikmesini Çizme
Geometrik Çizim
2. Adım
1. Adım
A
•
Sembol ve Gösterimler
B
Cetvelinizi kullanarak bir [AB] çiziniz.
A
B
ha
Pergelinizi |AB| nin yarısından fazla
olacak şekilde açınız ve merkezi A olan
şekildeki gibi iki yay çiziniz.
4. Adım
3. Adım
C
C
A
B
A
D
D
Pergelin açıklığını bozmadan merkezi
B olan bir önceki yayları kesen iki yay
daha çiziniz. Yayların kesim noktalarını
C ve D olarak isimlendiriniz.
814
B
C ve D noktalarını cetvelle birleştiriniz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenar Orta Dikme ve Yükseklikleri
Yukarıdaki geometrik çizim çalışması sonucunda pergel ve cetvel kullanarak [AB] nın
orta dikmesini çizdiniz. Çizmiş olduğunuz CD doğrusunun niçin [AB] nın orta dikmesi
olduğunu açıklayalım:
C ve D noktalarını yandaki şekildeki gibi A ve B noktaları ile birleştirelim.
C
A
Yaylar çizilirken pergelin açıklığı değiştirilmediğinden
|AC| = |AD| = |BC| = |BD| olur.
B
Bu durumda |BC| = |AC| , |BD| = |AD| ve |CD| = |CD|
D
D
D
olduğundan CAD , CBD (K. K. K. Eşlik Kuralı) dir.
Benzer üçgenlerin karşılıklı açıları eş olduğundan
% %
ACD , BCD dir.
C
A
ACB üçgeni ikizkenar ve [CD] , C açısının açıortayı
olduğundan hem kenarortay hem de yüksekliktir.
B
Dolayısıyla bu doğru [AB] nın orta dikmesidir.
D
Yukarıdaki çizimde A ve B merkezli yaylar çizilirken pergelin açıklığı bozulmadığından
A ve B noktalarına eşit uzaklıktaki iki nokta (C ve D noktaları) belirlenmiştir. Bu ilişki bir
doğru parçasının kenar orta dikmesi üzerinde alınan her noktanın doğru parçasının
uç noktalarına eşit uzaklıkta olduğunu göstermektedir. Buna göre kenar orta dikmeler
için aşağıdaki sonucu yazabiliriz.
Sonuç
Bir doğru parçasının orta dikmesi üzerinde
alınan her nokta, doğru parçasının uç
noktalarına eşit uzaklıktadır.
C
B
P
Eğer CP, doğrusu [AB] nın orta dikmesi ise
|CA| = |CB| dir.
A
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
815
Bölüm
4.3
Üçgenin Yardımcı Elemanları
1
Şekilde DC doğrusu [AB] nın orta dikmesi ve
A
|DA| = 2x + 14
|DB| = 4x + 2
C
2x + 14
olduğuna göre |BD| nu bulalım.
D
4x + 2
B
Bir doğru parçasının orta dikmesi üzerinde alınan her nokta doğru parçasının uç noktalarına eşit uzaklıkta olduğundan |DB| = |DA| dır.
Buradan 4x + 2 = 2x + 14 eşitliğinden x = 6 ve |BD| = 4x + 2 = 4 · 6 + 2 = 26 olarak bulunur.
Bir doğru parçasının orta dikmesi üzerinde alınan her noktanın doğru parçasının uç
noktalarına eşit uzaklıkta olduğunu öğrendik. Aşağıdaki sonuç bunun karşıtının da
doğru olduğunu belirtmektedir.
Sonuç
Bir doğru parçasının uç noktalarından eşit
uzaklıkta bulunan her nokta, bu doğru parçasının orta dikmesi üzerindedir.
D
K
A
B
Eğer |DA| = |DB| ise D noktası [AB] nın orta
dikmesi üzerindedir.
2
A
Yandaki şekilde
8
B
|AB| = |AC| = 8 cm
8
5
E
|BE| = |EC| = 5 cm
5
C
12
|CD| = 12 cm
A, E, D noktaları doğrusal
olduğuna göre |BD| değerini bulalım.
D
816
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenar Orta Dikme ve Yükseklikleri
Bir doğru parçasının uç noktalarından eşit uzaklıkta bulunan bir nokta bu doğru parçasının orta dikmesi üzerinde olduğundan [AE], [BC] nın orta dikmesidir. Bu durumda
[AE] ⊥ [BC] dir. A, E, D noktaları doğrusal olduğundan D noktası da [BC] nın orta dikmesi
üzerindedir. Dolayısıyla |DC| = |DB| = 12 cm dir.
Matematik atölyesinde bir üçgeninin kenar orta dikmelerinin tek noktada kesiştiğini
belirlediniz. Aşağıdaki teorem ulaştığımız bu sonucu ifade etmektedir.
Teorem
A
Bir üçgenin kenar orta dikmeleri tek
noktada kesişir.
L
N
K
C
H
B
İspat
Verilenler: ABC bir üçgen, N, L ve H noktaları kenarların orta noktaları
İstenen: Kenar orta dikmeler bir noktada kesişir.
A
L
K
C
H
B
Dikkat
Bir üçgenin kenar orta dikmeleri üçgenin köşelerinden
geçmek zorunda değildir.
Şimdi de K noktasını A ile birleştirelim. Benzer sebeplerden dolayı |AK| = |KC| ... (**) dir.
A
L
N
K
B
Bir ABC üçgeninin AC ve BC kenarlarına ait kenar orta
dikmelerini çizelim. “Bu orta dikmelerin kesim noktası K
olsun. K noktasını üçgenin B ve C köşelerine birleştirelim. Bir doğru parçasının orta dikmesi üzerinde alınan
her nokta doğru parçasının uç noktalarına eşit uzaklıkta
olduğundan |KB| = |KC| ... (*) dir.
H
C
(*) ve (**) dan |AK| = |BK| olur. Bu durumda K noktası, A
ve B noktalarına eşit uzaklıkta olur. Bir doğru parçasının
uç noktalarına eşit uzaklıktaki her nokta doğru parçasının orta dikmesi üzerinde olduğundan K noktası [AB]
nin orta dikmesi üzerindedir. Bu ise üçgenin kenar orta
dikmelerinin bir noktada kesiştiğini gösterir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
817
Bölüm
4.3
Üçgenin Yardımcı Elemanları
Yukarıdaki ispattan aşağıdaki sonuca ulaşılabilir.
Sonuç
A
Bir üçgenin kenar orta dikmelerinin kesişim noktası üçgenin köşe noktalarından
eşit uzaklıktadır.
L
N
K
B
C
H
Üçgenin kenar orta dikmelerinin kesim noktası üçgenin köşelerine eşit uzaklıkta
olduğundan, merkezi üçgenin kenar orta dikmelerinin kesim noktası olmak üzere
üçgenin köşe noktalarından bir çember geçer. Bu çembere üçgenin çevrel çemberi
ve bu çemberin merkezi olan kenar orta dikmelerinin kesim noktasına da üçgenin
çevrel çemberinin merkezi denir.
Aşağıdaki çizim çalışmasında verilen bir üçgenin çevrel çemberinin dinamik geometri
yazılımı kullanılarak nasıl çizilebileceği adım adım gösterilmiştir.
Üçgenin Çevrel Çemberini Çizme
Geometrik Çizim
2. Adım
1. Adım
A
A
B
B
O
C
Bir dinamik geometri yazılımı kullanarak bir ABC üçgeni çiziniz. Yazılımın
“orta dikme” özelliğini kullanarak ABC
üçgeninin kenar orta dikmelerini çiziniz. Orta dikmelerin kesim noktasını “O”
olarak isimlendiriniz.
O
C
Yazılımın “Çember” özelliğini kullanarak
merkezi O olan ve üçgenin köşelerinden
geçen bir çember çiziniz. “
3. Adım
Üçgeni köşelerinden tutarak hareket ettiriniz. Üçgenin farklı durumları için çevrel
çemberi inceleyiniz.
818
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenar Orta Dikme ve Yükseklikleri
Yukarıdaki çizim etkinliğinde bir üçgenin çevrel çemberinin merkezinin her zaman üçgenin iç bölgesinde bulunmadığını gözlemlediniz. Farklı üçgen çeşitlerine göre çevrel
çemberin merkezi üçgenin içinde, üzerinde ya da dışında olmaktadır. Çevrel çemberin
merkezi, üçgen eğer dar açılı ise üçgenin iç bölgesinde, dik açılı ise üçgenin kenarında
ve geniş açılı ise üçgenin dışındadır.
İnceleyelim
Kâğıt katlayarak da bir
üçgenin çevrel çemberinin
merkezini belirleyebilirsiniz.
Bunun için;
1. Makasla bir üçgen kesiniz.
A
F
E
K
B
K
A
A
E
F
K
E
D
B
D
C
Dar açılı üçgen
F
C
B
Dik üçgen
D
C
2. Bir köşesinden tutup diğer
köşesiyle birleşene kadar
üçgeni katlayınız.
Geniş açılı üçgen
3
Şekildeki ABC üçgeninde
A
|AD| = |DC|
|BE| = |EC|
D
F
[BD] ⊥ [AC]
12
B
E
3. Kâğıdı tekrar açınız ve iz
yerini kaleminizle çiziniz.
[AE] ⊥ [BC]
C
|CF| = 12 br
olduğuna göre |FD| değerini bulalım.
4. Diğer kenarlar için de aynı
işlemleri tekrarlayınız.
|AD| = |DC| , |BE| = |EC| olduğundan F noktası ABC üçgeninin ağırlık merkezidir.
Ayrıca [AE] ⊥ [BC] , [BD] ⊥ [AC] ve D ve E noktaları bulundukları kenarların orta noktaları olduğundan [AE] ile [BD] sırasıyla [BC] ve [AC] kenarlarının kenar orta dikmeleridir.
5. Çizdiğiniz doğru parçalarının kesim noktası çevrel
çemberin merkezidir.
Bu durumda F noktası aynı zamanda ABC üçgeninin çevrel çemberinin merkezidir.
O halde F noktası ABC üçgeninin köşelerine eşit uzaklıktadır.
Bu durumda |CF| = |BF| = 12 br olur.
F noktası ağırlık merkezi olduğundan |BF| = 2|FD| ve buradan |FD| = 6 br olarak bulunur.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
819
Bölüm
4.3
Üçgenin Yardımcı Elemanları
4
Dikkat
A
F
yükseklik
B
Kocatepe İlkokulu, Fevzi Çakmak Ortaokulu
ve Zafer Lisesinin bulunduğu bir alana yeni
bir pastane açılmak istenmektedir. Açılacak
bu pastanenin her üç okula da eşit mesafede olması planlanmaktadır. Yandaki şekilde
her bir okulun bu alandaki konumları
verilmiştir.
C
E
D
kenar orta dikme
Buna göre pastanenin nereye yapılması
gerektiğini çizimle gösterelim.
Bir üçgenin yükseklikleri ile
kenar orta dikmelerinin aynı
doğrular olduğu düşüncesi
çok yaygın karşılaşılan bir
kavram yanılgısıdır.
Alandaki her üç binayı A, B ve C noktalarıyla
gösterirsek bir ABC üçgeni elde ederiz.
Pastanenin yapılması istenen yer üçgenin her
üç köşesinden de eşit uzaklıkta olmalıdır.
Buna göre bir üçgenin kenar orta dikmelerinin kesim noktası üçgenin köşelerinden eşit
uzaklıkta olduğundan ABC üçgeninin kenar
orta dikmelerinin kesim noktası olan G
noktası, pastanenin yapılacağı yerdir.
G Pastanenin yeri
B
D
A
F
E
C
Üçgenin Yüksekliği
Bir üçgenin bir köşesinden karşı kenara veya karşı kenarın uzantısına indirilen dik
doğrunun, karşı kenarda kestiği nokta ile köşeyi birleştiren doğru parçasına, üçgenin o kenarına ait yüksekliği denir.
A
A
B
820
D
6AD@ = 6BC@
Dar açılı üçgen
C
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
D
B
6AD@ = 6CB
Geniş açılı üçgen
C
Üçgenin Kenar Orta Dikme ve Yükseklikleri
Aşağıdaki çizim çalışmasında pergel-cetvel kullanılarak bir doğruya dışındaki bir noktadan dik doğrunun nasıl çizilebileceği açıklanmıştır.
Bir Doğruya Dışındaki Bir Noktadan Dik Doğru Çizme
Geometrik Çizim
1. Adım
2. Adım
A
A
d
d
C
D
Kâğıdınıza bir d doğrusu çiziniz ve bu
doğrunun dışında bir A noktası alınız.
Pergelinizi d doğrusunu iki noktada
kesecek şekilde açınız. Pergelinizin sivri
ucunu A noktasına koyarak d doğrusunu kesen iki yay çiziniz. Yayların d doğrusunu kestiği noktaları C ve D olarak
isimlendiriniz.
4. Adım
3. Adım
A
d
C
D
A
H
d
C
D
H
Pergelinizi |CD| nun yarısından fazla
olacak şekilde açınız. Pergelinizin sivri
ucunu D noktasına koyarak merkezi D
olan bir yay ve bu yayı kesen merkezi C
olan bir başka bir yay çiziniz. Bu yayların
kesim noktasını H olarak isimlendiriniz.
A ile H noktalarını birleştiren bir doğru
çiziniz. Çizdiğiniz AH doğrusu d doğrusuna dik bir doğrudur.
Yukarıdaki çizim çalışmasında bir doğruya dışındaki bir noktadan dik bir doğru çizdiniz. Benzer şekilde bir doğruya üzerindeki bir noktadan da dik doğru çizilebilir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
821
Bölüm
4.3
Üçgenin Yardımcı Elemanları
Üçgenin kenar orta dikmeleri ve yükseklikleri ile ilgili matematik atölyesinde üçgenin
yüksekliklerinin bir noktada kesiştiğini keşfetmiştiniz. Aşağıda üçgenin yüksekliklerinin niçin bir noktada kesiştiği açıklanmıştır.
İnceleyelim
Bazı üçgenlerde kenar orta
dikmeler ve yükseklikler
aynıdır. Bu üçgenler hangileridir?
Bir ABC üçgeni alalım. Öyle bir DEF üçgeni çizelim ki
DEF üçgeninin kenar orta noktaları ABC üçgeninin
köşe noktaları olsun.
D
C
Bir üçgenin kenar orta dikmelerinin bir noktada kesiştiğini biliyoruz. A, B ve C noktaları DEF üçgeninin
K
kenarlarının orta noktaları olduğundan ABC üçgeE
ninin kenarları DEF üçgeninin kenarlarına daima
B
F
paraleldir. Bu nedenle DEF üçgeninin kenar orta dikmeleri aynı zamanda ABC üçgeninin yükseklikleridir. Buradan ABC üçgeninin yüksekliklerinin bir noktada kesiştiği elde edilir.
A
Matematik Tarihi
Sonuç
A
E
F
Bir üçgenin yükseklikleri aynı noktada kesişir.
Bu noktaya üçgenin diklik merkezi denir.
H
Yandaki şekilde H diklik merkezidir.
Euler 1765’te herhangi bir
üçgenin diklik merkezinin,
çevrel çemberinin merkezinin ve ağırlık merkezinin doğrusal olduğunu
göstermiştir.
B
D
C
Yukarıdaki sonuca göre bir üçgenin yükseklikleri bir noktada kesişmektedir. Bu noktanın
yeri üçgenin açılarının türüne göre değişiklik göstermektedir. Aşağıdaki şekilde farklı üçgenlerin yüksekliklerinin kesim noktasının yeri gösterilmiştir.
Siz de bir dinamik geometri yazılımı yardımıyla
bir üçgen çiziniz ve bu üçgende bu üç özel noktayı
gözlemleyiniz.
A
D
F
DeVilliers (2005). A Generalization of the nine-point circle
and Euler line.
B
A
A
D
D
H
B
C
B
E
C
C
Pythagoras
Dar açılı üçgen
(F noktası diklik merkezi)
Dik üçgen
(B noktası diklik merkezi)
E
H
F
Geniş açılı üçgen
(F noktası diklik merkezi)
Yukarıdaki şekillerden diklik merkezi üçgen dar açılı ise üçgenin iç bölgesinde, dik açılı
ise dik kenarların kesiştiği köşede ve geniş açılı ise üçgenin dış bölgesinde olduğu görülmektedir.
822
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Kenar Orta Dikme ve Yükseklikleri
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme
1.
3.
A
E
Aşağıda verilen ifadelerden doğru olanlara “D”
yanlış olanlara “Y” harfi koyunuz.
G
D
(. . . . ) Üçgende iki yüksekliğin kesim noktasından üçüncü
yükseklik de geçer.
B
(. . . . ) Geniş açılı üçgenlerde diklik merkezi üçgeninin iç
bölgesindedir.
F
C
Şekilde ABC üçgeninin yükseklikleri gösterilmektedir. Ahmet ABC üçgeninde D noktasının ağırlık
BD
2
merkezi ve
= olduğunu iddia etmektedir.
BE
3
Ahmet’in bu iddiasını niçin doğru olmayacağını
açıklayınız.
(. . . . ) Üçgenin herhangi bir kenarının kenar orta dikmesi,
daima bu kenarın karşısındaki köşeden geçer.
(. . . . ) Bir eşkenar üçgenin kenarortayları ve yükseklikleri
aynı noktada kesişir.
(. . . . ) Herhangi bir üçgenin kenar orta dikmeleri ve yüksekliklerinin kesim noktası daima aynıdır.
Alıştırmalar
1.
H
4x – 2
A
2x + 4
A
1
HG ⊥ [AC]
|CD| = |AD| dir.
D
2.
Yandaki şekilde
G
3
C
C
Verilenlere göre |HC| değerini bulunuz.
2
B
Şekilde A, B, C noktalarında bulunan 1, 2, 3 numaralı oyuncular sırasıyla BC, AC ve AB kenarlarına en
kısa yoldan koşmak istiyorlar. A, B ve C noktalarının
oluşturduğu üçgen dar açılı üçgendir.
2.
Yandaki şekilde
A
x
Bu koşu esnasında üç oyuncu da aynı anda çarpıştıklarına göre çarpıştıkları yer neresidir?
10
O
y
B
C
O noktası ABC
üçgeninin kenar
orta dikmelerinin kesim
noktası olduğuna göre x ve y
değerleri kaçtır?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
823
Üçgenin Kenar Orta Dikme ve Yükseklikleri
KENDİMİZİ SINAYALIM
3.
Uygulama ve Problem Çözme
Yandaki şekilde
A
C
B
A
F
E
40°
Yandaki şekilde C
noktası ADB
üçgeninin diklik
merkezi
B
°
α
1.
20
H
H noktası ABC
üçgeninin hem
diklik merkezi
hem de çevrel
çemberin merkezidir.
C
Buna göre m (W
C) = a kaç derecedir?
[CF] , ACB açısının açıortayı,
[AB] ⊥ [CE]
D
%
m (ABC) = 40°
%
m (DAC) = 20°
%
ise m (FCE) kaç derecedir?
4.
Aşağıdaki üçgenlerde a ve β değerlerini bulunuz.
40°
b.
A
10°
E
F
B
α
D
C
70°
L
E
H
β
D
F
Yandaki şekilde D
noktası ABC üçgeninin diklik
merkezi
%
[AF] , BAC nın
açıortayı
A
M
K
H
2.
D
15°
a.
B
E
70°
F
C
[AC] ⊥ [DE]
%
%
m (DAF) = 15° , m (CDE) = 70° ise
%
m (DCB) kaç derecedir?
5.
Aşağıdaki üçgenlerde P noktası ABC üçgeninin diklik merkezi olduğuna göre a ve β değerleri kaçtır?
a.
b.
A
P
3.
20
H
°
P
B
α
Yanda verilen
ABC üçgeninde
A
30
50°
°
C
L
[AD] ⊥ [BC] dir.
10°
%
m (HCD) = 20°
β
M
B
60°
D
20°
C
%
ise m (ACH) kaç derecedir?
824
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
%
m (DBH) = 60°
%
m (HBA) = 10°
Üçgenin Kenar Orta Dikme ve Yükseklikleri
KENDİMİZİ SINAYALIM
4.
A
7.
A
[DE] // [AK]
E
10
B
Yandaki şekilde
F
C
D
K
%
%
m (BCD) = m (DCK)
E
F
K
%
m (BDC) = 90°
|AC| = 10 cm
|DE| = 8 cm
ise |BC| nu bulalım.
B
D
C
Bir üçgende diklik merkezinin yükseklikleri ayırdığı
parçaların uzunluklarının çarpımının sabit, yani
ABC üçgeninin diklik merkezi K ise
|KF| · |KC| = |KE| · |KB| = |KD| · |KA|
olduğunu gösteriniz.
5.
Yandaki ABC
üçgeninde H
diklik merkezidir.
A
5
E
4 H
|AE| = 5 br
12
C
|EB| = 12 br
|HE| = 4 br
B
ise |CH| kaç birimdir?
6.
İki yüksekliği eş olan üçgenin ikizkenar üçgen
olduğunu gösteriniz.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
825
Bölüm
4.3
Üçgenin Yardımcı Elemanları
BÖLÜM ÖZETİ
Açıortay
Bir üçgende iki dış açıortay ile bu dış açılara komşu olmayan iç açının açıortayı tek noktada kesişir. Bu nokta
üçgenin dış teğet çemberlerinden birinin merkezidir. Bir
üçgenin üç tane dış teğet çemberi vardır.
B
F
G
H
A
Açıortayların Oluşturduğu Açılar
E
C
B
Bir açının açıortayı üzerindeki herhangi bir nokta, açının
kollarına eşit uzaklıktadır.
D
İç Açıortay Teoremi
A
A
C
C nın iç açıortayları
ABC üçgeninde [BD], V
B nın ve [CD], W
%
m (W
A)
dir.
olmak üzere m (BDC) = 90° +
2
C
N
B
D
Bir üçgende, herhangi bir iç açıortayın karşı kenar üzerinde ayırdığı parçaların uzunlukları oranı, diğer iki kenarın
uzunlukları oranına eşittir. [AN], A açısının açıortayı olmak üzere
BN
AB
=
dir.
NC
AC
B
C
A
Bir üçgenin iç açıortayları üçgenin kenarlarından eşit
uzaklıkta bir noktada kesişir. Bu noktaya üçgenin iç teğet
çemberinin merkezi denir.
Dış Açıortay Teoremi
C nın dış açıortayları
ABC üçgeninde [BD], V
B nın ve [CD], W
%
m (W
A)
dir.
olmak üzere m (BDC) = 90° 2
A
E
A
D
B
C
B
E
Bir ABC üçgeninde, A açısının dış açıortayı BC kenarının
uzantısını E noktasında kesiyorsa,
826
EB
AB
=
dir.
EC
AC
C
ABC üçgeninde [BE], B açısına ait dış açıortay ve [CE], C
%
%
m (BAC)
açısına ait iç açıortay olmak üzere m (BEC) =
dir.
2
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Üçgenin Yardımcı Elemanları
Üçgende Kenarortay
A
Bir üçgenin kenarortayları aynı noktada kesişirler. Bu
noktaya üçgenin ağırlık merkezi denir. Bu nokta kenarortayı 2:1 oranında böler.
E
B
D
M
F
Üçgende Orta Dikme ve Yükseklik
C
C
Bir üçgenin kenar orta dikmeleri, üçgenin köşe noktalarından eşit uzaklıkta bulunan bir noktada kesişir. Bu
noktaya üçgenin çevrel çemberinin merkezi denir.
B
P
A
Eğer CP, [AB] nın orta dikmesi ise |CA| = |CB| dir.
A
E
F
B
C
H
B
A
D
D
C
Bir üçgenin yükseklikleri de bir noktada kesişir. Bu noktaya üçgenin diklik merkezi denir.
Bir doğru parçasının uç noktalarından eşit uzaklıkta bulunan bir nokta, bu doğru parçasının orta dikmesinin
üzerindedir.
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
827
Bölüm 4. 3. Üçgenin Yardımcı Elemanları
BÖLÜM DEĞERLENDİRME
1.
Yandaki şekilde
B
F
D
B
E
A
[BE // [CD
%
%
m (EBA) = m (ABC)
%
[CB] , ACD nın
açıortayı ve
5.
A
10
C
D
ise |BD| nun alabileceği tamsayı değerlerinin toplamı kaç birimdir?
C
G
6.
40
°
A
15
C
D
E
H
D
B
A
|CB| = 6 br
B
%
ise m (BAC) kaç derecedir?
3.
F
Yukarıdaki şekilde [AB // [DE
%
%
[DH] , EDF nın [AG] , BAC nın açıortayı ve
%
%
m (AGH) = 40° ise m (ACF) kaç derecedir?
10
6
B
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
C
E
A nın
Yukarıdaki ABC ve BDC üçgenlerinde [AE] , W
W
ve [DE] , D nın açıortaylardır.
|AC| = 15 br , |AB| = 6 br , |DC| = 10 br
ise |DB| kaç birimdir?
828
Yandaki ABC
üçgeninde
%
[CD] , ACB nın
açıortayı
|CA| = 10 br
6
°
D
E
F
%
m (ACB) = 30°
30
%
m (HFG) = 70°
%
ise m (ACD) kaç derecedir?
Yandaki şekilde
B
[AG] , [DH] açıortay
H
D
%
m (AEF) kaç derecedir?
A
[AB // [DE
G
C
2.
Yandaki şekilde
C
[AB // [CD
%
[AE] , BAC nın
%
[CE] , DCA nın
%
[EF] AEC nın
açıortayı ise
A
E
4.
Bölüm 4. 3. Üçgenin Yardımcı Elemanları
BÖLÜM DEĞERLENDİRME
7.
Yandaki ABC
üçgeninde B, E, D
ve C noktaları
doğrusaldır.
%
C [AE] , BAD nın
açıortayı
%
%
m (CBA) = m (DAC)
A
B
D
E
10.
B
Yandaki şekilde
D
C
9
G
5
B
D, F, G noktaları
doğrusal
|EG| = 9 br , |GB| = 5 br ise |AD| kaç birimdir?
Yandaki ABC
üçgeninde
A
B
D
C
|BC| = 6 br
|AB| + |AC| = 12 br
Yandaki şekilde
[AD] ⊥ [DC]
8
20
B
C
E ∈ [AD] ∩ [BC] dir.
[AE] ve [CE] açıortaylardır.
E
|AC| = 20 br
D
|AB| = 8 br
ise |CD| kaç birimdir?
12. A
Yandaki şekilde
A nın
[AD] , W
açıortayı
|AB| = |DC|
F
A
%
[DE] , ADG nın
açıortayıdır.
[EB] // [AD]
9.
11.
[DE] ⊥ [AB]
F
E
D 3 C
|BD| = 6 br , |DC| = 3 br ise |CF| kaç birimdir?
ise |DE| kaç birimdir?
A
6
Yandaki ABC üçgeninde [AD] , A açısının iç açıortayı, [AF] , A açısının dış açıortayıdır.
|CA| – |CD| = 3 br
8.
E
A
%
%
m (ECA) = m (DCB)
dir.
E
4
3
C
5
D
|CE| = 3 br
B
|EB| = 4 br
|CB| = 5 br
ise |AE| kaç birimdir?
ise |BD| kaç birimdir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
829
Bölüm 4. 3. Üçgenin Yardımcı Elemanları
BÖLÜM DEĞERLENDİRME
13.
Yandaki şeklide
A
16.
A, D ve E noktaları
doğrusaldır.
12
10
C
x+4
C
D
B
|BD| = 5 br
D
5
2x – 2
G
|AB| = 10 br
B
x
E
[AE] ∩ [BC] = {D}
6
Yandaki ABC
üçgeninde
A
E
D ve E noktaları sırasıyla BC
ve AB kenarlarının orta
noktalarıdır.
|DC| = 6 br
|GE| = x br , |CG| = x + 4 br , |AG| = 2x – 2 br
|AC| = 12 br
ise |GD| kaç birimdir?
ise |AD| · |DE| değerini bulunuz.
17. A
14.
Yandaki ABC
üçgeninde
A
F
E
B
G
8
D
|GE| + |GD| = 7 br
B
|EC| = 8 br
|AE| = |EB|
|BD| = |DC|
D
|FE| = 6 br
C
C
E
%
%
m (ABC) = m (ACF)
6
Yandaki ABC
üçgeninde
ise |AD| + |CE| kaç birimdir?
4|AF| = 3|AC|
ise |CD| kaç birimdir?
18.
15. B
Yandaki şekilde I,
ABC üçgeninin iç
teğet çemberinin
merkezidir.
12
C
I
G
F
6
H
J
F, J, D ve E noktaları doğrusal
4
D
A
8
E
[EF] // [CB]
|BC| = 12 br , |FJ| = 6 br , |JD| = 4 br , |DE| = 8 br
ise |AD| + |AJ| toplamı kaç birimdir?
830
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Yandaki ABC
üçgeninde
A
[BG] açıortay ve G
ağırlık merkezidir.
10
|AB| = 10 br
G
B
D
ise |DC| kaç birimdir?
C
Bölüm 4. 3. Üçgenin Yardımcı Elemanları
BÖLÜM DEĞERLENDİRME
19.
Yandaki şekilde
A
E
G
C
D
B
22.
G, ABC üçgeninin
ağırlık merkezidir.
46°
D
[BE] // [HF]
F
A
B
F
E
G
C
|GD| = |DF|
32
H
|HF| = 32 br
H
Yukarıdaki şekilde H noktası, ABC üçgeninin dışındadır. [HD] ⊥ [AB] , [HE] ⊥ [AC]
ise |BE| kaç birimdir?
|BD| = |DA| , |AE| = |EC|
%
%
m (FAG) = 46° ise m (GHF) kaç derecedir?
20.
A
D
23.
Yandaki şekilde O,
ABC üçgeninin
çevrel çemberinin
merkezidir.
A
α
B
E
C
A nın açıortaydır.
Yukarıdaki ABC üçgeninde [AE] , W
O
B
|AB| = |AD| = |DC| , |BC| = 15 br ise |ED| kaç birimdir?
25°
15°
C
%
%
m (OBC) = 15° , m (ACO) = 25°
%
ise m (BAO) = a kaç derecedir?
21.
Yandaki ABC üçgeninde G ağırlık
merkezidir.
A
K
F
E
[AD] ∩ [EF] = {K}
B
ise |AD| kaç birimdir?
Yandaki ABC
üçgeninin çevrel
çemberinin
merkezi O noktasıdır.
A
α
|KG| = 2 br
G
D
24.
C
B
35°
O
C
%
%
m (CBA) = 35° ise m (OAC) kaç derecedir?
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
831
Bölüm 4. 3. Üçgenin Yardımcı Elemanları
BÖLÜM DEĞERLENDİRME
25.
Yandaki ABC üçgeninde
H diklik merkezidir.
A
6
D
|AD| = 4 br
E
H
Yandaki ABC üçgeninde H diklik
merkezidir.
A
30°
4
28.
%
m (DAC) = 30°
|DB| = 8 br
C
8
%
m (FCB) = 20°
E
|AE| = 6 br
F
H
B
B
ise |EC| kaç birimdir?
20°
D
C
%
ise m (EBA) kaç derecedir?
26. A
E
4
C
6
H
D
6
Yandaki ABC
üçgeninde H diklik
merkezidir.
29.
Yandaki ABC
üçgeninde H diklik
merkezidir.
A
6
|BD| = |DC| = 6 br
|HE| = 2 br
|EC| = 4 br
2
E
H
B
3
B
ise |AB| kaç birimdir?
|CE| = 3 br
|AE| = 6 br
C
ise |BH| kaç birimdir?
27.
Yandaki ABC üçgeninde
H diklik merkezidir.
A
|AH| = 10 br
|HD| = 2 br
10
B
Yandaki ABC
üçgeninde H diklik
merkezidir.
A
|BH| = 4 br
E
4
30.
H
[HD] ⊥ [BC]
2
H
D
28
C
ise |HE| kaç birimdir?
°
B
D
%
ise m (CBA) kaç derecedir?
832
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
|BD| = |DC|
%
m (ACH) = 28°
C
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
ÜNİTE DEĞERLENDİRME – I
1.
Yandaki ABC
üçgeninde
A
3.
%
m^ABCh = 60°
%
m^ACBh = 40°
E
60°
B
α
20°
D
40°
C
A) 60
B) 70
C) 80
D) 90
A) 30
%
m^EDCh = 20°
%
%
%
m^BADh = m^DACh ise m^ADEh = a kaç derecedir?
Bir ABC üçgeninde A köşesinden çizilen yükseklik ile B köşesinden çizilen iç açıortay üçgenin
içinde yer alan H noktasında kesişmektedir.
%
%
m^AHBh = 110° ise m^BAHh kaç derecedir?
B) 40
C) 50
4.
D) 60
E) 70
A
E) 100
B
C
D
E
Aşağıdaki eşitliklerin hangisi sağlanırsa
O
O
ACB ile EDA üçgenleri eş olur?
A) |AC| = |BC|
B) |AB| = |DE|
D) |AC| = |CD|
2.
Yandaki
şekilde
A
x
[AB] ⊥ [BD]
C
B
B) 20
E) |AC| = |ED|
ABC ve DCE birer
dik üçgen
A
D
|AC| = |BC|
|DC| = |CE|
B
C
kaç derecedir?
D
A) 13
[AC] ⊥ [DC]
%
m^BDCh = 140°
%
m^BADh = x
5.
C) |BC| = |AE|
C) 27
D) 34
E) 40
E
olduğuna göre
A) 1
B)
1
2
| BD |
oranı nedir?
| AE |
C)
1
4
D) 2
E)
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
3
2
833
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
ÜNİTE DEĞERLENDİRME – I
6.
ABC ikizkenar üçgen ve |AB| = |AC| dir. Kenar uzunlukları birer tam sayı olmak üzere çevresi 24 cm
olan kaç farklı ABC üçgeni vardır?
A) 7
B) 6
C) 5
D) 4
9.
A
Şekildeki G,
ABC üçgeninin
ağırlık merkezi,
D
E) 3
E
[DE] // [BC] ve
G
|AD| = |EC|
B
7.
A
5
8
Yandaki şekilde
| AE |
oranı kaça eşittir?
| BD |
|AC| = 5 br
A) 1
B) 2
C) 3
olduğuna göre
D) 4
E) 5
|AB| = 8 br
C
E
C
4
|CD| = 4 br
x
|BE| = |EC| ise
D
B
|ED| = x in en
büyük tamsayı değeri kaçtır?
A) 7
B) 8
C) 9
D) 10
E) 11
10.
α
8.
x
|AB| = x
x
|BC| = y
E
D
B
B)
D)
834
y
+x
2
θ
C
y
–x
2
II. a = y
IV. a = x
C)
E)
I. x = β
III. x = θ
C
y
x+y
2
y
β
B
[DE] // [BC]
olduğuna göre |DE| nun x ve y cinsinden ifadesi nedir?
A)
d
ABC üçgeninde
%
%
m^ABDh = m^DBCh
A
Yandaki şekilde
ABC üçgeninin
AC ve BC
kenarlarını
kesen d doğrusu
çiziliyor.
A
x
+y
2
y–x
2
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Koşullarından hangisi veya hangileri tek başına
verilirse, şekilde daima benzer iki üçgen oluşur?
A) Yalnız IV
D) I, II, III
B) I ve IV
C) II ve III
E) I, II, IV
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
ÜNİTE DEĞERLENDİRME – I
11.
Şekildeki ABC
üçgeninde I,
üçgenin iç
I
teğet çemberiB
nin merkezi, K
ise dış teğet
C
K
T
çemberlerinden
birinin merkezidir. A, B, T
doğrusal olduğuna göre aşağıdaki ifadelerden
hangileri doğrudur?
A
I. A, I, K doğrusaldır.
13.
A
30°
B
D
75°
α
C
ABC bir üçgen
%
%
m^ABDh = m^DBCh
%
m^BACh = 30°
%
m^CADh = 75°
%
olduğuna göre m^BDCh = a kaç derecedir?
%
%
II. m^BICh + m^BKCh = 90° dir.
%
%
III. m^BICh > m^BKCh
A) 15
B) 20
C) 25
D) 30
E) 35
%
%
IV. m^ABIh + m^KBTh = 90° dir.
A) I, II ve III
B) I ve IV
D) I, III ve IV
C) III ve IV
E) I, II ve IV
14. A
3|AD| = 2|DC|
[AB] ⊥ [BC]
E
12.
[EF] ⊥ [DC]
x
A
D
F
7
6
C
%
%
m^ADEh = m^EDCh
|BC| = 10 br
10
B
B
C
8
Yukarıdaki resimde görüldüğü gibi A noktasından
ok yönünde hareket başlayan bir kişi [AB] ve [BC]
ye eşit uzaklıkta olan bir H noktasında durmak
istiyor.
olduğuna göre |EF| = x kaç br dir?
A) 2
B) 3
C) 4
D) 5
E) 6
Buna göre A dan ok yönünde kaç m yürümelidir?
A) 2
B) 2,5
C) 3
D) 3,5
E) 4
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
835
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
ÜNİTE DEĞERLENDİRME – II
1.
Yandaki
şekilde ABE
bir üçgen,
ABC eşkenar
üçgen, ADC
B
C
D
E
ve ADE ise
%
birer ikizkenar üçgen olmak üzere m^DAEh kaç
derecedir?
A
A) 35
B) 30
C) 25
D) 20
3.
ABC eşkenar
A
üçgen,
D
80°
B
H
F
|EB| = |BH|,
α
%
m^EDFh = 80°
C
olduğuna göre
E
%
m^DFCh = a kaç derecedir?
E) 15
A) 100
4.
B) 105
C) 110
D) 115
A
E) 120
D
F
E
2.
B
D
A
T
f
b
F
d
a
B
C
I. ha = hf
E
II. nA = Vf
Va, Vd a ve d kenarlarına ait kenarortay uzunlukları,
nB, nE B ve E açılarına ait açıortay uzunlukları ha:a
kenarına ait yüksekliğin uzunluğunu göstermek
üzere şekildeki ABC ve DEF üçgenleri için aşağıdakilerden hangileri daima doğrudur?
O
III. Va = Ve
IV. ha = nF
A) Yalnız I
O
O
O
B) I ve II
C) II, III ve IV
D) I, II ve IV
O
I. ABC , DEF ise Va = Vd
O
5.
II. nB = nE ise ABC , D EF
E) I ve IV
ABC üçgeninde
A
%
m^ADEh = 30°
%
%
m^ABC h = m^DCEh,
x
III. Va = ha ise ABC , ACB
IV. |AB| = |DE| , |AC| = |DF| ve bu üçgenlerin karşılıklı
O
O
herhangi birer açıları eş verildiğinde ABC , DEF
dir.
A) I ve III
D) I ve IV
B) II ve III
C) I, III ve IV
E) I, II ve III
30°
B
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
|AB| = |DC|,
E
|BD| = |EC|
D
C
%
olduğuna göre m^BADh = x kaç derecedir?
A) 50
836
T
ABC üçgeni ikizkenar, |AB| = |AC|, ABC ≅ FDE olduğuna göre aşağıdakilerden hangisi veya hangileri
doğrudur?
e
c
C
B) 45
C) 40
D) 35
E) 30
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
ÜNİTE DEĞERLENDİRME – II
6.
A
h
Yanda
verilenlere
göre en kısa
kenar
hangisidir?
D
70°
a
d
b
75°
B
c
A) h
60°
65°
80°
C
B) d
f
e
C) c
8.
E
D
C
A
Şekildeki
katlanabilir
merdiven uçları,
E ve F noktası
olan basamağından şekildeki gibi
katlanmış ve
diğer ucu yere
değdirilmiştir.
F
B
40°
E
D) b
E) a
A – B arası mesafe 300 cm olduğuna göre C – D
arası mesafe kaç cm’dir?
A) 180
7.
I
9.
II
A
B) 150
x
6
D
4
2
|KC| = |AD| = 6 br
K
A noktasından B noktasına gidecek biri I, II, III, IV
nolu yollardan gidince yürüyeceği mesafeler sırasıyla x, y, z, k br olduğuna göre x, y, z, k arasındaki
sıralama aşağıdakilerden hangileri olamaz?
I.
6
|DK| = 2 br
B
C
A) 5
B) 4
C)
II. y < z < x < k
10.
17
4
D)
11
2
E)
21
4
ABC üçgeninde
A
IV. y < z < k < x
|AD| = 12 br
V. x < y < z < k
A) Yalnız V
|KE| = 4 br
ise |AE| = x uzunluğunu bulunuz.
y<x<z<k
III. y < x < k < z
E) 50
%
%
m^CDAh = m^BEAh
E
IV
D) 75
Şekildeki ABC
üçgeninde,
A
B
III
C) 125
|DB| = 2br
12
B) III ve V
D) I, II ve IV
C) IV ve V
E) III, IV ve V
|BC| = 10 br
E
α
D
2
80°
B
|AE| = |EC| ve
10
C
%
m^ABCh = 80°
%
olduğuna göre m^ADEh = a kaç derecedir?
A) 20
B) 30
C) 35
D) 40
E) 50
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
837
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
ÜNİTE DEĞERLENDİRME – II
11.
ABC üçgeninde
A
14.
I. Ağırlık merkezi
%
m^ABDh = 30°
x
II. İç teğet çemberin merkezi
%
m^DBCh = 30°
30°
30°
III. Diklik merkezi
%
D
m^ACDh = 25°
25
°
25°
B
C
IV. Çevrel çemberin merkezi
%
m^DCBh = 25°
Yukarıdaki noktalardan hangileri daima üçgenin iç
bölgesindedir?
%
olduğuna göre m^DACh = x kaç derecedir?
A) 20
B) 25
C) 30
12.
A
D) 35
E) 40
A) I ve II
B) I ve IV
D) II ve IV
F
C) I, II ve III
E) I, III ve IV
15.
B
4
D
x
C
6
E
H I
Yandaki şekilde ABE bir üçgen B, A, F doğrusal
%
%
%
m^DAEh = 90° , m^BADh + m^CAEh = 90°
P G
|BD| = 4 cm , |CE| = 6 cm ise |DC| = x kaç cm’dir?
A) 1
13.
B) 2
C) 3
D) 4
A
6
H
G
B
D
2
x
C
3
E) 5
Yandaki
şekilde G
noktası ABC
üçgeninin
ağırlık merkezi
|GH| = 2 cm
|AD| = 6 cm
|DC| = 3 cm ve
%
%
m^ADHh = m^CDHh olduğuna göre |BC| = x kaç cm
dir?
A) 4
838
B) 6
C) 7
D) 8
E) 9
Ünite 4. Üçgenlerde Eşlik ve Benzerlik
Dar açılı üçgen şeklindeki düz bir alanın köşelerinde bulunan üç bisikletli, üçgenin iç bölgesinde
seçilecek bir bitiş noktasına doğru doğrusal bir yol
boyunca yarış yapacaklardır. Bitiş noktası P, G, H,
I noktalarından hangisi veya hangileri olursa üç
yarışmacı için de yarış pistinin uzunlukları kesinlikle
eşit olur?
(P: Çevrel çemberin merkezi, G: Ağırlık merkezi, H:
diklik merkezi, I: İç teğet çemberin merkezi)
A) Yalnız G
B) P ve G
D) P ve H
C) Yalnız P
E) I ve G
CEVAP ANAHTARI
3. Ünite: FONKSİYONLAR
Eğlenceli matematik soruları: 1. Bulmaca doldurma
Bölüm Adı: 3.1. Fonksiyon Kavramı ve Gösterimi
HAZIR MIYIZ?
1.a. 2x 1.b. y = 2x + 1 1.c. y = 3x + 1 1.ç. y = x2 2. x = 4, y = 10
4. AxB = {(1, 5), (1, 8),(2, 5), (2, 8),(3, 5), (3, 8)} 5. a = {1,4} B = {3,5,7} 6. 29 – 1
3x + 7
=8
2
x
12. 7 = 3x + 3 13. a, b, ç, d 14.a. – 2, – 1, 0, 1, 2 14.b. 7, 14, 21, 28, 35
2
14.c. 11, 17, 23, 29, 35 15.a. y = 3x + 1 15.b. y = 6x + 1 16.c. y = 2x – 5 16.10000, 40000
19. ( – 1, 4)
7. .( – 1,10), ( – 3,13), (5,1), (3,4), (1,7) 8. 7 9. 1 10. 18a + 4b 11.
Konu Adı: 3.1.1 Fonksiyon Kavramı
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.a. fonksiyon 1.b. tanım kümesi, değer kümesi 1.c. görüntü
kümesi 1.ç. bağımsız, bağımlı 4.a. fonksiyon 4.b. fonksiyon değil 1.c. fonksiyon değil
1. 4 tanesi fonksiyondur.
Alıştırmalar: 1. f(A) = {1, 8, – 6, – 13, – 20} 2. f(A) = {3, 5, 7, 9} 3. – 5/3 4 . 2 5. (14, 26]
6. ( – 7, – 1] 7. f( – 5) = – 22, f(7) = 38 8. f(3) = 36, f(6) = 60 9.a. 3x – 3 9.b. – 6x + 15
9.c 27x – 24 9.ç. 6x2 + 27 10.a. 3x – 3 10.b. 18x2 – 24x + 7 10.c. 2x2 + 4x + 1
10.d. 2x4 – 4x2 + 1 11.a. x2 + 6x + 10 11.b. x2 – 2x + 2 11.c. x2 – 12x + 37
11.d. x4 + 2x2 + 2 12.a. 4x2 – 5 12.b. x2 – 2x + 6 12.c. 16x2 + 48x + 31 12.ç. x4 – 2x2 – 4
13. [ – 19,31] 14. a = 2 15. c = – 17/2 16.a. 44 16.b. 8 16.c. 29 16.ç 5 17. f ve g eşit
fonksiyonlardır. 19. f ve g eşit fonksiyonlardır. 20.a. 12 20.b. 400 20.c. 2 20.ç. – 20
20.d. 24√2 20.e. 4π 21. I. Y = x + 7 II. Y = x – 4 III. Y = 2x IV. Y = 3x – 5
22. { – 7, – 3, – 1, – 6}, { – 44, – 86, – 98,16} 23. – 1/10
24. f(a) = 4a – 3 f(b + 1) = 4b + 1, f(2d) = 8d – 3 , f(3k + 1) = 12k + 1, f(c – 2) = 4c – 11
26.tanım kümeleri aynı olmadığından eşit fonksiyonlar değildir. 27. a = 4 28. Eşit
Fonksiyonlardır.
29. f (x + 1) =
f (x –1) =
2.
2x – 12
3x – 13
x – 11
x
x–24
, fa k =
, f ( 2x ) =
, f ( 3 x – 1) =
,
3
3
3
2
6
x – 13
x2
, f (x 2) =
–4 30. y = 2x – 3 31. b = – 11 32. d = 3/4
3
3
Konu Adı: 3.1.2 Birim, Sabit ve Doğrusal Fonksiyonlar
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.a. Birim fonksiyon. 1.b. sabit fonksiyon. 1.c. doğru. 2. d, d, d,
d, y, d 3.a. fonksiyon belirtmez, denklem belirtir. 3.b. fonksiyon belirtir. 3.c. fonksiyon
belirtmez, cebirsel ifadedir. 3.ç. Fonksiyon belirtir. 3.d. fonksiyon belirtmez, çember
denklemidir. 3.e. fonksiyon belirtir. 3.f. fonksiyon belirtir. 4. 1. fonksiyon değil 2. fonksix 2 x
yon belirtir 3. fonksiyon değil 5. f(x) = 5x, g(x) = a k –
+ 1 7. a = 1, b = 0
10
10
8. a = 2 9. f(1) = 1 10. 4 11. – 14 12. 89 13. 0 14. 5 15. doğrusal fonksiyon, sabit fonksiyon, birim fonksiyon. 16.a m = 4/3 17. a. f(x) = – 3x + 4 16.b – 11 16.c 28 16.ç – 3x + 1
1.a. A(3,2) 1.b. B(3, – 2) 1.c. C( – 3, 3) 1.ç. D( – 2, – 2) 2. A( – 2, – 3) 6. x = – 2, x = 2
7. x = – 2 8.x = 4 noktası 9. 2 12. y ∈ {2, 1, – 2, – 5} 13. x ∈ [0, 3] 14. y = – x + 1 doğrusunun
eğimi – 1, y = – 2x + 4 doğrusunun eğimi – 2, y = 2x + 4 doğrusunun eğimi 2, y = 3x – 6
doğrusunun eğimi 3 tür.
3.1. Bölüm Değerlendirme
Konu Adı: 3.2.1. Fonksiyon Grafiklerini Okuma ve Yorumlama
1.a. 5 1.b. – 3 1.c. 5 1.ç. 2a2 + 4a – 1 1.d. 2x4 – 3 1.e. 2x4 – 4x2 – 1
2. f : Z + → R, f(x) = x + 1/x , f(4) = 17/4 3. f : R – " R, f (x) = x +
1
,1
–17
, fc m =
x
4
4
6. A = {1, – 3/2,,5/2} 7. a = 5 8. f( – 1) = – 1, g(1) = – 1, f(1) = 1 – 2 = – 1, g( – 1) = – 3, f ve
g eşit fonksiyon değildir. 9. değer kümeleri eşit olmadığından fonksiyonlar eşit değildir.
10. eşit 11. eşit değil Değişken vardır(t) 12. 8 13. 35 14. 9/2 15. 6 16. –3
17. eşit değildir. x = 0 için g(0) = 1≠h(0) = –1 18. 2027/2 19. 17/2 20. –17
23. a. 6x + 1 23.b.13 23.c. 6x + 13 23.ç. 6x2 + 1 23.d. 6x2 – 11 23.e.6x2 – 12x + 7
24. – 31 25. f(x) = 5x – 1 f(x – 8) = 5x – 41 26. f(x) = 2x + 5 27. 32
Araştırma Soruları: 1.a. f(x) = ax + b ise b = 0 durumunda.
2. f(x) = ax + b ise f(x – y) = f(x) – f(y), a(x – y) + b = ax + b – ay – b, a(x – y) + b = a(x – y)
n
değeri lineer fonksiyonun eşitliğini sağlayan
olup eşit olmaz. 3. mx + n = 0 ⇒ x = –
m
değer dolayısıyla köktür. 4. Evet en az iki nokta bir doğru belirtir.
Bölüm Adı: 3.2 Fonksiyon Grafikleri
HAZIR MIYIZ?
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.a. x, y 1.b.grafik 1.c. tanım, değer 2.a. belirtir 2.b.belirtmez
2.c. belirtir 2.ç. belirtmez
Uygulama ve Problem Çözme: 1. f(A) = {6,10,12} 2. [1,4] 3. [2,5] 4. [ – 2, – 1/2] ∪ [1/2,2]
5. 4/3 6. 8 7. 3 8. – 10 9. 5 10. 0 11. a[ – 3,2]→[1,3] b.( – 1,2)→( – 1,3) şekilde ( – 1,1) noktası gösterilmeli 12.a. f:R→R 12.b.{0,1,3} 12.c.[0,3] 12.ç.{ – 1,0,1,2} 12.d.[ – 1,2] 13.a.
g:R→R 13.b. {0,1,3,4} 13.c. [3,4] 13.ç. [0,2] 13.d.{ – 3, – 2,0,1,2} 14.a.
x
–2
–1
0
1
2
y
19/12
11/12
1/4
–
5/12
–
15/12
17.a. 5,3,1, – 1, – 3 17.b. 2,1,0, – 1, – 3/2 18. fonksiyon, fonksiyon, değil, değil, değil 19.
a. değil 19.b. fonksiyon 19.c.fonksiyon 19.ç.fonksiyon 19.d. fonksiyon 19.e.değil 19.f.
fonksiyon 19.g. fonksiyon
Konu Adı: 3.2.2. f(x) = xn Biçimindeki Fonksiyonların Grafikleri
10.c.4x – 3 10.ç.6x – 5 10.d.x – 3 10.e.2 x2 – 3 11.a.1 11.b.2 c.(0,∞) 12.a.9 12.b. 3
KENDİMİZİ SINAYALIM
12.c.7 ve 16 13. a = 5/2 14.n = 4 15.c = – 5 16. t = – 10 17. n = 5 18. – 10 19.1/30 20.7
Kavrama ve Muhakeme: 1. f ve h için n negatif çift tam sayı g ve k da ise n negatif tek
tamsayıdır. 2. g, f, h 3.a. – 5,1,5 3.b. – 4,9, – 1 3.c. [1,4] ç.[ – 2,6] 4.a. 4,0,4 4.b. a nın bir
gerçek sayısı yok b = 0, c = 1 4.c. [1,16] 4.ç. [1,3] veya [ – 1, – 3] 5.a. – 1,0,8 5.b. – 2,1,3
5.c. [ – 8,8] 5.ç. [1,2] 6.a. – 1/3, – 1,1,1/3,1/4 6.b.1, b nin gerçek değeri yok 6.c.[1/2,1]
6.ç. [–1, –1/2]
Konu Adı: 3.2.3 Doğrusal Fonksiyonlarla İlgili Uygulamalar
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.4 2.a.2 2.b.1/3 2.c.2/3 2.ç.tanımsız 2.d.0 3.a.1 3.b. – 4/3
3.c.0 3.ç.tanımsız 4. – 5/2< – 2/3<1<2<3 5. c 6.a. – 10
6.b. f:[0,90]→[0,900], f(x) = – 10x + 900 6.c. – 10 6.ç.90 sn 7.a. f:N→N,f(x) = 900x + 2000
7.b.15 500
Konu Adı: 3.2.4. y = f(x) Fonksiyonunu Grafiği ile f(x) = 0 Denklemi Arasındaki
İlişki
21.1/6 22. ( – ∞ – 1/2]∞(1/2,∞) 23.b. (5,21) 24. (0,9) 26.Evet, çünkü değer kümesinde
boşta eleman yok 27.b. Harcanan benzin miktarı = Alınan yol/10
28.a. (f(x) = 3000 + 600.x) b.21 000 29.a. 6 km 29.b. 24 30.a.3 31. ne örten ne de
birebir: i, v örten:ii, vii bire bir: iii hem bire bir hem örten: iv, iv 32. f ne birebirdir, ne de
örtendir, g birebir değildir ama örtendir, h birebir ancak örten değildir, m birebir ve
örtendir. 33.a.9 33.b.11 33.c.6a – 5 33.ç.10x – 5 34.a.45 34.b.9a2 + 12a
35. f(x) = x + 2 36.3x + 4y = 12 37.25 38. – 4 veya 6 39.5 40.a.{ – 1,1} 40.b.{ – 1/2,2}
40.c.[ – 1/2,0) 40.ç.(0,1/2] 41.5 42.a. – 1 b.x4 + 3 c. – 2x2 – 1 45.a.{2,6,8} 45.b.[0,2]
45.c.[2,6] 46.a.{ – 4,0,3} 46.b.{ – 3, – 2, – 1} 46.c. ( – 4, – 3] 47.a.{ – 2,2,0,1,4}
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1. 4,16 2.a. ( – 9/5, – 3/5) 2.b. ( – 7/5,6/5)
3. f(x) = x + 1, g(x) = 5 – x 4.a. – 1,4 4.b. – 2 4.c. – 3/2, 4.ç. – 2,1,3 4.d.0 4.e. – 2/3 6.
6 7.a. x = 1/2, y = – 1 7.b.x = – 1, y = 1, 7.c. x = 3, y = – 2, 7.ç. x = 3, 7.d. y = 1 8. c = 0
9. – 1,1,3 10. 2 11. 2 12. 1
47.b.{ – 2, – 1,0.,1,2} 47.c.[ – 3, – 1]U[1,3] 47.ç.[1,2]
Konu Adı: 3.2.5 Parçalı Tanımlı Verilen Fonksiyonlar ve Grafikleri
Ünite Testi – III
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 4.a = 1, b = – 3 5.a. p(t) = 25 + 20(t – 1) 6.a.124 6.b. birinci
tarife p(t) = 25 + 0,33(t – 250) ikinci tarife p(t) = 5 + 0,1t ikinci tarife daha uygun.
Ünite Testi – II
1. B 2. D 3. C 4. A 5. C 6. E 7. B 8. A 9. A 10. C 11. B 12. C 13. C
1. A 2. A 3. D 4. A 5. D 6. C 7. C 8. D 9. D 10. C 11. B 12. D 13. D
Ünite Testi – IV
Konu Adı: 3.2.6 Bire Bir ve Örten Fonksiyonlar
1. C 2. B 3. C 4. C 5. B 6. C 7. A 8. A 9. E 10. D 11. E 12. D 13. B 14. C 15. A 16. B
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 2.Bire birdir 3.Örtendir
Ünite Testi – V
Alıştırmalar: 2.a. bire bir ve örten 2.b.ne bire bir ne de örten c.bire bir ama örten değil,
ne bire bir ne de örten 3.a. ne birebir ne de örten 3.b.bire bir ama örten değil 4.a. ne
birebir ne de örten 4.b. bire bir ama örten değil 5. F bire bir ve örten, G ne bire bir ne
de örten H bire bir ve örten, f 1 – 1 ama örten değil, h 1 – 1 değil ama örten 7. i.Bire bir
değil, örten değil ii.Bire bir değil , örten değil iii.Bire bir fakat örten değil iv.Bire bir fakat
örten değil v.Bire bir değil örten değil vı.Bire bir fakat örten değil vıı.Bire bir fakat örten
değil vııı.Bire bir ve örten
1. D 2. D 3. B 4. E 5. C 6. E 7. A 8. B 9. A 10. E 11. D 12. E 13. B 14. A 15. A 16. C
Ünite Testi – VI
1. A 2. B 3. D 4. C 5. C 6. A 7. C 8. A 9. E 10. A 11. C 12. E 13. B 14. D
3.2. Bölüm Değerlendirme
1.a. x,y 1.b. Grafiksel 1.c. tanım, görüntü 1.ç. pozitif, büyüdükçe y eksenine 1.d.
negatif, küçüldükçe y eksenine 1.e. f(x) = 0 1.f. x – eksenine, bir noktada 1.g. bire bir
ve görüntü kümesi R 2. f(A) = {–6,3, 9, 18} 3. f(A) = {–5, –7, –9, –11, –13} 4.a. Tanım
kümesi : [–2,4], değer kümesi: R, görüntü kümesi: [ – 8,10] 5. a. f:[1, 8]→[4, 32]
5.b. g : [d, a]U [b, c]→{m} U [n, k) 5.c. h: R→R 6. a,b,c fonksiyondur. 7. m + n = –1
8. f(3) = 15 9. 5/3 11.a. 1 11.b. – 2 11.c. 3 11.ç. 4/3 11.d. 0 11.e. 0 11.f. – 4 11.g. –1
11.ğ. –1 11.h. 1 11.ı. 7 11.i. –0.3 13.a. f(a) = k, f(b) = l, f(c) = n 13.b. Tanımsız 14.a. bire
bir, örten 14.b. bire bir değil, örten 14.c. bire bir, örten 14.ç. bire bir değil, örten
15.a. Ç = { – 3} 15.b. Ç = { – 3,4} 15.c. Ç = {3} 15.ç. Ç = { – 2} 15.d. Ç = { – 5, – 2,2}
15.e. Ç = { – 4,6} 15.f. Ç = {2} 15.g. Ç = {2} 15.h. Ç = {0} 15.i. Ç = {0} 16. 18 17.E 18.D
19.C 20.A 21.B 22.A 23.B 26.A 27. C 28.a. (0,5] 28.b. f(A) = {5,7} 28.c. [0,7]
28.ç. [ – 1,2]U[4,5] 29.a. f : [ – 2,2]→[ – 4,4] 29.b. f(A) = { – 1,0,1} 29.c. f(B) = [0,4]
Ünite Testi – VII
29.ç. C = [0,2] 29.d. D = {0,1, – 2} 30.b. f(x) = x/10 31.a. [1,4] 31.b. (1,2) 31.c. 1
1. g, f, ı, c, d, ç, e, b, a, h 2. Ø, {E}, ⊥, //, 90o, doğrusal 3.a. {6} 3.b. (–∞, 3) 3.c. {3}
3.ç. (–∞, –9) 3.d. {72} 3.e. (0, 11) 4. 1-3-5-7, 2-4-6-8
31.ç. [ – 1,0] 31.d. 0 32.e. f (x) = (
C
F
– 10
14
0
32
10
50
3x + 3, 0 < x ≤ 5
33.f.
2x + 3
x >5
24
75,2
37
98,6
1. B 2. E 3. A 4. C 5. B 6. A 7. B 8. C 9. E 10. D 11. A 12. B 13. B 14. C 15. D
4. ÜNİTE: EŞLİK VE BENZERLİK
Bölüm Adı: 4.1. Eşlik
HAZIR MIYIZ?
Konu Adı: 4.1.1. Üçgende Açılar
100
KENDİMİZİ SINAYALIM
212
Kavrama ve Muhakeme: 1.a. açıortay 1.b. kenarortay 1.c. yükseklik 2.a. D 2.b. D
2.c. Y 2.ç. D 2.d. D 2.e. Y 2.f. D 2.g. D 2.h. Y3.a. D 3.b. D 3.c. Y 3.ç. D 3.d. Y
4.a. 180° 4.b.90° 5.a. D; D; Y 5.b. D; D; Y 5.c. D;Y;D;D 6. x > y > z
Ünite Değerlendirme – I:
y
1.a. y = 2x b. – 1 1.c. y = x2 1ç. y + 1 = x 2.a. y çıktısı x çıktısına eşittir. 2.b. Bütün
2
x girdileri için y çıktısı 2 dir. 2.c. y çıktısı x girdisinin 2 katının 3 eksiğidir. 2.ç. y çıktısı x
girdisinin karesidir. 2.d. y çıktısı x girdisinin küpüdür, 2.e. y çıktısı x girdisinin mutlak
değeridir. 3.a.Tanım kümesi [1,3] tür. Değer kümesi [ – 2,4] tür. Görüntü kümesi
f([1,3]) = [ –1,3] tür. c. (1, 3/2, 9/4, 11/4, 3) 4. (III.) 5. I,II, III 6. I, III 7. a,b,c 8.a. – 1
4 5 –1
8.b. – 1/3 8.c.0 8.ç. 1 8.d.
9.a.0 b.2 c. ç.4 d. 10.a. 2x – 1 10.b. 2x – 5
3
Alıştırmalar: 1.a.70° 1.b. 110° 1.c. 70° 1.d.110° 1.e. 50o 2. a = 28° b = 62° c = 30°
3. e = 86°, d = 94° 4. x = 60°, y = 80° 5. x = 40°, y = 90° 6. x = 40°, y = 78° 7. m = 13
8. a = 80°, b = 40°, c = 60°, d = 120° 9. a = 80o 10. 90° 11. 65° 12. 85° 13. a = 40°
b = 20°, c = 30°, d = 80°, e = 30° 14. 180° 15. a = 20°, b = 135°, c = 115°
Uygulama ve Problem Çözme: 1. 90° 2. 135° 3. 105° 4. a = 70°, b = 70°, i = 20°
5. 50° 6. 180° 7. 40° 8. 120° 9. 10. 50° 11. a = 80°, b = 90° 12. 75° 13. 45° < x < 60°
14. 20° 15. 140° 16. a + 2b = 180° 17. 30° 18. 130° 19. 265°
Konu Adı: 4.1.2. Üçgenlerin Eşliği
D
KENDİMİZİ SINAYALIM
D
D
D
D
D
D
Kavrama ve Muhakeme: 1.a. ABC , EDF 1.b. XYZ , PRS 1.c. HKJ , PLR 2.a. D
D
D
D
D
2.b. D 2.c. Y 2.ç. Y 3.a. CAB , DCE (K.A.K) 3.b. ABD , CBD (K.A.K.)
D
D
D
D
D
D
D
D
3.c. ABD , ACD (K.K.K.) 3.ç. ABC , DCB (A.K.A) 3.d. ABC , ADC (A.K.A.)
3.e. ACD , DBA (A.K.A)
Alıştırmalar: 1. 7 2. 1 3. 8 4. 5 7. x = a + b
Uygulama ve Problem Çözme: 5.a. A.K.A. 5.b. |CE|
Konu Adı: 4.1.3. İkizkenar ve Eşkenar üçgen
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.a. D 1.b. D 1.c. Y 1.ç. D 1.d. D 1.e. Y 1.f. D
Alıştırmalar: 1.a. 20° 1.b. 70° 1.c. 20° 1.ç. 115° 1.d. 10° 2. 3. 30° 4.a. 50° 4.b. 60°
4.c. 60° 4.ç. 30° 4.d. 42°
Uygulama ve Problem Çözme: 1. 2. 60 3. x = z = 62,5°, y = 55° 4. x = a + b 5. 50°
6. x = a 7. 20° 8. 120° 9. 60° 10. 40° 11. 80° 13. 60° 15. 120°
Konu Adı: 4.1.4. Üçgenin Kenarları İle Açıları Arasındaki İlişkiler
KENDİMİZİ SINAYALIM
%
%
Kavrama ve Muhakeme: 1. |AB| < |BD| ; |AD| < |AB| ; |DC| > |BC| 2. m (BCE) , m (CBE)
%
%
%
%
%
%
m (BAE) , m (BEA) ; m (DBE) , m (BDE) ; m (ECD) , m (EDC) 3.a. D 3.b. D 3.c. D
4.a. D 4.b. D 4.c. Y 4.ç. Y 4.d. D 4.e. Y 4.f. Y 5. a, b, ç 6. a, b, c, d 7.a. D 7.b. Y
7.c. D 7.ç. Y
Alıştırmalar: 1.a. b < a < c 1.b. a < b < c 1.c. c > b > a 1.ç.e > g > f 1.d. d > c > b > a
1.e. e < d < f 1.f.d > e > f 1.g. e > a = b = d > c 2.a. b 2.b. e 2.c. h 2.ç. f 3.a. d 3.b.a
3.c. c 3.ç. d 4. x > y > z 5.a. Oluşur 5.b.Oluşmaz 5.c.Oluşmaz 5.ç.Oluşur 5.d. Oluşur
6.a. 3 < x < 7 6.b. 0 < x < 20 6.c. 3 < x < 6 6.ç. 8 < x < 16 7. c > b > a 8. 17
Uygulama ve Problem Çözme: 1. 59° 2. 39° 3. 0 4. z > x > y > t > p > k 5. z > x > y
6. 30° 7.h 8. 4 9. 69° 10. 65° 11. 7 12. x > 1 (Y), x > 3/2 (D), 3/2 < x < 5 (Y), x < 5 (Y)
13. 1 14. 35 15. 18 16. 29 17. 4 18. 4 19. En küçük 21 br ve en büyük 25 br 20. 37
21. 48 22. 10 23. 5 24. z > y > x 25. 37 26. 79 27. Sadece şekil III 28. 8 ≤ x ≤ 16
29. B noktası 30. 39 31.i. 57 31.ii. 28
4.1. Bölüm Değerlendirme
1. 105° 2. 80° 3. 112,5° 4. 120° 5. 35° 6. 14 7. 60° 8. 20° 9. 3 10. 6 11. C 12. b 13. A
14. D 15. E 16. 53 17. 27 18. 16 19. B 20. E
Bölüm Adı: 4.2. Üçgenlerin Benzerliği
HAZIR MIYIZ?
6
11
5
4
5
10
2.b.
2.c.
2.ç.
2.d. b – ç 3. a, e 4. a = 4, r = , k =
, b = 13
7
13
6
6
3
6
y = 6, –6 5. 18 6. x = 6, 15, 18 y = 15, 20, 35
2.a.
Konu Adı: 4.2.1. Üçgende Orantılı Doğru Parçaları
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.a. D 1.b. D 1.c.Y 2.a. |AC| 2.b. |EG| 2.c. |DF| 2.ç. |AE| 3.G
4.a. // 4.b. // 4.c. //
5
3
5.b.
5.c. 2 6. 20
Alıştırmalar: 1. 8 2. x = 4, y = 1 3. 24 4.a. 6 4.b. 12 5.a.
2
4
7. x = 32, y = 45
27
9
3.
4. 8 6. |FG| = 24, |GH| = 48, |KL| = 96
Uygulama ve Problem Çözme: 1. 6 2.
2
2
7.a. 36 7.b. 72 8. 4 9. 9 10. III
Konu Adı: 4.2.2. Üçgenlerin Benzerliği
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.a. |AC|, |EF| 1.b. m ( W
D), m ( V
E), m ( V
F) 2.a. |AB| 2.b. |AC|
2.c. |AC| 2.ç. |EC| 3.a.D 3.b.D 3.c.Y 3.ç.D 4.a.D 4.b.Y 4.c.D 5.a.D 5.b. Y 5.c. D 6.a. D
6.b. Y 6.c. D 6.ç. D 6.d. Y 6.e. Y
D
D
D
Alıştırmalar: 1.a. FDE (A.A.), 1.b. CDE (A.A.) 1.c. MLK (K.A.K.) 1.ç. LMK (K.K.K.)
D
20
2.e. x = 6, y = 6
1.d. MNP (K.K.K.) 2.a. 8 2.b. 2 2.c. 15 2.ç. x = 12, y = 3 2.d.
3
1
3
3
3
3
Uygulama ve Problem Çözme: 1. 18 2. 7 3.a.
3.b.
3.c.
4.a.
4.b.
2
2
4
2
7
1
2
16
4.c.
5.a.2 5.b. 2 6. 1 7. 6 8. 5 9.
10. 24 11.40 12.14 13.3 14.19 15. 16. 2
3
5
5
1
7
1
17. 10 18.
19.
20.2 21. 6 22. 5 23. 4 24. 18 25.20 26.a.
26.b.40
6
20
16
15
81
36
26.c.
27.3 28.
29.5 30.4 31.16 32.1 33.
34.70° 36.15 37.4 38.5
2
16
5
Konu Adı: 4.2.3. Üçgenlerin Benzerliğini Problem Çözme ve Modellemede
Kullanma
KENDİMİZİ SINAYALIM
Problemler: 1.8 2.60 3.60 4.9 5. 27 6.5,4 7.8 8.
21
9.8,5 10.36
16
4.2. Bölüm Değerlendirme
7
9
8
3. 6 4. 7 5.
6. 12 7. 4 8. 15 9. 2 10. 3 3 11.
12. 6 13. 5 14. 2
1. 16 2.
2
2
3
15
15.
16. 6 17. 2 26 18. 6 2 19. 12 20. 10 21. 12 22. 6 23. 7 24. 25,48
7
Bölüm Adı: 4.3. Üçgenin Yardımcı Elemanları
HAZIR MIYIZ?
1.10o 3. [CE] 4. D,Y,D,D 5. a. T,H,G,E 5.b. T,J,K,D 5.c.K 5. ç. E
Konu Adı: 4.3.1. Açıortay
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.b 2. D, Y, Y, D, D 3. a. |BC| 3. b. |AC| 4. D,D,D,Y
33
6. 500 7. 1250 8. 500 9. 800
Alıştırmalar: 1. a 2. 6 3. 20 4. 4 5.
5
7
15 9
4
5
Uygulama ve Problem Çözme: 1.
2.
3. 700 4.
5.
,
2
2 2
3
3
Konu Adı: 4.3.2. Üçgende Kenarortay
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1.a.Kenarortaylarının 1.b. 2:1
27
cm
Alıştırmalar: 1. 18 2. 2 cm 3. 2 cm 4. 6br 5.
2
16
br 2.30 cm 3.3 cm 4.6 cm 5. 2
Uygulama ve Problem Çözme 1.a. 4 br, 8br 1.b.
3
6. 8 cm 7.16 cm 8. 9. 15 cm 10. 14 cm 11.30 cm 13. 6 br
Konu Adı: 4.3.3. Üçgenin Kenar Orta Dikme ve Yükseklikleri
KENDİMİZİ SINAYALIM
Kavrama ve Muhakeme: 1. D, Y, Y, D, Y 2.Diklik merkezi
Alıştırmalar: 1. 10 2. 10,10 3. 60° 4. a.40 b. 10 5. a. 50 5.b. 40
Uygulama ve Problem Çözme: 1.50 2. 20 3. 10 4. 6 5. 11
4.3. Bölüm Değerlendirme
1. 45 2. 45 3. 80 4. 40 5. 14 6. 4 7. 3 8. 4 9.2 10. 9 11. 15 12. 6 13. 30 14. 8 15. 11
16. 3 17. 21 18. 5 19. 24 20. 5 21. 12 22. 67 23. 50 24. 55 25. 2 26. 18 27. 5 28. 40
29. 7 30. 59
Ünite Değerlendirme – I
1.C 2.B 3.E 4.E 5.A 6.C 7. D 8.B 9.D. 10. E 11.D 12. C 13. A 14. C
Ünite Değerlendirme – II
1.E 2. A 3.C 4. D 5. E 6. C 7. B 8. E 9. E 10. D 11. D 12. B
13.B 14. A 15.C
Sözlük
A
açı: Aynı doğru üzerinde bulunmayan, başlangıç noktaları ortak iki ışının kesişimi. Işınlar açının kolları, ortak
başlangıç nokta da açının köşesi olarak adlandırılır.
açı-kenar-açı (A.K.A.) eşlik kuralı: İki üçgenin köşeleri arasında kurulan bire bir eşlemede, karşılıklı ikişer açı ve bu
açıların arasında kalan kenarların eşliğini ifade eden kural.
açıklık: Bir veri grubunda en büyük değer ile en küçük
değer arasındaki fark.
açıortay: Bir açıyı iki eş açıya ayıran ışın.
ağırlık merkezi (üçgen): Bir üçgenin kenarortaylarının
kesiştiği nokta.
ağırlıklı ortalama: Bir veri grubundaki her bir verinin belirli bir ağırlık değeri ile çarpımının toplamının verilerin
sayısına bölünmesi ile elde edilen değer.
akış diyagramı ispat biçimi: Geometride, bir teoremin
ispatında ifadelerin mantıksal bir sıra içinde ve bu ifadelerin gerekçelerinin ise hemen altlarındaki kutularda yer
aldığı gösterim biçimi.
alan: Bir yüzeyin bulunduğu düzlemde kapladığı yer. Bir
yüzeyi kaplamak için gerekli birim karelerin sayısı.
alt çeyrek: Bir veri grubunda veriler küçükten büyüğe
sıralandığında ortanca terim, veri grubunu terim sayıları
eşit olacak şekilde iki gruba ayırır. Sol tarafta kalan veri
grubu alt grup olmak üzere, alt grubun ortancasına alt
çeyrek denir.
alt küme: Bir A kümesinin elemanlarından bazılarının
oluşturduğu küme. Boş küme (∅) ve kümenin kendisi de
A kümesinin bir alt kümesidir.
altın oran: Değeri
irrasyonel sayı.
1+ 5
= 1, 6180339887... olan bir
2
analitik düzlem: Dik kesişen iki koordinat doğrusunun
oluşturduğu yapının belirttiği düzlem. Analitik düzlem
üzerindeki her bir nokta elemanları gerçek sayı olan
sıralı ikililere karşılık gelir.
aritmetik ortalama: Bir veri grubundaki sayıların toplamının, veri sayısına bölünmesi ile elde edilen değer.
asal sayı: 1 ve kendisinden başka pozitif tam sayı böleni
olmayan doğal sayı.
ayrık kümeler: Ortak elemanı olmayan kümeler.
B
bağımlı değişken: Bağımsız değişkene bağlı olarak değeri değişen değişken.
bağımsız değişken: Bağımlı değişkenlerde bir değişime
neden olmak için manipüle edilen değişken.
benzer terimler: Aynı değişkenleri içeren ve bu değişkenlerin kuvvetlerinin aynı, katsayıların aynı veya farklı
olduğu terimler.
bileşen: Bir bileşim ya da birleşimi oluşturan öğelerden
her biri.
bire bir fonksiyon: Tanım kümesindeki her bir elemanın
görüntüsünün diğer elemanların görüntülerinden farklı
olduğu fonksiyonlar.
birim fonksiyon: Tanım kümesindeki her değeri kendisiyle eşleyen fonksiyon.
boş küme: Hiç elemanı olmayan küme.
bilimsel gösterim: 1 ≤ a < 10, a ∈ R, b ∈ Z olmak üzere
bir sayının a · 10b şeklindeki gösterimi.
birim çember: Merkezi (0, 0) noktası (orijin) ve yarıçapı 1
birim olan çember.
birleşim kümesi: İki kümenin elemanlarının tamamının
oluşturduğu küme.
bütünler açılar: Ölçüleri toplamı 180° olan iki açı.
Ç
çelişki: Doğruluğu (veya yanlışlığı) kabul edilen durum
ilgili tutarsızlık.
çelişki yöntemiyle ispat: Verilen ifadenin tersinin doğru
olduğunu kabul edip bir çelişki elde etmeye dayalı ispat
biçimi.
çevrel çember: Bir çokgenin tüm köşelerinden geçen
çember. Örneğin, bir üçgenin kenar orta dikmelerinin
kesim noktası üçgenin çevrel çemberinin merkezidir.
çeyrekler açığı: Üst çeyrek ile alt çeyrek arasındaki fark.
çizgi grafiği: İlgili verilerin bir dizi nokta (sıralı ikili) ile
gösterildiği ve bu noktaların düz çizgilerle birleştirildiği
bir tür grafik. Çizgi grafiği genellikle bir niceliğin zamana
bağlı değişimini göstermek için kullanılır.
çözüm kümesi: Bir denklemi ya da eşitsizliği sağlayan
tüm değerlerin oluşturduğu kümesi.
D
daire grafiği: Bir niceliğin bütün içindeki oranının daire
üzerinde dilimlerle ifade edildiği grafik türü.
değer kümesi: Fonksiyonun tanımlı olduğu “çıktı” değerlerinin oluşturduğu küme.
denklem: İçinde en az bir bilinmeyenin bulunduğu
eşitlik.
değişim oranı (hızı): Bir nicelikteki değişimin, başka bir
niceliğin değişimine oranı.
değişken: Bir problem ya da bir dizi işlem bağlamında
değişen (farklı değerler alan) değer.
dış açı: Bir çokgende herhangi bir iç açının bütünleyeni.
dış açıortay: Bir çokgenin bir dış açısını iki eş parçaya
ayıran ışın.
dış merkez: bk. dış teğet çemberin merkezi.
dış teğet çemberin merkezi (üçgen): Üçgenin iki dış
açıortayı ile bu dış açılara komşu olmayan iç açısının
açıortayının kesim noktası.
eş üçgenler: Karşılıklı açıları ve kenarları eş olan üçgenler.
eşit fonksiyon: Tanım ve görüntü kümeleri aynı, tanım
kümesindeki her bir elemanın görüntüsünün de aynı
olduğu fonksiyonlar.
eşit kümeler: Elemanları aynı olan kümeler.
eşitlik: İçinde “=” sembolü bulunan matematik cümlesi.
eşitsizlik: İçinde <, >, ≤, ≥ veya ≠ sembollerinden en az
birinin bulunduğu matematik cümlesi.
etkisiz eleman: Bir küme ve üzerinde bir işlem tanımlandığında kümedeki her elemanı verilen işleme göre yine
kendisine dönüştüren eleman.
evren: İçinde bir cismin bulunabileceği yerlerin tümünü
gösteren kavram, bütün var olanları içinde bulunduran
şey.
evrensel küme: Üzerinde işlem yapılan tüm kümelere ait
elemanları içine alan küme.
F-G-H
diklik merkezi: Üçgenin yüksekliklerin kesim noktası.
fonksiyon: Bir kümenin (tanım kümesinin) her bir elemanını başka bir kümenin (değer kümesinin) bir ve yalnız
bir elemanına eşleyen ilişki.
dik kenar: Dik üçgende dik açıyı oluşturan kenarlardan
her biri.
görüntü kümesi: Tanım kümesindeki elemanların fonksiyon altındaki görüntülerinin oluşturduğu küme.
dik üçgen: İç açılarından biri 90° olan üçgen.
grup genişliği: Bir histogramda açıklık değerinin
grup sayısına bölümüne en yakın tam sayı. Örneğin
açıklık ! 29
= 5, 8 . 6 " grup genişliği.
grup sayısı ! 5
dik açı: Ölçüsü 90° olan açı.
dikey doğru testi: Bir grafiğin x-eksenine dikey doğrular
çizilerek bir grafiğin fonksiyon grafiği olup olmadığını
anlama yöntemi.
doğrusal fonksiyon: Tanım ve değer kümesi reel sayılar
olan f(x) = ax + b (a ≠ 0 ve b ∈ R) biçimindeki fonksiyon.
doğru orantı: Değişkenlerden biri artarken (veya azalırken), diğerinin de arttığı (veya azaldığı) orantı.
E
eş açı: Ölçüleri eşit olan açılar.
eş doğru parçaları: Uzunlukları eşit olan doğru parçaları.
eşkenar üçgen: Üç kenarının uzunlukları birbirine eşit
olan üçgen.
gerçek sayılar: Doğal sayılar, tam sayılar, rasyonel sayılar
ve irrasyonel sayılar kümesinin hepsini kapsayan ve R ile
gösterilen sayı kümesi.
hipotenüs: Bir dik üçgende dik açının karşısındaki kenar.
histogram: Veri genişlikleri eşit olan farklı aralıklardaki
veri sayılarını gösteren grafik türü.
İ
iç ters açı: Paralel iki doğruyu kesen üçüncü bir doğrunun iki yanında ve paralellerin içinde altlı üstlü ortaya
çıkan dört açıdan her biri.
iç açı: Bir çokgenin ardışık iki kenarının oluşturduğu ve
çokgenin içinde bulunan açı.
iç açıortay: Bir çokgenin bir iç açısını iki eş parçaya ayıran
ışın.
iç merkez: bk. iç teğet çemberin merkezi.
iç teğet çemberin merkezi (üçgen): Bir üçgende iç açıortayların kesiştiği nokta.
a
c
içler dışlar çarpımı: = olmak üzere a ve d değerleb
d
rinin (dışlar) b ve c değerleriyle çarpımının eşit olması:
a·d=b·c
ilişkisizlik: Değişkenler arasında artma veya azalmayla ilgili herhangi bir ilişki söz konusu olmadığında bu durum
ilişkisizlik olarak adlandırılır.
kesin olay: Olma/gerçekleşme olasılığı 1 olan olay.
kesişim kümesi: İki kümenin ortak elemanlarının oluşturduğu küme.
kenar-açı-kenar (K. A. K.) eşlik kuralı: İki üçgen arasında
kurulan birebir eşlemede, karşılıklı ikişer kenar ve bu
kenarların oluşturduğu açıların eşliğini ifade eden kural.
kenar-kenar-kenar (K.K.K.) eşlik kuralı: İki üçgenin köşeleri arasında kurulan birebir eşlemede, karşılıklı kenarların eşliğini ifade eden kural.
kenarortay: Üçgenin bir köşesini karşısındaki kenarın
orta noktasına birleştiren doğru parçası.
kesikli veri: Sürekli verilerin aksine, sonlu veya sayılabilir
belli bir aralıkta her değeri alamayan veriler. Örneğin;
kişi sayısı, araç sayısı vb.
Kosinüs Teoremi: Üçgenin iki kenar uzunluğu ve bu kenarların oluşturduğu açının ölçüsü ile üçüncü kenarının
uzunluğu arasındaki ilişkiyi ifade eden teorem.
koordinat düzlemi: bk. analitik düzlem.
iki kolonlu ispat biçimi: Geometride, bir teoremin ispatında ifade ve ifadelerin gerekçelerinin karşılıklı iki sütun
şeklinde yer aldığı ispat biçimi.
koordinat doğrusu: Gerçek sayıların, bir doğrunun
noktaları ile bire bir eşleştirilmesi ile oluşturulan sayı
doğrusu.
iki kümenin farkı: Bir kümede olup diğerinde olmayan
elemanların kümesi.
kutu grafiği: Bir veri grubundaki en küçük değer, en büyük değer, alt çeyrek, üst çeyrek ve ortanca değerlerini
gösteren bir tür grafik.
ikizkenar üçgen: Kenarlarından herhangi ikisi eş olan
üçgen.
imkansız olay: Gerçekleşme olasılığı olmayan olay.
küme: İyi tanımlanmış birbirinden farklı nesnelerden
oluşan topluluk.
kümenin elemanları: Bir kümeyi oluşturan nesneler.
irrasyonel sayılar: İki tam sayının birbirine bölümü şeklinde yazılamayan sayılar.
ispat: Bilinen matematiksel kural, özellik, sonuç veya
tanımları kullanarak bir yargının doğru veya yanlış olduğunun gösterilmesi.
K
kapsama: Bir kümenin başka bir kümenin elemanlarının
hepsini içermesi.
karekök: Bir sayının eş iki çarpanından biri.
kartezyen çarpım: İlk bileşeni A kümesinden ikinci bileşeni
B kümesinden alınarak oluşturulan sıralı ikililerin kümesi.
L–M–N
liste yöntemi: Küme elemanlarının, küme parantezleri
içinde her eleman arasına virgül konularak liste şeklinde
herhangi bir sırayla verildiği gösterim biçimi.
medyan: bk. ortanca.
merkezi eğilim ölçüsü: Bir sayı dizisini temsil eden tepe
değer, ortanca ve aritmetik ortalama değerleri.
merkezi yayılım ölçüsü: Bir sayı dizisindeki terimlerin
birbirine yakınlığını veya uzaklığını belirten standart
sapma, açıklık ve çeyrekler açıklığı değerleri.
mod: bk. tepe değer.
mutlak değer: Bir gerçek sayının sayı doğrusu üzerinde
sıfıra olan uzaklığı.
-x , x < 0
mutlak değer fonksiyonu: f: R " R + , f (x) = (
x , x≥0
ifadesi ile tanımlanan ve tanım kümesindeki her gerçek
sayıyı, sayı doğrusu üzerinde orijine olan uzaklığına
eşleyen fonksiyon.
negatif yönlü ilişki: İki farklı değişkenden biri artarken
diğer değişken azalıyorsa bu iki değişken arasındaki
ilişkiye negatif yönlü ilişki.
O
oran: İki çokluğun (niceliğin) bölme şeklinde birbiri ile
a
karşılaştırılması: a : b ,
b
orantı: İki ya da daha fazla oranın eşitliği.
orta dikme: Bir doğru parçasına orta noktasından dik
olan doğru.
S
sabit: Değişmeden kalan değer.
sabit fonksiyon: Tanım kümesinin bütün elemanlarını değer kümesinden yalnızca bir eleman ile eşleyen
fonksiyon.
saçılma grafiği: bk. serpme grafiği.
serpme grafiği: İki farklı değişken arasındaki ilişkinin
yönünü ve kuvvetini gözlemlemek için verilerin sıralı
ikililer olarak grafik üzerinde gösterildiği grafik türü.
sıralı ikili: A kümesinden alınan bir a elemanı ile B kümesinden alınan bir b elemanı kullanılarak oluşturulan (a, b)
şeklindeki yeni eleman.
simetrik fark: (A – B) ve (B – A) kümelerinin birleşimi:
(A – B) ∪ (B – A)
ortak özellik yöntemi: Bir kümeyi elemanlarının taşıdığı
şartları veya özellikleri belirterek ifade eden gösterim biçimi.
Sinüs Teoremi: Üçgenin kenar uzunlukları ve bu kenarların karşılarındaki açı ölçülerinin sinüs değerleri arasındaki ilişkiyi ifade eden teorem.
ortanca: Bir veri grubu küçükten büyüğe sıralandığında
veri grubunu eşit sayıda iki gruba ayıran değer.
sonlu küme: Eleman sayısı bir doğal sayı ile ifade edilebilen küme.
örten fonksiyon: Değer kümesindeki her elemanın tanım
kümesinden en az bir elemanla eşleştiği fonksiyon.
sonsuz: Verilmiş olan her büyüklükten daha büyük olan.
P-R
paradoks: Doğru olduğu varsayıldığında çelişki ürettiği gibi yanlış olduğu varsayıldığında da çelişki üreten
yargısal ifade.
standart sapma: Bir sayı dizisindeki elemanların aritmetik ortalamaya yakın olup olmadığı hakkında bilgi veren
merkezi yayılım ölçüsü.
sonsuz küme: Sonlu olmayan küme.
paragraf ispat biçimi: Geometride, bir teoremin ispatının
paragraf şeklinde detaylı açıklamaların birlikte verildiği
ispat biçimi.
sürekli veri: Kesikli verilerin aksine belli bir aralıkta bütün
değerleri alabilen veriler. Örneğin; bir cismin kütlesi ve
boyu, zaman, uzaklık vb.
parçalı tanımlı fonksiyon: Tanım kümesinin ayrık alt kümelerinde farklı kurallarla tanımlı olan fonksiyonlar.
sütun grafiği: Verilerin eksenler üzerinde sütunlarla veya
çubuklarla ifade edildiği grafik türü.
Pisagor Teoremi: Bir dik üçgende, hipotenüs (c) ile dik
kenarların (a ve b) uzunlukları arasındaki ilişkiyi ifade
T
D
eden teorem: ABC dik üçgeni ⇔ c2 = a2 + b2
pozitif yönlü ilişki: İki farklı değişkenden biri artarken
diğer değişkende artıyorsa bu iki değişken arasındaki
ilişkiye pozitif yönlü ilişki denir.
rasyonel sayı: a, b ∈ Z (b ≠ 0) ve a, b aralarında asal olmak
a
üzere,
şeklinde bir kesir olarak ifade edilebilen sayı.
b
Tanım kümesi: Bir fonksiyonun tanımlı olduğu küme.
teorem: Doğruluğu ya da yanlışlığı bir akıl yürütmeler
silsilesi ile ispatlanabilen matematiksel ifade.
tepe değer: Bir veri grubunda en çok tekrar eden değer.
ters orantı: Değişkenlerden biri artarken diğeri azalan
orantı.
trigonometrik oranlar: Bir dik üçgenin kenar uzunlukları
arasındaki oranlar.
tümler açılar: Ölçüleri toplamı 90° olan açılar.
tümleyen küme: İstenen kümede olmayıp evrensel
kümede olan elemanların kümesi.
U-Ü
uzay: bk. evren.
üçgen: Doğrusal olmayan üç noktayı, ikişer ikişer birleştiren doğru parçalarının oluşturduğu geometrik şekil.
üçgenin dış teğet çemberleri: Bir üçgende kenarlara
dıştan teğet olan çemberler.
üçgen eşitsizliği: Bir üçgende, herhangi iki kenar uzunluğunun toplamının üçüncü kenarın uzunluğundan büyük
olması.
üst çeyrek: Bir veri grubunda veriler küçükten büyüğe
sıralandığında ortanca terim, veri grubunu terim sayıları
eşit olacak şekilde iki gruba ayırır. Sağ tarafta kalan veri
grubu üst grup olmak üzere, üst grubun ortancasına üst
çeyrek denir.
V-Y
Venn şeması: Küme elemanlarının kapalı bir eğri veya
çokgenin içinde, her bir elemanın yanına birer nokta
konularak gösterildiği gösterim biçimi.
vücut kitle indeksi: Vücut kütlesinin (kg) boy uzunluğunun (m) karesine oranı ile hesaplanan ve bir insanın vücudundaki yağ oranının tahmini göstergesi olan bir ölçü.
yardımcı çizim: Bir teoremi ispatlayabilmek ya da bir
problemi çözebilmek için kullanılan ek çizim.
yatay doğru testi: x-eksenine paralel doğrular çizerek
verilen fonksiyon grafiğinden fonksiyonun bire bir veya
örtenliğini ortaya koymakta kullanılan bir yöntem.
yöndeş açı: Paralel iki doğru bir kesenle kesildiğinde,
kesenin aynı tarafında kalan aynı yönlü açılar.
yükseklik: Üçgenin bir köşesinden karşı kenara indirilen
dik doğru parçası.
Kaynakça
Angel, A. R., Abbott, C. D., & Runde, D. C. (2004). A Survey of Mathematics with Applications. New York, NY: AddisonWesley.
Aufmann, R. N., Lockwood, J. S., Nation, R. D., & Clegg, D. K. (2010). Mathematical Excursions (2nd ed.). Boston: Brooks/
Cole Cengage Learning.
Bello, I. (2009). Basic college Mathematics (3rd ed.). New York: McGraw-Hill Companies.
Boyer, B. C., Merzbach, U.C. ve Asimov, I. (1991). A History of Mathematics. New York: John Wiley & Sons.
Baki, A. (2008). Kuramdan Uygulamaya Matematik Eğitimi. Trabzon: Harf Yayıncılık.
Barnes A. (2007). Encyclopedia of Trigonometry. Delhi: Global Media.
Cajori F. (1928). A History of Mathematical Notations: Volume 1, Notations In Elementary Mathematics. London: The Open
Court Company Publishers.
Cajori F. (1930). A History of Elementary Mathematics. London: Macmillan.
DeVilliers, M. (2005). A Generalization of the nine-point circle and Euler line. Pythagoras, 61, 31-35.
Gökdal, F. (1999). Heron ve Brahmagupta Formülleri. Matematik Dünyası, 2, 20-24.
Göker, L., (1997). Matematik Tarihi ve Türk İslam Matematikçilerinin Yeri. İstanbul: MEB Yayınları.
Keijzer, R., Abels, M., Wijers, M., Brinker, L. J., Shew, J. A., Cole, B. R., & Pligge, M. A. (2006). Ratios and rates. Mathematics
in Context. Chicago: Encyclopædia Britannica, Inc.
Krebs, E. R. (2004). Groundbreaking Scientific Experiments, Inventions and Discoveries of the Middle Ages and the
Renaissance. London: Greenwood Pub.
Lial, M. L., Hornsby, J., & McGinnis, T. (2012). Beginning and intermediate algebra (5th ed.). Boston: Pearson Education.
McKeague, C. P. (2010). Basic Mathematics (7th ed.). Belmont: Brooks/Cole Cengage Learning.
Miller, J., O’Neill, M., & Hyde, N. (2009). Basic college mathematics (2nd ed.). New York: McGraw-Hill Companies.
Murdock, J., Kamischke, E., ve Kamischke, E. (2007). Discovering Algebra: An Investigative Approach (2nd ed.).
Emeryville, CA: Key Curriculum Press.
Pickover, C. A. (2009). The Math Book. New York: Sterling Publishing.
Serra, M. (2008). Discovering Geometry: An Investigative Approach. Emeryville, CA: Key Curriculum Press.
T.C. Milli Eğitim Bakanlığı Talim ve Terbiye Kurulu Başkanlığı. (2013). Ortaöğretim Matematik Dersi (9, 10, 11 ve 12.
Sınıflar) Öğretim Programı. Ankara: T.C. Milli Eğitim Bakanlığı.
Topdemir, G. H. (2011). Hipparkhos ve Trigonometrinin Doğuşu. Bilim ve Teknik, 528, 88-90.
Türk Dil Kurumu. (2012). Yazım Kılavuzu. Ankara: Türk Dil Kurumu Yayınları.
Türk Dil Kurumu. (2011). Türkçe Sözlük. Ankara: Türk Dil Kurumu Yayınları.
Verma, S. (2008). The Little Book of Maths Theorems, Theories & Things. Sydney: New Holland Publishers.
Wells, D. (2011). Geometrinin Gizli Dünyası. İstanbul: Doruk Yayınları.
Yağcı, M. (2004). Fermat-Toricelli Noktası. Matematik Dünyası, 1, 58-61.
Görsel Kaynakçası
Ünite Sayfa Görselin Alındığı Web
Ünite Sayfa Görselin Alındığı Web
Ünite Sayfa Görselin Alındığı Web
No
No
Sayfası
No
No
Sayfası
No
No
Sayfası
3
438
www.123rf.com
3
563
www.aa.com.tr
4
716
www.123rf.com
3
438
www.123rf.com
3
563
www.123rf.com
4
716
www.123rf.com
3
439
Orijinal çizim
3
566
www.123rf.com
4
719
www.123rf.com
3
440
www.123rf.com
3
568
www.123rf.com
4
720
dijitalimaj.com
3
440
Orijinal çizim
3
570
Orijinal çizimler
4
720
Orijinal çizim
3
442
www.123rf.com
3
577
www.dijitalimaj.com
4
724
Orijinal çizim
3
442
Orijinal çizim
3
578
www.dijitalimaj.com
4
725
Orijinal çizimler
3
443
www.123rf.com
3
579
www.123rf.com
4
726
Orijinal çizimler
3
443
Orijinal çizim
3
580
www.123rf.com
4
726
dijitalimaj.com
3
444
www.123rf.com
3
580
www.123rf.com
4
732
Orijinal çizim
3
454
Orijinal çizim
3
596
Orijinal çizim
4
742
Orijinal çizimler
3
455
Orijinal fotoğrafler
3
615
Orijinal çizim
4
755
Orijinal çizimler
3
463
www.alamy.com/tr
4
631
www.alamy.com/tr
4
758
dijitalimaj.com
3
470
Orijinal çizimler
4
634
Orijinal çizim
4
758
Orijinal çizimler
3
473
Orijinal çizim
4
639
dijitalimaj.com
4
759
Orijinal çizimler
3
492
www.123rf.com
4
648
Orijinal çizim
4
760
Orijinal çizim
3
492
Orijinal çizim
4
650
dijitalimaj.com
4
760
dijitalimaj.com
3
499
www.123rf.com
4
655
www.123rf.com
4
761
Orijinal çizimler
3
508
www.123rf.com
4
656
dijitalimaj.com
4
762
Orijinal çizimler
3
509
www.123rf.com
4
660
Orijinal çizim
4
763
Orijinal çizimler
3
522
Orijial resimler
4
662
www.123rf.com
4
764
Orijinal çizimler
3
523
www.123rf.com
4
670
Orijinal çizimler
4
770
dijitalimaj.com
3
523
www.123rf.com
4
672
www.123rf.com
4
771
dijitalimaj.com
3
523
www.123rf.com
4
674
Orijinal çizimler
4
777
Orijinal çizimler
3
533
www.123rf.com
4
675
dijitalimaj.com
4
792
Orijinal çizim
3
534
www.123rf.com
4
688
Orijinal çizim
4
797
Orijinal çizim
3
535
www.123rf.com
4
692
Orijinal çizim
4
798
Orijinal çizim
3
543
www.123rf.com
4
693
Orijinal çizim
4
800
dijitalimaj.com
3
547
www.dijitalimaj.com
4
694
dijitalimaj.com
4
800
foto.aa.com.tr
3
548
www.123rf.com
4
694
Orijinal çizim
4
801
www.123rf.com
3
549
www.alamy.com/tr/
4
698
Orijinal çizim
4
812
dijitalimaj.com
3
549
www.alamy.com/tr/
4
702
Orijinal çizim
4
812
Orijinal çizimler
3
549
www.alamy.com/tr/
4
703
Orijinal çizim
4
818
Orijinal çizimler
3
561
Orijinal çizim
4
704
Orijinal çizim
4
819
Orijinal çizimler
3
562
Orijinal çizim
4
711
www.alamy.com/tr
4
820
dijitalimaj.com
3
562
www.123rf.com
4
712
Orijinal çizim
4
821
Orijinal çizimler
3
562
www.123rf.com
4
714
www.123rf.com
4
833
Orijinal çizim
4
835
Orijinal çizim
4
836
Orijinal çizim