WEEK I
İŞARET NEDİR?
Fiziksel büyüklükleri ifade etmekte kullandığımız bir gösterim şeklidir. Örnek olarak ısı, ışık şiddeti,
ses, basınç, ve elektriksel işaretler verilebilir. İşaretlerin işlenmesi elektronik sistemler tarafından
gerçekleştirildiği ve elektronik sistemler elektriksel işaretler üzerinden işlem yürüttükleri için, söz konusu
işaretlerin (ısı, ışık şiddeti, ses, basınç etc.) elektronik sistemlere uygulanması öncesi elektriksel işaretlere
dönüştürülmesi gereklidir. Bu görevi sensör (transducer) dediğimiz yapılar yerine getirmektedirler.
Örnek vermek gerekirse, bir microfona konuşan bir kişinin ses işaretleri, mikrofon aracılığıyla
elektriksel işarete dönüştürülür, bu elektriksel işaret electronik sistem vasıtasıyla kuvvetlendirilir, ve sonuçta
kuvvetlendirilmiş bu işaret tekrar ses işaretine dönüştürülür. Sonuçta bir kişinin herhangi bir elektronik sistem
kullanmaksızın üretebileceği ses şiddetinin çok üzerinde bir ses şiddeti elde edilebilmiş olur. Burada mikrofon
içerisinde bulunan sensor (transducer) ses dalgası basınc büyüklüğünü algılar ve elektriksel işarete karşılık
düşürür, elde edilen elektriksel işaret kuvvetlendirici (amplifier) yardımıyla istenilen ölçüde kuvvetlendirilir ve
çıkışta, kuvvetlendirilen elektriksel işaret, elektriksel işareti ses işaretine dönüştüren farklı bir transducer
kullanarak ses işaretine dönüştürülür.
Sonuç olarak, bir çok fiziksel işareti işlemek için elektriksel işatere dönüştürmek esastır ve, birçok farklı
fiziksel işareti elektriksel işarete dönüştüren birçok farklı sensor (transducer) mevcuttur.
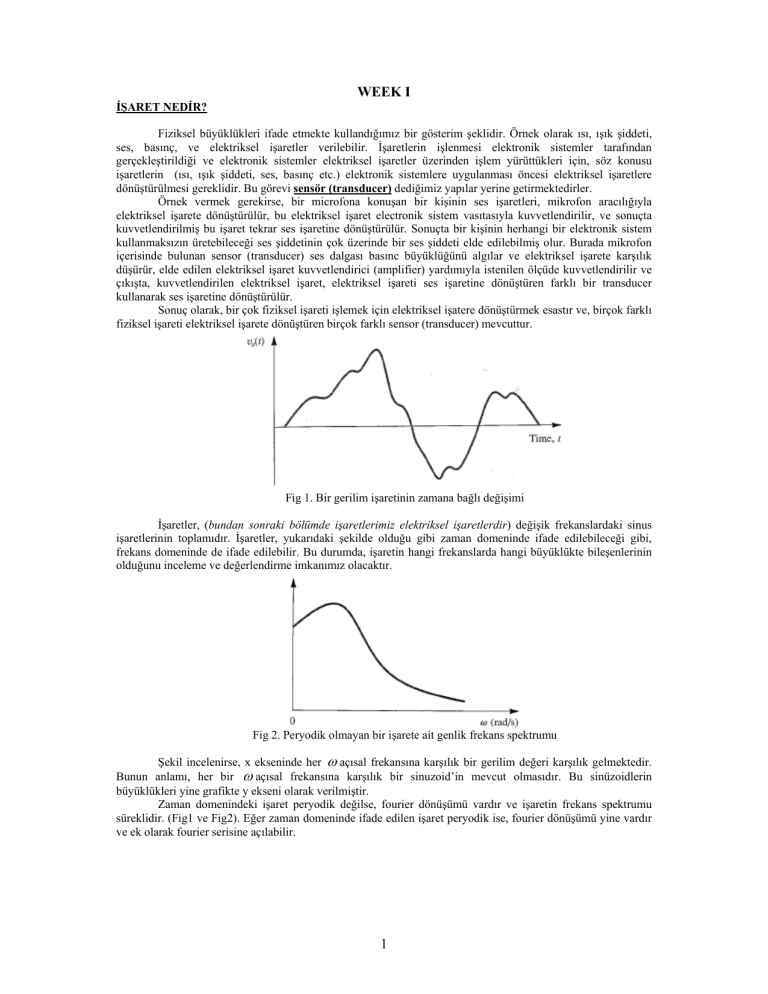
Fig 1. Bir gerilim işaretinin zamana bağlı değişimi
İşaretler, (bundan sonraki bölümde işaretlerimiz elektriksel işaretlerdir) değişik frekanslardaki sinus
işaretlerinin toplamıdır. İşaretler, yukarıdaki şekilde olduğu gibi zaman domeninde ifade edilebileceği gibi,
frekans domeninde de ifade edilebilir. Bu durumda, işaretin hangi frekanslarda hangi büyüklükte bileşenlerinin
olduğunu inceleme ve değerlendirme imkanımız olacaktır.
Fig 2. Peryodik olmayan bir işarete ait genlik frekans spektrumu
Şekil incelenirse, x ekseninde her ω açısal frekansına karşılık bir gerilim değeri karşılık gelmektedir.
Bunun anlamı, her bir ω açısal frekansına karşılık bir sinuzoid’in mevcut olmasıdır. Bu sinüzoidlerin
büyüklükleri yine grafikte y ekseni olarak verilmiştir.
Zaman domenindeki işaret peryodik değilse, fourier dönüşümü vardır ve işaretin frekans spektrumu
süreklidir. (Fig1 ve Fig2). Eğer zaman domeninde ifade edilen işaret peryodik ise, fourier dönüşümü yine vardır
ve ek olarak fourier serisine açılabilir.
1
Fig 3. Zaman domeninde verilen işaret
Şekilde verilen peryodik işarete ait fourier serisi açılımı aşağıdaki gibidir.
Yine, Fig 3’de zaman domeninde verilen peryodik işarete ait genlik frekans spektrumu Fig 4’de
verildiği gibidir.
Fig 4. Fig3 de verilen işarete ait genlik frekans spektrumu
Dikkat edilmesi gereken konu, frekans spektrumunun, eşitlikte verilen fourier serisinin grafiksel
gösterimi olduğudur. Sonuç olarak, zaman domeni işareti peryodik ise, fourier serisine açılabilir ancak zaman
domeni işareti peryodik değilse, o işaret fourier serisine açılamaz. Zaman domeninde peryodik işaretlerin genlik
frekans spektrumları ayrık iken, zamanda peryodik olmayan işaretlerin frekans spektrumları süreklidir.
Fourier dönüşümü ve serisi işaret işleme dersi konusu olup, burada derinlemesine incelenmeyecektir.
Ancak buradan çıkarmamız gereken ana fikir şudur ki, incelediğimiz, işlediğimiz işaretler, sinüzoidlerin toplamı
şeklindedir. O halde sinüzoidal işaretler bizim için oldukça önemlidir.
SİNÜZOİDAL İŞARET NEDİR?
Bir sinüzoidal işaret, genlik tepe değeri, frekansı, ve fazı ile en genel olarak tanımlanabilir. Fig 5.
Fig 5. Örnek sinus işareti
f =
1
Hz
T
f :frekans(Hz)
T : peryod (s)
2
ω = 2πf =
2π
rad/s ω : açısal frekans
T
Va : Sinüs işaretinin tepe değeri
RMS veya Efektir Değer =
Va
2
RMS: root mean square
RMS (efektif değer) bir sinüzoidal işarete ilişkin güç hesaplamakta kullanılır.
ANALOG ve DİJİTAL İŞARETLER
Analog işaretler, x eksenindeki her değerin y ekseninde herhangi bir değere karşılık düşebildiği işaretler
olarak tanımlanabilir. (Fig 1.) Analog işaretler, digital işaretlere dönüştürülürken, önce x ekseninden belli bir
sıklıkla (tasarımcı tarafından belirlenir) örnekler alınır. Bu aşamada işarete örneklenmiş işaret adı verilir. Fig 6.
Fig 6. Fig 1’deki işaret örneklendikten sonra
Örnekleme sıklığı, örnekleme frekansı veya örnekleme peryodu ile tanımlanır. Örnekleme peryodu Fig 6’daki
gösterim için t1 − t 0 şeklinde ifade edilebilir ve Ts ile ifade edilebilir. Yine örnekleme frekansı Fs =
1
olarak
Ts
ifade edilebilir. Figure 1’deki analog işareti, dijital işarete dönüştürmek için gereken ikinci adım ise, örneklenmiş
işareti quantalanmış işaret haline dönüştürmektir. Quantalama işleminde esas olan, genlik bilgilerini belli sayıda
digit kullanarak ifade etmektir. Mesela, 4 bit ile quantalama yapılıyorsa ve analog işaret genlik aralığı 32 ise
[0 V~32 V] bu durumda herbir seviye aralığı 1.25 V’a karşılık gelecektir. Şöyleki ;
0-1: 0001
1-3: 0010
3-5: 0011
etc… şeklinde.Basitçe görülebileceği üzere, kaç bit ile quantalama yaptığınız, quantalama yapılırken kaçınılmaz
olarak oluşacak hata miktarını düşürecektir. Ancak quantalama için kullanılacak olan bit sayısını arttırmakta,
gerekli hardware miktarını arttıracağı için ek maliyet anlamı taşıyacağından, tasarımcının bu noktada bir karar
vermesi yerindedir. Hem yeterli ölçüde hassas bir kuantalama hem de optimum harware (resource) kullanımı.
Qauntalama için kullandığınız bit sayısını arttırmakla, işlem çözünürlülüğünü arttırmış olursunuz. Tersi durum
3
da geçerlidir. Quantalama işlemi sonrasında, elde ettiğiniz işaret artık dijital bir işarettir. Günümüzde, bilinen
ismiyle ADC (analog digital converter) değişik yaklaşımlar kullanarak (trend örnekleme ve quantalama
teknikleri) esas olarak yukarıda anlatılan işlemi yapmaktadırlar. Girişine analog işareti kabul eden ve çıkışında
sayısal (digital) işaret üreten bir ADC yapısına ilişkin gösterim Fig 7’de verilmiştir.
Fig 7. ADC örneği
KUVVETLENDİRİCİLER (AMPLIFIERS)
En genel tanımı ile bir kuvvetlendirici, zayıf (küçük) bir giriş işaretini, kuvvetlendirerek büyük ve daha
anlamlı, ve yine işlenebilir hale dönüştürmek amacıyla oluşturulan elektronik sistemlerdir. Sensorler
(transducerlar) genel olarak, fiziksel büyüklüklerden, zayıf veya küçük elektriksel işaretler üretirler. Bu
işaretlerin işlenebilmesi için belli bir seviyeye çekilmeleri gereklidir ki bu işlemi kuvvetlendiriciler yapar.
Kuvvetlendiriciler, her zaman kuvvetlendirme işlemi yapmak durumunda değildir. Zayıflatma işlemi de
yapabilir. Bu noktada tasarımcı, elektronik sistemini, giriş işaretim ne, benim bu işaret üzerinde şu işlemi
yapabilmem için benim ihtiyacım olan (çalışmam gereken) gerilim veya akım seviyeleri ne sorularına cevap
vererek tasarımını yapar. Bu yüzden bazen giriş işaretinin zayıflatılması gerekebilir. Bu noktada da
kuvvetlendiriciler kullanılır. Bu kuvvetlendiricilerin kazançları 1’den küçüktür.
Kazanç, yükte mevcut olan gerilim, akım, veya gücün, kaynak tarafından sağlanan gerilime, akıma veya
güce oranı olarak ifade edilir. Sırasıyla bu oranlar, gerilim kazancı, akım kazancı, ve güç kazancı olarak
isimlendirilir. En genel olarak kazanç ;
x o (t ) = Ax s (t ) şeklinde ifade edilir.
x o (t ) :çıkıştaki yükte gözlenen (elde edilen) işaret
x s (t ) :giriş işareti
SORU : Bir kuvvetlendiriciye ait grafiksel gösterim nasıl olmalıdır ? Nasıl olmasını beklersiniz.
CEVAP: Yukarıdaki kazanç ifadesine bakılacak olunursa, bunun eğimi A olan birinci dereceden bir eğri olacağı
açıktır. Fig 8.
Fig 8. Kuvvetlendiriciye ait grafiksel gösterim ?
Evet, şekil 8’de gösterilen eğri, yukarıdaki kazanç ifadesini sağlıyor. Ancak bu gösterim her zaman doğru mu ?
Maalesef hayır. Kuvvetlendiriciler, belli bir gerilim (akım) seviyesine kadar, lineer olarak giriş işaretini başarıyla
kuvvetlendirir ancak, belli bir seviyenin üzerinde saturasyona (doyuma) maruz kalırlar. Bu durum Fig 9’da
gösterilmiştir. L+ ve L− bir kuvvetlendiriciye ait üst ve alt saturasyon noktalarını temsil etmektedir. Şekil
incelenecek olursa, saturasyon noktaları arasında giriş işaretinin başarıyla temsil edildiklerini gözlemlemekteyiz
ancak, saturasyon noktalarının aşılması durumunda, sistemin artık bir kuvvetlendirme yapmadığı görülmektedir.
4
Tasarımcının bu sebebden bu alt ve üst limitlere dikkat etmesi gereklidir aksi taktirde çıkışta bozulmuş
(distorsiyona uğramış) işaret elde edecektir.
Fig 9. Kuvvetlendiriciye ait giriş çıkış ilişkisi (transfer karakteristiği).
Girişe uygulanan sinus işaretinin çıkışa nasıl yansıdığını inceleyiniz.
Her kuvvetlendirici tasarımı, Fig 9’daki kadar lineer bir karakteristik göstermemektedir. Fig 9’da verilen
kuvvetlendirici tamamen lineer bir kuvvetlendiricidir. (saturasyon aralığı sınırları içerisinde). Ancak her
kuvvetlendirici bu denli lineer bir karakteristik ortaya koymamaktadır. Bu durum Fig 10.da gösterilmektedir.
Fig 10. Ideal olmayan kuvvetlendiriciye ilişkin transfer karakteristiği
5
Fig 10.’da gösterilen, bir kuvvetlendiriciye ait transfer karakteristiği üzerinde, giriş işaretinin yukarıdaki
bölümde olduğu gibi lineer olarak kuvvetlendirilebilmesi için, Fig 10’daki transfer eğrisi üzerinde lineer bir
bölge seçilmeli ve o lineer bölge içerisinde çalışılmalıdır. Bu gibi durumlarda ilk yapılması gereken nokta, Q ile
ifade edilen bir çalışma noktasının seçilmesidir. Q öyle bir noktadır ki, girişe girilen peryodik bir işaretin
maximum ve minimum noktalarında distorsiyon oluşmaz. Elbette girişe girilen işaretin büyüklüğü fazla ise,
distorsiyon kaçınılmazdır.
Örnek vermek gerekirse, girişte
v a (t ) gibi bir sinusoidal bir işaretiniz olsun. Sizin kuvvetlendiricinizin
gerilim transfer karakteristiği Fig 10.’da verildiği gibi olsun. Fig 10’daki grafiği de dikkate alacak olursanız,
sizin sinüzoidal işaretinizi olduğu gibi uygulamanız durumunda çıkışta elde edeceğiniz işaret (gerilim) L− ‘ye,
yani alt saturasyon gerilimine eşit bir değer olacaktır. Bu son ifadeyi değerlendiriken, Fig 9’dan da
faydalanabilirsiniz. Kuvvetlendirme işlemini düzgün bir şekilde yerine getirebilmeniz için, öncelikle giriş
sinüzoidal işaretinizi, Q dc çalışma noktasına taşımanız gerekmektedir. Ve bu sayede giriş sinus işaretinizin Q
etrafında salınım yapmasına imkan vermeniz gerekir. Yani bu durumda, girişe V I + v a (t ) şeklinde bir işaret
uygulamanız gerekir. V I ’nın ne olduğuna Fig 10’dan da bakınız. ( V I , Q noktasında çalışabilmek için girişe
uygulanması gereken işaretin DC bileşeni) Sonuçta, çıkışta, düzgün bir şekilde kuvvetlendirilmiş, ama içerisinde
DC bileşende barındıran bir işaret elde edilecektir. DC bileşeni bertaraf etmek için ise kapasite kullanılılır ve
elimizde asıl kuvvetlendirmek istediğimiz AC işarete ait kuvvetlendirilmiş çıkış kalacaktır.
Fig 10’daki eğriyi, Q noktası çevresinde lineer kabul edersek, Q noktasındaki eğim (yani türev) bize
gerilim kazancını verir.
GERİLİM KAZANCI:
vo
(çıkış geriliminin giriş gerilimine oranı)
vi
Giriş Gerilimi : Kaynak tarafından sağlanan gerilim. ( v i )
Gerilim Kazancı = Av =
Çıkış Gerilimi : Yüke aktarılan gerilim ( v o )
AKIM KAZANCI:
io
(çıkış akımının giriş akımına oranı)
ii
Giriş Akımı : Kaynak tarafından devreye verilen akım ( ii )
Çıkış Akımı : Yük üzerinden akan akım ( io )
Akım Kazancı = Ai =
Fig 10
GÜÇ KAZANCI:
Güç Kazancı = A p =
P vi
yükte _ harcanan _ güç
= o = oo
kaynak tan_ çekilen _ güç Pi
vi ii
2
GÜÇ: Bir devre elemanına ait güç hesaplarken, I R , V
2
R
, veya VI kullanılabilir. Devrenin güç harcaması
hesaplanırken üçüncü yani VI kullanılır. V kaynağın sağladığı gerilim ve
göstermektedir.
6
I da kaynaktan çekilen akımı
Desibel (decibel/db) kazançları ifade ederken, sıklıkla kullanılan bir gösterim şeklidir. Aşağıda sırasıyla
desibel olarak gerilim kazancı, akım kazancı, ve güç kazancı ifadeleri verilmiştir.
Gerilim Kazancı = 20 log | AV | db
AkımKazancı = 20 log | Ai | db
Güç Kazancı = 10 log |
A p | db
şeklindedir.
Bir kuvvetlendiricinin, elbette hiçbir başka kaynak kullanmaksızın, sadece kuvvetlendirilmesini
istediğimiz giriş işaretini uygulayarak, sözkonusu giriş işaretinin kuvvetlendirmesi beklenemez.
Kuvvetlendiriciler, DC (direct current) kaynaklar tarafından beslenirler. Bu DC kaynaklar, devrenin girişe
uygulanan küçük işaretin, çıkışta istenilen bir büyüklüğe çekilmesine olanak verir. Bir noktada asıl enerji
kaynağı DC beslemeler olup, girişe uygulanan küçük işaret sadece kuvvetlendirilmesi istenen işarettir. Giriş
kaynağından çekilen güç, DC beslemelerden çekilen gücün %1’i mertebelerindedir. Yine, bir kuvvetlendirici
yapısı içerisinde, harcanan toplam gücün büyük bir yüzdesi ısı enerjisi olarak ortaya çıkar, yüke aktarılan güç
gelen olarak ısı olarak kaybedilen gücün yarısı mertebesindedir. Değişik teknoloji ve tasarım stratejileri için bu
oran değişkenlik gösterebilmekte ancak, yine de ısı enerjisi olarak kaybedilen bu enerjinin kayda değer bir
büyüklükte olduğunu ve sonuçta devrenin verimi üzerinde olumsuz bir etki yarattığını söyleriz. Sizce, günümüz
mikroprocessorlarının üzerlerinde yer alan kocaman soğutucuların sebebi nedir ?
GENEL BİR GERİLİM KUVVETLENDİRİCİ YAPISI:
Her ne kadar bir kuvvetlendirici, 1~20(30) transistor içerebilir. Bir kuvvetlendirici yapısı, transistor
seviyesinde de incelenebileceği gibi, şimdilik model kurmak ve o model üzerinden değerlendirmekle yola
çıkacağız. Aşağıda, Fig 11’de genel bir gerilim kuvvetlendiricisine ait devre yapısı modeli verilmiştir.
Fig 11. Genel bir gerilim kuvvetlendirici devre yapısı modeli
7
Buna göre, (a) girişine uygulanmış bir işaretin olmadığı ve yine çıkışında bir yükün bulunmadığı yapıyı
göstermektedir. (b) de ise kuvvetlendirici girişine v s (t) şeklinde bir işaret uygulanan ve yük tarafında R L
direncinin bulunduğu kuvvetlendirici yapısını görmekteyiz.
Rs girişteki kaynağın iç direncini ifade etmektedir.
Ri devrenin (kuvvetlendiricinin) giriş direncini, Ro ise devrenin (kuvvetlendiricinin) çıkış direncini ifade
etmektedir. Avo yüksüz gerilim kazancını ifade etmektedir. (devrede RL mevcut değil iken).
v
RL
RL
vo = Avo vi
ve Av = o = Avo
R L + Ro
vi
R L + Ro
diğer taraftan;
vi = v s
şeklindedir. Sonuç olarak
Ri
Ri + Rs
vo
oranını elde etmek istersek, yukarıdaki eşitlikleri kullanarak,
vs
vo
Ri
RL
= Avo
vs
Ri + Rs RL + Ro
elde edilir. Bulunan bu değer kaynağın yük geriliminin kaynak gerilimine oranıdır.
ÇOK KATMANLI (KASKOT) KUVVETLENDİRİCİ YAPILARI :
Birçok durumda, istediğimiz kuvvetlendirmeyi sağlayabilmek, tek katmanlı bir kuvvetlendirici yapısı
ile mümkün olmayabilir. (sebeblerine ileriki bölümlerde değineceğiz) Bu gibi durumlarda, birden fazla
kuvvetlendiriciyi, ardışıl olarak (ardarda) bağlamak uygulanan yöntemdir. Böylece, istediğimiz özellikte bir
kuvvetlendirici yapısını elde edebilmek mümkün olmaktadır. Bu konuyu daha detaylı, bir örnek üzerinde
inceleyelim.
Kaskot kuvvetlendirici yapısının girişine uygulanan
v s kaynağının iç direnci R s =100 kΩ olsun. Üç
katmanlı kuvvetlendirici çıkışındaki yükümüz 100 Ω olsun. Fig 12’’yi incelersek, 1. kuvvetlendirici katmanını,
yüksek bir giriş direnci( Ri ) ve normal bir kazancı olan bir kuvvetlendirici yapısıdır. 2. kuvvetlendirici katmanı
ise, giriş direnci 1.ye göre daha düşük bir giriş direnci ama daha yüksek bir kazancı olan bir kuvvetlendirici
katmanıdır. Ve son olarak 3. kuvvetlendirici katmanı ise düşük bir çıkış direnci olan ve kazancı 1 olan bir
kuvvetlendirici yapısını göstermektedir.
Fig 12 Üç katmanlı kuvvetlendirici yapısı
Verilenler ışığı altında, gerilim kazancını, akım kazancını ve güç kazancını hesaplayalım.
8
vi 2
100kohm
=
*10 = 9.9V / V
vi1 100kohm + 1kohm
v i1
1M
=
= 0.909V / V
v s 1M Ω + 100 kΩ
vi 3
10kohm
=
*100 = 90.9V / V
vi 2 10kohm + 1kohm
Buna göre 3 kuvvetlendirici katının toplam kazancı (
vL
100ohm
=
= 0.909V / V
vi 3 100ohm + 10ohm
vL
) = 9.9 * 90.9 * 0.909 = 818V / V . (58.3 dB)
vi1
vL
v
) = 0.909 * ( L ) = 743.5V / V (57.4dB) olarak elde edilir.
vs
vi1
i
v 100ohm
Akım kazancı ( o ) = L
= 8.18 * 10 6 A / A (138.3dB) şeklindedir.
ii
vi1 1Mohm
Devrenin toplam kazancı (
Güç kazancı ise A p =
PL v L iO
=
= 818 * 8.18 * 10 6 = 66.9 * 10 8 W / W (98.3dB) şeklinde
PI
vi1ii
hesaplanabilir.
Yukarıdaki bölümde verilen genel (gerilim) kuvvetlendirici yapısının dışında, giriş/çıkış ilgilenilen
işaretin ne olduğuna bağlı olarak kuvvetlendirici çeşitleri aşağıdaki şekilde verilmiştir.
Fig 13
9
Fig 13’den çıkacak sonuç, ilgilenilen giriş işareti akım/gerilim, ve yine ilgilenilen çıkış işareti
akım/gerilim olabilir ve transfer ifadeleri bu durumlara göre 4 değişik şekilde oluşabilir. (Giriş ve Çıkış
dirençlerinin ideal durumlarda neden şekilde (Fig 13) gösterildiği değerleri aldığını düşününüz.)
Yine kazanç parametlerini inceleyiniz ve bağımlı kaynakların ürettikleri akım/gerilim ifadelerini
irdeleyiniz. Ro dirençlerinin 1 ve 4. durumlarda neden seri, 2 ve 3. durumlarda niçin bağımlı kaynaklara paralel
yerleştirilmesinin sebebi nedir. Bir akım kaynağını nasıl modellersiniz, benzer şekilde bir gerilim laynağını nasıl
modellersiniz ? (Norton ve Thevenin teoremlerini hatırlayınız.)
KUVVETLENDİRİCİLERİN FREKANS CEVABI:
Şu ana kadar, kuvvetlendiricilerin, sadece çıkış/giriş kazançları üzerinde konuşuldu. Bu anlatımın, daha
geniş ve geçerli bir şekli kuvvetlendiricilerin frekans cevabıdır. En genel anlamda, bir kuvvetlendiricinin frekans
karakteristiği iki bileşenden oluşur ki bunlar sırasıyla genlik karakteristiği ve frekans karakteristiği şeklindedir.
Bir devre resistif ise (sadece dirençlerden ibaret ise), söz konusu devrenin frekansa bağımlılığı yoktur.
Veya, frekansla birlikte transfer karakteristiği değişmez. Devre kapasite ve(veya) endüktans elemanları
barındırıyorsa devreye ait transfer ifadesinde ω açısal frekansı kendine yer bulur. Yani bu yeni durumda transfer
fonksiyonu frekansa bağlılık gösterecektir.
Biliyoruz ki, devre girişlerine uygulanan işaretler sinüs toplamları şeklinde işaretlerdir (mesela kare
dalga gibi), o halde kuvvetlendirici devre yapısının hangi frekanslarda ne şekilde davranacağını bilmemiz
gerekir. Bu bilgiyi bize o devreye ilişkin genlik frekans ve faz frekans eğrileri söylemektedir.
Frekans Genlik Karakteristiği: Bir devreye ilişkin, frekansın değişimine bağlı genliğin değişimini
gösteren karakteristik eğridir.
Frekans Faz Karakteristiği: Bir devreye ilişkin, frekansın değişimine bağlı olarak fazın değişimini
gösteren karakteristik eğridir.
Bu olguları, mesela bir kare dalga örneği üzerinden gösterelim. Bir kare dalga, sinüslerden ibaret bir
işarettir. Kare dalgayı oluşturuan her bir sinüsoidal işarete harmonik denir. Bu harmoniklerin frekansları n, 3n,
5n, ……. şeklindedir. Farzedelim ki, alçak geçiren bir filtre tasarladık. (Kuvvetlendirici) Bu durumda, alçak
geçiren filtrenin, kare dalgayı oluşturan harmoniklerden düşük frekanslı olanları geçirmesini, yüksek olanlarını
ise bastırmasını (filtrelemesini) bekleriz. Sonuç olarak filtre çıkışında, kare dalgadan daha farklı bir işaret elde
edeceğimiz açıktır.
Filtreler (Band Geçiren, Alçak Geçiren, Yüksek Geçiren, Band Söndüren, Tüm Geçiren etc) şeklinde
çeşitleri vardır. Bu bölümde, sadece temel, birinci dereceden pasif alçak geçiren filtre yapısı verilecek, ve yüksek
geçiren filtre yapısını sizin ders kitabından incelemeniz istenecektir.
Çıkış işaretine ait genlik değeri
Çıkış işaretine ait faz açısı
Fig 14. Giriş işareti, kuvvetlendirici çıkışında, genlik ve fazındaki değişim.
Vi sin ωt şeklindeki giriş işareti, kuvvetlendirici çıkışında, Vo sin(ωt + φ ) şekline dönüşmüştür.
Vo
Vi
genlik kazancını,
φ −0
ise, faz değişimini göstermektedir. Burada giriş işaretinin faz açısı 0’dır. Sonuç
olarak, kuvvetlendiriciler giriş işaretinin genliği ve fazı üzerinde etkilidirler. Açısal frekansın
genlik ve faz değerleri değişecektir.
H (ω ) =
Vo
Vi
ve
∠H (ω ) = φ
: Genlik ve faz frekans transfer fonksiyonları
10
(ω ) değişimi ile
Bu bölüm içerisinde en temel, birinci dereceden RC filtre yapıları verilecektir. Bir RC devresine ilişkin zaman
sabitinin τ = RC olduğunu ve biriminin sn olduğunu biliyorsunuz. Devre yapısı eğer RC değilde, R ve L
τ = L R şeklinde ifade edilir. ω o özel
karakteristiği üzerinde ω o frekansında, işaret 1
elemanlarından ibaret ise,
Genlik frekans
-3dB’dir. -3dB’in, 1
2
frekansı, köşe frekansı olarak adlandırılır.
2
kadar zayıflar, dB olarak zayıflama ise
sayısına eşitliğini gösteriniz.Sonuç olarak güç işaretin karesiyle orantılı olduğuna
göre, 3dB noktası gücün yarıya düştüğü frekanstır.
3dB Frekansları
Fig 15. Band Geçiren Bir Filtreye İlişkin Genlik Frekans Karakteristiği
band genişliği adı verilir. Band genişliği içerisinde işaret filtrelenmeden hemen
ω1 ve ω 2 aralığına
hemen olduğu gibi geçirilir iken, band sınırları dışında,
Bir RC devresine ilişkin olarak,
ωo =
1
τ
ω2 < ω
veya
ω < ω1 , işaret bastırılır. Yani filtrelenir.
şeklinde ifade edilir. Birimi radyan/saniyedir. Köşe frekansını Hz
(Hertz) cinsinden elde etmek isterseniz ne yapmalısınız ? Basitçe, f o =
ωo
2π
şeklindedir.
Fig 16. Sırasıyla alçak ve yüksek geçiren en basit RC filtre yapları
Fig. 16’da verilen devre yapılarına ait transfer fonksiyonlarını elde ediniz ve sol taraftaki devre yapısının neden
alçak geçiren ve sağ tarafta yer alan devre yapısının neden yüksek geçiren bir filtre yapısı olduğunu ifade ediniz.
Fig 17. Alçak ve yüksek geçiren filtre yapılarına ait eşitlikler
11
Fig 16’daki devre yapılarına ilişkin eşitlikler, fig 17’de verilmiştir. Bu eşitlikleri irdeleyiniz ve elde etmeye
çalışınız. Fig 17’de ilk satırda yer alan formül içerisindeki s ifadesi, jω => s dönüşümü yapılarak ikinci
satırdaki formüle dönüşür. S domeni ile ilgili bir incelememiz olmayacaktır, o sebebden s ifadesi yer alan
eşitlikleri göz ardı edebilirsiniz. (Bir kapasitenin empedansı :
1
, bir endüktansın empedansı : jωL ve bir
jωC
resistansın empedansı ise : R ’ olarak verilmektedir. ) Fig.17’de verilen ifadelerde yer alan K değerlerinin neler
olmaları gerektiğini, Fig 16’daki devre yapıları için bulunuz.
Fig 18. Fig 16’da verilen alçak geçiren filtre yapısına ilişkin genlik frekans ve faz frekans eğrileri
Fig 16’daki alçak geçiren filtre yapısı için, Fig 17’deki eşitliklerden faydalanarak, Fig 18’deki eğrileri,
matlab kullanarak çizdiriniz. (x ekseninin logaritmik çizildiğine dikkat edeniz)
Örnek Problem :
Fig 19
Rs : kaynak direnci, Ri : giriş direnci, Ro : çıkış direnci, RL: yük direnci
Ci : giriş kapasitesi
Vs : gerilim kaynağı
μ : kazanç faktörü şeklinde verilmektedir. Bu durumda;
12
a)
Vo
ifadesini, frekansın bir fonksiyonu olarak elde ediniz. Elde edilen bu eşitlikten yararlanarak, dc kazancı ve
Vi
3dB köşe frekansını elde ediniz.
b) Rs : 20kohm, Ri : 100kohm, Ro :200ohm , RL: 1kohm Ci : 60pF
frekansını, ve kazancın 0 dB’e düştüğü frekansı elde ediniz.
μ : 144 V/V alarak dc kazancı, 3dB köşe
c) vo (t ) ifadesini, aşağıda verilen herbir giriş gerilimi için hesaplayınız.
1.
vi = 0.1sin 10 2 t , V
2.
vi = 0.1sin 10 5 t , V
3.
vi = 0.1sin 10 6 t , V
4.
vi = 0.1sin 10 8 t , V
Çözüm:
a)
Vi
Zi
1
1
=
=
=
Vs Z i + Rs 1 + Rs [( 1 ) + jωC i ] 1 + ( Rs + jωC R )
i s
Ri
Ri
RL
R L + Ro
Vo = μVi
Vo
1
=μ
R
Vs
1+ ( s
dc kazanç =
Ri
) 1+ (
1
Ro
1
) 1 + jωCi [( Rs Ri ) /( Rs + Ri )]
RL
RR
τ = C i s i = C i ( Rs Ri )
Rs + Ri
Vo
Vs
=μ
ω =0
1+ (
1
Rs
Ri
) 1+ (
1
Ro
olarak
RL
)
ve
3 dB noktası (köşe frekansı) =
1
τ
=
1
olarak elde edilir.
Ci ( Rs Ri )
b) Soruda verilen değerler, birimleri de dikkate alarak yukarıdaki formüllerde yerlerine konulduklarında,
aşağıdaki sonuçlar elde edilir.
dc kazanç = 100V/V ;
3 dB noktası (köşe frekansı) =
ω o = 106 rad/sn
veya
fo =
10 6
= 159.2 kHz olarak
2π
elde edilir. Siz verilen değerleri yerlerine koyarak değerleri elde ediniz. Çünki birimlerden kaynaklı hatalar
sıklıkla yapılan hatalar arasında yer almaktadır.
Kazanç 100 V/V olarak bulunmuştu. (b) şıkkı. Yani 40 dB. Kazanç, köşe frekasınının devamında, 20dB/decade eğimle azalmaktadır. (decade : 10 katlık artımlara verilen addır.) Herbir decade için 20 dB azalma
sözkonusu ise, iki decade sonucunda, yani köşe frekansının 100 katı bir frekans değerinde, kazancın dB olarak
sıfır olacaktır. Sonuç olarak kazancın 0 dB olduğu frekans = 100* ω o = 15.92MHz olarak elde edilebilir.
13
c)
Verilen 4 farklı sinuzoidal giriş işaretine ait çıkış işaretlerini elde etmek için, söz konusu sinuzoidal
giriş işaretlerine ait frekanslardaki, ilgilendiğimiz devrenin kazancını ve fazını hesaplamamız gerekmektedir. İlk
durum için incelememizi yapalım.
i.
ω =102rad/sn olarak verilmiş.
| T ( jω ) |=
K
1 + j (ω
ϖo
)
K
=
1 + j (ω
∠T ( jω ) = φ = − tan 10
−1
−4
10
6
)
ω =10 2
≅ 100
≅ 0 derece
vi = 0.1sin 10 2 t , V olduğuna göre, vi = 10 sin 10 2 t , V şeklindedir.
ii.
ω =105rad/sn olarak verilmiş.
| T ( jω ) |=
K
1 + j (ω
ϖo
)
=
K
1 + j (ω
6
)
ω =105
≅ 99.5
10
∠T ( jω ) = φ = − tan 10 ≅ −5.7 derece
−1
−1
vi = 0.1sin 10 5 t ,V olduğuna göre, vi = 9.95 sin(10 5 t − 5.7 o )t ,V şeklindedir.
Diğer iki giriş işaretine ait çıkış gerilimlerinin ne olması gerektiğini elde ediniz.
Î Değişik çeşitlerdeki kuvvetlendirici ve filtre yapıları hakkında özet bilgi için, ders kitabınızdan sayfa
38’de bulunan, “Classification of Amplifiers Based on Frequency Response” okuyunuz.
INVERTER :
Sayısal elektroniğin temel yapısıdır. Birçok kompleks sayısal yapıya ışık tutması nedeni ile, verilmesi
ve anlaşılması önemlidir. En genel anlamda inverter, girişine uygulanan lojik 1(0)’a çıkış olarak 0(1) üreten
devre elemanıdır. Bir inverter’a ait giriş çıkış gerilim karakteristiği aşağıdaki şekilde verilmiştir.
Fig 20. İdeal inverter’a ait gerilim transfer karakteristiği
14
Fig 20. Inverter için gerilim transfer karakteristiği (Lineerleştirişmiş)
VOL : Çıkış düşük seviye
VOH : Çıkış yüksek seviye
VIL : Inverter’ın girişi 0 olarak yorumlayabilmesi (kabul edebilmesi) için tanımlı maksimum giriş değeri
VIH : Inverter’ın girişi 1 olarak yorumlayabilmesi (kabul edebilmesi) için tanımlı minimum giriş değeri
NM L : Düşük seviye gürültü marjı
NM H : Yüksek seviye gürültü marjı
Gürültü marjlarının yeterince yüksek olması, tasarımcının dikkate alması gereken önemli bir konudur. Çünki,
dikkatle bakılacak olunursa, bu gürültü marjları, dijital (sayısal) elektronik devre yapılarını, gürültü gibi dış
(external) bozucu kaynakların etkilerinden korur. Söz konusu bozucu, dış kaynaklı bu gürültü işaretler, genelde
düşük genlikli olup, sayısal devre yapısı içerisinde, tanımlı bu gürültü marjları nedeniyle kaybolurlar ve işlem
üzerinde negatif bir etki yaratmamış olurlar.
INVERTER ÇALIŞMA MANTIĞI :
Inverter, toprak (ground) ve besleme (supply) arasına, anahtar(lar) yerleştirilmesi ve bu hat üzerinden belli bir
noktada çıkış işaretinin alınması şeklinde çok kabaca ifade edilebilir. Aşağıda bazı inverter gerçeklemeleri
verilmiştir.
Fig 21. En basit inverter yapısı / Tek anahtarlı yapı
15
Fig 22 İki anahtarlı CMOS inverter yapısı
Fig 21’deki yapıda, anahtar (transistor) ile inverter yapısı oluşturulmuştur. İki durum vardır, bunlar
sırasıyla giriş düşük (low) veya yüksek (high) şeklindedir. Girişin düşük (low) olduğu durumda anahtar açık
olacak, (transistor kesimde olacak) ve çıkış gerilimi VDD, yani yüksek (high) olacaktır.
Sayısal tasarımlarda, bir transistörü, kabaca bir anahtar ve ona seri bir direnç elemanı olarak
modelleyebiliriz.
Girişin yüksek olduğu durumda ise, anahtar (transistor iletime geçecek) kapanacak. Anahtar kapalı
olduğu bu durumda devre bir gerilim bölücü şeklinde çalışmaya başlayacaktır. R direnci, RON direncinden
yeterince büyük seçilirse, vo çıkış gerilim değerinin, girişin yüksek (high) olduğu bu durum için, 0’a yakın bir
değer olacağını rahatlıkla söyleyebiliriz.
Voffset gerilimi, kullanılan anahtar elemanının bir bipolar transistor olması halinde karşılaştığımız,
transistor ün saturasyonda çalışması halinde modellerken kullandığımız oldukça düşük değerli bir gerilim
kaynağıdır.
Fig 22 için, siz düşününüz ve yorumlamaya çalışınız. Burada iki anahtar (transistor) kullanılmış, Fig
21’deki yapıya göre daha başarılı bir yapıdır.
Örnek Problem : Kitap Sayfa 46 / Example 1.6
Aşağıdaki şekilde, bir inverter yapısı verilmektedir. Fig 23. Voffset = 0.1V olarak verilmiştir. t=0 anında, girişin
yüksek seviyeden, düşük seviyeye geçtiğini farzederek (high=Îlow), çıkış
geriliminin (VOH+VOL)/2 değerine yükselmesi için geçen süreyi hesaplayınız.
Çözüm:
VOL = Voffset +
VDD − Voffset
R + Ron
Ron =0.55V
çıkış geriliminin (VOH+VOL)/2 değeri, VOH ve VOL değerlerinin aritmetik
ortalamasıdır. O halde
VOL değerinden, (VOH+VOL)/2 değerine ulaşmak için gereken süreyi;
Fig 23.
16
−t
0.5 = e τ eşitliğinden yararlanarak elde edebiliriz. Buradan, t= -(ln0.5)* τ olacaktır. τ yerine RC
değeri konulursa, sonuç aşağıdaki şekilde elde edilir.
t=0.69 RC = 6.9 ns.
Ders kitabınızda Chapter 1 konu anlatımı kısmını incelemenizi öneririm. Ek olarak kitabınızın sonunda yer alan
“APPENDIX” kısmında yer alan, C1, C2, D1, D2, D3, ….., D7, D8, D9 sayfalarındaki konu anlatımlarını
gözden geçiriniz. Ayrıca, yine kitabınızın konu anlatımı kısmı içerisinde yer alan çözümlü soruları da
inceleyiniz.
APPENDIX kısmında yer alan, G2 sayfasını çalışınız.
END OF WEEK I
17










