Veri Madenciliği
advertisement

Veri Madenciliği
Bölüm 8. Kümeleme 2
Doç. Dr. Suat Özdemir
http://ceng.gazi.edu.tr/~ozdemir
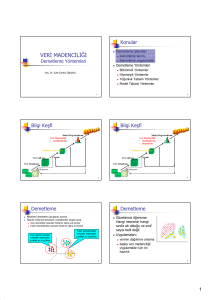
Demetleme - 2
§ Demetleme yöntemleri
– Yoğunluk tabanlı
– Model tabanlı
§ Outlier analizi
§ Değerlendirme
Veri Madenciliği
Doç. Dr. Suat Özdemir
Demetleme nedir?
§ Nesneleri demetlere (gruplara) ayırma
– Karakteristiklerden yararlanarak veri içindeki
benzerlikleri bulma ve benzer verileri demetler içinde
gruplama
§ Demet: birbirine benzeyen nesnelerden oluşan
grup
– Aynı demetteki nesneler birbirine daha çok benzer
– Farklı demetlerdeki nesneler birbirine daha az benzer
Veri Madenciliği
Doç. Dr. Suat Özdemir
Demetleme–Sınıflandırma Farkı
§ Demetleme: Gözetimsiz öğrenme (Unsupervised
learning)
– Hangi nesnenin hangi sınıfa ait olduğu ve sınıf sayısı belli değil
§ Sınıflandırma: Gözetimli öğrenme
(Supervised learning)
– Öğrenme kümesindeki sınıfların sayısı ve hangi nesnenin hangi sınıfta
olduğu biliniyor.
Veri Madenciliği
Doç. Dr. Suat Özdemir
Temel Demetleme Yaklaşımları
§ Bölünmeli yöntemler: Veriyi bölerek, her grubu
belirlenmiş bir kritere göre değerlendirir
§ Hiyerarşik yöntemler: Veri kümelerini (ya da
nesneleri) önceden belirlenmiş bir kritere göre
hiyerarşik olarak ayırır
§ Yoğunluk tabanlı yöntemler: Nesnelerin
yoğunluğuna göre demetleri oluşturur
§ Model tabanlı yöntemler: Her demetin bir
modele uyduğu varsayılır. Amaç bu modellere uyan
verileri gruplamak
Veri Madenciliği
Doç. Dr. Suat Özdemir
Bölmeli Yöntemler: K-means Demetleme
§ Bilinen bir k değeri için k-means demetleme
algoritmasının 4 aşaması vardır:
– Veri kümesi k altkümeye ayrılır (her demet bir altküme)
– Her demetin ortalaması hesaplanır: merkez nokta (demetteki
nesnelerin niteliklerinin ortalaması)
– Her nesne en yakın merkez noktanın olduğu demete dahil edilir
– Nesnelerin demetlenmesinde değişiklik olmayana kadar adım
2’ye geri dönülür.
Veri Madenciliği
Doç. Dr. Suat Özdemir
Hiyeraşik Yöntemler: Agglomerative Demetleme Algoritması
§ En çok kullanılan hiyeraşik demetleme algoritması
– Oldukça basit
§ En önemli işlem iki demet arasındaki yakınlığın bulunması
Veri Madenciliği
Doç. Dr. Suat Özdemir
Yoğunluk Tabanlı Yöntemler
§ Demetleme nesnelerin yoğunluğuna göre yapılır.
§ Başlıca özellikleri:
– Rasgele şekillerde demetler üretilebilir.
– Aykırı nesnelerden etkilenmez.
– Algoritmanın son bulması için yoğunluk parametresinin
verilmesi gerekir.
§ Başlıca yoğunluk tabanlı yöntemler:
– DBSCAN: Ester, et al. (KDD’96)
– OPTICS: Ankerst, et al (SIGMOD’99).
– DENCLUE: Hinneburg & D. Keim (KDD’98)
– CLIQUE: Agrawal, et al. (SIGMOD’98)
Veri Madenciliği
Doç. Dr. Suat Özdemir
DBSCAN
§ İki parametre:
– Eps: En büyük komşuluk yarıçapı
– MinPts: Eps yarıçaplı komşuluk bölgesinde bulunması gereken en
az nesne sayısı
• Neps(p): {q Є D | d(p,q)≤Eps}
§ Bir nesnenin Eps’si içinde MinPts kadar nesne varsa bu nesne
çekirdek nesne olarak adlandırılır
– |Neps(q)|≥MinPts
§ Doğrudan erişilebilir nesne: Eps ve MinPts koşulları altında
bir q nesnesinin doğrudan erişilebilir bir p nesnesi şu şartları
sağlar:
– p Є Neps(q)
– q çekirdek nesne
p
q
p nesnesine q nesnesiden doğrudan erişilebilir
Veri Madenciliği
Doç. Dr. Suat Özdemir
MinPts = 5
Eps = 1 cm
DBSCAN
§ Erişilebilir nesne:
– Eps ve MinPts koşulları altında q nesnesinin
erişilebilir bir p nesnesi olması için:
• p1,p2,...,pn nesne zinciri olması,
• p1=q, pn=p,
• pi+1 nesnesi pi den dogrudan erisilebilir
olmalidir
p
q
§ Yoğunluk bağlantılı nesne:
p1
– Eps ve MinPts koşulları altında q nesnesinin
yoğunluk bağlantılı nesnesi p şu koşulları
sağlar:
• D nesne kümesi içinde o diye hem p ye hem
de q ya erişebilen bir nesne varsa, p ve q
yoğunluk bağlantılı nesnelerdir
• p ve q nesneleri Eps ve MinPts koşulları
altında bir o nesnesinin erişilebilir nesnesidir.
p
q
o
Veri Madenciliği
Doç. Dr. Suat Özdemir
Örnek
§ MinPts=3
§ m,p,r çekirdek nesne
§ q nesnesi m nesnesinin doğrudan
erişilebilir nesnesi
§ m nesnesi q nesnesinin doğrudan
erişilebilir nesnesi değil (q çekirdek değil)
§ m nesnesi p nesnesinin doğrudan
erişilebilir nesnesi
§ q nesnesi p nesnesinin erişilebilir nesnesi
(çünkü m nesnesi p nesnesinin doğrudan
erişilebilir nesnesi)
§ p nesnesi q nesnesinin erişilebilir nesnesi
değil (çünkü q çekirdek nesne değil)
§ Aynı şekilde r nesnesi p nesnesinin
erişilebilir nesnesi
§ r,p ve q nesneleri yoğunluk bağlantılı
nesneler
Veri Madenciliği
Doç. Dr. Suat Özdemir
m
p
r
q
DBSCAN
§ Veri tabanındaki her nesnenin Eps yarıçaplı komşuluk
bölgesi araştırılır.
§ Bu bölgede MinPts’den daha fazla nesne bulunan p nesnesi
çekirdek nesne olacak şekilde demetler oluşturulur.
§ Çekirdek nesnelerin doğrudan erişilebilir nesneleri
bulunur.
§ Çekirdek nesnelerin erişilebilir nesneleri bulunur.
§ Yoğunluk bağlantılı demetler birleştirilir.
§ Hiçbir yeni nesne bir demete eklenemezse işlem sona erer.
§ Yer karmaşıklığı – O(n)
§ Zaman karmaşıklığı – O(nlogn)
– n: nesne sayısı
Veri Madenciliği
Doç. Dr. Suat Özdemir
DBSCAN
§ Gürültülü veritabanlarındaki değişik şekillerdeki demetleri
ortaya çıkarır
Outlier
Border
Core
Veri Madenciliği
Doç. Dr. Suat Özdemir
Eps = 1cm
MinPts = 5
DBSCAN Problemler
§ Kullanıcının minPts and eps eşik değerlerini
belirlemesi gerekir. Bu veri seti hakkında bilgi
sahibi olmayı gerektirir. Çok boyutlu veriler için
belirlenmesi güçtür.
§ Veri setinin dağılımı heryerde aynı olmayabilir.
– Bir bölgedeki yoğunluk diğer bölgelerden çok az olabilir. Ya hiç
demet oluşmaz ya da demetler içinde çok fazla gürültü olur.
§ minPts and eps eşik parametrelerden çok
etkilenir
Veri Madenciliği
Doç. Dr. Suat Özdemir
DBSCAN: Sensitive to Parameters
Veri Madenciliği
Doç. Dr. Suat Özdemir
When DBSCAN Works Well
Original Points
Clusters
• Resistant to Noise
• Can handle clusters of different shapes and sizes
Veri Madenciliği
Doç. Dr. Suat Özdemir
When DBSCAN Does NOT Work Well
(MinPts=4, Eps=9.75).
Original Points
• Varying densities
• High-dimensional data
Veri Madenciliği
Doç. Dr. Suat Özdemir
(MinPts=4, Eps=9.92)
DBSCAN: Determining EPS and MinPts
§
§
§
Idea is that for points in a cluster, their kth nearest
neighbors are at roughly the same distance
Noise points have the kth nearest neighbor at farther
distance
So, plot sorted distance of every point to its kth
nearest neighbor
Veri Madenciliği
Doç. Dr. Suat Özdemir
OPTICS: A Cluster-Ordering Method
§ It addresses one of DBSCAN's major weaknesses: the
problem of detecting meaningful clusters in data of
varying density.
§ DBSCAN Eps değerinden fazlaca etkilenir
– az youğunluklu demetler çok yoğunluklu demetleri içinde barındırır
– gizli kalmış desenler bulunamayabilir
– Çözüm?
• Birden çok Eps değeri üzerinden çalışılabilir
§ OPTICS: Demetleme yapısını ortaya çıkarmak için
nesneleri sıralar
– This cluster-ordering contains info equiv to the density-based
clusterings corresponding to a broad range of parameter settings
– Good for both automatic and interactive cluster analysis, including
finding intrinsic clustering structure
– Can be represented graphically or using visualization techniques
Veri Madenciliği
Doç. Dr. Suat Özdemir
OPTICS: Some Extension from DBSCAN
• Çekidek uzaklığı (core dist.) ve Erişilebilirlik uzaklığı (reachability
dist.)
• Önce tüm nesnelerin Çekidek uzaklığı ve Erişilebilirlik uzaklığı için
bir veri tabanı hazırlar
• Demetlemeye önce küçük Eps değerlerine göre erişilebilir
nesnelerden başlar (böylece yüksek yoğunluklu demetleri önce
bitirir)
Veri Madenciliği
Doç. Dr. Suat Özdemir
OPTICS: Some Extension from DBSCAN
Erişilebilirlik uzaklığı
Tanımsız
ε
ε‘
ε
Grafik olarak kolay ifade edilebilir. Veri Madenciliği
Doç. Dr. Suat Özdemir
Nesneler
OPTICS: Some Extension from DBSCAN
Veri Madenciliği
Doç. Dr. Suat Özdemir
Model Tabanlı Demetleme Yöntemleri
§ Veri kümesi için öngörülen matematiksel model en
uygun hale getiriliyor.
§ Verinin genel olarak belli olasılık dağılımlarının
karışımından geldiği kabul edilir.
§ Model tabanlı demetleme yöntemi
– Modelin yapısının belirlenmesi
– Modelin parametrelerinin belirlenmesi
§ Örnek EM (Expectation Maximization) Algoritması
Veri Madenciliği
Doç. Dr. Suat Özdemir
EM — Expectation Maximization
§ EM — Popüler bir iterative iyileştirme algoritması
§ k-means algoritmasının bir uzantısı olarak görülebilir
– Her nesne bir demete belli bir ağırlığa (olasılık dağılımı) göre
atanır
• Oluşan demetler arasında kesin sınırlar yoktur
– Yeni ortalamalar bu ağırlıklı ölçümlere göre hesaplanır
§ Ana fikir
– Tahmini bir parametre vektörü ile başlanır (expectation)
• Dağılımlar için merkez çap değerleri gibi
– Merkezler için iyileştirme yap (maximization)
– Demetlemeyi iterative bir şekilde yap
– Hızlı bir şekilde tamamlanır ancak herzaman en ideal çözüme
ulaşmayabilir
Veri Madenciliği
Doç. Dr. Suat Özdemir
EM — Expectation Maximization
Veri Madenciliği
Doç. Dr. Suat Özdemir
EM — Expectation Maximization
§ Örnekte verinin 2 demet oluşturduğunu ve bu demetlerin
normal dağılım özelliği gösterdiğini kabul ediyoruz.
§ Model: normal dağılım eğrisi
N(µ1,σ12)
Veri Madenciliği
Doç. Dr. Suat Özdemir
N(µ2,σ22)
Örnek
§ Aşağıdaki 51 örnek verinin
kabul edelim
§ 51 62 64 48 39
§ 43 47 51 64 62
§ 62 52 52 51 64
§ 64 64 62 63 52
§ 45 51 49 43 63
§ 42 65 48 65 64
§ 46 48 62 66 48
§ 45 49 43 65 64
§ 45 46 40 46 48
Veri Madenciliği
Doç. Dr. Suat Özdemir
bu iki normal dağılımdan geldiğini
51
48
64
42
48
41
Örnek
§ EM algoritması kabul edilen bu modelin parametrelerini
bulmaya çalışır
§ {s1, s2,…, sn} örnek veri setini temsil etsin.
§ Bu örnek için bulmamız gereken 5 parametre:
µ1, σ1, µ2, σ2, P(C1).
§ EM algoritması bu parametreler için tahmini değerlerle başlar.
Veri Madenciliği
Doç. Dr. Suat Özdemir
Örnek
§ P(C1)=0.5 olduğunu tahmin edelim.
Buna göre örnek veri setini 2’ye
bölelim
– {51(*2.5),52(*3),62(*5),63(*2),64(*8),65(*3),66(*1)};
– {51(*2.5),49(*2),48(*7),47(*1),46(*3),45(*3),43(*3),
42(*2),41(*1),40(*1),39(*1)};
– µ1=47.63;
– σ1 =3.79;
– µ2=58.53;
– σ2 =5.57.
Veri Madenciliği
Doç. Dr. Suat Özdemir
Örnek
§ Expectation Step: Herhangi bir si örneğinin bu
demetlere ait olma olasılığı aşağıdaki gibi hesaplanır:
Prob[xi | C1 ]Prob[C1 ] Prob[C1 ]
1
Prob[C1 | xi ] =
=
⋅
e
Prob[xi ]
Prob[xi ] 2π σ 1
(
xi − µ1 )2
−
Prob[xi | C2 ]Prob[C2 ] Prob[C2 ]
1
[
]
Prob C2 | xi =
=
⋅
e
Prob[xi ]
Prob[xi ] 2π σ 2
Prob[C1 | xi ]
pi =
,
Prob[C1 | xi ] + Prob[C2 | xi ]
where xi is attribute value of sample si .
Veri Madenciliği
Doç. Dr. Suat Özdemir
2σ 12
(
xi − µ 2 )2
−
2σ 22
Örnek
§ Örneğin değeri 52 olan örnek veri için:
0.5
1
Prob[C1 | 52] =
⋅
e
Prob[x52] 2π ⋅ (3.79)
0.5
=
⋅ 0.1357
Prob[x52]⋅ 2π
(
52 − 47.63)2
−
2⋅(3.79) 2
(
52 −58.53)2
−
0.5
1
2⋅(5.57 ) 2
Prob[C 2 | 52] =
⋅
e
Prob[x52] 2π ⋅ 5.57
0.5
=
⋅ 0.0903
Prob[x52]⋅ 2π
Prob[C1 | x52]
0.1357
pi =
=
= 0.600,
Prob[C1 | x52] + Prob[C 2 | x52] 0.1357 + 0.0903
Veri Madenciliği
Doç. Dr. Suat Özdemir
Örnek
§ Maximization Step: Bulunan bu değerlere göre
parametreler yeniden hesaplanır
n
n
∑px
i
µ1 =
i
i =1
n
∑ (1 − p ) x
i
; µ2 =
i =1
n
∑p
∑ (1 − p )
i
i
i =1
i =1
n
σ 12 =
i =1
n
∑p
i
i =1
n
∑p
i
Veri Madenciliği
Doç. Dr. Suat Özdemir
n
2
∑ pi (xi − µ1 )
P (C1 ) =
i
i =1
n
; σ 22 =
2
∑ (1 − pi )(xi − µ1 )
i =1
n
∑ (1 − p )
i
i =1
Örnek
§ Bu işlemler iteratif olarak tekrar edilir.
§ Genelde, aşağıdaki olabilirlik (likelihood) fonksiyonu
maksimize edilmeye çalışılır
∏ P(C )P[x |C ] + P(C )P[x |C ].
1
i
Veri Madenciliği
Doç. Dr. Suat Özdemir
i
1
2
i
2
Örnek
§ Parametreler belirlendiğinde herhangi bir si örneği
için aşağıdaki eşitsizlik sağlandığında si C1 sınıfına
dahil edilir:
Prob[C1 | xi ]
pi =
> 0.5,
Prob[C1 | xi ] + Prob[C2 | xi ]
Prob[xi | C1 ]Prob[C1 ] Prob[C1 ]
1
Prob[C1 | xi ] =
=
⋅
e
Prob[xi ]
Prob[xi ] 2π σ 1
(
xi − µ1 )2
−
Prob[xi | C2 ]Prob[C2 ] Prob[C2 ]
1
Prob[C2 | xi ] =
=
⋅
e
Prob[xi ]
Prob[xi ] 2π σ 2
§ Aksi durumda, si C2 sınıfına aittir.
Veri Madenciliği
Doç. Dr. Suat Özdemir
2σ 12
−
( xi − µ 2 )2
2σ 22
.
Çok boyutlu veride demetleme
§ Çok boyutlu veride (high-dimensional data) demetleme
– Problemler:
• İligisiz bir çok boyut olası demetleri gizleyebilir
• Uzaklık değerleri anlamsız hale gelir (eşit uzaklıklar)
• Demetler sadece alt uzaylarda olabilir
§ Methods
– Feature transformation: only effective if most dimensions are relevant
• PCA & SVD useful only when features are highly correlated/redundant
– Feature selection: wrapper or filter approaches
• useful to find a subspace where the data have nice clusters
– Subspace-clustering: find clusters in all the possible subspaces
• CLIQUE, ProClus, and frequent pattern-based clustering
Veri Madenciliği
Doç. Dr. Suat Özdemir
Boyut – Demet İlişkisi
§ Tek boyutta veri oldukça sıkışık olarak
görülür
§ Eklenen her boyut veriler arası uzaklığı
biraz daha açar
§ Çok fazla boyut verileri bir birinden çok
uzağa götürür, bu nedenle çok boyutlu
veriler oldukça seyrektir (sparse)
§ Eşit uzaklıklar nedeniyle uzaklık
ölçümleri anlamsız hale gelir
Veri Madenciliği
Doç. Dr. Suat Özdemir
CLIQUE (Clustering In QUEst)
§ Çok boyutlu veride daha iyi demetleme sonuçları verecek alt
uzayları bulmaya yarar
§ CLIQUE hem yoğunluk-tabanlı hem de grid-tabanlı bir sistem
olarak olarak düşünülebilir
– Her bir boyutu eşit aralıklara böler, küçük alanlar
oluşturulur
– Her verinin her boyutunda, küçük alanlar birim alana
düşen nesne sayısına göre incelenir ve yoğun bölgeler
bulunur
– Bir boyutta ki yoğun bölgeler birbirine bağlanarak
demetler oluşturulur
Veri Madenciliği
Doç. Dr. Suat Özdemir
40
50
20
30
40
Vacation
30
Vacation(
week)
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
Salary
(10,000)
20
age
60
30
Veri Madenciliği
Doç. Dr. Suat Özdemir
50
age
50
age
60
Demetleme Değerlendirme
§ En iyi demetleme algoritmasını seçmek zor
§ Verinin istatistiksel özelliğine, önişleme tekniklerine,
nitelik sayısına bağlı olarak algoritmaların avantajları
ve dezavantajları var
§ Aynı veri kümesi üzerinde farklı algoritmalar farklı
demetleme sonuçları üretebilir. Hangi demetlemenin
daha iyi olduğuna karar vermek gerekiyor
§ Uygulama alanını iyi incelemek gerekiyor
Veri Madenciliği
Doç. Dr. Suat Özdemir