T.C.
SELÇUK ÜNĠVERSĠTESĠ
FEN BĠLĠMLERĠ ENSTĠTÜSÜ
FABRĠKA BESLEMELERĠNDE HARMONĠK
ÖLÇÜMÜ VE FĠLTRE TASARIMI
Bahadır AKBAL
YÜKSEK LĠSANS TEZĠ
Elektrik-Elektronik Mühendisliği
Anabilim Dalı
Haziran-2011
KONYA
Her Hakkı Saklıdır
TEZ BĠLDĠRĠMĠ
Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde
edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait
olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.
DECLARATION PAGE
I hereby declare that all information in this document has been obtained and
presented in accordance with academic rules and ethical conduct. I also declare that, as
required by these rules and conduct, I have fully cited and referenced all materials and
results that are not original to this work.
İmza
Bahadır AKBAL
Tarih:
ÖZET
YÜKSEK LĠSANS TEZĠ
FABRĠKA BESLEMELERĠNDE HARMONĠK ÖLÇÜMÜ VE FĠLTRE
TASARIMI
Bahadır AKBAL
Selçuk Üniversitesi Fen Bilimleri Enstitüsü
Elektrik-Elektronik Mühendisliği Anabilim Dalı
DanıĢman: Doç. Dr. Abdullah ÜRKMEZ
2011, 104 Sayfa
Jüri
DanıĢman Doç. Dr. Abdullah ÜRKMEZ
Doç. Dr. Mehmet ÇUNKAġ
Yrd. Doç. Dr. Musa AYDIN
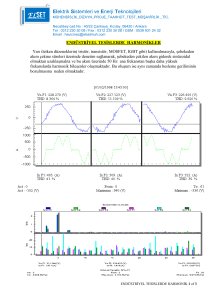
Bu çalışmada fabrika beslemelerindeki harmonikler, çeşitli yöntemlerle incelenmiş ve sistem için
gerekli pasif filtre tasarlanarak uygunluğu tesiste denenmiştir.
Elektrik tesislerinde, çeşitli sebeplerden dolayı sinüs biçimindeki akım ve gerilimin dalga şeklini
bozan harmonikler meydana gelir. Fabrikalarda, güç transformatörü ile kompanzasyon kondansatörlerinin
paralel rezonans oluşturması harmonik bozunumunu artırır. Harmonikler elektrik makinelerinde, enerji
tesisinin çeşitli elemanlarında, elektronik cihazlarda vb. birçok alanda çeşitli kayıplara, arızalara ve hasara
neden olurlar.
Fabrikalar harmonik filtrelemede genellikle seri reaktörlü pasif filtre kullanmaktadır. Seri
reaktörlü pasif filtre, transformatör ile kondansatörler arasındaki paralel rezonans frekansını değiştirerek
harmonik bozunum oranını azaltır.
Bu çalışmada fabrika beslemelerindeki harmonikler, 3 farklı yöntemle incelenmiştir. Bu
yöntemler, harmonik analizörü ile fabrika girişindeki orta gerilim ve alçak gerilim baralarından yapılan
ölçümler, MATLAB programı ile yapılan simülasyon ve tesisin tek hat şeması çıkarılarak yapılan
matematiksel hesaplamadır. Bu 3 yöntemin sonuçları karşılaştırıldığında gerçek ölçümle aralarında çok
küçük farklılıklar olduğu görülmüştür. Bu sonuçlara göre herhangi bir tesisin harmonik analizi, 3
yöntemden biri ile yapılarak uygun filtre tasarlanabileceği gösterilmiştir.
Anahtar Kelimeler: Harmonik, harmonik analiz, pasif filtre, rezonans,.
iv
ABSTRACT
MS THESIS
THE MEASUREMENT OF HARMONIC IN FACTORY SUPPLY AND DESIGN
OF HARMONIC FILTERS
Bahadır AKBAL
THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE
OF SELÇUK UNIVERSITY
THE DEGREE OF MASTER OF SCIENCE
IN ELECTRICAL AND ELECTRONICS ENGINEERING
Advisor: Assoc. Prof. Abdullah ÜRKMEZ
2011, 104 Pages
Jury
Advisor Assoc. Prof. Abdullah ÜRKMEZ
Assoc. Prof. Mehmet ÇUNKAġ
Assist. Prof. Dr. Musa AYDIN
In this study, harmonics in factory supply were analyzed with various methods and a passive
filter which is required for system was designed and examined in the factory.
In electrical systems, harmonics disrupting sinusoidal current and voltage waveform occur. In
the factories, parallel resonance of power transformer with compensation capacitors increase harmonic
distortion. Harmonics cause various losses, fault, and damages in many areas such as various components
of energy system, and electronic equipments.
Factories usually use passive filter with serial reactor to filter harmonics. The passive filter with
serial reactor decrease harmonic distortion by changing parallel resonance frequency between transformer
and capacitors.
In this study, harmonics in factory supply were analyzed with 3 different methods. These
methods are measurements from low voltage and medium voltage busbars in factory supply with
harmonic analyzer, simulation with Matlab software, and mathematical computations by taking one-line
diagram of the factory. It was observed that there was very little difference between results of 3 methods
and real measurements. According to these results, it was shown that appropriate filter can be designed by
analyzing harmonics of any factory with one of the 3 methods.
Keywords: Harmonic, harmonic analysis, passive filter, resonance.
v
ÖNSÖZ
Mühendislik mesleğini edinene kadar emeği geçen ve Elektrik Elektronik
Mühendisliğinin inceliklerini öğreterek bu mesleği sevmeme vesile olan hocalarıma,
ayrıca yüksek lisans eğitimimde bana desteğini esirgemeyen,
kıymetli hocam
Doç. Dr. Abdullah ÜRKMEZ‟e saygılarımı ve teşekkürlerimi arz ederim.
Öğretim hayatım boyunca her türlü maddi manevi desteğini esirgemeyen çok
değerli babam Erol AKBAL, annem Nurgül AKBAL,
kardeşim ve eşim‟e, ayrıca
yüksek lisans eğitimim için birçok olanak sağlayan Ramazan KOÇAK‟ a teşekkürü bir
borç bilirim.
Bahadır AKBAL
KONYA-2011
vi
ĠÇĠNDEKĠLER
TEZ BĠLDĠRĠMĠ ………………………………………………………….…………. iii
ÖZET ......................................................................................................................... iv
ABSTRACT .................................................................................................................v
ÖNSÖZ ...................................................................................................................... vi
ĠÇĠNDEKĠLER ........................................................................................................ vii
SĠMGELER VE KISALTMALAR........................................................................... ix
1. GĠRĠġ .......................................................................................................................1
2. KAYNAK ARAġTIRMASI ....................................................................................3
3. HARMONĠKLER....................................................................................................7
3.1. Reaktif Güç Kompanzasyonu ..............................................................................7
3.2. Harmonikler .......................................................................................................9
3.2.1. Harmonik üreteçleri ................................................................................... 10
3.2.1.1. Güç transformatörleri ..........................................................................10
3.2.1.2. Alternatörler ......................................................................................... 12
3.2.2.3. Statik dönüştürücüler ............................................................................ 12
3.2.1.4. Ark fırını ............................................................................................. 13
3.2.1.5. Gaz boşalma ilkesine göre çalışan aydınlatma elemanları .................... 14
3.2.2. Harmoniklerin etkileri ................................................................................ 15
3.2.2.1. Güç transformatörleri üzerindeki etkileri .............................................. 15
3.2.2.2. Döner elektrik makineleri üzerindeki etkileri ........................................ 16
3.2.2.3. Kesici ve sigortalar üzerindeki etkileri .................................................. 17
3.2.2.4. Kondansatörler üzerindeki etkileri ....................................................... 17
3.2.2.5. İletkenler üzerindeki etkileri ................................................................. 17
3.2.2.6. Rezonans etkisi .................................................................................... 19
3.2.3. Diversite etkisi ........................................................................................... 21
3.2.4. Harmonik bozunum sınırları ve harmoniklerin oluşum durumları ............... 21
3.2.5. Elektrik tesislerinde bulunan harmonik çeşitleri ......................................... 23
3.2.6. Harmoniklerin matematiksel analizi ........................................................... 24
3.2.7 Güç transformatörlerinin bağlantı gruplarına göre harmonik analizi ............ 28
3.2.7.1. Primer sargısının Yy0 bağlantı gurubunda harmonik analizi ................. 29
3.2.7.2. Primer sargısının üçgen bağlantı gurubunda harmonik analizi .............. 32
3.2.8. Harmoniklere karşı alınan önlemler ............................................................ 35
3.2.8.1. Alternatörlerde harmoniklere karşı alınan bazı önlemler ....................... 36
3.2.8.1.1. Sargı kirişleme faktörü ile belli harmoniklerin yok edilmesi ....... 36
3.2.8.1.2. Sargı yayılma faktörü ile belli harmoniklerin yok edilmesi ..........38
3.2.8.2. Statik dönüştürücülerde belli harmoniklerin yok edilmesi ..................... 39
3.2.8.3. Güç transformatörlerinde belli harmoniklerin yok edilmesi .................. 39
3.2.9. Pasif filtreler .............................................................................................. 41
3.2.9.1. Seri pasif filtreler ................................................................................. 41
3.2.9.1. Paralel pasif filtreler ............................................................................. 42
3.2.9.1. Tek ayarlı paralel pasif filtreler ....................................................... 42
vii
3.2.9.2. Çift ayarlı paralel pasif filtreler ....................................................... 43
3.2.9.3. Seri reaktörlü paralel pasif filtreler ................................................. 43
4. MATERYAL VE YÖNTEM ................................................................................ 47
4.1. Harmonik Analizinde Kullanılan Ölçü Cihazları ............................................... 47
4.1.1. Amprobe Genius 5080E harmonik analizörü ............................................... 47
4.1.2. Simeas P660 harmonik analizörü ............................................................... 48
4.1.3. Entes MPR63 harmonik analizörü ............................................................... 49
4.1.4. Circutor AR5 harmonik analizörü .............................................................. 50
4.2. Harmonik Ölçümleri ......................................................................................... 51
4.2.1. Güç transformatörü boşta çalışırken yapılan ölçümler ................................. 51
4.2.2. Harmonik filtre kullanılmayan tesislerde yapılan ölçümler .......................... 53
4.2.2.1. Alçı fabrikasına ait 1250kVA gücündeki güç transformatörün alçak
.
gerilim barasında yapılan ölçümler ..................................................... 53
4.2.2.2. Metal işleme fabrikasına ait 1000kVA gücündeki güç transformatörün
.
alçak gerilim barasında yapılan ölçümler ............................................ 56
4.2.3. Seri reaktörlü pasif filtreli sistemlerde yapılan ölçümler .............................. 51
4.2.4. Seri reaktörlü pasif filtre hesaplamaları ....................................................... 65
4.2.5. Kompanzasyon sisteminin ve seri reaktörlü pasif filtrenin harmonikler
.
üzerindeki etkisi ile ilgili simülasyonlar ...................................................... 69
5. ARAġTIRMA SONUÇLARI VE TARTIġMA ................................................... 76
5.1. Güç Transformatörü Boşta Çalışırken Harmoniklerin Durumu .......................... 76
5.2. Kompanzasyon Kondansatörleri Devrede Değilken Harmoniklerin Durumu ..... 76
5.3. Kompanzasyon Kondansatörleri Devredeyken Harmoniklerin Durumu ............. 77
5.4. Seri Reaktörlü Pasif Filtreli Tesislerde Harmoniklerin Durumu ......................... 78
5.5. Paralel Rezonans Frekansı, Harmonik Akım ve Gerilimin Matematiksel Olarak
.
Hesaplanması.................................................................................................... 79
6. SONUÇLAR VE ÖNERĠLER .............................................................................. 93
6.1. Sonuçlar ...........................................................................................................93
6.2. Öneriler ............................................................................................................ 95
KAYNAKLAR ..........................................................................................................98
EKLER .................................................................................................................... 100
ÖZGEÇMĠġ............................................................................................................. 104
viii
SĠMGELER VE KISALTMALAR
Simgeler
α20
: Sıcaklık katsayısı
B
: Manyetik alan
C
: Kapasitans
cosφ : Güç faktörü
D
: Transformatörde verim düşüklüğü
E
: Elektrik alanı
f
: Şebeke frekansı
fr
: Rezonans frekansı
h
: Harmonik
Ib
: Bacak akımı
Ih
: Harmonik akımı
In
: Nominal akım
Irms
: Akımın etkin değeri
Ij
: Boyunduruk akımı
Iμ
: Mıknatıslanma akımı
I0
: Ortalama akım
I1
: 1.hamonik akımı
Iωt
: Akımın ani değeri
K
: K Faktörü
L
: Endüktans
ix
n
: Harmonik derecesi
P
: Aktif güç
PEC
: Kaçak akı kayıpları
p
: Filtreleme faktörü
Q
: Reaktif güç
Qpr
: Transformatörün rezonans gücü
R
rdc
: Omik direnç
: Doğru akım direnci
s
: Kirişleme faktörü
S
: Görünür güç
SN
: Nominal güç
Ur
: Kondansatörün anma gerilimi
UC
: Kondansatör uç gerilimi
uk
: Bağıl kısa devre gerilimi
Vωt
: Gerilimin ani değeri
V0
: Gerilimin ortalama değeri
V1
: 1.harmoniğin gerilimi
Vrms : Gerilimin etkin değeri
XL
: Endüktif direnç
XC
: Kapasitif direnç
Ys
: Deri etkisi ile oluşan direnç
Yp
: Yaklaşım etkisi ile olan oluşan direnç
Ztr
: Transformatör empedansı
x
ZH
: Hat empedansı
Zk
: Kablo empedansı
Zy
: Yük empedansı
Zt
: Toplam empedans
β
: Bobinler arası faz farkı açısı
β1
: 1.harmoniğe ait bobinler arası faz farkı
βn
: n.harmoniğe ait bobinler arası faz farkı
Φj
: Boyunduruk akısı
Φb
: Bacak akısı
Φ
: Manyetik akı
ξs
: Sargı kirişleme faktörü
ξsn
: n.harmoniğe ait sargı kirişleme faktörü
ξn
: n.harmoniğe ait sargı yayılma faktörü
γn
: Kirişlenmiş bobinde faz farkı açısı
φ
: Akım ile gerilim arasındaki açı
φ1
: Kompanzasyondan önce, akım ve gerilim arasındaki açı
φ2
: Kompanzasyondan sonra, akım ve gerilim arasındaki açı
τp
: Kutup adımı ,Sargılar arası mesafe
Kısaltmalar:
AG
: Alçak Gerilim
IEEE : Institute of Elektrical and Elektronics Engineers (U.S.A) (Elektrik ve Elektronik
Mühendisleri Enstitüsü)
OG
: Orta Gerilim
xi
THD : Toplam Harmonik Distorsiyon
THB : Toplam Harmonik Bozunum
THBI : Akımdaki Toplam Harmonik Bozunum
TSE : Türk Standartları Enstitüsü
THBV: Gerilimdeki Toplam Harmonik Bozunum
xii
1
1.GĠRĠġ
Elektrik enerjisi günümüzde de çok önemli bir enerji türü olup, çok yaygın bir
kullanım alanı vardır. Bu alanlar, endüstriyel tesisler, ev ve ticarethaneler, tarımsal
amaçlı kullanım ve benzeri gibi sıralanabilir. Günlük yaşantımızda birçok kolaylığın
sağlanmasında kullanılan elektrik enerjisinin, diğer enerji türlerinde olduğu gibi verimli
kullanılması gerekmektedir. Elektrik enerjisinin verimi güç kalitesiyle belirlenir.
Güç kalitesi elektriğin akım, gerilim ve frekans değerlerinin belirli sınırlar içinde
tutulması, ayrıca akım ve gerilimin dalga biçiminin sinüs şeklinde olmasıyla ifade
edilen bir kavramdır. Güç kalitesi standartlara ne kadar yaklaştırılırsa, elektrik
enerjisinin verimi de o kadar artmış olur. Güç kalitesi düşük seviyelerde tutulursa hem
kullanılan enerjideki kayıplar artmış ve hem de kullanılan cihazdan alınan verim
düşmüş olur.
Elektrik enerjisinin kullanımındaki en büyük ölçüt cihazın anma görünür
gücüdür ve S ile sembolize edilmektedir. Güç transformatörleri ve alternatörlerin
güçleri görünür güç ile ifade edilir. Görünür gücün bileşenleri ise aktif ve reaktif güçtür.
Aktif güç bir elektrik makinesi veya elektrikle çalışan cihaz için iş yapan faydalı
güçtür. Reaktif güç ise endüktif ve kapasitif karakterli olup cihazın çalışmasını sağlayan
güçtür. Reaktif güç elektrik hattında ve cihazlarda kayıplara ve arızalara neden
olmaktadır. Bu yüzden elektrik enerjisinin kullanımında verimi düşüren faktörlerdendir.
Reaktif güç kompanzasyonu, güç kalitesini artırma yönündeki en büyük
çalışmalardan birisidir. Reaktif güç kompanzasyonu endüktif karakterli yüklerde
kondansatörlerle yapılırken, kapasitif karakterli yüklerde endüktif reaktörlerle
yapılmaktadır.
Reaktif güç kompanzasyonu ile güç faktörü istenilen seviyeye çıkarılarak güç
kalitesi yükseltilir. Bu sayede kayıplar ve arızalar en aza indirgenmiş olur.
Güç kalitesini yükseltmek için reaktif güç kompanzasyonunun yanında
harmonik kompanzasyonu da yapılmalıdır. Böylece hem cosφ 1‟e yaklaştırılarak akım
ve gerilim arasındaki faz farkı azaltılır, hem de akım ve gerilim dalga şekli sinüs
biçimine yaklaştırılır.
Harmoniklerin
kompanzasyonu,
elektrik
cihazlarının
teçhizatlarındaki
değişiklerle yapılacağı gibi, filtreler ile de yapılmaktadır. Fakat en verimli sonuçlar
filtre kullanılmasıyla elde edilmektedir.
2
Elektrik tesislerinde, harmoniklerin filtrelenmesinde aktif veya pasif filtre
kullanılmaktadır. Fabrikalarda genellikle pasif filtre kullanılmaktadır. Bunun nedeni
maliyetinin aktif filtreye göre düşük ve kullanımının kolay olmasıdır.
Bu tezin amacı;
-
Harmonik
kompanzasyonu
yapılırken
aynı
zamanda
reaktif
güç
kompanzasyonunun da yapılması,
-
Fabrika beslemelerinde baskın harmoniklerin tespit edilerek buna uygun
pasif filtrenin tasarlanması,
-
Tasarlanan pasif filtrenin uygunluğunun denenmesi için, pasif filtrenin
tasarlandığı fabrika modellenerek simülasyonunun yapılması,
-
Fabrika beslemelerinde harmonik analizörü ile yapılan ölçüm sonuçlarının,
simülasyon sonuçları ve matematiksel hesap sonuçları ile yakınlığının
gösterilmesi,
biçiminde sıralanabilir.
Bu tezde;
-
Birinci bölüm, tezin amacının anlatıldığı ,”GİRİŞ” giriş bölümünden,
-
İkinci
bölüm,
harmonikler
alanında
çeşitli
çalışmaların
yapıldığı,
“KAYNAK ARAŞTIRMASI” bölümünden,
-
Üçüncü
bölüm,
reaktif
güç
kompanzasyonunun
nasıl
yapıldığı,
harmoniklerin ne olduğu, elektrik tesislerine etkilerinin ne olduğu, ve
harmonik kompanzasyonu için kullanılan
pasif filtre çeşitleri ile seri
reaktörlü pasif filtrenin nasıl tasarlandığının anlatıldığı, “HARMONİKLER”
bölümünden,
-
Dördüncü bölüm, fabrika beslemelerinde harmonik
ölçümlerinin nasıl
yapıldığı ve ölçümler yapılırken hangi materyallerin kullanıldığının
anlatıldığı, “MATERYAL VE YÖNTEM” bölümünden,
-
Beşinci bölüm, fabrika beslemelerinde harmonik analizörü ile yapılan ölçüm
sonuçları, filtreli ve filtresiz tesisler için yapılan simülasyon sonuçları ve
filtresiz bir fabrikanın matematiksel yöntemle yapılan harmonik analiz
sonuçlarının
değerlendirildiği,
”ARAŞTIRMA
SONUÇLARI
VE
TARTIŞMA” bölümünden,
-
Altıncı bölüm, tüm bu çalmaların sonunda elde edilen sonuçların ve
önerilerin değerlendirildiği, “SONUÇLAR VE ÖNERİLER” bölümünden
oluşmaktadır.
3
2. KAYNAK ARAġTIRMASI
Akım ve gerilim harmonikleri elektrik tesislerinde ve şebekede ciddi sorunlara
neden olmaktadır. Harmoniklerin şebekelerde nasıl üretildiği ve dağıldığı, sisteme nasıl
zarar verdiği, bunların etkilerinin nasıl azalacağı konularında çeşitli çalışmalar
yapılmıştır.
Chowdhury ve ark. (1999) “An Investigation of the Harmonic Characteristics of
Transformer Excitation Current Under Nonsinusoidal Supply Voltage” adlı makalede,
25kVA gücündeki tek fazlı bir trafonun giriş akım ve gerilimindeki harmonikler
incelemiştir.
Rao ve ark.(1998) “Analysis of resonance problems and harmonic fitler design
in power factor correction capacitor applications” adlı makalede, harmoniklerin
kompanzasyon
kondansatörlerine
etkisini
incelemişlerdir.
Harmoniklerin
kondansatörleri paralel rezonansa soktuğu görülmüş ve bu konuda simülasyon
yapılmıştır.
Tsukamoto ve ark. (2000) “Advanced Technology to Identify Harmonics
Characteristics And Results of Measuring” adlı bildiride,
harmonik kaynakları ve
kullanılır güç sistemi arasındaki etkileşimi açıkça gösterebilmek için ileri düzey ölçü
aletlerini incelemiştir.
Puskarich ve ark. (2001) “Harmonic Experiences with a Large
Load-
Commutated Inverter Drive” adlı makalede, büyük Petro kimyasal işletmelerdeki ,
büyük inverterlerin neden olduğu, giderilmesi zor olan harmoniklerin yüksek geçiren
filtre ile filtrelenmesi incelemiştir.
Chen ve ark. (2003) “Stochastic harmonic analysis of mass rapid transit power
systems with uncontrolled rectifiers” adlı makalede, hızlı ulaşım sistemlerinin harmonik
analizini yapmıştır. Trafo olmaksızın 12 darbeli kontrolsüz doğrultucu matematiksel
olarak da türetilmiştir. Güç talebinde harmoniklerin oranı ve ani kalkış esnasındaki
harmoniklerin oranı incelenmiştir. Buna göre harmoniklerin ortalama değeri ve standart
sapması bu metot ile hesaplanmış ayrıca simülasyon yapılmıştır.
Pamplona ve ark. (2004) “Harmonic Passive Filter Planning In Radial
Distribution Systems Using Genetic Algorithms” adlı makalede, radyal dağıtım
sistemlerinde pasif filtre kullanılmasına yönelik çalışmalar yapmıştır. Ayrıca 15 yollu
radyal bir sistemin simülasyonu yapılmıştır.
4
Sağlam (2005)
Yıldız Teknik Üniversitesi Fen Bilimleri Enstitüsünde
hazırlamış olduğu “Dağıtım Transformatörlerinin Bağlantı Gruplarına Göre Harmonik
Simülasyonu” adlı Yüksek Lisans Tezinde, dağıtım transformatörlerinin Dyn1, Dyn11
ve Yyn bağlantı gruplarının harmonik olayına etkilerinin neler olduğu hedeflenmiş olup,
nonlineer yük kompozisyonu ile bir OG/AG sistem içerisinde farklı durumlar için
MATLAB Simulink ile modelleyerek bu etkileri gözlemlemiştir.
Mau ve ark. (2007) “ Planning Approaches for the Strategic Placement of
Passive Harmonic Filters in Radial Distribution Networks” adlı makalede OG
fiderlerinin baralarındaki harmoniklerin incelenmesini
yapmıştır. 11kV‟ luk radyal
dağıtım fideri üzerine simülasyon yapılmıştır.
Şahin (2006) Kocaeli Üniversitesi Fen Bilimleri Enstitüsünde hazırlamış olduğu
“Harmoniklerin yer altı güç Kablolarına etkisinin belirlenmesi “ adlı Yüksek Lisans
Tezinde, harmoniklerin yeraltı güç kablolarına etkilerinin belirlenmesi ve harmonik
etkilerinin azaltılması için öneri sunulması amaçlanmıştır. Bunu gerçekleştirmek için bir
OG sistemde harmonik ölçümü yapılmış, alınan harmonik değerleri doğrultusunda bir
MATLAB/SIMULINK modeli oluşturulmuş ve bu modelden alınan sonuçlar
değerlendirilmiştir.
Başman (2006) Sakarya Üniversitesi Fen Bilimleri Enstitüsünde hazırlamış
olduğu ” Elektrik Enerji Sistemlerinde Harmonik ve Filtreleme “ adlı Yüksek Lisans
Tezinde, aktif ve Pasif Filtreler anlatılmıştır. Ayrıca MATLAB programında bunlarla
alakalı simülasyon yapılmıştır.
Gezegin (2006) Ondokuzmayıs Üniversitesi Fen Bilimleri Enstitüsünde
hazırlamış olduğu “ Harmoniklerin süzülmesi Ve Tepkin Güç Kompanzasyonu İçin
Melez Koşut Etkin Güç Süzgeçleri “ adlı Yüksek Lisans Tezinde, harmonik filtreleme
yöntemleri incelenmiştir. Seri ve paralel oluşlarına göre aktif ve pasif filtreler
incelenmiştir. Ayrıca aktif ve pasif filtrelerin birlikte kullanılmasıyla oluşturulan melez
filtreler incelenmiştir.
İlaslaner (2006) Gazi Üniversitesi Fen Bilimleri Enstitüsünde hazırlamış olduğu
“ Güç Kalitesinde Harmonikler ve Filtrelenmesi “ adlı Yüksek Lisans Tezinde, halen
TEİAS tarafından kullanılan bir enerji nakil hattının (Akdağmadeni – Tokat Enerji
Nakil Hattının) simülasyonu yapılmış, enerji kalitesi için gerekli uygulamalar hat
üzerinde denenmiş ve özellikle elektriksel bileşenler için kararlılık çalışmaları
sağlanmıştır. Tezde enerji kalitesi için karma bir filtre kullanılmıştır.
5
Liang ve ark. (2008) “ Investigation of Non-Linear Devices Modeled as a
Harmonic Current Source” adlı makalede, gerilim kaynaklı ve akım kaynaklı sürücüler
karşılaştırılmıştır. Sürücülerin yükü arttıkça gerilim harmoniklerinde artış, akım
harmoniklerinde ise azalış saptanmıştır. Ayrıca empedansı yüksek olan sert sistemde
harmoniklerin fazla varlık gösterememesine karşın, düşük empedanslı zayıf sistemlerde
harmonikler
yükselmiştir.
Buna
dayanarak
empedansla
harmoniğin
ilişkisi
araştırılmıştır.
Vlahinic ve ark. (2008) “ Indices for Harmonic Distortion Monitoring of Power
Distribution Systems” adlı bildiride, akım ve gerilimdeki bozulmayı toplam bozulma
oranı ile karşılaştırma metodu kullanarak harmonik analizi yapılmıştır.
Bhattacharyya ve ark. (2009) “Harmonic Current Interaction at a Low Voltage
Customer‟s Installation” adlı bildiride, ev kullanıcılarının ürettiği harmonikleri
incelemiştir. Bu çalışmaları TU/Eindhoven„da bulunan güç kalitesi laboratuvarında
gerçekleştirmişlerdir.
Ayrıca
bilgisayar
ortamında
simülasyon
yaparak
ev
kullanıcılarının şebekeyi nasıl etkilediği ve bazı cihazların ürettiği harmoniklerin
miktarı ölçülmüş. Diversite olayı incelenmiştir.
Browne ve ark. (2009) “Allocated Harmonic Quantities as the Basis for Source
Detection” adlı makalede, harmoniklerin şebekede dağılımı üzerine çalışma yapılmıştır.
Bilinen en iyi standartların IEEE 519 ve IEC/TR 61000-3 olduğu belirtilmiştir.
Bunlardan birincisi dağıtım ve iletim sisteminde, ikincisi ise harmoniklerin
yansıtılmasında etkilidir. Thevenin ve Norton yöntemleri kullanılarak harmoniklerin
şebekeye dağılımının nasıl olduğu incelenmiştir.
Ünsal ve ark. (2009) “Dumlupınar Üniversitesi Merkez Kampüsü Elektrik
Kalitesinin Ölçüm Sonuçları”
adlı makalede Dumlupınar Üniversitesi Merkez
Kampüsün de tüketilen elektrik enerjisinin kalitesini incelemiştir. Çalışma kapsamında,
kampüse sağlanan şebeke geriliminin ne zaman ve hangi sıklıkla belirlenen standartların
dışına çıktığı ve kesintiye uğradığı incelenmiştir. Bu amaçla elektrik şebekesi
gerilimindeki dalgalanmaları kaydeden beş adet voltaj kayıt cihazı kampüsün ana
binalarına yerleştirilerek her binanın gerilimlerindeki dalgalanmalar kaydedilmiştir.
Cihaz kayıtları, periyodik olarak bilgisayara aktarılarak incelenmiş ve dalgalanmaların
en sık olduğu zamanlar ve süreleri tespit edilmeye çalışılmıştır.
Keramati ve ark. (2009) “New Control Technique for Compensation of Netural
Current Harmonics in Three-Phase Four -Wire Systems” adlı bildiride, MATLAB
programı kullanılarak seri aktif filtre ile güç kompanzasyonu yapılmıştır.
6
Ekiz ve ark. (2009) “Fabrikalardaki Harmoniklerin MATLAB/SIMULINK
Kullanılarak Modellenmesi “ adlı makalede bir fabrikanın gerçek verileri kullanılarak
simülasyonu yapılmıştır.
Zile (2009) “ Nominal Parametre Temeline Dayanan Harmonik Çalışmalar İçin
Trafo Modelleri” adlı makalede bilgisayar simülasyonları ve ölçümleri karşılaştırmıştır.
Modeller 50 Hz temelli seçilmiştir. Sargıların ve nüvenin doğrusal olmayan etkilerine
bağlı olan frekans incelenmiştir.
Boduroğlu (1988) “ Transformatörler” adlı kitapta, transformatörlerde,
mıknatıslanma
akımından
dolayı
meydana
gelen
harmonikler
incelenmiştir.
Transformatörlerin bağlantı gruplarına göre harmoniklerin nasıl değiştiği ve
transformatörlerde harmonik kompanzasyonunun üzerine çalışmalar yapılmıştır.
Arifoğlu (2002)
yılında basılan ” Güç Sistemlerinin Bilgisayar Destekli
Analizi” adlı kitapta, harmonikler matematiksel olarak analiz edilmiştir. Elektrik
tesislerinde harmoniklerin oluşumu ve elektrikli cihazlarda meydana getirdiği etkiler
işlenmiştir.
Boduroğlu (1988) “Döner Alternatif Akım Makinalarına Giriş” adlı kitapta,
senkron alternatörlerde harmoniklerin oluşumu incelenmiştir. Senkron alternatörlerde
harmoniklerin kompanzasyonu için sargı kirişleme ve sargı yayılma faktörleri
anlatılmıştır.
Whittle (2010) “How capacitors affect harmonics, and what is resonance?” adlı
yazıda, güç kondansatörlerinin paralel rezonansa etkisi ve paralel rezonans durumunda
harmoniklerin davranışı incelenmiştir. Seri reaktörlü pasif filtre ile harmonik
filtrelenmesi gösterilmiştir.
7
3. HARMONĠKLER
Harmonikler akım ve gerilimin dalga biçimini bozar. Akım ve gerilimin dalga
biçimlerinin bozulması elektrikli cihazlarda verim düşüklüğüne, arızalara ve yanlış
çalışmalara neden olmaktadır. Bu yüzden harmonik kompanzasyonu güç kalitesinin
iyileştirme çalışmalarında büyük rol oynamaktadır.
Güç kalitesini iyileştirme çalışmalarında, harmonik kompanzasyonunun yanında
reaktif güç kompanzasyonunun da önemi büyüktür. Bu yüzde tez çalışmasında reaktif
güç kompanzasyonuna da değinilmiştir.
3.1. Reaktif Güç Kompanzasyonu
Tesislerde tüketilen elektrik aktif güç olarak adlandırılır. Makineler cihazlar bu
tükettikleri aktif güce göre elektriksel olarak değerlendirilirler. Aktif gücün yanında
sistemden cihazlar reaktif güç de çekmektedir. Reaktif güç ise makinelerin ve cihazların
aktif çalışmalarına katkıda bulunmazlar. Aksine hatlarda kayıplara, cihazlarda
ısınmalara, transformatörlerde aşırı yüklenmelere ve bunun gibi olumsuz durumlara
neden olmaktadır.
Reaktif güç endüktif ve kapasitif olmak üzere iki çeşittir. Endüktif karakterli
reaktif güç genellikle sargılı cihazlar tarafından çekilir. Bu reaktif güce sargılardan
geçen ve mağnetik alanı oluşturan mıknatıslanma akımı neden olmaktadır. Kapasitif
karakterli reaktif güç ise kapasitif karakterli cihazlar tarafından çekilmektedir. Buna
örnek olarak kondansatörler ve yeraltı kabloları verilebilir. Endüktif ve kapasitif güçler
arasında 180 ° faz farkı vardır.
Eğer şebekede endüktif enerji çoğunluktaysa cihazların ısınmasına, hatlardaki
kaybın artmasına, gerilimin düşmesine ve bunun gibi sorunların ortaya çıkmasına neden
olur. Kapasitif enerji çoksa bu sefer gerilimin aşırı artmasına neden olur.
S görünür güç, P aktif güç, Q ise reaktif güç olarak bilinir. Bunlar Şekil 1.1‟ de
gösterilmiştir.
IP
φ
P
IQ
S
Q
ġekil 3.1. Aktif güç ile reaktif gücün vektörel toplamı
8
Burada φ akımla gerilim arasındaki açıyı göstermektedir. Reaktif güç
kompanzasyonu sayesinde akımla gerilim arasındaki açı küçülür. Güç faktörü denilen
cos φ „nin 1 olması demek, reaktif güç kompanzasyonunun yapıldığına ve sistemdeki
reaktif güç oranlarının standartlar içinde olduğu anlamına gelmektedir. Günümüz
itibariyle elektrik idaresi tarafından kullanılan reaktif oranlar, endüktif için %20
kapasitif içi %15‟ dir.
Bu standartların aşımı halinde şebekeden çekilen enerji elektrik faturasına reaktif
bedel olarak eklenmektedir. Bir fabrika kurulmadan önce reaktif güç ihtiyacı
hesaplanmalı ve standart değerler kompanzasyon sistemiyle yakalanmalıdır.
Kompanzasyon için gerekli reaktif güç hesabı aşağıdaki gibi yapılır:
Kompanzasyondan önceki reaktif güç denklem (3.1) ile hesaplanır. Kompanzasyondan
sonraki reaktif güç ise denklem (3.2) ile hesaplanır.
Q1 = P1. tan φ 1
( 3.1 )
Q2 = P1 . tan φ 2
( 3.2 )
Reaktif gücün Q1 den Q2 seviyesine gelebilmesi için gerekli reaktör veya kapasitör
Denklem (3.3) ile hesaplanır.
Qc= Q1 - Q2 = P1 ( tan φ 1 - tan φ 2 )
( 3.3 )
Denklem (3.4)‟ de cos φ1 ve cos φ2 nin yerine konulmasıyla tanφ1 ve tanφ2 hesaplanır.
tanφ = 1 cos 2 / cos φ
( 3.4 )
denklem (3.5) de açıların farkı k ile gösterilmektedir. bu değer denklem (3.3)‟ de yerine
konulursa denklem (3.6) elde edilir.
tan φ 1 - tan φ 2 = k
( 3.5 )
Qc= k . P1
( 3.6 )
Güç kalitesini etkileyen diğer faktörler ise;
-
Gerilim çökmesi
-
Gerilim yükselmesi
-
Elektrik kesintileri,
-
Gerilim dalgalanmaları
-
Ani gerilim sıçramaları,
-
Akım ve gerilim harmonikleri,
9
-
Güç ve frekans değişimleri
-
Gürültü ( EMG ),
-
Faz dengesizlikleri, şeklinde sıralanabilir.
Yukarıda sıralanmış güç kalitesi sorunlarının çeşitli çözümleri bulunmaktadır.
Bu tezde güç kalitesi sorunlarından Harmonikler üzerine çalışma yapılmıştır.
3.2. Harmonikler
Lineer olmayan elemanların akım ve gerilimleri de lineer değildir. Yani tam
sinüs şeklinde değildir. Zamana göre değişen ve sinüs şeklinde olmayan bu akım ve
gerilimler harmonikli akım ve gerilimler olarak adlandırılır. Akım ve gerilimin dalga
şeklini bozan yüksek frekanslı bileşenler harmonik olarak adlandırılır.
Harmoniklerin akım ve gerilimleri farklı frekanslarda ve farklı genliklerde
olabilirler. Cihazların arızalanmasına, koruma elemanlarının gereksiz açmalarına ve
teçhizatlarda kayıplara neden olmaktadırlar. Harmonikler çeşitli elektrik tesislerindeki
cihaz ve alıcılarda üretilmekte ve besleme hattı üzerinden elektrik şebekesine
yayılmaktadır. Böylece sadece üretildiği yeri değil, diğer tesisleri de etkilemektedir.
Harmoniklerin etkilerini azaltmak için Harmonik filtreler kullanılır. Filtreler, tesisin
durumuna göre ve harmoniğin derecesine göre aktif veya pasif filtreler olarak
seçilebilir.
Aktif filtre kullanımında,
belirlenen harmoniklerin ters faz açısında ve eşit
genlikte akım uygulanarak harmoniğin bastırılmasına çalışılır. Aktif filtre harmoniklerin
kompanzasyonunu yaparken reaktif güç kompanzasyonu da yapmaktadır. Aktif filtrenin
en
önemli
avantajlarından
birisi
değişen
yük
durumuna
kolayca
uyum
sağlayabilmesidir. Bu sayede harmoniklerin filtrelenmesinde kesin çözümler elde edilir.
Fakat maliyetinin yüksek olması kullanımını kısıtlamaktadır.
Pasif filtreler ise rezonans ilkesine göre çalışır. Öncelikle baskın olan harmonik
ve sistemin paralel rezonans frekansı belirlenir. Belirlenen harmoniğin frekansına göre
filtre tasarlanır. Pasif filtre çeşidine göre, harmonik frekansında veya harmonik frekans
değerine yakın olmayan bir noktada rezonans oluşturur. Rezonans direncine göre
harmoniklerin etkileri bastırılır.
10
Kullanım kolaylığı ve maliyetinin ucuz olması nedeniyle endüstriyel tesislerde
genellikle pasif filtreler kullanılmaktadır. Pasif filtrelerin en büyük sakıncası değişen
yük durumuna ayak uydurma zorluğudur. Örneğin sistemde 7. harmonik baskınken
herhangi bir yük değişiminde 5. harmonik baskın duruma geldiğinde fitrede değişiklik
yapmak gerekmektedir. Filtreler tasarlanırken bu türlü değişimlerin de göz önünde
bulundurulması gerekir.
Bu tezde pasif filtre tasarımı üzerinde durulmuştur. Pasif filtrenin harmonik
oranını nasıl değiştirdiği, fabrika beslemelerinde kullanıldığında ne kadar etkili olduğu
araştırılmıştır. Pasif filtrenin olduğu ve pasif filtrenin olmadığı tesislerde ölçümler
yapılarak, bu tesislerdeki sorunlar belirlenmiştir. Ayrıca tasarlanan ve gerçekleştirilen
filtre tesise takılarak ölçümler yapılmıştır.
3.2.1. Harmonik üreteçleri
Elektrik tesislerinde harmonikler değişik durumlarda üretilmektedir. Harmonik
üreten elemanlar:
-
Güç transformatörü, alternatör gibi demir manyetik nüveli cihazlar
-
Ark fırınları
-
Statik dönüştürücüler; doğrultucu, evirici, çevirici kıyıcı vb. güç elektroniği
elemanları
-
Telsiz ve radyo gibi elemanlar
-
Gaz boşalmalı lambalar
-
Fotovoltaik güç sistemlerinde bulunan güç elektroniği devreleri
-
DC iletim sisteminde bulunan güç elektroniği devreleri
şeklinde sıralanabilir.
3.2.1.1. Güç transformatörleri
Güç transformatörleri, demir nüvelerinden dolayı harmonik üretirler. Sinüzoidal
gerilimle çalışma altında ve lineer mıknatıslanma bölgesinde sinüzoidal çıkış verecek
11
şekilde tasarlanır. Nominal değerler aşılırsa nüve doyar ve harmonikler artar. Bunlar
demir nüvenin B= f(H) karakteristiğinin doğrusal olmayışından kaynaklanmaktadır
(Bilge, 2008).
Şekil 3.2 de histerezis eğrisi ve zamanla sinüs şeklinde değişen Φ, B veya E‟nin
ani değerlerinden faydalanarak çizilen mıknatıslanma akımının şekli gösterilmektedir.
Histeresis eğrisi ile Φ, B veya E‟nin dalga şekline göre mıknatıslanma akımının şekli
de değişmektedir. Bu durum mıknatıslanma akımını oluşturan harmonikleri de
etkilemektedir.
ġekil 3.2. Tek fazlı transformatörün mıknatıslanma akımı
Mıknatıslanma akımı harmonikleri, yüklenmenin az olduğu günün erken
saatlerinde en üst seviyeye ulaşır. Çünkü sistemin yükü az olduğundan transformatör
uçlarındaki gerilim yükselir ve aşırı uyarmadan dolayı harmonikler artar. Aşırı uyarma
ile 3, 5 ve 7. dereceden harmonikler oluşur. Çizelge 3.1‟ de güç transformatörünün
harmonik spektrum değerleri gösterilmektedir (Başman,2006).
Çizelge 3.1. Transformatörün Harmonik Spektrumu
Harmonik Derecesi (n)
% In/Iμ
3
0,5
5
0,2
7
0,05
9
0,026
12
3.2.1.2. Alternatörler
Alternatörler, uyartım alanının şekline, manyetik devrenin doymaya ulaşmasına
veya manyetik direncin değişimine bağlı olarak harmonikler üretirler. Makine hızına ve
endüvi oluk sayısına bağlı olarak döner makineler akım harmoniği üretirler.
2л
mg
Temel dalga
BoĢluklar/kutup
Meydana gelen dalga
ġekil 3.3. Kutup altındaki manyetik indüksiyon şekli
Şekil 3.3‟ de kutup altındaki manyetik indüksiyonun şekli gösterilmektedir.
Endüvinin oluklu olmasından dolayı meydana gelen alan değişmeleri gerilim eğrisinde
bozulmalar meydana getirir. Böylece temel dalga üzerinde yüksek frekanslı titreşimler
oluşur.
3.2.1.3. Statik dönüĢtürücüler
Doğrultucu, evirici, çevirici 1 ve 3 fazlı komutasyonlu konverterler statik
dönüştürücüler olarak adlandırılır. DC iletim sistemleri, akü ve fotovoltaik sistemler
komutasyonlu konverterler üzerinden beslenirler. Bunlar 3 ve 3‟ ün katı harmonikler
üretirler.
Statik dönüştürücülerde, harmonik dereceleri denklem (3.7) ile hesaplanır.
n k. p 1
(3.7)
Burada p darbe sayısı, n harmonik derecesi, k ise herhangi bir sayıdır. 6 darbeli
doğrultucuda 5, 7, 11 ve 13 dereceli harmonikler, 12 darbeli doğrultucuda 11, 13 ve 23
dereceli harmonikler üretilmektedir (Bilge, 2008).
13
Çizelge 3.2‟ de çeşitli doğrultucuların akım dalga şekilleri gösterilmektedir.
Burada farklı darbe sayısına sahip doğrultucuların toplam harmonik bozunumları ve
dalga şekilleri de farklı olmaktadır.
Çizelge 3.2. Çeşitli Doğrultuculardan Akım Dalga Şekilleri
Tek fazlı doğrultucu
6 darbeli doğrultucu
(filtre kondansatörlü)
6 darbeli doğrultucu
(filtre kond. ve
bsatırıcılı)
6 darbeli statik
evirici
(filtreli bastırıcılı)
6 darbeli statik
evirici
(filtreli bastırıcılı)
3.2.1.4. Ark fırını
Ark fırınları, kaynak makineleri gibi normal işlemlerini elektrik arkı ile
sürdüren tesisler, önemli harmonik kaynakları arasında sayılırlar. Ark direncinin
doğrusal olmaması, yani ateşleyicinin elektrotlarının akım gerilim karakteristiğinin
doğrusal olmaması, harmoniklerin ortaya çıkmasına neden olur. Ark olayının
başlamasının ardından ark gerilimi azalırken, ark akımı artar. Bu anda ark olayında
negatif direnç etkisi görülür. Ark fırınlarının direnç değişimi dengesiz olduğundan
şebekedeki harmoniklerde dengesiz olur. Onun için ark fırınlarının modellenmesi
zordur.
Şekil 3.4‟ de ark fırınının malzemeyi eritme ve inceltme anındaki akım ile
frekansın ilişkisi gösterilmektedir.
14
(a)
(b)
ġekil 3.4. (a) Ark fırınının eritme anındaki Akım-Frekans ilişkisi, (b) Ark fırınının inceltme
anındaki Akım-Frekans (Eroğlu, 2009)
3.2.1.5 Gaz boĢalma ilkesine göre çalıĢan aydınlatma elemanları
Flüoresan, civa, yüksek basınçlı sodyum buharlı lambalar gibi gaz deşarjlı
aydınlatma elemanları, şebekeden harmonikli akımların çekilmesine neden olurlar. Bu
ilke ile çalışan aydınlatma elemanları doğrusal olmayan akım ve gerilim karakteristiğine
sahip olduğu için harmonik üretirler. Bu tip aydınlatma elemanları negatif direnç etkisi
gösterir ve 3 ile 3 ün katı olan harmonikleri üreterek ısınmalara neden olmaktadır.
Çizelge 3.3‟ de manyetik balastlı bir floresan lambanın meydana getirdiği harmonikler
gösterilmektedir (Bilge, 2008).
Çizelge 3.3. Manyetik balastlı floresan lambanın harmonikleri
Harmonik (n)
I
(%)
I n/I1
1
3
5
7
9
11
13
15
17
19
21
100
19,9
7,4
3,2
2,4
1,8
0,8
0,4
0,1
0,2
0,1
Şekil 3.5 (a) aydınlatma elemanlarında akımın dalga şeklini göstermektedir.
Buradan da görüldüğü gibi akımın dalga şekli son derece bozuktur. Şekil 1.5 (b) ise bu
aydınlatma elemanlarına ait harmonik grafiğini göstermektedir. Burada küçük dereceli
harmoniklerin daha baskın olduğu görülmektedir.
15
(a)
(b)
ġekil 3.5. (a) Aydınlatma elemanlarının akım dalga şekli (b) Aydınlatma elemanlarının
harmonik grafiği
3.2.2. Harmoniklerin etkileri
Harmonikler enerji üretim, iletim ve dağıtım sistemlerinde gerilim düşümleri
yaparak, manyetik alanı bozar. Böylece akım ve gerilimin dalga şekli bozulur. Elektrik
enerji sistemlerinde cihazlar saf sinüs dalga şeklinde çalışmak üzere tasarlanmıştır.
Akım ve gerilimin dalga şeklinin belli bir değerden daha fazla bozulması cihazların
çalışmalarında aksaklıklar meydana getirir.
3.2.2.1. Güç transformatörleri üzerindeki etkileri
Akım harmonikleri transformatörlerde kaçak akıları artırarak bakır kayıplarında
artışa neden olurlar. Gerilim harmonikleri ise demir kayıplarına ve yalıtım
zorlanmalarına neden olur. Ayrıca harmonikler, güç transformatörü ile kompanzasyon
kondansatörlerinin paralel rezonansa girmesine neden olurlar.
Kaçak akı kayıpları sinüs olmayan dalga şeklinin kaybıdır. Yüklü çalışmada
bakır kayıpları i²R dir ve sargılarda ısınma meydana getirmektedir. Ayrıca bağlantı
yerlerindeki manyetik akıdan dolayı kaçak kayıplarının artmasına neden olur.
Manyetik çekirdekli bir elemanda oluşan demir kayıpları uygulanan gerilimin
şekline bağlıdır. Yani gerilim harmoniklerine bağlıdır. Kaçak akı kayıpları denklem
(3.8) ile hesaplanmaktadır (Sağlam, 2005).
16
PEC PEC R
h max
h 1
I
h h
IR
2
2
(3.8)
Bir güç transformatörünün rezonans gücü denklem (3.9) ile hesaplanmaktadır.
Qpr
S
n .%uk .sin k
(3.9)
2
S : Transformatör gücü (kVA) ,
n : Harmonik mertebesi
% uk : Transformatörün bağıl kısa devre gerilimi
Güç transformatörlerinde, sinüzoidal olmayan akımlarla beslenen yükleri
besleyebilme kapasitesinin bir ölçütü olarak kabul edilen ve standart güç
transformatörlerinin harmonik akımlara bağlı olarak nominal akım ve gerilimde
meydana gelen düşüşlerin tayinine yarayan büyüklük, K faktörü olarak nitelendirilir.
Transformatörün etkin akımına göre normlaştırıldığında K faktörü değeri denklem
(3.10) ile hesaplanır (Sağlam, 2005).
n
K n. I h I1
i 1
2
1 THD
2
1
( 3.10 )
Standart transformatörün anma değerindeki düşümün hesaplanmasında (IEEE
C57.110 1986‟da) denklem (3.11) kullanılmaktadır.
D = 1,15/(1+ 0,150.K)
( 3.11 )
D, transformatör gücündeki azalma. Yani harmonikli akımla yüklenen transformatörün
verebileceği en büyük güç değeri
SN; transformatörün nominal gücü,
SH = D . S N
( 3.12 )
olarak hesaplanır (İlaslaner, 2006).
3.2.2.2. Döner elektrik makinelerinde etkileri
Harmonikler alternatörlerde uyartım alanını bozarak saf sinüs dalgası
üretilmesini engeller. Ayrıca ısıl kayıpları artırır ve aşırı ısınmalara neden olur.
Alternatörün gürültülü çalışmasına neden olur.
Reaktanslar harmonik frekansları nedeniyle artmaktadır. Harmonikler de aynı
frekansta gerilim indükler ve bu gerilimler nedeniyle harmonik akımları akar. Böylece
faydalı akı bozulur. Alanın bozulmasıyla moment zayıflar.
motorlarda aşırı ısınmalara neden olur.
Harmonikler ayrıca
17
3.2.2.3. Kesici ve sigortalarda harmonik etkileri
Kesiciler, kontakların fazla yüklenmesini engellemek için akım sıfır noktasından
geçerken açma yapar. Harmoniklerin frekansları temel frekanstan farklı olduğundan
akım sıfır noktasından geçerken, harmonik akımlarından dolayı, toplamda sıfır
olmayacaktır. Böylece kısa devre esnasında veya herhangi bir zamanda kesici açmak
istediğinde, harmonik akımları tarafından kontakları zorlanacaktır. Bu durum eriyen
telli sigortalar için de geçerlidir. Ayrıca harmonik akımlar kontaklarda ısıl kayıplar
oluşturarak kesici ve şalterlerde ısınmaya neden olurlar.
3.2.2.4. Kondansatörler üzerindeki harmonik etkileri
Kondansatörlerde frekansın artmasıyla direnç düşmektedir. Direncin düşmesi
sonucunda kondansatörün çektiği akım artar. Bu da kondansatörlerin ısınmasına ve
ömrünün azalmasına neden olur. Tedbir alınmazsa kondansatörler patlar.
3.2.2.5. Ġletkenlerde harmonik etkileri
Harmoniklerin şebeke iletkenleri ve güç kablolarına da olumsuz etkileri
olmaktadır. İletkenler endüktif özelliklidir. Harmoniklerin frekansının yüksek
olmasından dolayı iletken ve kabloların dirençleri artar. Bu da ısıl kayıpları artırır.
Ayrıca deri etkisi ve yaklaşım etkisi nedeniyle iletkenlerin empedansları artmakta ve
akım taşıma kapasiteleri de düşmektedir. Deri ve yaklaşım etkileri nedeniyle alternatif
akım direnci doğru akım direncine göre büyümektedir.
rac = rdc (1+Ys+Yp)
(3.13)
Ys: Deri etkisiyle ek olan direnç, Yp: Yaklaşım etkisi nedeniyle oluşan direnç
Rdc : DC direnç, α20: Sıcaklık katsayısı ,
rdc=R20[ 1+ α20( θ-20)]
(3.14)
R20=ρ20/S
(3.15)
18
Çizelge 3.4. Malzemeye göre α20 ve ρ20 değerleri
α20 [K-1]
ρ20 [Ω/m]
Bakır
3,93.10-3
1,7241.10-8
Alüminyum
4,03.10-3
2,8264.10-8
Kurşun ve ya Kurşun alaşımı
4,0.10-3
21,04.10-8
Çelik
4,5.10-3
13,8.10-8
Bronz
3,0.10-3
3,5.10-8
Paslanmas çelik
ihmal
70.10-8
Alimünyum
4,03.10-3
2,84.10-8
Malzeme
a) İletken
b) kılıf ve Zırh
Çizelge 3.4‟de malzemeye göre α20 ve ρ20 değerleri gösterilmektedir. Bu
değerler malzemeye göre farklı değerler almaktadır. Bu ise iletkenin direnç değerini
etkilemektedir (Şahin, 2006).
Deri etkisi nedeniyle iletken merkezindeki akım yoğunluğu düşmektedir.
Homojen bir iletkenin merkezi yakınlarındaki kuvvet çizgilerinin yoğunlaşmasıyla,
iletkenin merkezindeki boyuna bileşen, kenardaki boyuna bileşenden büyük olur.
Bundan dolayı merkezdeki zıt EMK artar. Böylece merkezdeki akı daha da düşer ve
akım merkezden kenarlara doğru kayar. Frekansın artmasıyla akımın merkezden
kenarlara doğru kayması daha da artar. Harmoniklerin frekansları yüksek olduğundan
dolayı, deri etkisini artırıcı yönde etki yaparlar (Şahin, 2006).
Tek damarlı iletkenlerde deri etkisi daha güçlüdür. Onun için iletkenler çok
damarlı yapılarak deri etkisi mümkün olduğunca azaltılmaya çalışılmıştır.
Şekil 3.6 bir iletkenden geçen akımın, frekansın etkisiyle iletkenin merkezinden
kenarlara doğru nasıl dağıldığını göstermektedir. Burada DC akım kullanıldığında deri
etkisinin görülmediği, fakat alternatif akım da frekans arttıkça deri etkisinin nasıl arttığı
gösterilmekledir.
Doğru akım için iletken etrafındaki
kullanılabilir alan
“DC Direnç”
Düşük frekanslı alternatif akım için
iletken etrafındaki kullanılabilir alan
“AC Direnç”
Yüksek frekanslı alternatif akım için
iletken etrafındaki kullanılabilir alan
“AC Direnç”
ġekil 3.6. Frekansın iletkendeki akım dağılımına etkisi
19
Deri etkisi denklem (3.16) ve (3.17) ile hesaplanır.
Ys= Xs4 /(192+0,8 Xs4 )
( 3.16 )
Xs4= (8πf/ rdc)x10-7x ks
( 3.17)
Ks: iletkenin tipine göre değişen deri etki sayısı. Çizelge 3.5‟ de gösterilmektedir.
Alternatif akım taşıyan iletkenler, içinden geçen akımdan dolayı çevresinde
manyetik alan oluşturur. Bu manyetik alan yanından giden diğer iletkenin akısını bozar.
Bu nedenle iletkenin direnci artmış olur. Bu etkiye yaklaşım etkisi denir.
Harmonikli akım taşıyan kabloların üreteceği manyetik alanın etkisi daha
fazladır. Bu nedenle direnç artışı daha fazla olur. Bu durumda yaklaşım etkisi daha
güçlenir. IEC`nin 1982 tarihli 60287 numaralı yayınına göre, iki iletkenli kablo veya tek
iletkenli iki kablo durumu için, d iletken çapı (mm) ve s iki kablo veya iki iletken
arasındaki merkezden merkeze mesafe (mm) olmak üzere aşağıdaki eşitlikteki gibi
hesaplanmaktadır. İletkenler arası merkezden merkeze mesafe iletken çapının on katını
aşarsa bu ilave kayıplar ihmal edilebilmektedir (Şahin, 2006).
X
dc 2
dc 2
1,18
Yp
0,312
4
X
192 0,8 X p4 s
s
p
0,
27
192 0,8 X p4
4
p
X p2
8 f 7
10 k p
rdc
(3.18)
(3.19)
kp: iletkenin tipine göre değişen yaklaşım etkisi katsayısıdır ve Çizelge 3.5‟ de
verilmektedir (Şahin, 2006).
Çizelge1.5. ks ve kp değerleri
İletken
ks
kp
Yuvarlak telli
1
0,8
Yuvarlak kompakt
1
0,8
Yuvarlak parçalı
0,435
0,37
Dilimli
1
0,8
3.2.2.6. Rezonans etkisi
Periyodik bir kuvvetin etkisi altındaki bir sistem, salınımlar sergiler ve eğer etki
frekansı sistemin doğal frekansına eşit ise, bu salınımların genliği sınırsız artma
20
eğilimine girer. Sonuç olarak sistem, belli bir genlikten sonra bütünlüğünü veya
bulunduğu durumu koruyamayarak ya dağılır ya da bozunur. Buna rezonans denir.
Rezonans anında endüktif ve kapasitif dirençler birbirlerine eşittir. Rezonansın çeşidine
göre, aşırı akım ve gerilimler ortaya çıkar. Sistem rezonansı, harmonik frekanslarından
birine yakın bir değerde oluşursa, aşırı seviyede harmonik akım ve gerilimleri ortaya
çıkacaktır. Herhangi bir sistemin rezonans frekansı denklem (3.20)‟ de gösterilmektedir.
Burada L sistemde bulunan toplam endüktans, C ise sistemde bulunan toplam
kapasitansı niteler.
f
1
(3.20)
2 LC
Seri rezonansta, rezonans frekansında X L ve XC dirençleri birbirlerine eşitlenir.
Bu durumda toplam direnç omik dirence eşit olur. Şekil 1.7, seri rezonans anında
toplam empedansı göstermektedir. Bu durumda, kapasitif ve endüktif dirençler
birbirlerine eşitlendiği için sistemde sadece omik direnç kalır. Omik direnç toplam
empedansa göre düşük olduğu için sistemde aşırı akımlar meydana gelmektedir.
Paralel rezonansta ise rezonans frekansında toplam empedans artar. Toplam
empedans arttığı için, küçük akımlarda dahi büyük gerilimler oluşabilir.
Şekil 1.8 de paralel rezonans anında toplam empedans eğrisi gösterilmektedir.
bu eğriden de görüldüğü gibi paralel rezonans frekansına doğru, toplam empedans
artmaktadır.
ZT(Ω)
Kapasitif
Bölge
Endüktif
Bölge
ġekil 3.7. Seri rezonans durumunda direnç eğrisi
21
ZT(Ω)
Endüktif
Bölge
Kapasitif
Bölge
ġekil 3.8. Paralel rezonans durumunda direnç eğrisi
3.2.3. Diversite etkisi
Elektrik şebekesinde çeşitli yükler bulunmaktadır. Bu çeşitli yükler çeşitli
oranlarda ve derecelerde harmonikler üretir. Bir cihazın akımındaki harmonik
bozunumu çok yüksek olmasına rağmen, şebekedeki bozunum o kadar yüksek
olmamaktadır.
Örneğin bir sürücünün akımdaki bozunum oranı % 85 civarında
ölçülmüşken, ana bara akımının bozunum oranı %10-20 civarındadır. Cihazda görünen
oranın ana barada görünen orandan yüksek olması diversite etkisi olarak adlandırılır.
Bunun sebebi farklı faz açıklarındaki harmoniklerin birbirlerini yok etmesidir
(Bhattacharyya, ve ark., 2009).
3.2.4. Harmonik bozunum sınırları ve oluĢum durumları
Elektrik tesislerinde harmonik bozunum sınırları aşağıdaki gibi belirlenebilir;
THBV < % 2,5 ve THBI < %10 ise tesiste harmoniklerden dolayı bir enerji
kirliliği yoktur denilebilir.
THBV < % 2,5-3 ve THBI > %10 ise tesiste harmonikler giderilse iyi olur.
Fakat giderilmesi zorunlu değildir. Yani çok ciddi sorunlara yol açmazlar.
THBV > % 3 ve THBI > %10 ise tesiste rezonans riski yüksektir. Harmoniklerin
bir an önce bastırılması gerekmektedir. Çeşitli açılardan zararlar meydana gelebilir.
22
Ayrıca tesiste harmonik üreten yüklerin toplam görünür
gücü,
güç
transformatörünün görünür gücünün %25‟i kadarsa, harmoniklerden dolayı arızalar
meydana gelir. Bu durumda tesis için harmonik filtre tasarlanmalıdır.
Harmoniklerin oluşumunda, yükün etkili olmasının yanında, besleme gerilimi de
etkilidir. Yani;
-
Sinüs beslemeli doğrusal olmayan devrelerde besleme gerilimi tarafında
temiz sinüs dalgalı gerilim bulunurken, doğrusal olmayan devrede doğrusal
olmayan elemanlar nedeniyle harmonikler oluşmaktadır.
-
Nonsinüzoidal beslemeli lineer devrede ise yük lineer olmasına karşın,
besleme
gerilimi
nonsinüzoidal
olduğundan,
gerilimde
harmonikler
oluşacaktır. Gerilimde oluşan harmonikler akıma da yansıyacaktır.
-
Nonsinüsoidal beslemeli nonlineer devrede, hem akımda hem de gerilimde
çeşitli derecelerde harmonikler vardır. Akım ve gerilimin harmonik
yönünden temiz olmamasından dolayı, çeşitli dereceden harmonikler
üretilmektedir (Arifoğlu,2002).
IEEE (International Electrical Electronics Engineers) tarafından getirilen
sınırlamalar hem akım hem de gerilim harmoniklerini kapsaması nedeniyle daha etkin
ve sınırlayıcı olmaktadır. Ayrıca IEEE sınırlamasında yüklere tek tek değil, toplu olarak
sınırlama getirilmektedir. IEEE-519 standardında, elektrik dağıtım şirketleri için şebeke
bara gerilim bozulumu, müşteriler içinse doğrusal olmayan yükler tarafından üretilen
harmonik akımları ile ilgili sınırlamalar getirilmiştir. Üretici firmanın sorumluluğunda
olan gerilim harmonik bozulum değeri, IEEE tarafından, Çizelge 3.6‟ daki gibi
sınırlandırılmıştır. Burada her bir harmonik için ve toplamda harmonik bozulumu için
ayrı ayrı iki sınırlama verilmiştir.
Çizelge 3.6. IEEE gerilim için harmonik bozunum sınırları
Temel Harmonik Büyüklüğü
THB Vn
(%)
(%)
Vn < 69kV
3
5
69 < Vn < 161kV
1,5
2,5
Vn > 161kV
1
1,5
Bara Gerilimi (Vn)
23
Çizelge 3.7‟ de, IEEE‟nin akımdaki bozunum için belirlediği sınır değerler
gösterilmektedir (Bilge, 2008).
Çizelge 3.7. IEEE akım için harmonik bozunum sınırları
Vn<69kV
In/I1
n<11
11<n<17
17<n<23
23<n<35
n<35
THB
<20
4
2
1,5
0,6
0,3
5
20-50
7
3,5
2,5
1
0,5
8
50-100
10
4,5
4
1,5
0,7
12
100-1000
12
5,5
5
2
1
15
>1000
15
7
6
2,5
1,4
20
69<Vn<161kV
<20
2
1
0,75
0,3
0,15
2,5
20-50
3,5
1,75
1,25
0,5
0,25
4
50-100
5
2,25
2
0,75
0,35
6
100-1000
6
2,75
2,5
1
0,5
7,5
>1000
7,5
3,5
3
1,25
0,7
10
Vn>161kV
<50
2
1
0,75
0,3
0,15
2,5
>50
3
1,5
1,15
0,5
0,22
4
3.2.6. Elektrik tesislerinde bulunan harmonik çeĢitleri
Elektrik tesislerinde çeşitli derecelerde ve miktarlarda harmonikler meydana
gelmektedir. Harmoniklerin çeşitli derecelerde ve miktarlarda meydana gelmesinin
birçok nedeni bulunmaktadır. Bunları yükün cinsi, çalışma gerilimi, yüklenme akımları,
güç transformatörlerinin bağlantı grupları ve benzeri nedenler etkilemektedir.
Elektrik tesislerinde genellikle tek dereceli harmonikler görülmektedir. En
yaygın harmonikler 3.,5. ve 7. dereceden harmoniklerdir. Forier serisine göre harmonik
analizi yapıldığında, harmoniklerin derecesi arttıkça etkileri azalmaktadır.
Tek fazlı yüklerin ağırlıkta olduğu tesislerde 3. harmonikler baskındır. Üç fazlı
sistemlerde üretilen 3. harmonikler arasında 120 derece faz farkı bulunmaz. Bu yüzden
yıldız bağlı güç transformatörlerinde yıldız noktasında 3. harmonik akımları
sıfırlanmaz.
Aralarında faz farkı bulunmayan 3.harmonik akımları sıfır noktasında
sıfırlanmadığı için, bu noktada 3. harmonik akım değeri 3 katına çıkar. Eğer nötr
noktası topraklı ise harmonik akımları toprağa akar, topraklı değilse bu akımlar nötr
noktasında birikerek, fazlar arasında dengesizliğe yol açar.
24
Üçüncü harmonik akımlarının arasında 120 derece faz farkının bulunmadığı,
denklem (3.21), (3.22) ve (3.23) den de görülmektedir.
Ih3R= Ih3Rmax . cosωt
( 3.21 )
Ih3S= Ih3Smax . cos( 3ωt+3x2л/3)
( 3.22 )
Ih3T= Ih3Tmax . cos( 3ωt+3x4л/3)
( 3.23 )
Bağıntılarından da anlaşıldığı üzere 3 ve 3 ün katı harmonikler arasında faz farkı
bulunmamaktadır.
Üç fazlı yüklerin ağırlıkta olduğu tesislerde ise genellikle 5. ve 7. dereceden
harmonikler baskındır. Bu harmonikler nötr noktasında sıfırlandıklarından dolayı, nötr
iletkenine baskı yapmazlar. Yapılan ölçümlerde ve simülasyonlarda üç fazlı yüklerin
ağırlıkta olduğu tesislerde 5. ve 7. dereceden olan harmoniklerin baskın olduğu tespit
edilmiştir.
Şebekelerde genellikle Üçgen/Yıldız bağlı trafolar kullanıldığından, enerji nakil
hatlarında 5.ve 7. dereceden harmonikler baskındır. Çünkü 3. harmonik akımlarına
üçgen sargılarda kapalı çevrim oluşturulur. Bu kapalı çevrim sayesinde, 3. harmonik
akımları üçgen sargılarda dolaşır ve OG şebekesine geçemez.
AG şebekelerinde ise değişik dereceden harmonikleri görmek mümkündür.
Bunlar 3, 5, 7, 9 ve 11 gibi sıralanabilir. Bu harmoniklerin baskınlığı kullanılan yükün
özelliğine göre ve tesisin rezonans frekansına göre değişmektedir.
Bunlara ek olarak, güç transformatörleri mıknatıslanma akımından dolayı
harmonik üretmektedir. Güç transformatörlerinde harmoniklerin en yüksek olduğu an,
boşta çalışmalarının yüksek olduğu andır. Çünkü boşta çalışma esnasında çekilen akım
azalır. Böylece mıknatıslanma akımının oranı artar. Ayrıca transformatörün geriliminin
artmasıyla, nüvesi doyuma ulaşır. Nüvenin doyuma ulaşması harmonik oranlarını artırır.
3.2.7. Harmoniklerin matematiksel analizi
Tüm periyodik fonksiyonlar Fourier Serisi olarak adlandırılan bir seriye
açıldıklarında birinci terimi bir sabit, diğer terimleri ise bir değişkenin katlarının sinüs
ve kosinüslerinden oluşan bir seri halinde yazılabilirler.
Sinüzoidal olmayan bir gerilim, matematiksel olarak denklem (3.24)‟ de gösterilmiştir.
v(t ) V0 V1 sin(t 1 ) V2 sin(2t 2 ) ... Vn sin(nt n )
Burada;
(3.24)
25
v(t ) : Ani değer,
V0 : v(t ) eğrisinin ortalama değeri,
V1 : v(t ) eğrisinin ana harmonik bileşenin maksimum değeri,
Vn : v(t ) eğrisinin n. harmonik bileşenin maksimum değeri,
: Referansa göre açı farkı,
olarak gösterilmiştir. Denklem (3.24) de gösterilen gerilimin ifadesi sinωt ve cosωt
şeklinde açılırsa denklem (3.25) elde edilir.
v(t ) V0 a1 sin t a2 sin 2t ... an sin nt b1 cos t b2 cos 2t ... bn cos nt (3.25)
Denklem (3.25), v(ωt) fonksiyonunun Fourier açılımı olarak bilinir. Bu ifade de
ortalama gerilim, denklem (3.26) ile ifade olur ( Arifoğlu, 2002).
2л
1
V0
2л
v(t )dt
(3.26)
0
2л
1
an v(t )sin(nt )dt (n=0,1,2,…)
л0
(3.27)
2л
1
bn v(t ) cos(nt )dt (n=0,1,2,…)
л0
(3.28)
an sin nt bn cos nt Vn sin(nt n )
(3.29)
Vn (an2 bn2 )1/2
(3.30)
n arctan
bn
an
(3.31)
Katsayılar yukarıdaki denklemler kullanılarak bulunur. v(ωt) fonksiyonun alacağı özel
durumlara göre denklem (3.26), (3.27), (3.28) hesaplanabilir. Bu durumlar;
1- Verilen v(ωt) fonksiyonu v(-ωt) = - v(ωt) eşitliğini sağlıyorsa bn=0,
2- Verilen v(ωt) fonksiyonu v(-ωt) = v(ωt) eşitliğini sağlıyorsa an=0,
3- Verilen v(ωt) fonksiyonu v(ωt+л) = - v(ωt) eşitliğini sağlıyorsa a2n= b2n=0 (çift
dereceden harmonikler yok olur.)
Şekil 1.9‟ da verilen eğri Fourier harmonik analizi ile incelenmiştir. Burada
eğri
ωt eksenine göre simetrik olduğundan
v(-ωt) = v(ωt) eşitliğini sağladığı için a n=0 olur.
V0 =0 olur.
v( ωt) fonksiyonu,
26
ġekil 3.9. v(ωt) fonksiyonu
1
1
v(t ) cos(nt )dt
л 0
л
2л
bn
л /2
1cos(nt )dt
л
л /2
л /2
л
л /2
л /2
л /2
1cos(nt )dt 1cos(nt )dt 1cos(nt )dt
л /2
4
4
nл
1cos(nt )dt sin
л 0
2
лn
olacaktır. Bu ifadeye göre;
4
4
4
4
b1 , b2 0, b3 , b4 0, b5 , b6 0, b7 ...
л
3л
5л
7л
elde edilir. an ve bn değerleri denklem (3.25) de yerine konulursa;
v(t )
4
1
1
1
1
cos(
t
)
cos(3
t
)
cos(5
t
)
cos(7
t
)
cos(9t )...
л
3
5
7
9
elde edilir. Burada v(ωt+л) = - v(ωt) eşitliğini sağladığı için a2n= b2n=0 olacağından, bn
katsayısının analizinde çift dereceden harmoniklerin ortadan kalktığı görülmüştür.
v(ωt) eğrisi sonsuz sayıda sinüzoidal eğrinin toplamı şeklinde yazılabilir.
Şekil 3.10‟ da v1(ωt) eğrisi sonsuz sayıda değil de 1,3 ve 5. dereceden harmoniklerin
toplamından oluşmaktadır.
Şekil 3.10‟ da v1(ωt) eğrisi sonsuz sayıda olmadığı görülmektedir. Şekil 3.11‟ de
ise v2(ωt) eğrisi gösterilmektedir. Bu eğri ise 7, 9 ve 11. dereceden harmoniklerin ilave
edilmesiyle oluşmuştur.
v2(ωt) eğrisi, v1(ωt) eğrisi ile kıyaslandığında, v(ωt) eğrisine daha çok benzediği
görülmektedir.
Toplam akım ve gerilimin genlik değerleri denklem (3.32) ve (3.33)‟ de
verilmiştir. Toplam Harmonik Bozunum (THB) harmoniklerin incelenmesinde ölçüt
olarak alınır. Akım için toplam harmonik bozunum denklem (3.35)‟ de, gerilim için
toplam harmonik bozunum ise denklem (3.34)‟ de gösterilmektedir (Arifoğlu, 2002).
27
ġekil 3.10. v1(ωt) eğrisinin ve harmoniklerin gösterimi
ġekil 3.11. v2(ωt) eğrisi ve harmoniklerin gösterimi
n
I rms I12 I 32 I 52 ... I n2 I12 I k2
(3.32)
k 2
n
Vrms V12 V32 V52 ... Vn2 V12 Vk2
(3.33)
k 2
12
n U2
THDV n2
n 2 U1
(3.34)
12
n I2
THDI n2
n 2 I1
(3.35)
28
3.2.8. Güç transformatörlerinin bağlantı gruplarına göre harmonik analizi
Elektrik dağıtımında OG‟yi AG‟ye dönüştürmek için,
üç fazlı güç
transformatörleri kullanılmaktadır. Üç fazlı güç transformatörleri kullanım amaçlarına
göre değişik biçimde bağlantı gruplarına sahiptir. Bu bağlantı grupları Şekil 3.12‟ de
gösterilmektedir.
Üç fazlı güç transformatörlerinde harmoniklerin etkisi, bağlantı gruplarına göre
ve çekirdek tipine göre değişim göstermektedir. Güç transformatörünün mıknatıslanma
akımı ve kullanıcıların yük çeşidi harmoniklerin oranlarını ve derecelerini
belirlemektedir.
Şekil
3.12‟de
üç
fazlı
güç
transformatörlerinin
bağlantı
grupları
gösterilmektedir. Üç fazlı güç transformatörlerinde mıknatıslanma akımının şekli,
transformatörün bağlantı gurubuna ve transformatörün nüvesinin yapıldığı manyetik
malzemeye
bağlıdır.
Mıknatıslanma
akımına
nüvenin
etkisi
Şekil
3.2‟den
anlaşılmaktadır. Nüvenin manyetik özelliği ne kadar iyi ise histerezis eğrisi o derece
incelir ve doğrusal şekle yaklaşır. Bu durumda mıknatıslanma akımı harmonikleri
azalır. Mıknatıslanma akımının dalga şeklide sinüse yaklaşır.
Bağlantı gurubunun etkisini daha iyi anlamak için, bağlantı gruplarına göre
mıknatıslanma akımının değişimini ayrı ayrı incelemek gerekir.
29
Tasarım
Vektör Diyagramı
Devre konfigürasyonu
Sekonder
yıldız noktası
Yok
%10 yük
kapasitesi
Tam yük
kapasitesi
Tam yük
kapasitesi
Yok
Tam yük
kapasitesi
Yok
%10 yük
kapasitesi
Tam yük
kapasitesi
Tam yük
kapasitesi
Yok
Tam yük
kapasitesi
ġekil 3.12. Güç transformatörlerinin bağlantı grupları
1.2.7.1. Primer sargısının Yy0 bağlantı gurubunda harmonik analizi
Bu bağlantı gurubunda primer ve sekonder sargılar yıldız/yıldız olarak
bağlanmıştır. Primer ve sekonder sargılarında nötr hattı bulunup bulunmayışına göre
mıknatıslanma akımının durumu incelenmiştir (Boduroğlu, 1988).
30
a) Primer yıldız sargısında nötr hattının mevcut olduğu ve sekonder yıldız
sargısında nötrün yalıtıldığı durumda mıknatıslanma akımının durumu
Bu tip güç transformatörleri çok yaygın kullanılmaz. Kullanılsa bile küçük güçlü
yüklerin çalıştırılması için kullanılır. Bu tip transformatörlerin mıknatıslanma akımının
incelenmesinde, iki durumu birbirinden ayırt etmek gerekir. Güç transformatörlerinin
manyetik devreleri birbirinden bağımsız olacağı gibi birbirlerine bağımlıda olabilirler.
Manyetik devresi bağımsız olan güç transformatörleri, Mantel tipi ve 3 adet tek
fazlı transformatörden oluşan güç transformatörleridir. Bu güç transformatörlerinde tek
fazlı transformatörlerde görünen tek dereceli harmoniklerin hepsi görünür. Faz
akımlarının (n) inci mertebeden harmonikleri arasındaki faz farkı denklem (3.35)‟ e
eşittir (Boduroğlu, 1988).
n n. n.120 n.
1
2
3
(3.35)
Denklem 3.19‟dan da görüleceği gibi üç ve üçün katı olan harmonikler aynı
fazdadırlar. Bu harmonikler nötr noktasındaki toplamları sıfıra eşit değildir. Üçün
katından farklı olan harmonikler ise nötr noktasında sıfıra eşittir. Çünkü bunların
arasındaki faz farkı 120 derecedir.
Manyetik devresi birbirlerine bağımlı olan güç transformatörleri ise, çekirdek
tipi güç transformatörleridir. Bunların orta fazının akı yolu daha kısa olduğundan dolayı
akımları simetrik değildir. Yani orta fazın akımı daha düşüktür. Bu durum
mıknatıslanma akımına etkir. Orta fazın mıknatıslanma akımı, diğer iki fazın
mıknatıslanma akımına göre daha düşüktür. Mıknatıslanma akımlarının Iµ1, Iµ2, Iµ3,
olarak nitelenirse, Iµ2 akımının dengeleyicisi olarak Iµ0 akımı gelecektir. Bu durumda
sıfır hattından geçen akım Iµ0 akımıdır. Bunlar şekil 3.13‟ de gösterilmektedir.
Iµ0
Iµ2
Iµ3
Iµ0
Iµ1
Iµ2
Iµ1
Iµ3
ġekil 3.13 Çekirdek tip güç transformatörüne ait mıknatıslanma akımları.
Burada mıknatıslanma akımları için Iµ1+ Iµ2+ Iµ3+ Iµ0=0 yazılabilir.
31
b) Primer yıldız sargısında nötr hattının mevcut olmadığı durum
Üç fazlı güç transformatörlerinde, üç ve üçün katı harmoniklerin arasında faz
farkı bulunmadığından nötr noktasında sıfırlanmazlar.
Üç fazlı güç transformatörlerinde, üç ve üçün katı harmoniklerin arasında faz
farkı bulunmadığından nötr noktasında sıfırlanmazlar. Nötr noktası topraklı ise bu
akımlar burada toplanırlar ve toprağa akarlar. Eğer güç transformatörünün nötr noktası
topraklanmamışsa, bu durumda üç ve üçün katı harmonikler sıfır noktasında yığılırlar
ve sargılardan geçemezler. Diğer tek dereceden harmonikler ise nötr noktasında
sıfırlandığı için sargılardan geçecektir. Bu durumda Şekil 3.14‟de gösterilen
mıknatıslanma akımı eğrisinden 3 ve üçün katı harmonikler çıkarılır. Bu durumda i2
akımı elde edilir. i2 akımı denklem (3.36) ile gösterilmektedir. Bu durum şekil 3.14 ile
ifade edilir (Boduroğlu, 1988).
i2 = i - i3
(3.36)
Φ
i
Φ
Φ=f (i)
Φ1
Φ2
i
i-i3
i
i
t
i3
ġekil 3.14. Yıldız bağlı transformatörün nötrünün topraksız durumunda mıknatıslanma akımının
ve manyetik akının şekli
Şekil 3.14 ‟e bakıldığında, i2 mıknatıslanma akımı, i akımına göre daha yatıktır.
Buradan terse doğru giderek Φ2 manyetik akı eğrisi elde edildiğinde, Φ1 manyetik akı
çizgisine göre daha yatık olduğu görülmektedir. Bunun nedeni üçüncü harmoniğin
manyetik alana geçmesidir. Bu durumda her üç bacakta alanın üçüncü harmoniği
bulunacaktır. Serbest kuvvet çizgi yolları bulunan transformatörlerde ( örn. Mantel Tip)
aynı fazda bulunan bu manyetik akılar devrelerini bu yollardan tamamlarlar. Manyetik
devreleri bağımsız olmayan güç transformatörlerinde (örn. Çekirdek tip) alanda bulunan
üç ve üçün katı harmonikler devrelerini çekirdek içinde tamamlayamazlar. Bu durumda
harmonikler hava veya yağ içinde kendilerine yol seçerler. Eğer imkân olursa
32
transformatör kabına atlarlar. Bu şekilde mıknatıslanmaya cebri mıknatıslanma denilir.
Bu yüksek frekanslı harmonikler gövdenin ısınmasına neden olur. Ayrıca aynı fazda
bulunan bu manyetik akılar sargılarda aynı fazda gerilim indüklerler. Üç ve üçün
katında bulunan gerilimler hatlarda rezonans sonucunda yüksek gerilimlerin meydana
gelmesine neden olur.
Simetrik olmayan çekirdek tipi transformatörlerde, orta fazın mıknatıslanma
akımını dengeleyen mıknatıslanma akımı olan Iµ0, nötr noktası topraklamadığında, diğer
sargılara dağılır ve her bir sargıda 1/3 oranında bulunur. Her bir sargıya dağılan bu akım
buralarda manyetik akılar meydana getirir. Bu tip güç transformatörlerinde devresini
çekirdekten tamamlayamaz. Bu durumda devresini transformatör kabından tamamlar.
Aynı fazda olan bu akılar aynı fazda gerilim indükleyerek nötr noktasının kaymasına
neden olurlar (Boduroğlu, 1988).
3.2.7.2. Primer sargısının üçgen bağlantı gurubunda harmonik analizi
Primer sargısı üçgen olan güç transformatörlerinde üç ve üçün katı harmonikler
oluşur. Aynı fazda olan bu harmonik akımları üçgen olarak bağlanan sargıların içinde
akabilirler. Üç ve üçün katı olan bu harmonikler, yalnızca kapalı çevrim oluşturan bu
üçgen sargıda akacaklarından dolayı şebekeye geçemezler.
Üçgen bağlantıda, bacaklardaki simetrisizlikten kaynaklanan mıknatıslanma
akımlarının eşitsizliğinin bir sakıncası kalmaz. Çünkü mıknatıslanma akımları eşit
olmasa da şebekeden çekilen akımlar eşittir.
Zig zag bağlı güç transformatörleri, sadece sekonder kısmında kullanıldığından
mıknatıslanma akımlarının incelenmesi bu kısımda teoride kalacaktır. Şayet bu primer
tarafı zig zag bağlanıp nötr hattı topraklanırsa, nötr hattından yüksek değerde üçüncü
harmonik akımları akar (Boduroğlu, 1988).
Değişik bağlantı grupları, çeşitli durumlar gözetilerek değerlendirilmiştir. Bu
durumlar Sağlam‟a (2005) ait yüksek lisans tezinde incelenmiştir. Bağlantı grubu olarak
Dyn1, Dyn11 ve Yyn bağlantı grupları için simülasyonlar yapılmıştır.
Aynı harmonikli yük komposizyonunda yapılan simülasyonlar sonucunda,
harmonikli akımlardan dolayı Dyn11 bağlantılı dağıtım transformatörünün primer ve
sekonder tarafında oluşan gerilim düşümleri, Dyn1 ve Yyn bağlantı gruplu
transformatörlere göre daha fazla olmuştur. Dyn1 bağlantı grubunun sekonder
tarafındaki gerilim 387 V iken, Dyn11 için bu 371 V ve Yyn için 380 V olmuştur. Bu
33
sonuçlardan görüldüğü üzere harmonikli akımların en fazla gerilim düşümüne neden
olduğu grup Dyn11 bağlantı grubudur. Dyn11 bu bağlantı grupları içerisinde harmonikli
yük akısından gerilim düşümü olarak en fazla etkilenen grup olmuştur. Burada Dyn
bağlantı gruplarında faz farkı arttıkça oluşan gerilim düşümünün arttığını söylemek
mümkün olmaktadır.
Bu bağlantı gruplarını sekonder akımlar açısından değerlendirmek gerekirse ki
bu akıma yüklenme akımı demek doğru olur, en az yüklenen bağlantı grubu olarak Yyn
görülmektedir. Yüklenme akımlarına bakıldığında Dyn1 için 1855 A, Dyn11 için
2024 A ve Yyn için 1839 A olmaktadır. Buradan görüldüğü üzere Dyn11 bağlantı grubu
sistemdeki harmonikli akımdan dolayı en fazla yüklenen transformatör grubu
olmaktadır. Böylece fazla yüklenmeden dolayı arızaya ve transformatör ömrünün
kısalmasına en yakın bağlantı grubu olarak Dyn11 bağlantı grubu görülmektedir. Ayrıca
bu durum primer tarafındaki akımlar için de geçerlidir. Burada Dyn bağlantı gruplarında
faz farkı arttıkça oluşan kayıpların arttığını söylemek mümkündür.
Transformatörlere asenkron motorlar bağlanmış ve asenkron motorun kaynaktan
çektiği akımlar Dyn1 bağlantı grubunda 80 A, Dyn11 bağlantı grubunda 76.69 A ve
Yyn bağlantı grubunda 78.37 A olmaktadır. Burada Dyn11 bağlantı grubunda motor
yüklerinin harmonikli akıştan en fazla etkilendiklerini ve çalışma akımlarının azaldığını
söylemek mümkündür.
Transformatör empedansının endüktans bileşeni % 20 arttırılarak Dyn1, Dyn11
ve Yyn bağlantı grupları için simülasyonlar yapılmış ve referans simülasyon ile
karşılaştırılmıştır. Sonuçlara göre yüklenme durumunun en fazla ve gerilim düşümünün
de en çok Dyn11 bağlantı grubunda olduğu görülmüştür. Fakat transformatör
empedansının arttırılması durumunda yüklenme akımı olarak esas alınan sekonder akım
değeri % 1.17 azalarak, örneğin Dyn11 için 2024 A‟den 2001 A‟e gerilemiştir.
Sekonder akım distorsiyonu her üç bağlantı grubu için % 28 azalma ile
iyileşmeye gitmektedir. Bu durum bağlantı gruplarının primer tarafları için de geçerli
bir durumdur. Sonuç olarak transformatör empedansının arttırılmasıyla harmonikli yük
akısının sistem üzerindeki etkisi azalmaktadır.
Motor yükleri, mevcut yük kompozisyonuna göre % 213 arttırılarak Dyn1,
Dyn11 ve Yyn bağlantı grupları için simülasyonlar yapılmış ve referans simülasyon ile
karşılaştırılmıştır. Sonuçlara göre Dyn1, Dyn11 ve Yyn gruplarında primer ve sekonder
gerilimleri, referans simülasyondaki primer ve sekonder gerilimlere oranla azalmış ve
referans simülasyona göre gerilim düşümü artmıştır. Harmonik akımların, motor
34
yükünün arttırılması durumunda Dyn11 bağlantı grubunu diğer gruplara göre daha fazla
yüklediğini söylemek mümkündür.
Bu durum için toplam Harmonik akım ve gerilim bozunumları dikkate
alındığında her bağlantı Pasif yük, mevcut yük kompozisyonuna göre % 50 arttırılarak
Dyn1, Dyn11 ve Yyn bağlantı grupları için simülasyonlar yapılmış ve referans
simülasyon sonuçları ile karşılaştırılmıştır. Sonuçlara göre pasif yükün % 50
arttırılmasıyla, Dyn1, Dyn11 ve Yyn bağlantı gruplarında primer ve sekonder gerilimler
referans simülasyona göre azalmış, gerilim düşümü artmıştır. Gerilim düşümünün
artmasının nedeni sistemdeki yük büyüklüğünün artmış olmasıdır. Yüklenme akımı da
artan bu lineer yüke göre düzgün bir artış sağlanmıştır.
Pasif yükün bu oranda arttırılması sistemin lineerliğini arttırmış olduğundan
toplam harmonik akım ve gerilim bozunumlarında büyük azalmalar oluşmuştur.
Örneğin referans simülasyona göre pasif yükün arttırılması durumunda Dyn11 bağlantı
grubunda toplam harmonik akım bozunumunda % 64 bir azalma olmuştur.
Sistemdeki mevcut 3 fazlı pasif yük 1000 kW değerden 100 kW değere
düşürüldükten sonra, A, B, C fazlarına sırasıyla 100 kW, 300 kW ve 500 kW
değerlerinde tek fazlı pasif yükler eklenerek dengesiz bir sistem elde edilmiştir.
Sonuçlara göre dengesiz yüklenme şartlarının oluşturulmasıyla, Dyn1, Dyn11 ve Yyn
bağlantı gruplarında primer gerilimler gelişi güzel değişim gösterirken ve sekonder
gerilimler için dengesiz olarak daha az yüklenen A fazında artış oluşmuştur. Sekonder
akımlara bakıldığında üç bağlantı grubu için de dengesizliğin en fazla olduğu C fazında
yüklenme oldukça artmaktadır. Örneğin bu artış Dyn11 bağlantı grubu için referans
simülasyon değerine göre en fazla dengesiz yüklenen C fazı için % 67 oranında
oluşmuştur.
Bu durum değişikliği toplam harmonik akım ve gerilim bozunumları açısından
incelendiğinde, akım bozunumunda dengesiz yüklenmenin en az olduğu A fazında
büyük değişimler oluşmuştur. Sekonder akım bozunumu A fazında % 36.19 iken C
fazında % 2.88 olmaktadır.
Dyn1, Dyn11 ve Yyn bağlantı grupları akım bozunumu, gerilim bozunumu,
yüklenme durumu ve gerilim düşümü değerlerine göre incelenerek en kötü durumların
neler olduğu belirlenmiştir. Bu durumlar motor yükünün arttırılması ve dengesiz
yüklenme olarak ortaya çıkmıştır. Bu durumların tespit edilmesinin ardından 3 fazlı
pasif yük 1000 kW değerden 100 kW değere düşürüldükten sonra, A, B, C fazlarına
sırasıyla 200 kW, 300 kW ve 400 kW değerlerinde tek fazlı pasif yükler eklenmiş ve
35
sistemdeki motor yük değerleri de % 213 arttırılarak bu şartlar oluşturulmuştur. Sadece
dengesizlik durumuna veya sadece motor yüklerinin arttırılması durumuna bakıldığında,
her ikisinin birden bulunması dengesizlikle ilişkili olarak yüklenmeyi arttırmıştır.
Bu durumu bozunum açısından değerlendirmek gerekirse dengesizliğe motor
yükünün artmasının eklenmiş olmasıyla yine dengesiz bir biçimde bozunumların arttığı
görülmektedir. En az yüklenen A fazında akım ve gerilim bozunumları en yüksek
olmaktadır (Sağlam, 2005).
Güç transformatörleri boşta çalışırken aktif akım çekme yüzdeleri çok düşer ve
mıknatıslanma akımı oranı en üst seviyelere ulaşır. Ayrıca transformatör boşta
çalıştığında, nüve doyuma ulaşır ve gerilimi yükselir. Bu nedenle transformatörler boşta
çalışırken titreşimleri fazla olur.
Boşta çalışma durumunda, mıknatıslanma akımının artması, manyetik çekirdeğin
doyuma gitmesi ve çekilen akımın çok küçük olmasından dolayı harmoniklerin oranları
%90 seviyelerine kadar yükselmektedir.
1600kVA gücündeki transformatörün OG barasından güç analizörü ile ölçümler
yapılmıştır. Bu ölçüm sonuçları, Çizelge 3.8‟ de gösterilmektedir.
Çizelge 3.8 Güç Transformatörünün boşta çalışması durumunda harmonik oranları
Harmonik Oranları
Akım Harmonikleri
Gerilim Harmonikleri
L1
L2
L3
L1
L2
L3
I3
45%
43%
45%
V3
0.5%
0.4%
0.5%
I5
62%
60%
61%
V5
0.8%
0.6%
0.8%
I7
37%
37%
36%
V7
1.1%
1.1%
1.1%
THDI
255%
255%
255%
THDV
4.3%
4.3%
4.2%
3.2.8. Harmoniklere karĢı alınan önlemler
Harmoniklerin üretilmesini engellemek veya etkilerini en aza indirmek için
elektrikli cihazların içyapılarında düzenlemeler yapılabilir. Bu düzenlemelerin
yetmediği durumlarda harmonik filtreler kullanılır.
36
3.2.8.1. Alternatörlerde harmoniklere karĢı alınan bazı önlemler
Senkron alternatörlerde harmonikleri yok etmek veya etkilerini en aza indirmek
için çeşitli yöntemler kullanılmaktadır. Bunlar sargı kirişleme faktörü, sargı yayılma
faktörü ve olukların sarılma oranlarıdır.
3.2.8.1.1. Sargı kiriĢleme faktörü ile belirli harmoniklerin yok edilmesi
Çap bobinlerde iki bobin yanı arasında 180° faz farkı bulunmaktadır.
Kirişlenmiş iki bobin yanı arasındaki faz farkının 180° farklı olduğu kabul edilsin. Bu
durumda bobin yanı gerilimlerinin geometrik toplamları, cebirsel toplamlarından küçük
olacaktır. Şekil 3.15‟ de bu tür kirişlenmiş bir bobin incelenmiştir (Boduroğlu, 1988).
ġekil 3.15. Kirişlenmiş bobin (Boduroğlu, 1988).
Şekil 3.15‟ de iletkenlerin gerilimlerinin toplamından oluşan E 1 ve E2 gerilimleri
arasında, bobin yanları arasında kutup adımı τp den farklı uzaklık bulunduğundan, β gibi
bir faz farkı vardır. y= τp olsa idi, bu takdirde β sıfıra eşit olacaktı. Yani faz farkı
oluşmayacaktı.
y≠ τp olması durumunda bobin yanı gerilimlerin geometrik toplamı, cebirsel
toplamından küçük olur. Gerilimin geometrik ve cebirsel toplamları sargı kirişleme
faktörünü verir. Sargı kirişleme faktörü denklem (3.37)‟ de gösterilmektedir.
s
E
E1 E2
Kirişleme faktörü her bir harmonik için yazılabilir. Denklem (3.38)‟ de
(3.37)
37
n. harmonik için kirişleme faktörü gösterilmektedir.
sn
En
(3.38)
E1n E2 n
Çap bobinde iki bobin arasındaki faz farkı л „ ye eşittir. n. harmonikte faz farkı
ise n.л ‟ye eşittir. Kirişlenmiş bir bobinde faz farkı ise denklem (3.39)‟ da
gösterilmektedir.
n n.
y
.
p
(3.39)
Kirişlenmiş bir bobinde gerilimlere ait fazörlerdeki faz farkını oluşturan β değeri
1.harmonik için denklem (3.40)‟ da ve n.harmonik için bu değer denklem (3.41)‟ de
gösterilmektedir.
1
y
p
.
n n. n.
(3.40)
y
p
.
(3.41)
Kirişleme faktörünü s ile gösterilirse bu durumda β değeri 1.harmonik için
denklem (3.42) ve n.harmonik için denklem (1.43)‟ deki gibi olur.
1
s
p
n n.
.
s
p
(3.42)
.
(3.43)
Buradaki gerilim ifadeleri 1.harmonik için denklem (3.44) de gösterilmektedir.
n. harmonik için bu değer denklem (3.45)‟ de gösterilmektedir.
E 2 E1.cos
1
(3.44)
2
En 2 E1.cos n.
1
2
(3.45)
Bu ifadeler denklem (1.38)‟ de yerine konursa n. harmonik için kirişleme faktörü
bulunur. n. harmonik için kirişleme faktörü denklem (3.46)‟ da gösterilmektedir.
sn cos
n.1
2
(3.46)
Sargı kirişleme faktörü ile bazı harmonikler yok edilebilir. Denklem (3.41) ve
denklem (3.46)‟ daki ifadeler yerlerine konulursa denklem (3.47) elde edilir. Bu
38
denklemin çözülmesiyle sargı kirişleme faktörü bulunur. Bu ifade denklem (3.48) de
gösterilmektedir.
sn cos(
n. n. y
. )
2
2 p
(3.47)
sn sin
n. y
.
2 p
(3.48)
Eğer 5.harmonik yok edilmek istenirse sargıları 1/5 oranında kirişlemek gerekir. Yani
4
y p olmalıdır. Bu ifade denklem (3.48)‟ de yerine yazılırsa;
5
s 5 sin
5. 4 p
.
sin 2 0
2 5p
elde edilir (Boduroğlu, 1988).
s 5 0 olması 5.harmoniğin yok edilmesi demektir.
3.2.8.1.2. Sargı yayılma faktörü ile belli harmoniklerin yok edilmesi
Senkron alternatörlerde, sargı yayılma faktörü kullanılarak üç ve üçün katı
harmonikler yok edilebilir. Bir tabakalı bir fazlı sargıda bir kutupta var olan Q oluktan
yalnız q miktarı sarılmış olacağından bu gibi sargı için sargı yayılma faktörü denklem
(3.49)‟ da gösterilmektedir (Boduroğlu, 1988).
n
sin n.q.
1
q.sin n.
1
2
(3.49)
2
Bir fazlı bir sargıda ya da turbo alternatörde, kutup taksimatının 2/3‟ü sarılırsa
üç ve üçün katı harmonikler yok olur. q.γ1 =
2
ye eşittir. Bu değerler denklem (3.49)‟
3
da yerine yazılırsa;
n
sin n.
3
q.sin n.
1
olarak bulunur. Burada üç ve üçün katı harmonikler için n 0 olur.
2
Bu şekilde üç ve üçün katı harmonikler yok edilebilir (Boduroğlu, 1988).
Bunlardan başka, özellikle motorlarda stator sargılarına ait oluklar eğri yapılarak
yüksek harmoniklerin meydana gelmesi engellenir. Ayrıca olukların ağızları kapatılarak
yine yüksek harmoniklerin oluşumu engellenir.
39
Eğer alternatör 4 iletkenli bir şebekeye bağlı ise nötr hattı, zig zag bağlı bir
bobinle oluşturulan sanal yıldız noktasına bağlanır. Statör sargı adımlarının uygun
seçilmesiyle ve kirişleme yolu ile alan eğrisindeki 3, 5 ve 7. harmonikler elenir.
3.2.8.2.Statik dönüĢtürücülerde belli harmoniklerin yok edilmesi
Dönüştürücülerde harmonik derecesi n=kxp±1 idi. Burada darbe sayısı artırılırsa
küçük dereceli harmonikler yok edilir. Harmonik akımları;
I5=I1/5 I7=I1/7 şeklindedir. Darbe sayısı artırılıp küçük dereceli harmoniklerin
giderilmesi ile akımları da düşecektir (Bilge, 2008).
3.2.8.3. Güç Transformatörlerinde belli harmoniklerin yok edilmesi
Güç transformatörlerinde mıknatıslanma akımındaki yüksek harmoniklerin
etkilerini artırmamak için manyetik endüksiyon 1,3 T (13000 G) altında tutulur.
Manyetik
endüksiyonun düşük
tutulması transformatör
nüvesinden daha
az
yararlanmaya neden olur. Manyetik endüksiyonun artması sonucu üçüncü ve yedinci
harmoniklerde artış görülür. Transformatör çekirdeğinden tam olarak yararlanabilmek
için endüksiyonun 1,6T seviyelerinde olması gerekir.
Tersiyer sargılar üçgen bağlanarak 3. harmoniğin etkisi giderilir. Bu durumda
tersiyer sargı 3. harmonik akımlarına kısa devre yolu oluşturur.
Güç transformatörlerinde bağlantı gurubuna göre harmonik kompanzasyonu
yapılabilir. Güç transformatörünün primer sargısı üçgen bağlanırsa 3.harmonik akımları
her fazın sargısından dolaşabilir. Böylece bir kapalı çevrim oluşur. Üçgen sargı
içerisinde dolaşan 3.harmonik OG şebekesine geçemez.
3. ve 7. harmoniğin etkisi, soğuk haddelenmiş ve kristalleri yönlendirilmiş
saclar kullanılarak azaltılabilir. Bu durumda güç transformatörünün nüvesinin histerezis
eğrisi düzeltilmiş olur. Bunun sonucunda mıknatıslanma akımı sinüs biçimine yaklaşır.
Böylece harmoniklerin bir kısmı kompanze edilmiş olur.
Güç transformatörünün boyundurukları manyetik olarak üçgen bağlanarak 5. ve
7. harmonikler yok edilebilir. Şekil 3.16‟ da boyundurukları üçgen bağlı bir güç
transformatörü gösterilmektedir. Şekilden de görüldüğü üzere bacak akısı olan Φb ,
boyunduruk akısı olan Φj ve Φj‟‟ ne bölünmektedir. Boyunduruk akıları bacak akılarına
nazaran ileride veya geride olmak üzere 30° faz açılarına sahiptirler. Bu akıların
40
uyarılması için 5. ve 7. harmoniklere ihtiyaç vardır. Beşinci harmonikte 150° ve 7.
harmonikte ise 210° faz farkı bulunmaktadır (Boduroğlu, 1988).
Φj’ Φj
3
2
Φb
1
ġekil 3.16. Boyundurukları üçgen bağlanmış çekirdek tip güç transformatörü (Boduroğlu, 1988).
Simetrik halde iki boyunduruk, manyetik olarak bağlı bulundukları bacağın 5. ve
7. harmoniklerine, ters yönde harmoniklerle uyarılırlar. Relüktansların uygun bir şekilde
seçilmesiyle, karşılıklı ters etkiden dolayı, yüksek endüksiyonlarda bile 5. ve 7.
harmonik kompanze edilir. Bir bacağa yerleştirilen sargı çekirdeği mıknatıslamak,
bacak ve boyunduruklar için gerekli manyeto motor kuvvetini sağlamaktadır. Yani bu
sargı, bacak ve boyunduruklar için gerekli toplam mıknatıslanma akımını sağlamalıdır.
Bu durumda akımın ifadesi denklem (3.50)‟ de gösterilmektedir (Boduroğlu, 1988).
ia ib i1 i2
(3.50)
Bir bacak için, akımın ifadesi denklem (3.51)‟ de gösterilmiştir.
ib ib1 2 sin t ib5 2 sin 5t ib 7 2 sin 7t ...
(3.51)
Bir boyunduruk için akımın ifadesi denklem (3.52)‟ de gösterilmiştir.
i j ' i j1 2 sin(t 30) i j 5 2 sin(t 150) i j 7 2 sin(t 210) ...
(3.52)
Diğer boyunduruk için akımın ifadesi denklem (3.53)‟ de gösterilmiştir.
i j '' i j1 2 sin(t 30) i j 5 2 sin(t 150) i j 7 2 sin(t 210) ...
(3.53)
Bu akımların toplamı denklem (3.54)‟ de gösterilmektedir.
i 2(ib1 3i j1 )sin t 2(ib5 3i j 5 )sin 5t 2(ib7 3i j 7 )sin 7t ...
(3.54)
Bacak ve boyundurukların manyetik geçirgenlikleri uygun seçilirse, ib5 3i j 5 ve
ib 7 3i j 7 sağlanarak mıknatıslanma akımındaki 5.ve 7.harmonikler yok edilir.
41
Bu anlatılanların dışında şebeke ve tesislerin korunmasına yönelik aktif ve pasif
filtreler tasarlanmalıdır. Sanayi uygulamalarında pasif filtreler yaygın kullanıldığı için,
bu tezde pasif filtre tasarımı üzerinde durulmuştur.
3.2.9. Pasif filtreler
Pasif filtreler, yüke paralel olarak veya seri olarak bağlanır. Rezonans ilkesine
göre çalışan bu filtreler temel frekans haricindeki frekansları sönümler. Filtreler
Genellikle kondansatör ve reaktör gruplarından oluşur. Bazı durumlarda omik dirençler
de seri olarak bağlanır. Pasif filtreler ile ilgili Gezgin (2006) yüksek lisans tezinde
hesaplamalar yaparak filtrelerin işlevleri üzerinde çalışmalar yapmıştır.
Pasif filtrelerde amaç, yok edilmek istenen harmonik bileşen frekansında
rezonansa gelecek reaktör ve kondansatörü belirlemektir. Reaktör ve kondansatör seri
rezonans veya paralel rezonans oluşturarak harmonik akımlara, yüksek direnç veya
alçak direnç göstererek sönümlenmelerini sağlar.
Pasif filtreler harmonikleri filtreleme gibi faydaları bulunmasına karşın,
kullanım esnasında sakıncalı durumları da vardır. Bu durumlar;
- Kaynak empedansı filtre karakteristiğini etkilemesi,
- Özel frekanslarda meydana gelen kaynak ve pasif filtre arasındaki paralel
rezonans, kaynak üzerindeki harmonik akımlarının artmasına neden olması,
- Pasif filtreler güç frekansında tepkin güç ürettiklerinden, üretilen tepkin gücün
baralardaki güç katsayısını istenen değerlerin üzerine çıkartması olarak sıralanabilir.
3.2.9.1. Seri pasif filtreler
Seri pasif filtreler Harmonik kaynağı ile şebeke arasına seri olarak bağlanır.
Şekil 1.17‟ de seri pasif filtrenin bağlantısı görülmektedir. Ayarlandığı frekansta yüksek
empedans göstererek harmoniği bastırmaya çalışır. En önemli devre elemanı
endüktanstır. Seri filtreler aynı zamanda yük akımı da taşımak zorundadırlar. Bu yüzden
enerji nakil hatlarında gerilim düşümlerine ve bozunumlara sebebiyet verirler.
Genellikle tek fazlı yüklerin süzülmesinde kullanılırlar. Seri filtrelerin en önemli
sakıncalarından biri, devreye seri bağlandıklarından tam yük akımını da taşıma ve hat
geriliminden yalıtılmalıdır. Bunun yanında seri filtrelerin şebeke ile rezonans sorunu
yoktur (Gezegin,2006).
42
L
Doğrusal
Olmayan Yük
C
SES
ġekil 3.17. Seri pasif filtrenin şebeke bağlantısı
3.2.9.2.Paralel pasif filtreler
Paralel pasif filtrelerde kendi içlerinde bulunan reaktör ve kondansatörün,
harmonik frekansında, seri rezonansa gelmesiyle düşük empedanslı bir yol oluşturulur.
İstenmeyen harmonik akımları bu düşük empedanslı paralel yol yardımıyla toprağa
akıtılarak sistem içinde dolaşımı engellenir. Maliyet ve kullanılabilirlik açısından
paralel filtreler ön plana çıkar. Paralel pasif filtreler, reaktif güç kompanzasyonu da
sağlar. Fakat en büyük dezavantajı sistem ile rezonansa girebilmesidir (Gezegin,2006).
3.2.9.2.1.Tek ayarlı pasif filtreler
Tek ayarlı pasif filtrelerin rezonans frekansı tekdir. Bu rezonans frekansı baskın
olan harmoniğin frekansına ayarlanır. Tek ayarlı pasif filtreler, harmoniklere rezonans
frekansında düşük empedans veya kısa devre yolu oluşturarak, bu harmoniğin toprağa
akmalarını sağlar. Böylece harmonik sistemden uzaklaştırılmış olur.
Şekil 3.18 de tek ayarlı pasif filtreye ait devre elemanları ve empedans grafiği
gösterilmektedir (Gezegin, 2006).
Z
C
L
R
R
fr
f
ġekil 3.18. Tek ayarlı pasif filtrenin devre elemanları ve empedans grafiği
43
3.2.9.2.2. Çift ayarlı pasif filtre ile harmoniklerin yok edilmesi
Çift ayarlı pasif filtreler, iki ayrı frekansta harmonik filtrelemek için kullanılır.
Bu harmonik frekanslarında, filtre içindeki kondansatör ve reaktörler rezonans
oluştururlar. Rezonans esnasında düşük empedans veya kısa devre yolu ile harmonikler
toprağa akarak sistemden uzaklaşırlar. Şekil 1.19 da çift ayarlı pasif filtreye ait devre
elemanları ve empedans grafiği gösterilmektedir. Bu grafikte iki farklı rezonans frekansı
görülmektedir (Gezegin,2006).
C1
Z
L1
R1
C2
L2
R3
R2
R
fr1
fr2
f
ġekil 3.19. Çift ayarlı pasif filtrenin devre elemanları ve empedans grafiği
3.2.9.2.3. Seri reaktörlü pasif filtreler
Seri reaktörlü filtreler, rezonans ilkesine göre çalışarak harmoniklerin
filtrelenmesini sağlarlar. Elektrik tesislerinde, güç transformatörü ile kompanzasyon
kondansatörleri, belli bir frekans değerinde paralel rezonans oluştururlar. Paralel
rezonans esnasında toplam empedans artar. Harmonik kaynakları sabit akım kaynağı
gibi davranır. Eğer harmonik frekansı sistemin rezonans frekansında ise harmonik
akımları yüksek bir dirençle karşılaşacaktır. Bu durumda akım sabit olduğu için
harmoniklerin gerilimi artacak ve ana gerilim dalgasını bozacaktır. Bozulan gerilim
dalgası daha büyük harmonik akımlarının oluşmasına neden olur.
44
Paralel pasif filtreler sistemin rezonans frekansını, kendi rezonans frekansına
çeker. Yani başka bir değişle sistemin rezonans frekansını, harmonik oluşmayan bir
frekans noktasına kaydırırlar.
Filtresiz
Z
[ohm]
ġebeke
Filtreli
ffr
fr
250 350
550
f [Hz]
ġekil 3.20. Harmonikli durumda, normal şebeke çalışmasında ve filtreli durumda empedans
durumu
Şekil 3.20 de sistemin çeşitli durumlardaki toplam empedansı gösterilmektedir.
Harmonik oranının az olduğu durum yani, kompanzasyon sistemi devrede değilken,
şebeke empedansı doğrusaldır. Kompanzasyon sistemi devreye girince paralel
rezonansın etkisiyle toplam empedans artarak, 5.harmonik frekansında en üst seviyeye
ulaşır. Bu durumda eğer sistemde 5.harmonik varsa, 5.harmonik gerilimi artacak ve
1. harmoniğin gerilimini bozacaktır. Böylece akımdaki bozunum oranı da artacaktır.
Seri reaktörlü pasif filtrenin devreye girmesiyle paralel rezonans frekansı 210 Hz
seviyesine çekilmiş ve bu frekans değerinden sonra empedans doğrusal artmaya
başlamıştır. 210 Hz frekans değerinde harmonik bulunmadığından, harmoniklerin
genlikleri de artmayacaktır. Bu yöntem harmonik sorunu olan tesislerde kullanılan en
basit yöntemdir. Bilindiği üzere harmonikler kondansatörler üzerinde aşırı akımlar
oluşturarak zarar görmesine neden olur. Seri reaktörler harmoniklere karşı yüksek
empedans
göstererek,
kompanzasyon
kondansatörlerini
harmoniklerin
zararlı
etkilerinden korur.
Seri reaktörlü pasif filtreler seçilirken filtreleme faktörlerine göre seçilir.
Filtreleme faktörü p ile ifade edilmektedir ve denklem (1.55)‟ de gösterilmektedir.
Seri reaktörlü pasif filtrenin reaktör ve kondansatör değerleri filtreleme faktörü
ile belirlenir.
p = XL/XC
farklı frekanslardaki p değerleri aşağıda sıralanmıştır;
135Hz rezonans frekansında p= %13,7
( 3.55 )
45
189Hz rezonans frekansında p=%7
210Hz rezonans frekansında p=%5,6 dır.
Reaktör
Kondansatör
L
C
ġekil 3.21. Seri reaktörlü filtre devre elemanları ve şebekeye bağlantı şeması
Şekil 3.21‟ de seri reaktörlü filtre elemanları ve bağlantı şekli gösterilmektedir.
Seri reaktörlü filtrelerde harmoniklerden dolayı kondansatör uç gerilimi artmaktadır.
Kondansatörlerdeki
bu
gerilim
artışı
denklem
(3.55)‟de
gösterilmektedir.
Kondansatörün uç geriliminin değişmesi kapasitesini de değiştirir. Dolayısıyla bu
durum kondansatörün gücünün değişmesine neden olur. Değişen güç denklem (3.56)‟da
gösterilmektedir.
Uc= U/(1-p)
( 3.55 )
Q0= (Un/Ur)² x Qr
( 3.56 )
Burada;
Q0= Şebeke geriliminde işletme reaktif gücü (kVAr),
Un= Şebeke gerilimi (V)
Qr= Anma reaktif gücü (kVAr), Ur= Kondansatör anma gerilimini (V) dir.
Bir elektrik tesisinin toplam kapasitif güç ihtiyacı belirlendikten sonra
kondansatör güçleri belirlenir. Bu kondansatörler belirli kademelere göre sıralanırlar.
Her bir kademe için kondansatörler tahsis edildikten sonra filtre tasarlama aşamasına
geçilir. Seçilen kondansatör güçlerine göre reaktörler seçilir. Reaktör güçleri
kondansatör güçleri ile aynı güçte olmalıdır. Kademede bulunan reaktörlerin empedansı
kondansatör kapasitansı ile uygun frekansta rezonans oluşturacak şekilde seçilmelidir.
Reaktörün empedansı hesaplanırken öncelikle denklem (3.57) ile harmonik
derecesi belirlenir. Daha sonda filtreleme faktörü denklem (3.58) ile hesaplanır.
Filtreleme faktörü hesaplandıktan sonra, kondansatör gücü daha önce belirlendiği için
XC hesaplanır. Ve denklem (3.59) ile XL hesaplanır. Tüm bu veriler denklem 3.60‟ da
yerine konularak, reaktörün endüktansı hesaplanır. Buradan yola çıkarak harmonik
filtrede kullanılacak reaktörün endüktansı hesaplanıp gereken reaktör tespit edilir:
46
ωn/ω = n
( 3.57 )
1/n² = p
( 3.58 )
p = XL/XC
( 3.59 )
L=(XC.p)/(2лf)
( 3.60 )
Burada;
ωn=Rezonans frekansı
ω= Şebeke frekansıdır.
47
4. MATERYAL VE YÖNTEM
Bu kısımda çeşitli fabrikalarda Alçak Gerilim (AG) veya orta gerilim (OG)
baralarından, harmonikleri analiz etme amaçlı ölçümler yapılmıştır. Bu ölçümler çeşitli
harmonik
analizörler
kullanılarak
gerçekleştirilmiştir.
Ölçümlerde
kullanılan
analizörlerin özellikleri bölüm 3.1. de açıklanmıştır.
Kullanılan harmonik analizörleri akım bilgisini, (AG) ve (OG) baralarında
bulunan akım trafolarından almaktadır. Gerilim bilgisini, AG barasından doğrudan
temin ederken, orta gerilim barasındaki gerilim trafosundan temin etmektedir.
Fabrikalarda ölçümler, tesisteki farklı çalışma koşulları değerlendirilerek
yapılmıştır. Öncelikle güç transformatörünün boşta ve yükte çalışma durumlarına göre
ölçümler yapılarak sonuçları değerlendirilmiştir.
Harmonik bozunum oranının değişimi üzerinde, kompanzasyon sisteminin
etkisini incelemek için güç transformatörü yüklü çalışırken, kompanzasyon sistemi
devre dışı bırakılmış ve bu durumda ölçümler yapılmıştır. Yine güç transformatörü
yüklü çalışırken, kompanzasyon sistemi devreye alınarak ölçümler yapılmıştır. Giriş
kısmında da bahsedildiği gibi, kompanzasyon sistemi devreye alınınca, paralel
rezonansın etkisiyle harmonik bozunum oranı artmıştır.
Seri reaktörlü pasif filtre kullanan farklı fabrikaların AG ve OG baralarında
ölçümler yapılmıştır. Bu ölçüm sonuçlarına bakıldığında, harmonik oranlarının standart
değerlerde olduğu görülmüştür.
4.1. Harmonik Analizinde Kullanılan Ölçüm Cihazları
Harmoniklerin analizinde çeşitli ölçü aletleri kullanılmıştır. Bunların bazıları
hem (OG) ve hem de (AG) gerilimde ölçümler yapabilmektedir.
4.1.1. Amprobe Genius 5080E harmonik analizörü
Amprobe Genius 5080E harmonik analizörü, tek fazda ölçüm yapabilmektedir.
Üç faz için ayrı ayrı ölçümler yaparak bu değerleri hafızasına kayıt edebilir. Enerji
analizörü olarak kullanılmasının yanı sıra çevrim empedansı, toprak direnci, toprak
özgül direnci gibi ölçümlerde yapabilmektedir.
48
Analizör gerekli ölçümleri yapabilmek için akım bilgisini, AG barasında
bulunan akım transformatöründen veya 200 A akım değerine kadar ölçüm yapabilen,
akım transformatörlü klemp vasıtasıyla alır. Gerilim bilgisini, eğer ölçüm AG
barasından yapılıyorsa doğrudan baradan, ölçüm OG barasından yapılıyorsa, gerilim
transformatöründen sağlar.
Enerji analizörü olarak akım gerilim dalga biçimlerini, akım gerilim dalga
genliklerini, harmonik akım ve gerilim değerlerini, harmonik grafiklerini, aktif reaktif
ve tam güç değerlerini göstermektedir.
ġekil 4.1. Amprobe Genius 5080E enerji analizörünün bağlantı şeması
Şekil 4.1‟de
Amprobe
Genius 5080E analizörünün
bağlantı şeması
görülmektedir. Tek fazdan ölçüm yapabildiği için her faz için akım trafosu ve gerilim
uçları değişmektedir. Bu yüzden ölçülen gerilim faz-faz arası değil de faz-nötr arasıdır.
4.1.2. Simeas P 660 harmonik analizörü
Simeas P 660 analizörü, panoya sabit olarak montaj edilir. Yani taşınabilirliği
yoktur. AG ve orta gerilim barasından ölçümler yapılabilmektedir. Bunun için
analizörde hem akım transformatörü hem de gerilim transformatörü için girişler
bulunmaktadır.
Analizör gerekli ölçümleri yapabilmek için, akım bilgisini AG veya OG akım
transformatöründen sağlar. Gerilim bilgisini, AG‟ de direkt baradan, orta gerilimde
ölçüm yapılıyorsa gerilim transformatöründen sağlar.
49
Siemens firmasının ürettiği bu analizörün akım gerilim dalga biçimleri,
harmonik oranları ve bunların grafikleri, akım gerilim değerleri, kayıt yapabilme
özelliği sayesinde aşırı ve düşük değerdeki akım ve gerilim değerlerini saptayabilme
gibi özellikleri bulunmaktadır.
Bağlantı Noktaları
k
l k
lk
u
x
l
X
U
L1
L2
L3
N
K
u
x
u
x
X
U
X
U
L
K
L
K
L
ġekil 4.2. SIMEAS P660 enerji analizörünün bağlantı şeması
Şekil 4.2‟ de SIMEAS P660 enerji analizörünün bir OG şebekesinde, akım ve
gerilim transformatörü ile yapılan ölçümün bağlantı şeması gösterilmektedir.
4.1.3. Entes MPR 63 Ģebeke analizörü
Entes MPR 63 şebeke analizörü, Simeas 660 gibi sabit montajlı analizördür. Bu
analizörde farklı olarak osiloskop özelliği yoktur. Yani akım ve gerilim dalga şekillerini
gösterememektedir. Fakat istenilen diğer tüm değerleri sayısal olarak verebilmektedir.
RS 485 seri haberleşme bağlantısı ile bilgisayar veya herhangi bir ağa bağlanabilir.
Analizör gerekli ölçümleri yapabilmek için, akım bilgisini AG veya OG akım
transformatöründen sağlar. Gerilim bilgisini, AG de direkt baradan, orta gerilimde
ölçüm yapılıyorsa gerilim transformatöründen sağlar.
Şekil 4.3‟ de bu analizörün bir AG şebekesinde bağlantı şekli gösterilmiştir.
50
K
L1
L2
L3
L
K
k
L
K
l
k
L1
L1
L2
L
l k
L2
l
L3
L3
ġekil 4.3. ENTES MPR 63 enerji analizörüne ait bağlantı şeması
4.1.4. Circutor AR5 harmonik analizörü
Circutor AR5 harmonik analizörünün taşınabilir özelliği sayesinde çeşitli
tesislerde ölçümler yapılmıştır. Osiloskop, aktif ve reaktif güç ölçme, harmonik analiz
grafikleri çıkarabilme, her üç fazdan aynı anda ölçüm yapma, güç faktörü ölçme
özellikleri sayesinde harmonikler detaylı bir şekilde incelenmiştir.
Analizör ölçüm için akım bilgisini, AG barasında ölçüm yapılıyorsa, akım
transformatörlü
klemplerinden
veya
direkt
AG
barasında
bulunan
akım
transformatörlerinden sağlar. OG de akım bilgisi OG akım transformatöründen
sağlanmaktadır. Gerilim bilgisi, AG tesislerinde AG barasından doğrudan temin
edilirken OG tesislerinde gerilim transformatöründen sağlanır.
Şekil 4.4 de üç fazlı bir sitemde ölçüm için bağlantı şekli verilmiştir. Daha
değişik bağlantı çeşitleri de bulunmaktadır.
51
L1
L2
L3
Akım giriĢleri
Gerilim giriĢleri
ġekil 4.4. CICUTOR AR5 enerji analizörüne ait bağlantı şeması
4.2 Harmonik Ölçümleri
Ölçüm yapan cihazlar bağlantı şekilleri gösterilerek anlatılmıştır. Bu cihazlar ile
çeşitli şartlarda ölçümler yapılmıştır. Bunlar:
-
Güç transformatörü boşta çalışırken yapılan ölçüm,
-
Filtresiz tesislerde ölçüm,
-
Filtreli tesiste yapılan ölçüm, şeklinde sıralanabilir.
4.2.1. Güç transformatörü boĢta çalıĢırken yapılan ölçüm
1600kVA gücünde güç transformatörü boşta çalıştırılırken MPR63 analizörü ile
ölçümler yapılmıştır. Bu ölçümler güç transformatörünün OG barasından, akım ve
gerilim transformatörlerinden alınan bilgiler ile yapılmıştır. Bu analizörün bağlantısı
Şekil 4.5‟ de gösterilmektedir. Bu yapılan ölçümlerin sonucu Çizelge 4.1‟ de
gösterilmektedir.
52
ġekil 4.5. MPR 63 Analizörünün 1600kVA trafo postası tek hat şemasındaki bağlantısı
Çizelge 4.1. 1600kVA trafonun boşta çalışmasında oluşan akım harmonikleri ve oranları
Ih / f
L1
L2
L3
I2
1,3%
3,2%
1,8%
I3
7,7%
4,5%
48,5%
I5
62,4%
69,4%
64,8%
I7
37,5%
37,6%
38,6%
I9
1,9%
11,3%
11,5%
I11
10,4%
10,1%
10,5%
I13
5,5%
5,3%
4,6%
THD I
75,6%
92,5%
91,8%
Σ THDI
259%
MPR 63 enerji analizörünün osiloskop özelliği olmadığından akım ve gerilime
ait dalga şekilleri elde edilememiştir. Fakat akım ve gerilimdeki harmonik derecelerine
göre bozunum oranları ile ilgili ölçümler yapılmıştır. Gerilimdeki harmonik bozunum
oranları Çizelge 4.2‟ de gösterilmektedir.
Çizelge 4.2. 1600kVA trafonun boşta çalışması durumunda oluşan akım harmonikleri ve oranları
Vh / f
L1
L2
L3
V3
0,2%
0,5%
0,5%
V5
0,5%
0,8%
0,5%
V7
1,1%
1,1%
1,3%
THD V
Σ THD V
4,3%
4,2%
4,3%
4,3%
53
4.2. Harmonik filtre bulunmayan tesislerde yapılan ölçümler
Fabrikalarda kompanzasyon sistemleri, reaktif gücün dengede tutulması için
kullanılır. Harmonik bozunum oranları kompanzasyon sisteminin devrede olup
olmayışına göre değişiklik göstermektedir.
İki ayrı tesiste iki farklı enerji analizörü ile ölçüm yapılmıştır. Bu tesislerden
birisi 1250kVA gücünde transformatöre sahip bir alçı fabrikası, diğeri ise 1000kVA
gücünde transformatöre sahip metal işleyen bir fabrikadır. Alçı fabrikasında alçı işleme
sırasına göre taş kırma, mikser, fırın kısımları bulunmaktadır. Metal işleyen fabrikada
ise kaynak makineleri, presler, kompresörler gibi cihazlar çalışmaktadır. Yükün
çoğunluğunu
presler
oluşturmaktadır.
Pres
makinalarında
asenkron
motorlar
bulunmaktadır. Bu asenkron motorlar sürücüler ile kontrol edilmektedir. Dolayısıyla
asenkron motor sürücüleri ağırlıktadır. Bu fabrikalarda CIRCUTOR ve AMPROBE
marka harmonik analizörleri ile ölçümler yapılmıştır. Alçı fabrikasındaki ölçümler
CIRCUTOR marka analizör ile metal işleyen fabrikada ise AMPROBE marka analizör
kullanılarak ölçüm yapılmıştır. Ölçümler esnasında kompanzasyon kondansatörleri
devreye alınıp çıkarılarak harmoniklerin değişimi gözlenmiştir.
4.2.2.1. Alçı fabrikasına ait 1250kVA gücündeki güç transformatörünün AG
barasında yapılan ölçümler
Şekil 4.5‟ de Alçı fabrikasına ait tek hat şeması ve enerji analizörünün bağlantı
şekli gösterilmektedir. Burada şekilden de anlaşıldığı üzere güç transformatörünün AG
barasından ölçüm yapılmaktadır. Bu ölçüm sonuçlarına ait değerler Çizelge 3.3‟ de
gösterilmektedir.
Çizelge 4.3‟ de kompanzasyon devrede iken ve kompanzasyon devrede değilken
yapılan ölçüm sonuçları bulunmaktadır. Saat 13.25 ile 13.28 arasında kompanzasyon
kondansatörleri devre dışı bırakılmıştır. Kompanzasyon kondansatörleri devrede
olmadığında, harmoniklerin akım ve gerilim değeri oldukça düşük seviyededir. Fakat
kompanzasyon kondansatörleri devreye girdiğinde harmoniklerin oranlarında artış
görülmektedir.
54
31,5/0,4 kV
1250 kVA
Güç transformatörü
2000/5 A Akım transformatörü
Güç
Analizörü
2000 A Kompakt Ģalter
ġekil 4.5. Alçı fabrikasına ait tek hat şeması ve güç analizörünün bağlantısı
Çizelge 4.3. Alçı fabrikasına ait harmonik değerleri
Kompanzasyon Devrede
Gerilim (P-P)
Akım
Güç faktörü
Aktif güç
Reaktif güç
THD V (Gerilim)
THD A (Akım)
V
A
cos φ
kW
kVAr
%
%
max
395
831
-0,97
549
7
3,6
21,3
min
391
485
0,99
318
0
2,9
13,2
Kompanzasyon Devrede Değil
max
385
1165
0,80
497
555
0,9
2,5
min
380
761
0,7
329
289
0,7
2,2
Şekil 4.6‟ da ise toplam harmonik bozunum spektrumu görülmektedir. Şekillere
bakıldığında, kompanzasyon kondansatörleri devrede iken akım ve gerilimdeki
harmonik bozunumunun standartların üzerinde olduğu görülmektedir.
55
ġekil 4.6. Alçı fabrikasına ait toplam harmonik bozunumu
Şekil 4.7‟ de fazlarda bulunan harmoniklerin dereceleri ve yüzde olarak oranları
gösterilmektedir. Bu tesiste akım ve gerilimde, 7. harmoniğin baskın olduğu
görülmektedir.
ġekil 4.7. Alçı fabrikasına ait harmonikler ve oranları
Şekil 4.8‟de ise akım ve gerilimin dalga şekilleri görülmektedir. Dalga
şekillerine bakıldığında, harmoniklerin etkisiyle akımın dalga şeklinin bozulduğu
görülmektedir. Gerilimdeki bozulma ise sınır değerlerdedir.
Grafikler ve şekiller incelendiğinde tesiste harmoniklerin var olduğu ve oranların
standart değerlerin üzerinde olduğu anlaşılmaktadır. Bu tesiste meydana gelen arızaların
çoğu harmoniklerden kaynaklanmaktadır.
56
ġekil 4.8. Alçı fabrikasına ait akım gerilim dalga şekilleri
4.2.2.2.Metal
iĢleme
fabrikasında
bulunan
1000kVA
gücündeki
güç
transformatörünün AG barasında yapılan ölçümler
Bu tesiste kompanzasyon sisteminde herhangi bir filtre bulunmamaktadır.
Harmonik Filtre bulunmayan bu tesiste harmonik analizine yönelik güç kalitesi
ölçümleri
yapılmıştır.
Yüklerin
çoğunluğunu
asenkron
motor
sürücüleri
oluşturmaktadır. Şekil 4.9‟ da metal işleme fabrikasına ait tek hat şemasında güç
analizörünün bağlantısı gösterilmektedir.
Bu bağlantı şeklinde, analizör akım bilgisini güç transformatörünün AG
barasında bulunan akım trafosundan, gerilim bilgisini ise AG barasından sağlamaktadır.
Ölçümler kompanzasyon devredeyken gerçekleştirilmiştir.
Şekil 4.10 da metal işleme fabrikasının 1.fazına ait akım gerilim dalga grafiği,
gerilime ait harmonik grafik ve akıma ait grafikler görülmektedir.
57
31,5/0,4 kV
1000 kVA
Güç transformatörü
1600/5 A Akım transformatörü
Güç
Analizör
ü
1600 A Kompakt Ģalter
ġekil 4.9. Metal işleme fabrikasına ait tek hat şeması ve güç analizörünün bağlantı şekli
5
20
600
15
300
3
0
10
-300
5
-600
0
(a)
0
4
8
12
16
20
24 28 32
3 5 7 9 11 13 15 17 19 21 23 27 29
(b)
(c)
ġekil 4.10. Metal işleme fabrikasına ait 1. fazın (a) Akım gerilim dalga grafiği (b) Gerilimine ait
harmonik grafiği (c) Akımına ait harmonik grafiği
Şekilden akımın dalga şeklinin bozuk,
akımda ve gerilimde 7. harmoniğin
baskın olduğu görülmektedir. Bu grafiklere ait sayısal veriler Çizelge 3.4‟ de
gösterilmektedir.
Çizelge 4.4. 1.faza ait ölçüm sonuçları
L1
h1
h3
h5
h7
THB
I
(A)
553,43
16,87
5,47
91,7
16,51%
V
(V)
328,97
0
0
8,45
2,66%
58
600
5
20
300
15
3
0
10
-300
5
0
-600
0
4
8
12
(a)
16 20
3 5 7 9 11 13 15 17 19 21 23 27 29
24 28 32
(b)
(c)
ġekil 4.11. Metal işleme fabrikasına ait 2. fazın (a) Akım gerilim dalga grafiği (b) Gerilimine ait
harmonik grafiği (c) Akımına ait harmonik grafiği
Şekil 4.11‟ de metal işleme fabrikasının 2. fazına ait akım gerilim dalga grafiği,
gerilime ait harmonik grafik ve akıma ait grafik görülmektedir. Şekilden akımın dalga
şeklinin bozuk olduğu,
akımda ve gerilimde 7. harmoniğin baskın olduğu
görülmektedir. Bu grafiklere ait sayısal veriler Çizelge 4.5‟ de gösterilmektedir.
Çizelge 4.5. 2.faza ait ölçüm sonuçları
L2
h1
h3
h5
h7
THB
(A)
1160.93
38,86
6,148
159,8
14,26%
V (V)
321.68
0
1,7
9,11
2,95%
I
20
5
600
15
300
0
10
3
-300
5
-600
0
0
4
(a)
8
12
24 28 30 32
(b)
3 5 7 9 11 13 15 17 19 21 23 25 27
(c)
ġekil 4.12. Metal işleme fabrikasına ait 3. fazın (a) Akım gerilim dalga grafiği (b) Gerilimine ait
harmonik grafiği (c) Akımına ait harmonik grafiği
Şekil 4.12‟ de metal işleme fabrikasının 3. fazına ait akım gerilim dalga grafiği,
gerilime ait harmonik grafik ve akıma ait grafik görülmektedir. Şekilden akımın dalga
59
şeklinin bozuk olduğu,
akımda ve gerilimde 7. harmoniğin baskın olduğu
görülmektedir. Bu grafiklere ait sayısal veriler Çizelge 4.6‟ da gösterilmektedir.
Çizelge 4.6. 3.faza ait ölçüm sonuçları
L3
h1
h3
h5
h7
THB
(A)
409,15A
13,4
3,19
56,68
14,34%
V (V)
321,68V
0
3,2
6
1,97%
I
Kompanzasyon kondansatörleri devreden çıkarılıp yeniden ölçümler yapılmıştır.
Bu durumda sistemdeki endüktif akımın arttığı gözlemlenmiştir. Bu ölçümde de bir
önceki gibi AG barasının akım transformatörlerinden akım bilgisi, AG barasından da
gerilim bilgisi alınmıştır.
Şekil 4.13‟de kompanzasyon kondansatörleri devre dışı iken, metal işleme
fabrikasının 1.fazına ait akım gerilim dalga grafiği, gerilime ait harmonik grafik ve
akıma ait grafik görülmektedir. Şekillere bakılınca harmoniklerin etkilerinin azaldığı
görülmektedir. Bu grafiklere ait sayısal veriler çizelge 4.7 de gösterilmektedir.
600
5
20
15
300
3
0
10
-300
5
-600
0
4
8
12
(a)
16 20 24 28 32
0
3 5 7 9 11 13 15 17 19 21 23 25 27
(b)
(c)
ġekil 4.13. Metal işleme fabrikasına ait 1. fazın (a) Akım gerilim dalga grafiği (b) Gerilimine ait
harmonik grafiği (c) Akımına ait harmonik grafiği
Çizelge 4.7. 1.faza ait ölçüm sonuçları
L1
h1
h2
h3
h5
h7
THB
I (A)
696,4
17,94
5,35
11,36
4,03
3,51%
V (V)
223,3
0
0
0
0
0%
Şekil 4.14‟ de kompanzasyon kondansatörleri devre dışı iken, metal işleme
fabrikasının 2. fazına ait akım gerilim dalga grafiği, akım ve gerilime ait harmonik
bozunum grafikleri görülmektedir.
60
600
5
20
300
15
3
0
10
-300
5
-600
0
0
4 8 12 16 20 24 28 32
(a)
3 5 7 9 11 13 15 17 21 23 25 27 29
(b)
(c)
ġekil 4.14. Metal işleme fabrikasına ait 1. fazın (a) Akım gerilim dalga grafiği (b) Gerilimine ait
harmonik grafiği (c) Akımına ait harmonik grafiği
Şekillere bakılınca harmoniklerin etkilerinin azaldığı görülmektedir. Bu
grafiklere ait sayısal veriler Çizelge 4.8‟ de gösterilmektedir.
Çizelge 4.8. 2.faza ait ölçüm sonuçları
L2
h1
h2
h3
h5
h7
THB
I (A)
605,61
0
14,09
6,3
0
2,75%
V (V)
224,3
0
0
0
0
0%
Şekil 4.15‟de kompanzasyon kondansatörleri devre dışıyken, metal işleme
fabrikasının 3. fazına ait akım gerilim dalga grafiği, gerilime ait harmonik grafik ve
akıma ait grafik görülmektedir.
600
5
20
300
15
0
3
10
-300
5
-600
0
0
4 8
(a)
12 16 20 24 28 32
(b)
3 5 7 9 11 13 15 17 21 23 25 27 29
(c)
ġekil 4.15. Metal işleme fabrikasına ait 1. fazın (a) Akım gerilim dalga grafiği (b) Gerilimine ait
harmonik grafiği (c) Akımına ait harmonik grafiği
Şekillere bakılınca harmoniklerin etkilerinin azaldığı görülmektedir. Bu
grafiklere ait sayısal veriler çizelge 4.9‟ da gösterilmektedir.
61
Çizelge 4.9. 3.faza ait ölçüm sonuçları
L3
h1
h2
h3
h5
h7
THB
I
393,72
0
9,74
2,51
0
2,89%
V
223,73
0
0
0
0
0%
4.2.3. Seri reaktörlü pasif filtreli sistemlerde yapılan ölçümler
Harmonik filtre tesis edilen sistemlere örnek olarak iki farklı fabrikada ölçümler
yapılmıştır. Bunlar Kalsit üretimi yapan bir fabrika ile Mercedes Benz Türk Kamyon
Fabrikasıdır. Kalsit fabrikası ile bundan önce ölçümler yapılan alçı fabrikasının yükleri
benzerlik göstermektedir.
Kalsit fabrikasında 2000kVA gücünde güç transformatörü bulunmaktadır. Bu
tesisteki kompanzasyon sisteminde seri reaktörlü pasif filtre mevcuttur.
Mercedes-Benz Türk Kamyon Fabrikasının kurulu gücü 9200kVA dır. Bu tesis
içinde
çalışan
çeşitli
güçlerde
güç
transformatörleri
bulunmaktadır.
Bu
transformatörlerin kompanzasyon sistemlerinde seri reaktörlü pasif filtreler mevcuttur.
Bu tesiste bulunan transformatörlerin içerisinden 2 tane 1600kVA gücündeki
transformatörün AG barasından ölçümler yapılmıştır. Ayrıca fabrikanın ana giriş
barasından ölçüm yapılmıştır. Ana giriş barası OG kısmında bulunmaktadır. Ana giriş
barasından, bütün transformatörlerin çektiği toplam güç ölçülmektedir. Her iki tesiste de
kullanılan seri reaktörlü pasif harmonik filtrelerin, filtreleme faktörü %5,67 oranındadır.
Kalsit fabrikasında kullanılan analizör AMPROBE GENIUS 8050E harmonik
analizörüdür. Bu ölçümde akım bilgisi, analizörün akım transformatörlü klemplerinden
sağlanmıştır. Gerilim bilgisi ise doğrudan AG barasından sağlanmıştır. Şekil 4.16‟ da
kalsit fabrikasına ait tek hat şeması ve harmonik analizörün bağlantı şekli
gösterilmektedir.
Çizelge 4.9‟ da kalsit fabrikasının AG barasına ait parametreler verilmiştir.
Burada gerilim harmonikleri standartların altında görülmektedir. Fakat akım
harmonikleri standartların biraz üstündedir. Buna rağmen tesiste harmonik sıkıntısı pek
görülmemektedir. Ölçüm 10:45 ile 11:00 saatleri arasında yapılmıştır. Ölçüme
kompanzasyon sistemi devrede iken başlanmış ve 10:52 ile 10:57 saatleri arasında
kompanzasyon sistemi devre dışı bırakılmıştır.
62
31,5/0,4 kV
2000 kVA
Güç transformatörü
3000/5 A Akım transformatörü
Güç
Analizörü
3200 A Kompakt Ģalter
ġekil 4.16. Kalsit fabrikasına ait tek hat şeması ve güç analizörünün bağlantısı
Çizelge 4.9. Kalsit fabrikasına ait parametreler
Kompanzasyon Devrede
Gerilim (P-P)
Akım
Güç faktörü
Aktif güç
Reaktif güç
THB V
THB I
V
A
cos φ
kW
kVArL
%
%
Kompanzasyon Devrede Değil
max
min
max
min
403
1705
-0,78
812
740
0,6
13,7
396
616
-0,99
339
0
0,5
6,2
393
1396
0,83
777
510
1,1
3,6
385
1083
0,82
737
501
1,0
3,1
Şekil 4.17‟ de her faza ait akım ve gerilimin toplam harmonik bozulma oranları
gösterilmektedir. Kompanzasyon kondansatörleri devre dışı iken harmonik oranları
düşmüştür.
63
ġekil 4.17. Kalsit fabrikasına ait toplam harmonik bozunum
ġekil 4.18. Kalsit fabrikasına ait akım ve gerilim harmonikleri
Şekil 4.18‟ de her faza ait akım ve gerilim harmonikleri ve bunlara ait bozunum
oranları verilmiştir.
Şekil 4.19‟ da akım ve gerilimin dalga şekilleri ve bunların anlık değerleri ile
harmonik bozunum oranları verilmiştir.
Ölçüm sonuçlarına bakıldığında kalsit fabrikasındaki harmonik seviyesi
standartlara yakın seviyelerdedir. Burada da kompanzasyon sistemi devre dışı
bırakıldığında harmonik oranları düşmektedir.
64
ġekil 4.19. Kalsit fabrikasına ait akım ve gerilimin dalga biçimleri
Mercedes Benz Türk Kamyon Fabrikasında yapılan ölçümlerde kompanzasyon
sistemi, çalışma esnasında aksaklıkların meydana gelmemesi için devre dışı
bırakılmamıştır. Bu tesiste 1600kVA gücündeki güç transformatörlerinin AG
barasından ölçümler Siemens marka, sabit pano montajlı harmonik analizörü ile
yapılmıştır. Analizör akım bilgisini AG barasındaki akım transformatörlerinden, gerilim
bilgisini de doğrudan AG barasından almaktadır. Çizelge 4.10 ve çizelge 4.11‟ de bu
iki 1600kVA gücündeki transformatörün AG baralarına ait ölçüm sonuçları
verilmektedir.
Çizelge 4.10. 1. 1600kVA ya ait parametreler
Harmonik Oranlar
Akım Harmonikleri Gerilim Harmonikleri
I5
4%
V5
0.5%
I7
6%
V7
1%
I11
1%
V11
0.5%
Akım: 863A Gerilim= 384V
Çizelge 4.11. 2. 1600kVA ya ait parametreler
Harmonik Oranları
Akım Harmonikleri
Gerilim Harmonikleri
I5
6%
V5
0.5%
I7
2%
V7
0.%
I11
1%
V11
0.5%
Akım: 785A Gerilim= 384V
65
Bu iki güç transformatörünün kompanzasyon sistemlerinde seri reaktörlü pasif
filtre kullanılmıştır. Bu filtrelerin, filtreleme faktörü %5,67 dir. Ölçüm sonuçlarına
bakıldığında harmonik bozunum oranlarının standartların altında olduğu görülmektedir.
Tesiste, 6 adet güç transformatörü aynı anda çalışmaktadır. Tesiste bulunan
transformatörlerin
kompanzasyon
sistemlerinde
seri
reaktörlü
pasif
filtreler
bulunmaktadır. Bu tesisisin elektrik sayacı OG barasında bulunmaktadır. Dolayısıyla
tesisin harmonik bozunumunu bulmak için OG barasından da ölçümler yapılmıştır.
OG barasından yapılan ölçümlerde Simens P660 marka, sabit montajlı,
harmonik
analizörü
kullanılmıştır.
Analizör
akım
bilgisini
OG
akım
transformatöründen, gerilim bilgisini de OG gerilim ölçü transformatöründen
almaktadır. OG barasının akım ve gerilim değerleri Çizelge 4.12‟ de gösterilmektedir.
Çizelge 4.13 de ise OG barasına ait harmonik bozunum oranları verilmiştir.
Çizelge 4.12. OG barasına ait akım ve gerilim değerleri
L1
L2
L3
Akım
A
46
54
48
Gerilim
kV
32
32
32
Çizelge 4.13. OG barasına ait harmonik bozunum oranları
Harmonik Bozunum Oranları
Akım Harmonikleri
Gerilim Harmonikleri
L1
L2
L3
L1
L2
L3
I5
5%
3%
4%
V5
0.3%
0.4%
0.19%
I7
3%
3%
2%
V7
0.4%
0.3%
0.33%
THB
8%
6%
5%
THB
0%
0%
0%
Ölçüm sonuçlarına bakıldığında AG şebekesinde yapılan harmonik filtreler, OG
şebekesinde olumlu yönde etki yapmaktadır. Filtreler, harmonik bozunum değerlerini
hem AG ve hem de OG şebekesinde standartların altında tutmuştur.
4.2.4. Seri reaktörlü pasif filtre hesaplamaları
Filtresiz sistemlerde kompanzasyon devreye alındığında harmoniklerin oranları
artmaktadır. Oranları artan harmonikler güç kalitesini bozarak çeşitli sorunlara neden
olurlar. Harmoniklerin olumsuz etkilerini yok etmek için filtreler tasarlanmalıdır.
66
Tasarlanacak olan filtre, aktif veya pasif olabilir. Aktif filtrelerin şebekeye uyumu pasif
filtrelere göre çok daha iyidir. Fakat maliyetleri yüksek olduğundan dolayı pek tercih
edilmemektedir. Pasif filtreler yük çeşidinin çok fazla değişmediği işletmelerde yaygın
olarak kullanılmaktadır.
Ölçümlere bakıldığında harmonik filtresi olmayan alçı fabrikasında ve metal
işleme fabrikasında kompanzasyon kondansatörleri devreye alındığında harmonik
oranları artmış ve standartların üstüne çıkmıştır. Mercedes Benz ve kalsit fabrikalarında
pasif harmonik filtre kullanıldığından, kompanzasyon sistemi devreye alındığında
harmonik oranları standartların altında kalmıştır.
Mercedes Benz ve kalsit fabrikalarında tasarlanmış filtreler ve bunların hesabı
incelenmiştir. Mercedes fabrikasında 5. Harmonik etkilidir. Bu harmoniğin etkisini
gidermek için 210 Hz rezonans frekansında pasif harmonik filtre kullanılmıştır.
5.harmonik frekansı 250 Hz‟ dir. Bu frekans değerinde paralel rezonans meydana
gelirse toplam empedans artacaktır. Harmoniklerin etkilerini bastırmak amacıyla
rezonans frekansı, seri reaktörlü pasif filtre ile 210 Hz değerine çekilmiştir. Böylece
250 Hz frekansındaki empedans değeri de düşürülmüştür.
Bu fabrikada 210 Hz rezonans frekansında tasarlanan seri reaktörlü pasif
filtrenin reaktör endüktansı L=622 mH ve gücü 40 kVAr, kondansatör kapasitansı
C= 3x77 µF ve gücü 40 kVAr, filtreleme faktörü %p=5,67 şeklindedir. Kullanılan bu
değerler standart değerlerdir.
Bu değerler hariç tutularak yeniden pasif harmonik filtre tasarlanmış ve
hesaplamalar sonucu tasarlanan filtre değerleri ile kullanılan filtrenin değerleri
karşılaştırılmıştır.
Tesiste ihtiyaç olan kompanzasyon gücü 920 kVAr dır. Bunu 12 kademe reaktif
güç kontrol rölesi ile yapacak olursak kademeler:
40+80+80+80+80+80+80+80+80+80+80+80 şeklinde sıralanacaktır. Sistemde
harmoniklerden dolayı kondansatörlerin üzerindeki gerilim artar. Bu gerilim artışı
kondansatörlerin kapasitelerini düşürür. Kondansatörler de kapasite düşümünü azaltmak
için gerilimi daha yüksek kondansatör seçilmelidir. Bu gerilim artışı denklem (4.1) ile
hesaplanmaktadır.
Uc= U/(1-p)
(4.1)
Burada filtreleme faktörü p = %5,67 seçildiğine göre Uc= 424 V değerinde
olmalıdır. Fakat standart üretim olarak Uc=440 V gerilimli kondansatörler vardır. bu
67
yüzden 440 V gerilimli kondansatörler seçilmiştir. Kondansatör gücünün değişimi
denklem (4.2) ile hesaplanmaktadır.
Q0= (Un/Uc)².Qr
(4.2)
Burada:
Q0= İşletme anındaki kondansatör gücü, Un= Şebeke gerilimi,
Uc = Kondansatör gerilimi ve Qr = Anma reaktif gücüdür.
Buna göre ilk kademe olan 40 kVAr kondansatör 400 V değerinde seçilirse,
gerilim artışında bunun değeri 33 kVAr seviyelerine inmektedir. Bunu engellemek için
400 V değerinde kondansatör seçilecekse 40 kVAr lık kondansatör yerine 50 kVAr
veya daha uygunu 440 V değerinde 40 kVAr kondansatör seçilmelidir.
Pasif harmonik filtrenin rezonans frekansı denklem (4.3) ile hesaplanmaktadır.
Bu rezonans frekansında pasif harmonik filtre için gerekli kondansatör ve reaktör
seçilmelidir.
Sistemde gerekli olan kompanzasyon gücü tespit edildikten sonra kondansatör
kademeleri seçilmiştir. Denklem (4.4) ile kapasitif direnç hesaplanmış ve XC = 4,84 Ω
olarak bulunmuştur. Filtreleme faktörü %5,67 olarak alınmıştır. Buna göre
denklem (4.5) ile endüktif direnç hesaplanmış ve XL= 0,274 Ω olarak bulunmuştur.
Pasif harmonik filtrenin endüktansı, denklem (4.6) ile hesaplanmış ve L= 870 mH
olarak bulunmuştur. Pasif harmonik filtrenin kapasitans değeri de denklem (4.7) ile
hesaplanmış ve C=66 µF olarak bulunmuştur.
fr =1/(2л√(L.C))
(4.3)
XC= U²/Q
(4.4)
p=XL/XC
(4.5)
L= XL/(2л.f)
(4.6)
C=1/(XC. 2л.f )
(4.7)
Tesiste kullanılan filtre değerleri ile hesaplanan değerler birbirlerine yakındır.
Bazı farklıkların çıkmasının sebebi, 400 V gerilimindeki kondansatörlerin seçilmiş
olmasıdır. Buradaki kondansatör güçleri 440 V değerine göre seçilmiştir.
Bu hesaplanan değerler, 40 kVAr gücündeki ilk kademe içindir. Diğer
kademeler 80 kVAr gücündedir. Bunlar için standart kondansatör ve reaktör olmadığı
için 2 tane 40 kVAr kondansatör paralel bağlanarak filtre yapılmıştır.
Kalsit fabrikasındaki kompanzasyon sistemi içinde seri reaktörlü pasif harmonik
filtre hesabı yapılmıştır. Kalsit fabrikasındaki kompanzasyon kademeleri:
25+50+100+100+100+100+100+100+100+100+100+100 biçiminde 12 kademelidir.
68
25kVAr filtre kademesi için, rezonans frekansı 210 Hz seçilmiştir. Bu kademede
kullanılacak olan kondansatörler 440 V gerilim değerindedir. Kullanılacak olan
kondansatör gücü belli olduğu için denklem (4.4) kullanılarak kapasitif direnç olan XC
hesaplanmıştır. Denklem (4.7)‟ nin kullanılmasıyla filtre kapasitansı C=413 µF olarak
hesaplanır. Filtreleme faktörü olan p, 210 Hz için %5,67 değerindedir. Bu değerden
yararlanılarak, denklem (4.5) ile endüktif direnç olan XL hesaplanır. Denklem (4.6) ile
filtre endüktansı L= 1,39 mH olarak hesaplanmıştır. Tesiste kullanılan filtrenin
endüktansı L= 1,22 mH, kapasitansı C= 411 µF gücü 25 kVAr ve gerilimi 440 V dur.
Hesaplanan filtre değerleri ile uygulamada kullanılan filtre değerleri birbirine yakındır.
Bu hesaplamalar 50 kVAr ve 100 kVAr filtre kademeleri için yapılmış ve
endüktans değerleri ile kapasitans değerleri hesaplanmıştır. 50 kVAr filtre kademesi
için L= 0,7 mH, C=821 µF olarak hesaplanmıştır. Tesiste kullanılan filtrenin endüktansı
L= 0,61mH, iki adet 25kVAr kondansatör kullanıldığı için, kapasitansı C= 2x(411 µF),
gücü 2x25kVAr ve gerilimi 440 V‟ dur.
100kVAr filtre kademesi için, L= 0,35 mH, C=1644 µF olarak hesaplanmıştır.
Tesiste kullanılan filtrenin endüktansı L= 0,31 mH, dört adet 25 kVAr kondansatör
kullanıldığı için, kapasitansı C= 4x(411 µF), gücü 4x25 kVAr ve gerilimi 440 V‟ dur.
Hesaplanan filtre değerleri ile uygulamada kullanılan filtre değerleri birbirine
yakındır. Kalsit fabrikasının ölçüm sonuçlarına bakıldığında, kullanılan seri reaktörlü
pasif filtrenin, harmonikleri filtrelemede etkili olduğu görülmektedir.
Alçı fabrikası ve metal işleme fabrikasının kompanzasyon sistemlerinde filtre
bulunmamaktadır. Bunların ölçüm sonuçlarından da anlaşılacağı üzere harmonik
bozunum oranları yüksek seviyelerdedir. Her iki fabrikada, harmoniklerin sebep olduğu
arızalar görülmektedir.
Alçı fabrikasında pasif harmonik filtre tasarlamak için sistemin reaktif güç
ihtiyacı 625kVAr olarak hesaplanmıştır. Pasif harmonik filtre kademelerinin sıralanışı,
25+50+50+50+50+50+50+50+50+50+50+100 kVAr şeklindedir.
25kVAr filtre kademesi için, rezonans frekansı 210 Hz seçilmiştir. Bu kademede
kullanılacak olan kondansatörler 440 V değerindedir. Kullanılacak olan kondansatör
gücü belli olduğu için denklem (4.4) kullanılarak kapasitif direnç olan X C
hesaplanmıştır. Denklem (4.7) ile pasif harmonik filtre kapasitesi olan C=413 µF olarak
bulunur. Filtreleme faktörü olan p, 210 Hz değerinde %5,67 değerindedir. Bu değerden
yararlanılarak, denklem (4.5) ile endüktif direnç olan XL hesaplanmıştır. Denklem (4.6)
ile filtre endüktansı olan L= 1,39 mH olarak bulunur.
69
Bu hesaplamalar 50 kVAr ve 100 kVAr filtre kademeleri için yapılmış ve
endüktans değerleri ile kapasitans değerleri hesaplanmıştır. 50 kVAr filtre kademesi
için, L= 0,7 mH, C=821 µF olarak hesaplanmıştır.
100kVAr filtre kademesi için, L= 0,35 mH, C=1644 µF olarak hesaplanmıştır.
Alçı fabrikası için tasarlanan filtrenin simülasyonu yapılmış ve olumlu sonuçlar
alınmıştır.
Metal işleme fabrikası için tespit edilen reaktif güç ihtiyacı 487,5 kVAr
değerindedir.
Burasının
kompanzasyon
kademeleri,
12,5+25+25+25+50+50+50+50+50+50+50+50kVAr şeklindedir.
12,5kVAr filtre kademesi için, rezonans frekansı 189 Hz seçilmiştir. Bu
kademede kullanılacak olan kondansatörler 440 V değerindedir. Kullanılacak olan
kondansatör gücü belli olduğu için denklem (4.4) kullanılarak kapasitif direnç olan XC
hesaplanmıştır. Denklem (4.7) nin kullanılmasıyla filtre kapasitesi olan C=209 µF
olarak hesaplanır. Filtreleme faktörü olan p, 189 Hz değerinde %7 değerindedir. Bu
değerden yararlanılarak, denklem (4.5) ile endüktif direnç olan X L hesaplanır. Denklem
(4.6) ile filtre endüktansı olan L= 3,4mH olarak hesaplanmıştır.
Bu hesaplamalar 25kVAr ve 50kVAr filtre kademeleri için de yapılmıştır.
25kVAr filtre kademesi için, L= 1,72mH, C=412 µF olarak hesaplanmıştır. 50kVAr
filtre kademesi için, L= 0,85mH, C=824 µF olarak hesaplanmıştır.
3.2.5. Kompanzasyon sisteminin harmonikler üzerindeki etkisi ve seri reaktörlü
pasif filtreleme ile ilgili simülasyonlar
Harmoniklerin etkilerini bilgisayar ortamında görebilmek için 1250kVA
gücünde transformatöre sahip Alçı fabrikası modellenmiştir. Modelleme yaparken
fabrikada bulunan yüklerin özellikleri temel alınmıştır.
Alçı fabrikasında kompanzasyon sistemi devrede olduğu ve olmadığı durumlar
için yapılan ölçümlerin sonuçlarına göre pasif filtre tasarımı yapılmıştır.
Ölçümün
yapıldığı
analizörden
rezonans
empedansı
ile
ilgili
bilgi
alınamamıştır. Fakat bilgisayarda rezonans empedansı ile ilgili bilgiler alınmıştır.
Rezonans empedansı, kompanzasyon sisteminde filtre kullanılma durumuna göre
değişim göstermektedir. Bu durumların OG hattının rezonans empedansına etkisi
incelenmiştir. OG hattına ait SIMULINK modeli EK-1‟de gösterilmektedir.
70
İlk olarak fabrikada kompanzasyon sistemi devre dışı bırakılmıştır. Bu
durumdaki AG ve OG baralarına ait rezonans empedansının değişimi, AG barasının
akım ve gerilim dalga şekilleri ve harmonik bozunum oranları gösterilmiştir. Bu duruma
ait SIMULINK modeli EK-2‟de gösterilmektedir.
Şekil 4.20 (a)‟ da kompanzasyon sistemi devrede değilken, AG barasına ait
rezonans grafiği Şekil 4.20 (b) ise OG barasına ait rezonans direncinin grafiği.
Bu grafik Şekil 3.20 ile kıyaslandığında normal değerde olduğu görülmektedir.
(a)
(b)
ġekil 4.20. (a) AG barasına ait rezonans empedansı grafiği (b) OG barasına ait rezonans
empedansı grafiği
(a)
(b)
ġekil 4.21. (a) AG barasına ait akımın dalga şekli (b) AG barasına ait akımın harmonik grafiği
Şekil 4.21 (a)‟da kompanzasyon sistemi devrede değilken, AG barasına ait
akımın dalga şekli görülmektedir. Şekil 4.21 (b) ise AG barasına ait akımın harmonik
grafiğini göstermektedir. Bu iki sonuca bakıldığında harmonik oranların standartlar
altında olduğu görülmektedir.
71
Şekil 4.22 (a)‟da kompanzasyon sistemi devrede değilken, AG barasına ait
gerilimin dalga şekli görülmektedir. Şekil 4.22 (b) ise
AG barasına ait gerilimin
harmonik grafiğini göstermektedir. Bu iki sonuca bakıldığında gerilimin dalga şeklinin
düzgün olduğu ve harmonik oranlarının standartların altında olduğu görülmektedir. Bu
sonuçlar Çizelge 4.14‟ de gösterilmektedir.
(a)
(b)
ġekil 4.22. (a) AG barasına ait gerilimin dalga şekli (b) AG barasına ait gerilimin harmonik
grafiği
Çizelge 4.14. Simülasyon sonuçlarına göre harmonik oranları
Harmonik Oranlar
Akım Harmonikleri
Gerilim Harmonikleri
I5
5,27%
V5
0.5%
I7
4,50%
V7
1%
Akım: 341.2 A Gerilim= 384V
İkinci durumda kompanzasyon sistemi devreye alınmıştır. Bu durumdaki AG ve
OG barasına ait rezonans direncinin değişimi, AG barasının akım ve gerilimin dalga
şekilleri ile harmonik oranlarını gösterilmiştir. Bu duruma ait SIMULINK modeli
EK-3‟de gösterilmektedir.
72
(a)
(b)
ġekil 4.23. (a) AG barasına ait rezonans empedansı grafiği (b) OG barasına ait rezonans
empedansı grafiği
Şekil 4.23 (a)‟da kompanzasyon sistemi devrede iken, AG barasına ait rezonans
grafiği görülmektedir. Bu grafik Şekil 3.20 ile kıyaslandığında, pasif harmonik filtresiz
kompanzasyon sisteminin eğrisine uymaktadır. Şekil 4.23 (b) ise OG barasına ait
rezonans direncinin grafiğini göstermektedir.
Şekil 4.24 (a)‟da kompanzasyon sistemi devrede iken, AG barasına ait akımın
dalga şekli görülmektedir. Şekil 4.24 (b) Kompanzasyon sistemi devrede iken, AG
barasına ait akımın harmonik grafiğini göstermektedir. . Bu iki sonuca bakıldığında
harmonik oranların standartların üzerinde olduğu görülmektedir.
(a)
(b)
ġekil 4.24. (a) AG barasına ait akımın dalga şekli (b) AG barasına ait akımın harmonik grafiği
Şekil 4.25 (a)‟da kompanzasyon sistemi devrede iken, AG barasına ait gerilimin
dalga şekli görülmektedir. Şekil 4.25 (b) Kompanzasyon sistemi devrede iken, AG
barasına ait gerilimin harmonik grafiğini göstermektedir. Bu sonuçlar Çizelge 4.15‟de
gösterilmektedir.
73
Çizelge 4.15‟e bakıldığında gerilimde artış meydana gelmektedir. Bu endüktif
güç kompanzasyonundan ileri gelmektedir.
(a)
(b)
ġekil 4.25. (a) AG barasına ait gerilimin dalga şekli (b) AG barasına ait gerilimin harmonik
grafiği
Çizelge 4.15. Simülasyon sonuçlarına göre harmonik oranları
Harmonik Bozunum Oranları
Akım Harmonikleri
Gerilim Harmonikleri
I5
7,56%
V5
1,17%
I7
19,44%
V7
4,25%
Akım: 451,1 A Gerilim= 397,6V
Üçüncü durumda, daha önceden bu fabrika için tasarlanan pasif harmonik
filtreler kullanılmıştır. Bu durumdaki AG ve OG barasına ait rezonans empedansının
değişimi, AG barasının akım ve gerilimin dalga şekilleri ile harmonik oranlarını
gösterilmiştir. Bu duruma ait SIMULINK modeli EK-4‟de gösterilmektedir.
Şekil 4.26 (a)‟da kompanzasyon sistemi devrede iken, AG barasına ait rezonans
grafiği görülmektedir. Bu grafik Şekil 3.20 ile kıyaslandığında, filtreli kompanzasyon
sisteminin eğrisine uymaktadır. Burada frekans 210 Hz yakınlarında tutularak empedans
artışı engellenir. Şekil 4.26 (b) OG barasına ait rezonans direncinin grafiğini
göstermektedir.
74
(a)
(b)
ġekil 4.26. (a) AG barasına ait rezonans empedansı grafiği (b) OG barasına ait rezonans
empedansı grafiği
(a)
(b)
ġekil 4.27. (a) AG barasına ait akımın dalga şekli (b) AG barasına ait akımın harmonik grafiği
Şekil 4.27 (a)‟da pasif harmonik filtreli bir sistemde, AG barasına ait akımın
dalga şekli görülmektedir. Şekil 4.27 (b) ise pasif harmonik filtreli bir sistemde, AG
barasına ait akımın harmonik grafiğini göstermektedir. Bu iki sonuca bakıldığında
harmonik bozunum oranların standartların altında olduğu görülmektedir.
Şekil 4.28 (a)‟da pasif harmonik filtreli sistemde, AG barasına ait gerilimin
dalga şekli görülmektedir. Şekil 4.28 (b) ise pasif harmonik filtreli sistemde,
AG
barasına ait gerilimin harmonik grafiğini göstermektedir. Bu grafiklerden, harmonik
bozunum oranlarının standartların altında olduğu görülmektedir. Burada paralel
rezonans frekansının 210 Hz seviyesine çekilmesiyle, paralel rezonans empedansı da o
frekans değerine çekilmiştir. 210 Hz seviyesinde harmonik bulunmadığı için
harmoniklerin genlikleri de artmamıştır. Bu sonuçlar Çizelge 4.16‟ da gösterilmektedir.
75
(a)
(b)
ġekil 4.28. (a) AG barasına ait gerilimin dalga şekli (b) AG barasına ait gerilimin harmonik
grafiği
Çizelge 4.16. Simülasyon sonuçlarına göre harmonik bozunum oranları
Harmonik Bozunum Oranları
Akım Harmonikleri
Gerilim Harmonikleri
I5
0,59%
V5
0,12%
I7
1,36%
V7
0,34%
Akım: 507,6 A Gerilim= 399,7V
76
5. ARAġTIRMA SONUÇLARI VE TARTIġMA
Farklı çalışma koşullarını değerlendirmek ve bunları birbiri ile karşılaştırmak
amacıyla, dört farklı fabrikanın enerji besleme sistemlerinde harmonik ölçümler
yapılmıştır. Ayrıca bu sistemlerin bilgisayar ortamında yapılan simülasyonları ile , pasif
harmonik filtrenin tesise uygunluğu test edilmiştir.
Yapılan bu ölçümler sıralanacak olursa ;
-
Güç transformatörü boşta çalışırken harmoniklerin oranları,
-
Kompanzasyon kondansatörleri devre dışı iken, harmonik grafiği ve akım ile
gerilimin dalga şekilleri,
-
Kompanzasyon kondansatörleri devre de iken, harmonik grafiği ve akım ile
gerilimin dalga şekilleri,
-
Pasif filtreli kompanzasyon sistemi devrede iken, harmonik grafiği ve akım
ile gerilimin dalga şekilleri,
-
Aynı özelliklerde tasarlanan tesisin bu durumlardaki rezonans empedansı,
harmonik grafiği ve akım ile gerilimin dalga şekilleri,
5.1. Güç Transformatörü BoĢta ÇalıĢtırıldığında Harmoniklerin Durumu
Sistemlerdeki güç transformatörleri boşta çalıştırıldığında akım harmoniklerinde
aşırı bir artış meydana gelmektedir. Çizelge 4.1 ve Çizelge 4.2 „ye bakıldığında
buradaki değerler akım harmoniklerinin %90 seviyelerine ulaştığını göstermektedir.
Güç transformatörü boşta çalışırken, transformatör şebekeye bağlanmış demir
nüveli bir bobin gibi davranır ve mıknatıslanma akımını çeker. Mıknatıslanma akımının
dalga şeklini, güç transformatörünün yapımında kullanılan nüvenin manyetik özelliği
etkilemektedir. Bölüm 3.2.1.1.‟ de de bahsedildiği gibi, kullanılan malzemenin
manyetik özelliği ne kadar iyiyse ve nüve doyuma gitmiyorsa mıknatıslanma akımının
dalga şekli sinüse o kadar çok yaklaşmaktadır (Şekil 3.2). Bunun sonucunda
mıknatıslanma akımının harmonik etkisi azalmaktadır.
77
5.2. Kompanzasyon Kondansatörleri Devrede Değilken Harmoniklerin Durumu
Kompanzasyon sistemi devreden çıkarıldığında harmonik bozunum oranları
ciddi bir şekilde düşmektedir. Akım ve gerilimin dalga şeklide sinüse yaklaşmaktadır.
Kompanzasyon sistemi devreden çıkarıldığında güç transformatörü paralel rezonansa
gelemediği için harmonik bozunum oranları düşer. Fakat bu durumda endüktif güç
çekimi arttığından güç faktörü düşmektedir.
ġekil 5.1. Kompanzasyon sistemi devre dışında iken harmonik akımları
Şekil 5.1‟ de kompanzasyon sistemi devre dışı olduğunda harmonik akımlarının
durumu görülmektedir. Bu durumda harmonik akımları transformatöre doğru
yönlenecektir (Whittle, 2010).
5.3. Kompanzasyon Kondansatörleri Devredeyken Harmoniklerin Durumu
İki ayrı fabrikada iki farklı analizörle kompanzasyon sistemi devredeyken
ölçümler yapılmıştır. Ölçüm sonuçlarında harmonik oranları standartların üzerinde
çıkmıştır. Bunun nedeni kompanzasyon kondansatörleri ile güç transformatörünün
paralel rezonansıdır.
Şekil 5.2, kompanzasyon kondansatörleri devrede iken harmonik akımlarını
göstermektedir. Bu durumda harmonik üreten yük sabit bir akım kaynağı gibi
modellenir.
Harmonik
frekansında
kompanzasyon
kondansatörleri
ile
güç
transformatörü paralel rezonansa gelirse toplam empedans yükselir. Yüksek empedansın
78
etkisiyle harmoniğin gerilimi artar ve temel gerilim dalgasını bozar. Bozulan gerilim
sonucunda yüksek değerde harmonikli akımlar oluşur (Whittle, 2010).
ġekil 5.2. Kompanzasyon sistemi devrede iken harmonik akımları
ġekil 5.3. Paralel rezonans esnasında harmonik akımının sirkülasyonu
Şekil 5.3‟de görüldüğü gibi paralel rezonans esnasında kondansatörlerde
depolanan
enerji
endüktansa
gönderilir.
Endüktansta
depolanan
enerji
ise
kondansatörlere devredilir (Whittle, 2010).
5.4. Seri Reaktörlü Pasif Harmonik Filtreli Tesislerde Harmoniklerin Durumu
Pasif harmonik filtrenin kullanıldığı tesislerde yapılan ölçüm sonuçlarında akım
ve gerilim harmoniklerinin seviyeleri standartların altında veya standartlara yakın
çıkmıştır. Bunun sebebi ise kullanılan pasif filtrenin, kompanzasyon kondansatörleri ile
güç transformatörü arasında oluşan paralel rezonans frekansını harmonik frekansından
uzaklaştırmasıdır. Rezonans frekansı harmonik frekanslarından farklı bir değere
79
çekilerek, harmonik akımlarının yüksek dirençle karşılaşması engellenir. Böylece
gerilim seviyeleri artamadığından temel gerilim dalgasını da bozamaz.
Şekil 4.4‟de pasif filtre ile rezonans frekansını kaydıran devre görülmektedir.
Tasarlanan harmonik filtrelerde filtreleme faktörü p ya %5,67 ya da %7 seçilmiştir.
Burada p=%5,67 210Hz ‟e , p=%7 ise 189 Hz ‟e denk gelmektedir. Yani rezonans
frekansı 210 Hz veya 189 Hz değerine çekilmektedir.
ġekil 5.4. Paralel rezonans frekansının pasif filtre kaydırılması
Şekil 3.20‟ ye bakıldığında şebeke empedansının doğrusal bir şekilde olduğu
görülmektedir. Kompanzasyon sisteminin devreye girmesiyle bu doğrusallık bozularak
empedans artmaktadır. Pasif filtre kullanılmasıyla paralel rezonans frekansı, fr
noktasına çekilir. Böylece sistemin rezonans frekansı harmonik frekanslarından
uzaklaştırılmış olur.
5.5. Paralel Rezonans Frekansı, Harmonik Akım ve Gerilimin Matematiksel
Olarak Hesaplanması
Rezonans olayının etkisini matematiksel olarak göstermek, ölçümlerle teorik
hesaplamaların hangi noktalarda en iyi seviyede örtüştüğünü saptamak için Alçı
fabrikasında yapılan ölçüm sonuçları, matematiksel olarak hesaplanmıştır. Buna göre
hesaplama sonucunda rezonans frekansını etkileyen parametreler tespit edilmiştir.
Şekil 5.5 de Alçı fabrikasının indirici merkezden itibaren AG barasına kadar olan tek
hat şeması gösterilmektedir.
80
1,1+j3,3 Ω
0,44+j0,71 Ω
477 MCM
266 MCM
3 AWG
11km
2km
500m
154/31.5kV
100MVA
0,321+j0,12 Ω
0,021+j0,0568 Ω
1x50+16mm²
XLPE
80m
31.5/0,4kV
1250kVA
0,09+j0,0028 Ω
5x50kVAr
ġekil 5.5. Alçı fabrikasına ait indirici merkezden AG devresine kadar olan
endüktif ve omik direnç diyagramı
Enerji nakil hattında bulunan iletkenler ve bunların 50 Hz frekansındaki
empedans değerleri kullanılarak hesaplamalar yapılmıştır. Hesaplamalar sonucunda elde
edilen veriler ile ölçülen değerler karşılaştırılmıştır. Buna göre en uygun hesaplama
noktası tespit edilmiştir.
İlk önce hat parametrelerinin paralel rezonans frekansına etkisi incelenmiştir.
Bazı literatürlerde rezonans frekansı hesaplanırken, enerji nakil hattının empedansı ile
kompanzasyon kondansatörleri hesaba katılmıştır (Currence ve ark., 1995). Bazı
literatürlerde ise rezonans frekansı için sadece güç transformatörü ile kompanzasyon
kondansatörlerinin hesaba katılması istenmiştir (Zheng ve ark., 2010). Hat
parametrelerini hesaba katarak paralel rezonans frekansı denklem (5.1)
ile
hesaplanmıştır.
f
1
2 LC
(5.1)
Burada L toplam endüktans, C ise fabrikanın çalışması esnasında devrede olan
kondansatörlerin toplam kapasitansıdır. Toplam endüktif direnç X L ile ifade
edilmektedir. 50 Hz frekans değerindeki toplam endüktif direnç;
XL=j(3,3+0,71+0,12+0,0568+0,008+0,00115+0,00124)= j4,1972 Ω
Toplam endüktans ise denklem (5.2) ile hesaplanmış ve L=0,0133 H olarak
bulunmuştur.
L
XL
2 f
(5.2 )
50 Hz frekans değerindeki toplam kapasitif direnç X c ile ifade edilmektedir.
Burada toplam kapasitif direnç denklem (5.3) ile hesaplanmıştır. Toplam kapasitans ise
denklem (5.4) ile hesaplanmış ve C=0,004975 F olarak bulunmuştur.
81
Xc
V2
Q
Xc
4002
0, 64ohm
250.103
C
(5.3)
1
2 fX c
(5.4)
Toplam hat parametreleri hesaplanırken enerji nakil hattının kapasitif etkisi
ihmal edilmiştir. Buradaki kapasite kompanzasyon kondansatörlerinin kapasitesinden
çok küçüktür. Bu veriler ile denklem (5.1) kullanılarak paralel rezonans frekansı;
f
1
19,56 Hz
2 0, 0133.0, 004975
olarak hesaplanmıştır. OG parametreleri de kullanıldığından toplam endüktans artmış ve
paralel rezonans frekansı olarak 19,56 Hz bulunmuştur.
Şekil 5.6‟da enerji nakil hattı, güç transformatörü, AG güç kabloları ile
kompanzasyon kondansatörlerinin paralel rezonans devresi gösterilmektedir.
RH +RK
XC
XH+XT+XK
ġekil 5.6. Havai hat, güç transformatörü ve AG güç kablolarının toplam empedansı ile
kompanzasyon kondansatörlerinin paralel rezonans devresi
Rezonans frekansındaki endüktif direnç denklem (5.5) ile hesaplanmıştır. Omik
direnç frekansın değişimden etkilenmediği için hepsinin toplamı alınmıştır.
X L 2 fL
X L 2 fL 2 .19,5.0,0133 j1,62 Ω
Omik direnç ise ; R= 1,92Ω
(5.5)
olarak hesaplanır.
Kompanzasyon sisteminin toplam kapasitesi denklem (5.4) ile hesaplanarak
C=0,004975 F olarak hesaplanmıştı. Rezonans frekansındaki kapasitif direnç ise
denklem (5.6) ile hesaplanmıştır.
XC
1
2 fC
(5.6)
82
1
1
j1, 64 Ω değerindedir.
2 fC j 2 .19,5.0, 004975
XC
Eşdeğer empedans denklem (5.7) ile hesaplanmıştır.
Rrez
( R jX L ).( jX C )
( R jX L jX C )
Rrez
(1,92 j1, 62).( j1, 64) 2, 65 j3,14 4,1 49,8
2,14 49, 2 Ω
(1,92 j1, 62 j1, 64) 1,92 j 0, 02 1,92 0,59
(5.7)
Diğer frekans değerleri için de aynı hesaplama yapılarak Şekil 5.7 elde
edilmiştir.
2,5
Empedans [ohm]
2
1,5
1
0,5
0
5
10
15
20
50
150
250
350
450
Frekans [Hz]
ġekil 5.7. Frekansa göre direnç değişimi
Şekil 5.7‟ den de görüldüğü gibi, en yüksek direnç değeri paralel rezonans frekansı
olan 19,56Hz değerindedir.
İkinci durumda OG hattı hariç tutularak, güç transformatörü ve AG güç kabloları ile
kompanzasyon kondansatörlerinin paralel rezonans durumu değerlendirilmiştir.
RK
XC
XT+XK
ġekil 5.8. Güç transformatörü ve AG güç kabloları ile kompanzasyon kondansatörlerinin paralel
rezonans devresi
83
Şekil 5.8‟ de güç transformatörü ve AG kablolarının toplam empedansları ile
kompanzasyon kondansatörünün paralel rezonans devresi görülmektedir. Bu devrenin
rezonans frekansı denklem (5.1) ile hesaplamıştır. 50 Hz frekansındaki toplam endüktif
direnç XL=j(0,008+0,00115+0,00124)= j0,01Ω olarak bulunmuştur.
Toplam endüktans denklem (5.2) ile hesaplanmış ve L = 33µH olarak bulunmuştur.
Toplam kapasitans olan C ise denklem (5.4) ile hesaplanmış ve C=0,004975 F olarak
bulunmuştur. Rezonans frekansı denklem (5.1) ile hesaplanmıştır.
f
1
2 33.106.0, 004975
392 Hz
Paralel rezonans frekansındaki eşdeğer direnci hesaplamak için X L ve XC
değerlerinin hesaplanması gerekmektedir. Çünkü endüktif ve kapasitif dirençlerin
değerleri frekansın değişiminden etkilenmektedir. Endüktif direnç olan X L denklem
(5.5) ile hesaplanmış ve XL = j0,0812Ω olarak bulunmuştur. Kapasitif direnç olan X C
ise denklem (5.6) ile hesaplanmış ve XC = -j0,0816Ω olarak bulunmuştur. Rezistif
direnç olan R = 0,09Ω olarak hesaplanmıştır. Eşdeğer rezonans empedansı ise denklem
(5.7) kullanılarak hesaplanmıştır. Direnç değeri farklı frekans değerlerinde hesaplanarak
Şekil 5.2 oluşturulmuştur.
Rrez
(0, 09 j 0, 0812).( j 0, 0816) 0, 0066 j 0, 0073 0, 0098 47,8
0,1 47,5
(0, 09 j 0, 0812 j 0, 0816)
0, 09 j 0, 0004
0, 09 0, 25
Şekil 5.9‟ da frekans değerine göre direnç değişim grafiği görülmektedir.
Grafiğe bakıldığında frekans 350 Hz değerindeyken direnç, diğer frekans değerlerine
göre daha yüksektir. Şekil 5.9, Şekil 4.23(a) ile karşılaştırıldığında aralarında 42 Hz fark
olduğu görülmüştür.
Ölçüm sonuçlarına bakıldığında baskın harmonik olarak 7. Harmonik
görülmektedir. Rezonans frekansını 350 Hz olarak alabiliriz. Hesaplamalara
bakıldığında rezonans frekansına ikinci durumda daha çok yaklaşıldığı görülmektedir.
Şekil 5.9‟ a bakıldığında rezonans frekansında yani 392 Hz değerinde direncin
en üst seviyeye ulaştığı görülmektedir. Yani rezonans frekansının oluşumunda
transformatör, AG güç kablosu ve kompanzasyon kondansatörlerinin etkisi olduğu
anlaşılmaktadır. Rezonans frekansının oluşumunda OG kabloları ve enerji nakil hattının
ciddi bir etkisi yoktur. Ölçülen ve hesaplanan rezonans frekansları arasında 42 Hz lik
bir fark görülmektedir. Bu fark, teoride hesaplanan güç transformatörünün endüktif
direnci ile kompanzasyon kondansatörlerinin kapasitif direncinin doğrusal olmayışından
84
kaynaklanmaktadır.
Çünkü
kondansatörlerin
yaşlanması
dikkate
alındığında
kapasitelerinde belli bir düşüş yaşanacaktır. Bu da kondansatörlerin dirençlerini
etkileyecektir. Hesaplama kısmında bu durumlar göz önünde bulundurulmadığından
dolayı fark oluşmaktadır.
0,14
Empedans [ohm]
0,12
0,1
0,08
0,06
0,04
0,02
0
50
150
250
350
450
550
650
750
850
950
1050
için
kendi
Frekans [Hz]
ġekil 5.9. Toplam direncin frekansa göre değişimi
OG
hattının
rezonans
frekansını
değerlendirmek
içindeki
parametrelerinden yararlanmak gerekmektedir. Yani transformatörün AG tarafı hesaba
katılmadan OG hattının kendi endüktansı ve kendi kapasitansı hesaplanmalı ve bu
değerler ile rezonans frekansı bulunmalıdır.
OG hattının rezonans frekansını hesaplamada hattın empedansı ve kapasitansı
önemlidir. OG hattında bulunan iletkenler 477 MCM, 266MCM, 3 AWG, 1x50+16mm2
XLPE (36kV) kablodan oluşmaktadır. İletkenlerin endüktif dirençleri üretici firmanın
kataloğundan alınmıştır. Kapasitansı ise denklem (5.8) ile hesaplanmıştır. XLPE
kablonun endüktif ve kapasitif direnç değerleri de katalogdan alınmıştır.
C
2
D
ln e
r
Burada r,
(5.8)
iletkenin
yarıçapı,
De
iletkenler
arası uzaklıktır.
ε değeri
ise
8,85.10-12 C²/Nm² dir. Denklem (5.5) kullanılarak iletkenlerin kapasiteleri F/m
cinsinden hesaplanmıştır. Bunlar aşağıda sıralanmıştır.
85
C477= 10,12.10-9 F/m, C266= 9,68.10-9 F/m, C3AWG= 8,47.10-9 F/m, CXLPE = 0,125 F/km
şeklindedir. Toplam endüktans ise endüktif dirençlerin toplanmasıyla bulunmuştur.
50Hz frekans değerindeki toplam endüktif direnç XL=j(0,0568+0,12+0,71+3,3)=j4,18Ω
dur. Denklem (5.2) ile endüktans L= 0,0133 H olarak bulunur. Toplam kapasitans olan
CT=0,000134F olarak hesaplanmıştır. Bu hesaplamalara göre rezonans frekansı denklem
(5.1) ile hesaplanmış ve f=119Hz olarak bulunmuştur.
Rezonans frekansındaki endüktif direnç denklem (5.5) ile hesaplanmıştır. Omik
direnç, frekansın değişimden etkilenmediği için hepsinin toplamı alınmıştır.
X L 2 .119.0,0133 j9,94 Ω olarak hesaplanır. Omik direnç ise R= 1,88Ω dur.
Enerji nakil hattının toplam kapasitesi CT= 0,000134 F olarak hesaplanmıştı.
Rezonans frekansındaki kapasitif direnç ise denklem (5.6) ile hesaplanmıştır.
XC
1
j9,98 Ω değerindedir.
j 2 .119.0, 000134
Eşdeğer direnç denklem (5.7) ile hesaplanmaktadır.
Rrez
(1,88 j9,94).( j9,98) 99, 2 j18, 7 100,9 10, 6
53, 69 10, 48 Ω
(1,88 j9,94 j9,92) 1,88 0, 004 1,88 0,12
Diğer frekans değerlerin de aynı hesaplama yapılarak Çizelge 5.3 elde edilmiştir.
Şekil 5.10‟ dan da görüldüğü gibi en yüksek direnç değeri, paralel rezonans
frekansı olan 119 Hz değerindedir. Çizelge 5.3 simülasyon sonuçlarından alınan OG
hattının rezonans direnci grafiği ile uyuşmaktadır.
Bu üç durumdan da görülüyor ki OG ve AG hatlarındaki rezonans olayları birbirini
ciddi anlamda etkilememektedir. Fakat OG hattının rezonans direnci AG hattının
rezonans direncinden daha büyüktür. Hesap yapılırken sistemler ayrı ayrı ele
alınmalıdır.
Sistemin rezonans frekansı hesaplandıktan sonra bu frekans değerine göre akım ve
gerilim hesaplaması yapılmıştır. Bu hesaplamalar yapılırken ölçüm sonuçları ile en
uygun sonuçların yakalandığı noktayı tespit etmek için 3 farklı durum göz önünde
bulundurulmuştur. Bunlardan birincisinde; sadece güç transformatörü ve AG güç
kablolarının empedans değerleri hesaba katılmış, ikincisinde; güç transformatörü, AG
güç kabloları ve enerji nakil hattına bağlantı yapılan OG kablosunun empedans
değerleri ile hesap yapılmış ve üçüncüsünde ise enerji nakil hattı dahil tüm empedans
değerleri ile kompanzasyon kondansatörleri ve bu transformatörden beslenen yük
direnci hesaba katılmıştır.
86
60
Empedans [ohm]
50
40
30
20
10
0
10
20
50
100
119
150
250
350
450
550
Frekans [Hz]
ġekil 5.10. Frekansa göre direnç değişimi
İlk olarak güç transformatörü ve AG güç kabloları ile kompanzasyon
kondansatörlerinin rezonansı esnasında yük ile birlikte meydana gelen 7.harmonik
akımının ve geriliminin değerleri hesaplanmıştır.
RK
XC
Zy
XT+XK
Z2
Z1
ġekil 5.11. Güç transformatörü, AG güç kabloları, kompanzasyon kondansatörleri ve yük direncinin
paralel rezonansını gösteren devre
Şekil 5.11‟ de güç transformatörü, güç kabloları, kompanzasyon kondansatörleri ve
yük direncini gösteren devre görülmektedir. Burada güç transformatörü ve AG kabloları
seri empedansı ile kompanzasyon kondansatörleri ve yük direnci paralel rezonans
oluşturmaktadır. Bu devreye göre eş değer empedans hesaplanmış ve buradan alınan eş
değer empedans değeri ile harmonik akımı hesaplanmıştır. Eş değer empedans
hesaplanırken ilk önce Z1 empedansı, daha sonra ise Z2 empedansı hesaplanmıştır.
Alçı fabrikasının ölçüm sonuçlarına göre 1. fazındaki akım 451 A, gerilimi ise
224,5 V (F-N) dur. Bu değerlere göre sistemde mevcut güç 321 kW dır. Bu esnadaki
kompanzasyon gücü ise 250kVAr dır. Rezonans frekansına en yakın harmonik derecesi
87
7. harmoniktir. Ölçüm sonuçlarına bakıldığında sistemde 7. harmonik oranının en
yüksek olduğu görülmektedir. Sistemde baskın olarak 7. harmonik olduğundan
7.harmoniğin akım ve gerilim değerleri hesaplanmıştır. 7. harmoniğin frekansı 350 Hz
olduğundan ,bu frekans değerinde endüktif ve kapasitif dirençler hesaplanmıştır.
Frekans değeri 50 Hz iken toplam endüktif yük olan X L= j0,0107 Ω, omik direnç olan
R= 0,09 Ω olarak hesaplanmıştır. Toplam endüktans ise denklem (5.2) ile hesaplanmış
ve L = 33 µH olarak bulunmuştur. Bu değerlere göre toplam endüktans denklem (5.5)
ile hesaplanmış ve 350 Hz frekans değerindeki toplam empedans hesaplanmıştır.
X L 2 .350.33.106 2,1.103 Ω
Zt= 0,09+j0,0021Ω
Z1 empedansı denklem (5.6) ile hesaplanmıştır.
Z1
X C .ZY
X C ZY
Z1
0, 476.( j 0,091) 0, 476 j 0,091 0,004 j 0,02
.
0,017 j 0,085 0,087 78,8 Ω
0, 476 j 0,091 0, 476 j 0,091
0, 234
(5.6 )
Z2 empedansı denklem (5.7) ile hesaplanmıştır.
Z2
Z2
Z1.Zt
Z1 Zt
(5.7)
(0,017 j 0,085).(0,09 j 0,0021) 0,0017 j 0,0076 0,0078 77, 4
0,057 38, 2
(0,017 j 0,085) (0,09 j 0,0021) 0,107 j 0,0871 0,137 39,14
Hesaplanan bu Z2 empedans değerine göre 7.harmoniğin akım ve gerilim
değerleri hesaplanmıştır. Bu hesaplamalar 3 faz için ayrı ayrı yapılmıştır. Çünkü her
fazın harmonik değerleri ayrı ayrı ölçülmüştür. Ayrıca fazlar arasında küçük de olsa
akım ve gerilim değerlerinde dengesizlik bulunmaktadır. Yük direnci her 3 fazda aynı
değerde kabul edilmiştir.
1.faz için akım değeri 451 A, gerilim değeri 224,5 V dur. Burada 7. harmonik
akımı %19,5 , 7. harmonik gerilimi ise %2,9 olarak ölçülmüştür. Gerilimdeki bozunum
%2,9 kabul edilirse, 7.harmonik akımının değeri denklem (5.8) ile hesaplanmıştır.
V= I.Z2
(5.8)
Bu hesap sonucuna göre 7. harmonik akımının değeri 114,2 A dir. Bu değer ise
temel akımın %25,3 değerine denk gelmektedir. Ölçüm sonucunda %19,5 bulunan
7. harmonik akım değeri, hesaplama sonucunda %25,3 olarak bulunmuştur.
88
7. harmonik akımının değeri %19,5 kabul edilerek, 7. harmoniğin gerilim değeri,
denklem (5.8) ile hesaplanmıştır. Bu hesap sonucuna göre 7. harmonik gerilimi 5,01 V
olmakta ve bu değer temel gerilimin %2,2‟ sini oluşturmaktadır. Bu hesaplamalar her
faz için ayrı ayrı yapılmıştır. Sonuçlar Çizelge 5.4‟ de gösterilmektedir.
Çizelge 5.3. 7. Harmoniğe ait akım ve gerilimin faz başına ölçülen ve hesaplanan değerleri
Temel Frekans
Dalgası
1.Faz
2.Faz
3.Faz
Ölçülen Değer
Hesaplanan değer
Akım (A)
451
87,9
19,50%
114,2
25,30%
Gerilim (V)
224,5
6,51
2,90%
5,01
2,20%
Akım (A)
481
72,15
15,00%
88,9
18,40%
Gerilim (V)
225,7
5,07
2,25%
4,11
1,80%
Akım (A)
493
64,09
13,00%
78,9
16,00%
Gerilim (V)
225,5
4,5
2,00%
3,6
1,60%
Çizelge 5.3‟ de 7. harmoniğe ait akım ve gerilim değerleri ile bunların temel
dalgaya olan oranları görülmektedir.
İkinci durumda; güç transformatörü, AG kabloları ve OG kablosunun
empedansları toplanarak hesaplamalar yapılmıştır. Güç transformatörü, AG ve OG
kablosu ile kompanzasyon kondansatörleri ve yük direncinden oluşan devre
Şekil
5.9‟ da gösterilmektedir.
Şekil
5.12‟
de
gösterilen
eşdeğer
devrenin
eşdeğer
empedansının
hesaplanmasıyla, 7.harmoniğin akım ve gerilim değerleri hesaplanmıştır. Eşdeğer
devrenin hesaplanması için öncelikle transformatör ve kabloların toplam empedans
değerleri hesaplanmıştır. 50 Hz frekans değerinde, toplam endüktif direnç değeri olan
XL ile toplam direnç değeri olan R aşağıda hesaplanmıştır.
RK+RYG
XC
Zy
XT+XK+XYG
Z2
Z1
ġekil 5.9. Güç transformatörü, AG ve OG kablosu ile kompanzasyon kondansatörleri ve yük
direncinden oluşan devre Şekil 2.6 da gösterilmektedir.
XL=j(0,008+0,00115+0,00124+0,0568)= j0,067Ω
89
R= (0,00386+0,086+0,021)=0,11Ω
50 Hz frekans değerindeki toplam endüktans denklem (5.2) ile hesaplanmış ve
L = 213µH olarak bulunmuştur. Endüktif direncin değeri frekansa göre değişmektedir.
Yaklaşık rezonans frekansı olarak 350Hz kabul edilirse, endüktif direnç denklem (5.5)
ile hesaplanmış ve XL=0,47 Ω olarak bulunmuştur. Toplam empedans değeri ise
denklem (5.9) da gösterilmektedir.
Zt Ztr Z k ZYG
(5.9)
Zt= 0,11+j0,47Ω olarak bulunur. Yük direncinin değişmediği varsayılmış ve 0,476 Ω
olarak alınmıştır.
Eşdeğer devreye bakıldığında Z1 ve Z2 empedansları görülmektedir. Bu
empedans değerlerinden Z1 empedansı denklem (5.6) ile, Z2 empedansı da denklem
(5.7) ile hesaplanmıştır.
Z1
0, 476.( j 0,091) 0, 476 j 0,091 0,004 j 0,02
.
0,017 j 0,085 0,087 78,8
0, 476 j 0,091 0, 476 j 0,091
0, 234
Z2
(0,017 j 0,085).(0,11 j 0, 47) 0,042 j 0,0014 0,042 1,9
0,103 72,9
(0,017 j 0,085) (0,11 j 0, 47) 0,127 j 0,385
0, 405 71
Z2 eşdeğer empedansı hesaplandıktan sonra 1. durumda yapılan hesaplamalar
sıra ile yapılmış ve 7. harmonik için Çizelge 5.5 oluşturulmuştur.
Çizelge 5.4‟ de güç transformatörü ve AG kablolarına ek olarak 1x50+16mm2
XLPE kablo parametreleri de eklenerek 7.harmonik akımı ve gerilimi hesaplanmıştır.
Çizelge 5.4. 7. Harmoniğe ait akım ve gerilimin faz başına ölçülen ve hesaplanan değerleri
Temel Frekans
Dalgası
1.Faz
2.Faz
3.Faz
Ölçülen Değer
Hesaplanan değer
Akım (A)
451
87,9
19,50%
63,2
14,00%
Gerilim (V)
224,5
6,51
2,90%
9,05
4,00%
Akım (A)
481
72,15
15,00%
49,2
10,20%
Gerilim (V)
225,7
5,07
2,25%
7,4
3,20%
Akım (A)
Gerilim (V)
493
225,5
64,09
4,5
13,00%
2,00%
43,6
6,6
8,80%
2,90%
Üçüncü durumda; toplam hat parametreleri OG yeraltı kablosu ve havai hat
parametreleri hesaba katılarak 7.harmonik için akım ve gerilim değerleri hesaplanmıştır.
90
RK+RH
XC
Zy
XT+XK+XH
Z2
Z1
ġekil 5.13. Güç transformatörü, AG kabloları, OG kablosu havai hat iletkenleri, kompanzasyon
kondansatörleri ve yük direncinden oluşan paralel rezonans devresi
Şekil 5.13‟ de üçüncü duruma ait paralel rezonans devre şeması görülmektedir.
Bu durumda, ikinci duruma göre toplam empedans artmıştır. Toplam endüktif direnç
50Hz frekans değerinde hesaplamış ve toplam endüktans,
denklem (5.2) ile
hesaplanmıştır.
XL=j(0,008+0,00115+0,00124+0,0568+0,12+0,71+3,3)=j4,2Ω ve L = 0,013 H olarak
bulunur. 350Hz değerindeki endüktif direnç ise denklem (5.5) kullanılarak
hesaplanmıştır. Toplam omik direnç de hesaplanarak, toplam empedans denklem
(5.9)‟ da gösterilmiştir.
X L 2 fL 2 .350.0,013 28,5 Ω
R= (0,00386+0,086+0,021+0,321+0,44+1,1)=1,9Ω
Zt Ztr Z k Z H
(5.9)
Zt= 1,9+j28,5Ω
Yük direncinin değişmediği varsayılarak Z1 empedansı denklem (5.6) kullanılarak
hesaplanmıştır.
Z1
0, 476.( j 0,091) 0, 476 j 0,091 0,004 j 0,02
.
0,017 j 0,085 0,087 78,8 Ω
0, 476 j 0,091 0, 476 j 0,091
0, 234
Z2 eşdeğer empedansı ise denklem (5.7) kullanılarak hesaplanmıştır.
Z2
(0,017 j 0,085).(1,9 j 28,5) 2, 43 j 0,32
2, 45 7,5
0,086 78,63 Ω
(0,017 j 0,085) (1,9 j 28,5) 1,92 j 28, 4 28, 46 86,13
Eşdeğer empedansın hesaplanmasıyla Çizelge 5.5 oluşturulmuştur.
Çizelge 5.4, 5.5 ve 5.6 incelendiğinde, 7. harmonik akım ve geriliminin, ölçüm
sonuçları ile hesaplama sonuçları arasındaki farkın en az olduğu durum 3. durumdur.
Harmonik akım ve gerilimin hesaplanmasında, rezonans frekansı hesabının aksine, OG
kablosu ve havai hat empedansı kullanılmalıdır. Çünkü rezonans olayı güç
transformatörünün AG empedansı ile kompanzasyon kondansatörlerinin arasında
gerçekleşmesine rağmen, rezonans esnasında yükselen empedansın etkisiyle bozulan
91
gerilim, OG barasına da yansımaktadır. Yani harmonik akımları OG kısmına da
geçerler. Dolayısıyla akım, OG kısmını da izlediği için buradaki direnç harmonik
akımının ve geriliminin genliğine etki etmektedir.
Çizelge 5.5. 7. Harmoniğe ait akım ve gerilimin faz başına ölçülen ve hesaplanan değerleri
Temel Frekans
Dalgası
1.Faz
2.Faz
3.Faz
Ölçülen Değer
Hesaplanan değer
Akım (A)
451
87,9
19,50%
75,69
16,70%
Gerilim (V)
224,5
6,51
2,90%
7,5
3,30%
Akım (A)
481
72,15
15,00%
59
12,00%
Gerilim (V)
225,7
5,07
2,25%
6,2
2,70%
Akım (A)
493
64,09
10,60%
52,3
8,00%
Gerilim (V)
225,5
4,5
2,00%
5,5
2,40%
Ölçüm sonuçları ve simülasyon sonuçları değerlendirilerek, hesaplamalarda en
uygun noktalar belirlenmiştir. Bu noktaların belirlenmesinde her üç çalışmanın da
çakıştığı ortak noktalar etkili olmuştur.
Bu tezde yapılan çalışmalar birçok literatürle karşılaştırılmıştır. Currence ve ark.
(1995), yaptıkları çalışmada orta ölçekli endüstriyel tesislerde harmoniklerden dolayı
meydana gelen rezonans olayını incelemişlerdir. Bu çalışmada paralel rezonans frekansı
bulunurken, toplam empedans hesabında, güç transformatörünün empedansının yanında
OG şebekesinin hat empedansı da eklenmiştir. Şebeke frekans değeri 60 Hz olarak
kabul edilmiştir. Bu durumda paralel rezonans frekansı 336 Hz olarak hesaplanmıştır.
Fakat tesiste 7. harmoniğin baskın olduğu kabul edilmiş ve hesaplamalarda rezonans
frekansı olarak 420 Hz seçilmiştir. Aradaki fark yaklaşık olarak 86 Hz dir.
Tez çalışmasında ise, toplam empedans olarak güç transformatörü ve güç
kablolarının empedansı alınmıştır. Paralel rezonans frekansı 392 Hz olarak hesaplanmış
ve paralel rezonans frekansı da 350 Hz olarak kabul edilmiştir. Ölçüm sonuçlarına
bakıldığında 7.harmoniğin baskın olduğu görülmüştür. Hesaplama ile ölçüm sonuçları
arasındaki fark 42 Hz dir. Görüldüğü üzere bu tezde hesaplanan rezonans frekansı
gerçeğe daha yakındır.
Harmonik akım ve gerilim hesabında, Currence ve ark. (1995), toplam empedans
hesabında, sadece güç transformatörünün empedansını almıştır. Bu durumda hesaplama
sonuçları ile ölçüm sonuçları arasında % 5 civarında bir fark oluşmuştur. Bu tezde ise
hesaplama sonuçları ile ölçüm sonuçları arasında % 3 civarında bir fark oluşmuştur.
92
Pongsnwat ve ark.(2004) harmonik akım ve gerilim hesabı için toplam
empedansı bu tezde kullanılan yöntem ile yapmıştır. Bildiride matematiksel sonuçlar
alınmamış fakat empedans hesaplamak için gereken formüller verilmiştir.
El-Sadek ve ark.(2006) 11kV luk bir tesisin paralel rezonans empedansını
hesaplamak için bazı formüller vermiştir. Bu formülleri elde etmek için kapasitörler,
sistem empedansı ve yük direnci paralel olarak alınmıştır. Matematiksel sonuçlara
gidilmemiş sadece formüller verilmiştir.
Zheng ve ark.(2010) AG tesisinin paralel rezonans frekansının hesabında
kullanılan formülde, transformatör empedansı ile kompanzasyon kondansatörlerinin
kapasitansını kullanmıştır. Bu çalışmada matematiksel sonuçlara yer verilmemiştir.
93
6.SONUÇLAR ve ÖNERĠLER
6.1 Sonuçlar
Harmoniklerin elektrik tesislerindeki olumsuz etkilerini önlemek amacıyla çeşitli
çalışmalar
yapılmıştır.
Harmoniklerin
oluşumunu
engellemek
için
güç
transformatörlerinde, alternatörlerde, statik dönüştürücülerde bir dizi önlemler
alınmıştır. Fakat bu önlemler elektrik cihazının bazı harmonikleri üretmesini engeller.
Sistemde yüksek oranda bulunan çeşitli derecedeki harmoniklerin bastırılmasında pasif
filtreler kullanılmıştır.
Pasif filtrenin uygulamalarda kullanılmasının sebebi, aktif filtrenin maliyetinin
yüksek olmasıdır. Pasif filtrelerin maliyetinin uygunluğu ve kullanımının kolay olması,
yük çeşidi değişmeyen fabrikalarda tercih sebebidir.
Elektrik
tesislerinde
harmoniklerin
artmasına
neden
olan
asıl
etken
kompanzasyon kondansatörleridir. Kompanzasyon kondansatörleri, tesiste bulunan güç
transformatörü ve güç kablolarının toplam endüktansı ile paralel
rezonans
oluşturmaktadır.
Paralel rezonans durumunda sistemin empedansı artar. Bu empedans değeri
paralel rezonans frekansında en yüksek değerine ulaşır. Rezonans frekansı harmonik
frekansında veya harmonik frekansına yakın bir değerde ise harmonik bozunum miktarı
artmaktadır. Çünkü harmonik üreteçleri sabit akım kaynağı olduğundan , harmonik
akımları yüksek empedansla karşılaşınca gerilimleri artar. Harmoniklerin geriliminin
artması, birinci harmonikteki gerilim düşümlerinin artmasına neden olur ve gerilimin
dalga şekli bozulur. Bozulan gerilim dalgası, sistemde daha büyük harmonik
akımlarının oluşmasına neden olur.
Pasif filtre kullanılmayan tesislerde yapılan ölçümlerde, kompanzasyon
kondansatörleri devreye alınınca harmonik bozunum oranları standart değerlerin üzerine
çıkmıştır. Kompanzasyon kondansatörleri devre dışı bırakıldığında ise paralel rezonans
olayı meydana gelmediğinden dolayı harmonik bozunum oranları düşmüştür.
Harmoniklerin genliklerinin artmasını engellemek için paralel rezonans
frekansını, harmoniklerin frekansından uzaklaştırmak gerekir. Bunun için seri reaktörlü
pasif filtre kullanılmıştır. Seri reaktörlü pasif filtre, paralel rezonans frekansını kendi
94
frekans noktasına çeker. Böylece harmonikler yüksek empedansla karşılaşamaz ve
gerilimlerinin genlikleri de artmaz.
Seri reaktörlü pasif filtre bulunan iki fabrikada ölçümler yapılmıştır. Bu
fabrikalar, kalsit fabrikası ve Mercedes Benz Türk Kamyon fabrikasıdır. Kalsit
fabrikasında, güç transformatörünün AG barasında ölçümler yapılmıştır. Bu tesiste
kompanzasyon sisteminde, filtreleme faktörü %5,67 olan seri reaktörlü pasif filtre
kullanılmıştır. Kompanzasyon sistemin devre dışı iken yapılan ölçümlerde, harmonik
bozunum oranları standart değerlerin altında çıkmıştır. Kompanzasyon sistemi devreye
alınınca kondansatörlerin de etkisiyle harmonik bozunum oranlarında artış olmuş, fakat
oranlar standartlara yakın değerde kalmıştır.
Mercedes Benz Türk Kamyon fabrikasında, hem AG hem de OG barasından
ölçümler yapılmıştır. Bu fabrikada çeşitli güçlerde, 6 adet güç transformatörü
bulunmaktadır. Bunların hepsinin kompanzasyon sisteminde, filtreleme faktörü %5,67
olan seri reaktörlü pasif filtre kullanılmıştır. Bu tesiste bulunan 1600kVA gücündeki
transformatörün AG barasından yapılan ölçümlerde, harmonik bozumun oranlarının
standartların altında olduğu görülmüştür. OG barasından yapılan ölçümlerde ise
harmonik bozunum oranlarının yine standartların altında olduğu görülmüştür.
Kalsit fabrikası ve Mercedes Benz Türk Kamyon fabrikasında yapılan ölçüm
sonuçlarında, seri reaktörlü pasif filtrelerin harmonikleri filtrelemede yararlı olduğu
görülmektedir. Filtreler AG deki harmonikleri bastırdığı için OG barasına da olumlu
etki yapmıştır. Seri reaktörlü harmonik filtre tasarımında kullanılan hesap yönteminin
doğruluğunu sınamak için bu fabrikalara yeniden filtre tasarlanmıştır. Seri reaktörlü
pasif filtre için hesaplanan kapasitans ve endüktans değerleri ile mevcut filtrenin
kapasitans ve endüktans değerleri birbirlerine yakındır.
Tüm bu çalışmaları bilgisayar ortamında görmek ve tasarlanan filtrelerin
uygunluğunu denemek için MATLAB/SIMULINK programı ile simülasyon yapılmıştır.
Simülasyon programında 7.harmonik ve 5.harmonik değerleri alçı fabrikasındaki
harmonik değerlerine yakın bir fabrika tasarlanmıştır. Bu fabrikada kompanzasyon
sistemi devre dışı iken yapılan ölçümlerde, harmonik bozunum oranları düşük
değerdedir. Şebeke empedansı da doğrusaldır.
Kompanzasyon sisteminde seri reaktörlü filtre yokken yapılan ölçümlerde,
harmonik bozunum oranlarının standartların çok üstünde olduğu görülmektedir. Paralel
rezonans frekansı 350Hz civarında ve toplam empedans, paralel rezonans frekansında
en üst seviyeye ulaşmıştır.
95
Kompanzasyon sisteminde, alçı fabrikası için tasarlanan seri reaktörlü pasif filtre
kullanıldığında, paralel rezonans frekansı 210 Hz değerine çekilmiştir. Toplam
empedans, frekansın 210 Hz değerinde en üst seviyeye ulaşmış ve bundan sonra
doğrusal olmuştur. 210 Hz seviyesinde harmonik bulunmadığından, harmonik bozunum
oranı standartların altında kalmıştır.
Simülasyon sonuçları, ölçüm sonuçlarına yakındır. Herhangi bir fabrika
kurulmadan önce yük analizi yapılarak pasif filtresi tasarlanabilir. Tasarlanan filtrenin
uygunluğu da bilgisayar ortamında denenebilir.
Simülasyon sonuçları ve gerçek ölçüm sonuçları birbirlerini desteklemektedir.
Bu sonuçları matematiksel olarak elde etmek için, yani simülasyon programları ve
harmonik analizörler olmadan, matematiksel harmonik analizi yapılmıştır. Bunun için
alçı fabrikası model alınmıştır. Alçı fabrikasındaki ölçüm sonuçlarında 7.harmonik
baskın çıkmıştı. Bu fabrikanın OG indirici merkezinden itibaren tek hat şeması çizilmiş
ve empedansı hesaplanmıştır.
Ölçülen rezonans frekansı yaklaşık olarak 350 Hz dir. Hesaplanan rezonans
frekansı ise 392 Hz dir. Bu fark, kullanılan elemanların karakteristiklerinin doğrusal
olmayışından kaynaklanmaktadır.
7.harmonik akımının hesaplama sonucunda elde edilen değeri ile ölçüm sonunda
elde edilen değeri karşılaştırıldığında hesaplanan değer yaklaşık olarak %3 daha düşük
çıkmıştır. 7.harmonik geriliminin hesaplama sonucunda elde edilen değeri ile ölçüm
sonunda elde edilen değeri arasında karşılaştırma yapılmıştır. Karşılaştırma sonucunda
%0,4 civarında bir fark oluşmuştur. Ölçüm sonuçları ile hesaplama sonuçlarının farklı
çıkmasının sebebi, kullanılan elemanların doğrusal olmayışıdır. Buna örnek olarak
kondansatörler verilmiştir. Kondansatörün kapasitesinin değişmesi bu sonuçları
doğrudan etkiler.
Bu çalışmada fabrikaların çeşitli durumlarında harmonik analizi yapılmıştır.
Gerçek ölçümler, simülasyon sonuçları ve matematiksel hesaplamaların birbirlerini
desteklediği görülmüştür. Bu çalışmalardan herhangi birisi yapılarak fabrikanın
harmonik analizi yapılabilir ve bu analize göre uygun filtre tasarlanabilir.
96
6.2 Öneriler
Bu çalışmanın sonuçlarına göre harmoniklerin oluşumunu engellemek ve baskın
olan harmonikleri filtrelemek için önlemler alınmalıdır. Harmoniklerin oluşumunu
engellemek için;
-
Güç transformatörlerinin nüvesinin yapıldığı malzemenin, manyetik özelliği
iyi olmalıdır. Bu mıknatıslanma akımının harmonik etkisini azaltacaktır.
-
Alternatörlerde baskın bulunan harmonikleri gidermek için sargı kirişleme
faktörü ve sargı yayılma faktörleri kullanmalıdır.
-
Statik dönüştürücülerde darbe sayısı harmonik derecesini belirlediği için
baskın
olan
harmonik
derecesi
belirlendikten
sonra
darbe
sayısı
ayarlanmalıdır.
-
Elektrik
arkı
doğrusal olmadığından
dolayı
en önemli
harmonik
üreticilerindendir. Bu sebepten dolayı ark ocaklarının bulunduğu tesislerde
filtre tesis edilmelidir.
Bu önlemler alındığında halen harmoniklerin etkileri giderilemiyorsa filtre
tasarlanmalıdır. Filtre tasarımında;
-
Kullanılacak filtre çeşidi aktif veya pasif filtre olabilir. Ekonomiklik ve
kullanılabilirlik göz önüne alınarak seçimin doğru yapılması gerekir.
-
Pasif filtre tasarlanırken seri veya paralel rezonans frekansı doğru bir şekilde
hesaplanmalıdır. Aksi takdirde belirlenen derecedeki harmonik bastırılamaz.
-
Kompanzasyon sisteminin kademelerinde bulunan pasif filtrelerin filtreleme
oranları aynı olmak zorundadır. Aksi takdirde rezonans frekansı bu
durumdan etkileneceği için filtre düzgün çalışmaz. Hatta bazı kademelerde
aşırı yüklenmeden dolayı arızalar meydana gelmektedir.
-
Pasif filtre tasarımında kondansatörlerin uç gerilimleri harmoniklerden
dolayı arttığı için kapasiteleri düşer. Bu durum göz önünde bulundurularak
kondansatörün gerilimi doğru seçilmelidir. Aksi takdirde kapasite kaybından
dolayı reaktif güç kompanzasyonu tam olarak yapılamaz.
97
Matematiksel olarak harmonikler analiz edilmiş ve ölçüm sonuçlarına yakın
değerler bulunmuştur. Matematiksel olarak harmonik derecesinin belirlenmesinde ve
harmonik analizinde bazı durumlar göz önünde bulundurulmalıdır. Bunlar;
-
Paralel rezonans, güç transformatörü ile kompanzasyon kondansatörleri
arasında gerçekleşmektedir. Paralel rezonans frekansını hesaplamak için güç
transformatörü ve AG güç kablolarının endüktansı toplanmalıdır. Kapasite
ise, devrede olan kondansatörlerin toplam kapasitansıdır. Hesaplardan ve
simülasyon sonuçlarından görüldü ki, OG kısmının endüktansı rezonans
frekansını etkilememektedir.
-
OG hattının rezonans frekansı hesaplanırken kendi hat parametreleri hesaba
katılmalıdır.
-
Baskın olan harmoniğin akım ve gerilim değeri hesaplanırken OG hattının
empedans ve kapasitansı değerleri hesaba katılmalıdır. Çünkü harmonikler
OG‟e de etki ettiği için transformatörün harmonikli akım çekmesine neden
olurlar.
98
KAYNAKLAR
Arifoğlu, U., 2002, Güç Sistemlerinin Bilgisayar Destekli Analizi, Alfa Yayınları,
No:1065, İstanbul, 305-309.
Başman, F., 2006, Elektrik Enerji Sistemlerinde Harmonik ve Filtreleme, Yüksek
Lisans Tezi, Sakarya Üniversitesi Fen Bilimleri Enstitüsü, Sakarya, 49-77.
Bhattacharyya, S., Myrzik, J., Kling, W., Cobben, S. and Van Casteren, J., 2009,
Harmonic Current Interaction at a Low Voltage Customer‟s Installation, 10th
International Conference on Electrical Power Quality and Utilisation, 2009.
EPQU 200., Lodz, 1 – 6.
Bilge, M., 2008, Güç Sistemlerinde Pasif Filtrelerle Eliminasyonu, Yüksek Lisans Tezi,
Kahramanmaraş Sütçü İmam Üniversitesi Fen Bilimleri Enstitüsü,
Kahramanmaraş, 17-24.
Boduroğlu, T., 1988, Döner Alternatif Akım Makinalarına Giriş, Beta Yayınları,
No:167,İstanbul, 140-152.
Boduroğlu, T., 1988, Transformatorlar, Beta Yayınları, No:155,İstanbul, 114-132.
Browne, T.J., Gosbell, V.J. and Perera, S., 2009, Allocated Harmonic Quantities as the
Basis for Source Detection, IEEE Power & Energy Society General Meeting,
2009, PES '09, Calgary, AB, 1 – 6.
Chowdhury, A.H., Grady, W.M. and Fuchs, E.F., 1999, An Investigation of the
Harmonic Characteristics of Transformer Excitation Current Under Nonsinusoidal
Supply Voltage, IEEE Transactions on Power Delivery, Volume: 14, Issue:2,
450 – 458.
Chen, C.S., Chuang, H.J. and Shiau, H.M., 2003, Stochastic harmonic analysis of mass
rapid transit power systems with uncontrolled rectifiers, , IEEE ProceedingsGeneration, Transmission and Distribution, Volume: 150, Issue:2, 224 – 232.
Ekiz A., Tümay M., 2009, Fabrikalardaki Harmoniklerin MATLAB/SIMULINK
Kullanılarak Modellenmesi, Elektrik-Elektronik-Bilgisayar, Mühendisliği 10.
Ulusal Kongresi, 2003,Lütfi Kırdar Kongre ve Sergi Sarayı, İstanbul,1-4.
Eroğlu, H., 2009, Bir Dağıtım Şebekesinin Güç Kalitesi ve Harmonikler Yönünden
İncelenmesi, Yüksek Lisans Tezi, Selçuk Üniversitesi Fen Bilimleri Enstitüsü,
Konya, 75.
Gezegin, C., 2006, Harmoniklerin süzülmesi ve Tepkin Güç Kompanzasyonu İçin
Melez Koşut Etkin Güç Süzgeçleri, Yüksek Lisans Tezi, Ondokuzmayıs
Üniversitesi Fen Bilimleri Enstitüsü, Samsun, 28-59.
İlaslanser, İ., 2006, Güç Kalitesinde Harmonikler Ve Filtrelenmesi, Yüksek Lisans Tezi,
Gazi Üniversitesi Fen Bilimleri Enstitüsü, Ankara, 34-40.
99
Keramati Z.J. and Farjah E., 2009, New Control Technique for Compensation of
Netural Current Harmonics in Three-Phase Four -Wire Systems, IEEE Buucharest
Power Tech Conferecence, June 28th-July 2nd 2009, Bucharest, Romania,1-6.
Liang X., and Jackson W., 2008, Investigation of Non-Linear Devices Modeled as a
Harmonic Current Source, Industrial and Commercial Power Systems Technical
Conference, 2008, ICPS 2008, IEEE/IAS, Clearwater Beach, FL, 1 – 7.
Mau T. A., and Milanovic J. V., 2007, Planning Approaches for the Strategic Placement
of Passive Harmonic Filters in Radial Distribution Networks, IEEE Transactions
on Power Delivery, Volume: 22 Issue:1, 347 – 353.
Pamplona, F.M.P. and Souza, B.A., 2004, Harmonic Passive Filter Planning In Radial
Distribution Systems Using Genetic Algorithms, Transmission and Distribution
Conference and Exposition: 2004 IEEE/P, Latin America, ES, 126 – 131.
Puskarich, K.A., Reid, W.E. and Hamer, P.S.,2001, Harmonic Experiences with a Large
Load-Commutated Inverter Drive, IEEE Transactions on Industry Applications,
Volume : 37 , Issue:1, 129-136.
Rao, N.D., Sporea, S.I. and Sawma, A., 1998, Analysis of resonance problems and
harmonic fitler desıgn in power factor correction capacitor applications, IEEE
Canadian Conference on Electrical and Computer Engineering, 1998., Waterloo,
Ont. , Canada, Vol.1, 293 – 296.
Sağlam, H., 2005, Dağıtım Transformatörlerinin Bağlantı Gruplarına Göre Harmonik
Simülasyonu, Yüksek Lisans Tezi, Yıldız Teknik Üniversitesi Fen Bilimleri
Enstitüsü, İstanbul,110-115 .
Şahin, Y.G., 2006, Harmoniklerin yer altı güç Kablolarına etkisinin belirlenmesi,
Yüksek Lisans Tezi, Kocaeli Üniversitesi Fen Bilimleri Enstitüsü, Kocaeli, 47-57.
Tsukamoto, M., Ogawa, S., Natsuda, Y., Minowa, Y. and Nishimura, S., 2000,
Advanced Technology to Identify, Harmonics Characteristics and Results of
Measuring, Proceedings. Ninth International Conference on Harmonics and
Quality of Power, 2000, Orlando, FL, USA, Vol:1, 341 – 346.
Ünsal A., Tunaboylu N.S., 2009, Dumlupınar Üniversitesi Merkez Kampüsü Elektrik
Kalitesinin Ölçüm Sonuçları, Eskişehir Osmangazi Üniversitesi Mühendislik
Mimarlık Fakültesi Dergisi, Cilt:XXII, Sayı:1, 2009,14-29.
Vlahinic, S., Brnobic, D., and Stojkovic, N., 2008, Indices for Harmonic Distortion
Monitoring of Power Distribution Systems, IEEE Transactions on
Instrumentation and Measurement, Volume: 58 Issue:5, 1771 – 1777.
Whittle, G., 2010, How capacitors affect harmonics, and what is resonance?,
Transmission and Distribution Journal, Energize- Nov. 2010, 26-28
Zile M., 2009, Nominal Parametre Temeline Dayanan Harmonik Çalışmalar İçin Trafo
Modelleri, 5. Uluslararası İleri Teknolojiler Sempozyumu (IATS’09), 13-15 Mayıs
2009, Karabük, Türkiye,1-4.
100
EKLER
EK-1 Alçı Fabrikasının yüksek ve alçak gerilim baralarına ait SIMULINK modeli
N
A
B
aA
bB
A
B
C
a
b
c
n2
477 MCM
11 km
Aa
Bb
Cc
266 MCM
Three -Phase
2 km
V-I Measurement 1
3 AWG
500 m
1x50 mm 2
XLPE
80 m
C
C
154 /31 .5kV
Discrete,
Ts= 1e-005 s.
B
c
cC
Three -Phase
V-I Measurement
154 kV
31 ,5 kV
b
Three -Phase Source
Vabc
Vabc
Iabc
Iabc
Vabc 1
Vabc1
Iabc 1
Iabc 1
A
a
A
B
C
a
b
c
n2
Three -Phase
Transformer
31 ,5/0,4 kV
1250 kVA
A
C
B
AKALCI
101
EK-2 Alçı fabrikasının kompanzasyon sistemi devre dışı durumuna ait SIMULINK
modeli
C
Aa
Three -Phase
Series RLC Load 2
B
30 kW
A
A
Three -Phase
Series RLC Load 1
C
1
Three -Phase
Series RLC Load
B
90 kW
A
Bb
Conn2
50 kW
C
B
Conn3
70 kW
B
2
Conn2
Ih 5
A
Cc
Conn3
50 kW
Conn1
Ih 7
Conn1
50 kW
C
C
Three -Phase
V-I Measurement 1
Alcak gerilim
B
3
Vabc1
Vabc111b]
Iabc 1b
Iabc 1
A
Three -Phase
Series RLC Load 3
102
EK-3 Alçı fabrikasının pasif filtresiz kompanzasyon sisteminin devrede olma durumuna
ait SIMULINK modeli
Three -Phase
Series RLC Load 1
B
90 kW
A
C
Three -Phase
Series RLC Load 2
B
30 kW
A
C
Aa
C
A
Three -Phase
Series RLC Load
50 kW
B
1
Conn2
A
Bb
Conn3
70 kW
C
B
Conn2
Ih 5
B
2
Conn3
50 kW
Conn1
Ih 7
Conn1
50 kW
A
Cc
250 kVAr
400 V
C
C
Three -Phase
V-I Measurement 1
C1
Alcak gerilim
B
3
Vabc1
Vabc 111b]
Iabc 1
Iabc 1b
A
Three -Phase
Series RLC Load 3
103
EK-4 Alçı fabrikasının pasif filtreli kompanzasyon sisteminin devrede olma durumuna
ait SIMULINK modeli
Three -Phase
Series RLC Load 1
B
90 kW
A
C
Three -Phase
Series RLC Load 2
B
30 kW
A
C
Aa
C
A
Three -Phase
Series RLC Load
50 kW
B
1
Conn2
A
Bb
Conn3
70 kW
C
B
Conn2
Ih 5
Conn1
Conn3
50 kW
Conn1
Ih 7
B
2
Three -Phase
Harmonic Filter
50 kW
A
Cc
250 kVAr
400 V
210 Hz
C
C
Three -Phase
V-I Measurement 1
Alcak gerilim
B
3
Vabc1
Vabc 111b]
Iabc 1
Iabc 1b
A
Three -Phase
Series RLC Load 3
104
ÖZGEÇMĠġ
KĠġĠSEL BĠLGĠLER
Adı Soyadı
Uyruğu
Doğum Yeri ve Tarihi
Telefon
Faks
e-mail
:
:
:
:
:
:
Bahadır AKBAL
T.C.
K.Maraş \ Elbistan 24.07.1983
0538 451 6636
bakbal@selcuk.edu.tr.
EĞĠTĠM
Derece
Lise
Üniversite
Adı, Ġlçe, Ġl
: Aksaray Lisesi ,Merkez, Aksaray
: Ġnönü Üniversitesi, Merkez ,Malatya
Bitirme Yılı
2000
2006
Ġġ DENEYĠMLERĠ
Yıl
2007
2011
Kurum
Koçak Mühendislik Ltd.ġti.
Selçuk Üniversitesi
UZMANLIK ALANI
Elektrik Tesisleri
YABANCI DĠLLER
Ġngilizce
Görevi
Mühendis
ArĢ. Gör.