−1
−1
b) f (2) + h (2) + 3 g (3) değeri kaçtır?
7) Aşağıdaki fonksiyonların tek fonksiyon veya çift
fonksiyon olup olmadıklarını araştırınız.
TANIM KÜMESĐ
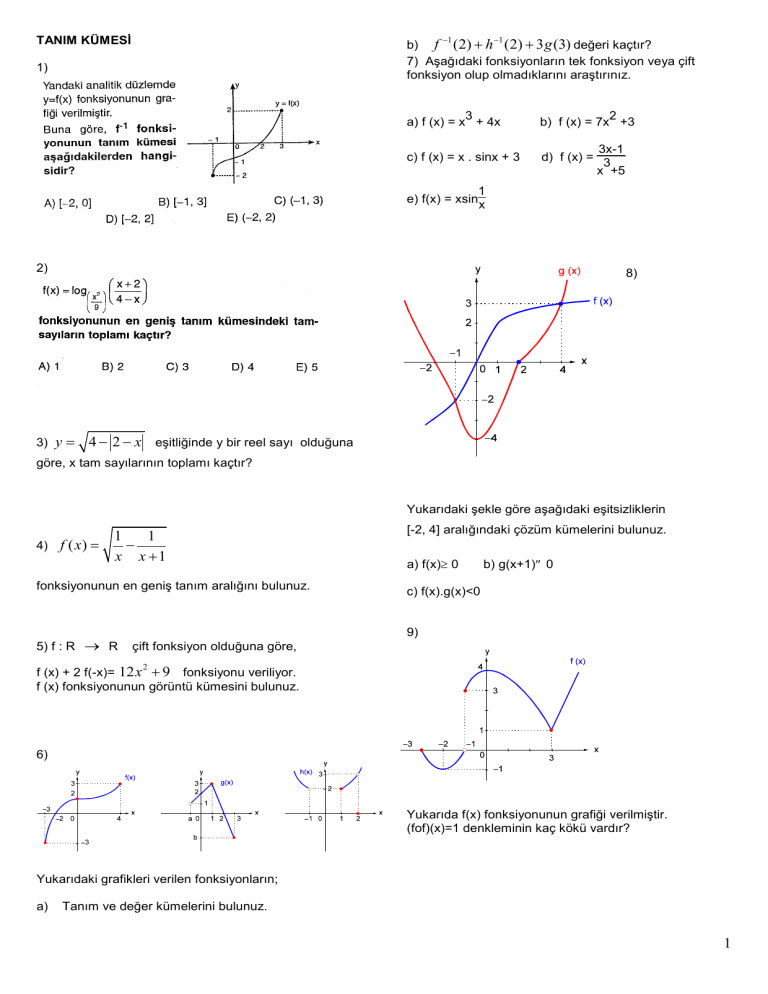
1)
3
a) f (x) = x + 4x
2
b) f (x) = 7x +3
c) f (x) = x . sinx + 3
3x-1
d) f (x) = 3
x +5
1
e) f(x) = xsin x
2)
3)
8)
y = 4 − 2 − x eşitliğinde y bir reel sayı olduğuna
göre, x tam sayılarının toplamı kaçtır?
Yukarıdaki şekle göre aşağıdaki eşitsizliklerin
4)
f ( x) =
1
1
−
x x +1
fonksiyonunun en geniş tanım aralığını bulunuz.
5) f : R
→ R çift fonksiyon olduğuna göre,
[-2, 4] aralığındaki çözüm kümelerini bulunuz.
a) f(x)≥ 0
b) g(x+1)≤ 0
c) f(x).g(x)<0
9)
f (x) + 2 f(-x)= 12 x + 9 fonksiyonu veriliyor.
f (x) fonksiyonunun görüntü kümesini bulunuz.
2
6)
Yukarıda f(x) fonksiyonunun grafiği verilmiştir.
(fof)(x)=1 denkleminin kaç kökü vardır?
Yukarıdaki grafikleri verilen fonksiyonların;
a)
Tanım ve değer kümelerini bulunuz.
1
10)
Aşağıda verilenlere göre istenenleri bulunuz.
-1
a) f(x+2)=f (3x-7) ise (fof)(4) kaçtır?
PARÇALI FONKSĐYONLAR
1)
-1
2
-1
b) f (1+log2x)=x -2x+1 ise f(1)+f (3) kaçtır?
+
c) f:R →R, f(x1.x2)= f(x1)+f(x2) veriliyor.
f(10)=1, f(2)=m, f(3)=n ise
f(15) in m ve n cinsinden ifadesini bulunuz.
2)
-1
d) f:[-3, ∞)→[2, ∞), f(x)=x²-6x+11 ise f (x)=?
e) f:[-7, -2)→B, f(x)=x²+2x-12 fonksiyonunun tersi var
olduğuna göre;
3)
i) B değerler kümesi ne olmalıdır?
-1
ii) Bu durumda f (x) fonksiyonunu bulunuz.
f) f:Q→Q olmak üzere
f(a+b)=f(a)+f(b), f(2)=3 olduğuna göre; f(5/2) kaçtır?
x y
+
g) x,y∈R için f(x)f(y) - f(xy) = y + x ise f(2) kaçtır?
h) x≠1 için f(x)+f(
1
3
3
) = x ise f(-1) kaçtır?
3
1-x
11) Aşağıdaki fonksiyonların ve ters fonksiyonlarının en
geniş tanım ve değer kümelerinin ne olduklarını
belirtip,ters fonksiyonlarını bulunuz:
3x-6
b) f(x)= x+7
a) f(x)=2x-3
2
d) f(x)= x - 8x + 10
f) f(x) =
x
c) f(x) = e +3
2x-3
e) f(x) = ln( x+7 )
2x-6 ,
x<1 ise
3+x ,
1
x ,
1≤x<5 ise
4)
5≤x ise
2
5)
8)
Yukarıda grafiği verilen f(x) fonksiyonuna bağlı
olarak
Fonksiyonlarının grafiklerini çiziniz.
9)
10)
x −1 − x = 1
Denkleminin çözüm kümesini bulunuz.
6)
SĐGNUM FONKSĐYONU
1)
2)
7)
3)
3
4)
9)
10)
5)
6)
7)
11)
12)
8)
13)
4
17)
14)
Yandaki grafiğe
göre aşağıdaki
denklem ve
eşitsizliklerin çözüm
kümelerini bulunuz.
a) sgn(f(x))=0
b) sgn(f(x))=1
c) sgn(f(x))= -1
d) x.sgn(f(x))<1
e) (x²-1).sgn(f(x)) < 0
18)
15)
Yukarıda f(x) fonksiyonunun grafiği verilmiştir.Buna göre;
Şekildeki grafik aşağıdaki fonksiyonlardan hangisine ait
olabilir?
A) f(x)=
C)
f ( x) = x + sgn x
f ( x) = x − sgn x
B)
f ( x) = x − 1
a) f(x)≤0 eşitsizliğini sağlayan tam sayılar kümesini
bulunuz.
b)
x 2 − x − 12
< 0 eşitsizliğinin çözüm kümesini
sgn ( f ( x) )
bulunuz.
D) f(x)=x.Sgn(x)
x
E) f(x)=Sgn(x)
16)
19) A⊂ R ve f:A→R olmak üzere
f ( x) =
x −5
1 − sgn ( x 2 − 9 x + 14 )
3
fonksiyonunun en geniş tanım kümesini bulunuz.
20) f:R→R fonksiyonunun grafiği aşağıda verilmiştir.
f(x) fonksiyonunun grafiğine bağlı olarak,
g ( x) =
x 2 sgn ( f ( x) )
fonksiyonunun grafiğini çiziniz.
x
Buna göre aşağıdaki fonksiyonların grafiklerini çiziniz.
a) -f(x)
f) f(x)
b) f(-x)
c) f(x-1)
d) f(x)-1
g) -f(x)
h) (x-1).sgn(f(x))
e) f(x)
5
TAM DEĞER FONKSĐYONU
7)
1)
8)
2)
9)
3)
10)
4)
11)
5)
12)
6)
13)
6
14)
Yukarıdaki şekilde, f (x) ve g(x) fonksiyonlarının
grafikleri verilmiştir.
( ( g ( x)) ) değeri kaçtır?
1 ≤ x < 2 olmak üzere, f f
18)
f ( x) =
1
fonksiyonunu tanımsız
x + 1 − 2 − 5
yapan tam sayılar kümesini bulunuz.
19) Aşağıdaki bağıntıların grafiklerini R² de çiziniz.
a) x+y=3
b) x-y=2
c) xx-1+y+2=2
d) x+2y-6=4
e) x-3-y+2≤4
3
f) y=sgn(x - 4x)
g)
x + 3
y − 2
=1
h) sgn(x²-x).sgn(y+2)=1
20)
15)
-1≤ x <1 olmak üzere;
x + y = 3
bağıntısının sınırladığı alan kaç birim karedir?
21) e doğal logaritmanın tabanı ve
f ( x) = x − x olduğuna göre, f(-e) değeri kaçtır?
16)
22) Aşağıdaki denklemlerin çözüm kümelerini bulunuz.
a) x − 3 x = 10
2
b)
x2 + x − 6
= −1
x
c) sgn
(
x 2− x =3
d)
2 x − 3 = 7
)
e) sgn ln x + 2 ln x − 3 + 1 = 0
g)
ı)
2
x − 2 x − 6 2 x − 3 = 0
x − 2. x = −1
x + 2 = x − 2
4 x + 2
i)
h)
2 − x = −1
3 f)
2x + 8 3 − x = −12
x + 1 − x + 1 = 6
2
2
17)
j)
l) 2 x − x = 3
1
3x = x + x + 3 k)
2x − 5 =5
2 m) x + 2 + 7
23) Aşağıdaki fonksiyonların en geniş tanım kümelerini
bulunuz.
1− x
a) f ( x ) =
2x + 4
f ( x) =
c)
1 − x3
4
x − 4x
3
1 − x2
x 2 − x − 20
b)
f ( x) =
d)
f ( x) = 25 −
x −5
2 x + 14
x2 − x
e) f ( x ) = log 2
( x −5 x ) x + 4
f)
f ( x) =
17
13 − 7 − x
27.
+ ln ( 9 x − x 2 ) −
Yukarıda y=f(x) fonksiyonunun grafiği verilmiştir.
x
sgn .f(x) = -1 denklemini çözünüz.
3
28.
x − 12
9 − x2
x. x. x =13 denkleminin çözüm kümesini
bulunuz.
29.
3
20 =
4
a
.
∑ k 2 ∑ sgn(k ) eşitliğini sağlayan a değerini
30
f ( x) =
g)
81 − 4 x 2
− x − x 2 sgn ( x 2 − x )
2
x
−
6
−
3
sgn( x − 2) − 1
3x + 6
h) f ( x ) = log x
+
sgn( x 2 − 1)
x −1
ı)
f ( x) =
i)
f ( x) =
24.
k =1
k =−2
bulunuz.
30.
− x 2 + x + 20
1 − sgn( x 2 − 5)
2− 2− 2− x
x − 1
31.
25.
32.
26.
33.
8