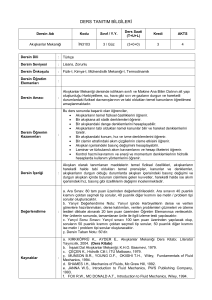
0216 AKIŞKANLAR MEKANİĞİ
2014/2015 Bahar Yarıyılı
BÖLÜM-I
Yrd. Doç. Dr. Adil KOÇ
1
1. GİRİŞ
1.1. Tanımlar ve Akışkanların Bazı Özellikleri
Akışkanlar Mekaniği, akışkanların durgun haldeki (akışkan statiği) ve hareket halindeki
(akışkan dinamiği) davranışları ve yine akışkanların diğer akışkanlar ve katılar ile oluşturdukları
sınırlardaki etkileşimleri ile ilgilenen bilim dalı olarak tanımlanır. Aynı zamanda, akışkanlar
mekaniği, akışkan hareketlerini ve bu hareketleri ortaya çıkaran ya da bu hareketler sonucunda
ortaya çıkan hız, basınç, kuvvet, enerji gibi fiziksel etkileri içeren momentum iletimi ve
mekanik enerji denkliklerini inceler.
1. Sıvıların Mekaniği veya Hidrodinamik (hidrolik, sıvıların boru ve kanallarda akışı),
2. Gazların Mekaniği veya Aerodinamik (Gaz dinamiği, gazların yüksek hızla lüleden akışı)
olmak üzere, akışkanlar mekaniğinin iki ana kolu vardır.
Akışkan, günlük hayatta sıvı ya da gaz adı altında bildiğimiz bütün maddeler akışkandır. Katı ve
sıvı arasındaki fark, maddelerin şeklini değiştirmek için uygulanan kayma gerilmesine karşı
gösterdikleri direnç ile anlaşılır. Katı madde, uygulanan kayma gerilimine karşı bir miktar
dayanım gösterirken (şekil değişimine uğrayarak direnç gösterir), sıvı madde ise çok az bir
kayma gerilmesinde bile şekil değiştirir. Gerilme birim zamandaki şekil değişimi ile doğru
orantılıdır (Şekil 1.1)
F
A
Katı
F
V
A
h
Akışkan
Şekil 1.1. Akışkan ve katının uygulanan kuvvetle davranışının farklılığı.
Statikte, birim alana etkiyen kuvvet gerilme olarak tanımlanır. Herhangi bir A yüzeyine etkiyen
bir F kuvvetini, Fn normal ve Ft teğetsel bileşenlerine ayırdığımızda bu kuvvetlerin oluşturduğu
gerilmeler aşağıdaki gibi tanımlanır, (Şekil 1.2).
Şekil 1.2. Bir akışkanın herhangi bir noktasında etki eden kuvvetler.
2
Bir yüzeyin birim alanına etki eden kuvvetin dik bileşeni normal gerilme (normal bileşen),
teğetsel bileşeni ise kayma gerilmesi olarak tanımlanır (Şekil.1.2). Durgun akışkanlarda normal
gerilme basınç olarak tanımlanır. Akışkanın hareketsiz olduğu hallerde kayma gerilmesinden söz
edilemez ve değeri sıfırdır.
Katılarda moleküller arası etkileşimler en güçlü olduğu halde gazlarda en düşüktür. Katılarda
moleküller arasındaki mesafeler kısa olduğundan, birbirlerine uyguladıkları çekim kuvvetleri
büyüktür ve moleküller konumlarını muhafaza ederler. Sıvılarda, moleküllerin birbirlerine göre
konumları sabit değildir ve moleküller serbestçe dönebilir ve yer değiştirebilirler. Gaz
molekülleri düzensiz hareket ederek birbirlerine ve içinde bulundukları kabın çeperlerine sürekli
olarak çarparlar. Gaz molekülleri aynı koşullarda sıvı ve katı haldeki moleküllere göre çok daha
yüksek enerjiye sahiptirler.
Gaz ve buhar kavramları birbirilerine karıştırılmakla birlikte farklı fiziksel özellikteki yapıları ifade
ederler. Bir maddenin buhar fazının sıcaklığı, kritik sıaklığının üzerinde ise gaz olarak
tanımlandığı halde, sıcaklığı yoğunlaşma koşullarına yakın olan hali ise buhar olarak bilinir.
Akışkanlar mekaniği, uçaklar, gemiler, denizaltılar, roketler, jet motorları, rüzgar türbinleri ve
biyomedikal cihazların yanında, elektronik ekipmanların soğutulması, su, ham petrol ve doğal
gazın taşınması gibi pekçok uygulamanın tasarım ve incelenmesinde önemli bir yere sahiptir.
Akışkanlar mekaniği uygulamalarında çok farklı akış problemleri ile karşılaşılır. Bu problemleri
gruplandırarak inceleyebilmek için bazı ortak özelliklerini dikkate almak uygun bir yaklaşımdır.
İki akışkan tabakanın birbirlerine göre bağıl hareketleri sırasında aralarında iç dirençten
kaynaklanan sürtünme kuvveti oluşur. Akışa karşı oluşan bu iç direnç viskozite olarak bilinir ve
viskozite, sıvılarda moleküller arasındaki çekim kuvvetlerinden, gazlarda ise moleküllerin
çarpışmalarından kaynaklanır. Sürtünme etkilerinin önemli olduğu akışlar viskoz akışlar olarak
tanımlanır.
Bütün deneysel çalışmalar, akışkanın üzerinden aktığı katı yüzeyinde (levha, boru, kanal, kanat,
vs.) akışkan hızının sıfır olduğunu göstermiştir. Katıya doğrudan temas eden akışkan viskoz
etkiler nedeniyle yüzeye “yapışır” ve kayma söz konusu olmadığından “kaymama koşulu” hali
gerçekleşir. Akışkanın akımı sırasında, kaymama koşulu nedeniyle akışa daldırılan plakanın her
iki tarafına yapışır ve viskoz etkilerin önemli olduğu plaka yüzeyine yakın ince sınır tabaka
“viskoz akış bölgesini” oluşturur. Plakanın her iki tarafında, plakanın varlığından etkilenmeyen
mesafede bulunan akış bölgesi ise “viskoz olmayan akış bölgesi” olarak tanımlanır.
Bir akış sırasında akışkanın yoğunluğunda değişiklik meydana gelmiyorsa “sıkıştırılamayan akış”
olarak tanımlanır ve sıkıştırılamayan akışta, akışkanın hacmi hareket süresince değişmez.
Sıvıların yoğunluğu genel olarak sabit olduğundan, sıvı akışları genellikle sıkıştırılamayan akış
olarak kabul edilir. Gaz akışlarında görülen yoğunluk farkının miktarı ve akışın sıkıştırılamaz
oluşu, Mach sayısına göre belirlenir. Ma < 0.3 olması durumunda akış sıkıştırılamaz olarak kabul
edilebilir.
3
Burada, c, deniz seviyesinde veya oda sıcaklığındaki havada 346 m/s değerini alan sıs hızıdır.
Bazı akışlar düzenli ve çalkantısız, bazı akışlar da oldukça düzensiz bir şekilde gerçekleşir.
Çalkantısız akışkan tabakaları, komşu akışkan taneciklerinin bir arada “ince tabakalar” halinde
hareketlerden ileri gelir ve “laminer akış” olarak tanımlanır. Genellikle yüksek akış hızlarında
gerçekleşen ve hız çalkantıları ile nitelenedirilen akış türü ise “türbülanslı akış” olarak
tanımlanır. Bir akışın türünü belirlemek için Reynolds Sayısı denen boyutsuz bir parametrenin
belirlenmesi gerekir.
Bazı akış sistemleri, pompa ya da fan gibi dış bir etki uygulanarak yapılabildiği için bu tür akışlar
“zorlanmış akış”, akış hareketi, daha ılık akışkanın yükselmesi veya soğuk akışkanın alçalması
şeklinde kendiliğinden gerçekleşiyorsa “doğal akış” olarak tanımlanır. Bir akışkan akımında,
akışın özellikleri “bir noktada zamanla herhangi bir değişime uğramıyorsa” daimi akış olarak
tanımlanır. Üniform akış ise, belli bir bölgede “konuma bağlı hiçbir değişim olmadan” meydana
gelen akış olarak tanımlanır. Türbin, kompresör, kazanlar, yoğuşturucu ve ısı değiştiriler gibi
birçok mühendislik uygulamasında kullanılan ekipman “daimi-akışlı makeneler” olarak kabul
edilir.
Bir akış hızı, temel boyutlardan yalnızca birine, her ikisine veya her üçüne göre değişiyorsa,
akışın sırasıyla, bir-, iki- ve üç- boyutlu olduğu söylenebilir. Bir borudaki daimi akışta, kaymama
koşulu nedeniyle, boru yüzeyindeki bütün noktalarda akışkanın hızı sıfırdır ve borunun giriş
bölgesinde hız, hem yarıçap (r) ve hemde uzunlukla (x) değiştiğinden akış iki boyutludur. Hız
profili girişten belli bir mesafe sonunda tamamen gelişir ve bu bölgenin sonundaki akış “tam
gelişmiş akış” olarak tanımlanır ve tam gelişmiş akış bir-boyutlu akış olarak bilinir (V = V(r)). Tam
gelişmiş akışta, hız profili herhangi bir eksenel x-konumunda aynıdır ve boru eksenine göre
simetridir (Şekil.1.3).
Gelişen hız profili, V = V(r, x)
Tam gelişmiş hız profili, V = V(r)
Şekil.1.3. Dairesel kesitli bir boruda hız profilinin gelişimi.
4
Akışkan viskozitesinin neden olduğu viskoz kayma kuvvetlerinin etkisinin hissedildiği akış
bölgesine hız sınır tabakası veya sadece sınır tabaka denir.
Üzerinde çalışılmak üzere seçilen bir madde, uzayda bir bölge veya bir reaksiyon ortamı
“sistem” olarak tanımlanır. Sistemin dışında kalan kütle ya da bölge “çevre”, sistemi
çevresinden ayıran sabit veya hareketli yüzey ise “sınır” olarak adlandırılır. Kapalı sistem
(kontrol kütlesi), sabit kütlelidir ve sınırlarından kütle geçişi yoktur ancak enerji geçişi iş veya ısı
şeklinde gerçekleşebilir. Sistem hem kapalı ve hemde enerji geçişi olmuyorsa, “yalıtılmış (izole)
sistem” olarak bilinir. İçinde gaz sıkıştırılmış bir piston-silindir düzeneğinde kütle geçişi olmadığı
için kapalı bir sistem, piston hareket edebildiği için yüzeyi hareketli sınır şeklinde değerlendirilir.
Açık sistem (kontrol hacmi, KH), uzayda uygun bir şekilde seçilmiş bir bölgedir. Kütle akışının
olduğu, kompresör, türbin yada lüle gibi cihazlar buna örnek olarak verilebilir. Kontrol
hacimlerinin çoğunda sınırlar sabittir ve hareketli sınırları yoktur.
Akışkanlar Mekaniği, temelde Mekanik (Newton) ve Termodinamik yasaları olmak üzere iki
bilim dalının ana kuralları üzerine inşa edilmiştir. Akışkanlar mekaniğinde karşılaşılan
problem(ler)i çözmek amacıyla basit mekanik ve termodinamik kanunları birlikte uygulanarak
çözüm yapılabilir. Ayrıca hareketi incelenen akışkanın fiziksel özellikleri ve hareket bölgesinin
çevresinden gelen şartların da etkisi büyük önem taşımaktadır. Akışkanlar mekaniği bu bilgileri
bir bütün oluşturacak şekilde birleştirirken ileri düzeyde matematik kullanmayı zorunlu kılar.
Akışkanlar mekaniği, kütlenin korunumu, enerjinin korunumu yasası (Termodinamiğin 1. yasası),
evrenin entropisinde azalmaya neden olan akışın mümkün olmadığı termodinamiğin II. Yasası,
(S 0) ve Newton’un hareket yasası (F = ma) olmak üzere dört temel prensibe dayanır.
Son yıllarda ısı enerjisi, mekanik enerji veya diğer enerji türlerinin transfer problemlerinin
incelenmesinde konunun akışkanlar mekaniği problemleri ile büyük benzerlik gösterdiği ve
yakın ilişki içinde olduğu görülmektedir. Akışkanlar mekaniği'nin kullanım alanları gerek
mühendislik uygulamalarında ve gerekse diğer bilimsel ve teknolojik araştırmalarda gün
geçtikçe yaygınlaşmaktadır.
İçten Yanmalı motorlar: Bilindiği gibi petroldeki kimyasal enerjiyi mekanik enerjiye dönüştüren
içten yanmalı motorlar termodinamikteki Açık Sistem’lere önemli bir örnek oluştururlar.
Atmosferden emilen havanın silindire dolması, burada piston tarafından sıkıştırılması, tutuşan
yakıtın yanması ve dolayısıyla yükselen sıcaklık ve basınçlar ve nihayet yanma sonunda egzos
gazlarının sistemi terk etmesi tipik bir akışkanlar mekaniği problemidir. Yine içten yanmalı
motorların su ile soğutulması halinde motor gövdesindeki fazla ısıyı alarak radyatörde havaya
bırakan soğutma sistemi de Kapalı Sistem’lere bir örnek oluşturur ve bu sistemdeki suyun
hareketi de bır Akışkanlar Mekaniği problemidir.
Su, Gaz ve Rüzgâr Türbinleri: Gerek akarsu enerjisini, gerek rüzgâr enerjisini ve gerekse
kimyasal enerjiyi mekanik enerjiye çeviren türbin sistemlerinde, sistemden akan akışkanın
hareketi çok önemli bir akışkanlar mekaniği problemidir.
Pompalar-Kompresörler: Günlük hayatta kullandığımız basit su pompaları, petrol kuyularında
kullanılan dev pompalar, kimyasal ürün (ilaç, petrol türevleri...) işlem hatlarında kullanılan
5
hassas derecelendirme pompaları, taşıtların fren sistemlerinde kullanılan servo-pompalar ve
bunların dâhil olduğu sistemlerin içindeki sıvı akışları, ısıtma-havalandırma sistemlerinde
kullanılan kompresör, vantilatör ve aspiratörler ve bu ekipmanların oluşturduğu gaz hareketleri
tipik akışkanlar mekaniği problemleridir. Hava (ve deniz) taşıtlarını havada (deniz
üstünde/altında) tutan, aero (hidro) dinamik kuvvettir; ayrıca bu taşıtların her türlü seyir ve
manevra hareketi de bu kuvvetin etkisi altında gerçekleşir. Benzer şekilde son yılların yüksek
hızlı kara taşıtlarında da bu kuvvetler, özellikle sürükleme adını verdiğimiz aerodinamik direnç
büyük önem kazanmıştır.
1.2. Boyutlar, Birimler ve Birim Sistemleri
Akışkanlar mekaniği ve diğer birçok mühendislik derslerinde karşılaşılan problemlerde, bazı
akışkanlar (özellikle su, hava,...) için, sabitler (yoğunluk, viskozite, vs.) çeşitli birim sistemlerinde
verilir. Herhangi bir fiziksel büyüklüğün anlamlı yorumlanabilmesi için boyutları ile birlikte
verilmesi gerekir, boyutları gösteren büyüklükler ise birim olarak tanımlanır. Ana boyutlar:
kütle, m, uzunluk L, zaman t ve sıcaklık T, vs., ikincil boyutlar (türetilmiş boyutlar) ana boyutlar
cinsinden ifade edilebilir: hız v, enerji E ve hacim V, vs. Uygulamada son yıllarda SI Birim Sistemi
gittikçe önem kazanmakta ise de gerek MKS ve gerekse FPS (İngiliz/Amerikan) Sistemleri hala
bazı ülkelerde yaygın bir şekilde kullanılmaktadır.
Mühendislik uygulamalarında, bütün denklemler boyutsal olarak homojen olmak zorundadır.
Boyutsal olarak homojen olmayan bir formülün kesinlikle yanlış olduğu ve boyutsal olarak
homojen olsa bile bir formülün de doğru olmasının gerekmediği bilinmelidir. Boyutsal
homojenlik, bir denklemde toplam halinde bulunan her bir terimin aynı birimde olduğundan
emin olunması gerekir. Birim dönüştürme oranları birimleri dönüştürmede oldukça kolaylık
sağlar. Günlük yaşamda çok sık kullandığımız uzunluk (L), zaman (t), hız (uzunluk/zaman, L/t)
gibi nicelikler boyutlarla ifade edilirler. Bir niceliğin sayısal değerini başka bir birimle ifade
etmek için çevirme faktörleri kullanılır.
Çizelge 1.1. Bazı temel birimler ve boyutları.
Temel Büyüklük
Adı
Sembolü Boyutu
Uzunluk Metre
m
L
Kütle Kilogram
kg
M
Zaman Saniye
s
T
Elektrik Akamı Amper
A
I
Termodinamik Sıcaklık Kelvin
K
K
Madde Miktarı
Mol
n
N
Işık Şiddeti Kandela
Cd
Iv
6
Çizelge.1.2. Bazı SI birimleri ve sembolleri.
Türetilmiş SI birimi
ve sembolü
Newton, N
Pascal, Pa
Joule, J
Watt, W
Coulomb, C
Volt, V
Farad, F
Ohm, W
Birim
Kuvvet
Basınç
Enerji, iş, ısı
Güç
Elektrik yükü
Elektriksel potansiyel
Elektrik kapasitesi
Elektriksel direnç
Temel ve diğer türetilmiş birimler
cinsinden ifadesi
1 N = 1 kg m/s2
1 Pa = 1 N/m2
1J=1Nm
1 W = 1 J/s
1 C = 1 Amp-s
1 V = 1 J/C
1 F = 1 C/V
1 W = 1 V/Amp
Çizelge 1.3. Çeşitli birim sistemleri.
İngiliz birim sistemi
Büyüklük
Uzunluk
Zaman
Kütle
Kuvvet
Kuvvet,
türetilmiş
gC
Mutlak
Gravitasyonel
Mühendislik
ft
s
lbm
ft
s
ft
s
lm
lbf
lbf
poundal
1
2
lbmft/lbs
CGS
mutlak
cm
s
g
CGS
gravitasyonel
cm
s
gf
dyne
1
2
sl-ft/lbfs
32.174
2
lbmft/lbfs
Metrik sistem
MKS
mutlak
m
s
kg
1
2
gcm/dyns
MKS
gravitasyonel
m
s
m
s
kg
kgf
Newton
981
2
gcm/gFs
SI
1
2
kgm/Ns
Newton
9.81
2
kgm/kgfs
1
2
kgm/Ns
Çizelge 1.3’de verilen gC temel ve türetilmiş kuvvet ve buna bağlı olarak enerji ve güç birimleri
ile birim sisteminin (İngiliz Birim Sistemi, FPS) diğer birimleri arasındaki uyumu sağlamak için
kullanılan bir çevirme faktörüdür. Ancak bu kullanım diğer birimlere dönüştürmede bazı
karışıklıkları beraberinde getirmektedir.
Bu karışıklığı (gc kullanımı) kaldırmak için SI birim sisteminde, kuvvet birimi Newton’un ikinci
yasasından türetilen ikincil bir boyut olarak değerlendirilir ve SI birim sisteminde kuvvet birimi
Newton (N) dur. Newton; 1 kg büyüklüğündeki bir kütleyi 1 m/s2 ivmelendirmek için gerekli olan
kuvvet olarak tanımlanır ve İngiliz birim sisteminde kuvvet birimi, pound-kuvvet (lbf) dur.
Ağırlık terimi, kütle ile karıştırılmakla birlikte bu iki büyüklük birbirinden farklı fiziksel
özelliklerdir. Ağırlık kütleyi de içine alan bir kuvvet olarak tanımlanır ve cisme etki eden
yerçekimi kuvveti (W) şeklinde ifade edilir.
7
Burada, m cismin kütlesi, g yerel yerçekimi ivmesidir (örneğin, 9.708 m/s2).
Çizelge 1.4. Temel birimlerle türetilen SI birimlerinden bazı örnekler.
Fiziksel
Büyüklük
Alan
Hacim
Hız
İvme
Basınç
Dalga Sayısı
Yoğunluk
Özgül hacim
Akım Yoğunluğu
Açısal hız
Özgül Ağırlık
Kinematik viskozite
Dinamik viskozite
Hacimsel debi
Açısal hız
Kuvvet
Momentum
Kayma gerilmesi
Enerji
Güç
SI türetilen birimler,
Sembol
m2
m3
m/s
m/s2
N/m2
m-1
kg/m3
m3/kg
Amp/m2
s-1
N/m3
m2/s
kg/m s
m3/s
s-1
N
Ns
N/m2
Joule
Watt
Boyutlar
L2
L3
L T-1
L T-2
M L-1T-2
L-1
M L-3
L3 M-1
AL-2
T-1
M L-2T-2
L2 T-1
M L-1T-1
L3 T-1
T-1
M L T-2
M L T-1
M L-1T-2
M L2T-2
M L2T-3
Enerjinin bir türü olan iş, kuvvet ile uygulanan mesafenin çarpımı kadardır ve birimi enerji birimi
olan Joule (J) dür, 1 J = 1 Nm, bir diğer enerji birim de kaloridir (cal), 1 cal = 4.187 J. İngiliz birim
sisteminde (FPS) enerji birimi Btu dur ve 1 Btu 68 oF sıcaklığındaki 1 lbm kütleye sahip suyun
sıcalığını 1 oF artırmak için gerekli olan enerji olarak tanımlanır, 1 Btu = 1.055 kJ.
Çizelge.1.5. Birimlerin as ve üst katları.
Birim
çarpanı
1012
109
106
103
102
10
10-1
Birim adı
ve sembolü
Tera, T
Giga, G
Mega, M
Kilo, k
Hekto, h
Deka, da
Deci, d
Birim çarpanı
10-2
10-3
10-6
10-9
10-12
10-15
10-18
8
Birim adı
ve sembolü
Centi, c
Mili, m
Mikro,
Nano, n
Piko, p
Femto, f
Atto, a
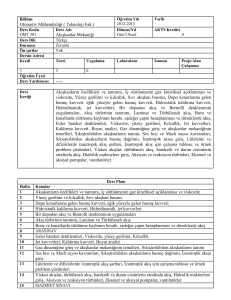
1.3. Problem Çözme Tekniği
Mühendislik uygulamarında, özellikle zor ve karmaşık görünen problemlerin çözümünde
sistemli bir yaklaşım büyük kolaylıklar sağlar. Bir mühendislik öğrencisi veya mühendis, karmaşık
ve zor görünen bir problemi, bir dizi basit problemin çözümüne indirgeyerek problemin
çözümünü gerçekleştirebilir. Bu amaçla aşağıdaki sıralama büyük kolaylıklar sağlar.
1. Problemin ifade edilmesi; problem, verilen bilgiler ve istenen büyüklükler şeklinde özetlenir.
2. Şematik çizim; incelenen fiziksel sistem gerçekçi bir şekilde hayali olarak tasarlanır ve şematik
olarak gösterilebilir.
3. Kabuller ve yaklaştırmalar; çözüme ulaşmak için uygun kabuller ve yaklaştırmalar yapılır ve
gerekli olduğu halde verilmeyen büyüklükler için uygun değerler alınır.
4. Fiziksel yasalar; problem ile ilgili tüm fiziksel yasa ve ilkeler uygulanıp yapılan kabuller ile
problem mümkün olan en basit şekle indirgenir.
5. Özellikler; problem çözümünde gerekli olduğu halde bilinmeyen özellikler, bilinen haller için
özellik bağıntıları ve/veya tablolardan bulunmalıdır.
6. Hesaplamalar; bilinmeyen niceliklerin belirlenmesi amacıyla bilinen büyüklükler,
basitleştirilmiş bağıntılarda yerine yazılarak ve uygun birim dönüşümleri uygulanarak
hesaplamalar yapılır.
7. Sorgulama, doğrulama ve irdeleme; elde edilen sonuçların doğru olduğu ve mantıklı değer
olarak alınabileceği muhakeme edilmelidir. Bulunan sonuçların sayısal olarak anlamlı olup
olmadığı ve gerçek fiziksel sistemlere uygulnabilirliği de gözden geçirilmelidir.
1.4. Doğruluk, Hassasiyet ve Anlamlı Rakamlar
Mühendislik uygulamalarında, sonuçlar verilirken, çok fazla basamak sayısının verilmesi,
olduğundan daha fazla bir hassasiyet anlamına geleceğinden istenmez. Mühendisler
kullandıkları birim sisteminden bağımsız olarak, sayıları yerinde kullanabilmek için doğruluk,
hassasiyet ve anlamlı basamaklar şeklinde olmasına dikkat etmelidirler. Mühendisler sayıların
yerinde ve doğru kullanımı konusunda aşağıdaki üç ilkeden kesinlikle haberdar olmalıdırlar;
1. Doğruluk hatası: Herhangi bir ölçümde okunan değerin gerçek değerden farkıdır. Okunan
değerlerin ortalamasının gerçek değere yakınlığıdır. Genellikle tekrarlayabilir sabit hatalarla
ilgilidir.
2. Hassasiyet hatası: Okunan bir değerin tüm okunan değerlerin ortalamasından farkıdır.
Ölçme aletinin çözünürlüğünün ve ölçümün tekrarlanabilirliğinin bir ölçüsüdür. Genellikle
rastgele hatalarla ilgilidir.
3. Anlamlı basamaklar: Önemli ve anlam taşıyan basamaklardır. Hesaplama yaparken, nihai
sonuç problemdeki en az hassasiyetli parametre kadar hassastır. Anlamlı basamakların
sayıları bilinmiyorsa, kabul edilen standart 3’tür. Tüm ödevlerde ve sınavlarda 3 anlamlı
basamağa göre işlem yapın.
9
1.5. Akışkanların Özellikleri
Bir sistemin herhangi bir karakteristiğine özellik denir. Bilinen bazı özellikler, Basınç, P, sıcaklık,
T, hacim, V ve kütle m, daha az biliniyor olmakla birlikte, viskozite, ısıl iletkenlik, elastiklik
modülü, ısıl genleşme katsayısı, buhar basıncı, yüzey gerilimi de sistemin özelikleri olarak bilinir.
Sistemin özellikleri yoğun özellikler ve yaygın özellikler olmak üzere iki gruba ayrılabilir.
Yoğun özellikler, sistemin kütlesinden bağımsızdırlar, sıcaklık, basınç ve yoğunluk. Yaygın
özellikler, değerleri sistemin büyüklüğüne bağlı olan özelliklerdir. Toplam kütle, toplam hacim
ve toplam momentum, vs. Birim kütle başına verilen özellikler özgül özellikler olarak adlandırılır.
Özgül hacim, v = V/m ve özgül toplam enerji e = E/m, vs.
A-Basınç
Katı cisimlerden farklı olarak akışkanlar bulundukları ortamı katı cidara kadar veya diğer bir
akışkan kütlesine kadar doldururlar. Temas yüzeylerinde "akışkanların molekül hareketleri yolu
ile ilettikleri kinetik enerjinin zamana göre ortalamasının birim alana düşen miktarı" akışkan
basıncını oluşturur. Sakin (durağan) akışkan kütleleri halinde bu basınç statik basınç adını alır ve
kaynağı yerçekimidir. Bu büyüklük deniz seviyesi referans alınarak ölçülür. Basınç, bir akışkan
tarafından birim alana uygulanan normal kuvvet olarak tanımlanır. Akışkanlardaki basıncın
katılardaki karşılığı, normal gerilmedir. Deniz seviyesinde serbest yüzeyli bütün akışkanların
basıncı hava basıncına (atmosferik basınca, Po) eşittir ve 25 oC sıcaklıkta Po = 760 mmHg dir.
Atmosferik basınca göre ifade edilen basınca gösterge basıncı (geyç pressure, etkin basınç,
efektif basınç) denir ve basınç biriminin sonuna "g" harfi konularak belirtilir (1 atmg, 14.7 psig).
Sıfır sıkıştırma gerilimi haline göre ifade edilen basınç (verilen bir konumdaki gerçek basınç) ise
mutlak basınç (absolut pressure) (Pm) olarak bilinir ve birimin sonuna "a" harfi konularak
belirtilir (1 atma, 14.7 psia). Gösterge basıncına (Pg) atmosferik basınç (Patm) eklenmek suretiyle
mutlak basınç (Pm), elde edilir (Şekil 1.4). gösterge basıncı pozitif veya negatif olabilir, ancak
atmosferik basıncın altındaki basınçlar “vakum basıncı” olarak bilinir ve atmosferik basınç ile
mutlak basınç arasındaki farktan ölçülür.
Birim yüzeye uygulanan kuvvet olarak bilinen basınç farklı birimlerle ifade edilebilir, örneğin,
N/m2, Pascal (Pa) olarak bilinir. Ancak Pascal birimi çok küçük bir değer olduğundan çoğunlukla
bunun 103 katı kPa ve 106 katı MPa birimleri kullanılır. Değişik birim sistemlerinde 1 atmosfer
(Po) için aşağıdaki eşleştirmeler yapılır;
1 Pa = 1N/m2, 1 kPa = 103 Pa, 1 MPa = 106 Pa
1 atm = 101325 Pa = 101.325 kPa = 1.01325 bar
1 Atm = 10333 kgf/m2 (mmH2O) = 1.013x105 N/m2 (Pa) = 14.71 lbf/in2 (psi) = 1.01325 bar
10
Şekil 1.4. Mutlak basınç, gösterge basıncı ve vakum basıncı arasındaki ilişki.
Atmosfere açık yüzeyi bulunan bir su kütlesinin serbest yüzeyi üzerindeki basınç o yükseklikteki
atmosfer basıncına eşittir. Ancak su yüzeyinin altında, su kütlesinin içinde, derinlik arttıkça
basıncın arttığı bilinmektedir. Suyun yoğunluğundaki değişimi hemen her zaman ihmal edilecek
kadar küçük kabul ettiğimizde bu basıncın derinlikle değişimi aşağıdaki gibi ifade edilir.
Basınç, durgun bir akışkan içinde yatay yönde
değişmediği halde, akışkanın ağırlığından dolayı
derinlikle önemli ölçüde artar.
Bu değişimi matematiksel olarak ifade etmek için,
Şekil.1.5’deki z yüksekliğinde, x uzunluğunda ve
birim derinlikteki dikdörtgen akışkan elemanı serbest
cisim diyagramında kuvvet denkliği yazmak gerekir.
Akışkanın yoğunluğunu () sabit kabul ederek zyönünde kuvvet denkliği,
Şekil 1.5. Dengede bulunan dikdörtgen bir
akışkan elemanının serbest cisim diyagramı.
Burada,
akışkan elemanının ağırlığıdır. (1.8) eşitliği
yeniden düzenlenirse aşağıdaki özgül ağırlık ( ) basınç ilişkisi elde edilir;
ile bölünür ve
Açık Hava (Atmosfer) Basıncı; bilindiği gibi açık hava basıncı yer küresinin etrafını saran hava
kütlelerinin ağırlığından kaynaklanır ve doğal olarak sıcaklık değişimleri ya da ölçüm noktasının
deniz seviyesinden yüksekliği ile değişmektedir. Sıcaklık değişimlerinin yoğunluk () değerini
sabit kabul edilebilecek kadar az etkilediği, dolayısıyla yüksekliklerin fazla değişmediği hallerde
bu basıncın yükseklikle değişimi aşağıdaki gibi (1.10 denklemi) kolayca hesaplanabilir. Burada, h,
serbest sıvı yüzeyinden itibaren olan sıvı derinliğidir.
11
Duran bir akışkan kütlesinin içinde bir noktadaki statik basınç bütün doğrultularda aynı değere
sahiptir. Duran akışkanlar için basıncın her nokta da eşit olma özelliğinden dolayı, = Po ve
= 0 olacağı için herhangi bir kap içinde bulunan bir akışkanın kap yüzeyine uygulayacağı
basınç her doğrultuda aynıdır. Serbest yüzeyli bir akışkan halinde bu basıncın değeri ancak
akışkanın ağırlığı ile değişir.
B-Sıcaklık
Moleküler enerji düzeyinin bir ölçüsü olarak düşünülen sıcaklık, farklı birimlerde yazılabilir. SI
birim sisteminde sıcaklık ölçeği Kelvin ölçeğidir ve K ile simgelenir.
MKS ve SI sistemlerinde;
FPS sisteminde;
Deniz seviyesinde, normal şartlarda, hava sıcaklığı, To = 273 + 25 oC = 298 K olarak bilinir.
Yoğunluk ve Özgül Ağırlık
Yoğunluk birim hacmin kütlesi, özgül hacim ise birim kütlenin hacmi olarak tanımlanır ve
aşağıdaki gibi matematiksel olarak ifade edilir.
Bir maddenin yoğunluğu, maddeyi oluşturan moleküllerin kütlesine ve yerleşim düzenine göre
aralarında kalan ro mesafesine bağlıdır. Basit moleküler katılarda bu mesafe sabit olduğundan
katıların yoğunluğu basınç ve sıcaklıkla değişmez. Sıvıların yoğunluğu, moleküllerin ağırlığına
değil, yapılarına ve molekülleri arasındaki van der Waals kuvvetlerinin ve özellikle de hidrojen
bağlarının varlığına bağlıdır. Katıların aksine sıvıların yoğunluğu sıcaklıkla değişir. Gazların
yoğunluğu, moleküler düzeyde basınçlarına ve basınçları ise iç enerjilerine bağlıdır. Katıların
aksine gazların yoğunluğu sıcaklık ve basınçla değişir. Yoğunluk, MKS: [kgks2/m4], SI: [kg/m3,
Ns2/m4]ve FPS: [lbf s2/ft4] gibi farklı birimlerle ifade edilir.
1 kg/m3 = 0.102 kgf s2/m4 = 1.94x10-3 lbf s2/ft4
12
Bir maddenin birim hacminin ağırlığı özgül ağırlık (
orantılı olarak aşağıdaki şekilde ifade edilir.
) olarak tanımlanır ve yoğunlukla doğru
Burada, g yerçekimi ivmesi ve s’nin birimi N/m3’tür.
Bazen bir maddenin yoğunluğu, çok bilinen bir maddenin yoğunluğu ile kıyaslanarak verilir ve
bu büyüklük “özgül yoğunluk, bağıl yoğunluk, spesifik gravite SG” gibi adlarla ifade edilir ve “bir
maddenin yoğunluğunun standart bir maddenin belirli bir sıcaklıktaki (+4 oC) yoğunluğuna
oranı” şeklinde tanımlanır.
Yağ ve petrol ürünleri için Amerikan Petrol Endüstrisi (API) tarafından geliştirilen oAPI
yoğunluğu, şeker endüstrisinde kullanılan oBrix, tuzlu su (salamura) ve sülfürik asit
çözeltilerinde kullanılan oBaume yoğunlukları, Archimedes yasasını esas alan yöntemlerle
ölçülür ve ampirik ifadelerle birbirlerine dönüştürülebilirler.
API ile SG arasında;
Brix ile SG arasında;
Baume ile SG arasında;
Gazların özgül ağırlığı (SGg) gazın yoğunluğunun (g) standart koşullar (0 oC, 1 atm) veya 15.5 oC
sıcaklıktaki havanın yoğunluğuna (h) oranı şeklinde verilir.
En önemli akışkanlar olan hava ve su için yoğunluk değerleri aşağıdaki gibi olmakla birlikte
havanın yoğunluğu sıcaklık ve basınç değerlerine göre değişiklik gösterir. "Normal şartlar"
dediğimiz Po = 1 atmosfer ve To = 298 K koşullarında aşağıdaki değere eşittir.
o, HAVA= 1.23 kg/m3 = 1/8 kgf s2/m4 = 2.4x10-3 lbf s2/ft4
o, SU = 1000 kg/m3 = 102 kgf s2/m4 = 1.94 lbf s2/ft4
İdeal gazların yoğunluğu, ideal gaz hal denkleminden faydalanılarak bulunur.
13
Bu eşitlikte, P mutlak basıncı, özgül hacmi, mutlak sıcaklığı, yoğunluğu ve R gaz sabitini
göstermektedir. R gaz sabiti her haz için farklıdır ve aşağıdaki gibi belirlenir. Bu eşitlikte, Rü
evrensel gaz sabitidir ve bütün gazlar için aynı değerdedir (8.314 J/molK)
Enerji ve Özgül Isılar
Toplam enerji, E, ısıl, mekanik, kinetik, potansiyel, elektrik, manyetik, kimyasal, ve nükleer enerji
gibi farklı şekillerde bulunur ve birimi çoğunlukla joule (J) veya kilo joule (kJ) dür.
Mikroskobik enerji;
İç enerji u, durgun (akmayan) akışkanlar için tanımlanır ve moleküler aktivitenin bir sonucu
olarak gösterilir.
Entalpi, akan bir akışkan için tanımlanır ve akış enerjisini (Pv =P/) yi içerir.
Makroskobik enerji;
Kinetik enerji Ke=V2/2;
Potansiyel enerji Pe = gz
Elektrik, manyetik, kimyasal ve nükleer enerjinin olmadığı durumlar için toplam enerji:
eakan= h + V2/2 + gz
Bir gazın iç enerjisinde ve entalpisinde meydana gelen diferansiyel ve sonlu değişimler, özgül
ısılar cinsinden (cv ve cp) aşağıdaki gibi ifade edilir.
Sıkıştırılabilirlik
Akışkanlar, sıcaklık artışı veya basınç azalması ile genleşirler, sıcaklık azalması veya basınç
artması ile sıkışırlar. Basınç ve sıcaklık değişimlerini, hacimdeki değişimle ilişkilendiren akışkan
özelliklerine ihtiyaç vardır. Hacim değişiminin miktarı, akışkana göre farklılık gösterdiğinden
hacim değişimlerini sıcaklık ve basınç değişimleri ile ilişkilendirmek gerekir. Bu ilişkiler hacimsel
elastiklik modülü (
sıkıştırılabilirlik katsayısı, Pa) ve hacimsel genleşme katsayılarıdır.
Büyük değeri, hacimde küçük bir değişime neden olmak için basınçta büyük bir değişim olması
gerektiğini gösterir, dolayısıyla büyük değerine sahip akışkanlar sıkıştırılamaz akışkan olarak
tanımlanır. İdeal bir gaz için,
14
Sıkıştırılabilirlik katsayısının tersine, izotermal sıkıştırılabilitlik, , denir. Bir akışkanın izotermal
sıkıştırılabilirliği, basınçtaki bir birimlik değişime karşılık hacim veya yoğunlukta meydana gelen
oransal değişime karşılık gelir ve aşağıdaki gibi tanımlanır.
T sıcaklığında bir ideal gazın,
Sıcaklık ve basıncın bir akışkan üzerindeki ortak etkileri, özgül hacmi, T ve P’nin bir fonksiyonu
olarak aşağıdaki gibi yazılabilir:
Viskozite (Kıvamlılık)
Kaymama koşulu, katı bir yüzey ile doğrudan temas halinde olan akışkanlar viskoz etkilerden
dolayı yüzeye “yapışırlar”. Çeperde kayma gerilmesi , tw yüzey sürükleme kuvveti olmak üzere,
aşağıdaki gibi ifade edilir ve yüzeyde sınır tabaka gelişiminin nedenidir. Kaymama koşuluna
neden olan akışkan özelliği viskozitedir. Akışkanlar mekaniği problemlerinin analitik ve sayısal
olarak modellenmesinde önemli bir sınır koşulu olarak kullanılmaktadır.
Şekil 1.6. Bir plaka üzerinde akan akışkanın hız dağılımı.
Akışkanın, sıkıştırılamaz ( = st., T = st.), yada sıkıştırılabilir fakat izentropik (s = st) hal
değişiminin her iki halinde de akışkan hareketinin çevreye enerji kaybetmeyeceği, yani hareket
bir defa başladığında ancak dış etkilerle değiştirilebileceği ya da durdurulabileceği bilinmektedir.
15
Viskozite bir akışkanın harekete karşı gösterdiği iç direnci temsil eder. Akan bir akışkanın bir
cisim üzerine akış yönünde uyguladığı kuvvete sürükleme kuvveti denir ve bu kuvvetin
büyüklüğü bir oranda viskoziteye bağlıdır. Gerçekte ise bir akışkanın herhangi bir hareketi
durmaksızın sürdüremediğini ve hareketi süresince çevreye enerji kaybederek sonunda durgun
hale geldiğini bilmeliyiz. İşte akışkanın çevreye enerji kaybetmesine yani sürtünme yolu ile
kendisini frenlemesine (dolayısıyla entropi artışına) neden olan akım mekanizmasına akışkanın
viskozluk özelliği adı verilir.
Aslında viskozluk veya viskozite, her hangi bir akışkanın bütün zerreleri için aynı derecede
etkilidir. Ancak, akışkanlar mekaniği açısından, etkilerinin özellikle önemli olduğu bölge akımın
katı cisim cidarına çok yakın olduğu yerdir. Viskozluk ayrıca farklı hızlara sahip akışkan
kütlelerinin değme yüzeylerinde de önem kazanır. Viskozite için bir bağıntı elde etmek üzere,
aralarında ℓ mesafe bulunan iki çok geniş plaka arasındaki akışkan tabakasını göz önüne alalım
(Şekil.1.7). Alttaki plaka sabit, üstteki plakaya bir F kuvveti uygulanarak çekildiğinde,
büyüklüğünde bir hızla hareket eder. Bu durumda, plaka ile akışkan arasındaki yüzey alanı A
olmak üzere, akışkan tabakasına etki eden kayma gerilmesi, = F/A şeklinde yazılır.
Şekil 1.7 Bir akışkan tabakada uygulanan kuvvet.
Kaymama koşulundan faydalanarak aşağıdaki eşitlikler yazılabilir; u(0) =0 ve u(ℓ) =
üzere, hız profili ve hız gradienti aşağıdaki gibi yazılır.
Su, hava, benzin ve yağlar gibi Newton tipi akışkanlar için kayma gerilmesi
ilişkisi aşağıdaki gibi tanımlanır;
olmak
ile viskozite
Bu eşitlikte, dinamik viskozite olarak tanımlanır ve birimi, kg/ms = Ns/m2, Pas şeklinde verilir.
0.1 Ns/m2 = 1 Poise, P = 0.1 Pas, 1 P = 100 cP (centipoise)
Newton tipi bir akışkan (Newtonian akışkan, kayma gerilmesi hız gradienti ile doğru orantılı)
tabakasına etki eden kayma kuvveti aşağıdaki gibi viskozite ile ilişkilendirilir;
16
Bu durumda alttaki plaka sabit tutulurken üstteki plakaya uygulanan kuvvet aşağıdaki gibi
yazılabilir;
Bir akışkanın dinamik viskozitesinin akışkanın o koşullardaki yoğunluğuna oranı Kinematik
viskozite olarak tanımlanır ve birimi Stoke (St = cm2/s) tur.
Bir akışkanın viskozitesi genel olarak sıcaklık ve basınçla değişir. Viskozite, sıvılarda moleküller
arasındaki çekim kuvvetleri, gazlarda ise moleküllerin çarpışması sonucu ortaya çıkar ve
sıcaklıkla büyük oranda değişir. Viskozite hesaplamalarında Hagen-Poiseuille eşitliği çok sık
kullanılır ve aşağıdaki gibi yazılır.
Bu eşitlikte, D, kapiler tüpün çapı, L, uzunluğu, ve sıvının yoğunluk ve viskozitesi, V haznenin
hacmi, t ise ölçüm süresini ifade eder.
Sıvıların viskozitesini ölçmek için, dönen viskozimetre çok sık kullanılır. Aralarında ℓ mesafe
bulunan iki eş merkezli silindir göz önüne alınır, içteki silindir döndürülürken dıştaki silindir sabit
tutuluyor. Kayma gerilmesinin tanımından faydalanarak, ℓ/R << 1 olması durumunda silindirler
iki düz plaka olarak düşünülebilir. Tork T ve teğetsel hız v = w R, ıslak yüzey alanı, A = 2 R L ve T
ve w ölçülerek, hesaplanır.
Şekil 1.8. Döner bir viskozimetre.
Bu eşitlikte, L silindirin uzunluğu, dev/dak olarak bilinen birim zamandaki dönme sayısıdır. Bir
tam dönme sırasında
radyan açısal yol alınır ve rad/dak ile dev/dak arasında
eşitlik yazılır.
17
Yüzey Gerilimi
Sıvı damlaları içleri sıvıyla dolu küresel balonlar gibidir ve sıvının yüzeyi ise gerilme altında
esnemiş zara benzer bir davranış sergiler. Buna neden olan çekme kuvveti moleküller arası
çekim kuvvetinden kaynaklanan yüzey gerilimidir ve s (N/m, J/m2) ile gösterilir. Yüzey
molekülüne etkiyen çekim kuvveti simetrik değildir. İçteki moleküller tarafından uygulanan
çekim kuvveti sıvıyı yüzey alanını minimuma indirmeye ve küresel bir şekil almaya zorlar.
Çizelge 1.6. Bazı maddelerin yüzey gerilimleri.
Şekil.1.9. Bir sıvının yüzey gerilimi.
Kılcallık Etkisi
Kılcallık etkisi, küçük çaplı bir boruda sıvının yükselmesi veya alçalmasıdır. Borudaki eğri yüzey
menisküs olarak adlandırılır. Suyun menüsküsü yukarı doğrudur çünkü su ıslatan bir akışkandır.
Civanın menüsküsü aşağı doğrudur çünkü civa ıslatmayan bir akışkandır. Kılcal yükselme
miktarını veren bağıntı şekildeki kuvvet dengesi ile elde edilebilir.
Şekil 1.10. Kılcal bir borudaki yükselme ve yüzey gerilimi.
Kılcal yükselmede, yükselen akışkanın ağırlığı (W), yüzey gerilimi kuvveti (Ft) ile dengelenir,
Kuvvet denkliği yazılarak kılcal yükselme (h) aşağıdaki gibi belirlenir.
18
Sıvı ortama enjekte edilen gazın oluşturduğu kabarcığa etkiyen yüzey gerilimi kuvveti de benzer
bir yaklaşımla belirlenebilir. Yarıçapı r olan bir gaz kabarcığının iki yarım küreden oluştuğu ve bu
iki yarım kürenin birleştiği çevre boyunca da yüzey gerilimi kuvvetinin uygulandığı
düşünüldüğünde,
19
UYGULAMA-1
Problem.1. Özgül yoğunluğu (bağıl yoğunluğu, SG) 0.8684 olan petrolün yoğunluğunu kg/m3,
g/cm3, lbm/ft3 ve lbm/gal (1 ft3 = 7.48 galon) birimlerinde ifade ederek eşdeğer API derecesini
hesaplayınız.
Çözüm-1. SG = 0.8684, su = 1000 kg/m3,
……………………………………………………….……………………………………………….
Problem.2. Karbondioksit gazını ideal gaz kabul ederek 0 oC sıcaklık ve 1 atm basınç koşullarında
MKS (m-kg-s) ve İngiliz birim sisteminde (FPS, ft-lbm-s), yoğunluğunu hesaplayınız ve spesifik
gravitenin (SG) birim sisteminden bağımsız olduğunu gösteriniz, (hava = 1.285 kg/m3(0oC, 1 atm)
CO2: 44 g/mol)
Çözüm-2. MKS’de, Standart koşullar; T = 273 K, P = 1 atm = 1.013*105 N/m2
İdeal gaz yasasından,
FPS de, Standart koşullar;
P = 1 atm (14.7 psi/1 atm)= 14.7 psi, R = 10.73 psia ft3/lbmol oR, M = 44 lbm/lbmol,
hava = 0.085 lbm/ft3
Görüldüğü gibi, SG her iki birim sistemi için de aynı çıkmış ve birim sisteminden bağımsız
olduğu belirlenmiştir.
20
Problem.3. Yandaki şekilde bazı akışkanlar
için kayma gerilmesi-hız gradienti değişimleri
verilmiştir. Her bir değişime sahip akışkanları
yorumlayınız.
Çözüm.3.
a) Newtonian akışkanlar, Newton’un
sürtünme yasasına göre hareket ederler.
Kayma gerilmesi hız gradientiyle doğru
orantılıdır. Bu akışkanlar için kayma
gerilmesi ile hız gradientini bir eksen
takımında gösterdiğimizde orjinden
geçenbir doğru elde ederiz. Doğrunun
eğimi dinamik viskoziteyi verir.
b) İdeal akışkanlarda kayma gerilmesine gösterilen direnç, sıfır olduğundan viskozite sıfırdır.
Buna göre, yatay eksen ideal akışkanlara denk gelir.
c) İdeal katı cisimlerde, herhangi bir kuvvet uygulanmasında şekil değiştirme oluşmayacağı için
düşey eksen elde edilir. Gerçek katı cisimlerde Hooke yasasına uyan bir miktar şekil
değiştirme meydana gelir ve bunun doğrusu düşey eksene yakındır.
d) Newtonian olmayan akışkanlarda oluşan şekil değiştirmede, kayma gerilmesi ile hız gradienti
orantılı değildir. Bu akışkanların şekil değiştirmesi, “plastik şekil değiştirmesi” olarak
tanımlanır.
e) İdeal plastikler, şekil değiştirmeden kayma gerilmesine bir miktar mukavemet gösterecek ve
daha sonra kayma gerilmesiyle orantılı olarak şekil değiştirecektir.
………………….……………………………………………….
Problem.4. Sabit yatay bir yüzey üzerindeki viskoz bir akışkanın akımındaki hız dağılımı, u (m/s),
y, yüzeyden itibaren düşey uzaklık (m);
şeklinde tanımlanmaktadır. Sıvının
-5
dinamik viskozitesi, = 8*10 kg/ms olduğuna göre, yüzeydeki ve y = 0.34 m mesafedeki
kayma gerilmesini hesaplayınız.
Çözüm.4. Kayma gerilimi tanımından aşağıdaki eşitlik yazılır;
21
Problem.5. Bir akışkanın hız dağılımı, u (m/s), y, yüzeyden itibaren düşey uzaklık (m), olmak
üzere,
şeklinde tanımlandığına göre, cidarda, cidardan 0.25 m ve 0.50 m mesafedeki
hız gradientlerini hesaplayınız. (Cevaplar: , 4.23 1/s, 3.36 1/s).
……………………………………………………….……………………………………………….
Problem.6. Bir sıvının dinamik viskozitesi = 2*10-4 kg s/m2 ve özgül ağırlığı = 0.913 ton/m3
olarak veriliyor. Bu sıvının serbest yüzeyine; u = 1.5 m/s büyüklüğünde bir hız verildiğinde
aşağıdaki koşullar için, 3, 6 ve 9 cm yüksekliklerdeki hız gradyenlerini ve kayma gerilimlerini
hesaplayınız.
a) Hız değişimi lineer,
b) Hız değişimi şekilde görüldüğü gibi tepe noktası A ve orjini B olan parabolik bir değişim
gösterdiği zaman.
Çözüm.6.
b)
22
……………………………………………………….……………………………………………….
Problem.7. Deniz suyunun yoğunluğu, basıncın 98 kPa olduğu serbest yüzeyinde 1030 kg/m3
olarak bilinmektedir. Deniz suyunun hacimsel elastiklik modülü (hacimsel sıkıştırılabilirlik
katsayısı, ) 2.34*109 N/m2 ve basıncın z derinliği ile
şeklinde değiştiğini kabul ederek
2500 m derinlikteki yoğunluk ve basıncı belirleyiniz (sıcaklık etkisini ihmal ediniz).
Çözüm.7. Hacimsel elastiklik modülü (
sıkıştırılabilirlik katsayısı, Pa) aşağıdaki gibi tanımlanır
(1. 21).
Bu yoğunluk değeri basınç eşitliğinde yazılır ve uygun sınır değerlerinde integre edilirse
aşağıdaki ilişki elde edilir.
23
Bu integraller bulunduktan sonra, z = 2500 m derinlikteki basınç ve yoğunluk değerleri
hesaplanabilir. Buna göre,
Eğer yoğunluğu başlangıç değeri gibi
kabul ederek çözüm yapılmış olsaydı aşağıdaki
değerler elde edilirdi;
% 0.55 mühendislik uygulamaları için kabul edilebilir hata değerleri arasındadır ve basınç
değerinin bu ifade ile hesaplanması büyük yanılgıya sebep olmayacaktır.
……………………………………………………….……………………………………………….
24
Problem.8. Yarıçapı R olan dairesel kesitli bir boruda viskozitesi olan bir akışkanın akışında
borudaki hız dağılımı aşağıda verildiği gibidir. Bu ifadede, umaks, boru ekseninde ulaşılan
maksimum hızı, r- eksen çizgisinden olan radyal mesafeyi, u(r) ise herhangi bir r- mesafesindeki
akış hızını göstermektedir. Bu sistemde birim boru uzunluğu başına akışkanın boru çeperine akış
yönünde uyguladığı direnç kuvveti için bir eşitlik türetiniz ve bulduğunuz ifadeden kuvvetin
yarıçaptan bağımsız olduğunu gösteriniz. Bu ifadeyi kullanarak, n = 2, R = 8 cm, umaks = 3 m/s,
L = 20 m, ve = 1*10
hesaplayınız.
-3
kg/ms olması durumunda bu direnç kuvvetinin sayısal değerini (N)
Çözüm.8. Önce kayma gerilmesi ifadesi oluşturulur. Bunun için aşağıdaki işlem serisi uygulanır;
……………………………………………………….……………………………………………….
Faydalanılan Kaynaklar
1. Çengel Yunus, Cimbala, Akışkanlar Mekaniği, Temelleri ve Uygulamaları, Güven, 2013.
2. Engin Tahsin, Sakarya Üniversitesi, Makine Mühendisliği Bölümü,
3. Uysal Bekir Zühtü, Gazi Üniversitesi, Kimya Mühendisliği Bölümü
4. Berber Rıdvan, Ankara Üniversitesi, Kimya Mühendisliği Bölümü,
5. Ilgaz Cemil vd.,. Akışkanlar Mekaniği ve Hidrolik Problemleri, Çağlayan Kitapevi,
25