ELEKTRİK ENERJİ DAĞITIMI

YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
Enerjinin Taşınması
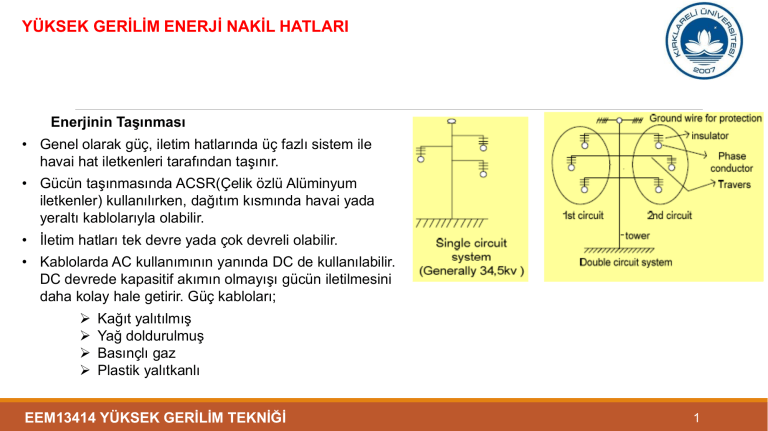
• Genel olarak güç, iletim hatlarında üç fazlı sistem ile
havai hat iletkenleri tarafından taşınır.
• Gücün taşınmasında ACSR(Çelik özlü Alüminyum
iletkenler) kullanılırken, dağıtım kısmında havai yada
yeraltı kablolarıyla olabilir.
• İletim hatları tek devre yada çok devreli olabilir.
• Kablolarda AC kullanımının yanında DC de kullanılabilir.
DC devrede kapasitif akımın olmayışı gücün iletilmesini
daha kolay hale getirir. Güç kabloları;




Kağıt yalıtılmış
Yağ doldurulmuş
Basınçlı gaz
Plastik yalıtkanlı
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
1
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
• Genelde enerji üç fazlı sistemler ile güç taşınırken HVDC olarak
taşımanın da kendine göre yararları vardır.
• Havai hatlar ile 500-600km’lik hatlar yada 50km uzunluğundaki kablolu
iletimde HVDC hatlar, AC iletime göre daha ekonomiktir.
• Üç fazlı sistemde faz ve hat gerilimleri aşağıdaki gibi verilebilir. İletim
hattında Nötr yoktur. Nötr dağıtım sisteminde bulunur.
𝑼: Fazlar arası gerilim, hat gerilimi
𝑼
𝟑
𝑼𝑭 : Faz gerilimi
𝑼𝑭 =
Üç fazlı sistemde güç
𝑷 = 𝟑. 𝑼. 𝑰. 𝒄𝒐𝒔𝝋(𝐖)
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
2
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
• Her iletim hattının bir 𝑹 direnci vardır.
• İletilen güç arttıkça direnç üzerindeki kayıplar da artar.
 Kayıplar, ısı salınımı olarak ortaya çıkar.
 Üç faz güç kayıplarına neden olur.
∆𝑷 = 𝟑. 𝑹. 𝑰𝟐
• Bağıl Güç Kayıpları
𝒑=
𝚫𝑷
𝑷
=
𝟑.𝑹.𝑰𝟐
=
𝟑.𝑼.𝑰.𝒄𝒐𝒔𝝋
𝟑.𝑹.𝑰
𝟑.𝑼.𝒄𝒐𝒔𝝋
=
𝟑.𝑹
𝑷
𝟑.𝑼.𝒄𝒐𝒔𝝋
𝟑.𝑼.𝒄𝒐𝒔𝝋
𝑹
𝒑 = 𝑷 ∙ 𝑼𝟐 .𝒄𝒐𝒔𝟐 𝝋
• İletim kayıplarının azaltılabilmesi için iletken direnci düşürülür, gerilim arttırılır ve güç katsayısı
yükseltilir.
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
3
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
• İletim kayıplarının azaltılabilmesi için
𝒍
 İletken direnci (𝑹 = 𝒌.𝑺) düşürülebilir,
 Güç katsayısı (𝒄𝒐𝒔𝝋) yükseltilebilir.
 Gerilim arttırılabilir (𝑼)
• Direnci düşürmek için iletkenin kesiti (𝑺) arttırılabilir.
Hattın uzunluğu sabit olduğunda bu durum uygun gibi görünse de iletkenin ağırlığını arttıracak,
daha büyük ve dayanıklı direklerin tasarımını gerektirecek ve dolayısıyla daha fazla maliyet
getirecektir.
• Güç katsayısını (𝒄𝒐𝒔𝝋) yükseltmek belli bir aralıkta yapılabilir. Güç katsayısını yükseltmek
kompanzasyon gerektirdiği için ek bir maliyet getirecektir.
• En uygun yol gerilimin arttırılmasıdır. Gerilimin arttırılmasıyla beraber bakır kayıpları (𝑰𝟐 . 𝑹) azalır.
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
4
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
• Bir iletim hattının gerçek eşdeğer devresinde hat sabitlerinin parametreleri hat
aralığı üzerinde eşit dağıldığı varsayılır.
• Bu yüzden, uzun bir iletim hattı eşdeğer devresi şekildeki gibi çizilebilir.
𝑹′ : İletim hattının birim uzunluğunun direnci (Ω/km)
𝑳: İletim hattının self indüktansı (H/km)
𝑪′ : Birim uzunluk kapasitansı (F/km)
𝑮′ : Birim uzunluk kaçak iletkenliği (S/km)
Uzun iletim hattının eş değer
devresi
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
5
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
Hattın kayıpsız olduğu kabul edildiği durumda
Bu durumda dalga (karakteristik) empedansı
𝒁 = 𝒋𝝎. 𝑳′ . 𝒍 ve
𝒁𝒐 =
𝑳′
𝑪′
=
𝒀 = 𝒋𝝎. 𝑪′ . 𝒍
𝑳
𝑪
Dalga empedansı, rezonans, yıldırım ve anahtarlama olaylarından kaynaklanan yürüyen dalgaya
karşı bir direnç elemanı gibi davranan empedanstır.
Yürüyen dalganın hızı (hem gerilim hem de akım dalgası) ışık hızına eşittir ve aşağıdaki ifade ile
hesaplanabilir.
𝒗=
𝟏
𝑳′ .𝑪′
(Dalga yayılım hızı)
Bu hız, kablolarda kablonun yalıtkanının dielektrik sabitine bağlıdır ve yaklaşık olarak ışık hızının
yarısıdır.
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
6
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
• Herhangi bir iletim hattı, karakteristik empedans değerine eşit bir omik yük ile yüklenmesi durumunda
hat sonundan yürüyen dalga yansıması olmaz ve kayıpsız olarak yük tarafına geçer. Bu durumda hattın
yükü Dalga Empedans Yükü(SIL:Surge Impedance Load) olarak verilir.
• SIL değeri aynı zamanda hattın yüklenebilirlik değerini de göstermektedir. SIL değeri aynı zamanda
Doğal Güç olarak da ifade edilmektedir. Doğal gücün değerini belirleyen gerilimin seviyedir. Bu
durumda güç iletiminde reaktif güç bulunmamaktadır.
𝑺𝑰𝑳 =
𝑼𝟐
𝒁𝑪
=
𝟑.𝑼𝟐𝑭
𝒁𝑪
• İletim hatları genellikle doğal güç ile yüklü değildir.
• Eğer 𝑫𝒐ğ𝒂𝒍 𝒈üç > İ𝒍𝒆𝒕𝒊𝒍𝒆𝒏 𝒈üç ise gerilim arttırılır. Bu durumda ek olarak
indüktans gereklidir.
• 𝑷𝟎 (Doğal güç) üç faz gücüdür.
𝑼
𝟑
𝑷𝟎 = 𝟑. 𝑹𝟎 . 𝑰𝟐 = 𝟑. 𝑹𝟎 . ( 𝑹 )𝟐
𝑼𝟐
𝑷𝟎 = 𝑹
𝟎
𝑶
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
7
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
Örnek: 𝑼 = 𝟑𝟖𝟎𝒌𝑽’luk tek devre (ikili demet) 𝟗𝟓𝟒𝑴𝑪𝑴 (cardinal) iletkenli bir enerji iletim
hattının yerden yüksekliği 𝒉 = 𝟑𝟏, 𝟕𝟓𝒎’dir.
a) Hattın karakteristik (dalga) empedansını hesaplayınız.
b) Hattın doğal gücünü bulunuz.
c) Hat doğal güç ile yüklendiğinde hattan geçen akımı, iletim kayıplarını ve
reaktif gücünü bulunuz.
d) Hattı doğal güç ile yüklemek için hattın sonuna bağlanacak elemanın
değerini hesaplayınız.
 Hat uzunluğu 𝒍 = 𝟓𝟎𝟎𝒌𝒎,
Öz iletkenlik 𝒌 = 𝟑𝟏, 𝟓𝟔𝒎/𝛀. 𝒎𝒎𝟐
 Işık Hızı
𝒗 = 𝟑. 𝟏𝟎𝟖 𝒎/𝒔
 Boşluğun dielektrik sabiti
𝜺𝟎 = 𝟖, 𝟖𝟓𝟒. 𝟏𝟎−𝟏𝟐 𝑭/𝒎
 Havanın bağıl dielektrik sabiti
𝜺𝒓 = 𝟏
 954MCM Cardinal iletkenine ait özellikler
– 𝒓 = 𝒊𝒍𝒆𝒕𝒌𝒆𝒏 𝒚𝒂𝒓𝚤ç𝒂𝒑𝚤 = 𝟏𝟓, 𝟐𝟏𝒎𝒎
– 𝒉 = 𝒚ü𝒌𝒔𝒆𝒌𝒍𝒊𝒌 (𝒎𝒎)
– 𝑻𝒐𝒑𝒍𝒂𝒎 𝑲𝒆𝒔𝒊𝒕 = 𝟓𝟒𝟕, 𝟑𝟒𝒎𝒎𝟐
𝟐.𝝅.𝜺
 Hattın birim uzunluğunun kapasitansı (𝑪′ ) 𝑪′ = 𝟐.𝒉 [𝑭/𝒎]
𝒍𝒏( 𝒓 )
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
8
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
a) Hattın birim uzunluğunun kapasitansı
𝟐.𝝅.𝜺
′
𝑪 =
𝒍𝒏(
𝟐.𝒉
)
𝒓
=
𝟐.𝝅.𝟏.𝟖,𝟖𝟓𝟒.𝟏𝟎−𝟏𝟐
𝟐.𝟑𝟏𝟕𝟓𝟎
𝒍𝒏(
)
𝟏𝟓,𝟐𝟏
−𝟏𝟐
𝑪′ = 𝟔, 𝟔𝟕𝟑. 𝟏𝟎
𝑭/𝒎
𝑪′ = 𝟔, 𝟔𝟕𝟑 𝒑𝑭/𝒎
Hattın karakteristik empedansı
𝒁𝑪 =
𝑳′
𝑪′
=
𝑳
𝑪
bağıntısından elde edilir. Bu formulde hattın
birim uzunluğunun endüktansı bilinmelidir. Dalga yayılım hızı
𝟏
𝒗=
𝟏
𝑳′ .𝑪′
formülünden
hattın
birim
endüktansı yalnız bırakılıp 𝑳′ = 𝒗𝟐 .𝑪′ denklemde yerine konularak;
𝒁𝑪 =
𝟏
𝑳′ .𝑪′
𝑪′
=
𝟏
𝒗𝟐 .𝑪
𝟏
′𝟐
𝟏
= 𝒗.𝑪′ = 𝟑.𝟏𝟎𝟖 .𝟔,𝟔𝟕.𝟏𝟎−𝟏𝟐 = 𝟒𝟗𝟗, 𝟓𝟐𝟓𝛀
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
9
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
b) Hattın gerilimi 𝑼 = 𝟑𝟖𝟎𝒌𝑽 = 𝟑𝟖𝟎𝟎𝟎𝟎𝑽 ve karakteristik empedansı 𝒁𝑪 ≅ 𝒁𝒐 = 𝟒𝟗𝟗, 𝟓𝟐𝟓𝛀 olduğuna
göre hattın doğal gücü,
𝑷𝒐 =
𝑼𝟐
𝒁𝒐
=
𝟑𝟖𝟎𝟎𝟎𝟎𝟐
𝟒𝟗𝟗,𝟓𝟐𝟓
= 𝟐𝟖𝟗, 𝟎𝟕𝟓. 𝟏𝟎𝟔 𝑾 = 𝟐𝟖𝟗, 𝟎𝟕𝟓𝑴𝑾
c) Doğal güç faz ile yıldız noktası arasına 𝒁𝒐 değerinde omik yük bağlandığındaki toplam güçtür.
𝑰=
𝑼/ 𝟑
𝒁𝒐
veya
𝑰=
𝑷𝒐
𝟑.𝑼.𝒄𝒐𝒔𝝋
Hatta doğal güç kullanıldığında reaktif güç çekilmediğinden hattın sonuna sadece omik direnç bağlı
olur. Bu durumda 𝒄𝒐𝒔𝝋 = 𝟏 olarak alınır.
𝑰=
𝑼/ 𝟑
𝒁𝒐
=
𝟑𝟖𝟎𝟎𝟎𝟎/ 𝟑
𝟒𝟗𝟗,𝟓𝟐𝟓
= 𝟒𝟑𝟗, 𝟐𝟎𝟑𝑨
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
10
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
Hat iletkenlerinin omik direnci ile ortaya çıkan ve iletkenlerdeki iletim kayıplarının toplamına eşit olan
toplam iletim kaybı
∆𝑷 = 𝟑. 𝑹. 𝑰𝟐 ile hesaplanır.
𝒍
𝑹 = 𝒌.𝑺
∆𝑷 =
𝒍
𝟑. 𝒌.𝑺 . 𝑰𝟐
=
𝟓𝟎𝟎.𝟏𝟎𝟑
𝟑. 𝟑𝟏,𝟓𝟔.𝟓𝟒𝟕,𝟑𝟒 . 𝟒𝟑𝟗, 𝟐𝟎𝟑𝟐
∆𝑷 = 𝟏𝟔, 𝟕𝟓𝟎. 𝟏𝟎𝟔 𝑾 = 𝟏𝟔, 𝟕𝟓𝑴𝑾
d) Hattın doğal güç ile yüklenmesi için hattın sonuna hattın dalga empedansına eşit değerde bir
empedans bağlanması gerekir.
𝒁𝒐 = 𝟒𝟗𝟗, 𝟓𝟐𝟓𝛀
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
11
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
Örnek: Üç fazlı bir iletim hattının uzunluğu 𝟒𝟎𝟎𝒌𝒎 dir. Hattın anma gerilim 𝟐𝟐𝟎𝒌𝑽 ve hattın
parametreleri 𝑹 = 𝟎, 𝟏𝜴/𝒌𝒎, 𝑳 = 𝟏, 𝟐𝟔𝒎𝑯/𝒌𝒎, 𝑪 = 𝟎, 𝟎𝟎𝟗𝝁𝑭/𝒌𝒎 ve 𝑮 = 𝟎 olduğuna göre,
a) Hattın dalga empedansını
b) Hattın direncini ihmal ederek dalganın yayılma hızını hesaplayınız. Dalganın hattın bir ucundan
diğer ucuna gidiş süresini bulunuz.
𝑳′
𝑪′
𝟏,𝟐𝟔.𝟏𝟎−𝟑
𝟗.𝟏𝟎−𝟗
Hattın dalga empedansı
𝒁𝟎 =
Dalga yayılım hızı
𝒗=
Dalganın bir uçtan bir uca
𝒕 = 𝒗 = 𝟐𝟗𝟔𝟗𝟓𝟕𝒌𝒎/𝒔 = 𝟏, 𝟑𝟒𝟕. 𝟏𝟎−𝟑 𝒔
𝟏
𝑳′ .𝑪′
𝒍
=
=
= 𝟑𝟕𝟒, 𝟏𝟔𝟔𝜴
𝟏
𝟏,𝟐𝟔.𝟏𝟎−𝟑 .𝟗.𝟏𝟎−𝟗
= 𝟐𝟗𝟔𝟗𝟓𝟕𝒌𝒎/𝒔
𝟒𝟎𝟎𝒌𝒎
𝒕 = 𝟏, 𝟑𝟒𝟕𝒎𝒔
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
12
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
Örnek: Güç faktörü 𝒄𝒐𝒔𝝋 = 𝟎, 𝟖𝟓 olmak üzere maksimum 𝟏𝟎𝟎𝑴𝑽𝑨’lık bir güç iletimi için tesis edilen enerji
sisteminde iletim hattından maksimum 𝟒𝟎𝟎𝑨 akım çekilebilmektedir. İletim hattının uzunluğu 𝒍 = 𝟒𝟎𝟎𝒌𝒎
olup kullanılan iletkenin öz iletkenliği 𝒌 = 𝟑𝟓𝒎/𝜴𝒎𝒎𝟐 ve akım yoğunluğu 𝒋 = 𝟎, 𝟓𝑨/𝒎𝒎𝟐 ’dir.
a) Bu iletim sisteminin gerilimini belirleyiniz.
b) İletim hattındaki kayıp gücü bulunuz.
c) Standart gerilim için kayıp gücü hesaplayınız.
a) Enerji iletimi üç fazlı olarak yapıldığından görünür güç denklemi 𝑺 = 𝟑. 𝑼. 𝑰 ifadesinden devre
gerilimi
𝑼=
𝑺
𝟑.𝑰
=
𝟏𝟎𝟎.𝟏𝟎𝟔
𝟑.𝟒𝟎𝟎
= 𝟏𝟒𝟒, 𝟑𝟑𝟕𝒌𝑽
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
13
YÜKSEK GERİLİM ENERJİ NAKİL HATLARI
b) İletim hattında kullanılan iletkenin kesiti (𝑺) , akım yoğunluğu (𝑱) ile akım (𝑰) arasındaki ilişkiden
yararlanılarak hesaplanır.
𝑰
𝑰
𝟒𝟎𝟎
𝟎,𝟓
= 𝟖𝟎𝟎𝒎𝒎𝟐
Akım yoğunluğu
𝑱=𝑺 ⟹ 𝑺=𝑱=
Omik direncin değeri
𝑹 = 𝒌.𝑺 =
Üç fazlı devre için güç kaybı
∆𝑷 = 𝟑. 𝑹. 𝑰𝟐 = 𝟑. 𝟏𝟎, 𝟕𝟏𝟒. 𝟒𝟎𝟎𝟐 = 𝟓𝟏𝟒𝟐𝟕𝟐𝟎𝑾
∆𝑷 = 𝟓, 𝟏𝟒𝟑𝑴𝑾
𝒍
𝟑𝟎𝟎.𝟏𝟎𝟑
𝟑𝟓.𝟖𝟎𝟎
= 𝟏𝟎, 𝟕𝟏𝟒𝜴
c) Standart gerilim seviyesi 𝑼 = 𝟏𝟓𝟒𝒌𝑽 olarak alınırsa,
𝑺
𝟑.𝑼
𝟏𝟎𝟎.𝟏𝟎𝟔
𝟑.𝟏𝟓𝟒.𝟏𝟎𝟑
Yeni devre akımı
𝑰=
Akım yoğunluğu
𝑱=𝑺 ⟹ 𝑺=𝑱=
=
𝑰
𝒍
𝒌.𝑺
𝑰
𝟑𝟎𝟎.𝟏𝟎𝟑
𝟑𝟓.𝟕𝟒𝟗,𝟖𝟎𝟔
= 𝟑𝟕𝟒, 𝟗𝟎𝟑𝑨
𝟑𝟕𝟒,𝟗𝟎𝟑
𝟎,𝟓
= 𝟕𝟒𝟗, 𝟖𝟎𝟔𝒎𝒎𝟐
Omik direncin değeri
𝑹=
Üç fazlı devre için güç kaybı
∆𝑷 = 𝟑. 𝑹. 𝑰𝟐 = 𝟑. 𝟏𝟏, 𝟒𝟑𝟐. 𝟑𝟕𝟒, 𝟗𝟎𝟑𝟐 = 𝟒𝟖𝟐𝟎𝟑𝟖𝟎𝑾
∆𝑷 = 𝟒, 𝟖𝟐𝑴𝑾
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
=
= 𝟏𝟏, 𝟒𝟑𝟐𝜴
14
KAYNAKLAR
• Prof.Dr. Muzaffer Özkaya, Yüksek Gerilim Tekniği Cilt 1 ve Cilt 2 (Birsen Yayınevi)
• Prof.Dr. Özcan Kalenderli, Yüksek Gerilim Elemanları
• Yrd.Doç.Dr. C.V. BAYSAL Yüksek Gerilim Tekniği Ders Notları
EEM13414 YÜKSEK GERİLİM TEKNİĞİ
15