durgun magnetizma - SABİS

T.C.
SAKARYA ÜNİVERSİTESİ
FEN EDEBİYAT FAKÜLTESİ
FİZİK BÖLÜMÜ
DURGUN MAGNETİZMA
HASAN UTKU
G100202013
Yrd. Doç. Dr. Zemine ZENGİNERLER
ŞEKİL LİSTESİ
Şekil 5.1 Yükler
2
Şekil 5.2 Zıt ve Aynı Yönlü Akımlar
3
Şekil 5.3Telin magnetik alan yönünde kıvrılması
3
Şekil 5.4 Parçacığın bir Hell üzerinde hareket etmesi
4
Şekil 5.5 Elektrik kuvvetinin baskın hale gelmesi
5
Şekil5.6 Akışa paralel uzanmış şerit
9
Şekil 5.7 Akışa paralel uzanmış sonsuz kesitli tüp
10
Şekil 5.8 Kararlı bir I akımı taşıyan tel
13
Şekil 5.9 İki paralel tel arasındaki çekim kuvveti
14
BÖLÜM 5 DURGUN MAGNETİZMA
5.1 Lorentz Kuvvet Yasası
5.1.1 Magnetik Alanlar
Elektrodinamiğin temel problemini anımsayacak olursak bir grup yüke sahibiz q1,q2,q3 …
(‘’kaynak’’ yükleri) ve bunların diğer bir Q yükü(‘’deneme’’yükü) üzerine uyguladığı kuvveti
hesaplamak istiyoruz.Toplanabilirlik ilkesine göre ,tek bir kaynak yükünün kuvvetini bulmak
yeterlidir.Daha sonra toplam tek tek bu kuvvetlerin tümünün vektör toplamıdır.Şu ana kadar
dikkatimizi kaynak yükünün durgun olduğu (ama deneme yükünün durgun olması gerekmez )
en basit hale ,durgun elektriğe yönelmiş durumdaydık.Hareket halindeki yükler arasındaki
kuvvetleri inceleyelim.
.
.Q
.q .
1
.
.q
.
.
.q
2
3
Kaynak Yükleri
Şekil 5.1
Deneme Yükü
Yükler
İnceleyeceğimiz konular arasında nelerin bulunduğuna dair size bir fikir vermek
açısından,şöyle bir gösteri deneyi kurduğunu düşününüz:İki tel ,birkaç santimetre aralıklı
olarak ,tavandan aşağı asılıdır.Tellerden birinden akım yukarı doğru akacak ve diğerinden
aşağı gelecek şekilde bir akımı başlatacak olursam ,teller dışarı açılırlar.Yani birbirini
iterler.Bunu bir örnekle açıklayacak olursak bataryanın telleri yüklediğini ve kuvvetin de
basitçe benzer yüklerin itmesinden kaynaklandığını varsayabiliriz.Ben bu tellerin yakınında
bir deneme yükü tutabilirdim fakat üzerinde hiçbir kuvvet olmazdı,çünkü teller aslında
elektriksel olarak nötrdür.(Telden aşağı elektronların aktığı doğrudur.İşte tam olarak da akım
budur.Fakat verilen herhangi bir parçacık üzerinde ne kadar hareketli negatif yük varsa tam o
kadar da durgun pozitif yükler vardır.) Bundan başka gösteri deneyimi akım her iki telde de
yukarı doğru akacak şekilde bağlayabilirim.
"f t.
.,..
(a)Zıt yönlü akımlar iter.
(b)Aynı yönlü akımlar çeker.
Şekil 5.2 Zıt ve Aynı Yönlü Akımlar
Paralel akımların çekilmesine ve anti paralel akıların itilmesine ne tür kuvvetler sebep olursa
olsun ,onlar durgun elektrik yapıda değildir.Magnetik bir kuvvettir.Durgun bir yük etrafındaki
uzayda yalnızca bir elektrik alan E oluşturduğu halde ,hareketli bir yük buna ek olarak bir
magnetik alan B doğurur.Gerçekte ,magnetik alanların algılanması pratikte çok daha
kolaydır.Ger eksinim duyacağımız tek şey bir izci pusulasıdır.Şimdi,akım taşıyan bir telin
yakınında bir pusulayı tutacak olursak , çok tuhaf bir şey keşfederiz.Alan tele doğru
yönelmemiştir,telden öteye doğru da değildir,fakat daha çok telin etrafında dolanır.Gerçekte
teli sağ elimizle kavrarsak başparmak akımın yönünde olmak üzere başparmaklarımız
magnetik alanın yönünde kıvrılırlar.
)/
Şekil 5.3 Telin magnetik alan yönünde kıvrılması
5.1.2 Magnetik Kuvvetler
Bir B magnetik alanı içinde v hızıyla hareket eden bir Q yükü üzerindeki magnetik kuvvet ,
Fmag=Q(v x B)
(5.1)
İle verilir.Bu lorentz kuvveti yasası olarak bilinir.Elektrik ve magnetik alanların her ikisinin
varlığında,Q üzerindeki net kuvvet ,
F=Q[E+(v x B)]
(5.2)
olurdu.
Örnek 1:
Siklotron Hareketi
Bir yüklü parçacığın bir magnetik alan içindeki ilk örnek hareketi,magnetik kuvvetin merkezcil
ivmeyi sağladığı dairesel bir harekettir.Şekil 5.3 ‘ de düzgün bir magnetik alan sayfanın içine
doğrudur.Q yükü saatin tersi yönde v hızıyla R yarıçaplı bir daire etrafında hareket ederse
,magnetik kuvvet içeriye doğru yönelmiş ve sabit bir QvB büyüklüğündedir.Düzgün dairesel
hareketi sürdürmeye tam yeterlidir:
QvB=m V2 /R veya p=QBR
(5.3)
Burada m parçacığın kütlesi ve p=mv onun momentumudur.Denklemdeki siklotron formülü
olarak bilinir.Çünkü bir siklotrondaki modern parçacık hızlandırıcılarının ilki , bir parçacığın
hareketini tanımlar.O aynı zamanda bir parçacığın momentumunu deneysel olarak bulmak
için basit bir deneysel teknik önerir.Parçacığı bilinen bir magnetik alanın içinden geçiriniz ve
dairesel yörüngesinin yarıçapının ölçünüz.Bu aslında temel parçacıkların momentumlarını
ölçmenin standart yoludur.
Yükün B’ye dik bir düzlemde hareket ettiğini kabul ettik.Parçacık B ‘ ye paralel bir v1 ilave
hızıyla harekete başlarsa,hareketin bu bileşeni magnetik alan tarafından değiştirilmez ve
parçacık bir hells üzerinde hareket eder.
Şekil 5.4
Parçacığın bir Hell üzerinde hareket etmesi
Örnek 2: Sikloid Hareketi
Magnetik alana dik durumda düzgün bir elektrik alanını koyarsak daha yabancı bir yörünge
meydana gelir.Örneğin şekil 5.6 ‘da gösterildiği gibi,B x-yönünde ve E z-yönünde
olsun.Durgun bir parçacık başlangıç noktasından serbest bırakılıyor,hangi yörüngeyi izler?
İlk önce nitel olarak düşünelim.Bşlangıçta parçacık durgundur,bu yüzden magnetik alan
sıfırdır ve elektirik alan parçacığı z yönünde hızlandırır.Parçacık hız kazandıkça ,bir magnetik
kuvvet doğar ve Denklem 5.1’e göre bu kuvvet yükü sağa doğru çeker.Onun daha hızlı
gitmesiyle Fmag ‘da daha kuvvetli hale gelir; sonunda ,bu kuvvet onu geriye y-eksenine doğru
büker.Bu noktada parçacık elektrik kuvvete karşı hareket etmektedir,
Şekil 5.5 Elektrik kuvvetinin baskın hale gelmesi
O nedenle yavaşlamaya başlar.O zaman magnetik kuvvet azalır ve elektrik kuvveti baskın
hale gelir ve yükü şekil 5.6’ daki a noktasında durgun hale getirir.Orada tüm işlem yeniden
başlar,parçacık b noktasına taşınır ve böylece devam eder.
Şimdi incelemeyi nicel olarak yapalım:x yönünde bir kuvvet olmadığından dolayı herhangi bir
t anında parçacığın konumu (0,y(t),z(t)) vektörü ile tanımlanabilir:bu yüzden hız
v=(0 ,y ,z)
olur,burada noktalar zamana göre türevleri göstermektedir.Böylece
x y z
vXB =
0 y z
B 0 0
= Bzy – Byz
elde edilir.Burdan Newto’un ikinci yasasını uygulayarak ,
F= Q ( E+ v X B ) = Q ( Ez + Bzy – Byz)=ma=m(yy+zz)
Veya y ve z bileşenlerini ayrı ayrı işleme sokarak ,
QBz = my, QE-QBy=mz
Uygunluk için,
W=QB/m
(5.4)
Tanımını yapalım.(Bu herhangi bir elektrik alanın yokluğunda parçacığın dönme hareketini
yapacağı siklotron frekansıdır.) O zaman hareket denklemleri ,
Y=wz
z= w(E/B –y)
(5.5)
Şeklini alırlar.Bunların genel çözümü şu şekilde olacaktır.
y(t)=C1.coswt + C2..coswt – (E/B)t+C3
(5.6)
z(t)=C2.coswt –C1.sinwt+C4
(5.7)
Fakat parçacık,(y(0)=z(0)=0) başlangıç noktasından,durgun olarak (y(0)=z(0)=0) başlamıştı ,
bu dört koşul C1,C2,C3 ve C4 sabitlerini belirler.
Y(t)=E/wB (wt-sinwt), z(t)=E/Wb (1-coswt)
(5.8)
Bu şekli ile yanıt fazla aydınlatıcı değildir ,fakat
R=E/Wb
(5.9)
tanımını yapar ve sin2wt+cos2wt =1 trigonometrik özdeşliğinden faydalanarak sinüs ve
kosinüsleri elersek
(y-Rwt)2+ (z-R)2=R2
(5.10)
buluruz.B u merkezi (0,Rwt,R)y- yönünde
v=wR=E/B
(5.11)
hızı ile ilerleyen R yarıçaplı bir dairenin denklemidir.Parçacık,sanki y-ekseni üzerinde v hızıyla
yuvarlanan bir tekerleğin çevresi üzerinde bir nokta imiş gibi hareket eder.Bu yolla
oluşturulan eğri bir sikloid adını alır.Varsayabileceğimiz gibi hareket tümüyle E yönünde bir
hareket olmayıp,ona diktir.
Magnetik kuvvet yasasının (denk 5.1) bir özelliği dikkate değerdir:
Magnetik kuvvet iş yapmaz.
İşi hesaplarsak,Q bir dl=vdt miktarı kadar hareket ettiğinde yapılan iş
dWmag=Fmag.dl =Q(v x B ).vdt= 0
(5.12)
bulunur.Bunun sebebi (vxB )’nin v’ ye dik olması ve dolayısıyla (vxB),v=0 olmasıdır.Magnetik
kuvvetler parçacığın hareket doğrultusunu değiştirebilirler,fakat onu hızlandıramaz veya
yavaşlatamazlar.Magnetik kuvvetlerin iş yapmaması Lorentz kuvvet yasasının doğrudan bir
sonucudur.
5.1.3 Akımlar
Bir teldeki akım bir noktadan birim zamanda geçen yüktür.Tanımlamayla,sola doğru hareket
eden negatif yükler sağa doğru hareket eden pozitif yüklerle aynı sonucu verir.Bu,uygun bir
gerçek olan , hareketli yükleri ilgilendiren olguların hemen hemen tümü yük ile hızın
çarpımına dayanır gerçeğini yansıtır.-Q ile v’nin işaretini değiştirirseniz aynı sonucu elde
edemezsiniz,böylece hangi hareketli yüke sahip olduğunuzun bir önemi yoktur.Uygulamada
genellikle hareketli olanlar negatig-f yüklü elektronlardır.Elektrik akımına zıt yönde.Bunun
yol açtığı önemsiz karışıklıklardan sakınmak için gerçekte bir yüzyıl kadar önce Benjamin
Franklin’in talihsiz kabulünden beri herkesin yaptığı gibi,hareketli olanların pozitif yükler
olduğunu varsayacak olursak;akım saniyede kulon ve Amper (A) cinsinden ölçülür.
1A=1 C/s
(5.13)
Bir tel boyunca v hızıyla giden λ çizgi yükü bir ,
I=λv
(5.14)
akımını oluşturur.Çünkü bir Δt zaman aralığında bir P noktasından , λvΔt yükünü taşıyan bir
vΔt uzunluğu geçer.Akım aslında bir vektördür.
Akım taşıyan bir parça üzerindeki magnetik kuvvet ,açıkça
Fmag=∫ (v xB)dq=∫ (v x B) λ dl= ∫ ( I x B)dl
(5.15)
İle verilir.I ile dl aynı yönde olduğu sürece ,bu ifadeyi
Fmag=ʃ I (dl x B)
(5.16)
şeklinde de yazabiliriz.Tipik olarak ,akım tel boyunca büyüklük olarak sabittir.Ve bu halde I
integralin dışına çıkar:
Fmag= I ʃ (dl x B )
(5.17)
Yük bir yüzey üzerinden aktığında bu akışı şu şekilde tanımlanan K yüzey akımı yoğunluğu ile
açıklarız:Akışa paralel uzanmış(Şekil 5.13) sonsuz küçük dl genişliğinde bir şerit düşünelim.Bu
şeritteki akım dI ise yüzey akımı yoğunluğu
˔
K=dl /dl
(5.18)
İle verilir.K akışa dik birim genişlik başına akımdır.Özel olarak,hareketli yüzey yoğunluğu σ ise
ve hızı ise,
K=σv
(5.19)
Genel olarak, σ ‘ daki veya v’deki değişmeleri yansıtacak şekilde K yüzey üzerinde noktadan
noktaya değişmektedir.Yüzey akımı üzerindeki magnetik kuvvet şu şekilde verilir,
Fmag= ʃ (v x B)ʃ σ da = ʃ (K x B ) da
Şekil 5.6 Akışa paralel uzanmış şerit
(5.20)
Yük akışı üç boyutlu bir bölgenin her yerine dağılmışsa bu akışı şu şekilde tanımlanan J hacim
akım yoğunluğu ile açıklarız.Akışa paralel uzanmış (Şekil 5.14) sonsuz küçük da enine kesitli
bir tüp düşünelim.Bu tüpteki akım dL ise hacim yoğunluğu
J= dL/da
˔
(5.21)
İle verilir.J akışa dik birim yüzey başına akımdır.Hacim yük yoğunluğu (hareketli) ƍ ve hızı v
ise, bu durumda
J= ƍv
(5.22)
O halde hacim akımı üzerindeki magnetik kuvvet
Fmag= ʃ (v x B ) ƍ dτ = ʃ (J x B ) dτ
olur.
Şekil 5.7 Akışa paralel uzanmış sonsuz kesitli tüp
(5.23)
Örnek: (a) Bir I akımı a yarıçaplı dairesel enine kesitli bir telin üzerine düzgün şekilde
dağılmıştır.Hacim yoğunluğu J’ yi bulunuz.
Çözüm: Akışa dik alan ∏r2 ‘ dir. Böylece ,
J= I/ ∏a2
Olacaktır.
(b) Teldeki akım yoğunluğunun eksenden olan uzaklıkla orantılı olduğunu varsayıyoruz,
J = ks (Burada k bir sabittir)
Çözüm: J s ile değiştiği için Denklem 5.25 in integralini almalıyız.Gölgeli kısımdaki (Şekil 5.14)
akım Ja ‘dır ve da = s ds dΦ ile verilir.Böylece
I= ʃ (ks) (s.ds.dΦ)=2∏k ʃ s2 sd = 2∏ka3 /3
Denklem 5.21 ‘ e göre bir S yüzeyinden geçen akım
I= ʃ J.da
˔ = ʃ J.da
(5.24)
olarak yazılabilir.(Nokta çarpım da ‘nın uygun bileşenini almak için uygun bir işlev görür.)
Özelikle ,birim zamandaki bir V hacminden çıkan toplam yük
ʃ J.da = ʃ (▼.J) dτ
ile verilir.Yük korunduğundan dolayı,yüzeyden her ne kadar çıkmışsa içeride geriye kalanların
zararına olarak çıkmış olmalıdır:
ʃ ( ▼.J) dτ= - d/ dt ʃ p.dτ =- ʃ (dp/dt)dτ
(Eksi işareti dışarıya doğru olan bir akışın V içinde kalan yükü azalttığı gerçeğini yansıtır.) Bu
her hacim için geçerli olduğundan dolayı
▼.J= -dp/dt
(5.25)
sonucuna varırız.Bu yerel yük korunumunun kesin matematiksel ifadesidir ve buna süreklilik
denklemi denir.
5.2 Biot Savart Yasası
5.2.1 Kararlı Akımlar
Durağan yükler zamanla sabit elektrik alanlar üretir,durgun elektrik terimi buradan ileri
gelir.Durağan akımlar zaman içinde sabit olan magnetik alanlar üretirler,kararlı akımların
teorisine durgun magnetizma adı verilir.
Kararlı akım deyince ,değişmeksizin ve herhangi bir yerde yük birikmesi olmaksızın sonsuza
dek devam eden bir akışı kastediyorum.Elbette ,uygulamada gerçek bir kararlı akım diye bir
şey yoktur,gerçek bir durağan yük bulunmadığı gibi mesela .Bu anlamda durgun elektrik ve
durgun manyetizma yalnızca ders kitaplarında bulunan yapay dünyaları açıklarlar.Bununlar
beraber ,gerçek dalgalanmalar makul derecede yavaş kaldığı sürece onlar uygun yaklaşımları
temsil ederler.Gerçekte birçok maksat için durgun manyetizma bir saniyede 60 kez yön
değiştiren mesken akımları için çok iyi uygulanır.
Bir kararlı akım bir telde aktığında,akımın büyüklüğü I tel boyunca her yerde aynı
olmalıdır.Aksi halde bir yerde yük biriktiriyor olacaktır ve o bir kararlı akım olmaktan
çıkardı.Aynı nedenle durgun manyetizmada dp/dt=0 ‘ dır.Ve buradan süreklilik denklemi
haline gelir.
▼.v = 0
5.2.2 Kararlı Bir Akımın Magnetik Alanı
Kararlı bir çizgi akımının magnetik alanı Biot-Savart yasasıyla verilir.
B(r)=μ0/4∏ ʃ I x ȓ/ ȓ2 dl= μ0 /4∏ . I ʃ dl x ȓ / ȓ 4
(5.26)
İntegral akımın yolu boyunca akış yönündedir.dl’nin tel boyunca bir uzunluk elemanıdır ve ȓ
her zamanki gibi kaynaktan r noktasına olan vektördür.μ0 sabiti serbest uzayın geçirgenliği
adını alır.
μ0 = 4∏ x 10-7 N/A2
(5.27)
Bu birimler ,B ‘ nin kendisi amper metre başına Newton cinsinden (Lorentz Kuvveti yasasının
gerektirdiği gibi) veya tesla (T) olarak bulunacak şekilde,
1T=1N/(A.m)
(5.28)
Durgun manyetizma için başlangıç noktası olması bakımından,Biot-Savart yasası durgun
elektrikteki Coulomb yasasının oynadığı rolün benzeri bir rol oynar.Gerçekten 1/ ȓ2 bağlılığı
her iki yasada da ortaktır.
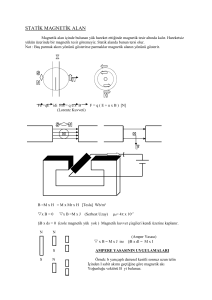
Örnek:Kararlı bi I akımı taşıyan uzun düz bir telden bir S uzaklığındaki magnetik alanı bulunuz.
Çözüm:
Şekil 5.8 Kararlı bir I akımı taşıyan tel
dȊ sin α = dȊ cosθ
Ȋ=s/cos2θ.dθ bulunur ve s= ȓ.cosθ ‘dan da şunu yazabiliriz.
1/ ȓ2 =cos2θ /s2
Böylece ,
B=μ0 .I /4∏ ʃ (cos2θ/s2 ).(s/cos2θ)cosθ.dθ
= μ0 .I ʃ cosθ.dθ=μ0.I/4∏s (sin θ2 – sinθ1)
(5.29)
Denklem 5.29 herhangi bir düz tel parçasının alanını,başlangıç ve son açılar θ 1 ve θ2
cinsinden verir.Elbette sonlu bir parça kendisi asla kararlı bir akım taşıyamaz fakat o kapalı
bir devrenin bir parçası olabilir.O zaman Denklem 5.29 onun toplam alana katkısını temsil
eder.Sonsuz bir tel halinde θ1=- ∏/2 ve θ2 =∏/2 dir.O halde
B= μ0 .I /2∏s
(5.30)
elde ederiz.
Alanın telden olan uzaklığın tersi ile orantılı olduğuna dikkat edecek olursam,benzer şekilde
sonsuz bir yükün elektrik alanda olduğu gibi.Telin aşağısındaki bölgede ,B sayfanın içine
doğru yönelmiştir.
I1
I2
d
(1)
(2)
Şekil 5.9 İki paralel tel arasındaki çekim kuvveti
Bir uygulama olarak I1 ve I2 akımlarını taşıyan d uzaklığı kadar aralıklı iki uzun paralel tel
arasındaki çekim kuvvetini bulalım:
B= μ0 .I / 2∏d
Dir ve sayfanın içine doğrudur.Lorentz kuvveti yasası (1)’e doğru yönelmiş
F=I2(μ0 I1 / 2∏d) ʃ dl
büyüklüğünde bir kuvvet öngörür.Toplam kuvvet,sürpriz olmayacak şekilde sonsuzdur ,fakat
birim uzunluk başına kuvvet şu şekilde verilir.
f = μ0 / 2∏ . I1.I2/d
Akımlar antiparalel ise (biri yukarı diğeri aşağı) kuvvet iticidir.
(5.31)