BÖLÜM 2 ELEKTRON
TEORİSİ
HAZIRLIK ÇALIŞMALARI
1. Madde nedir ve uzayda hangi hâllerde bulunur? Araştırınız.
2. Maddenin en küçük parçasına ne denir ve yapısı nasıldır? Araştırınız.
3. Elektronlar, proton etrafında niçin dönerler? Araştırınız.
4. İletkenlik ve yalıtkanlığın, maddenin atom yapısı ile ilgisini araştırınız.
2.1. MADDENİN YAPISI
Uzayda yer kaplayan ve kütlesi olan her şeye madde denir. Maddenin en kısa tanımı
böyledir. Ancak her madde normal şartlarda katı, sıvı ve gaz hâlinde bulunur ve tüm maddeler
elektrik yükü yönünden nötrdür.
Elektrikle ilgili olayları anlamak için maddenin yapısına ait özellikleri araştırmak gerekir.
Maddeler atom veya moleküllerden oluşur. Her maddenin atom veya molekülü diğer
maddelerden farklı yapıdadır.
Aynı cins atomlardan oluşan maddelere element, ayrı cins moleküllerden oluşan
maddelere bileşik denir. Şekil 2.1'de görüldüğü gibi hidrojen bir elementtir ve hidrojen
atomlarından oluşur. Oksijen de bir elementtir ve oksijen atomlarından oluşur. Su, bir bileşiktir ve
su molekülünden oluşur. Su molekülünün yapısında iki hidrojen ve bir oksijen atomu vardır.
Elementler bölünmek istenen en küçük parçalarında bile kendi özelliklerini taşır. Bileşikler ise
çeşitli ayrıştırma yöntemleri ile elementlere dönüştürülebilir.
Bazı özelliklerinin birbirine benzemesi sebebi ile elementler, metaller ve ametaller olmak
üzere iki esas gruba ayrılır. Yüzeyi parlak olan ve dövülerek işlenebilen elementlere metal
denir. Demir, çinko, bakır metaldir. Yüzeyi parlak olmayan ve dövülerek şekil verilemeyen
elementlere ametal denir. Hidrojen, oksijen, azot, kükürt ametaldir. Bugüne kadar 109 element
bulunmuştur.
2.2. ATOM VE YAPISI
Maddenin, özelliklerini taşıyan en küçük parçasına atom denir. Atomun yapısı henüz bir
mikroskop altında incelenmemekle beraber, kimyasal, fiziksel, elektriksel olaylara karşı gösterdiği
davranışlardan yola çıkılarak, atomun gerçeğe uygun yapısı bulunmuştur. Buna göre atom, küre
şeklindedir. Bu küresel yapı içinde bir çekirdek ve etrafında yörünge hareketi yapan elektronlar
vardır. Çekirdek içinde proton ve nötronlar vardır. Nötronlar yüksüz, protonlar ise pozitif yüklüdür.
Elektronların negatif yüklü olduğu ve proton ve elektronların elektrik yüklerinin birbirini
dengelediği görülmüştür. Bunun sonucu olarak atomun toplam elektrik yükünün normalde sıfır
olduğu ispat edilmiştir.
Şekil 2.2'de karbon atomunun yapısı görülmektedir. Karbon atomunda çekirdekte 6 adet
pozitif yüklü proton, 6 adet yüksüz nötron vardır. Birinci yörünge kabuğunda 2 adet, ikinci
yörünge kabuğunda 4 adet olmak üzere toplam 6 adet negatif yüklü elektron vardır. Her elektron
merkezkaç kuvvete sahiptir. Çekirdekteki protonlar hareketsizdir ve merkezkaç kuvvete sahip
olan elektronları kendine doğru çekerler. Bu yüzden elektronlar bir yörünge etrafında dönmek
zorunda kalır.
Şekil 2.3'te hidrojen atomu ve elektronun hareketi gösterilmiştir.
Bir maddeyi meydana getiren atomlardaki elektron ve proton sayısı eşittir. Protonlar
çekirdekte, elektronlar ise yörünge kabuklarında bulunur ve daima hareket halindedirler. Yörünge
kabukları K, L, M, N, O, P, Q olmak üzere 7 kabuktan oluşur. Tablo 2.1'de kabuklar ve her
kabukta bağımsız yörünge hareketi yapan elektron sayıları verilmiştir.
Tablo 2.1: Atomun yörüngelerinde yer alan toplam elektron sayıları
Kabuk sembolü
K
L
M
N
O
P
Q
En fazla elektron sayısı
2
8
18
32
50
72
98
2.3. SERBEST ELEKTRONLAR
Atomun yapısındaki K kabuğundaki yörüngelerde dönen elektronlar, çekirdeğe en yakın
elektronlardır. Bu elektronların çekirdekle aralarındaki bağ, diğer üst yörünge elektronlarına göre
çok daha kuvvetlidir. Çekirdeğin en az kuvvetle çektiği elektronlar ise atomun son yörüngesindeki
elektronlardır. Çekirdeğe en zayıf kuvvetle bağlı olan bu elektronlara serbest elektron denir.
Serbest elektronlar fiziksel ve kimyasal özelliklere etki eden elektronlardır.
Elektrik akımını ileten serbest elektronların önemi çok büyüktür. Bir devreden akım
geçmesi ve geçen akımın büyüklüğü serbest elektronların çokluğuna bağlıdır.
Bakır atomunun yapısında 29 proton, 34 nötron ve 29 elektron vardır. Bakır atomunun
yapısı ve bakır atomunda serbest elektronların hareketi Şekil 2.4.a'da görülmektedir. Bakır,
elektrikte çok kullanılan iyi bir iletkendir. Bakır atomunun en dış yörüngesindeki 1 elektron
serbest elektrondur. Bu elektronun çekirdekle olan bağı zayıftır. Şekil 2.4.b'de ise bakır
atomunun sadece serbest elektronu çizilerek elektronun diğer yörüngelere geçişi gösterilmiştir.
Serbest elektronlar ısı, ışık, elektrik gibi etkilerle kolayca yörünge değiştirirler.
2.4. İLETKENLER, YALITKANLAR VE YARI İLETKENLER
Elektrikte, elektrik akımını ileten malzemelere iletken, iletmeyen malzemelere yalıtkan,
normal şartlarda iletken olmayan ancak değişik etkilerle iletken hâle geçebilen malzemelere yarı
iletken malzemeler denir.
Maddelerin elektrik akımını iyi iletmesi ya da iletmemesi atom yapılarına bağlıdır. En dış
yörüngesinde 4'ten az serbest elektronu olan maddeler iletken, serbest elektronu 4 olan
maddeler yarı iletken ve serbest elektronu 4'ten fazla olan maddeler yalıtkandır. Bu sıralamadan
anlaşılacağı gibi atomun en dış yörüngesinde serbest elektronları az olanlar çekirdek ve birbiri ile
olan bağları zayıf olduğu ve kolayca yörünge değiştirebildiği için iletken, en dış yörüngesinde
fazla elektron olanların çekirdek ve birbiri ile olan bağları kuvvetli olduğu için yalıtkan
maddelerdir.
İletkenler, elektrikle çalışan her türlü araç, gerecin yapımında, elektrik akımının
iletilmesinde; yalıtkanlar, elektrik akımı geçen tellerin, makine, alet ve cihazların yalıtılmasında;
yarı iletkenler, elektronik elemanların yapımında geniş ölçüde kullanılmaktadır.
Elektrikte kullanılan en iyi iletkenler, altın, gümüş, bakır, alüminyum gibi metallerdir. En
iyi yalıtkanlar ise porselen, PVC, mika, amyant gibi malzemelerdir. Yarı iletken olarak da
genellikle germanyum ve silisyum kullanılır (Şekil 2.5).
BÖLÜM 4
ELEKTRİK AKIMI VE GERİLİM
HAZIRLIK ÇALIŞMALARI
1. Bir elektrik devresindeki elektron hareketini araştırınız.
2. Elektrik akımının şiddetini ölçen aletler devreye nasıl bağlanmalıdır? Araştırınız.
3. Elektrikte potansiyel kelimesi genelde ve elektrikte neyi ifade eder? Araştırınız.
4. EMK ve gerilim arasındaki farkı araştırınız.
5. Volta pilinin yapısını ve ürettiği gerilim değerini araştırınız.
6. Gerilim nasıl ölçülür? Araştırınız.
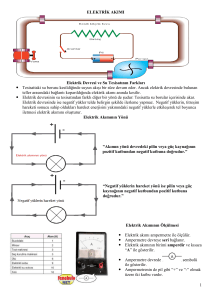
4.1. ELEKTRİK AKIMININ TANIMI
Elektrik akımına kısaca elektron akışı diyebiliriz. Şekil 4.1.a ve b'de üretecin (-)
kutbundaki fazla elektronlar üreteci ampule bağlayan teller içinden ve ampulün teli içinden
geçerek üretecin (+) kutbuna ulaşmaktadır. İnce ve az akımda çabuk ısınan ve ısıya dayanıklı
flâman ışık verir hâle gelinceye kadar kızarır ve ısı enerjisi ışığa dönüşür. Elektrik akımının ışığa
dönüştüğü görünen bir olay olduğu hâlde, iletken içinden akan elektronlar görünmez. Üreteci
ampule bağlayan telin içindeki olaylar ise şekil 4.2'de görülmektedir. Üretecin (-) ucundaki
elektronlar iletken atomlarının serbest elektronlarını harekete geçirir ve bu atomların
yörüngelerini kullanarak ilerlemek suretiyle pilin (+) kutbuna kadar gelirler. Bu açıklama,
görünmeyen bir olayın açıklaması gibi ise de bilimsel bir açıklamadır. Şekil 4.3'te elektronların
iletken içinden akışı gösterilmiştir. Elektrik akımı, bir elektron akışıdır ve elektronların hareket
yönü (-)'den (+)'ya doğrudur. Ancak teknikte elektrik akımının (+)'dan (-)'ye aktığı kabul
edilmiştir. Bu yüzden elektrikle uğraşanlar, elektrik akımının (+)'dan (-)'ye doğru aktığını kabul
ederek yönünü şekil 4.1.b'deki gibi çizerler, elektronikle uğraşanlar daha çok, elektron hareketi
ile ilgilendikleri için elektronların hareket yönünü şekil 4.1.a' daki gibi gösterirler.
4.2. AKIM ŞİDDETİ VE BİRİMLERİ
Bir elektrik devresinden 1 saniyede akan yük miktarına akım şiddeti denir. Eğer bir
devreden 1 saniyede 1 kulonluk elektrik yükü geçiyorsa bu devrenin akım şiddeti 1 amperdir.
•»16
Elektrik yük birimi kulondur ve 1 kulon 624x10 adet elektron yüküne eşittir. Bir elektrik
devresinden belli bir zamanda geçen yük miktarı biliniyorsa bu devredeki akım şiddeti;
Q
I = ------- (amper) formülü ile bulunur.
t
Bu formülde kullanılan ifadeler ve anlamları aşağıda verildiği gibidir: I
: Akım şiddetidir. Birimi amperdir, A ile sembolize edilir. Q : Yük
miktarıdır. Birimi kulondur, C ile sembolize edilir. t : Zamandır.
Birimi saniyedir, s ile sembolize edilir.
Akım şiddetinin as katlan miliamper ve mikroamperdir. Bu birimler genel olarak zayıf
akım tesisleri ve elektronikte kullanılır.
1 amper = 103 miliamper (mA),
1 amper = 106 mikroamper (uA) dir.
Örnek 4.1: Bir elektrik alıcısının çektiği akım 2 amper olarak ölçüldüğüne göre bu
devreden 4 sn içinde geçen yük miktarını ve elektron sayısını bulunuz.
Çözüm
Q = l • t den Q = 2 • 4 = 8 kulon
e = Q • 624 • 1016 = 8.624 • 1016= 4992.1016 elektron
4.3. AKIM YOĞUNLUĞU
Bir elektrik devresinde iletkenin 1 mm2 sinden geçen akım miktarına akım yoğunluğu
denir. Akım Yoğunluğu J ile gösterilir ve birimi A / mm2 dir.
I
j = ------- (A / mm )
S
Bu formülde kullanılan ifadeler ve anlamları şunlardır: J
Akım yoğunluğudur. Birimi A / mm2dir. I Akım
şiddetidir. Birimi A'dır. S İletken kesitidir. Birimi
mm2dir.
4.4. AKIM ŞİDDETİNİN ÖLÇÜLMESİ
Akımı ölçülmek istenen alıcıya seri bağlanmak suretiyle alıcının çektiği akımı ölçen
aletlere ampermetre denir. Alıcının çektiği akım, ampermetre üzerinden geçer ve bu akım, ölçü
aletinin yapısına göre analog veya dijital olarak isimlendirilir. Resim 4.1 .a ve b'de ampermetre
çeşitleri gösterilmiştir.
10
4.5. EMK VE GERİLİM
Bir üretecin boşta ölçülen potansiyel farkına EMK, yükte ölçülen potansiyel farkına
gerilim denir.
Bir üreteç olan pilin Şekil 4.7.a'da görüldüğü gibi alıcı devrede değilken ölçülen
potansiyel farkı yani boştaki potansiyel farkı, Şekil 4.7.b'deki bağlantıda ise alıcı devrede iken
yani yükteki potansiyel farkıdır. Bu iki ölçme arasında fark vardır. Boşta ölçülen değer, yükte
ölçülen değerden daha büyüktür. Bir kaynağın uçları arasındaki potansiyel fark yüksüz durumda
EMK (E), yüklü durumda gerilim (U) olarak adlandırılır. Her ikisinin de birimi volttur. EMK
üreteçlerin ürettiği enerjinin potansiyel farkını ifade ederken kullanılır. Örneğin, elektromotor
kuvveti 1,5 volt olan pil denilince yüksüz durumda 1,5 volt üreten pil anlaşılır.
4.5.1. Gerilimin tanımı
Gerilim, elektrik akımını meydana getiren kuvvettir. Bir elektrik devresinde iki nokta
arasında potansiyel fark varsa bu iki nokta arasında bulunan elemanlardan elektrik akımı geçer.
Bu durumu şekil 4.8'de görülen su sistemine benzetebiliriz. Burada A deposu yüksektedir ve
içindeki su yüksek potansiyel enerjiye sahiptir. B deposu alçaktadır ve içindeki su alçak
potansiyel enerjiye sahiptir. Depolar arası suyun akış yönü A'dan B'ye doğru olur.
15
Şekil 4.9'da ise sıvı pilin çinko elektrotu elektron almakta olup elektronları arttığı için (-),
bakır elektrot ise elektron vermekte olup elektron kaybettiği için (+) ile ifade edilerek bu iki
elektrot arasında elektron farkı, su örneğine benzer şekilde bir potansiyel fark yaratır. Bu iki
elektrot arasındaki elektron seviyesi farkına gerilim denir. Elektrotlar arasındaki potansiyel
farktan dolayı lâmba üzerinden geçen akım,lambanın ışık vermesini sağlar.
Genel anlamda bir elektrik devresinde gerilimi,devre üzerindeki iki nokta arasındaki
potansiyel fark olarak tanımlayabiliriz.
Şekil 4.9: Çinko klorür asidi içine daldırılan çinko ve bakır elektrotlar arasında
potansiyel farkı oluşumu, bu yüzden geçen elektrik akımı ve lâmbanın yanması
4.5.2. Gerilimin birimleri
Elektrik enerjisi üreteçleri, belli bir gerilim üretmek üzere yapılır. Her elektrik alıcısı da
belli bir gerilimde çalışacak şekilde yapılır. Bu yüzden bir elektrik alıcısı, yapıldığı gerilime uygun
gerilim üreten, bir üretece bağlanarak çalıştırılmalıdır.
Gerilim birimi volttur. Gerilim U ile birimi V ile gösterilir. Örneğin, 220 voltu tanımlamak
için; U = 220 volt yazılır.
Bir elektrik devresinde üzerinden 1 amper akım geçen 1 ohmluk direncin iki ucu
arasındaki gerilim 1 volttur denir.
Gerilim birimi olarak genelde volt (V) kullanılır. Yüksek gerilimler için kilovolt (kV),
düşük gerilimler için milivolt (mV) birimleri de kullanılır.
1 kilovolt = 103 volt, 1
milivolt = 10'3 volttur.
4.6. GERİLİMİN ÖLÇÜLMESİ
Gerilim ölçen aletlere voltmetre denir. Voltmetreler üzerinden geçen akımla doğru
orantılı olarak bağlandığı iki nokta arasındaki gerilim değerini gösteren aletlerdir.
Voltmetreler bağlandıkları iki nokta arasındaki gerilim değerini analog veya dijital olarak
gösterecek şekilde yapılır. Resim 4.3'te çeşitli yapıda voltmetreler görülmektedir.
16
5.1. DİRENCİN TANIMI
Direnç, bir etkiye karşı koyma kuvveti anlamını taşır. Elektrikte; elektrik akımının
geçmesine gösterilen zorluğa direnç denir.
Örneğin; evimizde 100 vvattlık lâmba 0,45 amper çekerken, ütümüz 3 ampere yakın akım
çeker. 100 vvattlık lâmba içinden geçen akımı 0,45 amperde sınırlarken ütü 3 amperde sınırlar.
Bu onların dirençlerinin farklı olduğunu gösterir. Direnci fazla olan lâmbadan az akım, direnci az
olan ütüden fazla akım geçer.
Ohm kanununa göre bir alıcının uçlarındaki gerilimin akıma bölümü (U /1) sabittir ve R
ile ifade edilir. R, ohm cinsinden o alıcının direncidir.
Ohm kanuna göre direncin tanımı:
Bir elektrik devresinden 1 voltluk gerilim altında 1 amperlik akım geçmesine sebeb
olan alıcının direnci 1 ohm'dur.
Standart 1 ohm'luk direnç, civaya göre tanımlanmıştır. 106,3 cm uzunluğunda ve 1 mm2
kesitinde, O °C [Celsius(selsiyus)]'taki civanın direncine 1 ohm denir.
5.2. DİRENÇ BİRİMLERİ
Direnç birimi ohm (n)'dur. Büyük dirençler için kiloohm (ko) ve megaohm (Mn) birimleri
kullanılır.
1 kiloohm (kn) = 103 ohm (n),
1 megaohm (Mn) = 106ohm (n) dur.
5.3. DİRENCİN ÖLÇÜLMESİ
Elektrikte kullanılan elemanların dirençleri çeşitli
metotlara göre ölçülebilir. "Ampermetre-voltmetre"
metodu veya "VVheatstone (Veston) köprüsü" (şekil 5.1)
ile yapılan ölçümler, en çok tercih edilen direnç ölçme
metotlarıdır. "Ampermetre-voltmetre" metodunda UII
oranı direncin değerini verir. "VVheatstone ohmmetresi" ile
yapılan ölçümde ise direnç değeri;
R2
Rx = R! --------- (Q) formülü ile hesaplanır.
R3
21
BÖLÜM 6
DOĞRU VE ALTERNATİF AKIM
HAZIRLIK ÇALIŞMALARI
1. Evinizde kullanılan doğru veya alternatif akım elektrikli cihazların cinsini araştırınız.
2. Doğru ve alternatif akım nedir? Araştırınız.
3. Doğru ve alternatif akımın kullanım alanlarını araştırınız.
4. Elektrik akımının etkilerini araştırınız.
6.1. DOĞRU AKIM VE ÖZELLİĞİ
Elektrik enerjisi çeşitli yollar ile elde edilir. En çok alternatif akım üretimi olduğu ve
alternatif akımın geniş bir kullanım alanı olduğu bir gerçektir. Ancak doğru gerilimin de kullanım
alanları fazladır ve bu gerilimi elde etmek için çeşitli üreteç ve doğrultmaçlar kullanılmaktadır.
Zamana göre yönü ve şiddeti değişmeyen akıma doğru akım denir. Doğru akım elektroliz
işlerinde, kaplamacılıkta, haberleşmede, ses ve görüntü cihazlarında, tramvay gibi taşıt araçlarında, hassas devir ayarı gerektiren makinelerde kullanılır. İstenen güç genellikle çok fazla
olmaz ve kaynak olarak alternatif akımı djpğru akıma çeviren doğrultmaçlar kullanılır. Dinamo, pil
ve akümülâtörler de küçük güçlerin kaîpanmasmda oldukça yaygın olarak kullanılır.
I
(akım, A)
Şekil 6.1'deki gibi bir devrenin çektiği akımın eğrisi Grafik 6.1'de gösterilmiştir. Devreye
tatbik edilen doğru gerilimdir ve bu gerilimden dolayı geçen doğru akım Grafik 6.1 .b'deki gibi
zamana göre hiç değişmemektedir. Devre 3 amper çekmektedir ve zamana göre çektiği akım her
zaman 3 amperdir ve yönü değişmez.
6.2. ALTERNATİF AKIM
Alternatif akım, zamana göre yönü ve şiddeti periyodik olarak değişen akımdır.
33
6.2.2. Değişim eğrisi
Şekil 6.2'deki alternatif akım devresinden geçen akımın eğrisi Grafik 6.2'deki gibi bir
sinüs eğrisidir.
I
Grafik 6.2: Alternatif akım eğrisi
6.2.3. Saykıl (periyot), frekans, dalga boyu tanımı
Alternatif akımın, "O" dan başlayan, (+) yönde maksimum, "O", (-) yönde maksimum ve
"O" oluncaya kadar Grafik 6.2'deki gibi çizilen sinüs eğrisine 1 saykıl (periyot) denir.
Alternatif akımın saniyedeki saykıl sayısına frekans denir. Birimi hertz (herz), saykıl/sn
veya periyot/sn'dir.
Sinüzoidal olarak değişen alternatif akımın bir eğrisinin metre olarak boyuna dalga boyu
denir. Bu tanım daha çok radyo ve televizyon yayın bantlarının tanımında kullanılır.
34
BÖLÜM 8
ELEKTRİĞİN TEMEL KANUNLARI
8.1. OHM KANUNU
Alman bilim adamı George Simon Ohm (Corc Saymın Om)
basit bir elektrik devresinde yaptığı deneyler sonucu akım, gerilim ve
direnç arasındaki ilişkileri ispat etmiştir.
Şekil 8.1'de görülen basit bir elektrik devresinde devre
gerilimi U ile gösterilir ve birimi volttur. Devre akımı I ile gösterilir ve
birimi amperdir. Devre direnci R ile gösterilir ve birimi ohm'dur.
Ohm kanununa göre bir elektrik devresinde gerilimin akıma
bölümü sabittir ve buna direnç denir.
Devre gerilimi artırılırsa akım da aynı oranda artmaktadır.
Direnç birimi Georg Simon Ohm'a izafeten ohm (om) olarak ifade
edilir, (n) harfi ile sembolize edilir.
Üzerinden 1 amper geçen ve uçlarındaki gerilim 1 volt olan direncin değeri 1 ohm'dur.
Ohm kanununu ispat etmek için iki deney yapılır.
8.1.1. Akımın gerilime göre değişmesi ve deneyi
Şekil 8.2'de ayarlı gerilim kaynağı ile çeşitli kademelerde gerilim ve akım değerleri
alınır. Alınan değerler bir tabloya yazılır (Tablo 8.1).
Tablo 8.1: Gerilim, akım ve direnç değerleri
I
Grafik 8.2: Ohm kanununa göre akımın dirence göre değişim eğrisi
Grafik 8.2'deki eğriden; bir elektrik devresinde direnç artırıldığı zaman akımın azaldığı ve
bu azalmanın dirençteki artma oranı kadar olduğu görülüyor.
Bu iki deneyden alınan sonuçlara göre Ohm kanunu şöyle tanımlanır: Bir elektrik
devresinden geçen akım (I), gerilim ( U ) ile doğru, direnç ( R ) ile ters orantılıdır.
Ohm kanununa göre devreden geçen akımın formülü;
I = U / R olur. Bu
formülden faydalanarak
R = U/I ve U = I • R formülleri elde edilir.
Bir elektrik devresinde bilinmeyen akım, gerilim ve direnç değerleri bu formüllerden
faydalanılarak bulunur.
Örnek 8.1: 220 voltluk kaynağa bağlanan ve direnci 40 ohm olan elektrik ocağından
geçen akımı bulunuz.
8.2. KİRCHHOFF (KİRŞOF) KANUNLARI
Alman fizikçi Kirchhoff un birinci Kirchhoff ve ikinci Kirchhoff olmak üzere iki elektrik
kanunu, seri, paralel ve karışık devre çözümlerini kolaylaştırmış, bilinmeyen akım ve gerilimlerin
kolaylıkla bulunması sağlanmıştır.
8.2.1. Kirchhoff un birinci kanunu (akımlar kanunu)
Elektrik devrelerinde bir düğüm noktasına gelen akımların toplamı, bu düğüm
noktasından giden akımların toplamına eşittir.
I = I1 + I2+I3+............ + !„
Şekil 8.4'te çizilen devrede A düğüm
noktasına gelen I akımı bu düğüm noktasından
ayrılan I,, I2,13 akımlarının toplamına eşittir.
I^It + 1,+ 13
Aynı devrenin B düğüm noktası için ise;
B düğüm noktasına gelen
Iı, I2,13 akımlarının toplamı bu düğüm
noktasından giden I akımına eşittir.
Iı+I2+I3 = I yazılır.
47
Paralel devrelerde Kirchhoff un akımlar kanunundan faydalanılarak bilinmeyen akımlar
bulanabilir.
Ölçülen I akım değeri 15 amper ve hesaplanan değere eşit olduğuna göre yapılan
ölçümler doğrudur.
Örnek 8.6: Şekil 8.4'teki paralel devrede I = 12 A, Iı = 3 A
ölçülmüştür. I2 akımını bulunuz.
ve I 3 - l A olarak
Çözüm
I = Iı + I2+I3 den I2 = I-(Iı+I3)
I2=12-(3 + l)
I2 = 8 A olarak bulunur.
8.2.2. Kirchhoff'un ikinci kanunu (gerilimler kanunu)
Seri bağlı elemanlardan oluşan kapalı bir elektrik devresinde kaynak gerilimlerin
toplamı, devredeki elemanlar üzerinde düşen gerilimlerin toplamına eşittir.
Şekil 8.5: A ve B noktaları arasına bağlı gerilini kaynağının ürettiği
gerilim ve bu gerilimin dirençler tarafından paylaşımı
Şekil 8.5'te R1f R2, R3 dirençleri seri bağlanarak ( U ) gerilimi üreten kaynak tarafından
beslenmektedir.
Kaynak gerilimi dirençler tarafından U1f U2, U3 olarak paylaşılmaktadır. A-B noktaları
arasına bağlı kaynağın ürettiği gerilim ( U ), dirençler üzerinde düşen gerilimlerin toplamına
eşittir.
U = U, + U2 + U3
Kirchhoffun ikinci (gerilimler) kanunundan faydalanarak seri devrelerde bilinmeyen
gerilimi bulmak mümkündür.
BÖLÜM 9
JOULE (JUL) KANUNU VE UYGULAMASI
9.1. ELEKTRİK AKIMININ ISI ENERJİSİNE DÖNÜŞÜMÜ
Isının insan hayatındaki önemi tartışılmaz. Isınmak, pişirmek, kaynatmak gibi önemli
işlerin yapılabilmesi için ısı enerjisi gerekir.
En büyük ısı kaynağı güneştir. Bu doğal ısı kaynağı dünyadaki canlılarında hayat
kaynağıdır. Güneş enerjisinin verdiği ısının dışında çeşitli yollar ile ısı enerjisi elde etmek
mümkündür. Isı enerjisi atomların parçalanması, yakıtların yakılması ile elde edildiği gibi elektrik
enerjisinden de elde edilebilir. Bu yolla elde edilen ısı enerjisi, pratik, kolay ve artıksız olduğu için
birçok alanda tercih edilir. Evlerimizde kullanılan ütü, fırın, ocak ve soba gibi ısı cihazları evimizin
vazgeçilmez birer aracı olmuştur.
Elektrikli ısıtıcılar genelde içinden akım geçen tel ısınır prensibine göre çalışır. Bunun
i dışında Foucoult (fuko) akımları, mağnetik ve kapasitif yüksek frekanslı ısıtıcılarda kullanılır.
9.2. JOULE KANUNUNUN TANIMLANMASI VE FORMÜLLERİ
Joule kanunu: İçinden akım geçen tel ısınır, meydana gelen ısı enerjisinin miktarı,
lakımın karesi, iletkenin direnci ve akımın geçiş süresi ile doğru orantılıdır.
Şekil9.1'de bir elektrik ocağı üzerine konan kap içinde bir miktar su ısıtılmaya
aşlanmıştır. Suyun ilk sıcaklığı 25° C'tur. Şekil 9.2'de bir süre sonra suyun sıcaklığının 75° C'a
ılaştığı görülüyor. Elektrik ocağının verdiği ısı enerjisi, suyu ısıtmıştır.
Elektrik ocağının ısıtıcı tellerinden geçen elektrik akımının meydana getirdiği ısı enerjisi
oule kanuna göre bulunur;
69
W = I 2 - R - t joule olur.
Formülde;
W, birimi "joule" olan ısı enerjisini,
I, ocağın çektiği akımı,
R, ocağın ısıtıcı tellerinin direncini,
t, saniye olarak ısıtma işlemi için geçen zamanı ifade eder.
Yukarıdaki formülde P = 12 • R formülüne göre I 2 • R yerine P konursa W =
P • t (joule) olarak ısı enerjisi bulunabilir.
Bu formülde P = U • I formülüne göre P yerine U • I yazılabilir, bu durumda ısı
enerjisi:
W = U it (joule) olur.
Bir ısıtma işinde 1 joulelük ısı enerjisi 0,239 veya yaklaşık olarak 0,24 kalorilik ısı miktarı
üretir. Belli bir zaman içinde yapılan ısıtma işinde kaç kalorilik ısı üretildiği ise;
Q = 0,24 ' W (kalori) formülü ile bulunur. W yerine, eşiti olan yukarıdaki
formüllerdeki değerleri yazılarak üretilen ısı miktarı;
Q = 0,24-I 2 -R-1 (kalori)
Q = 0,24 • P • t (kalori)
Q = 0,24 • U • I • t (kalori) olarak bulunabilir.
Bu formüllerden hangisinin kullanılacağı verilen değerlere bağlıdır. Bu eşitliklerden
faydalanarak bilinmeyen değerler bulunabilir.
9.3. MADDELERİN ISITILMASI
Maddeleri belli bir sıcaklıktan daha yüksek bir sıcaklığa getirmek için ne kadar ısı
verileceği, ısının kaç derece yükseltilmek istendiği, maddenin miktarı ve maddenin ısınma ısısına
bağlı olarak değişir. Verilmesi gereken ısı miktarı maddenin miktarı,yükseltilmek istenen sıcaklık
ve maddenin ısınma ısısı ile doğru orantılıdır. Bir maddenin sıcaklığını t, sıcaklığından t2
sıcaklığına getirmek için gerekli ısı miktarı;
Q = m ' c • (t2-tt) kalori formülü ile bulunur.
Bu formülde;
Q, ısı miktarı,
m, madde miktarı (gram),
c, ısınma ısısı (cal/gr),
(t2-t.,), son ve ilk sıcaklık farkı (derece) dir.
70
Maddeler; katı, sıvı veya gaz hâlinde bulunur ve bir durumdan diğerine geçebilir.
Maddenin bir durumdan diğerine geçebilmesi için ısı alması veya ısı kaybetmesi gerekir.
Dönüşüm katıdan sıvıya, sıvıdan gaz hâline doğrudur. Madde/er ısındıkça sıcaklıkları artar.
Bu artış verilen kalori miktarı ile doğru orantılıdır. Ancak sıcaklıktaki artış maddenin cinsi
ile ilgilidir. Aynı kaloriyi aldıkları hâlde sıcaklıklarındaki artış farklı olur.
Şekil 9.3'te 1 kg suyun 1 kW gücündeki bir ocakta 1 dakika ısıtılması sonucu, suyun
sıcaklığının 25° C'tan 35° C'a çıktığı, Şekil 9.4'te ise 1 kg yağın 1 kW gücündeki ocakta 1 dakika
ısıtıldığında sıcaklığının 25° C'tan 45° C'a çıktığı görülmektedir. Su ve yağa aynı güçteki ocaklar
ile aynı ısı verildiği hâlde yağ daha çok ısınmış, sıcaklığı daha fazla artmıştır.
Her maddenin yapısına bağlı olarak değişen bu özellik, ısınma ısısının farklı oluşundan
kaynaklanmaktadır.
Isınma ısısı : 1 gram maddenin sıcaklığını 1 derece arttırmak için verilmesi gereken ısı
miktarına o maddenin ısınma ısısı denir.
Isınma ısısı birimi kalori/gram (cal/gr) dır ve c ile gösterilir.
Suyun ısınma ısısı "1"dir. Çeşitli maddelerin ısınma ısıları da Tablo 9.1'de gösterilmiştir.
Tablo 9.1: Maddelerin ısınma ısısı
Maddenin cinsi
Alkol (etil)
Alüminyum
Bakır
Buz
Su
Cam
Isınma ısısı
(Cal/gr)
0,59
0,21
0,093
0,5
1
0,14
Maddenin cinsi
Civa
Demir
Çelik
Kalay
Kurşun
Platin
Isınma ısısı
(Cal/gr)
0,033
0,11
0,15
0,060
0,032
0,032
Bir ısıtma işleminde belli bir sıcaklığa yükseltilmek istenen maddenin ne kadar ısı alması
gerektiği;
Q = m c (t 2 -tı) formülü ile bulunur.
71
BÖLÜM 10
DOĞRU VE ALTERNATİF AKIMDA İŞ VE GÜÇ
10.1. MEKANİKTE İŞ, ENERJİ VE GÜÇ TANIMI VE BİRİMLERİ
Bir cismin uygulanan kuvvet doğrultusunda hareket ederek yol almasına iş denir.
Mekanikte iş formülü:
İş = kuvvet - yol W
=F-l
Tablo 10.1: Mekanikte kuvvet, yol ve iş birimleri
Kuvvet (F)
newton (N)
dyne
kg . kuvvet (kg)
Yol ( l )
metre (m)
santimetre (cm)
metre (m)
İş (W)
joule
erg
kgm
10.2. İŞ BİRİMLERİNİN BİRBİRİNE DÖNÜŞTÜRÜLMESİ
1 joule = 107 erg.
1 kgm = 9,8 joule = 10 joule
İş, devam eden bir olayı ifade eder.
Bir cisim bir kuvvet tarafından hareketlendirilmiş ve kuvvet doğrultusunda hareket
ediyorsa iş devam ediyor demektir.
Bir asansör, içine binen insanları zemin kattan 10. kata çıkarana kadar bir iş yapıyor
demektir. İnsanlar 10. kata geldiğinde asansörü bekletseler bile yapılan iş bitmiştir.
Bir insan pazar çantasını taşımak için onu kaldırması anında çantayı h yüksekliğine
kaldırana kadar iş yapar. Kaldırdığı anda iş bitmiştir.
İnsan çantayı kaldırmış vaziyette duruyorsa ya da çantayı hiç hareket ettirmeden
taşıyorsa iş devam etmiyor demektir.
İş yapabilme kabiliyetine enerji denir.
Enerji ve iş birbirine çok yakın kavramlar olduğu için her an karıştırılabilir. Enerji ile iş
arasındaki fark; enerjinin durumu, işin ise olayı göstermesidir.
74
Mekanik enerji iki durumda olabilir:
1. Kinetik enerji: Hareket enerjisi
2. Potansiyel enerji: Durgun enerji olarak ifade edilir.
Barajlarda su tribününden oldukça yukarıda duran su, potansiyel enerjiye sahiptir. Su
yolları açılıp hareketlenince, kinetik enerji kazanır ve tribünü döndürerek iş yapar. Tribün,
alternatörü döndürür ve mekanik enerji elektrik enerjisine çevrilir (Resim 10.1). Elektrik enerjisi
insanlar tarafından ısı, ışık enerjisine dönüştürülerek kullanılır
Resim 10.1: Barajda elektrik enerjisinin üretilmesi
Enerji birimi jouledür. Kinetik enerji;
1
Ek = -------- m • v 2
2
joule
m, kütle (kg) v, hız
(m/sn) dır.
Potansiyel enerji;
Ep = m.g.h (joule)
Bu formülde; m, kütle
(kg), g, yerçekimi
(m/sn2), h, yükseklik (m)
tir.
Belli bir zaman diliminde yapılan işe güç denir.
W
P = ----------
formülü ile bulunur.
t
75
Tablo 10.2: İş, güç ve zamanın değişik sistemlerdeki birimleri
Sembol
MKS
CGS
P (güç)
W (iş)
t (zaman)
watt (W)
joule
sn
erg / sn
erg
sn
Beygir
Gücü
HP
Mekanik
kgm /s
kgnı
sn
10.3. MEKANİK İŞİN ELEKTRİK İŞ VE GÜCÜNE DÖNÜŞTÜRÜLMESİ
Elektrikte iş birimi olarak joule ve güç birimi olarak watt kullanılır. Motor güçleri beygir
gücü olarak verilebilir.
Mekanikteki iş ve güç birimlerinin elektrik iş ve gücüne çevrilmesi Tablo 10.3'teki gibidir.
Tablo 10.3: Mekanikteki iş ve gücün elektrik iş ve gücüne dönüştürülmesi
Mekanik iş
1 kgnı
Mekanik güç
75 kgnı / sn
75 kgm / sn
Elektrik işi
9,8 joule
Elektrik gücü
1HP
0,736 kW
Motor güçlerinin beygir gücü olarak verilmesi durumunda wattlı güce, vvattlı güç olarak
verilmesi durumunda beygir gücüne dönüştürülmesi için;
1HP = 0,736 kW veya 1 HP = 736 W eşitlikleri kullanılır.
Örnek 10.1: 50 kg'lık kuvvetle itilen otomobili 20 m ileri götüren insan ne kadar joule'lük
iş yapmış olur?
Çözüm
W = 50 • 20 = 1000 kgm
W = 1000 • 9,8 = 9800 joule
Örnek 10.2: 75 kgm'lik mekanik iş kaç joule elektrik işi eder? Bu işi 1 sn de yapan
makinenin gücü nedir?
Çözüm
1 kgm ^
75 kg
_, 9,8 joule
ederse
"" ^ X X = 9,8 x
75 = 736 joule
W
736
P = ----------- = ------------- = 736 watt
t
1
Örnek 10.3: 250 kgm/sn gücünde bir su pompasını çeviren elektrik motorunun gücü ne
olmalıdır?
76
Çözüm
75 kgm/sn
-,
,- 736 W ederse
~><
250 kgm/sn --''
\X
250 x 736
X = ----------- — = 2453 watt
75
10.4. DOĞRU AKIMDA (D.A.) GÜÇ VE BİRİMLER
Aydınlatma ve ısıtma gibi diğer alıcılar için "watt" veya "kilowatt" birimleri kullanılır. Doğru
akımla çalışan elektrik alıcılarının güçleri ifade edilirken bunların yanı sıra "HP" birimi de
kullanılır.
Alıcılar doğru akım üretecinden çektiği enerjiyi işe çevirir. Alıcı ısıtıcı ise ısı işi,
aydınlatma ise aydınlatma işi, motor ise mekanik iş elde edilir.
Alıcıların birim zamanda yaptıkları işe ise güç denir.
Doğru akımda alıcıların güçleri; üreteç gerilimi ve akımı ile doğru orantılıdır.
t;. •
P = U • I watt olarak gücü verir. Güç formülünde
U yerine I • R yazılırsa güç; P = I - R - I = I2 -R
watt olur.
P = U • I formülünde I yerine U / R yazılırsa doğru akımda bilinen değerlere göre her
üç formülden güç bulunabilir.
U
U2
P = U • -------- = --------- (watt) olarak bulunur.
R
R
Bu formüllerde;
P, güç (W),
U, volt (V),
l, amper (A),
R, direnç (ohm) birimleri kullanılırsa sonuç watt olarak bulunur.
Güç biriminin üskatları ve askatları:
Üskatları:
1 megawatt ( MW) = 1 Q6 watt ( W)
1 kilowatt (kW) = 103 watt (W)
Askatları :
1 miliwatt ( mW) = 10~3 watt (W)
1 mikrowatt ( ^W) = 1 o"6 watt (W)
Buna göre aşağıdaki eşitliklerde yazılabilir:
-6
1 watt = 10 megavvatt
-3
1 watt = 10 kiloavvatt
3
1 watt = 10 milivvatt
-6
1 watt = 10 mikrovvatt
77
10.5. ALTERNATİF AKIMDA (AA) GÜÇ VE BİRİMLER
Alternatif akımda bir fazlı ve üç fazlı sistemler bulunmakta olup bu sistemlerde güç
hesabı ayrı ayrı incelenecektir.
10.5.1. Bir fazlı alternatif akımda güç
Doğru akımda sadece omik direnç vardır ve R ile ifade edilir. Ancak AA dirençleri omik
direnç (R), endüktif direnç (XL) ve kapasitif direnç (Xc) olmak üzere üç değişik alıcı tipi vardır.
AA'da çalışan alıcılar direnç yapılarının özelliği ile anılır ve dirençleri bakımından üç tip alıcı
vardır:
1. Omik alıcı
2. Endüktif alıcı
3. Kapasitif alıcı
1. Omik alıcılar
Bir fazlı AA omik alıcıları için güç formülleri; DA güç formülleri ile aynıdır ve
P=U-I
watt olarak hesaplanır.
2. Endüktif alıcılar
AA'da motor gibi bobinleri olan alıcıların (endüktif alıcılar) güçleri hesaplanırken güç
faktörünün dikkate alınması gerekir. Güç faktörü coş cp ile gösterilir ve her alıcıya göre O ile 1
arasında değişen bir değeri vardır. Güç; aşağıdaki formül ile hesaplanır.
P = U • I • coş 9 (watt)
3. Kapasitif alıcılar
Yapısında ve devrelerinde kondansatör olan alıcılardır. Bu alıcılarda da güç faktörünün
dikkate alınması gerekir. Güç; aşağıdaki formül ile hesaplanır.
P = U • I • coş <p (watt)
10.5.2. Üç fazlı AA'da güç
Üç fazlı alıcılar genelde omik (ısıtıcılar, aydınlatma vb.), endüktif (motorlar, endüksiyon
fırınları vb.) kapasitif (kondansatörlü motorlar vb.) alıcılardır.
Üç fazlı omik alıcılarda güç
Akkor telli lâmba, elektrik sobası gibi yapısında bobin ve kondansatör bulundurmayan
devrelerin harcadığı güçtür.
P =V3 • U • I (watt) formülü ile bulunur.
Üç fazlı endüktif alıcılarda güç
Röle, transformatör ve alternatif akım motorları gibi yapısında bobin bulunduran alıcıların
harcadıkları güçtür.
P =\/3 • U • I • coş <p (watt) formülü ile bulunur.
78
10.5.3. Aktif, reaktif ve görünür güçler
Alternatif akımda alıcının cinsine göre harcadıkları güçler aktif, reaktif ve görünür güçler
olarak da sınıflandırılır. Çünkü alternatif akımda omik, endüktif ve kapasitif özelliklerine göre
alıcılar aktif güçlerinin yanı sıra reaktif güç de harcarlar. Omik alıcıların harcadıkları güce aktif
güç, endüktif ve kapasitif yüklerin harcadıkları güce ise reaktif güç denir. Aktif ve reaktif güçlerin
vektörel toplamı alıcının görünür gücünü verir. Transformatör ve alternatör gibi bazı alıcılar
görünür güçleri ile bilinir. Aktif ve reaktif güçler ayrı sayaçlarla ölçülür. Her iki güç için de ayrı ayrı
ücret ödenir. Burada iş yapan güç aktif güçtür. Reaktif güçten dolayı harcanan enerji, enerji
hatlarının boşuna yüklenmesine ve işletmelerin gereksiz ücret ödemelerine neden olur. Bu
kaybın önlenmesi için reaktif gücü yok edecek ya da minimuma indirecek kompanzasyon
devreleri kurulur. Kompanzasyon devreleri; güç kat sayısı anlamına gelen coş 9' nin 1 olması ya
da 1' e yaklaştırılmasın! sağlayan devrelerdir.
Bu güçler aşağıdaki formüller ile ifade edilir.
Aktif güç için P = U • I • coş 9 (watt)
Reaktif güç için Q = U • I • sin 9 VAR ("volt amper reaktif kısaltması)
Görünür güç için S = U • I VA ("volt amper" kısaltması)
10.6. GÜÇ PROBLEMLERİ
1. 9 V'luk bir pil devresine bağlanan lâmba 0,55 A akım çekmektedir. Lâmbanın gücünü
hesaplayınız.
Çözüm
P = U • I formülünden;
P = 9- 0,5 = 4,5 W bulunur.
2. 1000 vvattlık bir elektrikli ütünün 200 volt gerilimde çekeceği akım şiddetini
hesaplayınız.
Çözüm
P = U • I formülünden;
1 = P/U = 1000/200 = 5 A bulunur.
3. 120 V gerilimde 3 amper akım çeken bir fazlı motorun güç kat sayısı 0,75'tir. Bu
motorun gücünü hesaplayınız.
Çözüm
P = U • I • coş cp formülünden;
P= 120-3-0,75 P = 231 W
bulunur.
79
10.7. ELEKTRİK AKIMININ İŞE ÇEVRİLMESİ
Elektrik almaçları kaynaktan çektikleri akım ile bir iş yaparlar. Yaptıkları işin çeşitli elektrik enerjisi
olarak karşılığı, alıcının çektiği akım miktarı ve gerilim ile doğru orantılıdır. Bilindiği gibi elektrik
yük miktarı kulon olup Q ile ifade edilir. Buna göre;
W = U • Q ile bulunur. Q = I • t
olduğundan Q yerine I • t konursa;
W = U • I • t watt saniye (Wsn) olarak iş bulunabilir.
Elektrik işi Şekil 10.1'deki bağlantı ile hesaplanabilir.
Şekil 10.1'deki lâmbanın çektiği akım ve lâmbaya verilen gerilim ölçülür ve lâmbanın
devrede kalma süresi saniye olarak kronometreden ölçülürse lâmbanın yaptığı iş;
W = U • I • t (Wsn) formülü ile bulunabilir.
Elektrik işi; gerilim, akım ve zamanla doğru orantılıdır.
1 mekanik iş = 1 elektrik iş 1
Nm = 1 VVsn'dir.
10.8. ELEKTRİK İŞİNİN SAYAÇLA ÖLÇÜLMESİ
Elektrik enerjisi elektrik santrallerinde üretilir ve abonelere satılır. Aboneler, kullandıkları
elektrik enerjisi miktarı kadar ücret öderler. Kullanılan elektrik enerjisini (elektrik işini) watt saat
(Wh) ve kilovvatt saat (kvVh) cinsinde ölçen aletlere de elektrik sayacı denir. Sayaçlar müşterilerin
harcadığı elektrik enerjisini veya elektrikle yapılan işi ölçer.
Gücü 1 kW olan alıcı, 1 saat çalıştığında sayaç, yapılan işi 1 kWh olarak gösterir.
Sayaçlar, bu ölçmeyi yaparken devrenin akımı ve gerilimi çarpımı kadar bir kuvvetle dönen
disklerine dişliler ile bağlı numaratörü çevirerek yapar.
Elektrikteki iş formülü W = U • I • t formülünde U . I yerine P konularak güç ve zamanın
çarpımı olarak aşağıdaki gibi belirtilebilir:
W=P-t
81
Bu formülde kullanılan ifadeler ve anlamları:
P : Alıcıların gücü (watt)
W : Elektrik işi (kWh)
U : Alıcılara uygulanan gerilim (volt)
l : Alıcıların çektiği akım (amper)
t : Alıcıların çalışma süresi (saat)
Formülden de anlaşılacağı gibi Wh, bir vvattlık, kWh ise bir kilowatt'lık bir elektrik
cihazının bir saatte sarf ettiği elektrik işidir. Aşağıda bir fazlı indüksiyon sayacının devreye
bağlantı şeması görülmektedir (Şekil 10.2).
0,88- 25.000 = 22.000TL bulunur.
~>v
v
10.9. VERİM (RANDIMAN) VE HESAPLANMASI
Elektrik enerjisinin mekanik enerjiye veya mekanik enerjinin elektrik enerjisine dönüşümü
[sırasında birtakım kayıplar oluşur. Bu kayıpların sebep olduğu güce kayıp güç (P«) denir.
Bu sebeple hiçbir zaman verilen güç, alınan güce eşit olmaz. Alman gücün verilen güce
(oranına verim denir.
% 100 verimli bir makine yapılmamıştır. Alınan güç (P/0, verilen güç (Pv) ve kayıp güç
\) olmak üzere kayıp güç ve verim aşağıdaki formüllerle belirtilebilir:
l
PK
Î|
= PV-PA
= PA/(PA+PK)
« = ------ —
Pv
10.10. MAKSİMUM GÜÇ TEOREMİ
Kapalı bir elektrik devresinde, üretecin alıcıya en büyük gücü verebilmesi için üretecin iç
direnci ile alıcının iç dirençleri birbirine eşit olmalıdır. Üretecin maksimum güç verdiği anda verim
yaklaşık olarak % 50'ye düştüğü için bu uygulama kuvvetli akım sistemlerinde kullanılmaz. Fakat
zayıf akım sistemlerinde kullanılır. Devre dirençli bir devre olduğu için akımla gerilim arasında faz
farkı "O" ve güç kat sayısı "1" dir.
Bu devrede R = r olduğundan alıcıdan geçen akım şiddeti (I) için;
E
I =
formülü yazılabilir.
2•R
Ohm kanununa göre U = I • R olduğundan akım şiddeti (I ) yerine yukarıdaki formül
konulacak olursa alıcıya uygulanan gerilim için;
E
U = -------.R
E
U = ------
2-R
bulunur.
2
Güç formülü P = U • I olduğundan akım şiddeti (I) ve gerilim (U) yerine yukarıdaki
formüller konulacak olursa alıcının harcadığı veya üreteçten verilen maksimum güç (PM) için;
E
PM = -------2
E
• -----2-R
PM
E2
= ------4-R
84
PM
E-I
= -----2
formülleri yazılabilir.