EEM211 ELEKTRİK DEVRELERİ-I
Prof. Dr. Selçuk YILDIRIM
Siirt Üniversitesi
Elektrik-Elektronik Mühendisliği
Kaynak (Ders Kitabı):
Fundamentals of Electric Circuits
Charles K. Alexander
Matthew N.O. Sadiku
McGraw Hill, 5th edition
ISBN: 978-0073380575, 2013.
2. Bölüm: Temel Kanunlar
2.1 Giriş
1. Bölümde, akım, gerilim ve güç gibi temel kavramlardan
bahsedilmişti. Verilen bir devrede bu değerleri bulmak için bazı temel
kanunları bilmek gerekir. Bu kanunlar, Ohm kanunu ve Kirchhoff kanunlarıdır.
2.2 Ohm Kanunu
• Malzemeler genelde, elektrik yükünün akışını engelleme şeklinde bir
karakteristik davranışa sahiptirler. Bu fiziksel özellik veya yetenek, direnç
olarak bilinir ve R sembolü ile gösterilir.
• A kesit alanına sahip herhangi bir malzemenin direnci, A kesiti ile 𝑙
uzunluğuna bağlıdır.
• Direnci matematiksel şekilde, 𝑅 = 𝜌
𝑙
𝐴
olarak gösterebiliriz.
• Burada, 𝜌 ohm-metre cinsinden malzemenin öz direnci olarak bilinir.
12.10.2015
2
• Tablo 2.1’de bazı genel malzemeler için 𝜌 değerleri verilmiştir ve hangi
malzemelerin iletkenler, yalıtkanlar ve yarı iletkenler için kullanıldığı
gösterilmiştir.
Bazı malzemelerin öz dirençleri:
12.10.2015
3
• Direnç, en basit pasif elemandır.
• Şekil 2.1’de direnç ve direncin devre sembolü verilmiştir.
• Ohm Kanunu: Bir direncin uçlarındaki 𝑣 gerilimi, dirençten
geçen 𝑖 akımıyla doğru orantılıdır.
𝑣 ∝𝑖
• Matematiksel şekilde Ohm Kanunu;
𝑣=𝑖𝑅
olarak tanımlanır.
• Bir elemanın direnci; elektrik akımının
akışını engelleme yeteneği olarak
tanımlanır ve ohm (Ω) ile ölçülür.
𝑅=
𝑣
𝑖
12.10.2015
ve 1 Ω = 1 V/A ’dir.
4
• Akım akışı yüksek potansiyelden düşük
potansiyele doğru olduğunda,
𝑣=𝑖𝑅
olur.
• Eğer akım düşük potansiyelden yüksek
potansiyele doğru akarsa,
𝑣 = −𝑖 𝑅 olur.
• 𝑅 = 0 olan bir eleman kısa devre
olarak isimlendirilir.
𝑣 = 𝑖 𝑅 = 0 olur.
(Akım herhangi bir değer olabilir, gerilim sıfırdır.)
• Bir kısa devre, direnci sıfıra yaklaşan
bir devre elemanıdır. (Şekil2.2a).
• 𝑅 = ∞ olan bir eleman açık devre
olarak bilinir. Açık devre için,
𝑣
𝑖 = lim = 0
olur.
𝑅→∞ 𝑅
(Gerilim herhangi bir değer olabilir, akım sıfırdır.)
• Bir açık devre, direnci sonsuza yaklaşan
bir devre elemanıdır. (Şekil2.2b).
12.10.2015
5
• Bir direnç sabit veya değişken olabilir.
• Şekil 2.3’de iki sabit direnç türü gösterilmiştir.
a) Tel sarımlı direnç, b) karbon film direnç
• Değişken dirençler ayarlanabilen dirençlerdir.
• Şekil 2.4a)’da değişken bir direnç sembolü
gösterilmiştir.
• Şekil2.4b)’deki değişken bir direnç genellikle
potansiyometre veya kısaca pot olarak bilinir.
12.10.2015
6
• Potansiyometre, hareketli bir kontağı bulunan üç uçlu
bir elemandır.
• Şekil 2.5’te pot örnekleri verilmiştir.
• Şekil 2.6’da bir
görülmektedir.
12.10.2015
devre
kartındaki
dirençler
7
• Bütün dirençler Ohm kanununu sağlamazlar.
• Lineer direnç Ohm kanununu sağlar.
Şekil 2.7a)’da gösterildiği gibi akım-gerilim
karakteristiği lineerdir ve direnci sabittir.
• Nonlineer direnç Ohm kanununu
sağlamaz.
Şekil 2.7b)’de akım-gerilim karakteristiği
gösterildiği gibi direnci akımla değişir.
• Ampül ve diyot, nonlineer (doğrusal
olmayan) dirençlere örnek olarak
gösterilebilir.
12.10.2015
8
• R direncinin tersi, iletkenlik olarak isimlendirilir ve devre
analizinde kullanılan faydalı bir büyüklüktür.
• İletkenlik G ile gösterilir:
1 𝑖
𝐺= =
𝑅 𝑣
• İletkenlik, bir elemanın elektrik akımını ne kadar iyi ilettiğinin
ölçüsüdür.
• İletkenliğin birimi siemes (S) veya mho (℧) ’dur.
1 S = 1℧ = 1 A/V
• İletkenlik, bir elemanın elektrik akımını iletme yeteneğidir.
• Aynı direnç, ohm veya siemens cinsinden ifade edilebilir.
• Örnek olarak, 10 Ω ile 0.1 S aynıdır.
𝑖 = 𝐺𝑣
şeklinde yazılabilir.
12.10.2015
9
• Bir direnç tarafından harcanan güç 𝑅 cinsinden,
2
𝑣
𝑝 = 𝑣𝑖 = 𝑖 2 𝑅 =
𝑅
• Bir direnç tarafından harcanan güç 𝐺 cinsinden ,
2
𝑖
𝑝 = 𝑣𝑖 = 𝑣 2 𝐺 =
𝐺
şeklinde ifade edilebilir.
Bu denklemleri şöyle yorumlayabiliriz:
1. Bir dirençte harcanan güç, hem akımın hem de gerilimin
nonlineer bir fonksiyonudur.
2. Direnç (𝑅) ve iletkenlik (𝐺) pozitif büyüklükler
olduğundan, bir dirençte harcanan güç her zaman
pozitiftir.
Böylece, direnç daima devreden güç çeker.
12.10.2015
10
Örnek 2.1: Bir elektrikli ütü 120 V’da 2 A akım çekmektedir.
Direncini bulunuz.
Çözüm: Ohm kanunundan,
𝑣 120
𝑅= =
= 60 Ω
𝑖
2
Ödev 2.1: Bir tost makinesinin temel bileşeni (rezistans),
elektrik enerjisini ısı enerjisine dönüştüren elektriksel bir
elemandır. Buna göre, 15 Ω ’luk bir rezistansı olan bir tost
makinesi 110 V ’da ne kadar akım çeker? (7.333 A)
Ödev 2.2: Şekil 2.9’daki
devrede, 𝑣 gerilimini,
𝐺 iletkenliğini ve
𝑝 gücünü hesaplayınız.
30 V, 100 µ𝑠, 90 mW
12.10.2015
11
Örnek 2.2: Şekil 2.8’de gösterilen devrede 𝑖 akımını, 𝐺
iletkenliğini ve 𝑝 gücünü hesaplayınız.
Çözüm: Direnç ve gerilim kaynağı aynı uçlara bağlandığından,
dirençteki gerilim düşümü gerilim kaynağı kadar olur. Burada
akım,
𝑣
30
𝑖= =
= 6 mA
3
𝑅 5 x 10
İletkenlik,
𝐺=
1
𝑅
=
1
5 x 103
= 0.2 mS
Güç değişik yollarla hesaplanabilir:
𝑝 = 𝑣𝑖 = 30 6x10−3 = 180 mW
𝑝 = 𝑖 2 𝑅 = (6x10−3 )2 5x103 = 180 mW
𝑝 = 𝑣 2 𝐺 = (30)2 0.2x10−3 = 180 mW
12.10.2015
12
Örnek 2.2: 20𝑠𝑖𝑛𝜋𝑡 V’luk bir gerilim kaynağı,
5 kΩ’luk bir dirence bağlanmıştır. Dirençten geçen
akımı ve harcanan gücü bulunuz.
𝑖=
𝑣
𝑅
=
20𝑠𝑖𝑛𝜋𝑡
5 x 103
= 4𝑠𝑖𝑛𝜋𝑡 mA
Buradan,
𝑝 = 𝑣𝑖 = 80𝑠𝑖𝑛2 𝜋𝑡 mW
Ödev 2.3: Bir direnç 𝑣 = 15𝑐𝑜𝑠𝑡V’luk bir kaynağa
bağlandığında, 30𝑐𝑜𝑠 2 𝑡 mW anlık güç çekmektedir.
𝑖 ve 𝑅 ’yi bulunuz.
(2𝑐𝑜𝑠𝑡 mA, 7.5 kΩ)
12.10.2015
13
2.3 Düğüm, Dal ve Çevre Kavramları
• Bir elektrik devresinin elemanları birbirleriyle çeşitli şekillerde
bağlanabildiğinden dolayı, devre topolojisinin temel kavramlarını
öğrenmemiz gerekir.
• Devre topolojisinde, devredeki elemanların yerleştirilmesiyle ilgili
özellikleri ve devre bağlantılarını inceleyeceğiz.
• Dal; akım kaynağı, gerilim kaynağı veya direnç gibi iki uçlu tek bir
elemanı ifade eder.
• Şekil 2.10 ’daki devrede,
10 V ’luk gerilim kaynağı,
2 A ’lik akım kaynağı ve
3 adet direnç olmak üzere
5 adet dal vardır.
12.10.2015
14
• Düğüm; iki veya daha fazla dalın arasındaki bağlantı noktasıdır.
• Düğüm, bir devrede genellikle bir nokta ile gösterilir. Eğer iki
düğümü bir kısa devre birleştiriyorsa, iki düğüm tek bir düğüm
oluşturur.
• Şekil 2.10’daki devrede, a, b ve c olmak üzere üç düğüm vardır.
• b düğümüne iletken tellerle bağlı olan üç nokta tek bir düğüm
oluşturur. Aynı durum c düğümünü oluşturan dört nokta için de
geçerlidir.
• Şekil 2.10’daki devreyi,
Şekil 2.11’deki gibi sadece
üç düğümle tekrar çizebiliriz.
12.10.2015
15
• Çevre; bir devrede herhangi bir kapalı yoldur.
• Çevre, bir düğümden başlanarak, herhangi bir düğümden
birden fazla geçmeksizin başlangıç düğümüne tekrar
gelinmesiyle oluşturulan kapalı bir yoldur.
• Bir çevre, diğer bir bağımsız çevrede bulunmayan en az bir dalı
içeriyorsa bağımsız çevre olarak isimlendirilir.
• Bağımsız çevreler veya yollar bağımsız denklem sistemleri
oluştururlar.
• Şekil 2.11’de, 2 Ω’luk direnç ile oluşturulan abca çevresi
bağımsızdır.
• 3 Ω’luk direnç ve akım kaynağı ile oluşturulan ikinci bir çevre
bağımsızdır.
• Üçüncü çevre, 2 Ω’luk direnç ile buna paralel bağlı 3 Ω’luk
dirençten oluşur. Bu çevre de bağımsızdır.
• Şekil 2.11’de, üç bağımsız çevre bulunmaktadır.
12.10.2015
16
• 𝑏 adet dal, 𝑛 adet düğüm ve 𝑙 adet bağımsız
çevreden oluşan bir devre için devre topolojisinin
temel teoremi,
𝑏 =𝑙+𝑛−1
• 𝑏 = 5, 𝑛 = 3 ise 𝑙 = 3 olur.
• İki veya daha fazla eleman, sadece bir düğümü
paylaşıyorsa seri bağlıdır ve sonuç olarak aynı akım
geçer.
• İki veya daha fazla eleman, aynı iki düğüme bağlıysa
paralel bağlıdır ve sonuç olarak aynı gerilim
düşümüne sahiptirler.
12.10.2015
17
• Örnek 2.4: Şekil 2.12’deki devrede dal ve düğüm sayısınız bulunuz.
• Çözüm: Devrede 4 eleman bulunduğundan, dört dal vardır:
10 V, 5 Ω, 6 Ω ve 2 A.
• Şekil 2.13’deki devrede bulunan üç düğüm tanımlanmıştır.
• 5 Ω ’luk direnç ile 10 V ’luk gerilim kaynağının her ikisinden aynı
akım geçeceğinden seri bağlıdırlar.
• 6 Ω ’luk direnç ile 2 A ’lik akım kaynağının her ikisi de aynı
düğümlere (2 ve 3 nolu düğümler) bağlandığından paralel
bağlıdırlar.
12.10.2015
18
• Ödev 2.4: Şekil 2.14’deki devrede kaç dal ve düğüm
vardır?
•
•
•
•
•
Cevap:
Devrede 5 dal mevcuttur.
Şekil 2.15’te tanımlandığı gibi 3 düğüm vardır.
1 Ω ’luk ve 2 Ω ’luk dirençler paraleldir.
4 Ω’luk direnç ile 10 V’luk gerilim kaynağı da paraleldir.
12.10.2015
19
2.4 Kirchhoff Kanunları
• Ohm kanunu, devrelerin analizi için tek başına yeterli
değildir. Ohm kanunu ile Kirchhoff’un iki kanunu
birleştirildiğinde elektrik devrelerinin büyük bir kısmı
analiz edilebilir.
• Bu kanunlar;
• Kirchhoff akım kanunu (KAK) ve
• Kirchhoff gerilim kanunu (KGK) olarak bilinir.
• Kirchhoff’un birinci kanunu, bir sistemdeki yüklerin
cebirsel toplamı değişmez, şeklinde bilinen yüklerin
korunumu kanununa dayanır.
• Kirchhoff akım kanunu (KAK): Bir düğüme (veya kapalı
bir sınıra) giren akımların cebirsel toplamı sıfırdır.
12.10.2015
20
•
Kirchhoff akım kanunu (KAK) matematiksel olarak;
𝑁
𝑖𝑛 = 0
𝑛=1
•
şeklinde ifade edilir. Burada 𝑁, düğüme bağlı dal sayısı ve 𝑖𝑛 ise 𝑛. düğüme giren
(veya düğümden çıkan) akımdır.
•
Bu kanuna göre, düğüme giren akımlar pozitif, düğümden çıkan akımlar negatif
veya tam tersi alınabilir.
Kirchhoff akım kanununun ispatı için, bir düğümden akan akımların
•
𝑖𝑘 𝑡 , 𝑘 = 1,2, … , olduğunu kabul edelim. Düğümdeki akımların cebirsel toplamı,
𝑖 𝑇 𝑡 = 𝑖1 𝑡 + 𝑖2 𝑡 + 𝑖3 𝑡 + ⋯
•
Bu denklemin her iki tarafının integralin alırsak,
𝑞𝑇 𝑡 = 𝑞1 𝑡 + 𝑞2 𝑡 + 𝑞3 𝑡 + ⋯
olur. Burada 𝑞𝑘 𝑡 =
•
𝑖𝑘 𝑡 𝑑𝑡 ve 𝑞𝑇 𝑡 =
𝑖 𝑇 𝑡 𝑑𝑡 ’dir.
Ancak elektrik yükünün korunumu kanununa göre, düğümdeki elektrik yüklerinin
cebirsel toplamı değişmez, yani düğüm net yük depolamaz. Böylece,
𝑞𝑘 𝑡 = 0 → 𝑖 𝑇 𝑡 = 0
olur ve Kirchhoff akım kanunu sağlanmış olur.
12.10.2015
21
• Şekil 2.16’daki düğüme Kirchhoff akım kanunu uygulanırsa,
𝑖1 + −𝑖2 + 𝑖3 + 𝑖4 + −𝑖5 = 0
• 𝑖1 , 𝑖3 ve 𝑖4 düğüme giren akımlar,
• 𝑖2 ve 𝑖5 düğümden çıkan akımlardır.
Terimler yeniden düzenlenirse,
𝑖1 + 𝑖3 + 𝑖4 = 𝑖2 + 𝑖5
olur ve Kirchhoff akım kanununun
diğer bir şekli elde edilmiş olur:
• Bir düğüme giren akımların toplamı, düğümden çıkan
akımların toplamına eşittir.
• Kirchhoff akım kanunu kapalı bir
sınıra da uygulanabilir.
• Şekil 2.17’deki devrede görüldüğü gibi,
• Kapalı yüzeye giren toplam akım,
yüzeyden çıkan toplam akıma eşittir.
12.10.2015
22
• Kirchhoff akım kanununun basit bir uygulaması paralel akım
kaynaklarının birleştirilmesidir.
• Birleştirilen akım, ayrı kaynaklar tarafından verilen
akımların cebirsel toplamıdır.
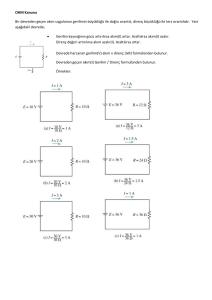
• Örneğin, Şekil 2.18(a)’daki akım kaynakları, Şekil 2.18(b)
’deki gibi birleştirilebilir.
• Birleştirilen (eşdeğer) akım kaynağı,
𝑎 düğümüne Kirchhoff akım kanunu
uygulanarak bulunabilir:
𝐼𝑇 + 𝐼2 = 𝐼1 + 𝐼3 veya
𝐼𝑇 = 𝐼1 − 𝐼2 + 𝐼3
• Akımları 𝐼1 ve 𝐼2 olan iki farklı
akım kaynağı 𝐼1 = 𝐼2
olmadıkça seri bağlanamaz.
12.10.2015
23
• Kirchooff’un ikinci kanunu, enerjinin korunumu prensibine dayanan
Kirchhoff gerilim kanunu (KGK)’dur.
• Kirchhoff gerilim kanunu (KGK): Kapalı bir çevredeki bütün gerilimlerin
cebirsel toplamı sıfırdır.
• Kirchhoff gerilim kanunu (KGK) matematiksel olarak;
𝑀
𝑣𝑚 = 0
𝑚=1
• şeklinde ifade edilir. Burada 𝑀 , çevredeki gerilimlerin sayısı (veya
çevredeki dal sayısı) ve 𝑣𝑚 ise 𝑚. gerilimidir.
• Kirchhoff gerilim kanununu göstermek için Şekil 2.19’daki devreyi göz
önüne alalım. Çevre etrafında gidildiğinde ilk karşılaşılan ucun polaritesi,
her bir gerilimin işareti olarak belirlenir. Herhangi bir daldan başlayarak,
çevre etrafında saat yönünde veya saat yönünün tersinde gidilebilir.
• Şekil 2.19’da gösterildiği gibi gerilim kaynağı
ile başladığımızı ve çevre etrafında saat
yönünde gittiğimizi kabul edelim.
• Örneğin, 3. dala ulaştığımızda karşılaşılan
ilk uç pozitif olduğundan +𝑣3 alırız.
• 4. dala ilk olarak negatif uçtan ulaştığımız
için −𝑣4 alırız.
12.10.2015
24
• Böylece Kirchhoff gerilim kanunundan,
−𝑣1 + 𝑣2 + 𝑣3 − 𝑣4 + 𝑣5 = 0
elde edilir. Terimler yeniden düzenlenirse,
𝑣2 + 𝑣3 + 𝑣5 = 𝑣1 + 𝑣4
olarak elde edilen Kirchhoff gerilim kanunu diğer bir şekilde yorumlanabilir:
Düşen gerilimlerin toplamı = Yükselen gerilimlerin toplamı
• Gerilim kaynakları seri bağlandığında, toplam gerilimi elde etmek için
Kirchhoff gerilim kanunu uygulanabilir. Birleştirilen gerilim, ayrı kaynakların
gerilimlerinin cebirsel toplamıdır.
• Örneğin, Şekil 2.20(a)’da gösterilen gerilim
kaynakları için, Kirchhoff gerilim kanunu
uygulanarak, Şekil 2.20(b) ’deki birleştirilen
(eşdeğer) gerilim kaynağı elde edilir.
−𝑉𝑎𝑏 + 𝑉1 + 𝑉2 − 𝑉3 = 0
veya
𝑉𝑎𝑏 = 𝑉𝑆 = 𝑉1 + 𝑉2 − 𝑉3
• Gerilimleri 𝑉1 ve 𝑉2 olan iki farklı gerilim
kaynağı 𝑉1 = 𝑉2 olmadıkça paralel bağlanamaz.
12.10.2015
25
2.5 Seri Dirençler ve Gerilim Bölme
• Şekil 2.29’daki devrede her iki dirençten de aynı 𝑖 akımı
geçtiğinden dolayı bu dirençler seri bağlıdır.
• Her bir dirence Ohm kanununu uygularsak,
𝑣1 = 𝑖𝑅1 ,
𝑣2 = 𝑖𝑅2
elde ederiz. Devredeki çevreye saat yönünde giderek
Kirchhoff gerilim kanunu uygularsak,
−𝑣 + 𝑣1 + 𝑣2 = 0
olur. Buradan,
𝑣 = 𝑣1 + 𝑣2 = 𝑖(𝑅1 + 𝑅2 )
𝑖=
𝑣
𝑅1 +𝑅2
𝑣 = 𝑖𝑅𝑒ş
𝑅𝑒ş = 𝑅1 + 𝑅2
şeklinde iki direnç bir eşdeğer dirençle gösterilebilir.
12.10.2015
26
2.5 Seri Dirençler ve Gerilim Bölme
• Şekil 2.29’daki devre, Şekil 2.30’daki eşdeğer devre ile gösterilebilir.
Her iki devre, 𝑎 − 𝑏
uçlarında aynı gerilim-akım ilişkisi
gösterdiğinden eşdeğerdir. Eşdeğer devre, bir devrenin analizini
basitleştirdiği için faydalıdır.
• Herhangi bir sayıdaki seri bağlı dirençlerin eşdeğer direnci, ayrı
dirençlerin toplamıdır.
• Seri bağlı 𝑁 direnç için eşdeğer direnç:
𝑅𝑒ş = 𝑅1 + 𝑅2 + ⋯ + 𝑅𝑁 =
𝑁
𝑛=1 𝑅𝑛
Her bir dirençteki gerilim düşümü;
𝑣1 =
𝑅1
𝑣
𝑅1 +𝑅2
ve
𝑣2 =
𝑅2
𝑣
𝑅1 +𝑅2
şeklinde elde edilir.
• 𝑣 kaynak gerilimi, dirençler arasında direnç değerleriyle doğru
orantılı olarak bölünür; büyük dirençte büyük gerilim düşümü olur.
• Buna gerilim bölme kuralı denir ve Şekil 2.29’daki devre gerilim
bölen devre olarak isimlendirilir.
12.10.2015
27
2.6 Paralel Dirençler ve Akım Bölme
• Şekil 2.31’deki devrede iki direnç paralel bağlıdır ve bundan dolayı her
dirençte de aynı gerilim düşümü olur.
• Ohm kanunundan,
𝑣1 = 𝑖1 𝑅1 ,
𝑣2 = 𝑖2 𝑅2
veya
𝑖1 =
𝑣
𝑅1
𝑖2 =
ve
𝑣
𝑅2
yazılır. 𝑎 düğümüne Kirchhoff akım
kanunu uygulanırsa toplam akım,
𝑖 = 𝑖1 + 𝑖2
olur. Buradan,
𝑣
𝑣
1
1
𝑣
𝑖1 =
+
=𝑣
+
=
𝑅1 𝑅2
𝑅1 𝑅2
𝑅𝑒ş
elde edilir. Burada 𝑅𝑒ş paralel bağlı dirençlerin eşdeğer direncidir.
1
𝑅𝑒ş
12.10.2015
=
1
𝑅1
+
1
𝑅2
yazılır ve eşdeğer direnç, 𝑅𝑒ş =
𝑅1 𝑅2
𝑅1 +𝑅2
olur.
28
2.6 Paralel Dirençler ve Akım Bölme
•
•
•
•
Paralel bağlı iki direncin eşdeğer direnci, iki direncin çarpımının toplamına
bölümüne eşittir.
𝑅1 = 𝑅2 ise, 𝑅𝑒ş = 𝑅1 /2 olur.
N sayıda direncin paralel bağlandığı bir devrede eşdeğer direnç,
1
𝑅𝑒ş
=
1
𝑅1
+
1
𝑅2
+ ⋯+
1
𝑅𝑁
•
Genellikle paralel dirençler ile çalışıldığında, dirençten daha çok iletkenlik kullanılır.
•
𝐺𝑒ş = 𝐺1 + 𝐺2 + 𝐺3 + ⋯ + 𝐺𝑁
•
•
Paralel bağlı dirençlerin eşdeğer iletkenliği, ayrı ayrı iletkenliklerinin toplamıdır.
1
1
1
1
1
Burada iletkenlikler; 𝐺𝑒ş = 𝑅 , 𝐺1 = 𝑅 , 𝐺2 = 𝑅 , 𝐺3 = 𝑅 , … , 𝐺𝑁 = 𝑅 ,
•
Paralel bağlı dirençlerin eşdeğer iletkenliği,
seri bağlı dirençlerin eşdeğer direnciyle
aynı yolla elde edilir.
Seri bağlı dirençlerin eşdeğer iletkenliği ise,
paralel bağlı dirençlerin eşdeğer direnciyle
aynı yolla elde edilir.
•
•
𝑒ş
1
𝐺𝑒ş
1
1
1
1
2
3
2
3
𝑁
1
= 𝐺 + 𝐺 + 𝐺 + ⋯+ 𝐺
12.10.2015
1
𝑁
29
2.6 Paralel Dirençler ve Akım Bölme
• Şekil 2.31’deki 𝑎 düğümüne giren toplam 𝑖 akımı verildiğinde, 𝑖1 ve
𝑖2 nasıl elde edilir? Eşdeğer direncin aynı gerilime sahip olduğunu
biliyoruz.
𝑣 = 𝑖𝑅𝑒ş =
𝑖𝑅1 𝑅2
𝑅1 +𝑅2
Burada, 𝑖1 =
𝑖1 =
𝑅2 𝑖
veya
𝑅1 +𝑅2
𝑖1 =
𝐺1 𝑖
𝐺1 +𝐺2
𝑖2 =
𝑅1 𝑖
veya
𝑅1 +𝑅2
𝑖2 =
𝐺2 𝑖
𝐺1 +𝐺2
𝑣
𝑅1
ve
𝑖2 =
𝑣
𝑅2
’yi yerine yazarsak,
şeklinde elde edilir.
• Toplam 𝑖 akımı, dirençler tarafından direnç değerleriyle ters orantılı
olarak paylaşılır; daha küçük dirençten daha büyük akım akar.
• Buna akım bölme kuralı denir ve Şekil 2.31’deki devre akım bölen
devre olarak bilinir.
12.10.2015
30
• Şekil 2.31’deki bir dirençlerden birisini sıfır kabul edelim.
Mesela, 𝑅2 = 0 olsun. Bu durumda Şekil 2.33(a)’da
gösterildiği gibi, 𝑅2 direnci kısa devre olur.
• 𝑖1 =
𝑅2 𝑖
𝑅1 +𝑅2
denkleminde,
𝑅2 = 0 ise 𝑖1 = 0 olur.
• 𝑖2 =
𝑅1 𝑖
𝑅1 +𝑅2
denkleminde,
𝑅2 = 0 ise 𝑖2 = 𝑖 olur.
• Bunun anlamı, 𝑖 akımının tamamının 𝑅1 direncini bypass
ederek (atlayarak), en küçük direnç yolu olan (𝑅2 = 0) kısa
devresinden aktığıdır.
• Bir devre, kısa devre edildiğinde iki durum meydana gelir:
1. Eşdeğer direnç, 𝑅𝑒ş = 0 olur. (𝑅2 = 0 ’da olduğu gibi)
2. Akımın tamamı kısa devreden geçer.
12.10.2015
31
• Diğer bir durumda, 𝑅2 = ∞ olduğunu kabul
edelim. Bu durumda Şekil 2.33(b)’de
gösterildiği gibi, 𝑅2 direnci açık devre olur.
• 𝑖 akımı, yine en küçük direnç yolu olan 𝑅1
direncinden akar.
• 𝑅𝑒ş =
𝑅1 𝑅2
𝑅1 +𝑅2
denkleminde
𝑅2 → ∞ için limit alarak,
eşdeğer direnci, 𝑅𝑒ş = 𝑅1
olarak elde ederiz.
12.10.2015
32
2.7 Yıldız Üçgen Dönüşümleri
• Devre analizinde çoğunlukla dirençlerin ne seri ne de paralel olduğu
durumlar ortaya çıkar. Örneğin, Şekil 2.46’daki köprü devreyi göz önüne
alalım.
• Bu şekilde birçok devre, üç uçlu eşdeğer devreler kullanılarak
basitleştirilebilir.
• Bunlar; Şekil 2.47’de gösterildiği gibi yıldız (Y) veya T devresi ile Şekil
2.48’de gösterildiği gibi üçgen (∆) veya pi (Π) devresi’dir.
• Bunlar, üç fazlı devrelerde ve elektrik filtrelerinde kullanılır.
• Buradaki amacımız, bir devrenin parçası olarak karşılaştığımızda nasıl
özdeşleştireceğimiz ve devre analizinde yıldız-üçgen dönüşümünün nasıl
uygulanacağıdır.
12.10.2015
33
Yıldız Üçgen Dönüşümleri
Üçgen Yıldız Dönüşümü:
• Mevcut üçgen devreyi yıldız bir devre ile
eşleştiriyoruz ve yıldız devredeki eşdeğer
direnci buluyoruz.
12.10.2015
34
Üçgen - Yıldız Dönüşümü
12.10.2015
35
Üçgen - Yıldız Dönüşümü
• Y devredeki her bir direnç, iki komşu Δ dalındaki
dirençlerin çarpımının, üç adet Δ direncin toplamına
bölümüdür.
12.10.2015
36
Yıldız - Üçgen Dönüşümü
• Yıldız bir devrenin üçgen bir devreye dönüşümünü elde etmek için,
• Yıldız – Üçgen Dönüşüm Kuralı:
• Δ devredeki her bir direnç, Y dirençlerin çarpımlarının toplamının, karşı
taraftaki Y direncine bölümüdür.
12.10.2015
37
Yıldız - Üçgen Dönüşümü
olduğunda, yıldız ve üçgen devreler dengelidir, denir.
Bu şartlar altında, dönüşüm formülleri şu şekilde olur:
12.10.2015
38
Doğru Akım Ölçü Aletlerinin Tasarımı
• Dirençler, akım akışını kontrol etmek için kullanılır.
• Direncin bu özelliğinin potansiyometre gibi çeşitli uygulamalarda avantajı
vardır.
• Potansiyometre, potansiyel ile metre kelimelerinden elde edilir ve
potansiyel ölçebilen anlamına gelir.
• Potansiyometre (veya kısaca pot), gerilim bölme prensibiyle çalışan üç uçlu
bir cihazdır.
• Aslında potansiyometre, ayarlanabilir
bir gerilim bölücüdür.
𝑉𝑜 = 𝑉𝑏𝑐 =
𝑅𝑏𝑐
𝑉
𝑅𝑎𝑐 𝑖
𝑅𝑎𝑐 = 𝑅𝑎𝑏 + 𝑅𝑏𝑐
• Potun kontağı c veya a ’ya doğru hareket ettirilerek V𝑜𝑢𝑡 çıkışı azaltılır veya
artırılır.
• Potansiyometre, radyo, televizyon vb. cihazlarda ses veya kademe kontrolü
için kullanılan bir gerilim düzenleyicidir.
12.10.2015
39
Doğru Akım Ölçü Aletlerinin Tasarımı
• Dirençlerin, akım akışını kontrol etmek için kullanıldığı diğer bir uygulama,
akım, gerilim ve direnç ölçmede kullanılan analog doğru akım ölçü aletleri
(ampermetre, voltmetre ve ohmmetre)’dir.
• Şekil 2.59’da gösterildiği gibi, bir elemana bağlanan voltmetre ve
ampermetreyi göz önüne alalım.
• Voltmetre, bir yükün uçlarındaki gerilimi
ölçmektedir ve bu yüzden elemana paralel
bağlanmıştır.
• Voltmetrenin devreden çektiği akımı minimize
etmek için kendisine paralel bağlı 𝑅𝑚 iç direnci
çok büyük (teorik olarak sonsuz) seçilir.
• Voltmetrenin ölçme sınırını genişletmek için, genellikle voltmetreye Şekil
2.60(b)’de gösterildiği gibi seri ön dirençler bağlanır.
• Şekil 2.60(b)’deki çok kademeli voltmetre, anahtarın 𝑅1 , 𝑅2 veya 𝑅3 ’e
bağlı olup olmamasına göre, sırasıyla 0-1 V, 0-10 V veya 0-100 V
gerilimlerini ölçebilir.
12.10.2015
40
Doğru Akım Ölçü Aletlerinin Tasarımı
• Şimdi Şekil 2.60(a)’daki tek kademeli voltmetrenin 𝑅𝑛 ön direnci ile Şekil
2.60(b)’deki çok kademeli voltmetrenin 𝑅𝑛 = 𝑅1 , 𝑅2 , 𝑅3 ön dirençlerini
hesaplayalım.
• Voltmetrenin 𝑅𝑚 iç direnci ile seri bağlanacak 𝑅𝑛 değerini bulmamız
gerekir. Herhangi bir tasarımda en kötü şartı göz önüne alırız.
• Burada, voltmetreden geçen maksimum
skala akımının, 𝐼𝑚𝑠 = 𝐼𝑚 olmasıyla
en kötü durum oluşur.
• 𝑅𝑛 ön direnci, 𝑅𝑚 iç direnci ile seri bağlı
olduğundan voltmetreden okunan
maksimum skala gerilimi 𝑉𝑚𝑠 ,
• Buradan,
𝑉𝑚𝑠 = 𝐼𝑚𝑠 (𝑅𝑛 + 𝑅𝑚 )
𝑅𝑛 =
elde ederiz.
12.10.2015
𝑉𝑚𝑠
𝐼𝑚𝑠
− 𝑅𝑚
41
Doğru Akım Ölçü Aletlerinin Tasarımı
• Benzer şekilde, ampermetre, seri olarak bağlandığı
yükten geçen akımı ölçmektedir.
• Şekil 61(a)’da gösterildiği gibi ampermetrenin kendisine
seri bağlı 𝑅𝑚 iç direnci, uçlarındaki gerilim düşümünü
minimize etmek için çok küçük (teorik olarak sıfır)
seçilir.
• Ampermetrenin ölçme sınırını genişletmek için,
genellikle ampermetreye Şekil 2.61(b)’de gösterildiği
gibi paralel (şönt) dirençler bağlanır.
• Şönt dirençler ampermetrenin, anahtarın 𝑅1 , 𝑅2 veya
𝑅3 ’e bağlı olup olmamasına göre, sırasıyla 0-10 mA, 0100 mA veya 0-1 A kademelerinde ölçüm yapmasını
sağlar.
12.10.2015
42
Doğru Akım Ölçü Aletlerinin Tasarımı
• Şimdi Şekil 2.61(a)’daki tek kademeli ampermetrenin 𝑅𝑛 şönt direnci ile
Şekil 2.61(b)’deki çok kademeli ampermetrenin 𝑅𝑛 = 𝑅1 , 𝑅2 , 𝑅3 şönt
dirençlerini elde edelim.
• 𝑅𝑚 ile 𝑅𝑛 paralel bağlı olduğundan,
ampermetreden okunan maksimum skala akımı,
𝐼 = 𝐼𝑚𝑠 = 𝐼𝑚 + 𝐼𝑛 ’dir.
Burada 𝐼𝑛 , şönt dirençten (𝑅𝑛 ) geçen akımdır.
• Akım bölme kuralını uygularsak,
𝐼𝑚 =
𝑅𝑛
𝐼
𝑅𝑛 +𝑅𝑚 𝑚𝑠
𝑅𝑛 =
𝐼𝑚
𝑅
𝐼𝑚𝑠 −𝐼𝑚 𝑚
veya
olur.
12.10.2015
43
• Örnek 2.17: Bir voltmetrenin iç direnci 𝑅𝑚 = 2 𝑘Ω ve maksimum skala
akımı 𝐼𝑚𝑠 = 100 𝜇𝐴 olduğuna göre, aşağıdaki ölçme alanlarında bir
voltmetre tasarlamak için gerekli ön direnç değerlerini hesaplayınız.
a) 0-1 V
b) 0-5 V
c) 0-50 V d) 0-100 V
Çözüm: a) 0-1 V alanında ölçme yapabilmek için,
1
𝑅1 =
− 2000 = 10000 − 2000 = 8 kΩ
100x10−6
b) 0-5 V alanında ölçme yapabilmek için,
5
𝑅2 =
− 2000 = 50000 − 2000 = 48 kΩ
−6
100x10
c) 0-50 V alanında ölçme yapabilmek için,
50
𝑅3 =
− 2000 = 500000 − 2000 = 498 kΩ
100x10−6
d) 0-100 V alanında ölçme yapabilmek için,
100
𝑅4 =
− 2000 = 1000000 − 2000 = 998 kΩ
100x10−6
12.10.2015
44