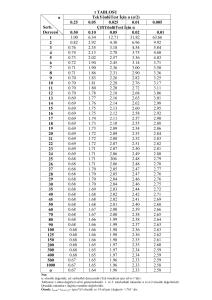
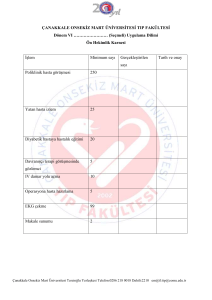
5. Ders
Dağılımlardan Rasgele Sayı Üretilmesi
Ters Dönüşüm Yöntemi
X sürekli bir rasgele değişken ve FX bu rasgele değişkenin dağılım
fonksiyonu olsun. Dağılımın destek kümesi üzerinde F dağılım fonksiyonu
artan ve bire-bir bir fonksiyon olmaktadır.
Y = FX ( X ) dönüşümü olarak tanımlanan Y rasgele değişkeni için
(
)
(
)
P (Y ≤ y ) = P ( FX ( X ) ≤ y ) = P X ≤ FY−1 ( y ) = FX FY−1 ( y ) = y
olup, Y ~ U (0,1) dır.
X sürekli bir rasgele değişken olmak üzere, FX ( X ) dönüşümüne X ‘in
Olasılık Đntegral Dönüşümü denir.
U ~ U (0,1)
olmak üzere,
FX−1 (U )
biçiminde tanımlanan rasgele
değişken için
P FX−1 (U ) ≤ x = P FX ( FX−1 (U )) ≤ FX ( x)
= P [U ≤ FX ( x)] = FX ( x) = P( X ≤ x)
dır. FX−1 (U ) rasgele değişkeni ile X rasgele değişkeni aynı dağılımlıdır. U (0,1)
düzgün dağılımdan üretilen U sayısı F −1 (U ) dönüşümü sonucu F dağılım
fonksiyonuna sahip dağılımdan üretilmiş olur. Kısaca, X rasgele değişkenin
dağılımından sayı üretmek için X = F −1 (U ) dönüşümü kullanılabilir. Đlgili
algoritma aşağıdaki gibidir.
Algoritma
1. U ( 0 , 1) dağılımından U üretilir
2. X = F −1 (U ) hesaplanır
1
Örnek: X rasgele değişkenin olasılık yoğunluk ve dağılım fonksiyonu,
0, x < 0
2 x , 0 ≤ x ≤ 1
f ( x) =
,
F ( x) = x 2 , 0 ≤ x ≤ 1
0, d . y.
1, x > 1
−1
1/ 2
olsun. X = F (U ) = U
= U dönüşümü ile X rasgele değişkeninin
dağılımından sayı üretilebilir.
>> u=rand(100,1) ; x=u.^(1/2) ; hist(x)
25
20
15
10
5
0
0.1
0.2
0.3
0.4
0.5
0.6
2
0.7
0.8
0.9
1
Örnek: X rasgele değişkeni ( a , b ) aralığında düzgün dağılıma sahip olsun. X in
olasılık yoğunluk fonksiyonu
1
f ( x) =
,
b−a
dağılım fonksiyonu,
0
x − a
F ( x) =
b − a
1
a≤ x≤b
, x<a
, a≤ x<b
, x≥b
ve
F − (u ) = F −1 (u ) = a + (b − a )u , 0 < u < 1
şeklinde olduğundan U ~ U ( 0 , 1) olmak üzere, ters dönüşüm yöntemine göre
X = F −1 (U ) = a + ( b − a )U
ile bu dağılımdan sayı üretilebilir.
Örnek: θ parametreli üstel dağılımın olasılık yoğunluk fonksiyonu
1 −θx
, x≥0
f ( x) = θ e
0
, d . y.
dağılım fonksiyonu,
0
F ( x) =
x
−
1 − e θ
, x<0
,
x≥0
ve
F −1 (u ) = −θ ln(1 − u ) , 0 < u < 1
olmak üzere,
X = F −1 (U ) = −θ ln(1 − U )
dönüşümü ile üretilen X rasgele sayıları üstel dağılımdan üretilmiş sayılardır.
U ~ U (0,1) için 1 − U rasgele değişkeninin de U (0,1) düzgün dağılımına sahip
olduğu gözönüne alınırsa, θ parametreli üstel dağılımdan sayı üretmek için
X = −θ ln(U ) dönüşümü de kullanılabilir.
3
4
Örnek: X ~ N(0,1) için,
x2
1 −2
f ( x) =
e
2π
1
F ( x) =
2π
x
∫e
, x∈R
−
t2
2 dt
, x∈R
−∞
>> x=-4:.1:4; plot(x,normpdf(x)); hold on;
plot(x,normcdf(x),'r')
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-4
-3
-2
-1
1
F ( x) =
2π
0
x
∫e
−
t2
2 dt
1
2
3
4
, x∈R
−∞
olmak üzere,
F −1 : (0,1) → R
u → F −1 (u )
olmak üzere, F −1 (u ) değerleri u ‘ya bağlı olarak açık bir şekilde kolayca
yazılıp hesaplanamamaktadır.
5
Matlab’daki norminv ve erfinv fonksiyonları yardımıyla F −1 (u ) , u ∈ (0,1)
değerlerinin hesaplanması.
1
F ( x) =
2π
x
∫e
−∞
−
t2
2 dt
=
1
x
(1 + erf ( )) , x ∈ R
2
2
F −1 : (0,1) → R
u → F −1 (u ) = norminv(u ) = 2erfinv(2u − 1)
6
>> u=rand(100,1);x=norminv(u);hist(x)
25
20
15
10
5
0
-3
-2
-1
0
1
2
3
15
20
25
30
>> x=norminv(u,15,5);hist(x)
25
20
15
10
5
0
0
5
10
7
Örnek: Cauchy dağılımına sahip X rasgele değişkenin olasılık yoğunluk
fonksiyonu
f ( x) =
1
, −∞ < x < ∞
π (1 + x 2 )
olmak üzere, dağılım fonksiyonu
1 1
F ( x) = + arctan(x) , x ∈ R
2 π
ve
F −1 (U ) = tan[π (U − 12 )] , U ∈ (0,1)
dır. BASIC dilinde,
X=TAN(3.14*(RND-0.5))
deyimi ile bu dağılımdan sayı üretilir.
Örnek:
X 1 , X 2 ,..., X n sürekli, bağımsız ve aynı F dağılımına sahip rasgele
değişkenler olmak üzere Yn = max( X 1 , X 2 ,..., X n ) ve Y1 = min( X 1 , X 2 ,..., X n )
sıra istatistiklerinden sayı üretelim. Yn ve Y1 sıra istatistiklerinin dağılım
fonksiyonları sırasıyla
FYn ( y ) = F X ( y )
n
FY1 ( y ) = 1 − 1 − F X ( y )
n
olmak üzere, bu fonksiyonların ters fonksiyonları dikkate alınarak
Yn = F X−1 (U 1/ n )
Y1 = F X−1 (1 − U 1/ n )
dönüşümleri bulunur. Özel olarak X 1 , X 2 ,..., X n rasgele değişkenlerinin
dağılımı U ( a , b ) olarak alınırsa,
Yn = a + (b − a )U 1 / n
Y1 = a + (b − a )(1 − U 1 / n )
dönüşümleri ile Yn ve Y1 rasgele değişkenlerinin dağılımlarından sayı üretilebilir.
Örnek: (Weibull Dağılımından sayı üretme)
8
Weibull dağılımına sahip X rasgele değişkenin olasılık yoğunluk
fonksiyonu
1 x c −1 − x
c e θ
f ( x) = θ θ
0
c −1
, x>0
, d. y
ile verilir ( θ > 0 ,c > 0 ). Dağılım fonksiyonu
F ( x) = 1 - e
x
−
θ
c
olmak üzere
1
F −1 ( y ) = θ ( −log ( y ) ) c
dır. Ters dönüşüm yöntemi ile bu dağılımdan sayı üretilebilir.
Örnek: (Laplace Dağılımından sayı üretme)
Laplace dağılımına sahip X rasgele değişkenin olasılık yoğunluk
fonksiyonu
x
1 −θ
f ( x) =
e
, -∞ < x < ∞
2θ
ile verilir. Dağılım fonksiyonu
1 θx
, x<0
e
2
F ( x) =
x
1 − 1 e − θ , x ≥ 0
2
biçimindedir. Ter dönüşüm yöntemine göre bu dağılımdan sayı üretecek
bilgisayar programı aşağıda verilmiştir.
INPUT "TETA=", TETA
IF RND < 0.5 THEN X=TETA*LOG(2*RND)
ELSE X=TETA*LOG(2-2*RND)
PRINT "X=",X
Örnek: (Lojistik dağılımından sayı üretme)
9
Lojistik dağılıma sahip
X
rasgele değişkenin olasılık yoğunluk
fonksiyonu.
f ( x) =
e
−
x −a
b
x −a
−
b1 + e b
2
, -∞ < x < ∞
biçiminde verilir. Dağılım fonksiyonu
1
F ( x) =
x −a
1+ e
−
b
olmak üzere
F −1 (U ) = a − b log( U1 − 1)
ile bu dağılımdan sayı üretilebilir.
10